2. 哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001
2. College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China
蓄能电站发电机组轴承运转时需要润滑,但是这会使机组运行过程中出现“甩油”和油雾溢出现象,在各大型电站中,都出现了这类问题。当油雾积累到一定程度时会从机组的转动部件和密封部件的结合处溢出,这会造成水车室的污染以及发电机定子线圈的损害[1]。
目前国内外各大型电站一般采用以下方式去解决“甩油”和油雾溢出问题:
1)在轴承的油槽盖外壁上安装呼吸器。呼吸器内部有互相交错的挡板,油槽内溢出的油雾能够沿着呼吸器的挡板排出。
2)通过改善油槽内部结构,减小油面波动,防止油雾溢出。
3)通过改善密封,控制“甩油”,封堵油雾。
4)在封闭式轴承内安装抽油装置,将油雾排放。
在轴承内配备传统的呼吸器的同时从油槽内部引出抽油雾装置,可以很好地解决机组运行过程中所产生的油雾问题。目前我国已经具备自主研发“油挡”和抽油装置的能力,但是仪器精度以及抽油装置的过滤性能和国外仍有差距[2]。抽油装置在中国水电站的应用是在三峡电厂的主机设备招标需求中首次提出的,因当时已经对机组内部的清洁及油雾问题开始重视,要求国外顶级设备商如美国通用电气、法国阿尔斯托姆等公司研发抽油设备以消除油雾对机组影响。目前国内大型的电站的抽油装置几乎全部使用国外设备。
上述的4种对蓄能电站发电机组轴承的油雾的处理方案均有一些缺陷,并没有彻底解决油雾外溢所带来的问题。
首先几乎所有的水轮发电机轴承设计时均设有呼吸器,但因为发电机封闭式轴承内部结构空间小、油槽内的油位较高,油槽内的油位上部空间无法加大到理想程度,造成油槽内油雾压力过高,呼吸器无法全部聚结通过的油雾,从而形成了油雾外泄的直接通道。
第二,从改善油槽内部结构防止油雾溢出方面着手,在已投运的发电机机组中改造难度巨大,很难实现。
第三,近十几年来国内外行业内的专家在改善轴承油槽密封方面进行了大量的探讨和实践,已经取得了成果,使机组内部的油污污染程度有了很大的降低。但是这只是“堵”的方法,密封严密了,油槽内部的油雾并不会减少,并且因为油槽在结构上还无法做到一个完全密闭的承压空间,这就造成了油雾会寻找出路,释放压力。
第四,使用抽油装置将油雾短时间内抽出,不对抽取量和补气量进行控制,会造成整个机组内部的气压变化。气压短时间的增加或者减少会造成与外界压差加大,可能会使内部的油雾激增,无法将油雾排净,而压差的增加也对机组安全运行造成危害。
针对上述问题,可以得出结论:使用抽油装置及时稳定排放出油雾并使轴承内部气压保持一个稳定的范围内,可以避免相关危害。本文提出了基于改进的遗传−PID控制算法的蓄能电站发电机组油雾排放控制策略,将自动控制的思想引入到发电机组油雾排放领域中。这一控制策略将变频调速原理和智能控制算法应用到机组油雾排放中,可以实现油雾智能排放,避免危害的发生。
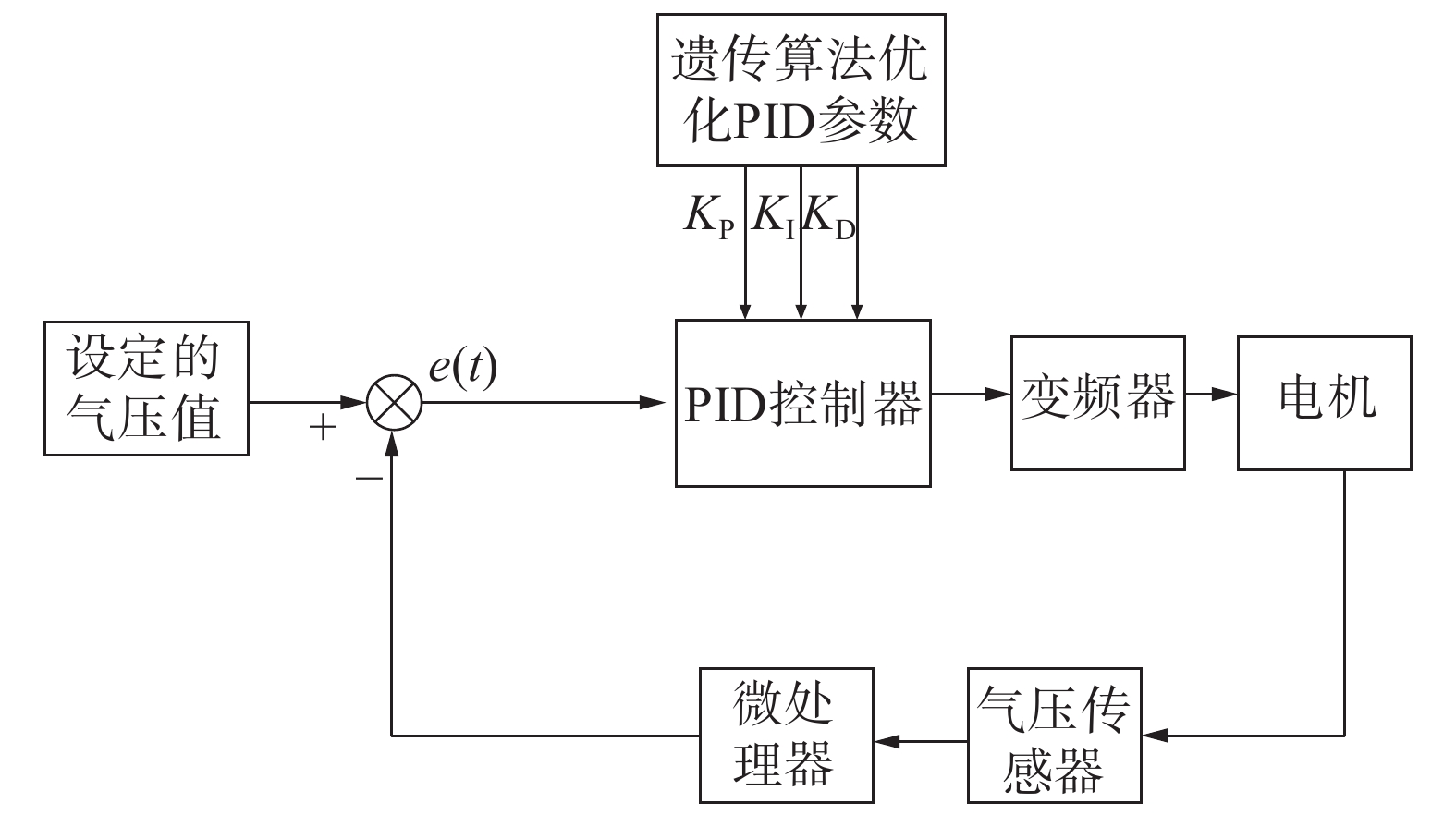
1 油雾排放系统的组成本文采用的方式是基于遗传−PID控制算法间接测量封闭式轴承内部气体压强,根据压强变化使用变频器控制抽油电机即三相异步电机的转速,从而控制排油流量。通过对传统遗传算法的遗传操作进行改进,不断优化系统的控制响应,实现蓄能电站发电机组轴承油雾智能排放。本系统的主要组成结构如图1所示。
|
Download:
|
| 图 1 发电机组轴承油雾排放系统框图 | |
当抽油电机抽取油雾的时,封闭式轴承中的油雾量产生变化,油雾在排放过程中会使发电机组封闭式轴承内部压力发生变化。当轴承内部气压与外界压差过大时会导致内部的油雾激增或大量减少,使得整个油雾排放系统不稳定,产生危险。所以系统通过单片机或者其他嵌入式系统设定发电机组所允许的内部气压最大值,该压力值与压力传感器反馈的数值进行比较,通过使用的控制算法进行处理,控制变频器调节抽油电机转速间接控制轴承内部的气压,逐步达到稳态,使发电机组的内部气压在一个合理的范围内,保证机组安全工作。
2 控制系统的设计控制策略是一个自动控制系统的核心,所以算法的选择至关重要。由于发电机组油雾排放系统结构较复杂,数学模型是高阶带有延时的线性系统,并且控制系统的阶跃响应要具备超调量较小、平稳性高的特点,所以用于设计控制策略的控制算法要能够满足上述的要求[3]。本文分别基于PID算法、传统遗传−PID算法和改进的遗传−PID算法设计控制器,通过仿真结果选取最优的控制策略。为了保证控制系统的平稳性,控制策略要求能够使控制系统超调量低于5%,控制精度小于2%。
2.1 PID算法的原理传统的PID算法的理想微分方程是:
| $ \begin{aligned}u\left( t \right) = & {K_{\rm{P}}}\left[ {e\left( t \right) + \frac{1}{{{T_l}}}\int\limits_0^i e \left( t \right){\rm{d}}t + {T_d}\frac{{{\rm{d}}e\left( t \right)}}{{{\rm{d}}t}}} \right] = \\ & {K_{\rm{P}}}e\left( t \right) + {K_{\rm{I}}}\int\limits_0^i e \left( t \right){\rm{d}}t + {K_{\rm{D}}}\frac{{{\rm{d}}e\left( t \right)}}{{{\rm{d}}t}} \end{aligned} $ | (1) |
式中:
由于在进行算法分析和程序设计时通常使用PC机或者嵌入式系统进行,通常将式(1)离散化从而得到离散PID表达式:
| $u\left( k \right) = {K_{\rm{P}}}e\left( k \right) + {K_{\rm{I}}}\mathop \sum \limits_{j = 0}^k e\left( j \right)T + {K_{\rm{D}}}\frac{{e\left( k \right) - e\left( {k - 1} \right)}}{T}$ |
式中:
传统的PID控制算法由于受到控制参数设定不良以及对复杂的运行工况适应较差的影响,通常达不到理想的控制效果,这使得基于传统PID算法设计的控制器的应用受到限制[5]。
遗传算法是一种全局优化、并行搜索的寻优方法,无需对目标函数微分,只依赖于适应度函数,即使在被控对象模型非线性的情况下,它仍可根据对象的输出情况对
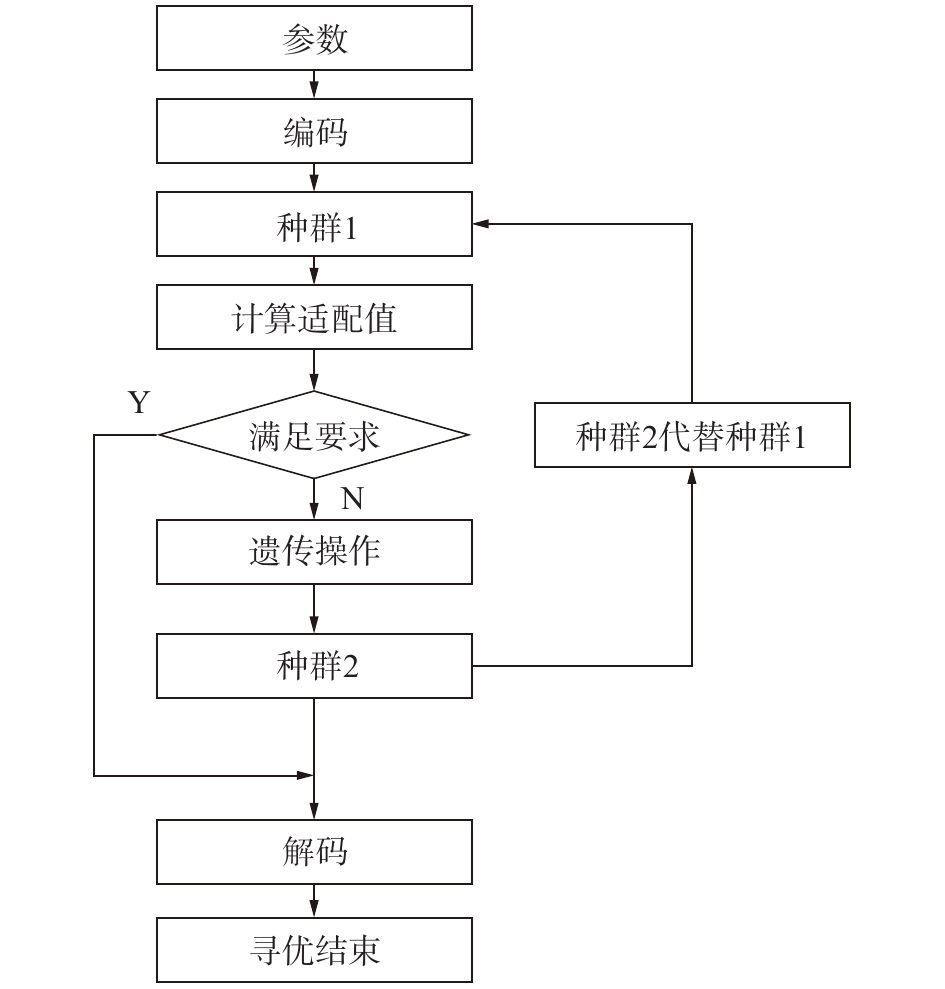
遗传算法是一种基于自然选择和自然遗传的迭代式自适应概率性搜索方法。遗传算法的搜索方法根植于进化和自然遗传学的机制,对特定的目标实现自动优化。遗传算法主要包括选择、交叉和变异3个步骤,其流程图如图2所示。
|
Download:
|
| 图 2 遗传算法流程 | |
遗传算法因为具备较强的全局收敛性和较少的优化目标的优点,被广泛应用到控制器设计中,但同时此算法存在如下缺点:
1)交叉算子概率和变异算子概率数值的设定对算法的优化效果有着直接的影响。而且对于传统的遗传算法,其交叉概率和变异概率的数值在算法的运行过程中是保持恒定不变的,无法满足实际运算的要求,对传统遗传算法的进化速度和收敛性产生影响[7]。
2)局部搜索能力较弱,容易陷入局部收敛。
3)初始种群是随机生成的,其运行效率较低。
2.3 遗传−PID控制器设计遗传−PID控制算法的原理,就是使用遗传算法对PID参数进行优化,其控制过程由如下:
1)首先对PID算法的3个参数
| $\left[ {{K_{{\rm{P}}1}},{K_{{\rm{P}}2}}, \cdots ,{K_{{\rm{I}}10}},{K_{{\rm{I}}1}},{K_{{\rm{I}}2}}, \cdots ,{K_{{\rm{I}}10}},{K_{{\rm{D}}1}},{K_{{\rm{D}}2}}, \cdots ,{K_{{\rm{D}}10}}} \right]$ |
在生成种群前,算法要在所设定的取值范围内随机产生M个染色体。种群由产生的M个染色体构成。遗传算法以此种群作为初始点开始进行迭代计算,初始种群如下。
| $ \left| {\begin{array}{*{20}{c}} {K_{\rm{P}}^1}&{K_{\rm{I}}^1}&{K_{\rm{D}}^1}\\ {K_{\rm{P}}^2}&{K_{\rm{I}}^2}&{K_{\rm{D}}^2}\\ \vdots & \vdots & \vdots \\ {K_{\rm{P}}^M}&{K_{\rm{I}}^M}&{K_{\rm{D}}^M} \end{array}} \right| $ |
2)确定每个个体的适应度,需要适应度函数来对其进行评价。控制系统的稳定性、准确性和快速性是用于衡量机组轴承油雾排放控制策略的3个重要指标。本文针对这3点并结合误差积分优劣的3个指标即时间乘绝对误差积分准则(ITAE)、绝对误差积分准则(IAE)和平方误差积分准则(ISE)[9],从而采用的目标函数如式(2)和(3)所示。
| $J = \int _0^\infty ({w_1}\left| {e\left( t \right)} \right| + {w_2}{u^2}\left( t \right)){\rm{d}}t + {w_3}{t_u}$ | (2) |
式中:w1、w2与w3为权值;
| $J = \int _0^\infty ({w_1}\left| {e\left( t \right)} \right| + {w_2}{u^2}\left( t \right) + {w_4}\left| {e\left( t \right)} \right|){\rm{d}}t + {w_3}{t_u}\;\;\left( {{w_4} \geqslant{w_1}} \right)$ | (3) |
适应度函数采用求最大值方式,其函数表达式为[10]:
| $F\left( {{x}} \right) = \frac{1}{J}$ |
3)计算并保存每一代的适配值,根据算法流程进行选择、交叉与变异的遗传操作,产生新的个体,计算它的适配值,并进行最优值的替换[11]。
4)每产生一个最优值便将迭代次数加一,将迭代次数与设定的最大迭代次数进行比较,如果二者数值相等则满足结束条件,将输出最优解,并对最优解进行解码得到对应的PID参数。
由2.2节可知,由于基本的遗传算法存在一些缺点,故对此算法进行一些改进以达到更好的控制效果,改进方法如下:
1)缩小种群搜索空间
为了提高遗传算法的运算效率,本文使用Zielgler−Nichols整定法对参数进行优化,得到
2)选择操作的改进
设某个个体的适应度值为
| ${P_i} = \frac{{{F_i}}}{{\displaystyle\sum\limits_{i = 1}^N {{F_i}} }}\;\;\left( {{\rm{i = 1,2,}} \cdots ,{{N}}} \right)$ |
当每个个体的适应度值比较大的时候,应增大其被选择的概率;当个体适应度值比较小的时候,应该缩小其被选择的概率。设
| $ F_i' = \left\{ {\begin{array}{*{20}{l}} {\bar F + \mu {{[\left( {{F_i} - \bar F} \right)/\mu ]}^\xi },{F_i} \geqslant \bar F}\\ {\bar F - \mu {{[\left( {{F_i} - \bar F} \right)/\mu ]}^\xi },{F_i} < \bar F} \end{array}} \right. $ |
式中:
| $\left\{ {\begin{array}{*{20}{l}} {\mu = \dfrac{1}{2}{\rm{min}}\left( {{\mu _1},{\mu _2}} \right)}\\ {{\mu _1} = {\rm{}}\mathop {{\rm{max}}}\limits_i {F_i} - \bar F}\\ {{\mu _2} = \bar F - {\rm{}}\mathop {{\rm{max}}}\limits_i {\rm{}}{F_i}} \end{array}} \right.$ |
3)交叉概率和变异概率数值选取的改进
本文中的控制策略针对传统遗传算法的交叉概率
| $\begin{aligned} {P_c} = & \left\{ {\begin{array}{*{20}{l}} {{p_{c_1}} - \dfrac{{{k_1}\left( {{F_c} - {F_{{\rm{avg}}}}} \right)}}{{{F_{{\rm{max}}}} - {F_{{\rm{avg}}}}}},{F_c} \geqslant {F_{{\rm{avg}}}}}\\ {{P_{c_1}} + \dfrac{{{k_1}\left( {{F_c} - {F_{{\rm{avg}}}}} \right)}}{{{F_{{\rm{max}}}} - {F_{{\rm{avg}}}}}},{F_c} < {F_{{\rm{avg}}}}} \end{array}} \right.\\ {P_m} = & \left\{ {\begin{array}{*{20}{l}} {{p_{m_1}} - \dfrac{{{k_2}\left( {{F_m} - {F_{{\rm{avg}}}}} \right)}}{{{F_{{\rm{max}}}} - {F_{{\rm{avg}}}}}},{F_m} \geqslant {F_{{\rm{avg}}}}}\\ {{P_{m_1}} + \dfrac{{{k_2}\left( {{F_m} - {F_{{\rm{avg}}}}} \right)}}{{{F_{{\rm{max}}}} - {F_{{\rm{avg}}}}}},{F_m} < {F_{{\rm{avg}}}}} \end{array}} \right. \end{aligned}$ |
式中:
本节针对传统PID控制器、传统遗传−PID控制器和改进的遗传−PID设计方案,并使用改进的遗传算法求解Rosernbrock函数全局极大值,分别在仿真平台软件MATLAB上编写程序,进行发电机组轴承油雾排放控制系统的仿真实验。
3.1 改进的遗传算法对函数的优化传统遗传算法的一个最大问题是容易陷入局部最优解,这一问题会使算法在优化PID参数时,无法找到最优解。为了验证改进的遗传算法是否解决了上述问题,本文选取了Rosernbrock函数作为被优化函数进行仿真实验,Rosernbrock函数的表达式为:
| $\left\{ {\begin{array}{*{20}{l}} {f\left( {{x_1},{x_2}} \right) = 100{{(x_1^2 - {x_2})}^2} + {{(1 - {x_1})}^2}}\\ {- 2.048 \leqslant {x_1} \leqslant 2.048}\\ { - 2.048 \leqslant {x_2} \leqslant 2.048} \end{array}} \right.$ |
如图3所示,该函数存在2个局部极大值点,分别是
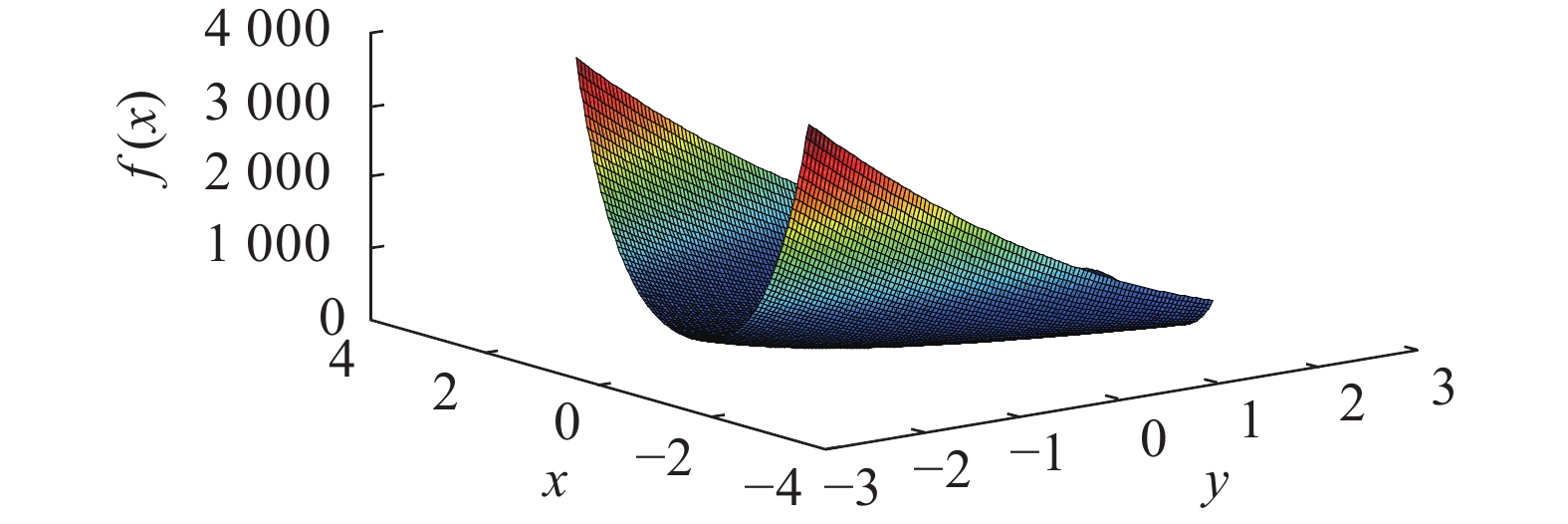
|
Download:
|
| 图 3 Rosernbrock函数三维图 | |
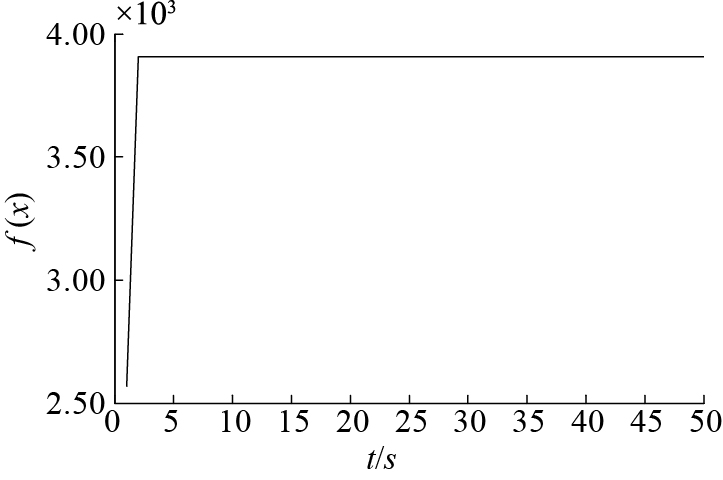
在仿真实验中,取
|
Download:
|
| 图 4 适应度函数优化过程 | |
发电机组油雾排放控制系统的被控对象的数学模型主要由变频器和三相异步电机组成(抽油电机可等效为异步电机),所以通常将该类模型等效为带有滞后和增益的高阶系统,可表示为:
| $G\left( s \right) = \frac{{400{e^{ - 20s}}}}{{{s^2} + 50s + 1}}$ |
试验过程中,首先通过常用的PID整定法,即Zielgler−Nichols整定法,来获得遗传−PID控制器的
改进的遗传−PID算法使用的样本个数为S=30,采样周期为0.01 s,交叉概率和变异概率初始数值分别为

|
Download:
|
| 图 5 改进的遗传−PID控制器阶跃响应 | |
|
Download:
|
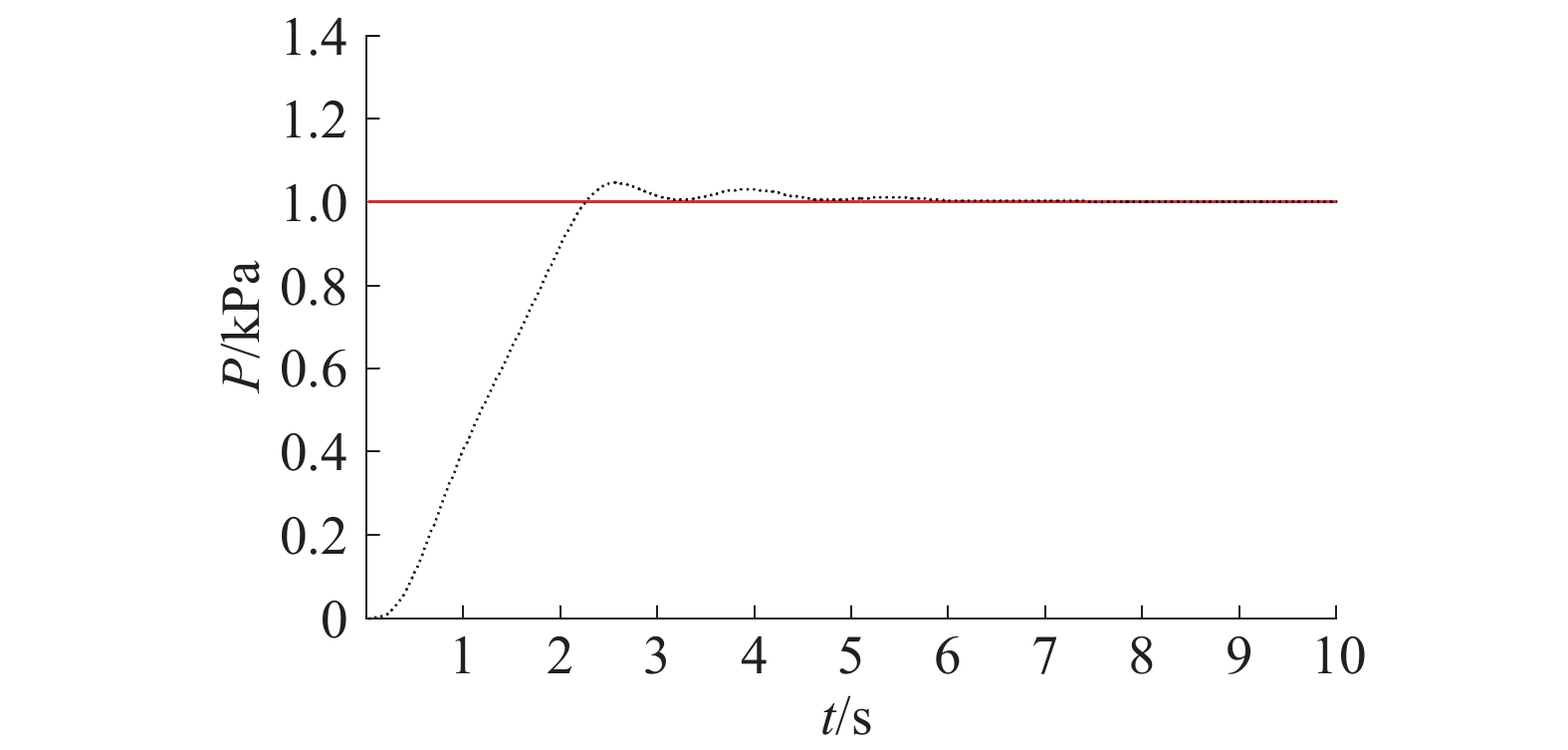
| 图 6 Z-N整定法优化的传统PID控制器阶跃响应 | |
|
Download:
|
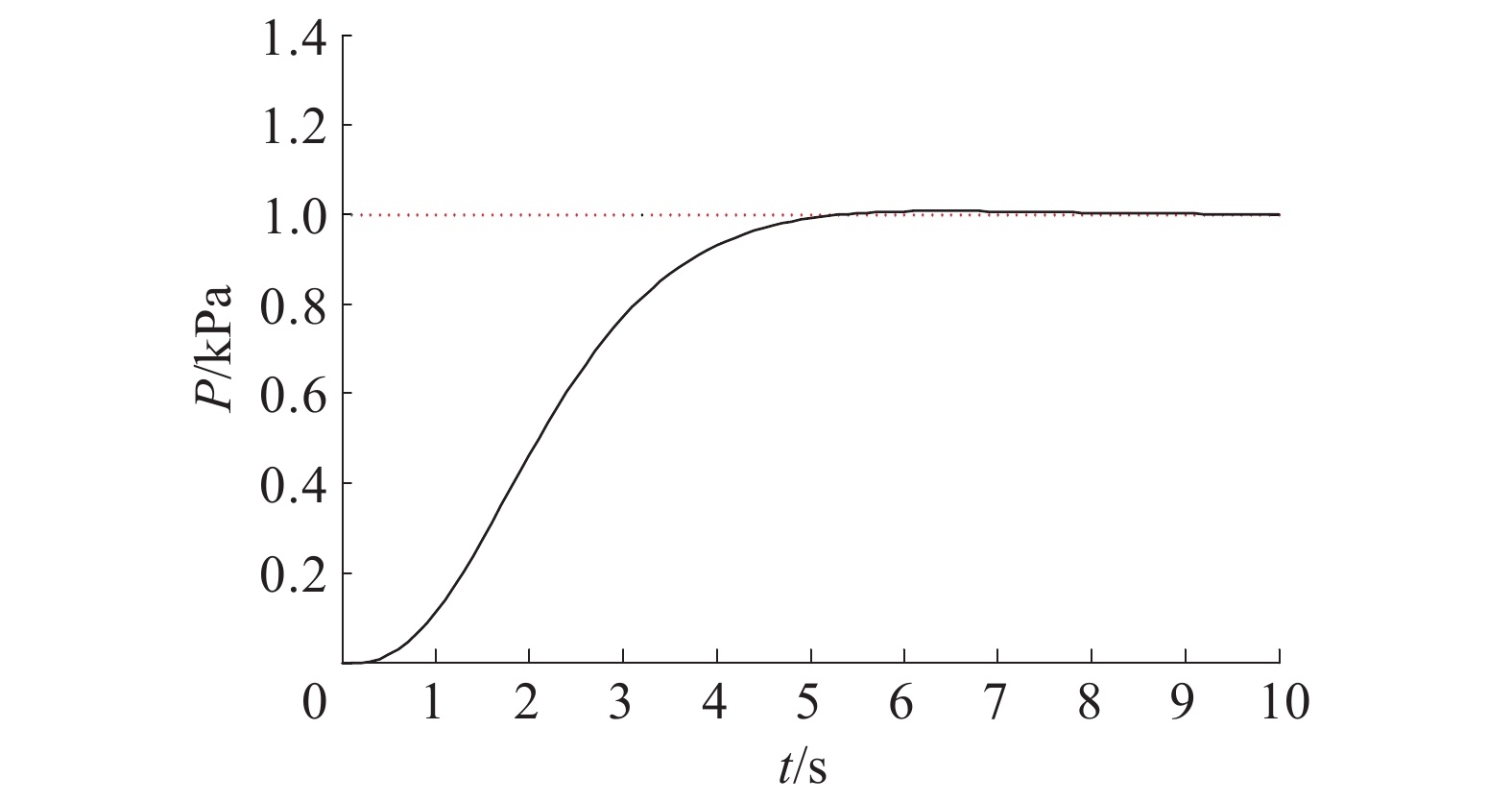
| 图 7 传统遗传−PID控制器阶跃响应 | |
|
|
表 1 传统PID算法、传统遗传−PID算法和改进的遗传−PID算法对比 |
由仿真结果和表1数据可以看到,尽管经过Zielgler−Nichols整定法优化后的传统PID控制器阶跃响应的上升时间为1.82 s,小于传统遗传−PID控制器的3.32 s;但是在超调量和调节时间2个重要指标上,传统遗传−PID控制器则优于传统PID控制器。传统遗传−PID算法的阶跃响应超调量仅为1.12%,调节时间为4.79 s,而传统PID算法的超调量高达6.83%,调节时间为5.50 s。改进的遗传−PID算法的上升时间为1.12 s,调节时间为3.61 s,超调量为0.6%,3个指标均优于传统遗传−PID算法。从上述实验结果可以得出,基于改进的遗传−PID算法的控制策略满足系统要求,控制效果更好。
4 结论本文提出了基于改进的遗传−PID算法的发电机组轴承油雾排控制策略,介绍了蓄能电站发电机组轴承油雾排放控制系统的组成。通过对基于传统PID算法的控制策略和基于传统遗传−PID算法的控制策略进行对比论证,并对传统的遗传−PID算法进行改进,在三者中选取最优的方案。
通过设定的参数指标和MATLAB仿真曲线对3种控制策略进行了比较,可以得到如下结论:
1)通过仿真结果可以看到,基于改进之后的遗传−PID算法的控制策略的超调量为0.06%,远远优于传统PID算法,满足指标要求和系统的稳定性。在调节时间这一重要指标上,改进之后的遗传−PID控制算法在针对高阶大滞后系统进行控制,调节时间仅为3.61 s,时间比传统PID算法减少了34.4%.
2)经过改进之后的遗传算法PID也大大改善传统遗传−PID算法效率慢、响应速度慢以及容易陷入局部极大值等问题。
3)遗传算法与PID算法结合,通过遗传算法的遗传操作和迭代计算对PID的3个参数进行在线优化并在此基础上进行一定的改进,从而使整个系统具有良好的稳定性、快速性和控制精度,满足油雾智能排放的要求。综上所述改进的遗传−PID算法的控制策略可应用到发电机组轴承油雾排放系统中,可以起到良好的控制效果。
| [1] |
张德选, 张晓刚. 巨型水轮发电机推力轴承甩油处理[J]. 水电站机电技术, 2016, 39(1): 68-71. ( 0) 0)
|
| [2] |
王伟, 孙文艳, 范江艳, 等. 大型水轮发电机组油雾问题分析与处理[J]. 水电与新能源, 2017, 31(2): 74-77. ( 0) 0)
|
| [3] |
OZANA S, DOCEKAL T. PID controller design based on global optimization technique with additional constraints[J]. Journal of electrical engineering, 2016, 67(3): 160-168. DOI:10.1515/jee-2016-0023 ( 0) 0)
|
| [4] |
JAMALUDIN J, RAHIM N A, HEW W P. Development of a self-tuning fuzzy logic controller for intelligent control of elevator systems[J]. Engineering applications of artificial intelligence, 2009, 22(8): 1167-1178. DOI:10.1016/j.engappai.2009.04.006 ( 0) 0)
|
| [5] |
熊四昌, 高玉科, 钱冰, 等. 基于容积补偿的气体泄漏检测遗传PID控制研究[J]. 机电工程, 2015, 32(3): 348-351. ( 0) 0)
|
| [6] |
张倩, 杨耀权. 基于遗传算法的PID控制器参数优化方法研究[J]. 电力科学与工程, 2011, 27(11): 53-57. DOI:10.3969/j.issn.1672-0792.2011.11.011 ( 0) 0)
|
| [7] |
尼文斌, 董金刚, 刘书伟, 等. 自适应遗传PID算法在风洞风速控制中的应用[J]. 实验流体力学, 2015, 29(5): 84-89. ( 0) 0)
|
| [8] |
陈永前, 曹艳琼, 于治明, 等. 基于遗传PID整定的单柱校正压装液压机控制[J]. 机械研究与应用, 2016, 29(3): 202-204. ( 0) 0)
|
| [9] |
张炳兰. 改进遗传算法PID在电液伺服系统的应用[J]. 自动化仪表, 2017, 38(8): 28-32. ( 0) 0)
|
| [10] |
张志文, 王沛元, 安柏楠, 等. 基于遗传算法PID的风电机组变桨控制[J]. 电力电子技术, 2017, 51(7): 37-39, 85. ( 0) 0)
|
| [11] |
刘金琨. 先进PID控制MATLAB仿真[M]. 4版. 北京: 电子工业出版社, 2016: 129-133.
( 0) 0)
|
| [12] |
HARRAG A, MESSALTI S. Variable step size modified P&O MPPT algorithm using GA-based hybrid offline/online PID controller[J]. Renewable and sustainable energy reviews, 2015, 49: 1247-1260. DOI:10.1016/j.rser.2015.05.003 ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


