图像匹配是针对不同视角、不同传感器获得的图像,通过匹配算法,找出图像之间纹理、特征、结构等的相似性和一致性,进而找出相似图像。图像匹配是图像领域中的热点问题,高精度的图像匹配能够更好地处理图像拼接、目标跟踪与识别等后续工作[1]。图像匹配算法可以分为基于灰度的图像匹配方法、基于变换域的图像匹配方法和基于特征的图像匹配方法这3大类[2]。其中基于特征的匹配方法抗噪性较好,匹配精度高,对图像中物体的旋转和遮挡方面具有更好的鲁棒性。选取合适的特征能够在图像的旋转、平移、尺度变换、视角变化、光照变化等条件下具有不变性。由于其优良的匹配性能,人们通常将基于特征的图像匹配作为主要的研究方法。
近年来,SIFT由于其旋转和尺度不变性、良好的光照适应性,受到研究者广泛关注[3]。杨世沛等[4]使用灰度均匀化和冗余分割树技术建立成更均匀、更宽的SIFT直方图,有效解决了光照变化过大时检测性能降低的问题。李彦等[5]使用SIFT算法,并通过数据库中已有的车牌标记来识别车牌汉字,并对其位置进行定位,提高了车牌识别效率。Ramu等[6]使用SIFT与随机样本一致性进行图像伪造检测,与现有的伪造检测方法相比,它可以提取更准确的结果。但是上述方法在提高准确率与效率的同时,并没有提高匹配所需的时间。主要原因是SIFT在构造高斯差分(difference of Gaussian,DoG)算子过程中,会产生较多不稳定的边缘点[7−8],而这些点在生成描述符时也要被一一计算。实验表明:SIFT特征点的提取时间占总时长的30%左右[9],从而导致匹配时间较长,难以进行实时性的应用。角点是图像领域中重要的局部特征。SCHMID[10]对多种角点算法进行比较,结果表明在物体旋转、平移和光照强度变化方面,Harris算法提取的角点特征是迄今为止稳定性最好的。但是Harris方法的不足是不具备空间多尺度性,且提取特征的数量远不如SIFT特征点,导致匹配不精准。
针对以上不足,对SIFT算法和Harris角点提取进行改进,提出一种新的图像匹配算法。首先,对输入图像构造高斯金字塔模型,在此模型中采用Harris角点提取特征,再使用Canny边缘算子提取出更多有意义的特征点;然后,通过建立梯度直方图的方法对上述特征点形成描述子;最后,采用欧式计算距离公式完成图像之间的匹配。
1 SIFT算法SIFT算法被认为是图像匹配效果最好的方法之一,它对物体的尺度变化、刚体变换、光照强度和遮挡都具有较好的稳定性。SIFT算法总共可分为4个阶段:尺度空间构建、特征点选择、方向确定和特征点描述。尺度空间构建的基本思想是在输入的图像模型中,通过高斯模糊函数连续地对尺度进行参数变换,最终得到多尺度空间序列。图像中某一尺度的空间函数L(x,y,σ)由可变参数的高斯函数G(x,y,σ)和原输入图像I(x,y)卷积得出
| $L(x, y, \sigma ) = G(x, y, \sigma ) * I(x, y)$ |
高斯函数为:
| $G(x, y, \sigma ) = \frac{1}{{2{\text π} {\sigma ^2}}}{e^{ - ({x^2} + {y^2})/2{\sigma ^2}}}$ |
式中:σ表示为尺度参数,σ越小,反应的局部点越清晰;反之σ越大,图像越模糊,越不能反应出图像的细节。
传统的SIFT算法是通过建立DoG函数方法来提取特征点。每一个尺度对应多幅图像。在不同尺度参数组成的多个层数图像中,高斯差分图像由某一相同尺度层的相邻图像作差值得出。将得到的差分图像与原图像I(x,y)做卷积得到的DOG函数:
| $\begin{aligned}f_{\rm DOG}(x, y, \sigma ) = & [G(x, y, n\sigma ) - G(x, y, \sigma )] * I(x, y)= \\ & L(x, y, n\sigma ) - L(x, y, \sigma ) \end{aligned}$ |
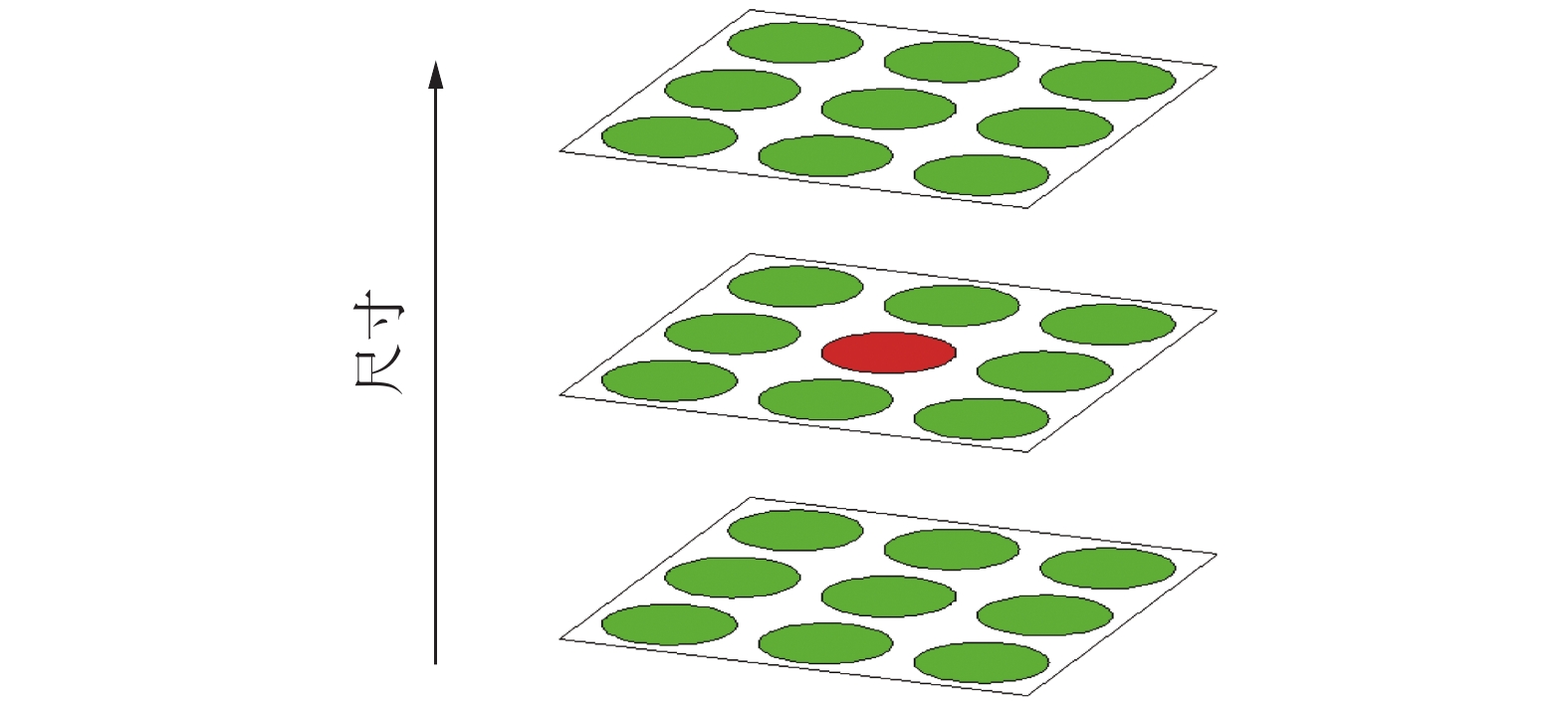
在得出DOG函数之后,计算不同尺度下的极值点。某一特征点通过周围邻域点的比较判断该特征点是否为极值点,如图1所示。其计算方法为确定某一尺度层的特征点,将它周围同层附近的8个相邻点和上下层相邻尺度的2×9个像素点,共26个检测点相比较,如果中心像素点是此邻域像素点的最大值或最小值,则该点为极值点。
|
Download:
|
| 图 1 DOG极值点检测 | |
通过以上计算得到的极值点并非都是稳定特征点,需要一些限制条件来排除响应较弱的极值点,筛选出精确、稳定的特征点。
为使特征点具有旋转不变性,采用高斯金字塔邻域像素梯度的幅值和方向计算特征点的值,如式(1)与式(2):
| $F(x, y) \!\!=\!\! \sqrt {{{{\text{(}}L(x \!\!+\!\! 1, y) - L(x \!\!-\!\! 1, y){\text{)}}}^{\text{2}}} \!\!+\!\! {{(L(x, y \!\!+\!\! 1) - L(x, y \!\!-\!\! 1))}^2}} $ | (1) |
| $H(x, y) = {\tan ^{ - 1}}(\frac{{L(x + 1, y) - L(x - 1, y)}}{{L(x, y + 1) - L(x, y - 1)}})$ | (2) |
式中:L表示特征点所对应的尺度空间;F(x,y)和H(x,y)为像素点的梯度幅值与方向。采用直方图的方法分别记录像素邻域内梯度的F和H,每个特征点的主方向为该点直方图最大峰值对应方向;同时也统计该点附近大于其主方向峰值80%的方向,将其标记为辅助方向,以增强鲁棒性。
在特征点的4×4邻域内,分别记录16个邻域中每个邻域内8个方向的梯度信息,形成128维特征描述向量。考虑到光照强度变化对特征点的干扰,再将得到的128维描述向量进行归一化,形成最终描述符。
2 改进的方法传统的SIFT匹配通过建立高斯金字塔模型,对每个塔模型的相邻层做差值得到近似极值点。但是通过这种方法求出的极值点包含很多不稳定点和无用点,导致特征点描述与后续的匹配时间过长。对此本文对以上的不足进行改进(如图2所示)。

|
Download:
|
| 图 2 改进的特征匹配算法 | |
首先,将原输入图像与高斯模糊函数作卷积计算,通过改变高斯模糊函数中尺度参数的大小得到多尺度空间,对其进行多尺度Harris角点提取,再使用Canny边缘提取算法对Harris角点进行修饰,提取出更多稳定的特征点,将得出的2种特征点进行融合,若有重合的特征点,对其进行合并处理;然后,使用传统SIFT算法中的描述子对特征点进行描述;最后,采用欧氏距离计算方法对上述提取的特征点进行特征点对的匹配,得到最终匹配结果。
2.1 多尺度Harris角点提取传统的Harris角点不具有空间尺度不变性。因此,本文引入高斯金字塔模型,将原输入图像I(x,y)与高斯模糊函数G(x,y,σ)作卷积计算,得到高斯尺度空间函数L(x,y,σ),然后进行Harris角点提取。对于大小为σ的尺度层,Harris角点的二阶矩公式为:
| $M(x, y, \sigma ) = \sum\limits_{x, y} {G(x, y, \sigma )} \left[ {\begin{array}{*{20}{c}} {I_x^2}&{{I_x}{I_y}} \\ {{I_x}{I_y}}&{I_y^2} \end{array}} \right]$ |
式中:G(x,y,σ)为带有尺度参数σ的高斯函数;Ix和Iy分别是原图像I(x,y)中在x方向和y方向上的导数梯度值。分别求出二阶矩M(x,y,σ)的行列式det M和迹trace M。在此基础求出角点的响应函数
| $Q(x, y) = \det M - k \times {\rm trace}\;{M^2}$ |
式中K为常数,通常取0.04~0.06。
当由公式求出的Q值小于本文设定阈值t时,就将Q值设为0。本文取K=0.05。最后,在3×3的邻域内进行非极大抑制,计算出某一区域的局部最大值,并将其记录为角点。
2.2 Canny边缘提取经典的Harris角点算法会出现特征点漏检的不足,而且Harris提取出的特征点数量远不如SIFT算法。对此本文提出一种多尺度Harris角点与Canny边缘提取相结合的算法,既对边缘特征点进行了改善;同时也增加了更多有用特征点,为改善特征匹配性能打下基础。
采用以下公式分别对每个尺度层计算图像的梯度大小和方向:
| $E(E) = \sqrt {I_x^2 + I_y^2} $ |
| $D(\theta ) = {\tan ^{ - 1}}(\frac{{{I_x}}}{{{I_y}}})$ |
式中:E(E)代表梯度大小;D(θ)表示梯度方向;Ix和Iy分别代表二维图像I(x,y)在x方向和y方向的梯度值。根据梯度计算结果对像素点进行极大值抑制,通过设定上下界阈值判断像素点是否为边界点。将提取后的特征点与Harris提取的角点进行融合,合并两者重复提取的特征点,得到最终特征点结果。
2.3 特征点描述和匹配本文采用SIFT算法描述符。以上述提取之后的特征点为中心,在其附近4×4的邻域小块内,每个小块分别赋予8个方向向量,共生成128维特征向量。再将生成的特征描述向量进行归一化,以减少光强度变化带来的影响。
为了得到2幅图像间的对应关系,本文采取BBF算法实现特征点对的匹配[3]。通过欧几里得度量公式计算2个特征点的距离大小,再利用KD树的性质分别记录距离最小值d1和次小值d2,将d1与d2的比值与设定阈值相比较,若d1/d2小于设定阈值,即视为匹配;否则视为不匹配。
3 实验结果与分析采用3组对比实验分析本文提出的算法,如图3~5。实验环境为Intel Core i5−4210 CPU, 2.9 GHz和内存4 GB的Windows7 PC机。实验结果分别与经典的SIFT和SURF[11]相比较,其中SIFT和SURF由VS2010的Opencv2.4.9实现,而本文算法在MATLAB 2014a中实现。实验图像来自于INRIA Holidays[12],图片分辨率均为800×600。

|
Download:
|
| 图 3 图像平移前后的匹配实验结果对比 | |

|
Download:
|
| 图 4 图像旋转后匹配实验结果对比 | |

|
Download:
|
| 图 5 图像平移加旋转后匹配实验结果对比 | |
通过以上图像对比分析,对实验结果数据进行记录与比较,对比结果如表1所示。
|
|
表 1 实验数据对比 |
其中,每幅图像都由2张图片组成,特征数量斜线前后的2个数字分别代表每幅图图左提取的特征点和图右提取的特征点数量。上述结果表明:改进算法的匹配正确率提高,速度明显快于SIFT,时间基本与SURF算法持平。尽管文中算法提取的特征点数量减少了一些,但是减少的点多为边缘不稳定的点,而大部分有用的特征点被保留了下来,并且本文算法具有良好的鲁棒性。
4 结论本文针对SIFT会产生大量不稳定边缘点的不足,提出一种多尺度Harris角点与Canny边缘提取结合的改进算法。结果表明:1)使用Harris角点代替传统的SIFT提取特征点方法能够有效地减少匹配时间;2)Harris角点与Canny边缘提取的结合增加了特征点提取数量,同时也提高了匹配正确率。因此,本算法在保证有效减少不稳定特征点的情况下,也提高了匹配精度和效率,更适用于图像匹配的应用。
| [1] |
YU Chuan, TIAN Lu, HU Han, et al. Progressive feature matching via triplet graph[C]//2015 IEEE International Conference on Image Processing. Quebec City, Canada, 2015: 1860−1864.
( 0) 0)
|
| [2] |
郭艾侠, 熊俊涛, 肖德琴, 等. 融合Harris与SIFT算法的荔枝采摘点计算与立体匹配[J]. 农业机械学报, 2015, 46(12): 11-17. DOI:10.6041/j.issn.1000-1298.2015.12.002 ( 0) 0)
|
| [3] |
LOWE D G. Distinctive image features from scale-invariant keypoints[C]//International Journal of Computer Vision. Hingham, USA, 2004: 91-110.
( 0) 0)
|
| [4] |
杨世沛, 陈杰, 周莉, 等. 一种基于SIFT的图像特征匹配方法[J]. 电子测量技术, 2014, 37(6): 50-53. DOI:10.3969/j.issn.1002-7300.2014.06.013 ( 0) 0)
|
| [5] |
李彦, 张洪博, 石莲英. 基于SIFT特征匹配的车牌识别方法[J]. 计算机工程与应用, 2016, 52(12): 194-200. DOI:10.3778/j.issn.1002-8331.1507-0188 ( 0) 0)
|
| [6] |
RAMU G, BABU S B G T. Image forgery detection for high resolution images using SIFT and RANSAC algorithm[C]//Proceedings of the 2nd International Conference on Communication and Electronics Systems. Coimbatore, India, 2017: 850−854.
( 0) 0)
|
| [7] |
程德志, 李言俊, 余瑞星. 基于改进SIFT算法的图像匹配方法[J]. 计算机仿真, 2011, 28(7): 285-289. DOI:10.3969/j.issn.1006-9348.2011.07.071 ( 0) 0)
|
| [8] |
向程谕, 王冬丽, 李建勋, 等. 基于改进SIFT特征的深度图像匹配[J]. 计算机应用, 2016, 36(S2): 135-138. ( 0) 0)
|
| [9] |
骞森, 朱剑英. 基于改进的SIFT特征的图像双向匹配算法[J]. 机械科学与技术, 2007, 26(9): 1179-1182. DOI:10.3321/j.issn:1003-8728.2007.09.021 ( 0) 0)
|
| [10] |
SCHMID C, MOHR R, BAUCKHAGE C. Evaluation of interest point detectors[J]. International journal of computer vision, 2000, 37(2): 151-72. DOI:10.1023/A:1008199403446 ( 0) 0)
|
| [11] |
BAY H, ESS A, TUYTELAARS T, et al. Speeded-up robust features (SURF)[J]. Computer vision and image understanding, 2008, 110(3): 346-359. DOI:10.1016/j.cviu.2007.09.014 ( 0) 0)
|
| [12] |
JEGOU H, DOUZE M, SCHMID C. Hamming embedding and weak geometric consistency for large scale image search[C]//Proceedings of the 10th European Conference on Computer Vision. Marseille, France, 2008: 304−317.
( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


