信号特征的提取方法主要为傅里叶变换、小波分析等，提取的特征参量主要为信号的幅值、能量、频率等。小波分析是目前常用的信号分解方法，经小波分解，时域信号可分解为不同频段的时域信号。但是小波变换不具有自适应性，小波基的选择比较困难，小波参数的选择将直接影响到最后的诊断结果^[1−4]，存在很大的人为因素的影响。同时共振解调存在与小波变换相同的缺陷，需要人为地选择一些参数，也不具有自适应性^[5−7]。

EMD算法是一种信号分解方法，把信号分解为一系列平稳的信号分量，且分量按频率由高到低排列，与小波分析相比不用人为地选择小波基。但是目前的研究主要考虑EMD分解的某一部分分量，摒弃了大量的信号特征信息，且特征参量多只考虑幅值、能量等信息^[8]。张志刚等^[9]在提取滚动轴承的故障特征时利用了灰色关联度和互信息来改进EMD算法，但是两者都只能度量EMD分量的一个尺度，也就是相关性。胡爱军等^[10]利用了峭度准则进行特征提取时只选择了一个固有模态函数（intrinsic mode function，IMF）分量，移除了大量的特征信息。

在特征的选择方面，众多学者在选择算法和特征评价中取得了丰硕的研究成果。要明确起关键作用的特征组，首先必须明确选择的算法，再者就是制定相应的评价准则对所提取的特征向量进行评价分析^[11]。同时，特征样本数越多就会造成模型越复杂，训练的速度也越慢，因此数据降维也是一个研究的热点。通常数据信号的降维从两个方面来考虑：其一就是直接提取特征子集抽取特征；其二就是用线性或者非线性的方式通过变换空间实现信号特征的降维。第2种方法是目前运用的主流。线性映射的方法主要有主成分分析（principal component analysis，PCA）、线性判别分析（linear discriminant analysis，LDA）。PCA可以提取信号主要的信息，但是该方法需要计算协方差矩阵，计算量较大；LDA原理比较简单，容易理解，但是计算较复杂；而利用核函数的特征降维方法最后的结果受核的选择的影响^[12]。

为了解决上面提到的问题，本文提出一种基于EMD的特征提取与识别方法。利用信号的信息熵构建基于信息熵的均值特征向量，同时引入模糊聚类对特征向量进行再选择，探讨不同聚类数下的特征向量对识别结果的影响。首先对信号数据进行EMD分解，求取各个分量的信息熵，基于信息熵构建均值特征向量；然后基于模糊聚类算法对均值向量进行特征降维选择；最后利用BP神经网络进行识别训练。

1 基于信息熵的特征向量构建 1.1 信息熵理论

熵是随机变量不确定性的度量。如果一个离散型随机变量 $X$ ，该随机变量的取值空间为A，概率密度函数 $p(x) = Pr (X = x), x \in A$ 。那么我们就可以把一个离散型随机变量 $X$ 的熵 $H(X)$ 记做^[13]

$H(X) = - \sum\limits_{x \in A} {p(x)\log p(x)} $

1.2 经验模态分解

EMD是一种会把信号分解为一系列平稳信号分量的分解方法，且分量按频率由高到低排列。目前在缺陷检测、状态监测、特征向量的构建以及信号去噪等方面得到了普遍且成熟的应用，取得了丰硕的学术成果。经验模态分解步骤如下：

假设待分解信号模型为：

$f(t) = s(t) + n(t)$

式中： $f(t)$ 表示含有噪声的观察信号； $s(t)$ 为观察信号； $n(t)$ 为Gaussian白噪声。

1）计算出信号 $f(t)$ 所有的极值点。

2）求取全部极大值点连接起来生成的包络线 ${u_0}(t)$ ，以及全部极小值点连接起来生成的包络线 ${v_0}(t)$ 。

3）对2条包络线求取平均值为 ${m_0}(t)$ ，表示为

${m_0}(t) = \frac{{{u_0}(t) + {v_0}(t)}}{2}$

(1)

并记信号与平均值 ${m_0}(t)$ 的差值为 ${h_0}(t)$ ，表示为

${h_0}(t) = f(t) - {m_0}(t)$

4）判断 ${h_0}(t)$ 是否满足差值 ${h_0}(t)$ 极值点数目和过零点数目的相差为0或者1；差值 ${h_0}(t)$ 的上下包络线由式（1）计算，所得的均值为0。若满足这2个条件，则 ${h_0}(t)$ 为IMF；否则，令 ${h_0}(t)$ 为 $f(t)$ 继续执行步骤1）到步骤3），获得一个合格的IMF，记为 ${c_1}(t)$ 。

5）记 ${r_1}(t) = f(t) - {c_1}(t)$ 为新的信号 $f(t)$ ，然后执行步骤1）到步骤4），获得第2个IMF分量，记为 ${c_2}(t)$ ，以及余项 ${r_2}(t) = {r_1}(t) - {c_2}(t)$ 。循环执行上述步骤，当余项 ${r_n}(t)$ 是一个单调信号或 ${r_n}(t)$ 的值已经达到阈值的要求时，分解完成。获得的 $n$ 个IMF分量分别用 ${c_1}(t), {c_2}(t), \cdots , {c_n}(t)$ 表示，余项记为 ${r_n}(t)$ ，到此整个分解过程结束。原始信号被分解为

$f(t) = \sum\limits_{k = 1}^n {{c_k}(t) + {r_n}(t)} $

1.3 构建基于信息熵的均值特征向量

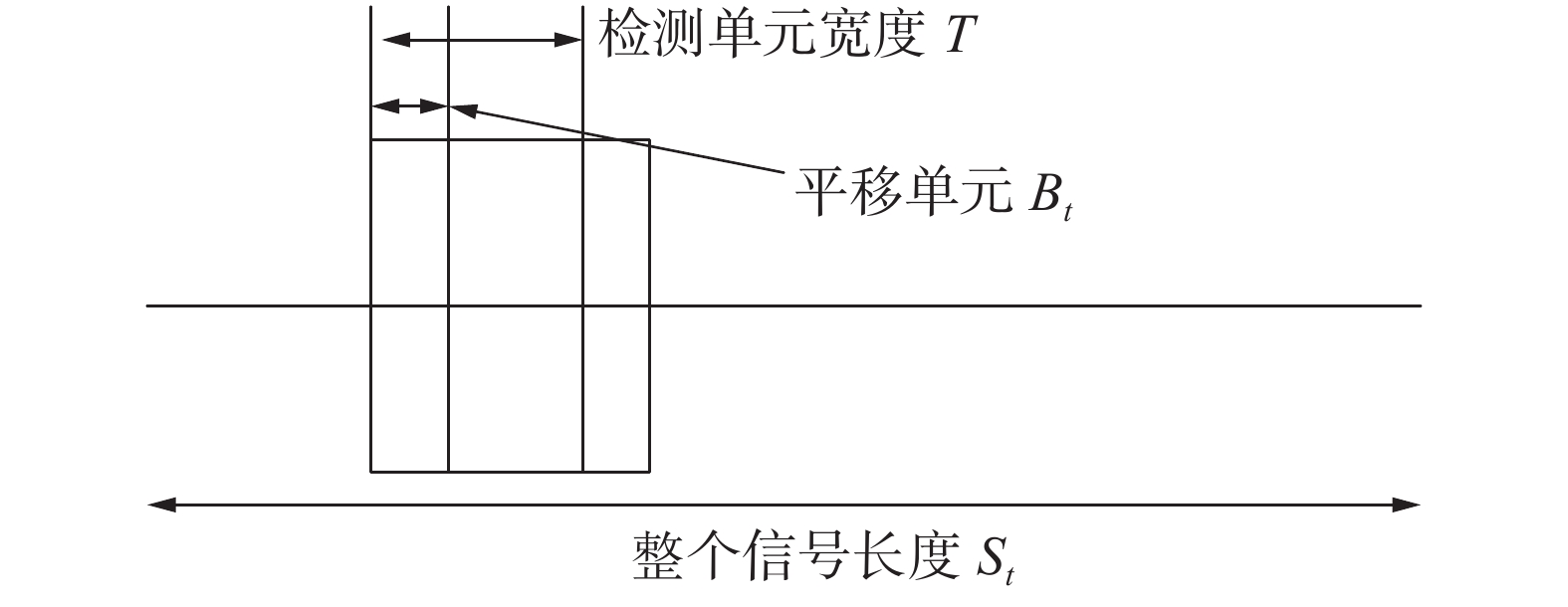
为了构建桩基缺陷数据的基于信息熵的均值特征向量，利用EMD方法对缺陷信号进行分解。分解后的分量为了方便求取信息熵，在时间轴上选取固定长度的信号作为一个检测单元，然后再依次平移检测单元，完成整个信号长度的计算。检测单元、平移距离如图1所示。

检测单元宽度T和平移距离 ${B_t}$ 是2个需要在文中进行选择的参数，它们的选择会决定桩基缺陷信号特征提取的合理性，所以在构建均值特征向量时，要充分考虑检测单元宽度和平移距离这2个参数。检测单元宽度的设定一般与信号的波长大致相同；平移距离决定了缺陷点在整个时间轴上的分辨率，平移距离越小，分辨率越高。参考相关文献知识，检测单元的平移距离与检测单元的宽度有关。综合考虑，步进长度的设定范围定为

$\frac{T}{8} < {B_t} < \frac{T}{4}。$

信息熵的求解重点是概率 $p$ 的求解。对于可以确认具体的取值范围的数据，可以直接根据每一个取值出现的次数确定概率。但是，对于本文所分解的桩基缺陷信号，数值的范围并不是确定的，如果进行变换，使其转换到一个整数范围的话，会造成数据的丢失，因此本文采用一种一维序列求取信息熵常用的方法。首先对信号在幅值范围内进行分块，通过计算幅值的最大值和最小值构成的区间，均分为 $N$ 块；然后计算时间轴上固定长度下每一块的数据个数占所有数据总数的比例，求出相应的概率；最后分别求取每个分量的信息熵后，求取它们的平均值，构建基于信息熵的均值特征向量。

2 基于模糊聚类的特征选择 2.1 模糊聚类

假设存在论域 $X$ ，则认为从该论域到[0，1]区间的映射关系记为 ${\mu _A}:X \to [0, 1]$ ，构成了该论域的一个模糊集。对于每一个 $x \in X$ ， ${\mu _{\rm{A}}}(x)$ 叫做元素 $x$ 对模糊集 $A$ 的隶属度。隶属度函数的值越大说明某一个元素属于该类的程度越强，但是再大也不会超过1；越小就说明越不属于该类，但是再小也不会超过0。其本质表示的是某一个元素是否属于一个类的程度。

模糊C均值聚类（fuzzy c-means，FCM）方法第一次由E Ruspini在论文中进行较完整的阐述。随着其他学者对该方法的进一步研究，把算法在具体的应用方法上进行了推广，开始应用于模糊聚类的相关领域。这种推广大大加速了FCM算法在实际工程中的应用。FCM算法进行聚类的主要原理是通过迭代的方式对目标函数进行计算更新，直到达到理想的聚类效果。通过隶属度函数，判断每一个元素属于一个类的程度，完成每一个类的划分，只要在程序中设定了聚类数，后续的处理将会自动地自适应完成^[14−15]。

FCM算法的目标函数为

${J_1}(U, P) = \sum\limits_{i = 1}^c {\sum\limits_{k = 1}^n {{u_{ik}}{{({d_{ik}})}^2}} } $

式中 ${u_{ik}}$ 表示 ${x_k}$ 与第i类样本的隶属度。

FCM算法执行步骤如下：

1）给定聚类数c（1<c<n）、模糊指数m（m>1）、最大迭代次数T、收敛的精度 $\varepsilon $ 、随机初始划分隶属度矩阵U，确定初始聚类中心以及距离；

2）根据公式 $\displaystyle{p_i} = \displaystyle\frac{{\displaystyle\sum\limits_{k = 1}^n {{{\left( {{u_{ik}}} \right)}^m}{x_k}} }}{{\displaystyle\sum\limits_{k = 1}^n {{{\left( {{u_{ik}}} \right)}^m}} }}$ ，计算类中心。

3）根据公式 $\displaystyle{u_{ij}} = \displaystyle\frac{1}{{\displaystyle\sum\limits_{i = 1}^c {{{\left[ {\displaystyle\frac{{{d_{jt}}}}{{{d_{it}}}}} \right]}^{ - \textstyle\frac{2}{{m - 1}}}}} }}$ 更新划分隶属度矩阵U。

4）判断是否满足停止条件（达到最大迭代次数或者达到收敛精度），如果满足就停止，否则继续执行步骤2）。

2.2 基于模糊聚类算法的数据处理

假定待处理的基于信息熵的均值向量为

${{X}} = \{ {x_1}, {x_2}, \cdots , {x_N}\} $

(1)

首先对式（2）重新进行构造，构成用于模糊聚类的输入矩阵。以长度 $n$ 进行分段，构成 $m$ 行 $n$ 列的矩阵且 $N = m \cdot n$ 。如果 $N$ 不能够刚好被 $n$ 整除，则在末尾补零处理。构造矩阵A如下：

${{A}} = \left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}&{\cdots }&{{x_{1n}}} \\ {{x_{21}}}&{{x_{22}}}&{\cdots }&{{x_{2n}}} \\ \vdots &{\cdots }&{\cdots }& \vdots \\ {{x_{m1}}}&{{x_{m2}}}&{\cdots }&{{x_{mn}}} \end{array}} \right]$

(2)

式（2）与（3）的对应关系如表1所示。

从矩阵A我们可以看出，该矩阵有 $m$ 行，确定聚类数 $c$ 后利用FCM算法生成 $c$ 个数目的聚类。对于相同聚类里面的行向量求取他们的平均值，生成 $c$ 行 $n$ 列的简化矩阵，简化矩阵表示如下

${{B}} = {\left[ {\begin{array}{*{20}{c}} {{y_{11}}}&{{y_{12}}}&{\cdots }&{{y_{1n}}} \\ {{y_{21}}}&{{y_{22}}}&{\cdots }&{{y_{2n}}} \\ \vdots &{\cdots }&{\cdots }& \vdots \\ {{y_{c1}}}&{{y_{c2}}}&{\cdots }&{{y_{cn}}} \end{array}} \right]_{c < m}}$

(3)

根据式（4）中的降维矩阵B生成新的特征向量，表示为 ${{F}} = \left\{ {{f_1}, {f_2}, \cdots , {f_N}} \right\}$ 。F与降维矩阵B之间的对应关系如表2所示。

这样原本的均值向量X就被简化为了特征向量F。然后把新构建的特征向量作为神经网络的输入用于对缺陷信息进行识别分类。

在应用FCM算法时，有 $c$ 和 $m$ 这2个参数需要考虑。2个参数的选择影响聚类的结果，从而对缺陷的识别产生影响。

本文聚类数 $c$ 考虑由识别分类结果最终确定。在数据的聚类中，可以根据 $L(c)$ 函数对聚类效果进行判断。

$L(c) = \displaystyle\frac{{\displaystyle\sum\limits_{i = 1}^c {\displaystyle\sum\limits_{j = 1}^n { u_{ij}^m } } ||{p_i} - \overline x |{|^2}/(c - 1)}}{{\displaystyle\sum\limits_{i = 1}^c {\displaystyle\sum\limits_{j = 1}^n { u_{ij}^m ||{x_j} - {p_i}|{|^2}/(n - c)} } }}$

(4)

式中 $\overline x = \displaystyle\frac{{\displaystyle\sum\limits_{i = 1}^c {\displaystyle\sum\limits_{j = 1}^n {u_{ij}^m{x_j}} } }}{n}$

但是在文中利用式（5）确定聚类数c并不可行，因为每一个缺陷我们有50组数据，但是对每一组数据来说都可能存在不同的最佳聚类数，这样就会导致构建的新特征向量维数不相同，也就无法作为神经网络的输入。以扩颈桩数据为例，第1、3组数据计算得到的 $L(c)$ 值如表3、4所示。

从表3我们可以看出，当 $c$ =4时， $L(c)$ 取得最大值，也就是聚类数为4时，会取得最优的聚类效果。从表 4我们可以看出，当 $c$ =3时， $L(c)$ 取得最大值，也就是当聚类数为3时，会取得最优的聚类效果。因此聚类数 $c$ 的选择只能通过识别的结果加以确定。

指数 $m$ 的选择会影响聚类的效果以及聚类是否准确。下面讨论指数 $m$ 的取值选择策略。如果 $m$ 设定的过小就会导致聚类比较宽泛，导致聚类效果受周围零星数据点的影响比较严重，使聚类出现偏差；而当 $m$ 设定过大的值时，就会导致考虑的数据范围过小，对周围零星数据点考虑不够，同样使得聚类结果产生偏差，进而会影响后续的信号识别训练。Pal等^[16−18]从聚类有效性中得出 $m$ 的最佳取值为 $m \in [1.5, 2.5]$ ，通常来说， $m$ 选取2.0比较合理，在本文中我们选取 $m$ =2。

利用模糊聚类算法对相空间重构后的矩阵进行聚类分析，对于同类的行向量合并，达到对重构的矩阵降维的效果；把降维后的矩阵再重构回一维特征向量，构建一种新的特征向量，实现对特征向量的选择。

3 实验仿真分析

根据上述的新的特征向量的构建规则对基于信息熵的均值向量进行优化处理。步骤总结如下：

1）把基于信息熵的均值特征向量进行相空间重构；

2）利用FCM算法进行聚类分析；

3）根据分类结果构造聚类后的矩阵；

4）根据聚类后的矩阵生成新的特征向量。

由基于信息熵的均值向量的仿真实验结果可知，基于信息熵的均值向量共有52个特征元素，在末尾补2个零元素，首先设定 $n$ 等于9，构造成6行9列的矩阵。以缩颈桩数据为例，构成的矩阵如下（保留两位小数）：

${{A}} = \left[ {\begin{array}{*{20}{c}} {{{34}}{{.59}}}&{{{35}}{{.57}}}&{{{34}}{{.18}}}&{{{33}}{{.88}}}&{{{34}}{{.58}}}&{{{34}}{{.46}}}&{{{34}}{{.42}}}&{{{34}}{{.58}}}&{{{35}}{{.68}}} \\ {35.78}&{36.09}&{34.73}&{34.53}&{33.72}&{33.76}&{34.26}&{35.27}&{34.64} \\ {35.58}&{33.89}&{35.27}&{35.14}&{36.23}&{34.39}&{35.18}&{36.37}&{35.76} \\ {35.13}&{34.26}&{33.82}&{33.73}&{34.69}&{34.49}&{33.95}&{36.24}&{35.53} \\ {35.53}&{32.25}&{35.40}&{35.97}&{35.71}&{34.45}&{34.45}&{35.37}&{36.10} \\ {36.56}&{35.66}&{29.20}&{20.98}&{14.17}&{10.31}&{1.10}&0&0 \end{array}} \right]$

(5)

对式（6）中的矩阵A进行模糊聚类算法处理，设定聚类数 $c$ 为3的情况下，可以得到隶属度矩阵 ${{U}}$ 为（为了方便表示，结果四舍五入并保留2位小数）：

${{U}} = \left[ {\begin{array}{*{20}{c}} {0.89}&{{{0}}{{.86}}}&{0.01}&{0.82}&{0.90}&{4.11 \times {{10}^{ - 12}}} \\ {5.80 \times {{10}^{ - 4}}}&{9.08 \times {{10}^{ - 4}}}&{2.16 \times {{10}^{ - 5}}}&{7.32 \times {{10}^{ - 4}}}&{5.64 \times {{10}^{ - 4}}}&{1.00} \\ {0.11}&{0.13}&{0.99}&{0.18}&{0.09}&{3.78 \times {{10}^{ - 12}}} \end{array}} \right]$

聚类结果如表5所示。

根据分类结果，生成新的优化特征向量，并利用该向量进行基于BP神经网络的识别训练，同时输出为设定的如表6所示的网络编号。

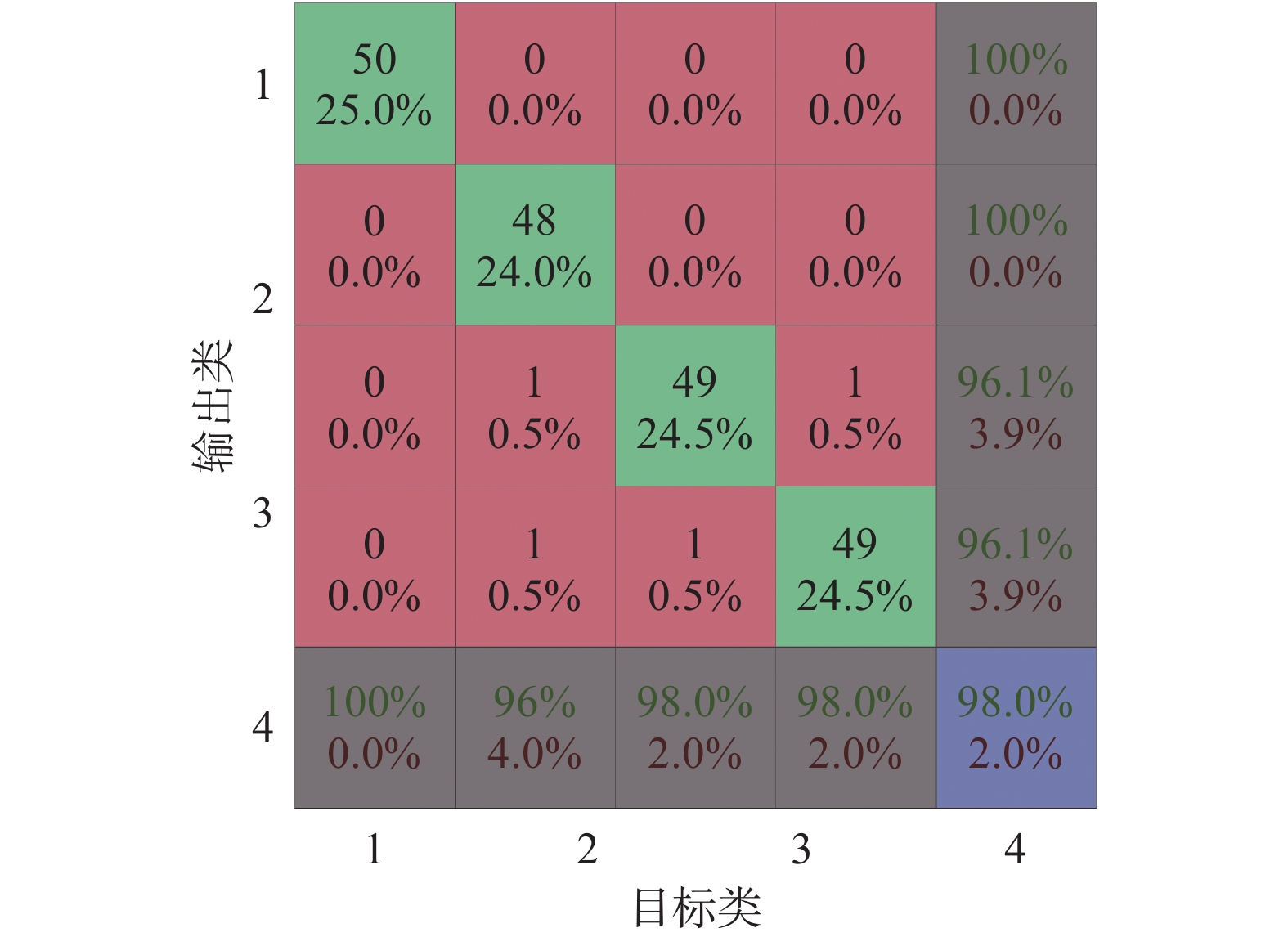
经过BP神经网络识别后，识别率与差错率如图2所示。

从图2的识别结果可以看出，基于模糊聚类处理的优化特征向量具有很好的识别结果，识别率达到了98%。然而单次的仿真实验具有一定的随意性，没有说服力。

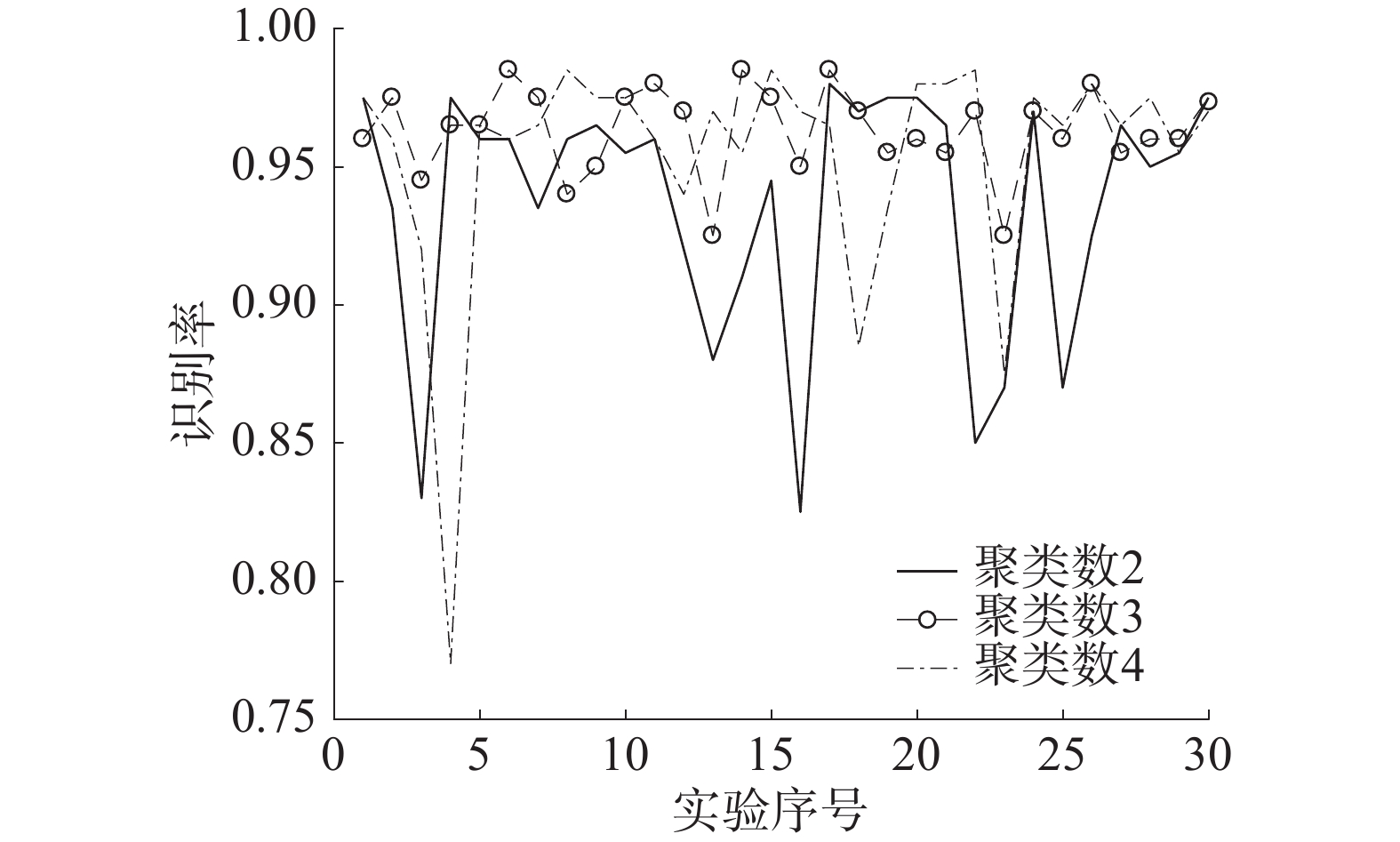
表7、图3为聚类数 $c$ 分别等于2、3、4时的识别率对比，数据为平均值。

从表7可以看出，在10、20、30次实验的情况下，聚类数为3时的识别率均高于当聚类数为2、4时的识别率；同时从图3可以看出，当聚类数为3时识别率最平稳，没有出现其他2种情况的大波动。

PCA降维是目前应用比较广泛的降维方法，本文对于2种算法在降维后，维数为3时的识别率和时间开销进行了分析，分析结果如表8所示。

从表8可以看出，2种方法相比，基于模糊聚类构建的新特征取得的识别率明显高于PCA方法构建的特征，同时所消耗的时间显著缩短。因而基于模糊聚类方法降维显著地优于PCA降维。

4 结论

本文主要解决桩基缺陷信号的特征提取、降维与识别。基于EMD分解构建了基于信息熵的均值特征向量；引入模糊聚类的相关技术方法，对基于信息熵的均值特征向量进行相空间重构然后进行降维，实现特征向量的降维选择。所取得的结论如下：1）通过30次仿真实验以及10次与PCA的对比实验验证了基于信息熵的均值特征向量以及基于模糊聚类构建的新特征向量取的了理想的识别效果；2）从识别率和稳定性2个方面考虑了不同聚类数对识别结果的影响，实验结果显示当聚类数为3时识别效果最好。

本文构建了一种有效的特征类型，具有实际的应用价值，但是在聚类数的选择中只能通过仿真实验获取，还需要进一步的研究。