压水堆堆内构件是压水反应堆重要的结构部件,其安全性直接关系着整个反应堆的可靠运行。然而流致振动造成的堆内构件事故不断发生,通常核电站设有堆内构件振动监测系统,以对其构件振动进行周期性监测;但现有振动监测系统对于非平稳信号缺乏有效的信号处理手段,容易湮灭信号的重要特征[1]。因此,要分析反应堆运行时堆内构件模态特征,首先就要去除从传感器监测振动信号中的噪声。
在堆内构件流致振动研究中,近年来中国核动力研究设计院采用实堆1∶5的模型,对秦山二期工程反应堆、ACP1000等堆型,进行了堆内构件流致振动试验研究[2-3]。国外则主要针对SMART、PHWR、AP1000等堆型,进行模型试验和数值分析相结合的研究[4-5]。由于流致振动领域涉及到多学科的交叉,不少机理至今仍然没有得到透彻的认识,而流致振动分析关键在于结构实体模型的建立以及模拟求解的方法。
因此,本文建立反应堆三维堆内构件简化模型,进行堆内构件邻近流体计算,最终得到正常状态和事故状态下的堆内构件流致振动响应。最后针对振动信号特征,进行基于改进小波包的去噪算法研究。本文能够为压水堆堆内构件流致振动研究提供思路,对其振动信号处理方法研究有改进创新之处。
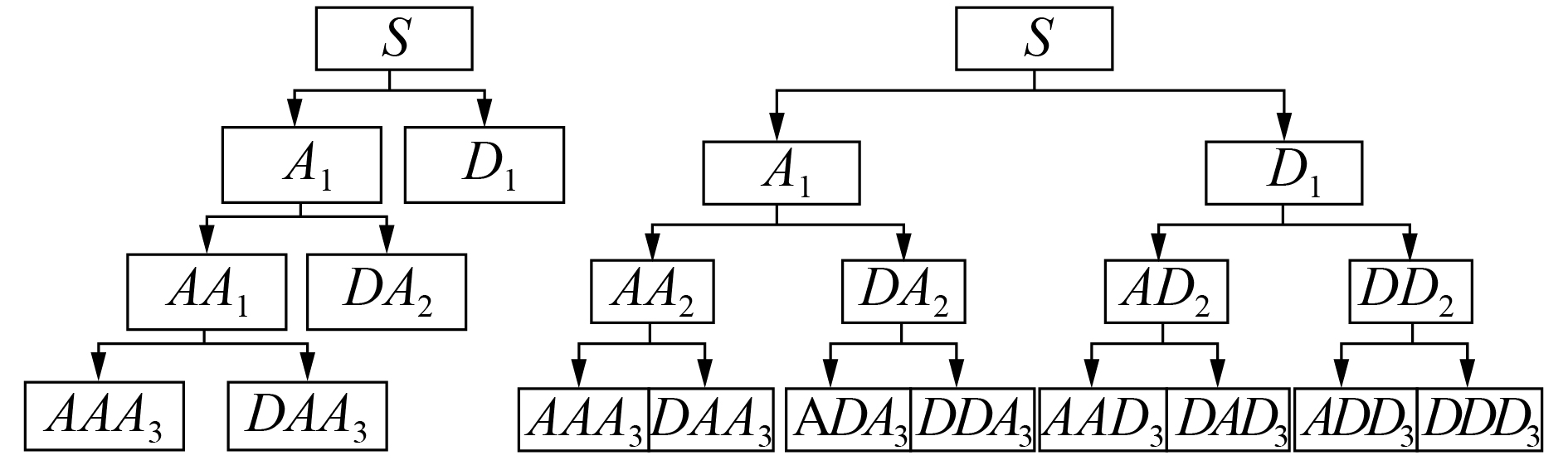
1 小波包变换去噪及其改进技术 1.1 小波包变换原理小波包变换对信号在全频带内进行多分辨率分解,继承小波变换所有良好时频局部化优点,也能对低、高频都进行细化处理,克服了小波变换分辨率不高的缺点。由图1可以看出2种方法的区别,其中S为原始信号,A表示低频,D表示高频,末尾的序号表示小波包分解的层数。
|
Download:
|
| 图 1 小波分解及小波包3层分解结构 | |
原始信号S经过3层小波包分解后可以表示为
| $\begin{aligned}S =& AA{A_3} + DA{A_3} + AD{A_3} + DD{A_3} + AA{D_3} +\\ & DA{D_3} + AD{D_3} + DD{D_3}\end{aligned}$ |
小波包理论的分解算法和重构算法的数学表达式如下[6]:
| $\left\{ \begin{array}{l}d_t^{j,{\rm{2}}k} = \displaystyle\sum\limits_p {{h_{p - 2t}}d_p^{j + 1,2k}} \\d_t^{j,{\rm{2}}k + {\rm{1}}} = \displaystyle\sum\limits_p {{g_{p - 2t}}d_p^{j + 1}} \end{array} \right.$ |
| $d_t^{j + 1,k} = \sum\nolimits_p {({h_{t - 2p}}d_p^{j,2k} + {g_{t - 2p}}d_p^{j,2k + 1})} $ |
式中:h、g为滤波器系数,d为小波包分解系数,p、t为分解层数,j、k为小波包节点号。
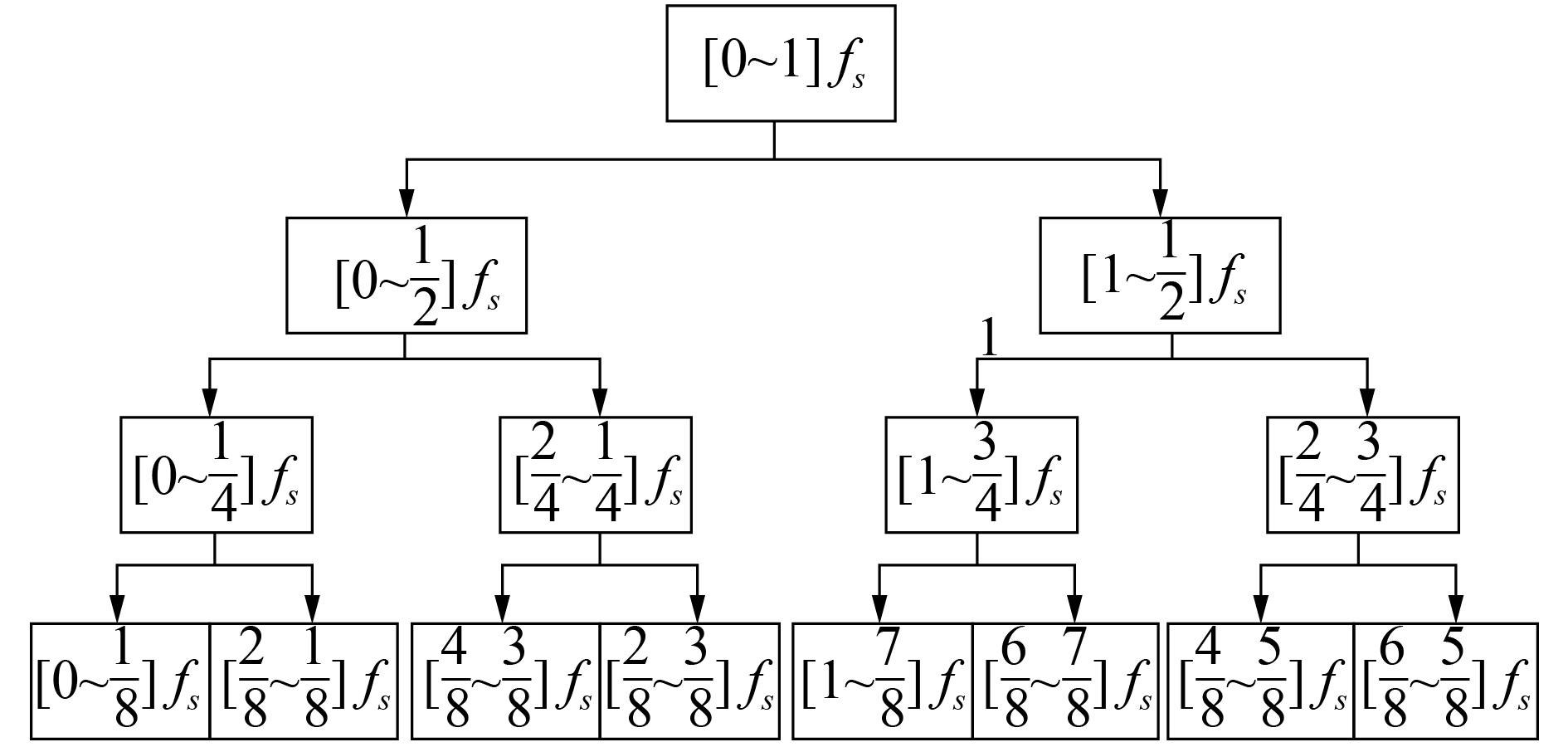
1.2 小波包的频带顺序重排技术在小波包经典分解算法中,对高低频部分均保留较高分解精度,但在每次小波包分解时采用隔点采样,即高通滤波器会进行一次“翻转”操作,造成采样频率减半从而导致小波包频带出现混乱排序现象[7],使得最终产生的小波包原始分解系数顺序未按照频率排序,其原始频率分解如图2所示。
|
Download:
|
| 图 2 小波包3层分解频率 | |
如图2所示,设信号采样频率为2fs,经3层小波包分解后,小波包分解系数出现频率排序混淆现象,而在对其进行多阈值处理时,需要频率顺序而非原始分解顺序。因此,要提高去噪信号信噪比,需要对小波包系数在阈值处理前进行频带排序。本文采样基于格雷排序的频带顺序重组方法[7],每经一次小波包分解的节点,通过高通滤波器就编码为“1”,通过低通滤波器就编码为“0”,这样,最终分解的分解节点按频带就形成了一个二进制码,3层格雷编码如图3所示。

|
Download:
|
| 图 3 3层小波包分解节点格雷编码 | |
如图3所示,方框中为该节点格雷编码,按格雷码顺序其节点应分别为(3,0)、(3,1)、(3,3)、(3,2)、(3,6)、(3,7)、(3,5)、(3,4)。可以发现,最终分解节点的格雷顺序就是正确的频率重组顺序。
1.3 改进小波包阈值及其阈值函数方法常用的小波包滤波方法主要有模极大值重构滤波、空域相关滤波法和小波包阈值滤波[1],其中阈值滤波由于原理简单、计算速度快而被广泛使用。在阈值选取中,单一阈值准则容易造成不充分去噪或者过度去噪问题,因此采用不同小波包系数尺度上的多阈值准则。传统4种阈值准则为:固定(sqtwolog) 阈值准则、自适应(rigrsure)阈值准则、启发式(heursure)阈值准则以及最小极大(minimax)阈值准则。其中,minimax规则和rigrsure规则去噪比较“保守”,容易导致去噪不明显;而sqtwolog规则和heursure规则去噪比较充分,但容易过度去噪[8]。
针对上述弊端,本文选用基于小波包系数能量选取阈值的方法。具体说来,在振动信号分析领域,若某信号经小波包分解后,在频率顺序下发现小波包系数低、中频段中能量分布较高,而高频段处系数能量极低,则可以认定有用信号集中于低、中频段,更适合采取rigrsure阈值准则、minimaxi阈值准则,而对于高频段采取sqtwolog阈值准则、heursure阈值准则。因此,所选阈值根据各频域段噪声与信号相对大小而变化,相比传统全局阈值处理更加合理。
Donoho[9]提出的软、硬阈值去噪法是工程上应用较为广泛的方法,同时也取得了很好的效果。但各方法也存在一定的缺陷,为克服硬阈值函数的不连续性及软阈值函数的恒定偏差,采用一种改进阈值函数进行振动信号去噪[10]:
| ${\bar \omega _{j,k}} = \left\{ {\begin{array}{*{20}{c}} {{\rm{sgn}}({\omega _{j,k}}) - (\left| {{\omega _{j,k}}} \right|\displaystyle\frac{{{T_{{\rm{thr}}}}}}{{{\rm{exp}}((\left| {{\omega _{j,k}}} \right| - {T_{thr}})/N)}}),{\rm{ }}\left| {{\omega _{j,k}}} \right| \geqslant {T_{{\rm{thr}}}}{\rm{ }}} \\ {0,{\rm{ }}\left| {{\omega _{j,k}}} \right| < {T_{{\rm{thr}}}}{\rm{ }}} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\end{array}} \right.$ |
式中:
基于上述改进技术,能够从多方面提高阈值处理后去噪信号的精确度,具体改进小波包阈值降噪算法按如下步骤进行:
1)一维信号的小波包分解。采用Shannon信息熵最优化选择基函数,选取使小波包系数熵最小基函数为最优基函数[10],确定分解层次N后对信号进行小波包分解。
2)小波包分解系数的阈值量化。通过小波包频带排序重组,得到各频段的小波包分解系数。选择改进的阈值及其阈值函数对小波包系数进行阈值处理。
3)小波包重构。利用阈值处理后的小波包系数进行小波重构。
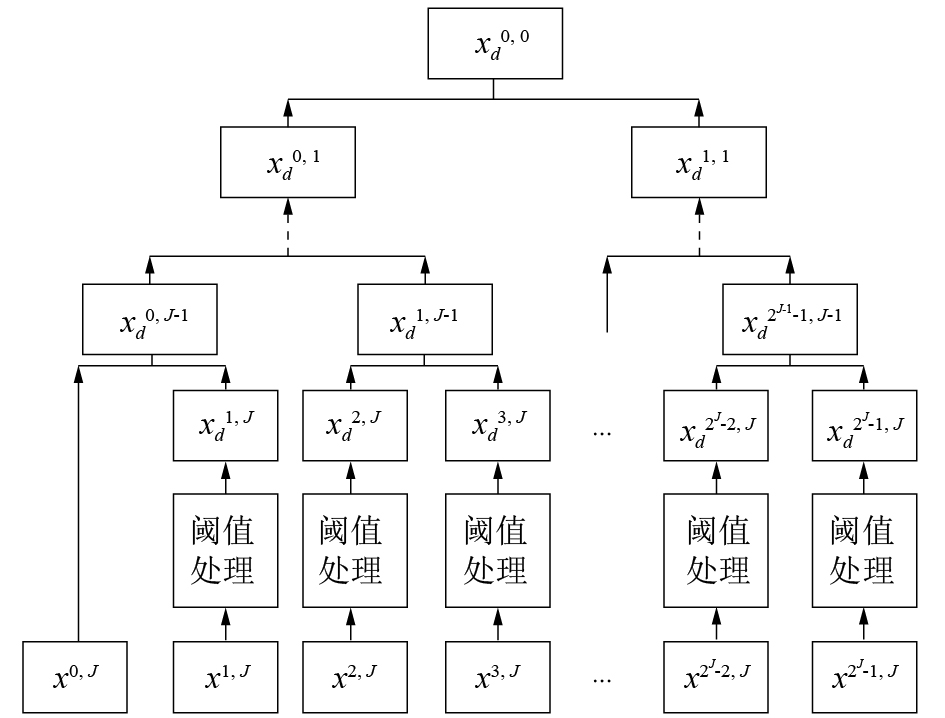
经频率重排后的小波包系数阈值处理降噪如图4所示。
|
Download:
|
| 图 4 小波包系数阈值处理算法框图 | |
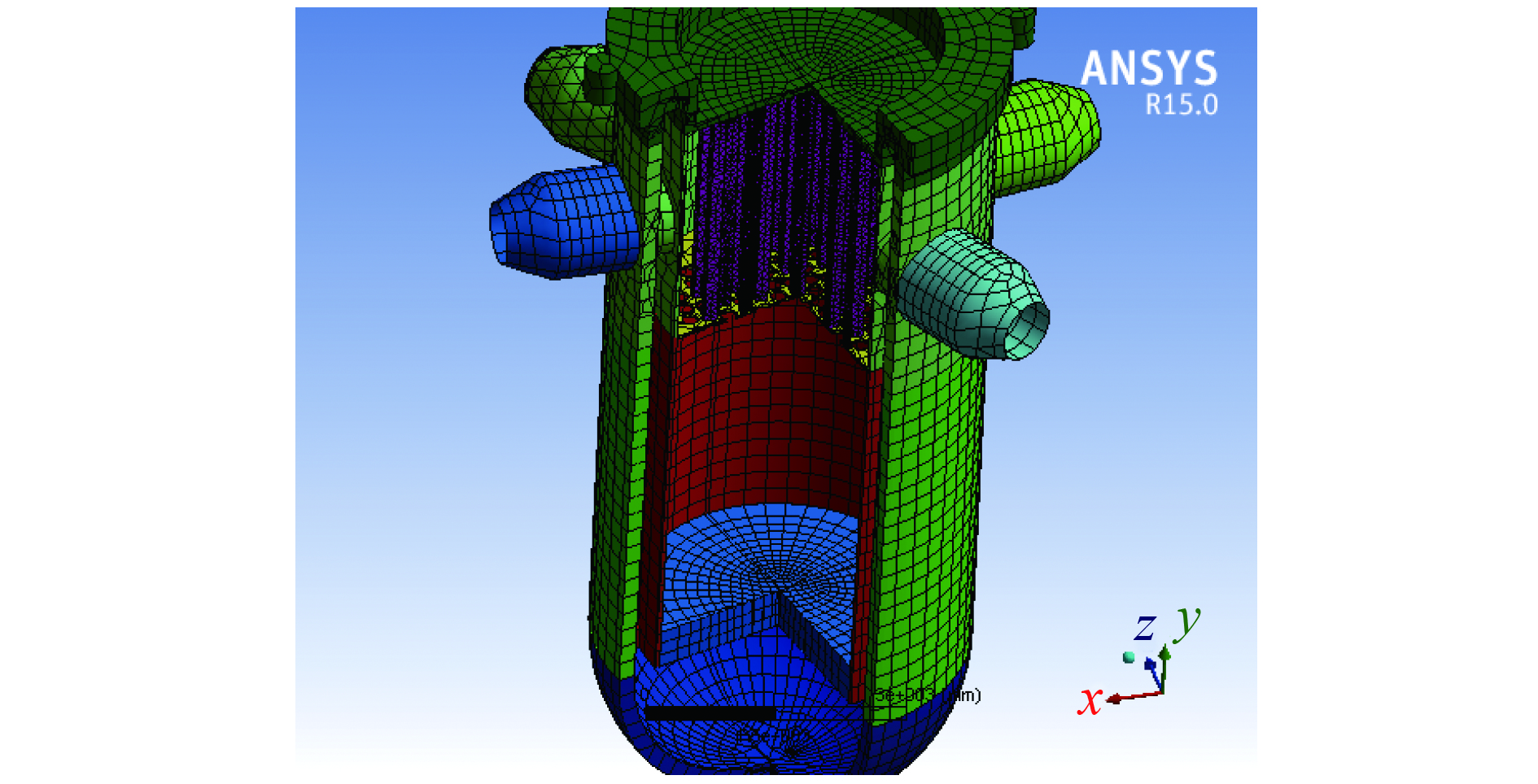
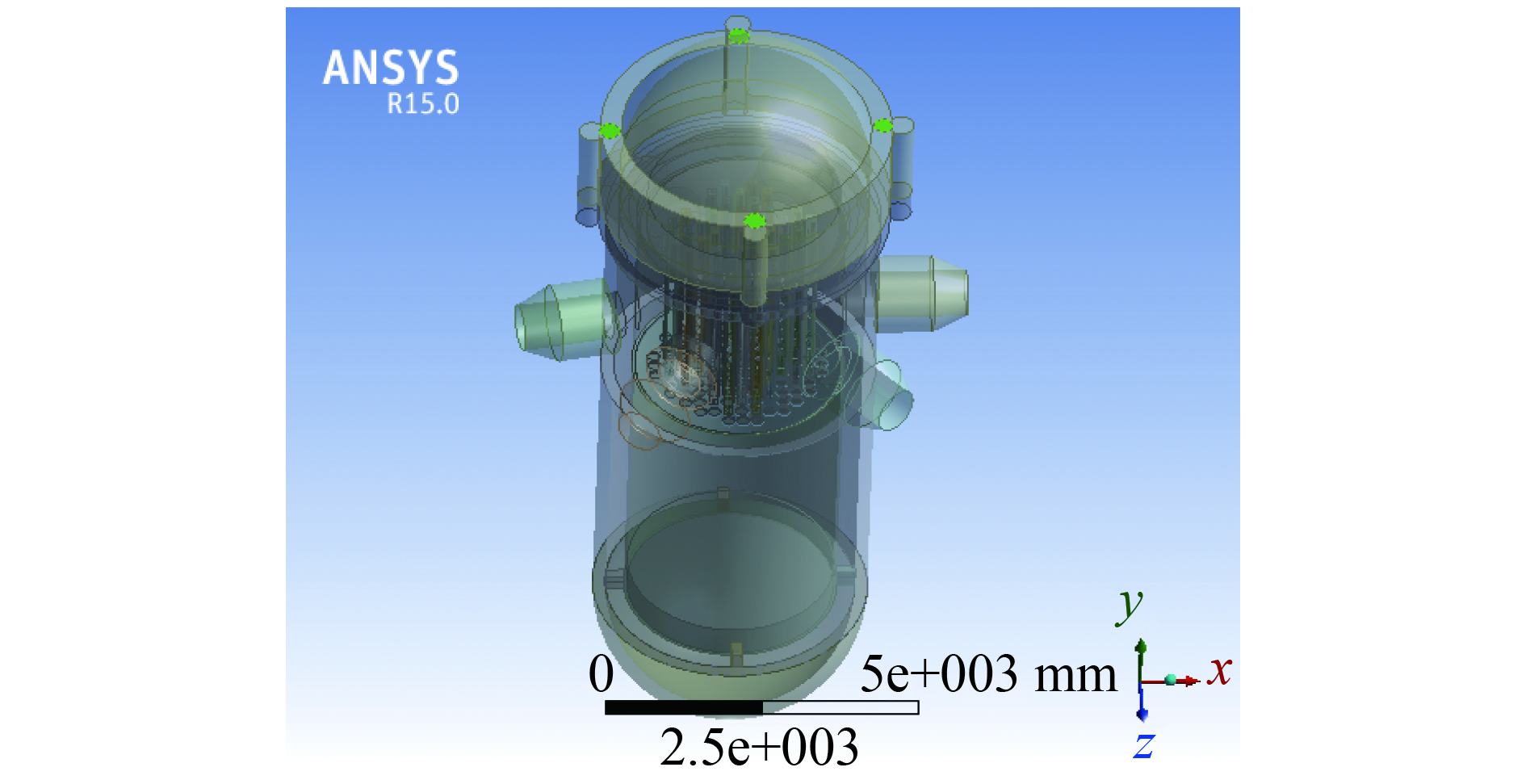
考虑到反应堆内部结构复杂、网格量庞大,对模型进行简化。由于该模型用于流致振动信号仿真计算,因此采用全尺寸比例模型。建模对象主要包括压力容器、堆芯吊篮、控制棒导向筒等流致振动重点关注部位。6个冷却剂进出管嘴中,每条环路的进出口管嘴相隔50°夹角。吊篮通过法兰固定在压力容器的内壁凸台上,其底部由压力容器内壁下部4个径向定位键约束。堆芯上板开设有37组导向筒,另外还有84个圆孔供冷却剂从堆芯流出。模型主要结构参数如表1所示[11]。模型网格划分如图5所示。
|
|
表 1 模型主要结构参数 |
|
Download:
|
| 图 5 有限元模型网格 | |
抽取吊篮外侧环腔流体域并进行网格划分,在Fluent模块中选择大涡模拟湍流模型对流体进行计算[12]。由于吊篮振动幅度较小,文中仅考虑单向流固耦合。设置流场入口速度为17 m/s,出口为open-flow边界条件,其他界面为壁面。在Solution Methods中采用SIMPLE算法,在Monitor中设置监测冷却剂入口冲击吊篮附近处脉动压力。网格最大尺寸30.0 mm,网格量为2×106,选择时间步数为1 000步每秒,计算5 s内流体流动情况。流体部分网格以及测点脉动压力时程变化曲线如图6、7所示。

|
Download:
|
| 图 6 吊篮外侧流体部分网格 | |

|
Download:
|
| 图 7 脉动压力时程 | |
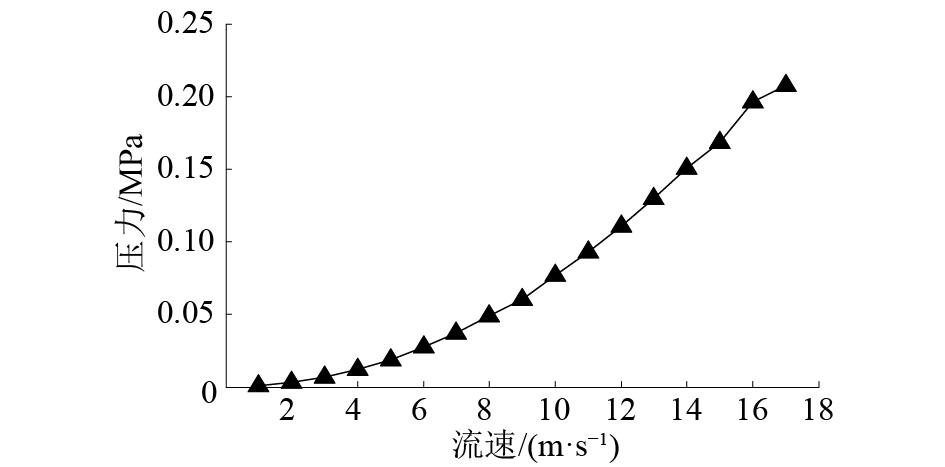
由图7可知,计算达到稳定后,脉动压力稳定在约0.207 2 MPa。同时计算发现冷却剂入口处对吊篮冲击力较大,该位置横向流动较为显著,结论与文献[13]相符。因此,在进行吊篮正常状态下流致振动模拟时,参考文献[1]中方法,在吊篮入水口附近施加相应叠加白噪声的脉动压力。图8给出了不同冷却剂入口速度下的脉动压力变化曲线,速度越大,压力越大,其关系近似成抛物线规律。因此,与文献[14]类似,可将压力脉动拟合成速度的函数。在可由冷却剂速度表示的事故工况下堆内构件流致振动模拟时,可以根据拟合的函数来推测堆内构件主要冲击部位流体的激励。
|
Download:
|
| 图 8 不同流速下冷却剂入口附近吊篮压力变化 | |
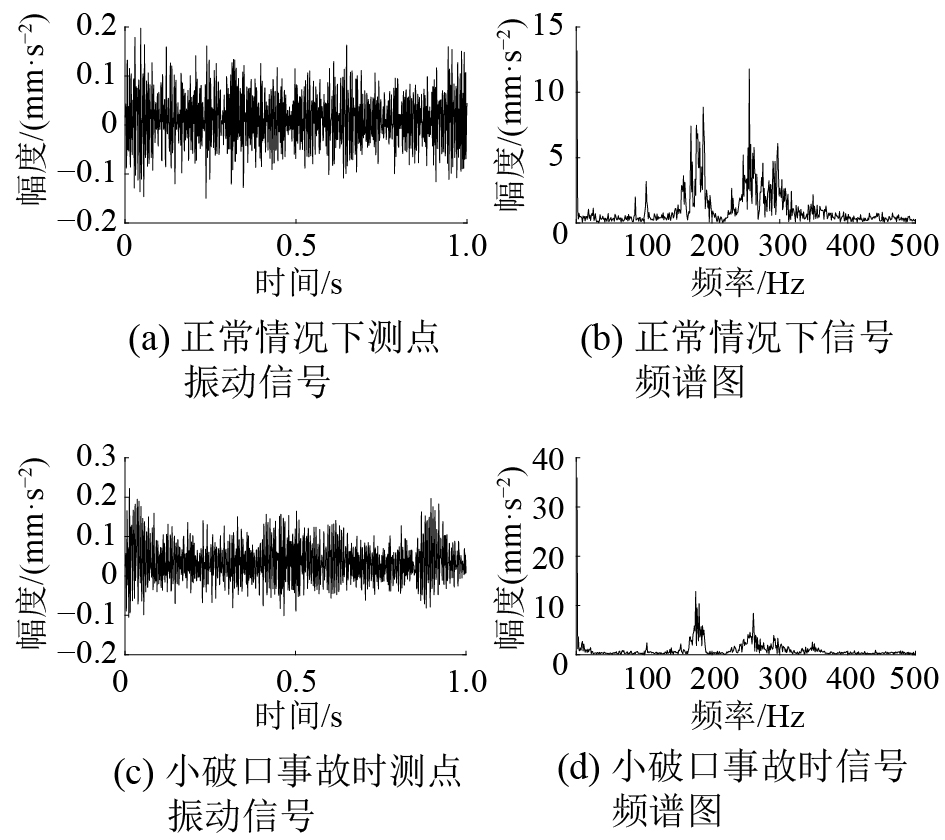
在Fluent模块中分别得出正常和事故情况下的脉动压力参数,将其作为初始条件输入Transient Structural模块中。流固耦合中对固体结构施加时间−历程载荷有3种方法,分别是利用函数方程、表格输入、多载荷步施加法[12],本文采用表格输入的方法施加载荷。测点布置参考实际振动监测系统传感器布置,设置在压力容器顶盖0°、90°、180°、270°这4个位置上[1],如图9所示。计算1 s内结构的流致振动响应,监测得到的测点处加速度信号如图10所示。
|
Download:
|
| 图 9 模型测点 | |
|
Download:
|
| 图 10 正常及小破口状态下测点加速度振动信号及其频谱 | |
为验证改进小波包去噪算法的有效性及优越性,以非平稳信号Doppler、Bumps叠加不同能量的噪声为对象,2种信号采样点数均为1 024点,使Doppler信噪比SNR=5 dB,Bumps信噪比SNR=10 dB。选用小波经典阈值去噪、小波包全局阈值去噪、文献[15]中FMC法及改进的小波包去噪算法对上述仿真信号进行去噪,得到每种方法的去噪对比及其信噪比。其中小波经典阈值去噪为信号经小波分解后,对小波系数进行传统阈值处理并重构,在信号降噪中广泛使用,选用此方法是为了对比小波及小波包对非平稳信号的去噪性能;小波包全局阈值去噪为基于固定阈值准则的小波包去噪方法,选用此方法的目的是与基于多阈值准则的小波包去噪对比效果;文献[15]的FMC法采用多阈值准则,与本文改进方法同时验证基于频率排序去噪的有效性,同时与本文改进阈值函数作为对比,验证其去噪效果。各方法均采用分解层次为3层、“db4”小波作为小波基,统一参数以充分验证方法的有效性。各种方法的去噪效果对比如图11、12所示。由图11、12可以看出,应用小波经典阈值去噪、小波包全局阈值去噪、文献[15]FMC方法以及本文改进的小波包阈值去噪方法,将Doppler信号SNR=10 dB分别提升至16.03、16.87、17.30、17.52 dB,将Bumps信号SNR=5 dB分别提升至12.37、13.18、15.00、15.70 dB。针对不同非平稳信号,文中改进的小波包算法去噪后信噪比均最大,去噪效果最好。通过分析可以得出几点结论:
1)基于小波变换的阈值去噪方法都可以不同程度地去噪,因此可以应用于反应堆堆内构件的振动监测领域;
2)小波包全局阈值算法去噪效果优于小波经典阈值算法,表明小波包去噪的整体精度高于小波去噪;
3)FMC法和文中改进算法均采用多阈值准则,且去噪效果均优于小波包全局阈值去噪,说明基于多阈值准则的去噪方法能够提高去噪精度;
4)相比于FMC法中方法,本文去噪算法改进了阈值函数,且去噪效果优于FMC算法,证明了基于改进阈值函数的小波包去噪方法的有效性。

|
Download:
|
| 图 11 含噪声Doppler信号去噪效果对比 | |

|
Download:
|
| 图 12 含噪声Bumps信号去噪效果对比 | |
在验证改进小波包去噪算法在实际流致振动信号处理中的有效性研究中,为模拟工程实际中传感器接收的信号,读取一组仿真得到的正常状态下吊篮流致振动信号中加入白噪声,使得信噪比SNR=5 dB,将其作为分析对象,进行改进去噪算法有效性验证。原始振动信号、加噪信号及其傅里叶变换幅频曲线如图13所示。

|
Download:
|
| 图 13 加噪前后信号及其幅频曲线对比 | |
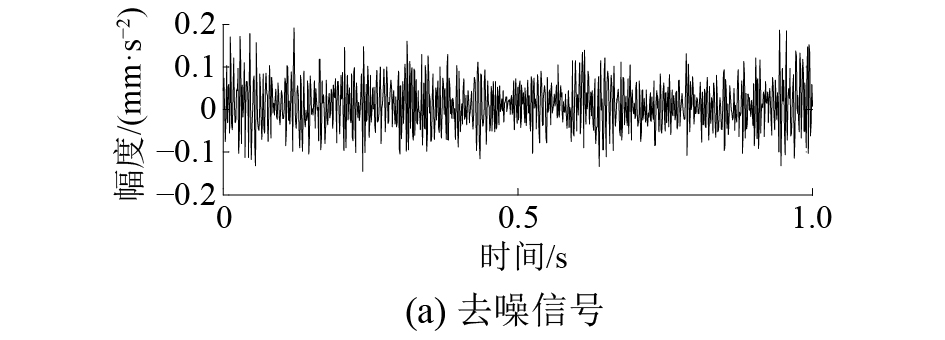
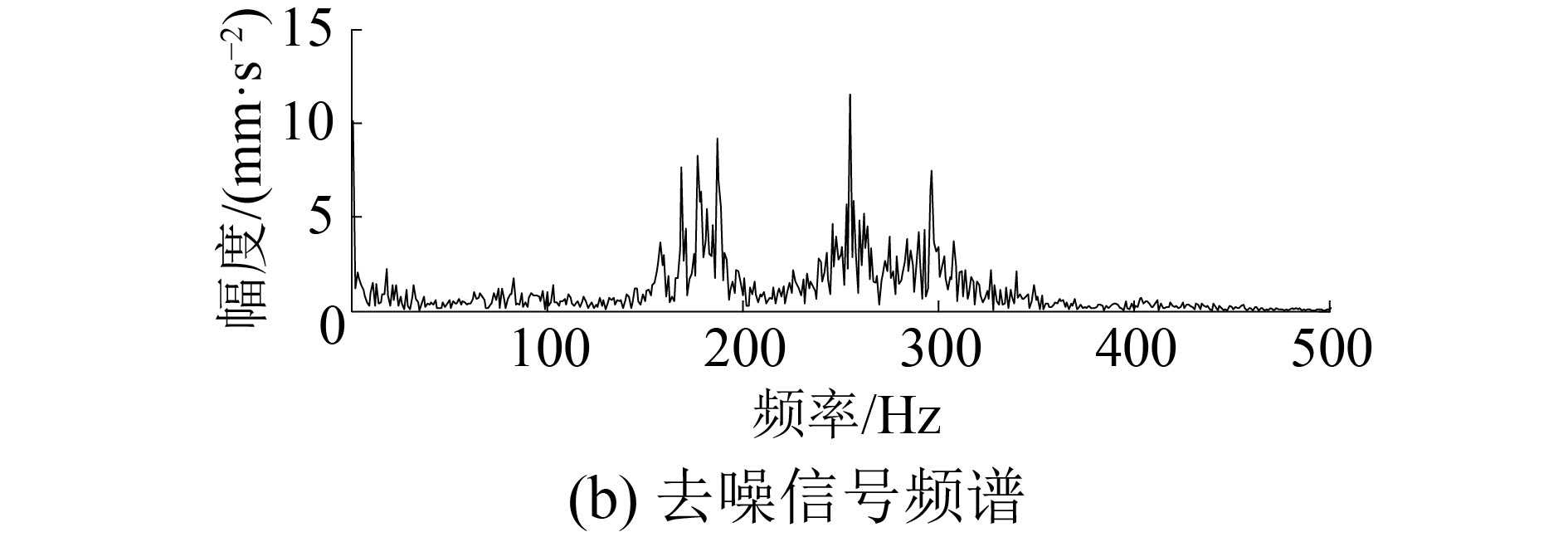
由图13可以看出,在低信噪比情况下,原始时域信号受到了噪声的污染,且信号在整个频域范围内都受到了噪声的干扰,不利于后续的特征提取。幅频曲线表明,振动信号在全频域中100、180、270 Hz等附近处有能量聚集,且各频率对应幅值均能反映出测点的工作状态。实际工程希望通过对探测器所获信号进行特征提取,反映出堆内构件的工作状态,因此,在进行去噪时需要保留整个频域信息以最大限度还原出测点实际振动情况,选取改进的小波包阈值去噪方法。首先对小波基函数进行选取,不同的小波包基函数对信号进行分解得到的小波包系数的熵有很大区别[10]。经计算发现,在常用小波包基函数中,采用sym2作为基函数时得到的熵值最小,因此选择sym2作为分析该振动信号的小波包基函数。采用改进阈值准则,同时应用改进阈值函数进行阈值量化,其去噪信号及其频谱如图14所示。同时,还应用小波包全局阈值及FMC算法进行了去噪,并计算其均方根误差(RMSE),效果对比如表2所示。
|
Download:
|
| 图 14 | |
|
Download:
|
| 图 14 去噪信号及其频谱 | |
|
|
表 2 去噪效果比较 |
由表2对比可以看出,文中改进的阈值方法去噪后均方根误差最小,信噪比最大,其去噪效果最好。由此可知,对于中高频率成分较多的振动信号,在阈值选取方面,采用多阈值处理相对于全局阈值去噪,不但可以充分去除噪声,而且高低频信息也能很好地保留;且改进的阈值函数较常用的软阈值函数去噪效果更好,有效提高了信噪比,充分验证了改进的小波包阈值去噪算法在堆内构件流致振动信号去噪中的可行性及有效性。
4 结论本文研究了一种压水堆堆内构件流致振动的信号去噪算法,着重探究了该方法的理论应用及工程仿真下的适用性。同时也研究了堆内构件在冷却剂环境下的流致振动特性,包括吊篮外侧流体域的压力以及堆内构件在流体激励下的加速度响应计算,得出结论如下:
1)采用大涡模拟湍流模型计算吊篮环腔流场,在入口速度为17 m/s时,吊篮在冷却剂入口附近脉动压力约为0.207 2 MPa,且其脉动压力随速度变化近似成抛物线增长规律,可为由入口速度表征的事故工况下流体激励数据提供参考。
2)通过理论分析及工程仿真应用,可得出传统小波及小波包对去除振动信号噪声均能提高一定量的信噪比,但传统小波去噪及小波包全局去噪并未充分考虑噪声在频带间的分布。针对核动力装置振动信号特征,应用文中改进多阈值及阈值函数方法进行去噪,相比传统软阈值函数,既能保证去噪信号的连续性又能快速减小恒定偏差,可以得到更好的去噪效果。
| [1] |
吕阳. 基于振动信号的堆内构件监测系统研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
( 0) 0)
|
| [2] |
喻丹萍, 胡永陶. 秦山核电二期工程反应堆堆内构件模型流致振动试验研究[J]. 核动力工程, 2003, 24(2增刊): 109-113. ( 0) 0)
|
| [3] |
喻丹萍, 马建中, 席志德, 等. 反应堆堆内构件流致振动试验研究综述[J]. 核动力工程, 2016, 37(S2): 47-51. ( 0) 0)
|
| [4] |
CHOI Y, LIM S, KO B H, et al. Dynamic characteristics identification of reactor internals in SMART considering fluid-structure interaction[J]. Nuclear engineering and design, 2013, 255: 202-211. DOI:10.1016/j.nucengdes.2012.10.010 ( 0) 0)
|
| [5] |
RAO A R. Experimental and analytical dynamic analysis of coolant channel and its internals of Indian 540MWe PHWR reactor[J]. Nuclear engineering and design, 2011, 241(3): 582-589. DOI:10.1016/j.nucengdes.2010.04.016 ( 0) 0)
|
| [6] |
MALLAT S G. A theory for multiresolution signal decomposition: the wavelet representation[J]. IEEE transactions on pattern analysis and machine intelligence, 1989, 11(7): 674-693. DOI:10.1109/34.192463 ( 0) 0)
|
| [7] |
李彬. 时频分析技术在AP1000特殊监测系统中的应用研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
( 0) 0)
|
| [8] |
康玉梅, 陈依珂, 胡淑婷, 等. 基于小波包分数幂阈值的声发射去噪研究[J]. 有色矿冶, 2016, 32(5): 16-20. DOI:10.3969/j.issn.1007-967X.2016.05.006 ( 0) 0)
|
| [9] |
DONOHO D L, JOHNSTONE I M, Kerkyacharian G, et al. Wavelet shrinkage: asymptopia[J]. Journal of the royal statistical society. Series b (methodological), 1995, 57(2): 301-369. ( 0) 0)
|
| [10] |
杨波, 夏虹, 张晓玉. 基于自适应阈值的小波包在松动部件信噪分离中的研究[J]. 原子能科学技术, 2014, 48(11): 2045-2050. DOI:10.7538/yzk.2014.48.11.2045 ( 0) 0)
|
| [11] |
欧阳予. 秦山核电工程[M]. 北京: 原子能出版社, 2000.
( 0) 0)
|
| [12] |
许京荆. ANSYS Workbench工程实例详解[M]. 北京: 人民邮电出版社, 2015.
( 0) 0)
|
| [13] |
席志德, 陈炳德, 李朋洲. 大涡模拟在计算反应堆吊篮流体激励力中的应用[J]. 核动力工程, 2008, 29(3): 28-31. ( 0) 0)
|
| [14] |
郭涛, 张涛, 赵威. 基于LES的直管流致振动分析[J]. 工程力学, 2012, 29(10): 340-346. ( 0) 0)
|
| [15] |
章浙涛, 朱建军, 匡翠林, 等. 小波包多阈值去噪法及其在形变分析中的应用[J]. 测绘学报, 2014, 43(1): 13-20. ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


