结构安全监测可用于对船舶的重要结构、敏感部位及船体的运动状态进行实时监测,并通过历史监测数据对当前海况下未来一段时间的船舶结构应力进行预测,为船舶决策者提供真实可靠的最新数据,为保障船上人员及物资安全提供科学依据[1]。
由于结构应力信号是典型的非平稳信号,直接用SVM进行预测效果不是很理想,所以考虑先对结构应力信号进行时频分析,然后再结合SVM,使得预测效果更优。对于非平稳信号的处理[2],先后提出了以经验模态分解(empirical mode decomposition, EMD)为核心的希尔伯特黄变换(Hilbert-Huang trans-form, HHT)和集合经验模态分解(ensemble empirical mode decomposition, EEMD)。EMD算法分解的稳定性不高,而且还会出现模态混叠的问题[3-4]。而EEMD虽然抑制了模态混叠的问题,但同时会引入噪声的低频成分混杂在相应频率的模态本征函数(intrinsic mode function,IMF)[5]分量中的问题。针对EEMD方法出现的问题,Yeh等[6]提出互补集合经验模态分解(CEEMD)。由于SVM具有良好的泛化能力和学习能力,克服了模型选择及非线性问题,解决了会出现局部最优解的问题,避免了“维数灾难”的出现,并且具有训练时间短、使用方便等优点[7-8],可成功应用到分类、识别及回归预测中。
本文将利用CEEMD方法对信号进行时频分解再结合SVM完成对结构应力的预测。
1 传感器的选择及布置 1.1 传感器的选择船舶结构应力监测对传感器的可靠性、使用寿命、物理量传递效率和测量精确度有着很高的要求。所以经过综合分析考虑选择管式和埋入式封装光纤光栅传感器相对而言更加适用于船舶结构应力监测。
1.2 传感器的布置无论是民船还是军船,船舶的结构复杂,空间紧凑,提供给船舶结构监测系统的传感器布置空间十分狭窄。目前对一艘舰船实施结构监测大概需要几十个或上百个监测点,传感器的排布是其主要的难点之一[9]。
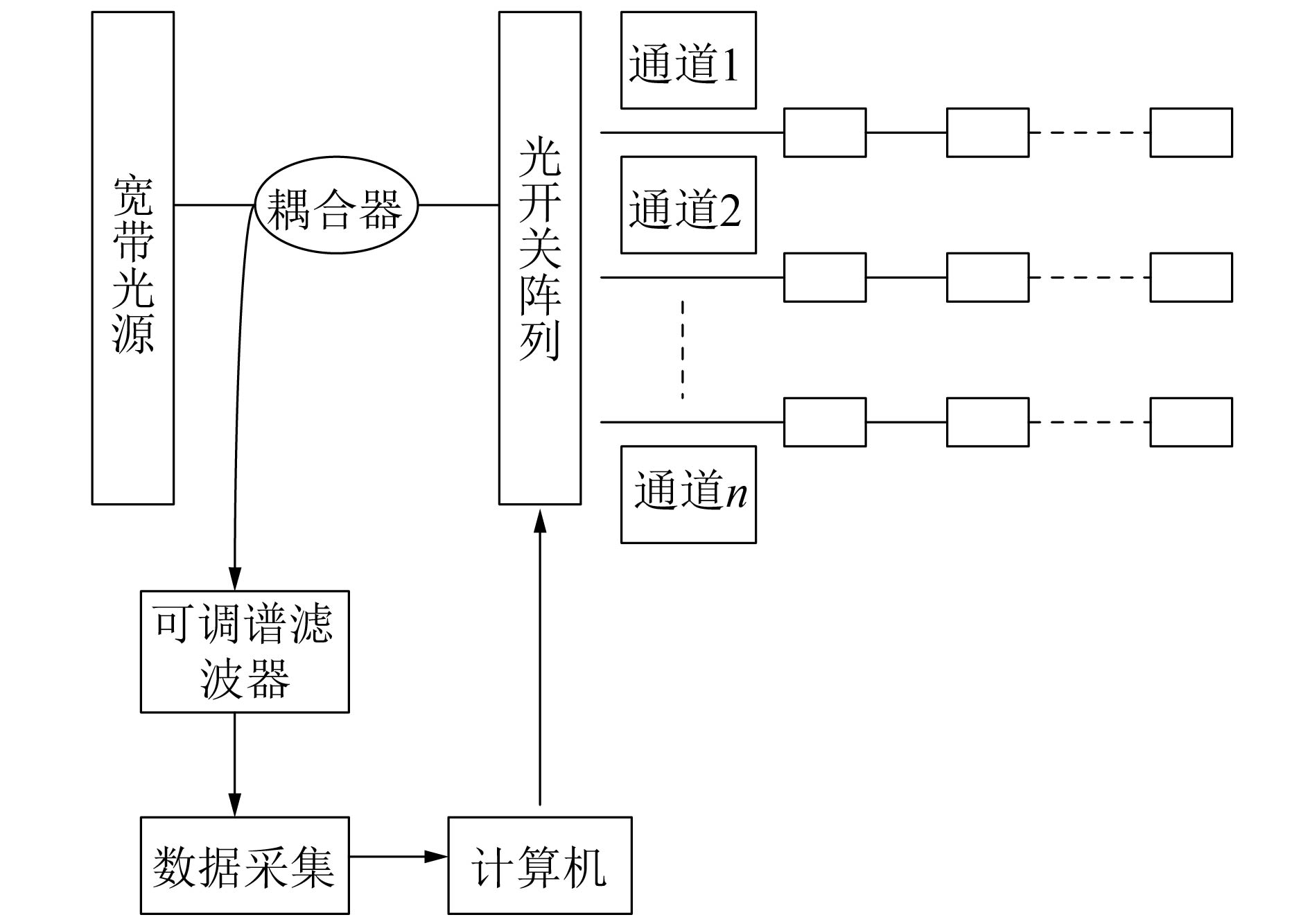
单独的空分复用、波分复用和时分复用技术都有其自身的不足,难以满足船舶结构应力监测的需求[10]。本文结合波分复用与空分复用技术,将全船的监测传感器进行分组:同一船舱内的传感器之间采用波分复用,不同船舱或甲板之间的传感器则采用空分复用的方法;不同波长的传感器采用波分复用方式串联,再利用空分复用方式并联。这种方法在充分利用了光源的同时有效地减小了传感器间的串扰。波分复用和空分复用结合的混合复用系统如图1所示。
|
Download:
|
| 图 1 波/空分复用混合复用技术结构示意 | |
CEEMD分解建立在EMD分解的基础上,主要包括3个步骤:
1)向原始信号中加入n组正负成对的辅助白噪声,这样就形成了2n个合成的信号。
| $\left[ {\begin{array}{*{20}{c}} {{S_1}} \\ {{S_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&1 \\ 1&{ - 1} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} X \\ N \end{array}} \right]$ |
式中:X表示原始信号;N表示辅助白噪声;
2)对2n个信号分别进行EMD分解,每个信号得到一组IMF分量,其中第j个信号的第k个IMF分量可表示为
3)通过多组分量合成方法得到原信号的第k个IMF的大小为
| ${C_k} = \frac{1}{{2n}}\sum\limits_{j = 1}^{2n} {{C_{jk}}} $ |
式中
本文选择的是改进的基于K次交叉验证法的网格搜索法。
1)K次交叉验证法
将原始数据平均分成K组,将每组数据分别进行一次验证集,其余的K−1组数据作为训练集,这样会得到K个模型,取这K个模型最终的验证集的分类准确率的平均数作为此K次交叉验证下分类器的性能指标。
2)改进的网格搜索法
针对网格搜索法[11]寻优时间过长的问题,提出一种改进的网格搜索法。
首先采用折中法获得的动态步长进行粗搜,即将选取范围的一半作为步长,利用K次交叉验证法计算这2组的分类准确率,选取准确率最高的一组作为新的范围,重复上述折中粗搜,直到寻得了局部最优参数。
然后,在寻得了局部最优参数之后,再在这组参数附近选择一个小区间,采用传统方法中的小步距进行二次精搜,找到最终的最优参数。
如果参数区间选择合理,那么改进的网格搜索法能够搜索出全局最优的参数,但由于这个区间的选择含有比较多的经验成分,所以通常情况下只能得到局部最优的参数。
2.3 CEEMD和SVM的预测模型本文将改进的CEEMD和SVM结合。具体步骤如下:
1)将原始序列先经过CEEMD的分解,得到若干IMF分量,获取对原信号贡献率最大的IMF分量,然后对各IMF分量进行提取,作为训练样本。
2)对SVM的核函数、错误惩罚参数C和核函数宽度G等参数进行选择。
其中常用的SVM的核函数如下:
a)线性核函数
| ${e_{\max }} = \max \left| {\frac{{{Y_i} - {Y_i}'}}{{{Y_i}}}} \right|$ |
b)多项式核函数(Polynomial)
| $K\left( {{x_i},{x_j}} \right) = {\left[ {\left( {{x_i},{x_j}} \right) + 1} \right]^d}$ |
c)径向基核函数(radial basis function, RBF)
| $K\left( {{x_i},{x_j}} \right) = \exp \left( { - \frac{{{{\left\| {{x_i} - {x_j}} \right\|}^2}}}{{2{\delta ^2}}}} \right)$ |
d)双曲正切核函数(Sinmoid)
| $K\left( {{x_i},{x_j}} \right) = \tanh \left[ {a\left( {{x_i} \cdot {x_j}} \right) + b} \right]$ |
RBF核函数的特征空间维数为无限维,并且其搜索查找为全网络搜索,当输入样本个数有限时,其特征空间为线性可分,在没有先验信息时,比其他核函数的总体性更好。综上,SVM的核函数选择RBF对样本数据进行非线性映射。
3)利用改进的基于K次交叉验证法的网格搜索法寻找最优的C和G。
4)在确定核函数、C、G之后,进行预测模型的训练。
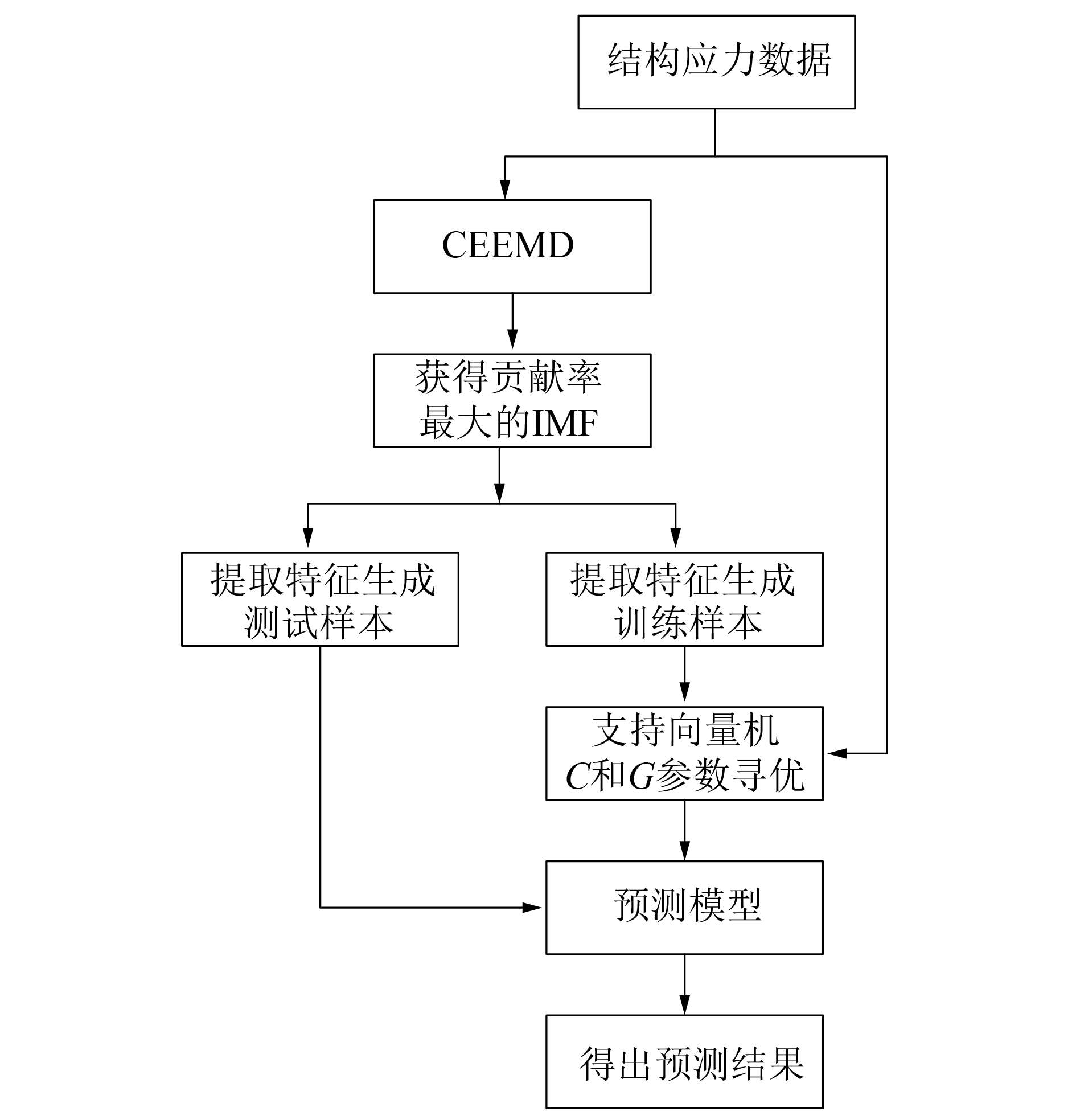
5)利用测试样本建立测试模型。具体预测模型的示意图如图2所示。
|
Download:
|
| 图 2 预测模型的示意 | |
利用平均绝对百分比误差emap、最大误差emax、平均误差ea等预测指标对预测模型进行分析[12-13]:
| ${e_{{\rm{map}}}} = \frac{1}{m}\sum\limits_{i = 1}^m {\frac{{{Y_i} - {Y_i}'}}{{{Y_i}}}} $ |
| ${e_{\max }} = \max \left| {\frac{{{Y_i} - {Y_i}'}}{{{Y_i}}}} \right|$ |
| ${e_a} = \frac{1}{m}\sum\limits_{i = 1}^m {\left( {{Y_i} - {Y_i}'} \right)} $ |
式中:
对于获得的结构应力信号,利用时间窗进行截取数据进行分析,对于滑窗中的数据进行CEEMD分解,分解得到的IMF分量,选择其贡献率最大的分量,对该分量进行特征提取。
本文中选用边际谱比例、分量相对幅度、样本熵[12]、能量熵等4个特征对船舶结构应力数据进行特征提取。
这里取了20组数据,将采集的结构应力信号各特征变量进行分类,结果如图3所示。

|
Download:
|
| 图 3 不同特征变量分类结果 | |
实验证明,利用上述特征进行特征提取,预测效果可达到最优效果。
3.2 CEEMD和SVM预测实验本文将某船模总长12.48 m、船宽1.568 m、设计吃水0.404 m、排水量4.672 t、航速6 kn,在高、低及混合海况下实验得到的10 h数据作为实验数据。采用滑窗对数据进行提取,采样频率为20 Hz,窗口长度为5 min,即滑窗可容纳的数据量为6 000。利用前5 min的数据进行特征提取来训练预测模型,预测不同海况下所对应的后15 s即将发生的结构应力数据。
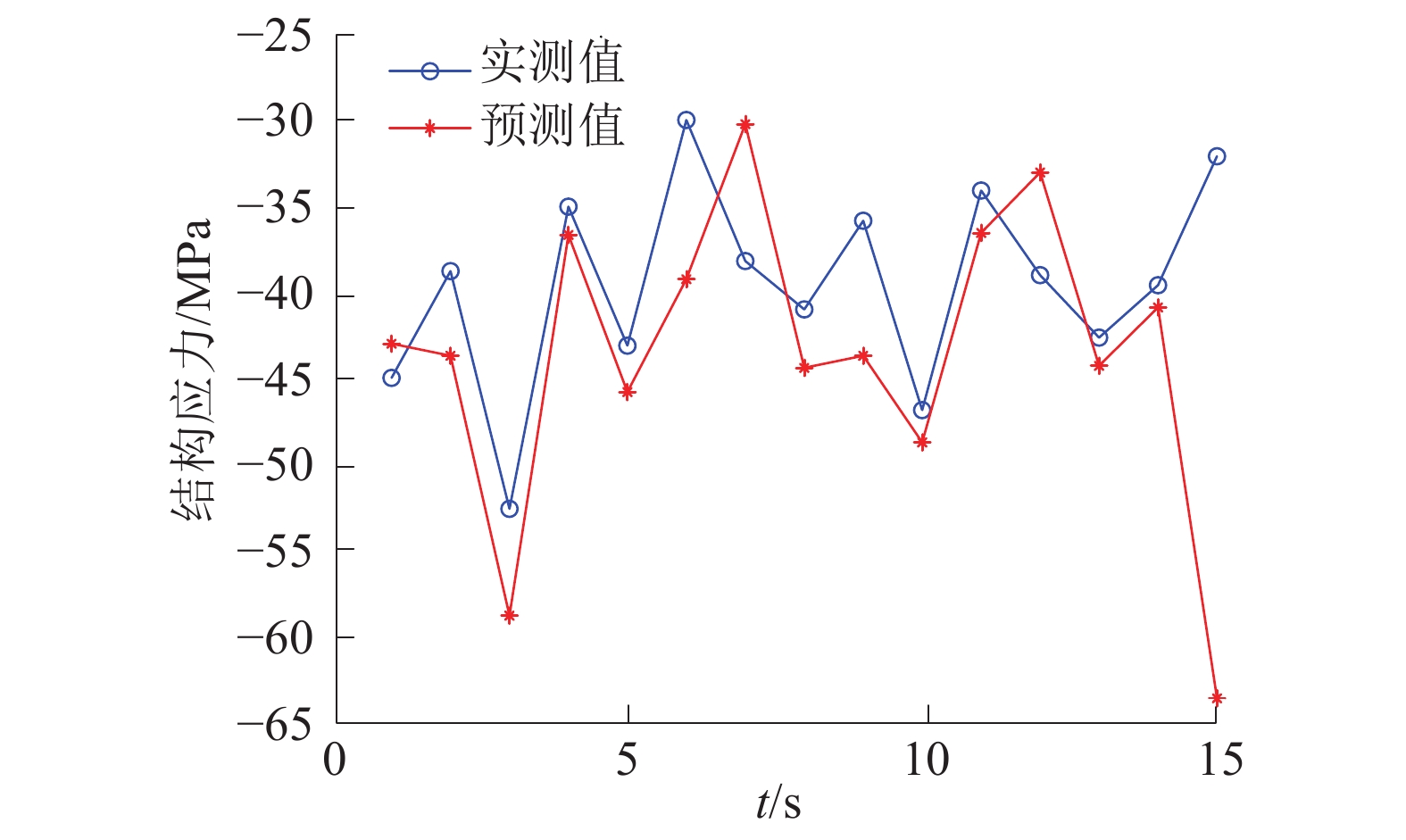
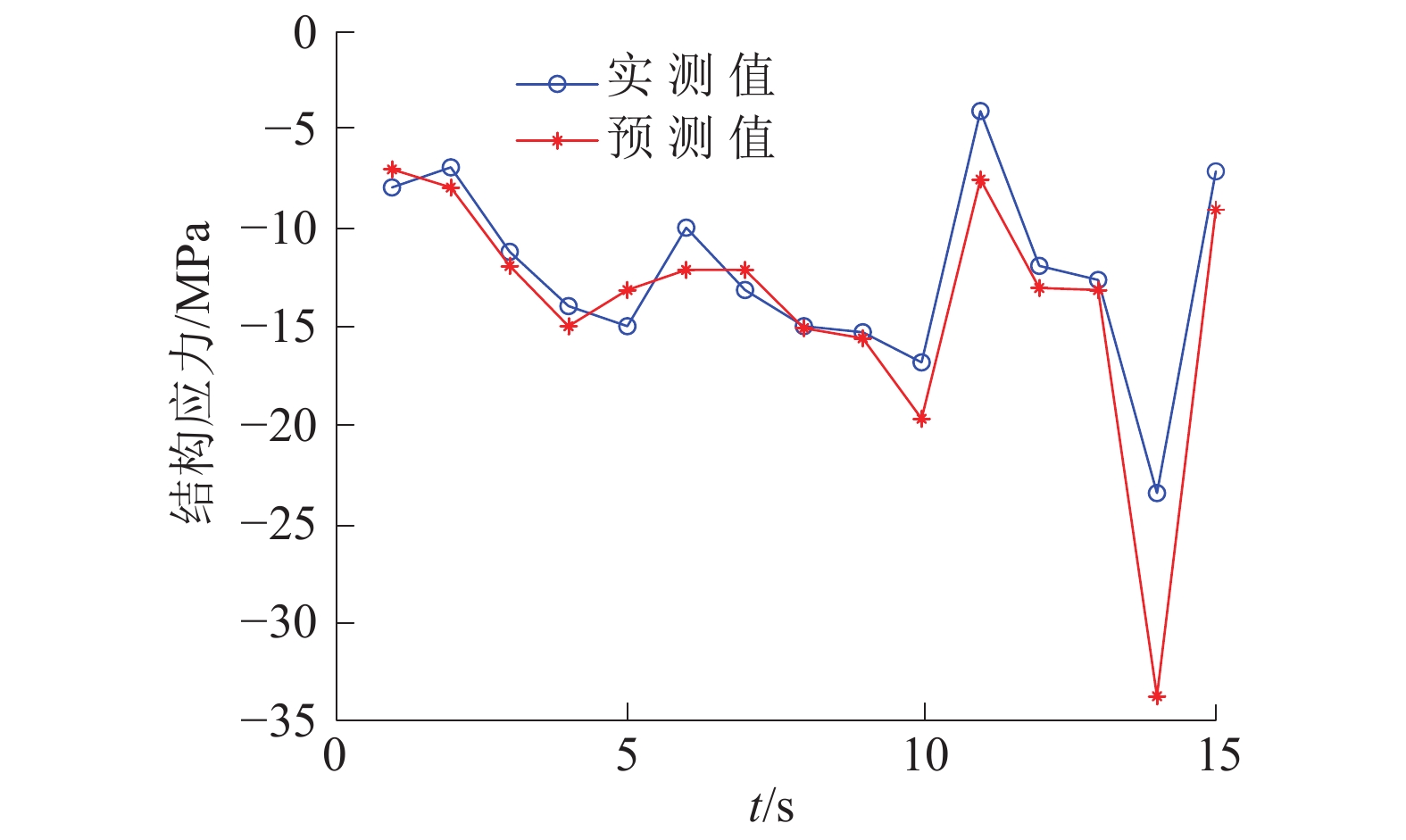
利用上述模型分别在高海况、低海况及混合海况中进行预测,结果如图4~6所示。
|
Download:
|
| 图 4 高海况下模型预测结果 | |
|
Download:
|
| 图 5 低海况下模型预测结果 | |

|
Download:
|
| 图 6 混合海况下模型预测结果 | |
不同海况下,该预测模型在不同海况中所对应的误差分析如表1所示。
|
|
表 1 不同海况的预测性能评价 |
为了验证本文所采用模型的优越性,在混合海况情况下,利用SVM、EMD+SVM、EEMD+SVM等模型进行预测研究,将其效果与本文提出的预测模型进行比较。混合海况下多种模型预测结果如图7所示。各模型预测误差结果分析如表2所示。

|
Download:
|
| 图 7 混合海况下多种模型预测结果对比 | |
|
|
表 2 各模型预测性能评价 |
从表2中可以看出,对比其他的预测方法,本文提出的CEEMD+SVM预测方法的平均绝对百分比误差为17.5%,较其他的预测模型具有更好的预测精度。同时从图7可以看出,本文提出的预测模型能够很好地预测出结构应力的变化趋势,验证了该方法的有效性。
4 结论本文进行如下工作:
1)考虑船舶监测系统的实际应用需求,完成对传感器类型及布置方法的讨论,综合考虑选用管式和埋入式封装光纤光栅传感器,通过波分复用和空分复用结合的混合复用的方法来满足监测过程中精度、传输效率及传感器间干扰的问题。
2)构建CEEMD和SVM预测模型,对SVM常用的参数寻优方法——网格搜索法,进行改进。
3)利用预测模型对高、低及混合海况情况下的船舶结构应力进行预测。
4)对于构建的预测模型,从以下两方面验证其准确性:一方面通过测试样本验证模型对高、低及混合海况的适应性,实验结果表明,该模型可以对3种情况下的结构应力进行较好的预测;另一方面,通过对SVM、EMD+SVM、EMD+SVM等模型的预测结果进行对比,结果表明,CEEMD+SVM预测模型对结构应力的预测效果及预测误差要优于其他几种预测模型。
| [1] |
杨帆. 舰船破舱稳性实时计算方法研究[D]. 大连: 大连理工大学, 2006: 12.
( 0) 0)
|
| [2] |
沙丹丹. 基于HHT和SVM的砰击检测算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2015: 3.
( 0) 0)
|
| [3] |
HUANG N E, SHEN Zheng, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the royal society A: mathematical, physical and engineering sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 ( 0) 0)
|
| [4] |
LEI Yaguo, LIN Jing, HE Zhengjia, et al. A review on empirical mode decomposition in fault diagnosis of rotating machinery[J]. Mechanical systems and signal processing, 2013, 35(1/2): 108-126. ( 0) 0)
|
| [5] |
WU Zhaohua, HUANG N. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in adaptive data analysis, 2008, 1(1): 1-41. ( 0) 0)
|
| [6] |
YEH J R, SHIEH J, HUANG N. Complementary ensemble empirical mode decomposition: a novel noise enhanced data analysis method[J]. Advances in adaptive data analysis, 2010, 2(2): 135-156. DOI:10.1142/S1793536910000422 ( 0) 0)
|
| [7] |
GUO Guodong, LI S Z. Contents-based audio classification and retrieval by support vector machines[J]. IEEE transactions on neural network, 2003, 14(1): 209-215. DOI:10.1109/TNN.2002.806626 ( 0) 0)
|
| [8] |
王军栋, 齐维贵. 基于EDM-SVM的江水浊度预测方法研究[J]. 电子学报, 2009(10): 2130-2133. DOI:10.3321/j.issn:0372-2112.2009.10.004 ( 0) 0)
|
| [9] |
张金涛. 光纤光栅传感器复用关键技术的研究与应用[D]. 合肥: 合肥工业大学, 2015.
( 0) 0)
|
| [10] |
曲健, 陈红岩, 刘文贞, 等. 基于改进网格搜索法的支持向量机在气体定量分析中的应用[J]. 传感技术学报, 2015, 28(5): 774-778. DOI:10.3969/j.issn.1004-1699.2015.05.027 ( 0) 0)
|
| [11] |
QIAO Meiying, MA Xiaoping, LAN Jianyi, et al. Time-series gas prediction model using LS-SVR within a Bayesian framework[J]. Mining science and technology, 2011, 21(1): 153-157. DOI:10.1016/j.mstc.2010.12.012 ( 0) 0)
|
| [12] |
吕震宇. 基于ELMD和KNN分类器的船体砰击载荷检测算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


