2. 哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001;
3. 福建省交通建设工程试验检测有限公司,福建 福州 350000
2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China;
3. Fujian traffic construction engineering test & Inspection Co., Ltd., Fuzhou 350000, China
季节性冻土地区渠道衬砌冻胀破坏现象普遍,给渠系工程的正常使用带来了严重影响,缩短了渠道衬砌的正常使用寿命,对工程后期的维护管理带来了严重的影响,同时增加了渠道工程的维护费用。因此,深入研究渠道工程的冻胀破坏机理和防冻胀措施,是水利工程中必须解决的工程技术难题。
渠道衬砌的冻胀破坏主要由衬砌体下的土体冻胀引起的,土体冻胀体积发生膨胀对衬砌体有挤压作用,最终会导致衬砌体的冻胀破坏。Ma等[1]利用核磁共振仪测定了不同温度和不同土应力下未冻土的含水量,阐明了渠道冻土产生的温度与土应力间的关系。王正中等[2]通过对大U型渠的冻胀试验的观测,得到了衬砌结构破坏部位的分布规律及成因。张茹[3]用数值模拟的方法研究了大U型混凝土衬砌渠道的冻胀破坏,总结了大U型混凝土渠道衬砌破坏的特点。
本文依托实际工程项目对矩型渠进行冻胀数值模拟,对比不同掺量EPS颗粒轻质土垫层情况的冻胀情况,分析该保温材料的保温效果;再对矩型渠进行室内模型试验,分析土体一个冻融循环的冻结特性和冻胀量变化情况。
1 矩型渠衬砌结构冻胀机理 1.1 模型介绍文中矩型渠为薄壁结构,代号UJ,混凝土强度等级为C50,抗冻性为F300。矩型渠及相关产品具有施工周期短、使用寿命长、强度等级高、抗冻性强和工程成本低等特点,可节省工程建设及维修保养投资。
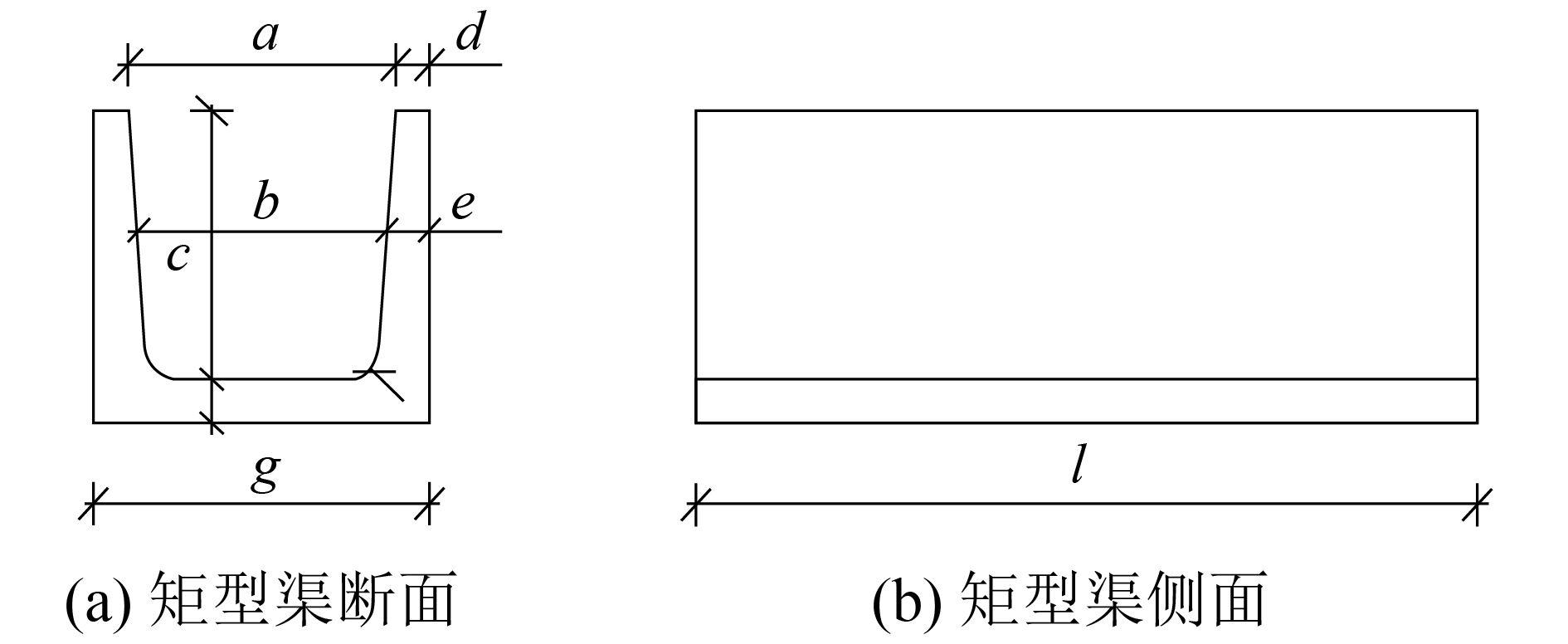
矩型渠综合造价与传统渠道相近,且易于安装、省工省时,能够提高灌溉水利用系数,增加灌溉面积和耕地面积,是目前国内传统混凝土U形渠、梯形渠升级换代产品。本文所述矩型渠长度为2 m,且型号较多可以适应不同工作环境,结构断面示意图见图1,具体技术参数见表1。
|
Download:
|
| 图 1 预制混凝土矩型渠典型断面 | |
|
|
表 1 预制混凝土矩型渠参数 |
渠道衬砌有一定抵抗变形的能力,但随着渠道运行时间的增长,渠道衬砌变形累积到一定程度,直至超过衬砌结构能承受的范围,渠道衬砌发生开裂、隆起等破坏现象,严重影响渠道的使用功能,给国民经济带大巨大损失。
1.2.1 冻土的相变温度场土体冻结和融化的热量迁移是一个极其复杂的过程,一般情况下,冻土中还存在固态冰。热迁移是热传导过程中热量传递的主要部分,可以通过相变热传导方程描述多年冻土的相变温度场[4]。若将热传递过程简化,忽略冰晶体融化时的水汽蒸发耗热量和质量迁移引起的化学势作用,只考虑介质水、土骨架的热传导和水的相态变化这些因素[5],可用偏微分方程表示冻土的温度场:
| $C\frac{{\partial T}}{{\partial t}} = {\rm div}(\lambda {\rm gard}T) + L{\rho _i}\frac{{\partial {\theta _i}}}{{\partial t}}$ |
温度边界条件:
| $T\left| {_s} \right. = {T_b}$ |
或
| $\frac{{\partial T}}{{\partial n}}\left| {_s} \right. = {T_b}$ |
或
| $\left( {\frac{{\partial T}}{{\partial n}} + T} \right)\left| {_s} \right. = {T_b}$ |
温度初始条件:
| $T\left| {_{t = 0}} \right. = {T_0}$ |
式中:T为环境温度的绝对值,K;θi为冰的体积含量,%;ρi为冰容重,kg/m3;C为介质的热容量,kJ/(m3·K);λ为介质导热系数,kJ/(s·m·K);L为介质的相变潜热,kJ/kg;S为边界条件,即
水分迁移主要是由相变温度场引起的,无论是在自然条件还是人工条件下,相变温度场的温度梯度对土体的冻结速率有很大关系,温度梯度越大,土体含水量越大,冻结速率也就越大[6]。对饱和水和非饱和水,其水分迁移方程可表示为
| $\frac{{\partial {\theta _w}}}{{\partial t}} = {\rm div}(k{\rm gard}\phi )$ |
水分初始条件:
| ${\theta _w}\left| {_{t = 0}} \right. = {\theta _0}$ |
式中:θw为水分体积含量,%;φ为水土势;k为介质的导水系数;θ0为初始含水量,%。
1.2.3 冻土的力学特性及本构模型冻土的微观组成和宏观特性有着密切的关系。安维东[7]、刘雄[8]、许强[9]等为了推出符合材料力学土体的本构模型,将冻土视为各向同性的线弹性材料,其表达式为
| ${{\varepsilon }} = {{S}} \cdot {{\sigma }}$ |
式中应力、应变和柔度矩阵分别为
| $ {{\varepsilon }} = \left[ \begin{array}{l}{{{\varepsilon }}_{{x}}}\\{{{\varepsilon }}_{{y}}}\\{{{\varepsilon }}_{{z}}}\\{{{\gamma }}_{{{yz}}}}\\{{{\gamma }}_{{{zx}}}}\\{{{\gamma }}_{{{xy}}}}\end{array} \right],\;\; {{\sigma }} = \left[ \begin{array}{l}{{{\sigma }}_{{x}}}\\{{{\sigma }}_{{y}}}\\{{{\sigma }}_{{z}}}\\{{{\tau }}_{{{yz}}}}\\{{{\tau }}_{{{zx}}}}\\{{{\tau }}_{{{xy}}}}\end{array} \right]$ |
式中各符号意义与弹性力学相一致。
由复合材料力学理论可知,横观同性指的是材料各个方向的力学性能相同,横向各观同性是正交各向异性的特例,应该满足对称性即
| $\frac{{{\mu _{xz}}}}{{{E_z}}} = \frac{{{\mu _{zx}}}}{{{E_x}}}$ | (1) |
式中:μij为冻土在j方向正应力作用下,i方向应变与j方向应变的比值,即泊松比;Ex、Ez为冻土x和z弹性方向的弹性模量。
式(1)可验证材料是否属于正交各向同性材料。
1.3 数值模拟条件假设1)假设土体内水分迁移发生在相变界面,气相和盐度的影响不予考虑。
2)假设土体的冻融过程是刚性的,土壤颗粒间没有变形且不可压缩,忽略温度变化带来的颗粒的热胀冷缩现象,只考虑土体冻胀引起的体积变化。
3)假设土体内部各个方向的渗透系数相等,即土体是均匀且各向同性:kx=ky=kz=k。
4)土体冻结过程中,未冻土的含水量和负温存在函数关系,两者处于动态联系中。
5)认为土体内部的质量迁移是液相迁移,即水和冰间的相变作用。
6)冻融过程不考虑下部融土层的压实效果;土体冻胀时,不计外部载荷对渠道衬砌的影响。
2 矩型渠冻胀数值模拟分析本次数值模拟采用EPS颗粒轻质土垫层作为保温措施,垫层20 cm厚布置在矩型渠底部,通过垫层影响土体冻深,进而影响土体的冻胀量。物理模型试验分为4种不同情况进行对比分析,通过模拟野外自然降温、升温的冻融过程,监测渠基土体的温度场、冻胀量及融沉量,综合各种情况的冻深、冻胀量判断不同掺量EPS颗粒轻质土垫层对矩型渠冻胀的影响,进而对矩型渠冻胀耐久性及稳定性进行分析评价。
2.1 有限元模型建立本文选取的矩型渠的尺寸和模拟条件和物理模型试验一致,矩型渠尺寸为2.0 m×0.5 m×0.5 m,换填垫层厚度0.2 m,土层厚度1.5 m,渠两侧土取0.92 m,钢筋取分布筋8Φ4@260,受力筋9Φ4@175,钢筋居中布置。矩型渠采用C50混凝土,膨胀系数取1.1×10−5[10]。钢筋采用HPB235低碳钢,膨胀系数取1.0×10−5[11],相关力学参数见表2。
|
|
表 2 混凝土及钢筋的力学参数 |
土体弹性模量随温度的变化而变化,弹性模量参照天津水泥工业设计有限公司土工试验结果,假设土体为各向同性体,参数见表3,冻土泊松比取0.3,融土泊松比取0.2。相变间区取−0.3 ℃~0.01 ℃[12],土体的相变潜热值取为334 700 J/kg[13]。
|
|
表 3 冻土的弹性模量 |
在温度场分析时,钢筋单元类型选用DC1D2,混凝土、垫层及土体的单元类型为DC3D8;在进行位移场分析时,钢筋的单元类型选用T3D2,混凝土、垫层和土体的单元类型为C3D8R,有限元模型如图2所示。

|
Download:
|
| 图 2 矩型渠有限元模型 | |
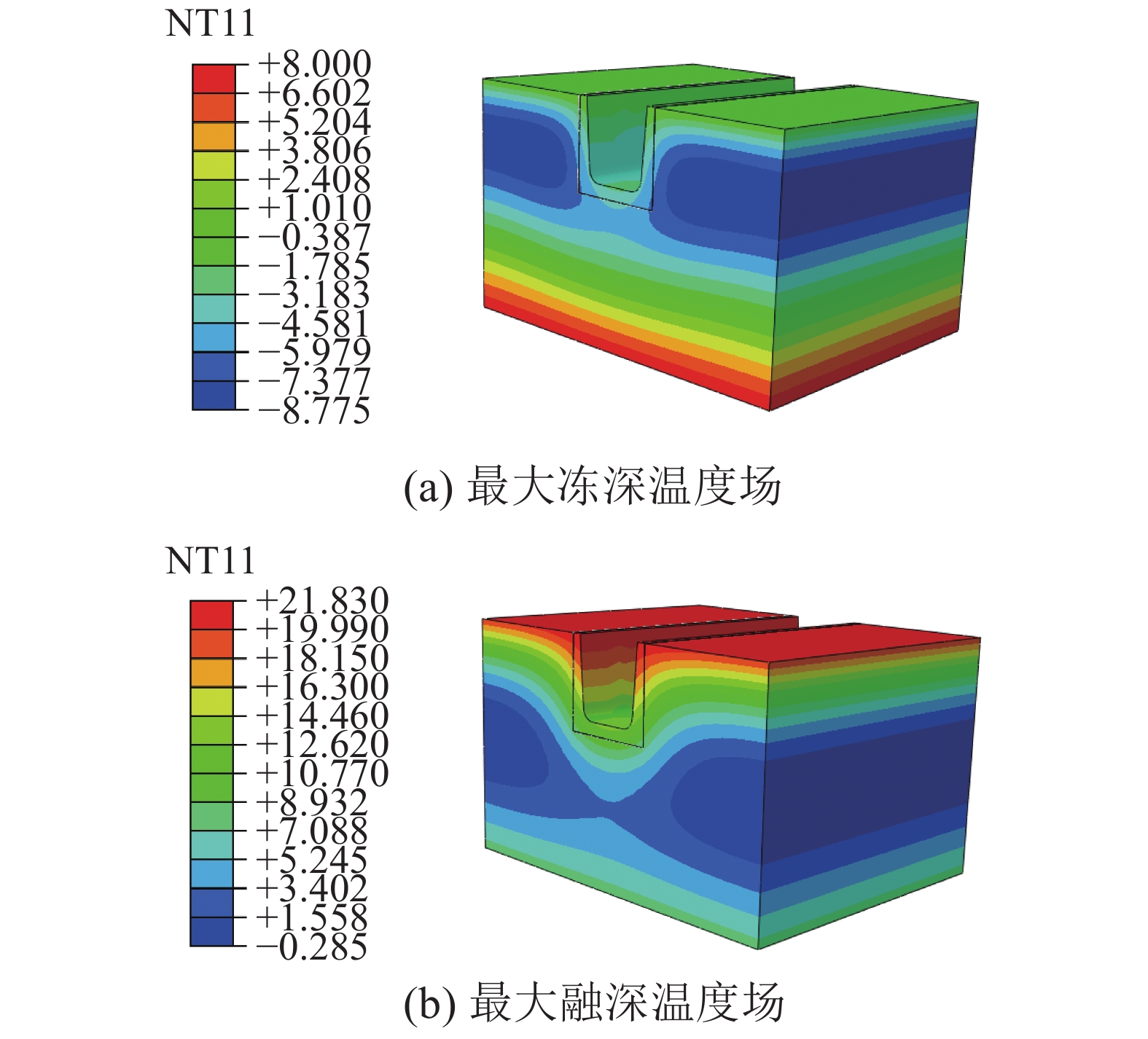
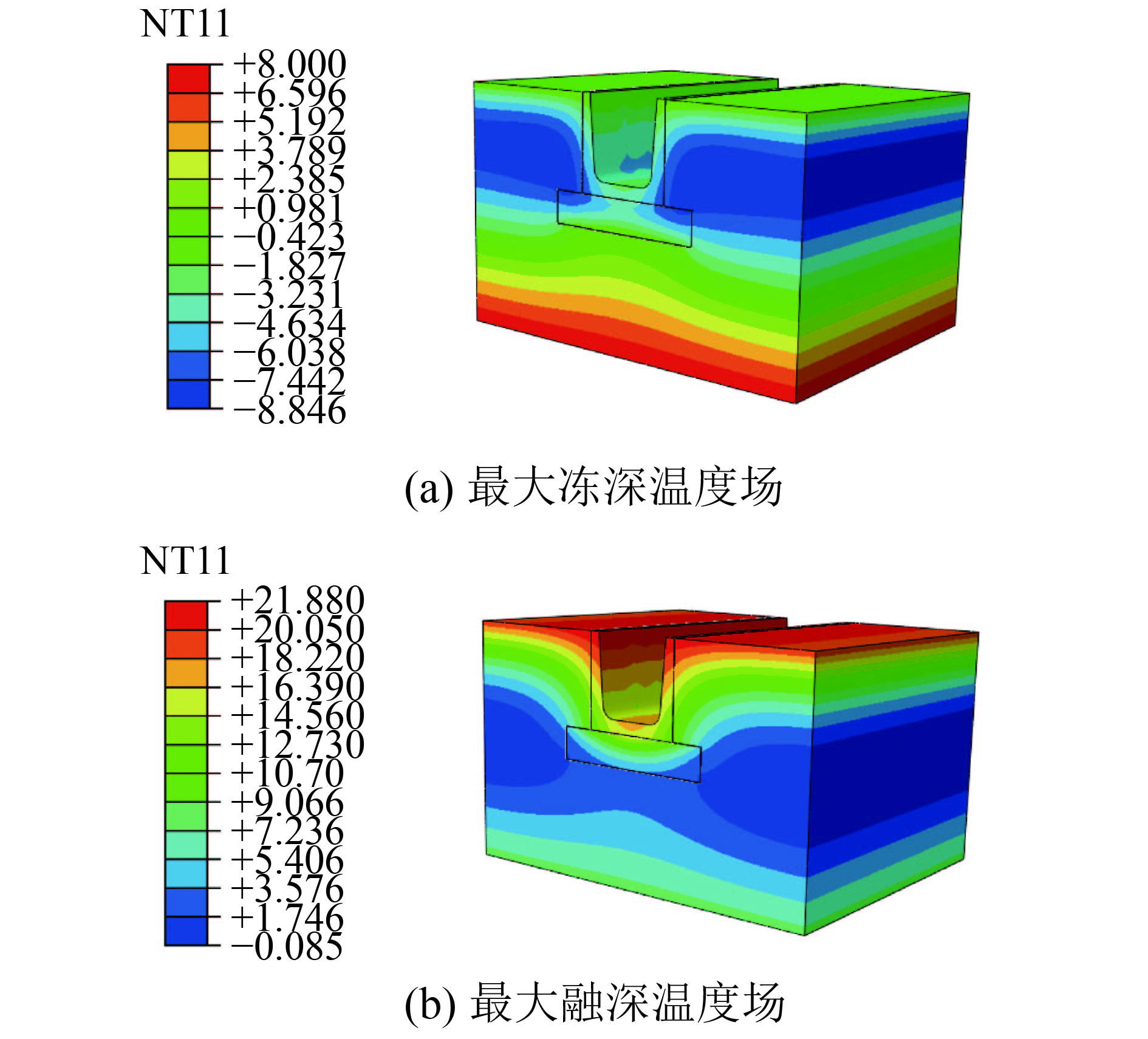
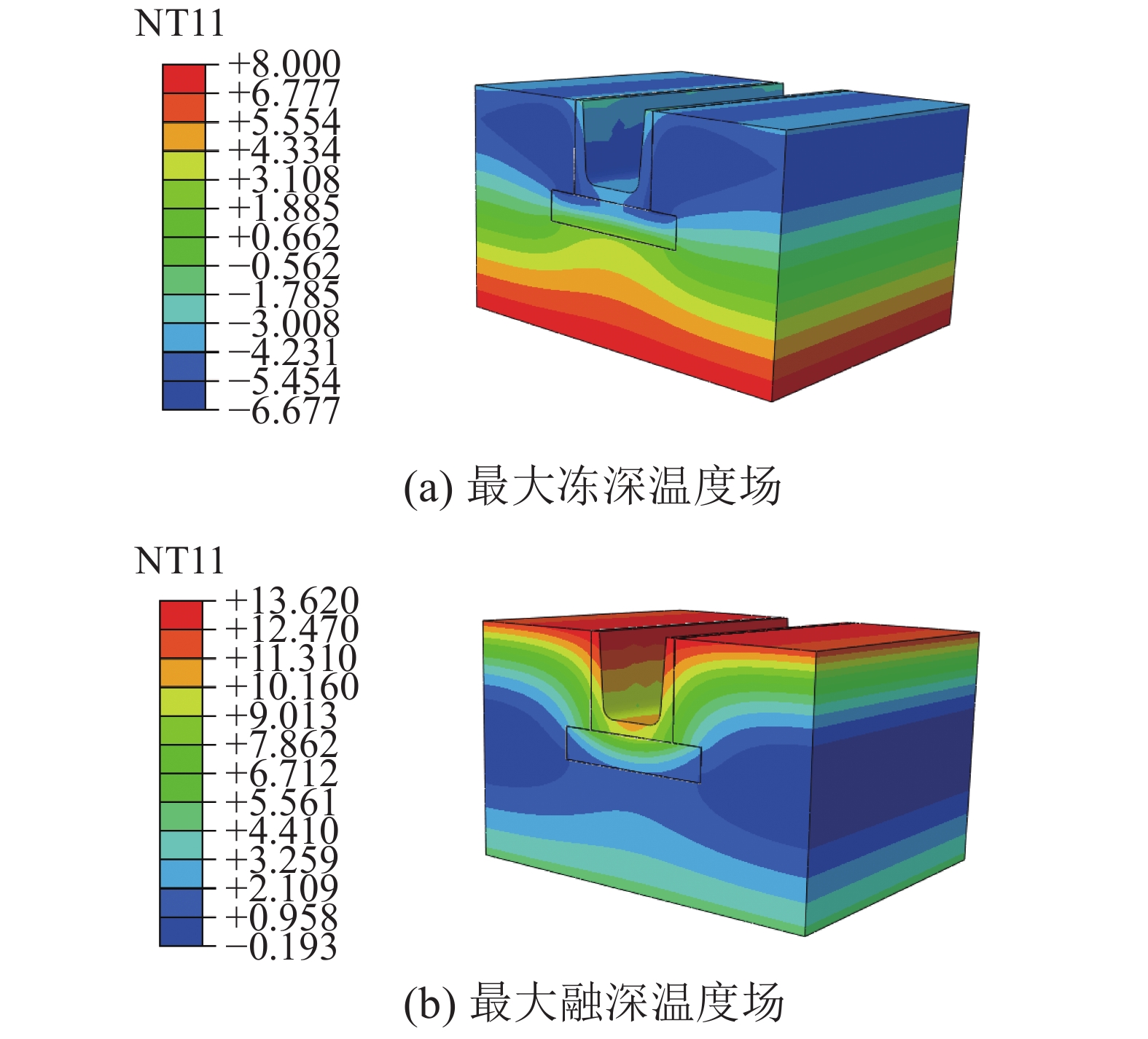
本次数值模拟给出不同掺量EPS颗粒轻质土的温度场云图,为了能更好地分析冻融循环过程中土体的冻结融化规律,现给出冻融过程中的最大冻深和最大融深温度场,如图3~6所示。
|
Download:
|
| 图 3 未掺EPS颗粒轻质土模型 | |
|
Download:
|
| 图 4 2%EPS颗粒轻质土模型 | |
|
Download:
|
| 图 5 3%EPS颗粒轻质土模型 | |

|
Download:
|
| 图 6 4%EPS颗粒轻质土模型 | |
根据冻结融化规律,由图3~6可以看出,渠基土的冻结融化是一个单向冻结、双向融化的过程。掺EPS颗粒轻质土垫层的土体冻深明显比未掺EPS颗粒轻质土垫层的冻深小。随着EPS颗粒轻质土掺量提高,土体的冻结深度变小,也就是EPS颗粒轻质土掺量越高,对土体的冻深削减越明显,保温效果也更明显。
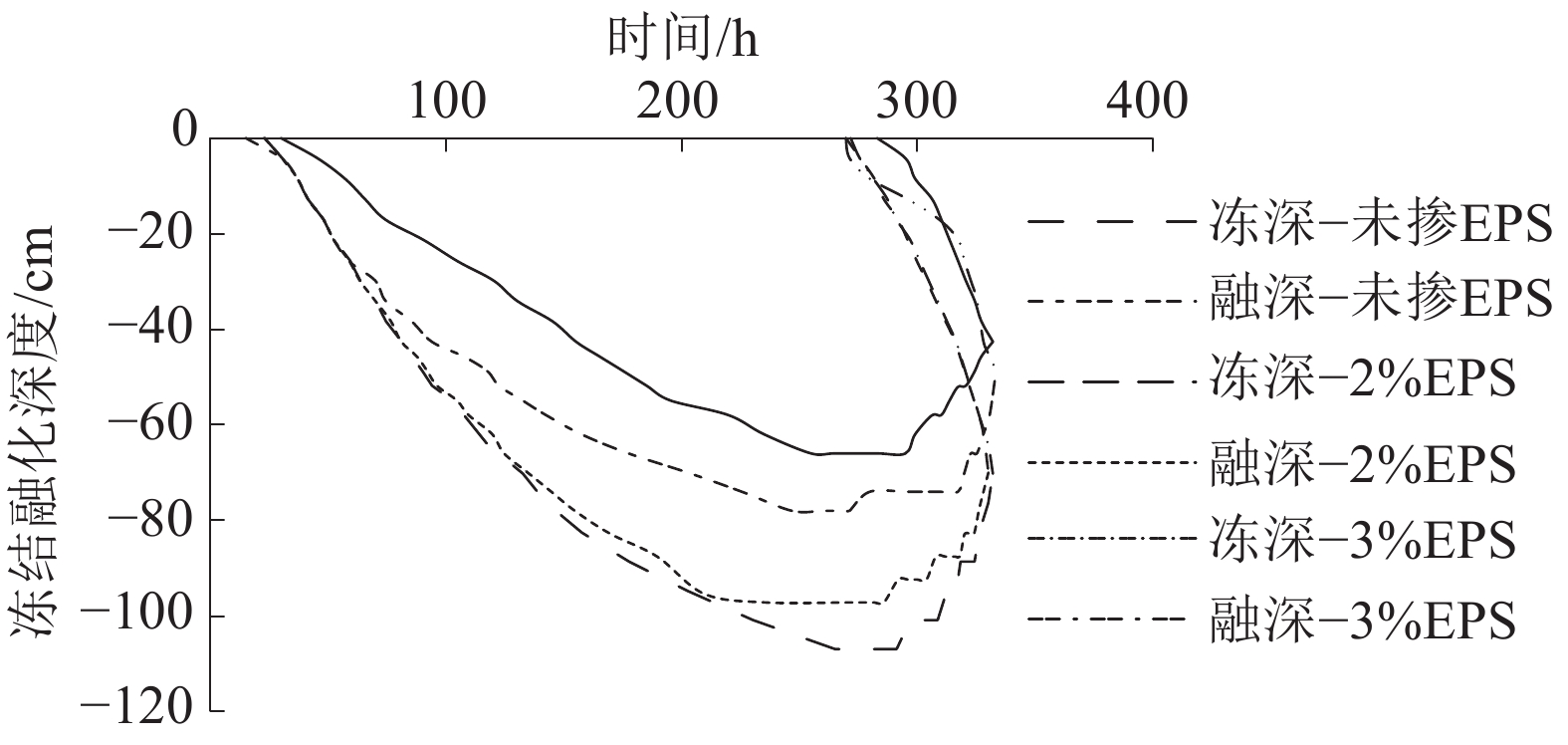
2.2.2 冻结融化深度分析根据温度场云图可以看出各时段的冻深和融深,将不同时段的冻深和融深值绘制成冻结融化曲线(图7),以此来更好地分析其冻结融化规律。
|
Download:
|
| 图 7 冻结融化曲线 | |
可以看出,整个冻结融化过程与试验模型冻结融化规律相似,最大冻深发生在270 h左右,270 h后土体开始融化,冻结深度减小,融化深度增大,直到330 h左右,冻结深度与融化深度相等,土体完全融化。从图7可以看出未掺EPS颗粒轻质土垫层时,土体的最大冻深为107 cm;2%EPS颗粒轻质土垫层时,土体的最大冻深为97.2 cm;3%EPS颗粒轻质土垫层时,土体的最大冻深为78 cm;4%EPS颗粒轻质土垫层时,土体的最大冻深为66 cm。随着EPS颗粒轻质土掺量越高,土体的冻深越小,保温效果越明显。从冻结融化曲线还可以看出,EPS颗粒轻质土掺量越高,土体的冻结速率也越慢。
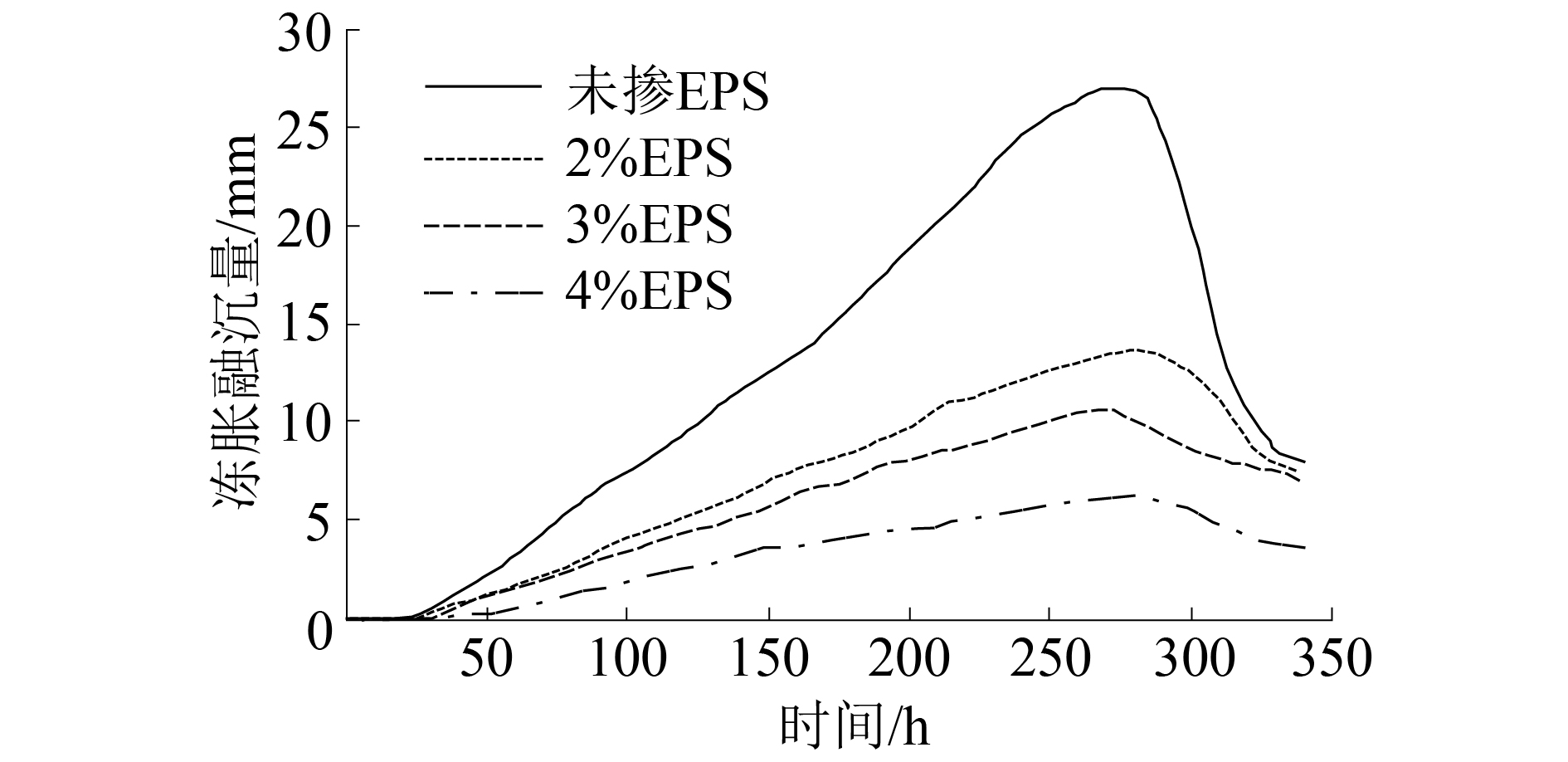
2.2.3 位移场分析本次模拟在求得模型温度场后,通过顺序热应力耦合的方法计算模型的位移场,不同时刻的冻胀融沉量,对比分析不同EPS轻质土掺量对土体冻胀融沉量的影响,如图8所示。
|
Download:
|
| 图 8 冻胀融沉量变化曲线 | |
整个冻融过程中,在不同掺量EPS颗粒轻质土情况下,土体的冻胀量都有相同趋势,土体在20 h左右出现冻胀量,也就是土体开始冻结;270~280 h时间段内出现最大冻胀量;之后土体开始融化,直至数值模拟结束土体完全融化。
从图8可以看出,未掺EPS颗粒轻质土的土体冻结速率较快,随着EPS颗粒轻质土掺量的提高,土体冻结速率降低;随着EPS颗粒轻质土掺量的增大,土体的最大冻胀量越小,残余变形也越小。
3 物理模型试验本次试验在黑龙江省季节性冻土区工程重点实验室内进行,同样采用EPS颗粒轻质土垫层作为矩型渠的保温措施,试验主要检测两方面:一是温度场的监测,监测土体内部温度场情况及实时环境温度变化情况;二是冻胀融沉量监测,监测土体的冻胀量。
3.1 试验装置及相关设备模型试验箱尺寸长4.5 m、宽3.0 m、高1.5 m。模型试验箱底层结构共分为3层:第1层是加热板,由直径为2 cm的铜管弯曲铺成;第2层先铺设5 cm厚的砂垫层,后在其上面加无纺布;第3层为补水层,先将弯曲的塑料管均匀铺设,并在塑料管周围铺上5 cm卵石,最后用无纺布将塑料管覆盖。箱底底层结构主要为模拟自然情况下土体单向冻结、双向融化提供条件,模型试验箱底部结构如图9所示。

|
Download:
|
| 图 9 模型试验箱底部结构 | |
数据采集系统包括DT515/615系列数据采集仪、PT100温度传感器、XLD系列温度巡检仪、WDL位移传感器。本次试验所用土体取自工程试验段现场,按照水利部行业标准要求进行试验[14]。
3.2 试验降温过程设计方案该模型的温度控制方案以试验温度控制曲线为主,模拟土体的整个冻结融化过程。根据哈尔滨地区野外实测资料,外界平均冻结期为213 d,根据相似准侧,取时间比尺Ct=16、几何比尺Cl=4、温度比尺Ct=1,确定本次模型试验历时13.125 d,在试验方案中的历时为320 h,本次试验为了能使土体完全融化,延长试验历时为330 h。
为模拟野外自然土体下卧层温度,同时避免发生双向冻结,从降温开始就控制底板温度,底板温度控制为8 ℃,温度控制曲线如图10所示。

|
Download:
|
| 图 10 试验温度控制曲线 | |

|
Download:
|
| 图 11 试验开始阶段 | |

|
Download:
|
| 图 12 试验结束阶段 | |
数值模拟与物理模型试验采用的降温曲线、试验条件及相关参数相同,现将模型试验结果与数值模拟结果进行对比分析。
3.3.1 冻结融化深度对比分析将物理模型试验与数值模拟结果进行对比。由于4种工况冻结融化规律相似,现给出4%EPS颗粒轻质土垫层模型的冻结融化深度曲线,如图13所示。

|
Download:
|
| 图 13 4%EPS颗粒轻质土 | |
从图13可以看出,未掺EPS颗粒轻质土的试验模型土体在259 h出现最大冻深,为110 cm;数值模拟土体在271 h出现最大冻深,为107 cm。2%EPS颗粒轻质土的试验模型土体在270 h出现最大冻深,为97.2 cm;数值模拟土体在253 h出现最大冻深,为93.1 cm。3%EPS颗粒轻质土试验模型土体在260 h出现最大冻深,为80 cm;数值模拟土体在270 h出现最大冻深,为78 cm。4%EPS颗粒轻质土试验模型土体在288 h出现最大冻深,为73.5 cm;数值模拟土体在265 h出现最大冻深,为66 cm。
从以上出现最大冻深的时间看,当外界环境温度接近0℃时,土体出现最大冻深,此后土体开始融化。对比试验和数值模拟结果,可以看出两者最大冻深误差不大,且出现最大冻深时间也接近。总的来说,数值模拟结果冻结速率相对平稳,而试验模型结果冻结速率有发生突变的情况,这可能是由于低温模型试验外界环境的温度曲线难以达到和数值模拟一样理想的情况,加上试验过程中测量的不及时和一些不可避免误差等原因造成。
3.3.2 冻胀量及残余变形对比分析将试验模型与数值模拟结果的土体残余变形及最大冻胀量列表如表4所示。
|
|
表 4 不同掺量EPS颗粒轻质土模型的冻胀融沉量 |
与数值模拟试验结果相比,物理模型试验结果的土体冻胀量和残余变形都偏小,且一个冻融循环后土体的残余变形为正值,也就是一个冻融循环后土体的冻结膨胀量大于土体融化沉降量,物理模型试验结果和数值模拟结果存在偏差,但偏差不大,从侧面验证了数值模拟方法的合理性。
3.4 误差分析由于本文物理模型试验与数值模拟结果存在误差,现对出现的误差进行分析。
1)在整个试验过程中,有些不可避免的因素。在试验模型开始阶段首先要对土体进行饱水处理,在实际试验条件下,试验土体可能不能完全饱水。为了模拟天然土体下卧暖土层温度,土体底部铺设弯曲铜管作为加热层,此外还有塑料水管对土体底部进行补水。整个试验都是在低温实验室完成的,当温度低到一定程度,底板处的水管可能会冻裂,导致土体底部的温度不易控制。
2)数值模拟参数的选取也存在误差。冻土本身是一个极其复杂的多相体,材料参数会因温度、相变、土体种类的不同而存在差别。本文模型参数有部分是按试验模型测得,还有部分是通过查相关资料获得的理论值。
3)本章在建立数学模型时做了简化,由于本模型是对工程实际模型的简化计算,故本文在建模过程中假设了一系列理想条件,如土壤介质的不可压缩性及渠基土的各向同性等。这些理想条件的假定,对模型简化固然有利,但对计算结果也带来了误差。
4 结论综合以上物理模型试验和数值模拟结果,得到如下结论:
1)本文在数值模拟时对模型进行了简化,数值模拟与物理模型试验有着相似的冻结融化规律,证明了数值模拟方法在季节性冻土区渠道防冻胀工程中的适用性;
2)季节性冻土地区的冻融变化是一个单向冻结、双向融化的过程。土体的温度在下降段接近0 ℃开始冻结,温度越低冻深越大,在温度上升段接近0 ℃土体出现最大冻深,此后土体开始融化;
3)用不同掺量EPS颗粒轻质土垫层作为渠道的保温措施,通过对比分析,发现EPS颗粒轻质土掺量越高,土体冻深和冻胀量都会降低,EPS颗粒轻质土垫层保温效果就越好。
| [1] |
MA Wei, WU Ziwang, ZHANG Lixin, et al. Analyses of process on the strength decrease in frozen soils under high confining pressures[J]. Cold regions science and technology, 1999, 29(1): 1-7. DOI:10.1016/S0165-232X(98)00020-2 ( 0) 0)
|
| [2] |
陈涛, 王正中, 张爱军. 大U形渠道冻胀机理试验研究[J]. 灌溉排水学报, 2006, 25(2): 8-11. ( 0) 0)
|
| [3] |
张茹. 大U形混凝土衬砌渠道冻胀破坏力学模型及数值模拟[D]. 杨凌: 西北农林科技大学, 2007.
( 0) 0)
|
| [4] |
张宇峰. 渠道防渗保温防冻胀技术标准化模式研究[D]. 杨凌: 西北农林科技大学, 2014.
( 0) 0)
|
| [5] |
NOORISHAD J, TSANG C F, WITHERSPOON P A. Coupled thermal-hydraulic-mechanical phenomena in saturated Fractured porous rocks: numerical approach[J]. Journal of geophysical research: solid earth, 1984, 89(B12): 10365-10373. DOI:10.1029/JB089iB12p10365 ( 0) 0)
|
| [6] |
高玉佳, 王清, 陈慧娥, 等. 温度对季节性冻土水分迁移的影响研究[J]. 工程地质学报, 2010, 18(5): 699-702. ( 0) 0)
|
| [7] |
安维东, 吴紫汪, 马巍, 等. 冻土的温度水分应力及其相互作用[M]. 兰州: 兰州大学出版社, 1989.
( 0) 0)
|
| [8] |
刘雄, 宁建国, 马巍. 冻土地区水渠的温度场和应力场数值分析[J]. 冰川冻土, 2005, 27(6): 932-938. DOI:10.3969/j.issn.1000-0240.2005.06.022 ( 0) 0)
|
| [9] |
许强, 彭功生, 李南生, 等. 土冻结过程中的水热力三场耦合数值分析[J]. 同济大学学报: 自然科学版, 2005, 33(10): 1281-1285. ( 0) 0)
|
| [10] |
刘旭东, 王正中, 闫长城, 等. 基于数值模拟的双层薄膜防渗衬砌渠道抗冻胀机理探讨[J]. 农业工程学报, 2011, 27(1): 29-35. DOI:10.3969/j.issn.1002-6819.2011.01.005 ( 0) 0)
|
| [11] |
中国建筑科学研究院. GB 50176-1993, 民用建筑热工设计规范[S]. 北京: 中国标准出版社, 1993.
( 0) 0)
|
| [12] |
孔德坤. 季冻区渠道冻胀试验及数值模拟分析[D]. 哈尔滨: 哈尔滨工程大学, 2017: 42-43.
( 0) 0)
|
| [13] |
张建荣, 刘照球, 刘文燕. 混凝土表面自然对流换热系数的实验研究[J]. 四川建筑科学研究, 2007, 33(5): 144-146. ( 0) 0)
|
| [14] |
中华人民共和国水利部. SL237-1999, 土工试验规程[S]. 北京: 中国水利水电出版社, 1999.
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


