2. 哈尔滨工程大学 理学院,黑龙江 哈尔滨 150001
2. College of Sciences, Harbin Engineering University, Harbin 150001, China
近年来,光纤加速度传感器的应用领域不断拓展,从惯性导航和制导传统以及水下潜艇探测等军事领域[1-3]逐渐发展到大地测量、地震勘探、石油钻井、隧道开凿、电子设备等民用领域[4-8],这也对传感器的性能提出了更高的要求。作为加速度传感器的一项重要性能指标,灵敏度成为了研究者们关注的焦点,如何有效地提高光纤加速度传感器的灵敏度,成为了目前限制光纤加速度传感器发展的一个主要难题。盘式光纤加速度计凭借弹性盘片一维尺寸(厚度)远小于其他两维尺寸(长、宽)的平面几何特性,大大缩小了传感器的尺寸,推动了光纤加速度传感器向小型化、实用化方向发展。然而,早期报道的盘式光纤加速度传感器的灵敏度通常不高,Geoffrey A. Cranch等[9]制作了不同尺寸、不同边界条件的盘式光纤加速度计,但并没有讨论不同尺寸、不同边界条件对灵敏度的具体影响;王永杰等[10]只讨论了不同边界条件时盘式光纤加速度传感器的粘贴区域与灵敏度关系。本文针对周边固支型盘式光纤加速度计,从弹性盘片尺寸、光纤盘粘贴区域以及光纤类型3个方面出发,提出了提高基于单层光纤盘的光纤加速度传感器的灵敏度方案,并综合三者的优化结果,提出了采用多层光纤敏感盘来实现灵敏度倍增的方案,并进行了有限元软件仿真,验证该方案的有效性。
1 系统结构及工作原理盘式光纤加速度传感器的系统结构如图1所示。作为光纤Michelson干涉仪干涉臂的2个光纤盘分别粘贴在同一弹性盘片的上、下表面,弹性盘片采用周边固支方式的方式与外部封装壳体固定,从而构成加速度传感单元。

|
Download:
|
| 图 1 盘式光纤加速度传感系统 | |
盘式光纤加速度传感器的工作原理为:在光纤Michelson干涉仪的传感光路中,引入光纤环形器和隔离器,构成差分形式的探测结构,用于降低光路噪声。当外界加速度信号施加在盘式光纤加速度传感器时,引起弹性盘片发生弯曲,弹性盘片表面产生与加速度信号相关的应变分布。弹性盘片将此应变分布传递给粘贴在其上、下表面的传感光纤,传感光纤受到等幅反向的应力作用而形成推挽结构,从而使传感光纤的长度发生变化引起光程差,进而引起光纤Michelson干涉仪的输出光相位发生变化。通过对光纤Michelson干涉仪输出光相位变化进行探测,实现对外界加速度的测量。
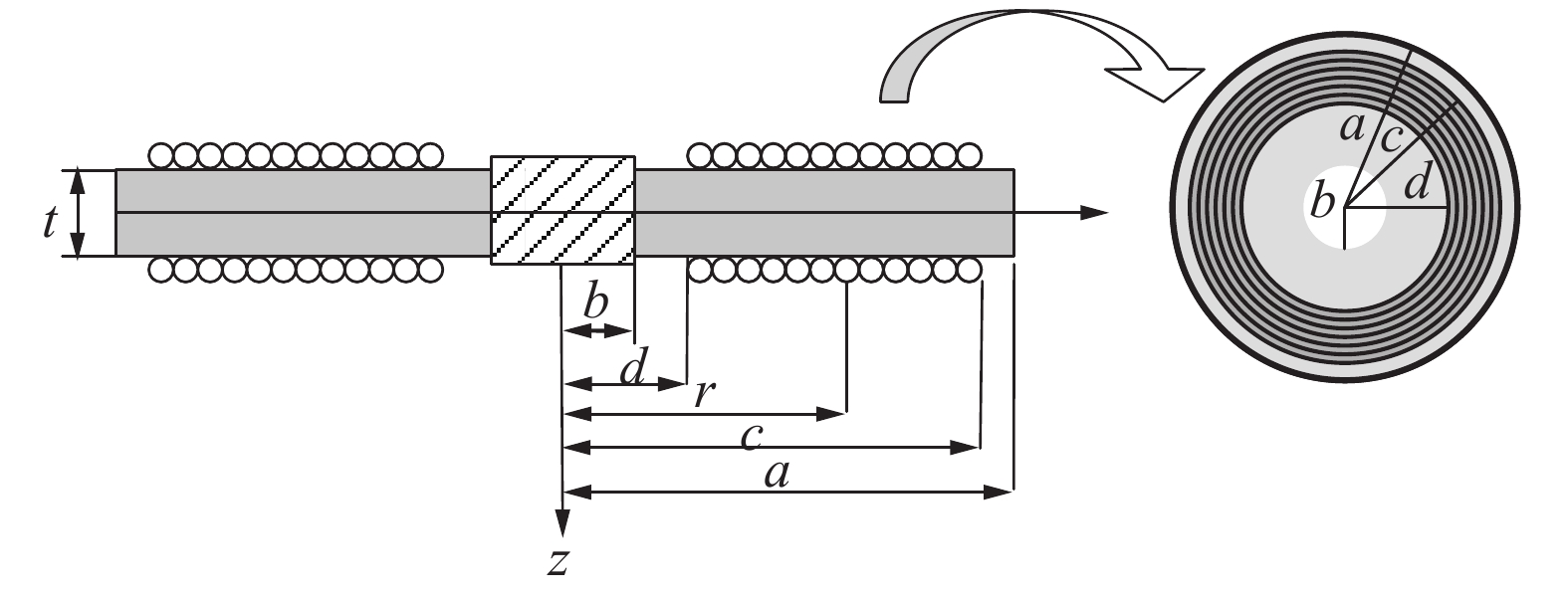
盘式光纤加速度传感器的坐标系统如图2所示。其中,弹性盘片的外半径为a、内半径为b、厚度为t,光纤盘的外半径为c、内半径为d。
|
Download:
|
| 图 2 盘式光纤加速度传感器坐标系统 | |
在外界加速度信号作用下,弹性盘片发生弯曲,其弯曲挠度方程为[11]
| $\frac{\rm d}{{{\rm d}r}}\left[ {\frac{1}{r}\frac{\rm d}{{{\rm d}r}}\left( {r\frac{{{\rm d}\omega }}{{{\rm d}r}}} \right)} \right] = \frac{{{Q_r}}}{{D'}}$ | (1) |
式中:
在如图2所示的盘式光纤加速度传感器坐标系统中,边界条件为
| $\omega \left| {_{r = a} = 0} \right.,\frac{{{\rm d}\omega }}{{{\rm d}r}}\left| {_{r = a} = 0} \right.,{M_r}\left| {_{r = b} = 0} \right.$ | (2) |
式中
由式(1)、(2)可得
| $\omega = \frac{{P{r^2}}}{{8\pi D^{^\prime}}} \left( {\ln \frac{r}{a}- 1} \right) + \frac{{P{r^2}}}{{16\pi D^{^\prime}}}{Q_1} + \frac{{P{a^2}{b^2}}}{{4\pi D^{^\prime}}}\ln \frac{r}{a}{Q_2} + \frac{{P{a^2}}}{{16\pi D^{^\prime}}}{Q_3}$ |
式中Q1、Q2和Q3为与盘片尺寸和材料相关的量:
| ${Q_1} = \frac{{(1 - \mu )({a^2} - {b^2}) - 2{b^2}(1 + \mu )\ln ({b \mathord{\left/ {\vphantom {b a}} \right.} a})}}{{{b^2}(1 + \mu ) + {a^2}(1 - \mu )}}$ |
| ${Q_2} = \frac{{1 + (1 + \mu )\ln ({b \mathord{\left/ {\vphantom {b a}} \right. } a})}}{{{b^2}(1 + \mu ) + {a^2}(1 - \mu )}}$ |
| ${Q_3} = \frac{{(1 - \mu ){a^2} + (3 + \mu ){b^2} + 2{b^2}(1 + \mu )\ln ({b \mathord{\left/ {\vphantom {b a}} \right. } a})}}{{{b^2}(1 + \mu ) + {a^2}(1 - \mu )}}$ |
在外界加速度信号作用下,弹性盘片表面产生应变分布,根据广义胡克定律,半径r处的径向应变εr和环向应变εθ为
| $\begin{split}{\varepsilon _r}(r) = & - \frac{t}{2}\frac{{{{\rm d}^2}\omega }}{{{\rm d}{r^2}}} = \\& - \frac{t}{2}\left[ {\frac{P}{{8\pi D^{^\prime}}}\left( {2\ln \frac{r}{a} \!+\! 1} \right) \!+\! \frac{P}{{8\pi D^{^\prime}}}{Q_1} \!-\! \frac{{P{a^2}{b^2}}}{{4\pi D^{^\prime}{r^2}}}{Q_2}} \right]\end{split}$ | (3) |
| $\begin{split}{\varepsilon _\theta }(r) & = - \frac{t}{{2r}}\frac{{d\omega }}{{dr}} = \\& \!-\! \frac{t}{2}\left[ \!{\frac{P}{{8\pi D^{^\prime}}}\left( {2\ln \frac{r}{a} \!-\! 1} \right) \!+\! \frac{P}{{8\pi D^{^\prime}}}{Q_1} \!+\! \frac{{P{a^2}{b^2}}}{{4\pi D^{^\prime}{r^2}}}{Q_2}} \!\right]\end{split}$ | (4) |
由外界加速度信号所引起的盘式光纤加速度传感器产生的相位变化可表示为
| $\Delta \phi = 0.79 \times 4\beta \times \Delta L$ | (5) |
式中:β=2πn/λ为光在光纤中的传播常数,λ为波长,n为光纤的折射率,
由式(3)~(5),盘式光纤加速度传感器的灵敏度S为
| $S = \frac{{\Delta \phi }}{{A/9.8}} = 2 \times 9.8 \times 0.79\frac{{12(1 - {{\mu '}^2})\pi {{m}}n}}{{\lambda DE{t^2}}}{Q_4}$ | (6) |
式中
盘式光纤加速度传感器的谐振频率
| ${f_{n{\kern 1pt} }} = \frac{{{\varLambda ^2} \cdot t}}{{2\pi \cdot {a^2}}}\sqrt {\frac{E}{{12(1 - {\mu ^2})\rho }}} $ | (7) |
式中:Λ2=10.216为谐振频率参数,ρ为弹性盘片材料的密度。
2 灵敏度增强方法分析 2.1 单层光纤敏感盘增敏分析由式(6)可知,盘式光纤加速度传感器的灵敏度S受到弹性盘片外半径a、内半径b、厚度t、光纤盘外半径c、内半径d、光纤直径D等结构参数的影响。以上结构参数可归纳为弹性盘片尺寸、光纤盘粘贴区域、传感光纤类型3种影响因素对光纤加速度传感器灵敏度的影响,下文分别对此3种因素对光纤加速度传感器灵敏度的影响进行分析。
弹性盘片尺寸中外半径a与光纤加速度传感器灵敏度的关系如图3所示,从图中可知,随着弹性盘片外半径a的增大,灵敏度也随之增大,但在光纤加速度传感器设计时,弹性盘片外半径a决定了加速度传感器的外结构尺寸,为保持光纤加速度传感器尺寸的小型化,因此弹性盘片外半径a并不能无限制的增大。与此同时,由式(7)可知,盘式光纤加速度传感器的谐振频率与外半径a的平方成反比。随着外半径a的增加,光纤加速度传感器的谐振频率会急剧减小。综上,弹性盘片外半径a应根据光纤加速度传感器的性能要求进行选择。

|
Download:
|
| 图 3 加速度灵敏度与弹性盘片外半径关系 | |
图4给出了当弹性盘片外半径一定时,弹性盘片内半径b与光纤加速度传感器灵敏度的关系。由图可知,光纤加速度传感器的灵敏度并不是随着弹性盘片内半径b的增加而减小,而是存在一个极值点使灵敏度达到最大。

|
Download:
|
| 图 4 加速度灵敏度与弹性盘片内半径关系 | |
盘式光纤加速度传感器中,作为传感臂的2个光纤盘粘贴在弹性盘片的上、下表面,感知弹性盘片在外界加速度作用下产生的径向应变和环向应变,并在两者的共同作用下,使传感光纤长度发生变化,从而产生相位变化,实现加速度的测量,因此光纤盘需粘贴在弹性盘片上应变敏感的区域内。图5为弹性盘片上表面在外界加速度作用下发生形变时其表面的应变分布与弹性盘片半径的关系,由图可知,弹性盘片表面的应变分布存在零点,即存在正应变和负应变的临界点r0,该临界点的公式为
| ${r_0} = \exp \left[ {\frac{{2{b^2}(1 + \mu )\ln \displaystyle\frac{b}{a} - (1 - \mu )({a^2} - {b^2})}}{{2{b^2}(1 + \mu ) + 2{a^2}(1 - \mu )}} + \ln a} \right]$ |

|
Download:
|
| 图 5 弹性盘片应变与弹性盘片半径关系 | |
在临界点r0以内的半径区域,弹性盘片受到正应变,引起传感光纤伸长,在临界点r0以外的半径区域,弹性盘片受到负应变,引起传感光纤收缩。若光纤盘的粘贴区域横跨临界点,光纤盘中的一部分传感光纤被拉伸,一部分传感光纤被收缩,从而降低了传感光纤对应变的感知,导致灵敏度降低。因此,光纤盘的粘贴区域并不是将传感光纤粘贴满弹性盘片表面便会取得最大的加速度,即光纤盘外半径c、内半径d的选择应尽量不跨临界点区域。
以上分析了弹性盘片尺寸、光纤盘粘贴区域2种因素对光纤加速度传感器灵敏度的影响,此外传感光纤类型对灵敏度也具有影响。传感光纤类型对灵敏度的影响主要体现在结构参数光纤直径D上。在弹性盘片尺寸、光纤盘粘贴区域确定后,为在有限的空间内实现灵敏度的提高便需要增加传感光纤的长度。图6为加速度灵敏度与传感光纤类型的关系,在传感光纤类型的选择上,我们选择了弯曲不敏感光纤(BI-SMF)和细径光纤(RC-SMF)进行分析。细径光纤一方面要比弯曲不敏感光纤的直径要小,其中弯曲不敏感光纤的光纤直径为250 μm(含涂覆层),细径光纤的光纤直径为165 μm(含涂覆层);另一方面,细径光纤要比弯曲不敏感光纤有更小的弯曲半径和弯曲损耗,可承受更小的缠绕半径。由图可知,细径光纤的灵敏度要明显大于弯曲不敏感光纤的灵敏度,因此在进行光纤加速度传感器设计时,可选择细径光纤作为传感光纤。

|
Download:
|
| 图 6 加速度灵敏度与传感光纤关系 | |
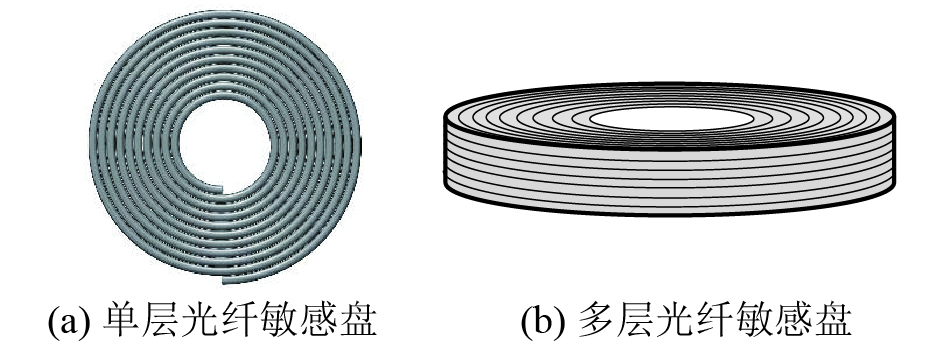
由灵敏度公式可知,ΔL是影响加速度灵敏度的一个重要参数,然而,对于单层光纤敏感盘(图7(a)所示)而言,受制于弹性盘片的尺寸以及光纤的粘贴区域,传感光纤的长度毕竟有限。本文在综合单层光纤敏感盘增敏结果的基础上,提出采用多层光纤敏感盘来实现灵敏度倍增的方案,多层敏感盘如图7(b)所示。
|
Download:
|
| 图 7 光纤敏感盘示意图 | |
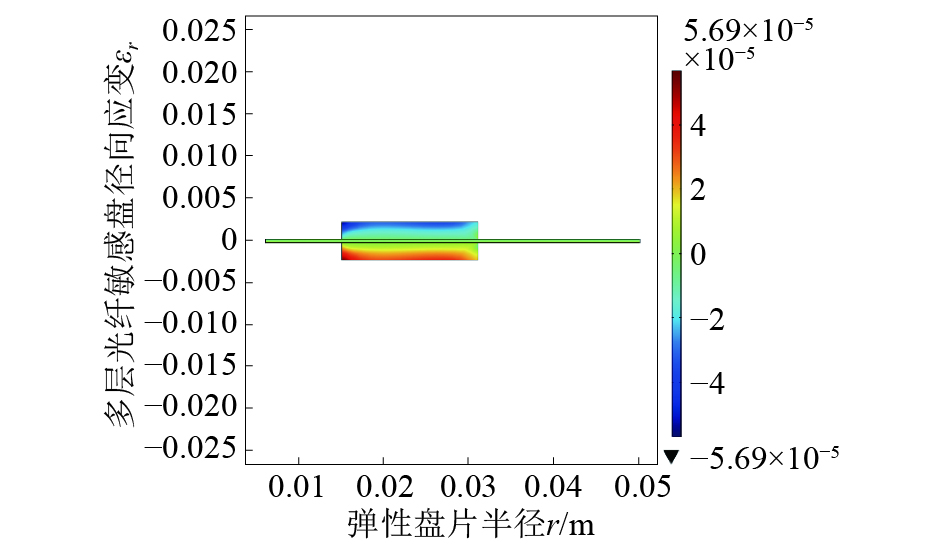
在加速度传感时,弹性盘片的形变逐层地传给多层光纤盘,每层光纤盘都将感受到盘片的应变,引起每层光纤长度的变化,从而有效地增加了ΔL,进而实现了灵敏度倍增。图8、9分别为多层光纤敏感盘的径向应变和环向应变剖面图,因剖面图左右对称,取一侧进行分析。以图中上方多层光纤盘为例,它的上表面的径向应变和环向应变的绝对值都比弹性盘片表面的大;同理,对于下方多层光纤盘来说,它的下表面的径向应变和环向应变的绝对值也都比弹性盘片表面的大。由此可证明,弹性盘片表面的应变能够有效地传递给光纤敏感盘。
|
Download:
|
| 图 8 多层光纤敏感盘径向应变 | |

|
Download:
|
| 图 9 多层光纤敏感盘环向应变 | |
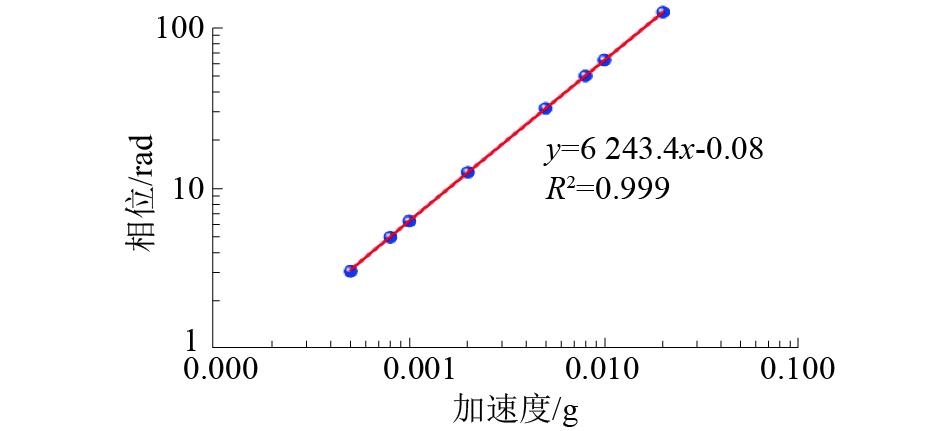
按照前面介绍的灵敏度增强方法,设计了基于多层光纤敏感盘的盘式光纤加速度计,如图10所示。图11为加速度测量曲线,由曲线可知,加速度值与相位具有很好的线性关系,曲线的斜率表示加速度计的灵敏度,为6 243.4 rad/g。图12所示为谐振频率测试曲线,从图中可以看出,待测的光纤加速度传感器的谐振频率在185 Hz附近,在100 Hz以内,其波动小于±3 dB,其工作带宽在100 Hz以内。

|
Download:
|
| 图 10 光纤加速度计样品 | |
|
Download:
|
| 图 11 加速度与解调的光相位关系 | |

|
Download:
|
| 图 12 谐振频率测试曲线 | |
本文通过对盘式光纤加速度计的灵敏度理论模型分析,探讨了影响盘式光纤加速度传感器的灵敏度的因素,并综合多因素优化,提出灵敏度增强方案,最后通过模型仿真及实验验证,得到如下结论:
1)盘式光纤加速度计的弹性盘片尺寸、光纤敏感盘尺以及光纤类型都会影响传感器灵敏度。
2)使用多层光纤敏感盘代替单层光纤敏感盘,能够有效实现盘式光纤加速度计的灵敏度增强。
| [1] |
倪明, 胡永明, 孟洲, 等. 光纤水听器探头技术研究[J]. 应用声学, 2003, 22(2): 1-7. DOI:10.11684/j.issn.1000-310X.2003.02.001 ( 0) 0)
|
| [2] |
MURASHKINA T I, MOTIN A V, BADEEVA E A. Manufacturing technology of a two-axial fiber-optic accelerometer[J]. Journal of physics: conference series, 2017, 803(1): 012102. ( 0) 0)
|
| [3] |
瞿柯林. 新型干涉型光纤水听器动态范围研究及在水下测量中的应用[D]. 杭州: 浙江大学, 2016: 1-7.
( 0) 0)
|
| [4] |
侯璐. 光纤地震测量信号解调系统的若干实用化研究[D]. 哈尔滨: 哈尔滨工程大学, 2016: 1-3.
( 0) 0)
|
| [5] |
张颖, 姚江淮, 魏江南, 等. 一种新型光纤加速度传感器的研究[J]. 光电子·激光, 2017, 28(4): 354-360. ( 0) 0)
|
| [6] |
MACDONALD G A. A review of low cost accelerometers for vehicle dynamics[J]. Sensors and actuators A: physical, 1990, 21(1/2/3): 303-307. ( 0) 0)
|
| [7] |
HAN Jing, ZHANG Wentao, JIANG Dongshan, et al. Fiber optic 3-component seismometer[J]. Photonic sensors, 2014, 4(2): 102-107. DOI:10.1007/s13320-014-0173-4 ( 0) 0)
|
| [8] |
LOPEZ-HIGNERA J M, MORANTE M A, COBO A. Simple low-frequency optical fiber accelerometer with large rotating machine monitoring applications[J]. Journal of lightwave technology, 1997, 15(7): 1120-1130. DOI:10.1109/50.596957 ( 0) 0)
|
| [9] |
CRANCH G A, NASH P J. High-responsivity fiber-optic flexural disk accelerometers[J]. Journal of lightwave technology, 2000, 18(9): 1233-1243. DOI:10.1109/50.871700 ( 0) 0)
|
| [10] |
王永杰, 李芳, 肖浩, 等. 盘片式光纤传感器灵敏度计算方法[J]. 光学学报, 2007, 27(8): 1387-1392. ( 0) 0)
|
| [11] |
范钦珊. 轴对称应力分析[M]. 北京: 高等教育出版社, 1985: 260-262.
( 0) 0)
|
| [12] |
BUCARO J A, LAGAKOS N. Lightweight fiber optic microphones and accelerometers[J]. Review of scientific instruments, 2001, 72(6): 2816-2821. DOI:10.1063/1.1372172 ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


