无人驾驶飞机(unmanned aerial vehicle，UAV)在过去几十年中发挥了重要作用。随着对高性能无人机的需求，混合型机翼无人机受到学者们的广泛关注。倾转旋翼无人机作为混合翼无人机的一个子群，可以按旋翼个数分为双倾旋翼无人机和四倾旋翼无人机。考虑到旋翼电机是否与机翼固连，倾转旋翼机可以分为旋翼机翼非共倾无人机和旋翼机翼共倾无人机。本文重点研究的是一种复合式四旋翼机翼共倾无人机，其具备直升机垂直起降和悬停的飞行特点，同时也具备固定翼无人机快速前飞和长航时的特点。

倾转旋翼无人机复杂的飞行器结构和高耦合的非线性动态模型使得倾转旋翼无人机的控制变得较为复杂。外部扰动、建模误差、控制过程中的时延等也对控制器设计提出了更高的要求。Cetinsoy等^[1-3]在其设计的倾转旋翼无人机SUVAI中采用了经典的PID控制，设计了位置控制器，随后在其最新的研究报告中采用了模型参考自适应(MRAC)设计了位置控制器。Gerardo以及Xinhua等^[4-7]在其各自所设计的倾转旋翼无人机中都采用了积分反步(Backstepping)的控制方法设计了控制器。另外一些机器学习的控制方法也被应用在了位置控制器的设计上^[8]。上述提及的控制方法能满足一定的控制要求，但对于倾转旋翼无人机中所存在的外部扰动、建模误差、时延等并没用针对性的处理，对集总扰动的鲁棒性不足。因此，本文在前期对所设计倾转旋翼无人机动态模型和姿态控制研究的基础上，针对位置控制中存在外部干扰、建模误差、时延等问题设计了基于扰动观测器的位置控制器，并通过所设计仿真场景验证了所设计控制器的有效性。

1 QTR动力学模型

如图1所示为QTR无人机的三维模型及坐标系示意图。

根据牛顿欧拉公式^[9]，QTR无人机的动力学模型可简要表示为

$\left[ {\begin{array}{*{20}{c}}{m{{{I}}_{3 \times 3}}} & {{{{O}}_{3 \times 3}}}\\{{{{O}}_{3 \times 3}}} & {{{{I}}_b}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{{{\dot{ V}}}_w}}\\{{{{\dot{ \Omega }}}_b}}\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}0\\{{{{\Omega }}_b} \times \left( {{{{I}}_b}{{{\Omega }}_b}} \right)}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{{{F}}_t}}\\{{{{M}}_t}}\end{array}} \right]$

式中： ${{{F}}_t}$ 为总推力项，由电机推力 ${{{F}}_{th}}$ 、机翼产生的升阻力 ${{{F}}_{{w}}}$ 、重力 ${{{F}}_{{g}}}$ 、阻力 ${{{F}}_d}$ 组成， ${{{F}}_t} = {{{R}}_{wb}}\left( {{{{F}}_{{\rm{th}}}} + {{{F}}_w} + {{{F}}_g}} \right)$ ，其中 ${{{R}}_{wb}}$ 表示机体系到大地系的坐标转换矩阵； ${{{M}}_t}$ 为总力矩项，由电机产生的力矩 ${{{M}}_{{\rm{th}}}}$ 、机翼的气动力矩 ${{{M}}_w}$ 、旋翼陀螺效应产生的力矩 ${{{M}}_{{\rm{gyro}}}}$ 组成， ${{{M}}_t} = {{{M}}_{{\rm{th}}}} + {{{M}}_w} + {{{M}}_{{\rm{gyro}}}}$ ； ${{{I}}_b} = {\left[ {{I_x},{I_y},{I_z}} \right]^{\rm{T}} }$ 表示三轴转动惯量； ${{{V}}_w}{\rm{ = }}{\left[ {\dot X,\dot Y,\dot Z} \right]^{\rm{T}}}$ 表示大地系下三轴方向的速度； ${{{\Omega }}_b} = {\left[ {p,q,r} \right]^{\rm{T}}}$ 表示机体系下的三轴角速度。

由文献[9]给出QTR的动力学方程为

$\left\{ \begin{aligned}& \ddot X = \frac{1}{m}\left[ {\left( {{c_\psi }{c_\theta }{c_{{\theta _w}}} - \left( {{c_\phi }{s_\theta }{c_\psi } + {s_\phi }{s_\psi }} \right){s_{{\theta _w}}}} \right){u_1} + {W_x} - {k_x}\dot X\left| {\dot X} \right|} \right]\\& \ddot Y = \frac{1}{m}\left[ {\left( {{s_\psi }{c_\theta }{c_{{\theta _w}}} - \left( {{c_\phi }{s_\theta }{s_\psi } - {s_\phi }{c_\psi }} \right){s_{{\theta _w}}}} \right){u_1} + {W_y} - {k_y}\dot Y\left| {\dot Y} \right|} \right]\\& \ddot Z = \frac{1}{m}\left[ {\left( { - {s_\theta }{c_{{\theta _w}}} - {c_\phi }{c_\theta }{s_{{\theta _w}}}} \right){u_1} + mg + {W_z} - {k_z}\dot Z\left| {\dot Z} \right|} \right]\\& \dot p = \frac{{{s_{{\theta _w}}}{u_2} - {c_{{\theta _w}}}{u_4}}}{{{I_x}}} + \frac{{{I_y} - {I_z}}}{{{I_x}}}qr - \frac{{{J_{{\rm{prop}}}}}}{{{I_x}}}q{\omega _p}{s_{{\theta _w}}}\\& \dot q = \frac{{{s_{{\theta _w}}}{u_3}}}{{{I_y}}} + \frac{{{I_z} - {I_x}}}{{{I_y}}}pr + \frac{{{J_{{\rm{prop}}}}}}{{{I_y}}}\left( {p{s_{{\theta _w}}} + r{c_{{\theta _w}}}} \right){\omega _p}\\& \dot r = \frac{{{c_{{\theta _w}}}{u_2} + {s_{{\theta _w}}}{u_4}}}{{{I_z}}} + \frac{{{I_x} - {I_y}}}{{{I_z}}}pq - \frac{{{J_{{\rm{prop}}}}}}{{{I_z}}}q{\omega _p}{c_{{\theta _w}}}\end{aligned} \right.$

(1)

式中： $m$ 表示QTR的质量；k_x、k_y、k_z表示大地系下三轴方向的气动阻力系数；W_x、W_y、W_z表示大地系下三轴方向上的机翼产生的气动力； ${\theta _w}$ 表示机翼倾转角(认为电机推力方向沿机体 ${z_b}$ 轴方向时为90°)； ${J_{{\rm{prop}}}}$ 表示旋翼转动惯量； ${\omega _p} = {\omega _1} - {\omega _2} - {\omega _3} + {\omega _4}$ 表示由旋翼转速所得的量；此外，为简化公式表达，其中c_(*)和s_(*)分别表示cos(*)和sin(*)。

2 基于扰动观测器的位置控制 2.1 系统不确定项问题描述

传统的控制器，如PID控制器、滑模控制器以及LQ控制器等需要基于线性化的系统模型进行控制器的设计。一般是将非线性的系统模型在平衡点附近将将影响较小的非线性项约去以得到线性化的模型进而设计控制器。此类控制器在设计过程中不仅忽略了系统模型固有的非线性项，同时对于存在的不确定项也未给予考虑，故而从本质上缺乏抗扰动的能力。因此，为设计具有抗扰动能力的控制器，首先需要将系统中存在的不确定项考虑到控制模型中。对于QTR无人机的位置控制，其主要的不确定项包含外部扰动、建模误差、控制时延等。

将外部扰动、建模误差、控制时延这3类不确定项考虑到系统模型中，系统模型可描述为如下形式：

$\left\{ \begin{array}{l}{\dot {{P}}} = {{{V}}_w}\\{{{\dot{ V}}}_w} = F({{x}}) + G({{x}})u(t - \tau ) + d({{x}},t)\end{array} \right.$

(2)

式中： ${{x}} = {\left[ {{{P}},{{{V}}_w}} \right]^{\rm{T}}}$ ， ${{P}}$ 、 ${{{V}}_w}$ 分别表示QTR的位置和速度， ${{P}} = {\left[ {X,Y,Z} \right]^{\rm{T}}}$ ； ${{F}}({{x}})$ 和 ${{G}}({{x}})$ 表示可建模的非线性系统模型函数； $d({{x}},t)$ 表示外部扰动及未模型化非线性项； $\tau $ 表示控制时延。 ${{F}}({{x}})$ 和 ${{G}}({{x}})$ 又可以描述为标称模型 ${{{F}}_n}({{x}})\text{、}{{{G}}_n}({{x}})$ 与建模误差模型 ${{{F}}_\Delta }({{x}})\text{、}$ ${{{G}}_\Delta }({{x}})$ 相加的形式，表示如下：

$F({{x}}){\rm{ = }}{F_n}({{x}}) + {F_\Delta }({{x}}),G({{x}}){\rm{ = }}{G_n}({{x}}) + {G_\Delta }({{x}})$

(3)

2.2 位置控制

在水平位置附近对QTR动力学模型式(1)进行小扰动线性化处理^[10-11]，且有 $\sin \theta \approx \theta ,\sin \phi \approx \phi $ 得：

$\left\{ \begin{array}{l}\ddot X = \displaystyle\frac{1}{m}\left[ {\left( {{c_\psi }{c_{{\theta _w}}} - \left( {{c_\phi }{c_\psi }\theta + {s_\psi }\phi } \right){s_{{\theta _w}}}} \right){u_1} + {W_x} - {k_x}\dot X\left| {\dot X} \right|} \right]\\[5pt]\ddot Y = \displaystyle\frac{1}{m}\left[ {\left( {{s_\psi }{c_{{\theta _w}}} - \left( {{c_\phi }{s_\psi }\theta - {c_\psi }\phi } \right){s_{{\theta _w}}}} \right){u_1} + {W_y} - {k_y}\dot Y\left| {\dot Y} \right|} \right]\\[5pt]\ddot Z = \displaystyle\frac{1}{m}\left[ {\left( { - {c_{{\theta _w}}}\theta - {c_\theta }{s_{{\theta _w}}}} \right){u_1} + mg + {W_z} - {k_z}\dot Z\left| {\dot Z} \right|} \right]\end{array} \right.$

由此可得线性化标称模型F_n(x), G_n(x)的表示如下：

${{{F}}_n}({{x}}) = \frac{1}{m}\left[ {\begin{array}{*{20}{c}} {{W_x} - {k_x}\dot X\left| {\dot X} \right|} \\[7pt] {{W_y} - {k_y}\dot Y\left| {\dot Y} \right|} \\[7pt] {{W_z} + mg - {k_z}\dot Z\left| {\dot Z} \right|} \end{array}} \right]$

(4)

${{{G}}_n}({{x}}) = \frac{1}{m}\left[ {\begin{array}{*{20}{c}} {{c_\psi }{s_{{\theta _w}}}{u_1}}&{{s_\psi }{s_{{\theta _w}}}{u_1}}&{{c_\psi }{c_{{\theta _w}}}} \\[9pt] {{s_\psi }{s_{{\theta _w}}}{u_1}}&{{c_\psi }{s_{{\theta _w}}}{u_1}}&{{s_\psi }{c_{{\theta _w}}}} \\[9pt] { - {c_{{\theta _w}}}}&0&{{c_\phi }{c_\theta }{s_{{\theta _w}}}} \end{array}} \right]$

(5)

对应的内环姿态控制器的输入量，即式(2)中所表示的状态量，可表示为

${{u}} = {\left[ {\theta ,\phi ,{u_1}} \right]^{\rm{T}}}$

(6)

根据式(2)~(6)，接下来进行位置控制器的设计。

首先根据式定义位置误差和速度误差分别如下：

${e_1} = {{P}} - {{{P}}_r},\;\;{e_2} = {{{V}}_w} - {\alpha _1}$

(7)

式中： ${{P}} = {\left[ {X,Y,Z} \right]^{\rm{T}}}$ 为当前位置， ${{{P}}_r} = {\left[ {{X_r},{Y_r},{Z_r}} \right]^{\rm{T}}}$ 为参考位置， ${{{V}}_w} = {\left[ {\dot X,\dot Y,\dot Z} \right]^{\rm{T}}}$ 为当前大地坐标系下的速度， ${\alpha _1}$ 为用以稳定 ${e_1}$ 的虚拟控制输入。

根据式(2)、(7)可得位置环表示如下：

${\dot e_1} = {e_2} + {\alpha _1} - {{\dot{ P}}_r}$

(8)

虚拟控制输入 ${\alpha _1}$ 可设计为如下：

${\alpha _1}{\rm{ = }} - {k_{1p}}{e_1} - {k_{1i}}\int\limits_0^t {{e_1}{\rm{d}}t} + {\dot {{P}}_r}$

(9)

式中( ${k_{1p}} > 0$ 、 ${k_{1i}} > 0$ )，然后对该虚拟输入量 ${\alpha _1}$ 求微分可得：

${\dot \alpha _1}{\rm{ = }} - {k_{1p}}{\dot e_1} - {k_{1i}}{e_1} + {{\ddot{ P}}_r} = - {k_{1p}}\left( {{V_w} - {{{\dot{ P}}}_r}} \right) - {k_{1i}}{e_1} + {{\ddot{ P}}_r}$

根据式(2)、(3)、(7)可得速度环表示如下：

$\begin{split}{{\dot e}_2} = & {{{\dot{ V}}}_w} - {{\dot \alpha }_1} = {{F}}({{x}}) + {{G}}({{x}})u\left( {t - \tau } \right) + d({{x}},t) - {{\dot \alpha }_1} = \\& {{{F}}_n}({{x}}) + {{{G}}_n}({{x}})u - {{\dot \alpha }_1} + d({{x}},t) + {{{F}}_\Delta }({{x}}) + {{{G}}_\Delta }({{x}})u\end{split}$

(10)

根据式(10)可将集总干扰 $w$ 表示为

$\begin{split}& w = d({{x}},t) + {{{F}}_\Delta }({{x}}) + {{{G}}_\Delta }({{x}})u(t - \tau ) = \\& \quad \quad {{\dot e}_2} - ({{{F}}_n}({{x}}) + {{{G}}_n}({{x}})u - {{\dot \alpha }_1})\end{split}$

(11)

考虑到存在小但时变的控制输入时延，其可能在一个采样周期内发生多次变化，所以式(11)中用 ${G_n}({{x}})u(t - \tau )$ 表示时延的影响在实际控制过程中存在问题。在此引入一个积分滤波器将集总干扰 $w$ 重新描述为如下形式：

$\tilde w = \frac{{{e_2} + {\alpha _1} - \displaystyle\int\limits_0^t {\left( {{{{F}}_n}({{x}}) + {{{G}}_n}({{x}})u(t)} \right){\rm{d}}t} }}{t}$

(12)

根据式(10)、(11)可得控制量 $u$ 为

$u = \frac{{{{\dot e}_2} + {{\dot \alpha }_1} - {{{F}}_n}({{x}}) - \tilde w}}{{{{{G}}_n}({{x}})}}$

将式(12)中的 ${\dot e_2}$ 替换为 $ - {k_2}{e_2}$ ，则控制输入量 $u$ 变为

$u = \frac{{ - {k_2}{e_2} + {{\dot \alpha }_1} - {{{F}}_n}({{x}}) - \tilde w}}{{{{{G}}_n}({{x}})}}$

(13)

由式(13)可知，内环姿态控制器输入量的补偿项为 $\hat w = {{\tilde w} / {{G_n}({{x}})}}$ ，即扰动观测器的输出量。图2给出了误差观测器控制原理框图。

2.3 位置控制稳定性证明

首先令 ${e_0} = \displaystyle\int\limits_0^t {{e_1}{\rm{d}}t} $ ，然后分别将式(9)代入式(8)，式(13)代入式(11)，可得如下误差状态方程组：

$\left\{ \begin{array}{l}{{\dot e}_0} = {e_1}\\[8pt]{{\dot e}_1} = {e_2} - {k_{1p}}{e_1} - {k_{1i}}{e_0}\\[8pt]{{\dot e}_2} = - {k_2}{e_2}\end{array} \right.$

取标量函数 $V = a{k_{1i}}{e_0}^2 + a{e_1}^2 + b{e_2}^2$ ( $a > 0$ 、 $b > 0$ )。

$\begin{aligned}\dot V = & 2a{k_{1i}}{e_0}{{\dot e}_0} + 2a{e_1}{{\dot e}_1} + 2b{e_2}{{\dot e}_2}{\rm{ = }}\\& 2a{k_{1i}}{e_0}{e_1} + 2a{e_1}{e_2} - 2{k_{1p}}{e_1}^2 - 2a{k_{1i}}{e_0}{e_1} - \\& 2b{k_2}{e_2}^2 = - 2a{k_{1p}}{e_1}^2 + 2a{e_1}{e_2} - 2b{k_2}{e_2}^2{\rm{ = }}\\& - a{({e_1} - {e_2})^2} - a(2{k_{1p}} - 1){e_1}^2 - (2b{k_2} - a){e_2}^2\end{aligned}$

要满足标量函数的一阶导 $\dot V \leqslant 0$ ，且仅在平衡点处取得 $\dot V{\rm{ = }}0$ ，则可知需要满足如下关系：

$2{k_{1p}} - 1 \geqslant 0, \;\; 2b{k_2} - a \geqslant 0$

则有 ${k_{1p}} \geqslant 0.5$ 、 ${k_2} \geqslant {a / {2b}} > 0$ ，总存在满足上述关系式的 $a$ 、 $b$ ，故可得系统是大范围渐进稳定的^[12]。

2.4 姿态控制

姿态控制器采用的是鲁棒伺服线性二次型最优控制器(robust servo linear quadratic regulator, RSLQR)^[13-14]。以滚转通道为例，状态量为 ${{x}} = {\left[ {\phi ,p} \right]^{\rm T}}$ ，线性配平后的滚转通道状态方程为 $\left[ {\begin{array}{*{20}{c}} {\dot \phi } \\ {\dot p} \end{array}} \right] \!=\! {{A}}\left[ \!\! {\begin{array}{*{20}{c}} \phi \\ p \end{array}} \!\! \right] \!+\! {{B}}{u_2}$ ，滚转角 $\phi $ 作为被控变量，其输出方程为 ${y_c} = {{{C}}_c}\left[ \!\! {\begin{array}{*{20}{c}} \phi \\ p \end{array}} \!\! \right] \!+\! {{D}}{u_2}$ 。根据RSLQR控制理论，RSLQR的控制结构如图3所示。在参考信号指令 $r$ 作用下，引入一个误差 $e = {y_c} - r$ 作为状态量进行增广，系统的滚转通道状态模型可改写为

$\dot { {z}} = {\tilde{ A}}{ z} + {\tilde{ B}}\mu ,{ z} = \left[ {\begin{array}{*{20}{c}} e \\ {\dot x} \end{array}} \right],\mu = {\dot u_2}$

选取合适的滚转通道状态量权重矩阵 ${{{Q}}_\phi }$ 阵和控制量权重矩阵 ${{{R}}_\phi }$ ，再根据所选取的 ${{{Q}}_\phi }$ 阵和 ${{{R}}_\phi }$ 阵求解相应的Riccati方程，进而获得状态反馈控制器增益矩阵 ${{K}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{k_1}}&{{k_2}}&{{k_3}} \end{array}} \right]$ 阵，完成姿态控制器的设计。

3 仿真实验

本节将设计飞行仿真场景对所设计位置控制器进行验证。首先，QTR在垂直模式下起飞，在6 s内达到10 m的高度；在第6 s时刻QTR切换到倾转过渡模式，经过4 s机翼由90°倾转到10°，在此倾转过程中保持俯仰角为0°及高度的稳定；然后在水平模式下前飞8 s后，在2 s内切换倾转角至30°，然后对半径为70 m的圆形轨迹段进行跟踪；最后切换到垂直模式降落 。

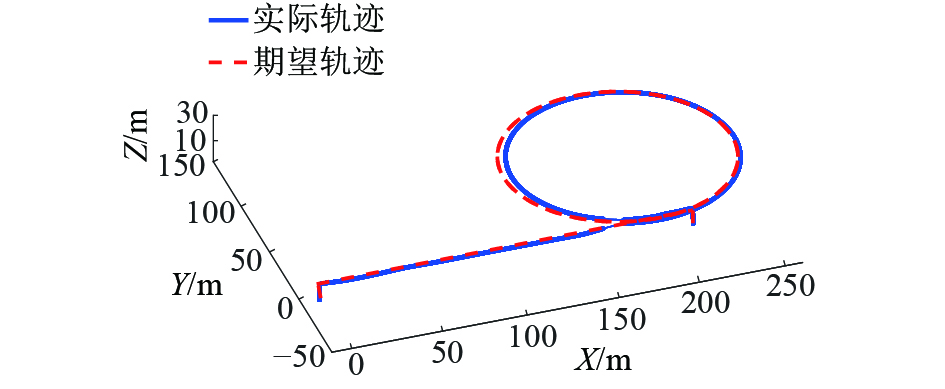
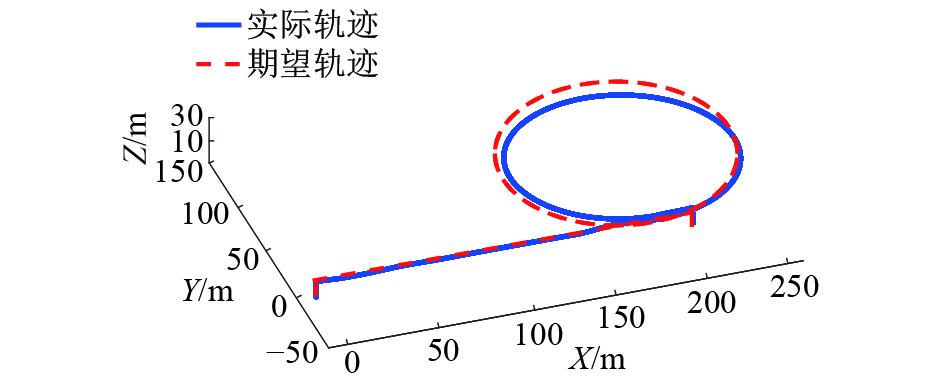
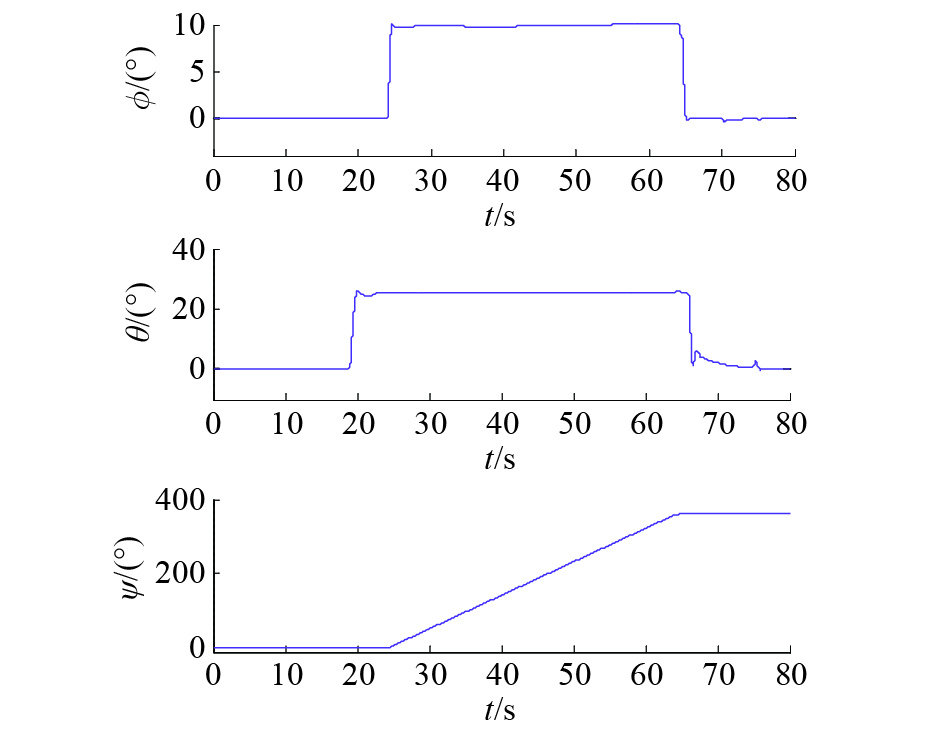
图4为仿真过程中本文所设计控制器下的QTR的期望轨迹与实际轨迹，可见实际轨迹基本能跟踪上期望轨迹。图5为与之对比未加扰动观测器的PID控制器下QTR的轨迹曲线，可见轨迹跟踪效果要劣于本文所设计的位置控制器。图6具体展示了仿真过程中QTR的位置及速度变化。图7为仿真过程中QTR的姿态角的变化情况，可以看出俯仰角在第20 s处变化到了25°，滚转角在24 s处变化到了10°以协调转弯的飞行方式跟踪半径为70 m的圆形期望轨迹段，同时从偏航角的改变可以看出QTR在轨迹跟随过程中不断调整机头方向朝向圆形轨迹切线方向以达到获得更大升力的效果。

4 结论

本文主要内容总结如下：

1) 设计了一种倾转旋翼无人机QTR；

2) 考虑了控制模型中的不确定项，基于扰动观测器设计了位置控制器，并证明了其稳定性；

3) 采用了鲁棒伺服线性二次型控制理论设计了姿态控制器。

主要针对所设计的倾转旋翼无人机QTR，考虑外部干扰动、建模误差以及输入时延的问题，提出并设计了一种基于误差观测器的位置控制器。通过设定的仿真场景，对位置控制器的有效性进行了验证，仿真结果表明所设计的基于误差观测器的位置控制器能良好的跟踪期望轨迹。在接下来的研究中将进一步完善基于误差观测器的位置控制器控制性能。