采用可变截面涡轮增压技术,既能使发动机在转速或负荷较低时,获得较高的转矩和增压压力,又能避免发动机过载而导致发动机承受过高的机械载荷和热负荷;同时也是加速涡轮增压系统瞬态响应,减小发动机排放的有效措施[1-2]。对于一台新研制的可变截面涡轮来说,设计性能和实际性能在一定程度上存在差异,并且可变截面涡轮 (VGT)实际性能对发动机与涡轮增压器以及可变截面涡轮与压气机之间的匹配有影响。因此对某型号可变截面涡轮进行性能实验,研究其实际性能具有重要意义,通过实验数据提出了预测可变截面涡轮流量特性的计算方法。
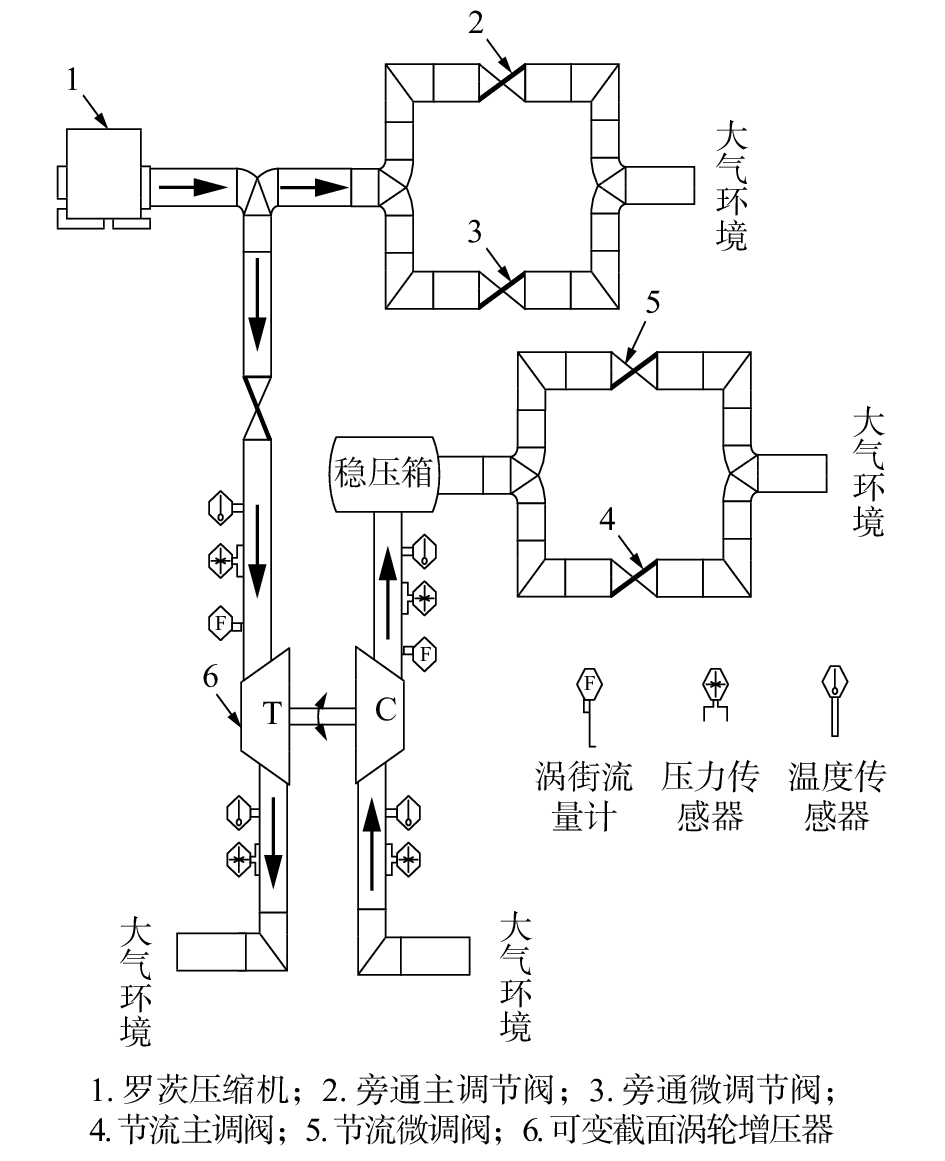
1 VGT性能实验 1.1 实验系统配置及实验原理可变截面涡轮试验系统由高压气源供给系统、高精度高灵敏度的数据采集系统、高精准的控制调节系统、高压滑油系统等组成。可变截面涡轮试验系统示意图如图1所示。试验中,由罗茨压缩机向可变截面涡轮试验系统提供一定流量的高压气体,驱动可变截面涡轮增压器对外做功。可变截面涡轮和压气机的进出口装有压力传感器和温度传感器,分别测量可变截面涡轮和压气机进出口的压力和温度。系统中的旁通主调阀和旁通微调阀,用来调节进入可变截面涡轮中气体的流量和压力。当旁通主调阀和旁通微调阀开度减小时,将会增加进入可变截面涡轮中气体的流量和压力,增压器转速升高,提高压气机出口压力。系统中的节流主调阀和节流微调阀,用来建立压气机出口压力。当节流主调阀和节流微调阀开度增大时,增压器转速下降,通过压气机的流量增大,压气机出口压力降低。通过联合调节旁通阀和节流阀,建立可变截面涡轮增压器中气体的稳定流动。
|
Download:
|
| 图 1 可变截面涡轮试验系统实验示意 | |
涡轮的主要特性包括流量特性和效率特性,本文采用涡轮折合流量
|
Download:
|
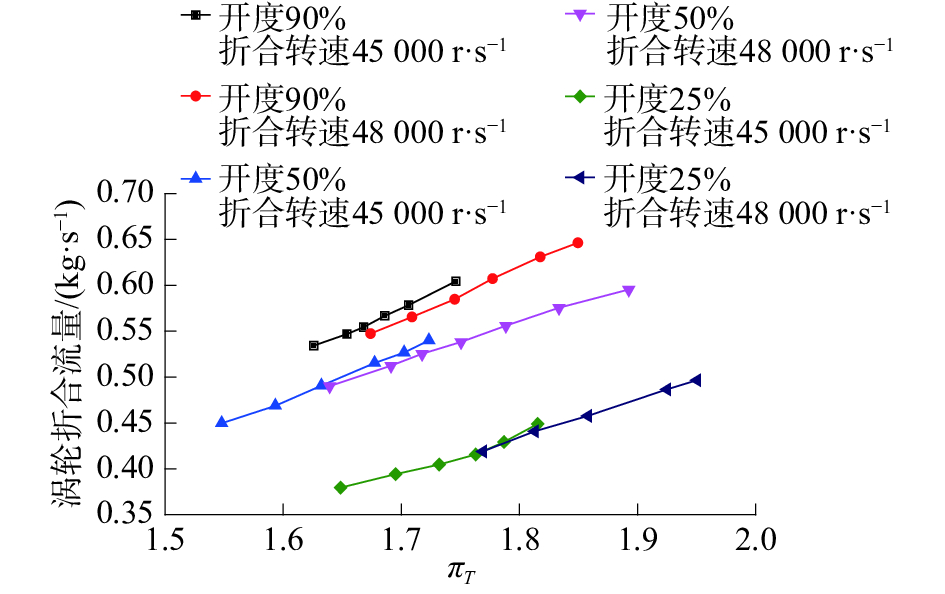
| 图 2 VGT流量特性 | |
|
Download:
|
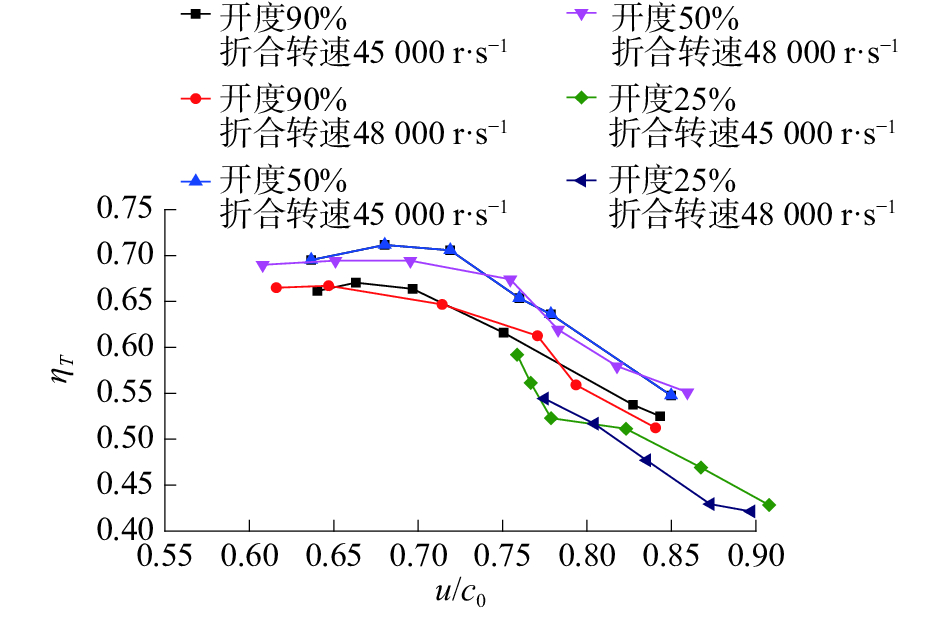
| 图 3 VGT效率特性 | |
由图2可以看出,相同喷嘴开度下,不同折合转速对涡轮折合流量的影响较小,并且在一定的膨胀比范围内,折合流量随膨胀比的增大而增大。相同膨胀比下,涡轮喷嘴环开度处于较小位置时的涡轮的折合流量比开度处于较大位置时的折合流量下降明显,有利于满足发动机低负荷或低速运行时,对小流量高压比进气的需求。
由图3可以看出,相同喷嘴环开度下,不同折合转速的效率特性相差很小。喷嘴环开度为50%时,具有涡轮的最高效率,而增大或减小开度时,涡轮效率均有所下降。喷嘴环开度的变化,并不会使涡轮总体效率产生显著的变化,当工况大幅度变化、VGT的喷嘴环开度随之大幅变化时,涡轮效率不会出现大幅的下降,因此能够获得稳定增压压力,提高发动机进气量,优化缸内燃烧,有助于提高发动机动力性和经济性。
2 VGT流量特性的预测方法如上所述,除了试验测定的方法来获取涡轮流量特性外,还可借助计算机,通过数值计算方法对涡轮流量特性进行预测。预测涡轮流量特性,不仅可以对涡轮的初期设计、涡轮增压器的匹配及涡轮与发动机的匹配提供指导,而且有利于涡轮变工况性能的研究[3-5]。预测可变截面涡轮流量特性,可以用于建立VGT与发动机匹配的简化控制模型,有助于实现可变截面涡轮增压器与发动机在全工况范围内的优化匹配[6-12]。
2.1 VGT流量的预测方法目前,广泛采用的计算涡轮流量特性的基本公式为
| $\frac{{{q_T}\sqrt {{T_T}^*} }}{{{P_T}^*}} = \mu {F_n}\sqrt {\frac{{2k}}{{R(k - 1)}}[{{(\frac{{{P_2}}}{{{P_T}^*}})}^{2/k}} - {{(\frac{{{P_2}}}{{{P_T}^*}})}^{(k + 1)/k}}]} $ |
式中:
从图2中可以看出,折合转速
| ${q_T}\sqrt {\frac{{{T_T}^*}}{{{T_0}^*}}} \frac{{{P_0}^*}}{{{P_T}^*}} = {m_{i1}} + {m_{i2}}{\pi _T}^2 + \frac{{{m_{i3}}}}{{{\pi _T}}}$ |
式中
| ${q_T}\sqrt {\frac{{{T_T}^*}}{{{T_0}^*}}} \frac{{{P_0}^*}}{{{P_T}^*}} = {S_m}({b_1} + {b_2}{\pi _T}^2) + {S_{m1_2}} + \frac{{({b_3} + {S_{m_2}}})}{{{\pi _T}}}$ |
为了考虑开度的不同对流量特性曲线产生的影响,建立可变截面涡轮全工况模型,引入的参变量
| $\begin{array}{l}{S_m} = {l_1} + {l_2}\alpha + {l_3}{\alpha ^2} + {l_4}{\alpha ^3}\\{S_{m_1}} = {c_1} + {c_2}\alpha + {c_3}{\alpha ^2} + {c_4}{\alpha ^3}\\{S_{m_2}} = {t_1}\exp ({t_2}\alpha )\end{array}$ |
各喷嘴环开度下参变量
|
|
表 1 涡轮流量特性系数 |
则可变截面涡轮流量特性的预测模型为
| $\begin{array}{l}{q_T}\sqrt {\displaystyle\frac{{{T_T}^*}}{{{T_0}^*}}} \displaystyle\frac{{{P_0}^*}}{{{P_T}^*}} = (0.094 \;7 + 6.253\alpha - 8.606{\alpha ^2} + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;3.246{\alpha ^3})(1.549 - 0.017 \;4{\pi _T}^2) + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(0.291 - 5.748\alpha + 8.223{\alpha ^2} - 2.745{\alpha ^3}) + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;[1.052\exp ( - 4.577\alpha ) - 1.473]/{\pi _T}\end{array}$ |
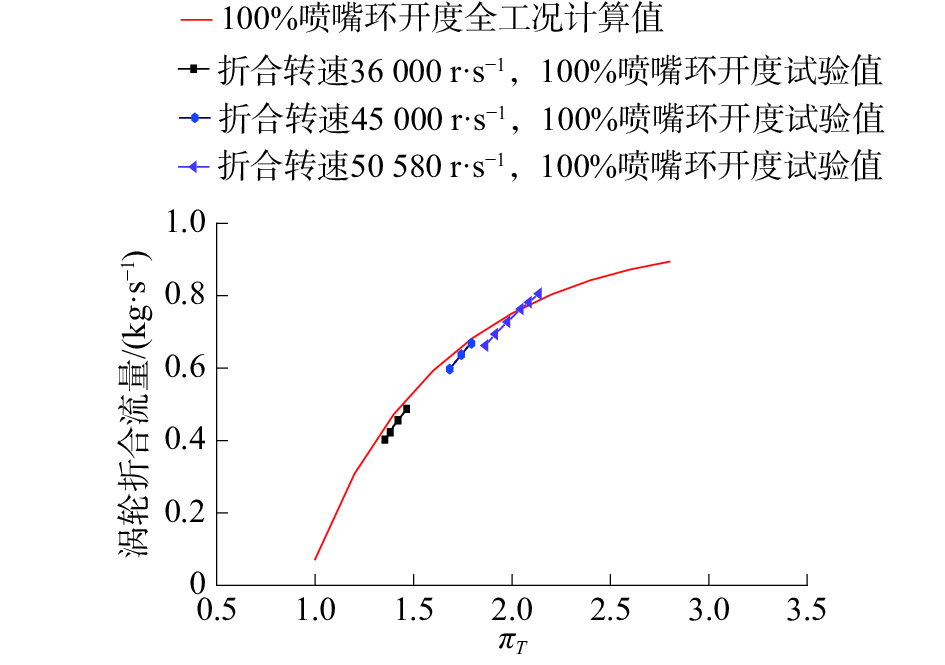
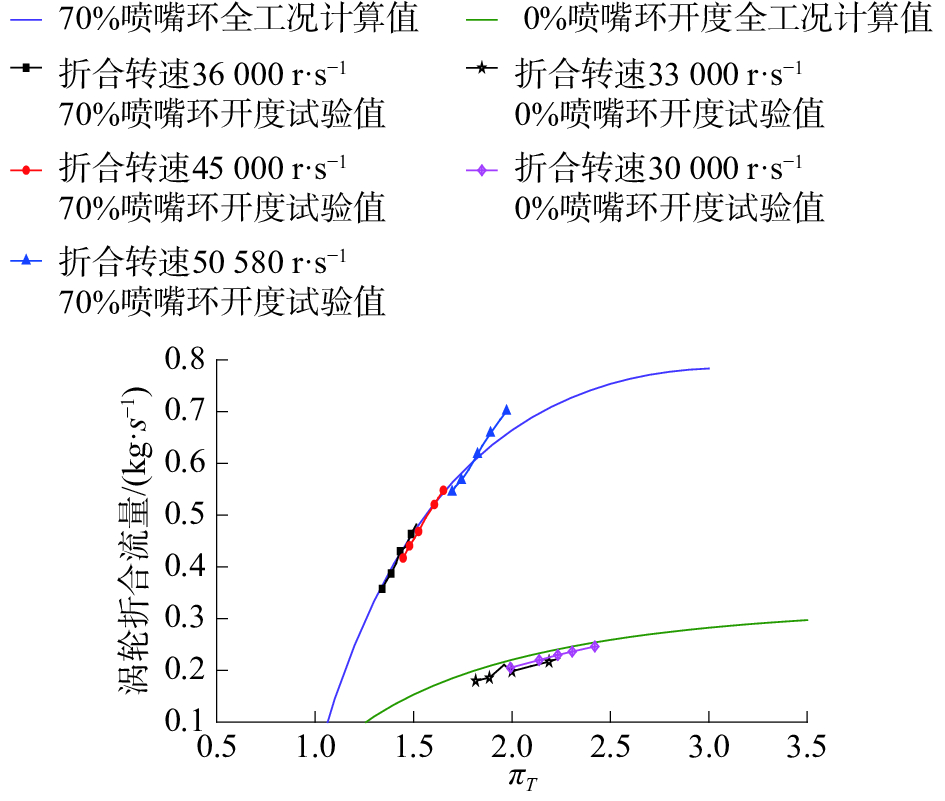
为了验证该方法的有效性,采用该方法预测了某种型号的可变截面涡轮在0%、70%和100%喷嘴环开度下的流量特性,并与实测的流量特性进行对比,如图4、5所示。从图4、5可以看出,试验值与实测值基本吻合。当预测精度要求小于5%时,该预测模型可以达到精度要求。该预测模型能够反映该型号可变截面涡轮的流量特性,有助于纠正试验中的错误数据。从试验中验证了这种预测方法能快速获得涡轮的流量特性,并且预测的流量特性具有较高的准确性。
|
Download:
|
| 图 4 某型VGT100%开度时预测流量与实测流量比较 | |
|
Download:
|
| 图 5 某型VGT0%和70%开度时预测流量与实测流量比较 | |
本文对某型可变截面涡轮性能试验进行介绍,依据实验数据提出了预测可变截面涡轮流量特性的方法,得出了以下结论:
1)可变截面涡轮转速,对流量特性的影响不明显。相同喷嘴环开度,通过可变截面涡轮的流量,随膨胀比的增大而增大;相同膨胀比,喷嘴环开度越小,通过可变截面涡轮的流量越小。
2)当喷嘴环开度小于50%时,相同膨胀比,通过可变截面涡轮的流量随开度的减小速率比喷嘴环开度大于50%,通过可变截面涡轮的流量随开度的减小速率大。
3)喷嘴环开度在50%时,可变截面涡轮的总体效率最高。当喷嘴环开度变化时,总体效率均有所下降。
4)利用最小二乘法,对实验数据进行处理,得出了基于实验数据的可变截面涡轮流量特性的预测方法。该预测方法优点在于,不需要涡轮的几何数据,并且该预测方法将可变截面涡轮流量特性,归一为涡轮膨胀比和喷嘴环开度的函数,由该预测模型得到的预测值与试验值比较,预测值具有较高的准确性。
| [1] |
张守动. 车用柴油机配VGT性能研究[D]. 武汉: 华中科技大学, 2014.
( 0) 0)
|
| [2] |
郭林福, 马朝臣, 施新, 等. VGT对柴油机经济性和动力性影响的试验研究[J]. 内燃机学报, 2004, 22(2): 116-121. DOI:10.3321/j.issn:1000-0909.2004.02.004 ( 0) 0)
|
| [3] |
郭林福. VGT电控增压系统的开发及其与柴油机优化匹配的研究[D]. 北京: 北京理工大学, 2003.
( 0) 0)
|
| [4] |
HATAMI M, CUIJPERS M C M, BOOT M D. Experimental optimization of the vanes geometry for a variable geometry turbocharger (VGT) using a design of experiment (DoE) approach[J]. Energy conversion and management, 2015, 106: 1057-1070. DOI:10.1016/j.enconman.2015.10.040 ( 0) 0)
|
| [5] |
TANCREZ M, GALINDO J, GUARDIOLA C, et al. Turbine adapted maps for turbocharger engine matching[J]. Experimental thermal and fluid science, 2011, 35(1): 146-153. DOI:10.1016/j.expthermflusci.2010.07.018 ( 0) 0)
|
| [6] |
CHAUVIN J, GRONDIN O, MOULIN P. Control oriented model of a variable geometry turbocharger in an engine with two EGR loops[J]. IFAC proceedings volumes, 2009, 42(26): 64-70. DOI:10.3182/20091130-3-FR-4008.00009 ( 0) 0)
|
| [7] |
WU Binyang, ZHAN Qiang, YU Xiaoyang, et al. Effects of Miller cycle and variable geometry turbocharger on combustion and emissions in steady and transient cold process[J]. Applied thermal engineering, 2017, 118: 621-629. DOI:10.1016/j.applthermaleng.2017.02.074 ( 0) 0)
|
| [8] |
陣内靖明, 有水大之, 田代直人, 等. 满足欧洲排放法规要求的车用柴油机可变截面涡轮增压器的开发[J]. 国外内燃机, 2014, 46(2): 25-30. DOI:10.3969/j.issn.2096-4870.2014.02.006 ( 0) 0)
|
| [9] |
董霏, 方存光. 可变截面废气涡轮增压器控制系统数学建型[J]. 科技资讯, 2014, 12(35): 81. DOI:10.3969/j.issn.1672-3791.2014.35.059 ( 0) 0)
|
| [10] |
倪计民, 刘越, 石秀勇, 等. 可变喷嘴涡轮增压及废气再循环系统改善柴油机排放性能[J]. 农业工程学报, 2016, 32(16): 82-88. DOI:10.11975/j.issn.1002-6819.2016.16.012 ( 0) 0)
|
| [11] |
詹志胜. 可变喷嘴涡轮增压器喷嘴环设计及非定常流场分析[D]. 北京: 北京理工大学, 2015.
( 0) 0)
|
| [12] |
TANG H, AKEHURST S, BRACE C J, et al. Optimisation of transient response of a gasoline engine with variable geometry turbine turbocharger[C]// Proceedings of the 11th International Conference on Turbochargers and Turbocharging. Amsterdam, Holland. 2014: 163-175.
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


