2. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001
2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
对于雨噪声研究, 有两类研究内容比较广泛, 一项是对雨噪声的功率谱研究[1-6], 另一项是对水滴或雨噪声信号进行研究探讨[7-14], 本文对雨噪声的研究主要基于单水滴信号, 通过对单水滴和多水滴时域波形的测量分析, 得到水滴声信号的主要波形及频谱特征, 据此模拟降雨噪声。
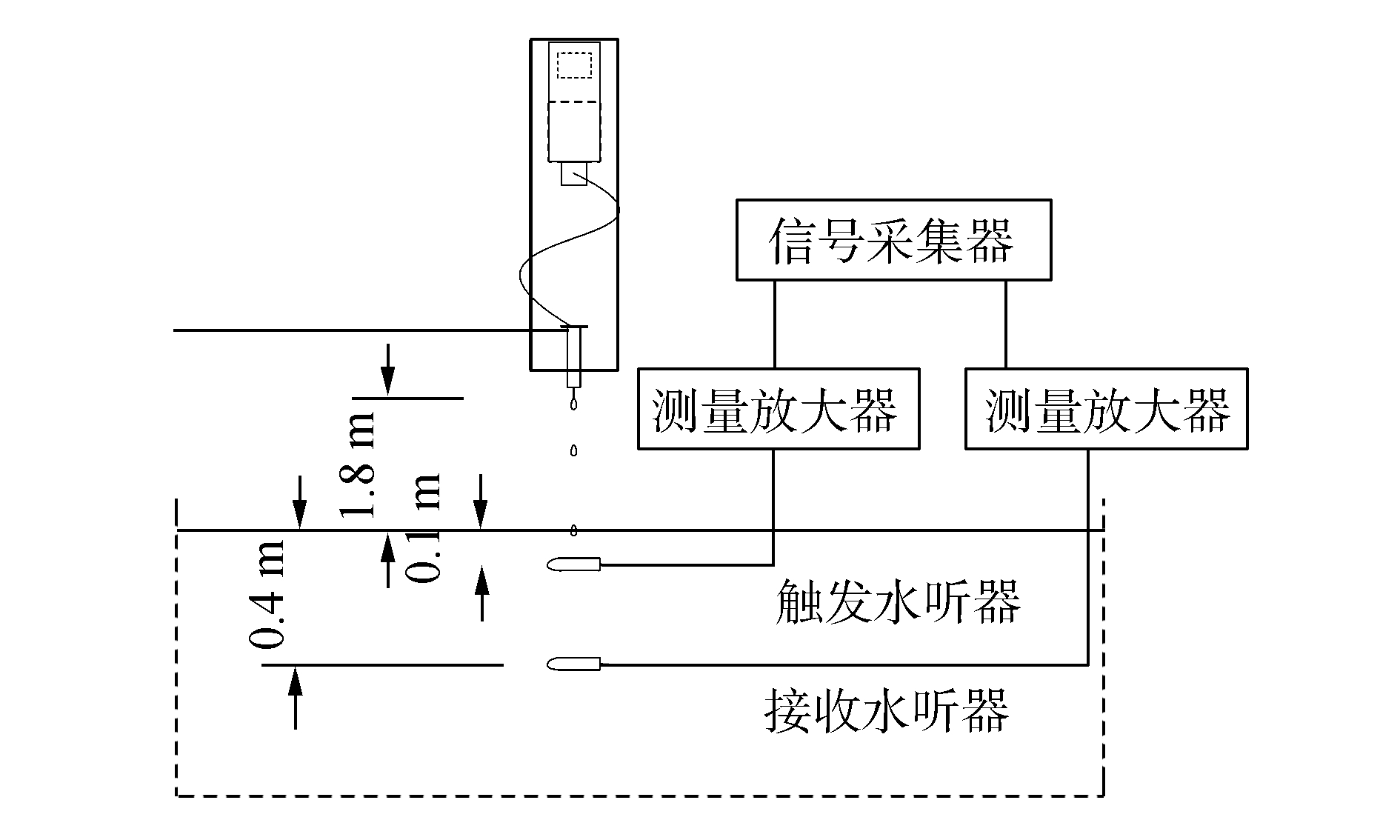
1 水滴声信号测量 1.1 单水滴声信号测量实验概况本节通过实验测量水滴溅落声, 研究其波形及频谱统计规律。实验在消声水池中进行, 测量框图如图 1所示。
|
Download:
|
| 图 1 水滴测量实验框图 | |
放置一个注射器针管, 针头距离水面1.8 m。其上固定水瓶, 水瓶底部开口以便进水, 保证水顺利流出。水瓶接输液管, 控制流速, 使得针头处缓慢形成水滴依靠自身重力滴下(约2~3 s一滴)。本实验中, 认为水滴大小是固定的。经测量, 水滴等效直径为3.3 mm。
1.2 多水滴声信号测量将容器底部穿孔并安置针头。在容器底部铺上滤纸, 以缓和水滴速度, 能使水成滴落下, 而不是直接流出。容器吊在固定的法兰盘下, 底部距水面1.8 m。位于水下0.4 m的标准水听器接收信号, 经过放大滤波接到采集器上。实验示意图如图 2所示。

|
Download:
|
| 图 2 多水滴实验示意 | |
一个完整的水滴声信号包含2种声信号, 一种为初始冲击声, 水滴冲击水表面时立即产生的信号, 每次水滴落下都会产生, 在时间上最早出现; 另一种为初始冲击声之后150~250 ms处呈衰减形式的波形, 可以是一组或几组波形, 这些波形可能是水滴的二次溅落、气泡破裂或气泡脉动产生的。这种衰减信号在频率上的变化很大, 说明这些小水滴或气泡大小并不总是一致的[9], 文中统称为非初始冲击声。
典型水滴声信号时域波形如图 3所示。图中可见, 在水下0.4 m处接收到的水滴噪声声压可达到2 Pa, 并且组成并不单一, 而是由几种波形组成。图 4展示了图 3中各个信号的细节, 两者在时间上是对应的。

|
Download:
|
| 图 3 水滴声信号 | |

|
Download:
|
| 图 4 水滴声信号细节 | |
从图 4中可以看到, 除了初始冲击声, 还有3个衰减信号。衰减信号可能是气泡或二次溅落的水滴产生的声信号。对其波形、幅度、频率进行统计分析, 可获得其统计规律。
对多组单水滴声信号的频谱进行平均, 结果如图 5所示。由图 5中可见, 能量较为均匀地分布在5~20 kHz, 在15 kHz左右存在1个能量较低区域, 在14 kHz和19 kHz左右存在线谱簇。

|
Download:
|
| 图 5 水滴声频谱 | |
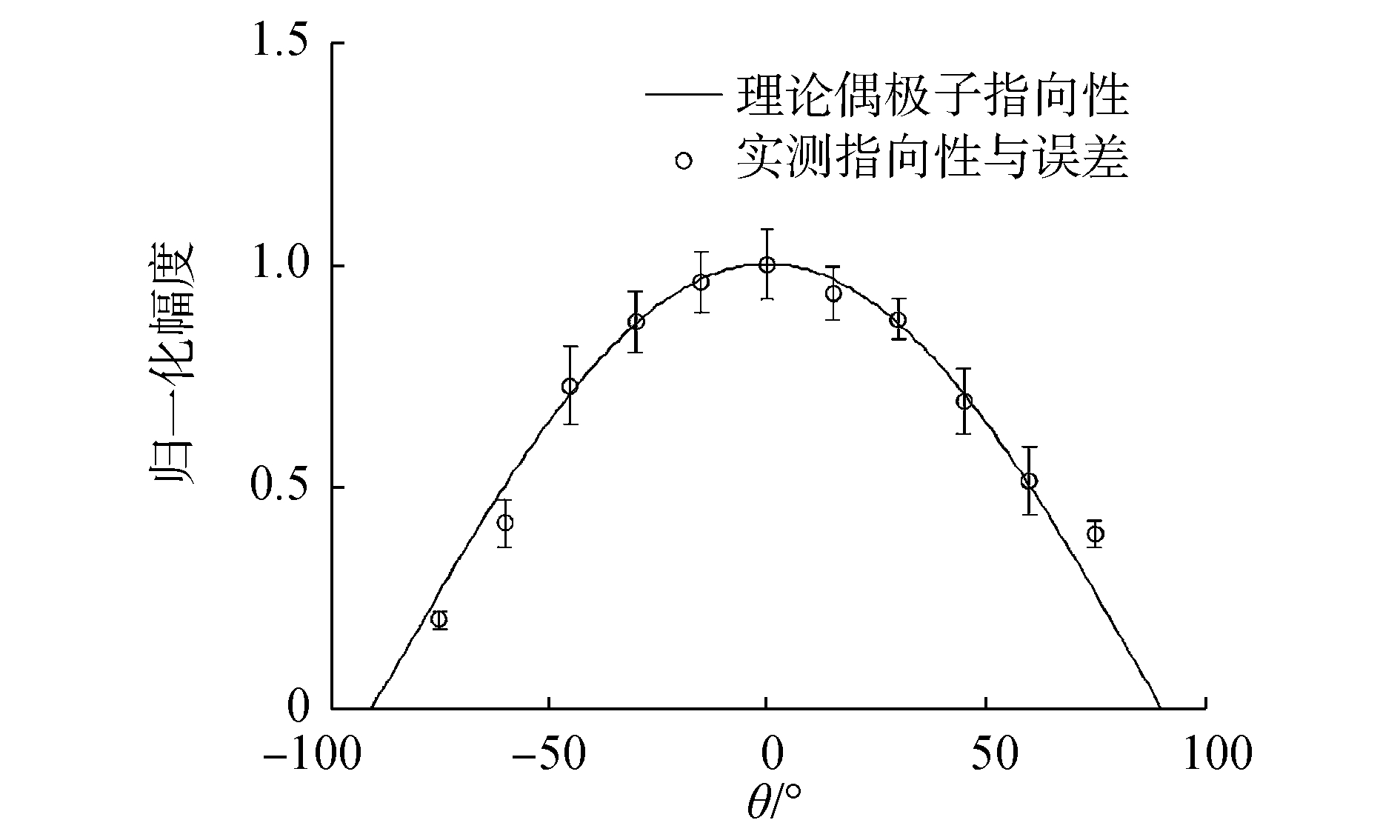
每一个水滴产生的声信号中都存在初始冲击声, 并且出现时间与持续时间较为固定, 因此根据初始冲击声的最大值进行指向性分析。实验共测量了11个角度, 从15°~165°(掠射角), 以15°为间隔, 每个角度下采集50个水滴样本, 水听器与水滴滴入点距离为0.5 m, 对同一位置的水滴声无法保证每次初始冲击声幅度是相同, 因此对50个水滴样本进行平均, 求误差, 并与偶极子指向性进行比较, 得到图 6。
|
Download:
|
| 图 6 指向性测量误差 | |
图 6中零度角为水滴正下方。可见, 在一定误差内, 初始冲击声指向性可以认为是与偶极子相同的。在小掠射角下, 由于信噪比较低, 因此误差较大。
2.2 单水滴声信号统计特性本文对水滴声统计的侧重点主要为幅度及波形特征。单水滴声信号测量实验中, 对单水滴声信号进行了分析与统计, 包括初始冲击声与非初始冲击声的幅度及波形特征。
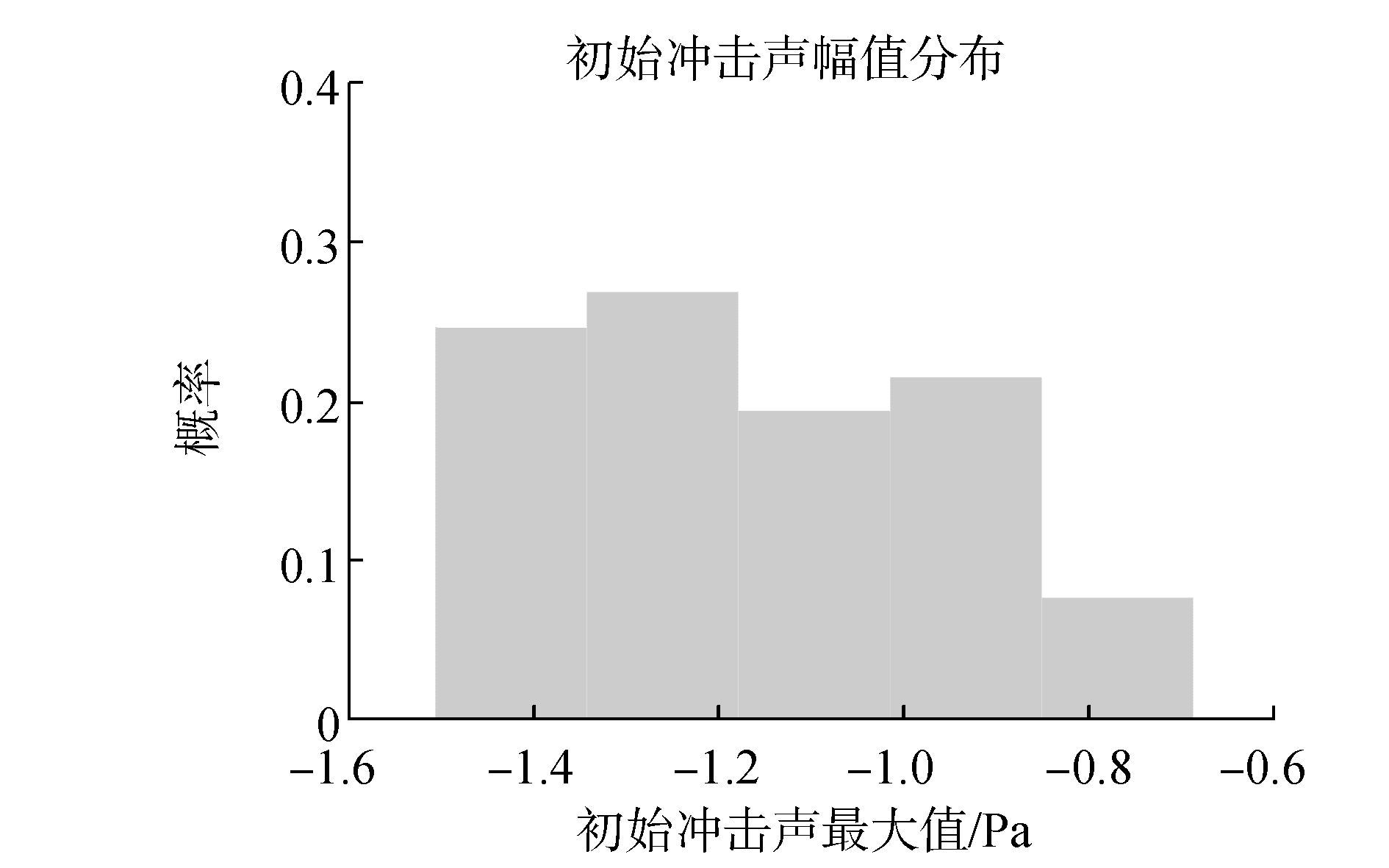
对初始冲击声幅值进行统计, 得到图 7。
|
Download:
|
| 图 7 初始冲声幅值分布 | |
除了初始冲击声, 其余声信号的出现时间并无一定规律。在本次实验的样本中, 一个水滴产生的声信号中, 非初始冲击声最多有3组, 出现组数与比例如图 8所示。

|
Download:
|
| 图 8 单次声信号出现非初始冲击声个数 | |
这些非冲击声波形组成也比较复杂, 按照波形分类一般分为4种[12]:A为指数衰减, B为阻尼振动衰减, C在波形上类似于辛格函数, D为近似调制的衰减信号。实验数据中各类波形如图 9所示。

|
Download:
|
| 图 9 4种声信号波形 | |
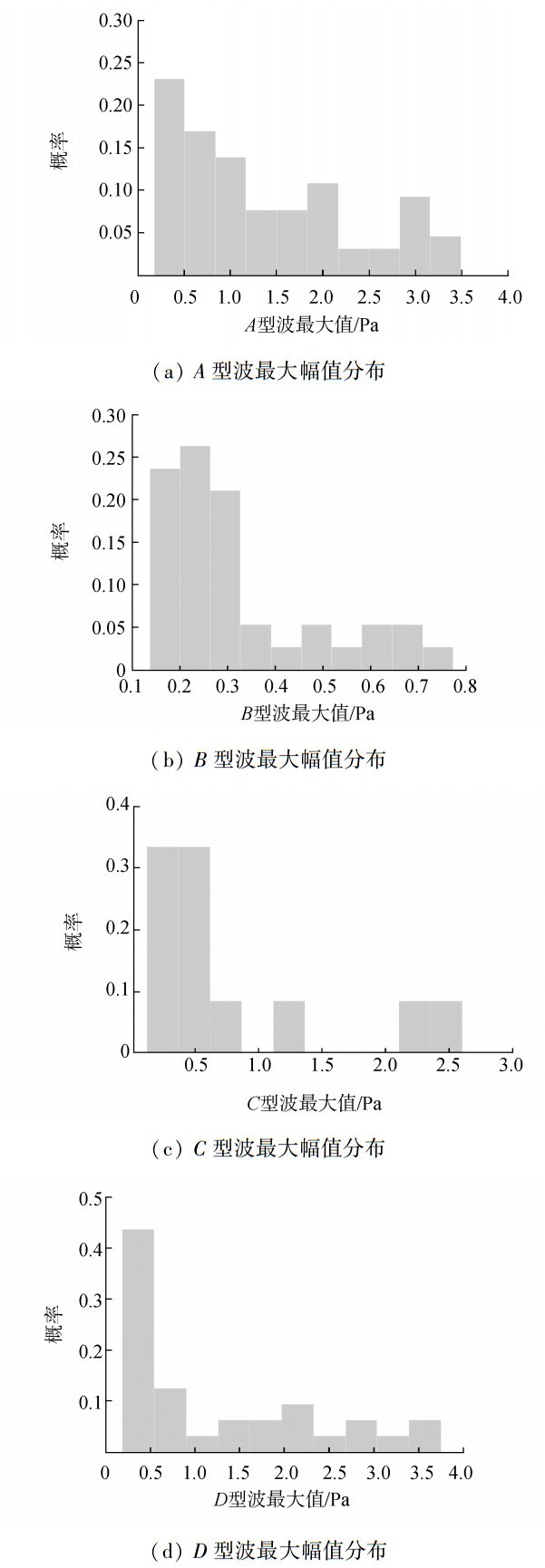
其中, A类波形比例最大, 约占50%, B和D近似, 各占20%, C类占比例最小, 仅有10%左右。按波形分类对幅值进行统计, 结果如图 10所示。
|
Download:
|
| 图 10 4种波形幅值分布 | |
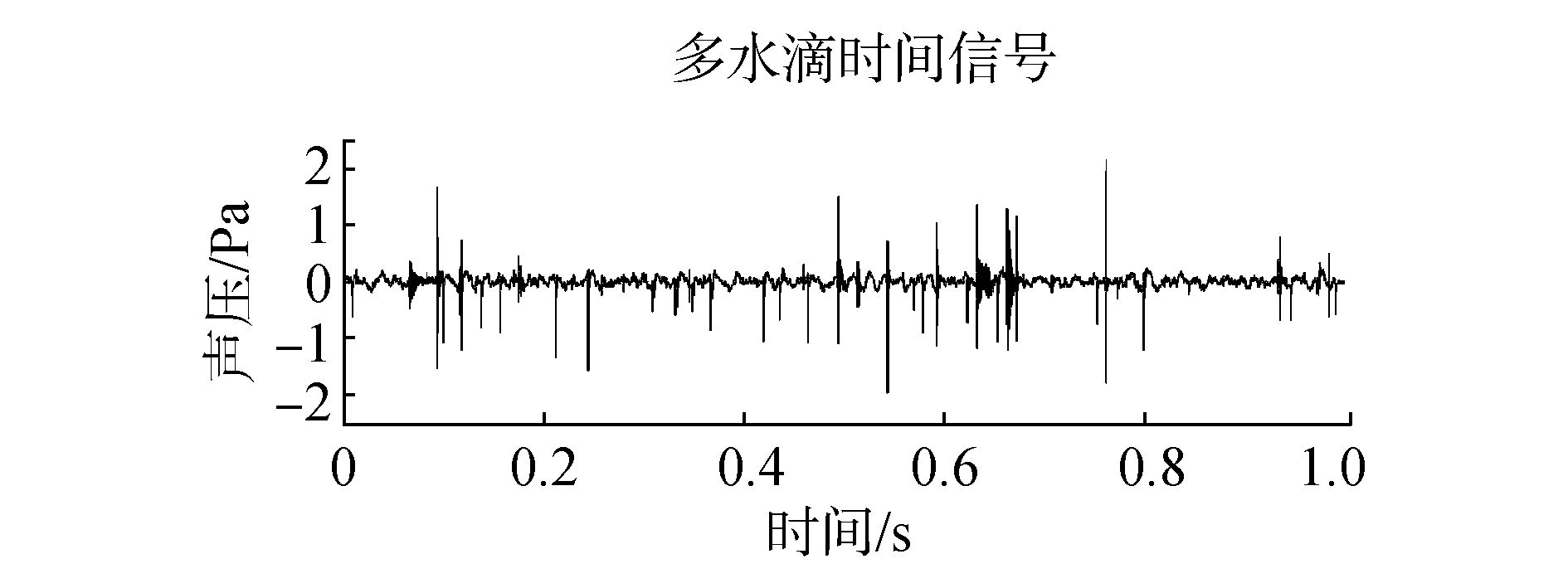
多水滴声信号时域波形如图 11。
|
Download:
|
| 图 11 多水滴声信号 | |
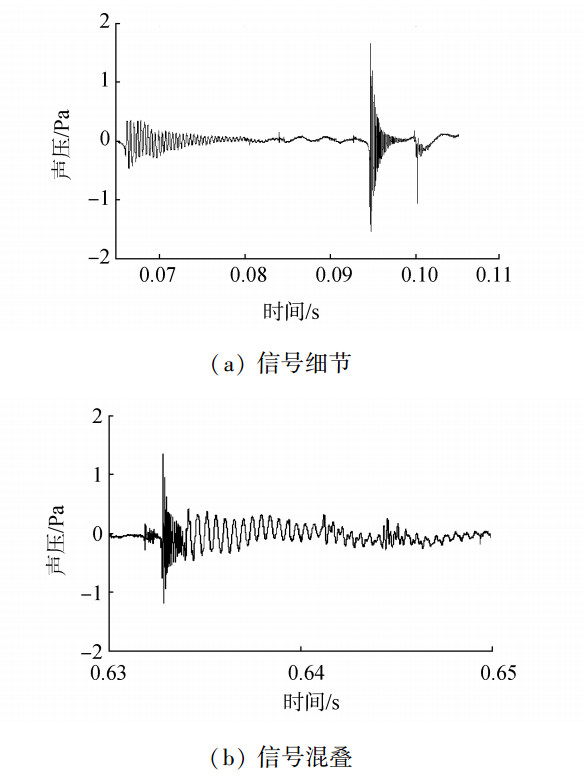
较明显的低频波动是由于多水滴落下的重力表面波的相互干扰。信号细节如图 12所示。
|
Download:
|
| 图 12 多水滴声信号细节 | |
对于多水滴信号, 由于同时落下的水滴并不足够多, 各个波形在时间上一般可以分得开。但是仍然有信号混叠的情况存在。
3 多水滴噪声的仿真从时间上, 多水滴信号可以看做单水滴信号以不同的时延的相加, 空间上则需要加入距离算子与指向性函数。设单水滴信号为S(t), 则接收点处接收到的第n个水滴到信号为Sn(t-τn)/Rn, 那么, 多水滴声信号可表示为
| $ {S_{{\rm{mul}}}} = \sum\limits_{n = 1}^N {{S_n}(t-{\tau _n})/{R_n}} $ |
单水滴信号可分解为初始冲击声与非初始冲击声, 从单水滴声信号中提取初始冲击声与非初始冲击声, 建立波形库。依据前文统计得到的各波形出现概率与幅度(如图 7、8和10所示), 从波形库中提取波形并叠加, 得到单水滴声信号S(t), 将单水滴声信号以不同时延叠加, 从而得到多水滴声信号。
其中, 根据分布函数生成随机数通常采用反变换法[15], 详细步骤如下:
1) 计算x的分布函数F(x), 令F(x)=y;
2) 解x=G(y), 即G=F-1;
3) 均匀分布产生yi, 则xi=G(yi)为所需变量。
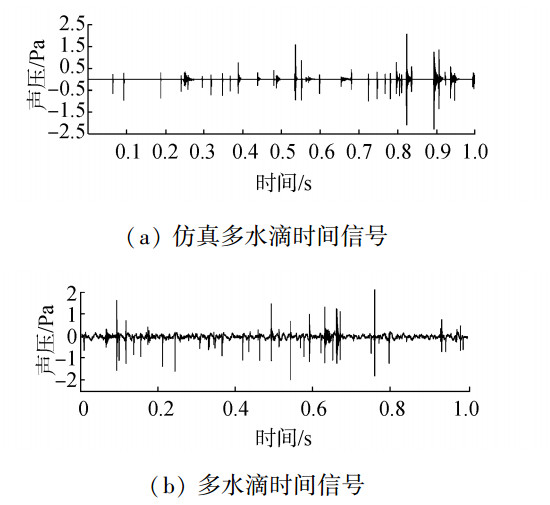
据此仿真多水滴声信号, 时域上的仿真信号和实测信号如图 13所示。
|
Download:
|
| 图 13 仿真与实测多水滴声信号 | |
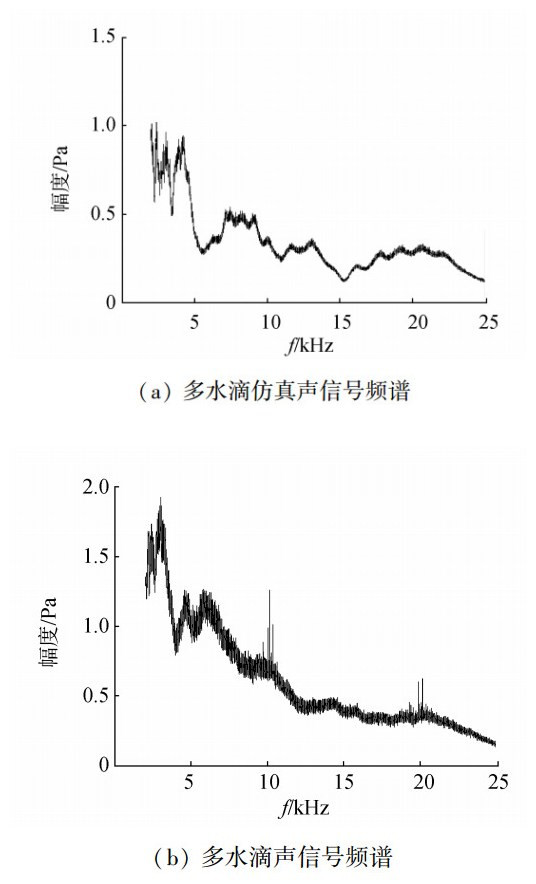
对仿真的多组单水滴信号进行处理, 得到其频谱。仿真时没有加入噪声, 因此得到的幅值大小不同。由图 13可见仿真与实验时域信号形式较为接近。图 14为仿真与实测多水滴声频谱图, 由图 14可见, 重构信号与实测信号在频谱形式较为接近, 与仿真信号相比, 实测信号只在幅值上有所增加, 这是由于在测量中背景噪声对其产生的影响。
|
Download:
|
| 图 14 仿真与实测多水滴声频谱 | |
1) 本文实验研究了水滴噪声信号的统计特性。从时域波形上可见, 水滴声信号的主要组成部分有初始冲击声和4种波形的非初始冲击声。统计得到单水滴声信号出现一组至三组非初始冲击声的概率, 初始冲击声的幅度分布, 得到了4种波形的比例及幅值分布。并对初始冲击声的指向性进行分析, 验证了水滴声指向性与偶极子相近。
2) 根据信号波形的分类建立了信号波形库。认为多水滴声信号为单水滴声信号的线性叠加, 根据统计结果从信号库中进行波形的选择, 配置幅度与时间, 从而得到仿真的多水滴声信号。和实验结果相比, 仿真信号在统计意义上符合雨滴噪声特性。因此, 本文仿真水滴信号的方法可用于实验环境中雨噪声的模拟。
| [1] |
VAGLE S, LARGE W G, FARMER D M. An evaluation of the WOTAN technique of inferring oceanic winds from underwater ambient sound[J]. Journal of atmospheric and oceanic technology, 1990, 7(4): 576-595. DOI:10.1175/1520-0426(1990)007<0576:AEOTWT>2.0.CO;2 ( 0) 0)
|
| [2] |
NYSTUEN J A. Acoustical rainfall analysis:rainfall drop size distribution using the underwater sound field[J]. Journal of atmospheric and oceanic technology, 1996, 13(1): 74-84. DOI:10.1175/1520-0426(1996)013<0074:ARARDS>2.0.CO;2 ( 0) 0)
|
| [3] |
MA B B, NYSTUEN J A, LIEN R C. Prediction of underwater sound levels from rain and wind[J]. The journal of the acoustical society of America, 2005, 117(6): 3555-3565. DOI:10.1121/1.1910283 ( 0) 0)
|
| [4] |
MA B B, NYSTUEN J A. Passive acoustic detection and measurement of rainfall at sea[J]. Journal of atmospheric and oceanic technology, 2005, 22(8): 1225-1248. DOI:10.1175/JTECH1773.1 ( 0) 0)
|
| [5] |
NYSTUEN J A, AMITAI E, ANAGNOSTOU E N, et al. Spatial averaging of oceanic rainfall variability using underwater sound:Ionian sea rainfall experiment 2004[J]. The journal of the acoustical society of America, 2008, 123(4): 1952-1962. DOI:10.1121/1.2871485 ( 0) 0)
|
| [6] |
刘贞文. 海上降雨的噪声特性研究[D]. 厦门: 厦门大学, 2012. http://dspace.xmu.edu.cn/handle/2288/52846?show=full
( 0) 0)
|
| [7] |
ASHOKAN M, LATHA G, RAMESH R. Analysis of shallow water ambient noise due to rain and derivation of rain parameters[J]. Applied acoustics, 2015, 88: 114-122. DOI:10.1016/j.apacoust.2014.08.010 ( 0) 0)
|
| [8] |
NYSTUEN J A. Rainfall measurements using underwater ambient noise[J]. The journal of the acoustical society of America, 1986, 79(4): 972-982. DOI:10.1121/1.393695 ( 0) 0)
|
| [9] |
MEDWIN H, KURGAN A. Impact and bubble sound from raindrops at normal and oblique incidence[J]. The journal of the acoustical society of America, 1990, 88(1): 413-418. DOI:10.1121/1.399918 ( 0) 0)
|
| [10] |
MEDWIN H, NYSTUEN J A, JACOBUS P W, et al. The anatomy of underwater rain noise[J]. The journal of the acoustical society of America, 1992, 92(3): 1613-1623. DOI:10.1121/1.403902 ( 0) 0)
|
| [11] |
NYSTUEN J A, OSTWALD L H JR. The hydroacoustics of a raindrop impact[J]. The journal of the acoustical society of America, 1992, 92(2): 1017-1021. DOI:10.1121/1.404030 ( 0) 0)
|
| [12] |
MEDWIN H, BEAKY M M. Bubble sources of the Knudsen sea noise spectra[J]. The journal of the acoustical society of America, 1989, 86(3): 1124-1130. DOI:10.1121/1.398104 ( 0) 0)
|
| [13] |
张卫强. 水滴溅落噪声特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2012. http://www.docin.com/p-1500758105.html
( 0) 0)
|
| [14] |
田茹妍. 水滴入水过程及其水噪声试验研究[D]. 沈阳: 沈阳农业大学, 2017.
( 0) 0)
|
| [15] |
叶其孝, 沈永欢. 实用数学手册[M]. 北京: 科学出版社, 2006.
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


