由于带外辐射低且能同时抵抗符号间干扰(inter-symbol interference，ISI)和载波间干扰(inter-channel interference，ICI)等特性，FBMC被视为5 G中重要的候选波形。但是FBMC系统中，子载波基函数的正交条件只在实数域上成立，使得子载波和符号间存在固有的虚部干扰，信道估计相比传统的OFDM系统更具有挑战性。FBMC中常用的信道估计方法主要分为干扰消除、干扰利用和干扰规避3种。干扰消除包括将周围数据置零、让周围干扰相互抵消和辅助导频法(auxiliary pilot, AP)等方法^[1]。干扰利用的典型代表为干扰近似法(interference approximation method，IAM)^[2-4]。干扰规避中最具代表性的为成对导频法(pair of pilots，POP)^[5]。上述这些方法为便于处理都假设信道慢变，且对模型进行了简化，采用这种不精确的模型会造成残余干扰，在高信噪比下存在性能瓶颈。文献[6]给出了线性最小均方误差(linear minimum mean square error，LMMSE)和加权最小二乘(weighted least square，WLS)两种时域信道估计方案。该方法不存在性能瓶颈且对时间同步误差不敏感。文献[7]给出了使WLS方法估计误差最小的导频。但是文献[6−7]为了减小数据对导频的干扰，用了几列0将导频与数据隔离，这种处理方法计算简单但效果并不是最优的。本文的方法是充分利用导频信息将2、3列导频设计为合适的数值来增强估计效果。此外，现有的方法只考虑了同一符号子载波上噪声的相关性，事实上相邻符号子载波上的噪声也是相关的。利用这种相关性能进一步增强信道估计效果。

1 系统模型

FBMC的基带输出信号s[k]的表达式为

$s\left[ k \right] = \sum\limits_{m = 0}^{M - 1} {\sum\limits_{n \in Z} {{a_{m,n}}} } g\left[ {k - n\frac{M}{2}} \right]{{{e}}^{{{j2\pi }}mk/M}}{{{e}}^{{{j\pi }}\left( {m + n} \right)/2}}$

经过长度为L的信道后，接收端的解调结果为

$\begin{split}{{\hat a}_{m,n}} & = \sum\limits_{l = 0}^{L - 1} {\sum\limits_{k = - \infty }^\infty {\sum\limits_{p = 0}^{M - 1} {\sum\limits_{q \in Z} {{a_{p,q}}g\left[ {k - l - q\frac{M}{2}} \right]} } } } g\left[ {k - n\frac{M}{2}} \right]\times \\& {{{e}}^{{{j2\pi }}\left( {p - m} \right)k/M}} \cdot {{{e}}^{{{j\pi }}\left( {p + q - m - n} \right)/2}} \cdot {{{e}}^{ - {{j2\pi }}pl/M}}h\left[ l \right] + {\eta _{m,n}}\end{split}$

解调符号的第一列用来进行信道估计，但是实际上由于FBMC相邻符号是重叠的，导频符号会受到相邻符号数据的干扰。因此通常在导频符号与数据之间插入几个全为零的符号来将干扰减少到一个可以接受的程度。为简单起见，假设符号间的干扰通过插入足够数量的全为零的符号全部消除，则接收的导频表达式为

$\begin{split}{{\hat a}_{m,0}} & = \sum\limits_{l = 0}^{L - 1} {\sum\limits_{k = - \infty }^\infty {\sum\limits_{p = 0}^{M - 1} {{a_{p,0}}} } } g\left[ {k - l} \right]g\left[ k \right]{{{e}}^{{{j2\pi }}\left( {p - m} \right)k/M}}\times \\& {{{e}}^{{{j\pi }}\left( {p - m} \right)/2}}{{{e}}^{ - {{j2\pi }}pl/M}}h\left[ l \right] + {\eta _{m,0}}\end{split}$

(1)

将式(1)表示为向量形式：

${{{r}}_{{0}}} = {{\varGamma h}} + {{{\eta }}_0}$

式中： ${{{r}}_0} = {\left[ {{{\hat a}_{0,0}},{{\hat a}_{1,0}}, \cdots ,{{\hat a}_{M - 1,0}}} \right]^{{T}}}$ ； ${{h}}$ 为采样后的信道响应， ${{h}} = {\left[ {h\left( 0 \right),h\left( 1 \right), \cdots ,h\left( {L - 1} \right)} \right]^{{T}}}$ ； ${{{\eta }}_0}$ 为噪声向量， ${{{\eta }}_0} = {\left[ {{\eta _{0,0}},{\eta _{1,0}}, \cdots ,{\eta _{M - 1,0}}} \right]^{{T}}}$ ； ${{\varGamma }}$ 是一个由导频符号与原型滤波器决定的 $M$ 行 $N$ 列的矩阵，其第 $m$ 行 $l$ 列的元素 ${\varGamma _{m,l}}$ 为

$\begin{split}{\varGamma _{m,l}} & = \sum\limits_{k = - \infty }^\infty {\sum\limits_{p = 0}^{M - 1} {{a_{p,0}}} } g\left[ {k - l} \right]g\left[ k \right]{{{e}}^{{{j2\pi }}\left( {p - m} \right){k / M}}} \times \\& {{{e}}^{{{j2\pi }}{{\left( {p - m} \right)} / 2}}}{{\mathop{ e}\nolimits} ^{ - {{j2\pi }}p{l / M}}}\end{split}$

由于子载波噪声之间的相关性，采用加权最小二乘法进行信道估计，信道响应 ${{h}}$ 的估计值为

${{\hat{ h}}_{{{WLS}}}} = {\left( {{{{\varGamma }}^{{H}}}{{{C}}^{ - 1}}{{\varGamma }}} \right)^{ - 1}}{{{\Gamma }}^{{H}}}{{{C}}^{ - 1}}{{{r}}_0}$

式中 ${{C}}$ 是噪声的协方差矩阵，具体表达式为

${{C}} = \left[ {\begin{array}{*{20}{c}} {{\sigma ^2}} & {{\sigma ^2}\zeta _{0,0}^{1,0}} & \cdots & {{\sigma ^2}\zeta _{0,0}^{M - 2,0}} & {{\sigma ^2}\zeta _{0,0}^{M - 1,0}} \\ [6pt] {{\sigma ^2}\zeta _{1,0}^{0,0}} & {{\sigma ^2}} & \cdots & {{\sigma ^2}\zeta _{1,0}^{M - 2,0}} & {{\sigma ^2}\zeta _{1,0}^{M - 1,0}} \\ [6pt] \vdots & \cdots & \cdots & \cdots & \vdots \\ [6pt] {{\sigma ^2}\zeta _{M - 2,0}^{0,0}} & {{\sigma ^2}\zeta _{M - 2,0}^{1,0}} & \cdots & {{\sigma ^2}} & {{\sigma ^2}\zeta _{M - 2,0}^{M - 1,0}} \\ [6pt] {{\sigma ^2}\zeta _{M - 1,0}^{0,0}} & {{\sigma ^2}\zeta _{M - 1,0}^{1,0}} & \cdots & {{\sigma ^2}\zeta _{M - 1,0}^{M - 2,0}} & {{\sigma ^2}} \end{array}} \right]$

(2)

式中 ${\sigma ^2}\zeta _{{m_1},0}^{{m_2},0}$ 表示 ${\eta _{{m_1},0}}$ 和 ${\eta _{{m_2},0}}$ 的协方差。时域估计方法的克拉美罗界为 ${{tr}}\left[ {{{\left( {{{{\Gamma }}^{{H}}}{{{C}}^{ - 1}}{{\Gamma }}} \right)}^{ - 1}}} \right]$ 。

2 算法扩展

当导频的后几列不为零时，接收的导频为

$\begin{split}{{\hat a}_{m,0}} & = \sum\limits_{l = 0}^{L - 1} {\sum\limits_{k = - \infty }^\infty {\sum\limits_{p = 0}^{M - 1} {\sum\limits_{q \in \Psi } {{a_{p,q}}g\left[ {k - l - q\frac{M}{2}} \right]} g\left[ k \right]} } } \times \\& {{{e}}^{{{j2\pi }}\left( {p - m} \right)k/M}}{{{e}}^{{{j\pi }}\left( {p + q - m} \right)/2}}{{{e}}^{ - {{j2\pi }}pl/M}}h\left[ l \right] + {\eta _{m,0}}\end{split}$

(3)

式中 $\varPsi $ 是导频符号列序号的集合，将式(3)记作

${{{r}}_{{0}}} = \left( {{{S}} + {{U}}} \right){{h}} + {{{\eta }}_{{0}}}$

(4)

式中：

${{{S}}_{m,l}} = \sum\limits_{k = - \infty }^\infty {{a_{m,0}}g\left[ {k - l} \right]g\left[ k \right]{{ e}^{ - j2\pi m{l / M}}}} ,$

$\begin{split}{{{U}}_{m,l}}& = \sum\limits_{k = - \infty }^\infty {\sum\limits_{p = 0,p \ne m}^{M - 1} {\sum\limits_{q \in \psi } {{a_{p,q}}} } } g\left[ {k - l - q\frac{M}{2}} \right]g\left[ k \right] \times \\[8pt]& {{{e}}^{j2\pi \left( {p - m} \right)k/M}}{{{e}}^{{{j\pi }}\left( {p + q - m} \right)/2}}{{{e}}^{ - {{j2\pi }}pl/M}}\end{split}$

此时 ${{h}}$ 的最大似然估计为

$\hat{ h}={\left( {{{\left( {{{S}} + {{U}}} \right)}^{{H}}}{{{C}}^{ - 1}}\left( {{{S}} + {{U}}} \right)} \right)^{ - 1}}{\left( {{{S}} + {{U}}} \right)^{{H}}}{{{C}}^{ - 1}}{{{r}}_0}$

估计误差下界为

${{tr}}\left\{ {{{\left[ {{{\left( {{{S}} + {{U}}} \right)}^{{H}}}{{{C}}^{ - 1}}\left( {{{S}} + {{U}}} \right)} \right]}^{ - 1}}} \right\}$

常见的导频形状分为全导频和稀疏导频两种情况，其具体结构见图1。下面将研究本文所提方法在两种结构下的导频设计问题。

2.1 全导频情况

全导频是指前三列全用来做导频的结构，这种方法的导频开销与传统的IAM方法一致。导频设计的原则就是为图1(a)中的前三列选择数值使式(4)最小，但是这个问题的求解异常困难。

为了简化问题的求解，假定导频数值范围为 ${{Y }} = \left\{ {{{1}},j, - 1, - j} \right\}$ ，求解出的导频满足以下形式：

$a = {1_{\frac{M}{4}}} \otimes b$

式中： ${1_{\frac{M}{4}}}$ 表示数值全为1，长度为M/4的向量， $ \otimes $ 表示克罗内克积，矩阵b具有如下形式：

${{b}} = {\left[ {\begin{array}{*{20}{c}} 1 & { - j} & { - 1} & j \\ { - j} & { - 1} & j & 1 \\ { - 1} & j & 1 & { - j} \end{array}} \right]^{{T}}}$

2.2 稀疏导频情况

文献[7]中的稀疏导频是只有一些孤立的子载波非零，周围都是空子载波。本文中的稀疏导频与文献[8−10]类似，所有导频符号均非零，一部分是观测点，用来信道估计，周围的起辅助作用，减小估计误差。由于观测点数只需等于或略大于信道时域响应长度，使得估计方程大大简化，求解也较为容易。缺点是由于方程组中方程数量变少，最小二乘估计的效果减弱，估计误差比全导频情况大。

本文假定导频点等间隔分布，导频中心点p的位置满足如下的关系：

$\left\{ {\left. p \right|p = {p_0} + i \cdot u + 1,i = 0,1, \cdots ,\left\lfloor {M/u} \right\rfloor } \right\},\;u = \left\lfloor {M/L} \right\rfloor $

式中：L为信道时域响应长度，M为子载波个数。为不失一般性，取 ${p_0} = 0$ 。

3 联合估计

通常情况下，相邻几个符号历经的信道响应保持不变，利用相邻列的导频信息联合估计能利用更多的有用信息，理论上可以取得更好的效果。详细过程表述如下：

第二列导频的接收结果为

$\begin{split}{{\hat a}_{m,1}} & = \sum\limits_{l = 0}^{L - 1} {\sum\limits_{k = - \infty }^\infty {\sum\limits_{p = 0}^{M - 1} {\sum\limits_{q = 0}^2 {{a_{p,q}}} } } } g\left[ {k - l - q\frac{M}{2}} \right]g\left[ {k - \frac{M}{2}} \right] \times \\& {{{e}}^{{{j2\pi }}\left( {p - m} \right)k/M}}{{\mathop{ e}\nolimits} ^{{{j\pi }}\left( {p + q - m - 1} \right)/2}}{{{e}}^{ - {{j2\pi }}pl/M}}h\left[ l \right] + {\eta _{m,1}}\end{split}$

(5)

记第一列导频估计的信道响应为 ${{\hat{ h}}_0}$ ，第二列导频估计的信道响应为 ${{\hat{ h}}_1}$ 。将式(3)、(5)分别记为

${{{r}}_0} = \left( {{{{S}}_0} + {{{U}}_0}} \right){{\hat{ h}}_0} + {{{\eta }}_0}$

${{{r}}_1} = \left( {{{{S}}_1} + {{{U}}_1}} \right){{\hat{ h}}_1} + {{{\eta }}_1}$

一种直观的方法是对2个估计值进行简单的等值加权处理，并将结果作为新的信道估计值，结果表示为

${\hat{ h}} = {{\left( {{{{\hat{ h}}}_0} + {{{\hat{ h}}}_1}} \right)} / 2}$

事实上，在FBMC/OQAM中，不仅相邻子载波间存在重叠，相邻的符号之间也是互相重叠的。这不仅造成接收后同一个符号相邻子载波上的噪声之间是相关的，而且相邻符号上的噪声也是相关的，在联合估计时应同时考虑到相邻子载波和相邻符号之间的相关性。

记 ${{r}} = \left[ {\begin{array}{*{20}{c}} {{{{r}}_0}} \\ {{{{r}}_1}} \end{array}} \right]$ ， ${{A}} = \left[ {\begin{array}{*{20}{c}} {{{{A}}_0}} \\ {{{{A}}_1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{S}}_0} + {{{U}}_0}} \\ {{{{S}}_1} + {{{U}}_1}} \end{array}} \right]$ ， ${{\eta}} = \left[ {\begin{array}{*{20}{c}} {{{{\eta }}_0}} \\ {{{{\eta }}_1}} \end{array}} \right]$ ，建立新方程组

${{r}} = {{Ah}} + {{\eta }}$

文献[6]中给出了单列导频估计的加权矩阵证明的详细过程，直接将相关结果列出： ${{E}}\left[ {{\eta _{m,0}}} \right] = 0$ ， ${{E}}\left[ {{\eta _{m,1}}} \right] = 0$ ， ${{Var}}\left[ {{\eta _{m,0}}} \right] = {\sigma ^2}$ ， ${{Var}}\left[ {{\eta _{m,1}}} \right] = {\sigma ^2}$ ， ${{Cov}}\left[ {{\eta _{{m_1},0}},{\eta _{{m_2},0}}} \right] = $ ${\sigma ^2}\displaystyle\sum\limits_{k = - \infty }^\infty {g\left[ k \right]} g\left[ k \right]{{{e}}^{{{j2}}\pi \left( {{m_2} - {m_1}} \right)k/M}} \times {{{e}}^{{{j}}\left( {{m_2} - {m_1}} \right)\pi /2}} = {\sigma ^2}\zeta _{{m_1},0}^{{m_2},0}$

现在给出不同符号子载波上噪声互协方差证明的详细过程：

$\begin{aligned}& {{Cov}}\left[ {{\eta _{{m_1},1}},{\eta _{{m_2},1}}} \right] = {{E}}\left[ {{\eta _{{m_1},1}}\eta _{{m_2},1}^ * } \right] - {{E}}\left[ {{\eta _{{m_1},1}}} \right]{{E}}\left[ {\eta _{{m_2},1}^ * } \right]{{ = }}\\& \quad { E}\left[ {\left( {\left( { - {{j}}} \right)\sum\limits_{k = - \infty }^{ + \infty } {\eta \left[ k \right]g\left[ {k - \frac{M}{2}} \right]} {{{e}}^{ - {{j2\pi }}{m_1}k/M}}{{{e}}^{ - {{j}}{m_1}{{\pi }}/2}}} \right)} \right. \times \\& \quad \left. {\left( {{{j}}\sum\limits_{k = - \infty }^{ + \infty } {{\eta ^ * }\left[ k \right]g\left[ {k - \frac{M}{2}} \right]{{{e}}^{{{j2\pi }}{m_2}k/M}}{{{e}}^{{{j\pi }}{m_2}/2}}} } \right)} \right] = \\& \quad {\sigma ^2}\sum\limits_{k = - \infty }^{ + \infty } {g\left[ {k - \frac{M}{2}} \right]} g\left[ {k - \frac{M}{2}} \right]{{{e}}^{{{j2\pi }}\left( {{m_2} - {m_1}} \right)k/M}}{{{e}}^{{{j}}\left( {{m_2} - {m_1}} \right){{\pi }}/2}} = \\& \quad {\sigma ^2}\zeta _{{m_{1,}}1}^{{m_2},1}\;{{ e}^{{{j\pi }}\left( {{m_2} - {m_1}} \right)}}{\sigma ^2}\zeta _{{m_1},0}^{{m_2},0}\end{aligned}$

同理可证

$\begin{split}& {{Cov}}\left[ {{\eta _{{m_1},1}},{\eta _{{m_2},0}}} \right] = - {{j}}{\sigma ^2}\sum\limits_{k = - \infty }^\infty {g\left[ k \right]} g\left[ {k - \frac{M}{2}} \right] \times\\& \quad \quad {{{e}}^{{{j2\pi }}\left( {{m_2} - {m_1}} \right)k/M}}{{{e}}^{{{j}}\left( {{m_2} - {m_1}} \right){{\pi }}/2}} = {\sigma ^2}\zeta _{{m_1},1}^{{m_2},0}\end{split}$

$\begin{split}& {{Cov}}\left[ {{\eta _{{m_1},0}},{\eta _{{m_2},1}}} \right] = { j}{\sigma ^2}\sum\limits_{k = - \infty }^{ + \infty } {g\left[ k \right]} g\left[ {k - \frac{M}{2}} \right] \times \\& \quad \quad {{{e}}^{{{j2\pi }}\left( {{m_2} - {m_1}} \right)k/M}}{{{e}}^{{{j}}\left( {{m_2} - {m_1}} \right){{\pi /2}}}} = {\sigma ^2}\zeta _{{m_1},0}^{{m_2},1}\end{split}$

噪声协方差矩阵 ${{V}}$ 的具体表达式见式(6)。

${ V}=\left[ {\begin{array}{*{20}{c}}{{\sigma ^2}} & {{\sigma ^2}\zeta _{0,0}^{1,0}} & \cdots &{{\sigma ^2}\zeta _{0,0}^{M - 2,0}}& {{\sigma ^2}\zeta _{0,0}^{M - 1,0}}& {{\sigma ^2}\zeta _{0,0}^{0,1}} & {{\sigma ^2}\zeta _{0,0}^{1,1}} & \cdots & {{\sigma ^2}\zeta _{0,0}^{M - 2,1}}& {{\sigma ^2}\zeta _{0,0}^{M - 1,1}}\\[5pt]{{\sigma ^2}\zeta _{1,0}^{0,0}}& {{\sigma ^2}}& \cdots & {{\sigma ^2}\zeta _{1,0}^{M - 2,0}}& {{\sigma ^2}\zeta _{1,0}^{M - 1,0}}& {{\sigma ^2}\zeta _{1,0}^{0,1}}& {{\sigma ^2}\zeta _{1,0}^{1,1}}& \cdots & {{\sigma ^2}\zeta _{1,0}^{M - 2,1}}& {{\sigma ^2}\zeta _{1,0}^{M - 1,1}}\\[5pt] \vdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \vdots \\[5pt] {{\sigma ^2}\zeta _{M - 2,0}^{0,0}}&{{\sigma ^2}\zeta _{M - 2,0}^{1,0}}& \cdots & {{\sigma ^2}}& {{\sigma ^2}\zeta _{M - 2,0}^{M - 1,0}}& {{\sigma ^2}\zeta _{M - 2,0}^{0,1}}& {{\sigma ^2}\zeta _{M - 2,0}^{1,1}}& \cdots & {{\sigma ^2}\zeta _{M - 2,0}^{M - 2,1}}& {{\sigma ^2}\zeta _{M - 2,0}^{M - 1,1}}\\[5pt]{{\sigma ^2}\zeta _{M - 1,0}^{0,0}}&{{\sigma ^2}\zeta _{M - 1,0}^{1,0}}& \cdots & {{\sigma ^2}\zeta _{M - 1,0}^{M - 2,0}}& {{\sigma ^2}}& {{\sigma ^2}\zeta _{M - 1,0}^{0,1}}& {{\sigma ^2}\zeta _{M - 1,0}^{1,1}}& \cdots & {{\sigma ^2}\zeta _{M - 1,0}^{M - 2,1}}& {{\sigma ^2}\zeta _{M - 1,0}^{M - 1,1}}\\[5pt]{{\sigma ^2}\zeta _{0,1}^{0,0}}& {{\sigma ^2}\zeta _{0,1}^{1,0}} & \cdots & {{\sigma ^2}\zeta _{0,1}^{M - 2,0}}& {{\sigma ^2}_{0,1}^{M - 1,0}}& {{\sigma ^2}} & {{\sigma ^2}\zeta _{0,1}^{1,1}}& \cdots & {{\sigma ^2}\zeta _{0,1}^{M - 2,1}}& {{\sigma ^2}\zeta _{0,1}^{M - 1,1}}\\[5pt]{{\sigma ^2}\zeta _{1,1}^{0,0}}& {{\sigma ^2}\zeta _{1,1}^{1,0}} & \cdots & {{\sigma ^2}\zeta _{1,1}^{M - 2,0}}& {{\sigma ^2}\zeta _{1,1}^{M - 1,0}}& {{\sigma ^2}\zeta _{1,1}^{0,1}}& {{\sigma ^2}}& \cdots & {{\sigma ^2}\zeta _{1,1}^{M - 2,1}}& {{\sigma ^2}\zeta _{1,1}^{M - 1,1}}\\[5pt] \vdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \vdots \\[5pt] {{\sigma ^2}\zeta _{M - 2,1}^{0,0}}& {{\sigma ^2}\zeta _{M - 2,1}^{1,0}}& \cdots & {{\sigma ^2}\zeta _{M - 2,1}^{M - 2,0}}& {{\sigma ^2}\zeta _{M - 2,1}^{M - 1,0}}& {{\sigma ^2}\zeta _{M - 2,1}^{0,1}}& {{\sigma ^2}\zeta _{M - 2,1}^{1,1}}& \cdots &{{\sigma ^2}}& {{\sigma ^2}\zeta _{M - 2,1}^{M - 1,1}}\\[5pt]{{\sigma ^2}\zeta _{M - 1,1}^{0,0}} & {{\sigma ^2}\zeta _{M - 1,1}^{1,0}}& \cdots & {{\sigma ^2}\zeta _{M - 1,1}^{M - 2,0}}& {{\sigma ^2}\zeta _{M - 1,1}^{M - 1,0}}& {{\sigma ^2}\zeta _{M - 1,1}^{0,1}}& {{\sigma ^2}\zeta _{M - 1,1}^{1,1}}& \cdots & {{\sigma ^2}\zeta _{M - 1,1}^{M - 2,1}}& {{\sigma ^2}}\end{array}} \right]$

(6)

将矩阵V进行如下形式分块：

${{V}} = \left[ {\begin{array}{*{20}{c}} {{{{V}}_1}} & {{{{V}}_2}} \\ {{{{V}}_3}} & {{{{V}}_4}} \end{array}} \right]$

(7)

式中： ${{{V}}_1}$ 就是式(2)中的C， ${{{V}}_2}$ 表示 ${{{\eta }}_0}{{{\eta }}_1}$ 的互协方差矩阵， ${{{V}}_3}$ 表示 ${{{\eta }}_1}{{{\eta }}_0}$ 的互协方差矩阵， ${{{V}}_4}$ 为 ${{{\eta }}_1}$ 的自相关矩阵。考虑到FBMC中，仅仅相邻子载波之间存在影响，上面的矩阵可以简化，简化后的矩阵之间存在着如下关系

${{{V}}_4} = {{{V}}_1}^{{T}}, \; {{{V}}_3} = {{{V}}_2}^{{H}}$

${{V}}$ 矩阵可简化为

${{V}} = \left[ {\begin{array}{*{20}{c}} {{{{V}}_1}} & {{{{V}}_2}} \\ {{{{V}}_2}^{{H}}} & {{{{V}}_1}^{{T}}} \end{array}} \right]$

此时信道时域响应 ${{h}}$ 的估计值 ${\hat{ h}}$ 为

${\hat{ h = }}{\left( {{{{A}}^{{H}}}{{{V}}^{{{ - 1}}}}{{A}}} \right)^{{{ - 1}}}}{{{A}}^{{H}}}{{{V}}^{{{ - 1}}}}{{r}}$

联合估计的克拉美罗界为

${{CRB}} = {{tr}}\left[ {{{\left( {{{{A}}^{{H}}}{{{V}}^{ - 1}}{{A}}} \right)}^{ - 1}}} \right]$

(8)

还可以将此方法推广到多个符号之间的联合估计，只需对方程进行扩展即可。值得一提的是，当采用具有良好时频聚焦性的原型滤波器时，相隔两列的符号上噪声之间的相关性很弱，可以不予考虑。

4 仿真结果

在仿真中，考虑了一个12 MHz带宽、256个子载波的FBMC系统，原型滤波器为4个符号长度的各向同性正交变换(isotropic orthogonal transform algorithm, IOTA)函数。信道采用ITU的车辆A模型，无多普勒频移。

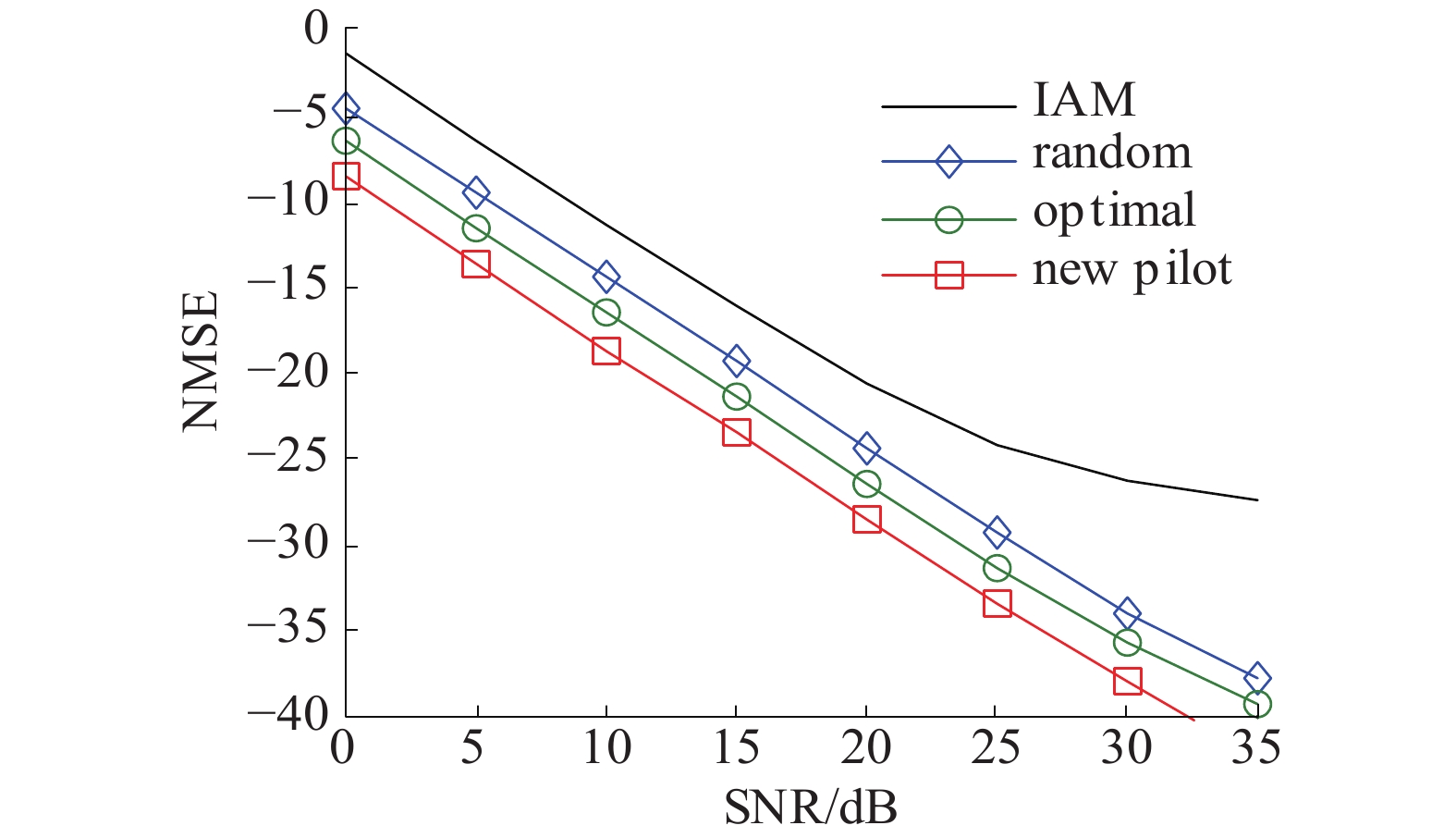
4.1 扩展后时域估计

对于前3列全部为导频的情况，仿真了3组导频，图2中random对应的是一组随机导频，optimal对应文献[7]中给出的最优导频，new pilot是上节提到的应用于本文算法的优化导频。采用归一化均方误差来衡量各种方法的性能，单位是dB。图中还给出了IAM方法的估计效果以作对比，IAM方法的估计误差可以参考文献[11]。

从图2的仿真结果可以看出，时域方法估计效果要好于IAM方法，在传统时域方法中最优导频优于随机导频，而本文方法则可以获得优于传统方法中最优导频的性能。结果表明导频非稀疏的情况下新方法的估计效果优于原有算法，且两者导频开销与计算复杂度一致。

稀疏情况如图3所示，仿真中考虑了2种导频形状。

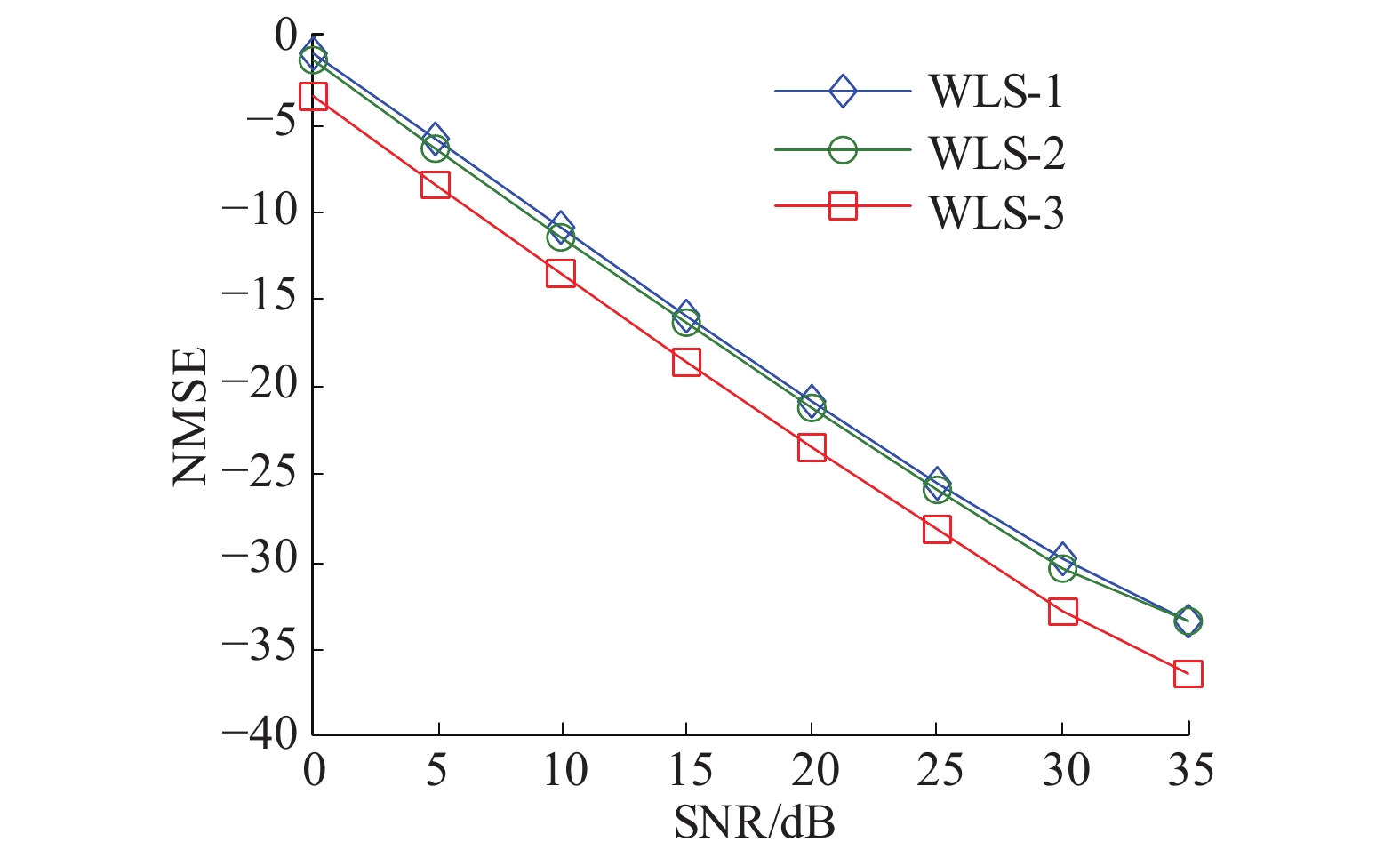
图4中WLS-1对应图3(a)中的导频形状，WLS-2和WLS-3都使用图3(b)中的形状，只是WLS-2对应的是一组随机数，WLS-3使用了一组优化解。结果显示在导频稀疏的情况下本文方法同样比传统方法有效。此外，使用优化解的误差小于随机值。对比图2、3可以发现导频非稀疏时估计效果比稀疏情况好。

4.2 联合估计

为减小干扰，采用了4列导频，同样对比了全导频和稀疏导频2种情况，每种情况都采用了2组导频来验证算法效果。

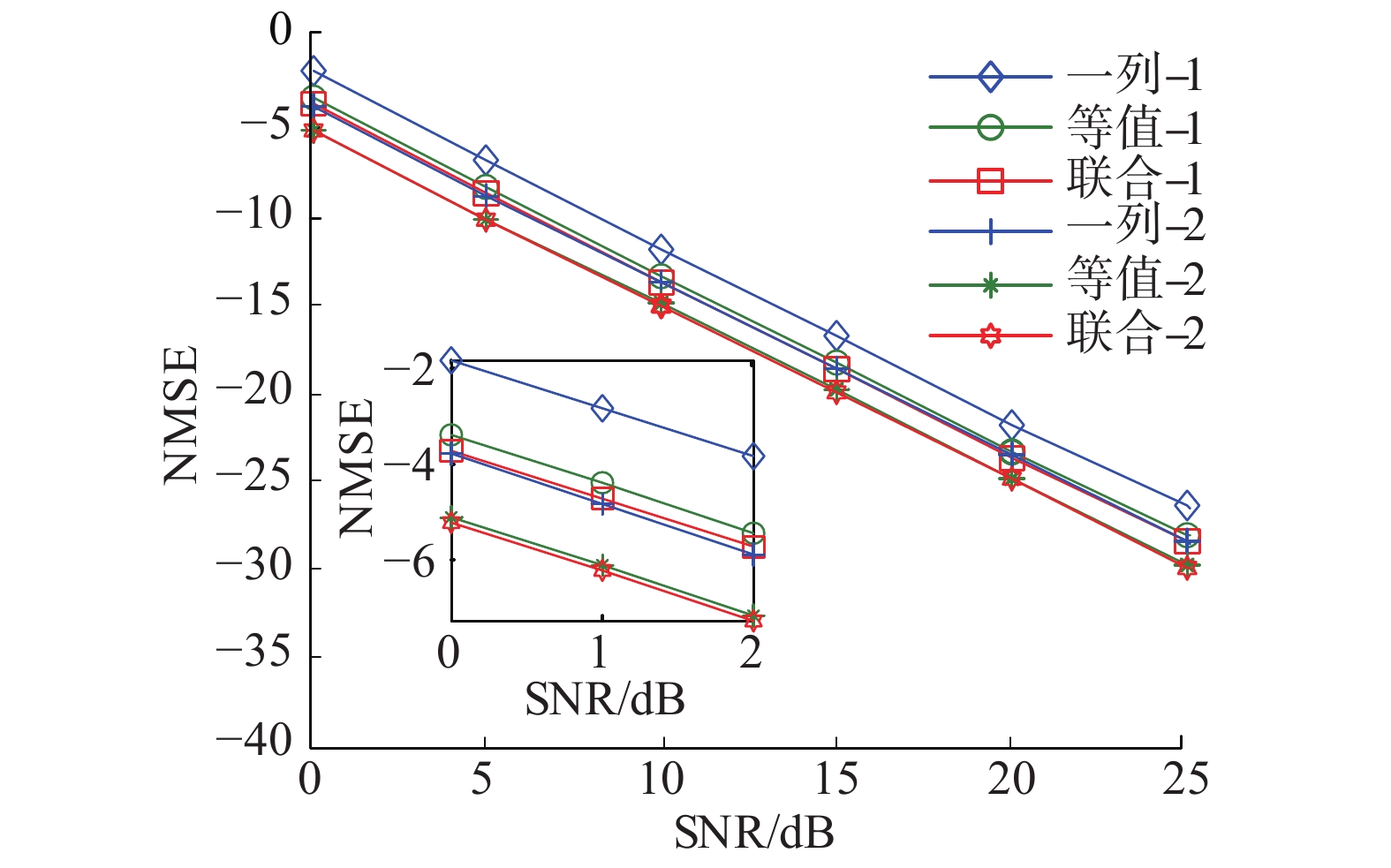
图5、6分别显示了导频非稀疏和稀疏情况的算法效果。图中“一列−1”表示使用第1组导频时单独一列的信道估计结果对应的误差曲线；“等值−1”表示使用第1组导频时相邻两列信道估计结果求平均值对应的误差曲线；“联合−1”表示使用第1组导频时按照本文方法进行联合估计对应的误差曲线。与此类似，“一列−2”、“等值−2”，“联合−2”分别表示使用另外一组导频相应情况对应的误差曲线。

从图5可以看出2组导频情况下联合估计效果均优于单独估计和2列结果求平均，区别在于第2组导频比第1组误差小。从图中还可以发现求平均值的方式获得的结果很接近联合估计，在对性能要求不高的场合可以用求平均值代替联合估计来减小复杂度。

在稀疏导频情况，由于观察的子载波之间不是连续的，所以式(7)中的矩阵 ${{{V}}_1}$ 和 ${{{V}}_4}$ 退化成值为σ²I(I是单位阵)的对角阵。 ${{{V}}_2}$ 和 ${{{V}}_3}$ 也退化为对角阵，且它们之间存在如下关系

${{{V}}_2} = {\sigma ^2}\zeta _{0,0}^{0,1}{{I}} , \; {{{V}}_3} = - {{{V}}_2}$

所以矩阵 ${{V}}$ 可以简化为

${{V}} = \left[ {\begin{array}{*{20}{c}} {{\sigma ^2}{{I}}} & {{\sigma ^2}\zeta _{0,0}^{0,1}{{I}}} \\ [8pt] { - {\sigma ^2}\zeta _{0,0}^{0,1}{{I}}} & {{\sigma ^2}{{I}}} \end{array}} \right]$

容易求得

${{{V}}^{{{ - }}1}} = \frac{1}{{{\sigma ^2}}} \cdot \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{1}{{1 - {\alpha ^2}}}{{I}}} & {\displaystyle\frac{{ - j\alpha }}{{1 - {\alpha ^2}}}{{I}}} \\ [8pt] {\displaystyle\frac{{j\alpha }}{{1 - {\alpha ^2}}}{{I}}} & {\displaystyle\frac{1}{{1 - {\alpha ^2}}}{{I}}} \end{array}} \right]$

式中 $\alpha = - j\zeta _{0,0}^{0,1}$ ，代入式(8)求得估计的克拉美罗界为

$\begin{split}& {\sigma ^2} \cdot {{tr}}\left[ {\left( {\frac{1}{{1 - {\alpha ^2}}} \cdot \left( {{{A}}_0^{{H}}{{{A}}_0}{{ + A}}_1^{{H}}{{{A}}_1}} \right)} \right.} \right. + \\& \frac{{{{j}}\alpha }}{{1 - {\alpha ^2}}}\left. {{{\left. {\left( {{{A}}_1^{{H}}{{{A}}_0} - {{A}}_0^{{H}}{{{A}}_1}} \right)} \right)}^{ - 1}}} \right]\end{split}$

从图6结果可以看出在导频稀疏的情况也有类似的特性，联合估计相对传统方式性能提升了约2 dB。结合图5、6的结果可以得知，本文提出的联合估计方式在导频非稀疏和稀疏情况下均有效。

5 结论

1) 本文分析了原有时域估计方式的缺陷，为充分利用导频数据，对估计方程进行了扩展，并针对导频稀疏和非稀疏两种情况进行了研究。

2) 通过限制导频数值范围和导频结构，分别求解出稀疏和非稀疏情况下的一组估计误差最小的导频。仿真结果表明，使用本文导频构造的观测矩阵进行信道估计，效果优于原有算法。

3) 针对能同时获得相邻两列估计结果的情况进行了研究，将两个估计方程联立，推导出加权矩阵的表达式并给出了联合估计的克拉美罗界。

4) 对联合估计的理论进行仿真验证，结果表明联合估计效果优于单独一列的估计结果，也优于两列结果求平均。此外，性能提升结果与导频相关，部分情况下可以用求平均来代替联合估计。联合估计方式的缺点是频谱效率降低且计算复杂度增大。