2. 中集海洋工程研究限有限公司, 山东 烟台 264670
2. CIMC Offshore Engineering Institute Co, Ltd., Yantai 264670, China
自1951年自升式平台诞生以来,已成为当今世界范围内应用最为广泛的油气钻井平台,并且数量仍在不断攀升。悬臂梁结构使得自升式钻井平台的作业能力发生了翻天覆地的变化,不仅功能上得到了大幅提高,能够在导管架生产平台上实施钻井作业、修井作业和钻调整井作业等[1],设计承载量也得到了减轻,因此建造成本投入也相应地降低。对悬臂梁结构进行研究,对于提高悬臂梁的承载能力、降低成本至关重要。
1 悬臂梁结构特点图 1为悬臂梁钻台截面建造实体图。悬臂梁结构位于自升式平台尾部甲板上,由两条互相平行的工字梁组成,在其上布置了钻台及井架结构。如图 1所示,中间为钻台,下方为两条平行的由工字梁组成的悬臂梁主梁。悬臂梁可在固定于尾部甲板的一对滑轨上前后滑动,并带动钻台及井架一起伸向平台尾端舷外[2]。

|
图 1 悬臂梁钻台截面建造实体图 |
通常所说的常规悬臂梁,是相对于平台船体的船长方向滑动而实现X方向的移动, 而钻台在悬臂梁上作相对于平台Y方向滑动[3],从而使钻台可以在一个矩形的区域内作业。悬臂梁两侧的主梁是承受荷载的主体,钻台的工作形式是在主梁上部左右移动,钢梁在滑轨上的伸出使得井架活动范围增大。当悬臂梁被滑移到最大悬出距离时,悬臂梁的各组件及钻井作业产生的载荷均会通过悬臂梁传递到主船体上,而直接承受这一载荷的为布置在主船体尾部的垫板,特别是在主梁下部面板与垫板发生接触的翼缘极易形成应力集中[4]。
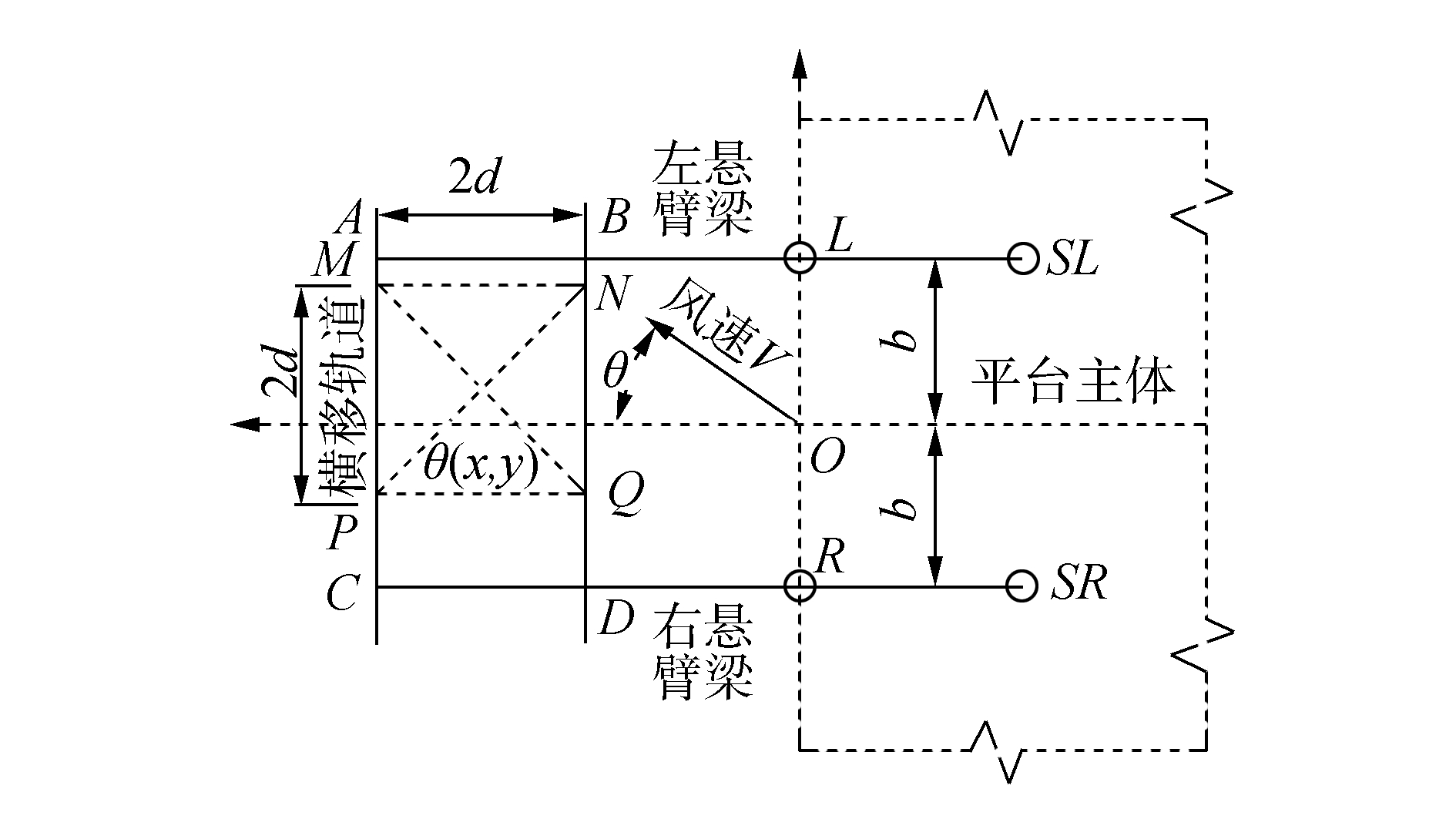
2 悬臂梁载荷评估悬臂梁在平台进行起下钻作业时承受的载荷最大,尤其是在悬臂梁处于距尾部最远且滑移到远离井心时最为危险,因此悬臂梁的各种极限工况的受力分析是悬臂梁设计的关键步骤,也是悬臂梁可靠性设计的必要过程[5]。为了便于进行悬臂梁各种极限工况载荷计算研究,建立图 2所示的计算坐标系[6],图中d为井架中心横向移动的距离。
|
图 2 悬臂梁计算坐标系 |
风载荷对悬臂梁的影响主要体现在迎风面积和距主梁底面的垂向尺寸上,因此,主要的影响因素取决于钻台围壁和井架,对悬臂梁产一个绕垂直方向的弯矩和水平面的剪切力[7]。设风速为V,方向与X轴呈θ角如图 2。
依据船级社相关规范,悬臂梁承受风载荷FW的计算公式如式(1)所示。
| $ {{\mathit{F}}_{\rm{W}}}\rm{=}\sum{{{\mathit{C}}_{\mathit{hi}}}{{\mathit{C}}_{\mathit{si}}}{{\mathit{S}}_{\mathit{i}}}\mathit{P}}\rm{ }\!\!~\!\!\rm{ } $ | (1) |
式中:Si为受风构件正投影面积,m2;Chi为受风构件高度系数,无量纲;Csi为受风构件形状系数,无量纲;P为风压,kN/m2。
弯矩MW可按式(2)计算:
| $ {{\mathit{M}}_{\rm{W}}}\rm{=}\sum{{{\mathit{C}}_{\mathit{hi}}}{{\mathit{C}}_{\mathit{si}}}{{\mathit{S}}_{\mathit{i}}}{{\mathit{Z}}_{\mathit{i}}}\mathit{P}} $ | (2) |
式中Zi为风载荷的作用点距离悬臂梁上缘的长度,m。
2.2 钻井载荷作用作为可变载荷的钻井载荷H,主要组成部分为大钩载荷、转盘载荷、立根盒载荷及隔水管张紧力等[8],是悬臂梁承受的主要载荷,其作用方向竖直向下并且通过转盘中心O'(x, y)[6]。则其对悬臂梁的剪力QH和弯矩MH为
| $ \begin{align} & \ \ \ {{\mathit{Q}}_{\mathit{H}}}\rm{=}\frac{\mathit{y}\rm{+}\mathit{b}}{\rm{2}\mathit{b}}\mathit{H} \\ & {{\mathit{M}}_{\mathit{H}}}\rm{=}\frac{\left( \mathit{y}\rm{+}\mathit{b} \right)\mathit{x}}{\rm{2}\mathit{b}}\mathit{H} \\ \end{align} $ |
由于悬臂梁可以沿平台的纵向滑动,同时,钻台可以在悬臂上进行横向滑动,根据悬臂梁的受力特点,当悬臂梁沿纵向滑移距离最远,且横向滑移最远的工况下,悬臂梁承载能力最差。而钻台位于横向的中心或者向主船体方向滑移时,悬臂梁承载能力会增大。因此,要根据悬臂梁的承载能力,计算出每个不同的工位的许用载荷。
2.3 钻台重量作用钻台由钢结构和设备组成,其中钢结构包括钻台本体和井架,设备主要为钻机、顶驱、卡盘等,它们的重量为悬臂梁固定载荷的一部分。设总重量为GD,重心为(x', y'),求得悬臂梁的剪力QD和弯矩MD为[6]
| $ \begin{array}{l} \;\;{Q_D}{\rm{ = }}\frac{{y'{\rm{ + }}b}}{{{\rm{2}}b}}{G_D}\\ {M_D}{\rm{ = }}\frac{{\left( {y'{\rm{ + }}b} \right)\mathit{x'}}}{{{\rm{2}}b}}{G_D} \end{array} $ |
横向轨道焊接悬臂的固定位置,其重量属于固定载荷,设其重量为GT,其重心为(x, 0);定义悬臂梁平均线密度为ρ,悬出平均部分的长度为(x+d), 则分别求得剪力QC及弯矩WC为[6]
| $ \begin{align} & \ \ \ {{\mathit{Q}}_{\mathit{C}}}\rm{=}{{\mathit{G}}_{\mathit{T}}}\rm{+}\mathit{\rho }\left( \mathit{x}\rm{+}\mathit{d} \right) \\ & {{\mathit{M}}_{\mathit{C}}}\rm{=}{{\mathit{G}}_{\mathit{T}}}\mathit{x}\rm{+}\frac{1}{2}\mathit{\rho }\left( \mathit{x}\rm{+}\mathit{d} \right){{\rm{ }\!\!~\!\!\rm{ }}^{\rm{2}}} \\ \end{align} $ |
参考现有成型自升式钻井平台的设计方案,选取研究的悬臂梁所处平台是一座独立三桩腿自升式钻井平台,设计此平台作业水深50 m,最大钻井深度7 000 m(4.5英寸钻杆),平台一次就位设计钻井数量为30口(井间距设定为2 m),平台的主要参数见表 1所示。
|
|
表 1 平台主要参数 |
悬臂梁的详细设计如图 3所示。

|
图 3 悬臂梁结构设计图 |
悬臂梁载荷设计确定见表 2。
|
|
表 2 悬臂梁设计载荷 |
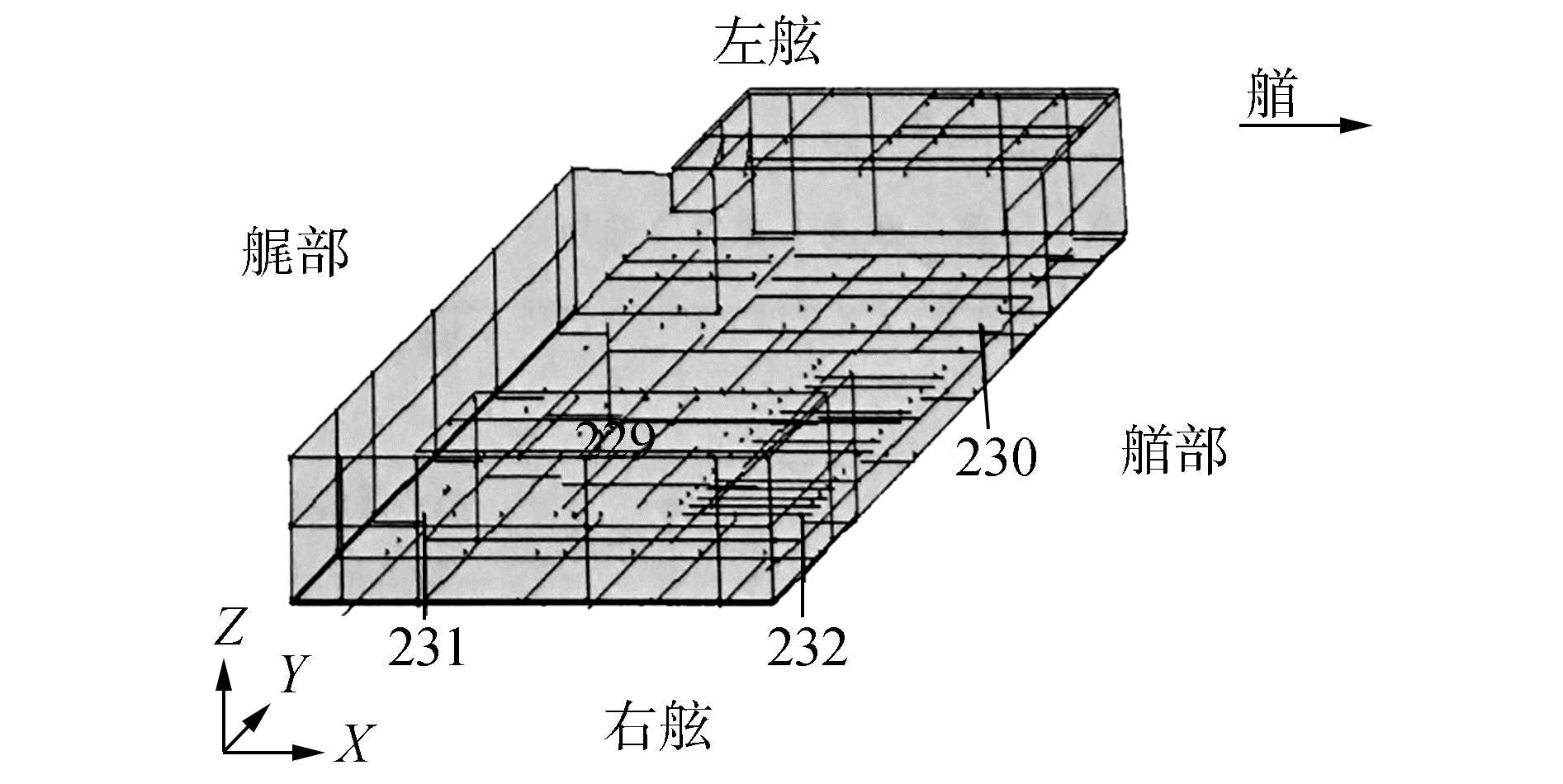
结构中,钻台工作状态下产生的载荷信息[9],根据成品设备样本中提供的钻台工作支反力,在确定了钻台的在悬臂梁上的位置后,对模型中钻台支点的位置定义为231,232, 230, 229,具体位置示意见图 4。钻台对悬臂梁产生的支反力和支反力矩信息见表 3。
|
图 4 钻台位置示意 |
|
|
表 3 钻台支反力信息表 |
有限元方法作为解决复杂工程问题的有效手段,不仅具有较高的计算精度,而且结果处理功能强大,能够直观地反映指定工况下结构响应特点[10]。使用Abaqus 6.10-1软件对悬臂梁进行结构校核,创建悬臂梁的有限元分析模型,进行有限元分析方法的前期处理基础。
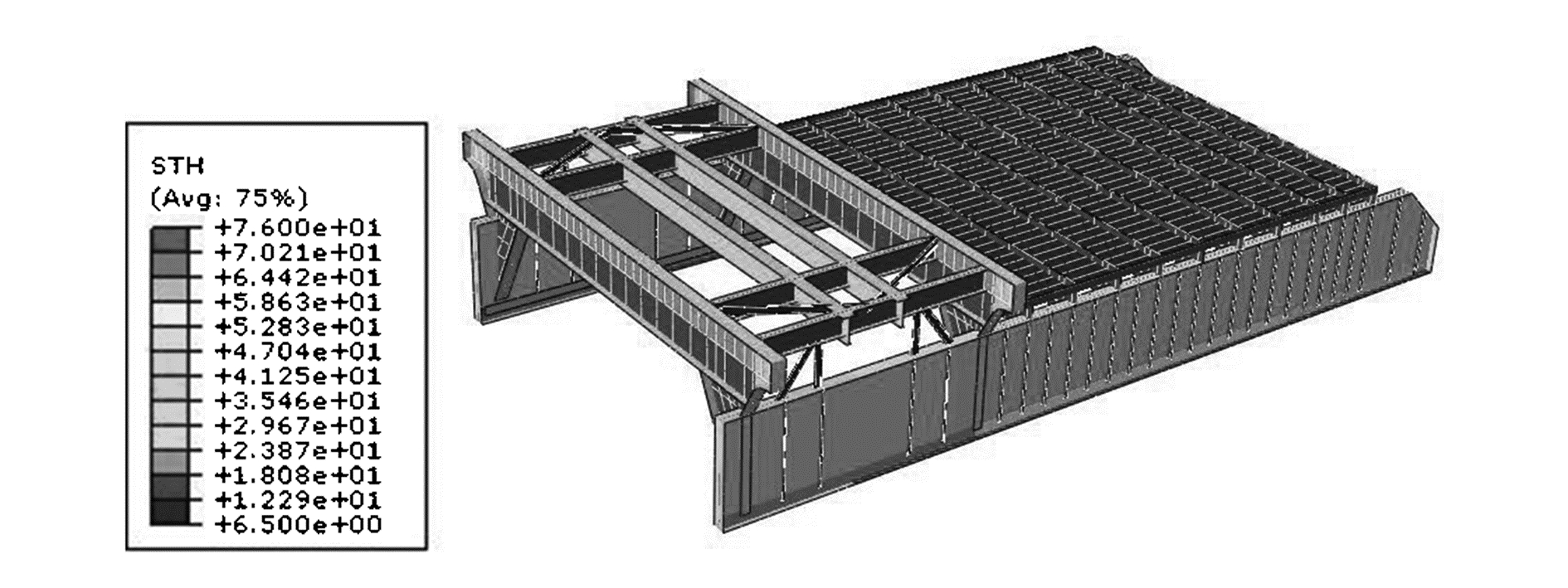
根据以上结构尺寸和材料属性,利用Abaqus 6.10-1软件建立有限元模型,并附加板厚属性,见图 5。
|
图 5 悬臂梁结构板厚划分 |
当需要校核悬臂梁纵向构件的强度时,其约束边界滑道基座(Push up和Hold up)采用铰支约束方式,是偏于安全的边界条件。当对钻台滑动支撑结构进行分析时,主要是校核悬臂梁横向支撑钻台的结构强度,在基座梁上面施加纵向约束;在悬臂梁工字梁腹板施加垂向约束;在悬臂梁工字梁底部面板一侧施加3个平动方向的约束,模拟悬臂梁在外伸时的可以扭转。在模型中,边界约束条件如表 4所示。
|
|
表 4 悬臂梁结构边界约束 |
根据悬臂梁的工作形式和工作状况,对悬臂梁工作时的载荷工况进行组合。每种工况组合及备注见表 5。
|
|
表 5 工况组合 |
在软件中,对不同载荷分别加载,按照表 5中组合工况,见图 6。

|
图 6 钻台偏移-15 ft悬臂梁加载形式 |
基于美国船级社规范[11]中的工作应力设计要求,对此设计中的悬臂梁结构进行强度校核[12]。其中,材料的许用应力为材料屈服应力值叠加组合工况系数后的应力值。规范中,对于板材结构强度校核,需要对结构应力进行Mises应力换算,换算公式如式(3):
| $ {{\mathit{\sigma }}_{\mathit{eqv}}}\rm{=}\sqrt{\mathit{\sigma }_{\mathit{x}}^{2}\rm{+}\mathit{\sigma }_{\mathit{y}}^{2}\rm{-}{{\mathit{\sigma }}_{\mathit{x}}}{{\mathit{\sigma }}_{\mathit{y}}}\rm{+}\mathit{\tau }_{\mathit{xy}}^{2}\rm{3}} $ | (3) |
式中:σx为计算出的结构在x方向的正应力值;σy为结构在y方向的应力值;τxy为结构的剪切应力。
悬臂梁工作方式为多种基本载荷的组合工况形式,因此,规范对此类组合工况的结构校核,要求对材料的屈服应力考虑1.11的安全系数,作为Mises许用应力的取值[13]。对于组合工况的分向应力,规范要求,在σx和σy两个方向的正应力,许用应力考虑1.25的安全系数[14],τxy的剪切应力校核时,考虑1.88的安全系数。具体材料系数选取及许用应力值见表 6所示。
|
|
表 6 材料许用应力值列表 |
综上所述,通过几次对有限元模型尺寸和板厚的调整,并反复进行有限元结构强度运算,最终对悬臂梁设计方案的有限元强度计算通过了板级强度规范要求,在得到的应力云图中,分别对Mises应力和x方向正应力、y方向正应力以及剪切应力值进行提取,并对应力值与许用应力大小进行比较,从而得到此结构的有效强度利用率值。结构强度及有效利用率列表见表 7~9所示。
|
|
表 7 材料AH36结构强度及利用率 |
|
|
表 8 材料EQ47结构强度及利用率 |
|
|
表 9 材料EQ56结构强度及利用率 |
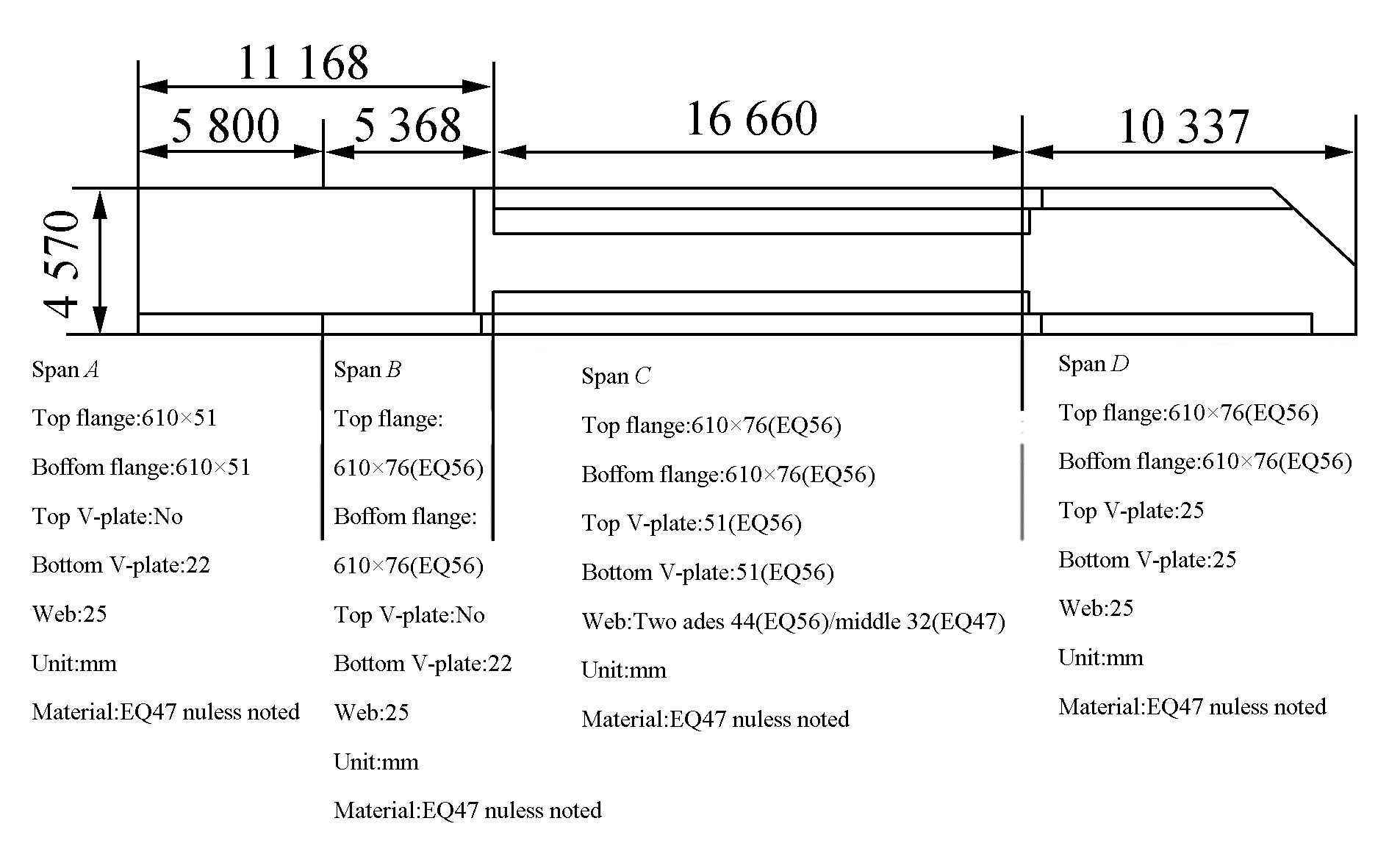
并根据悬臂梁的工作区域,将主梁分为4段不同的跨距。图 7为悬臂梁分段简易图,据悬臂梁结构的详细设计图纸,分别对图 7中划分的A、B、C、D共4段跨距上的截面求得截面属性。表 10为各悬臂梁截面属性。
|
图 7 悬臂梁分段简易图 |
|
|
表 10 悬臂梁截面属性 |
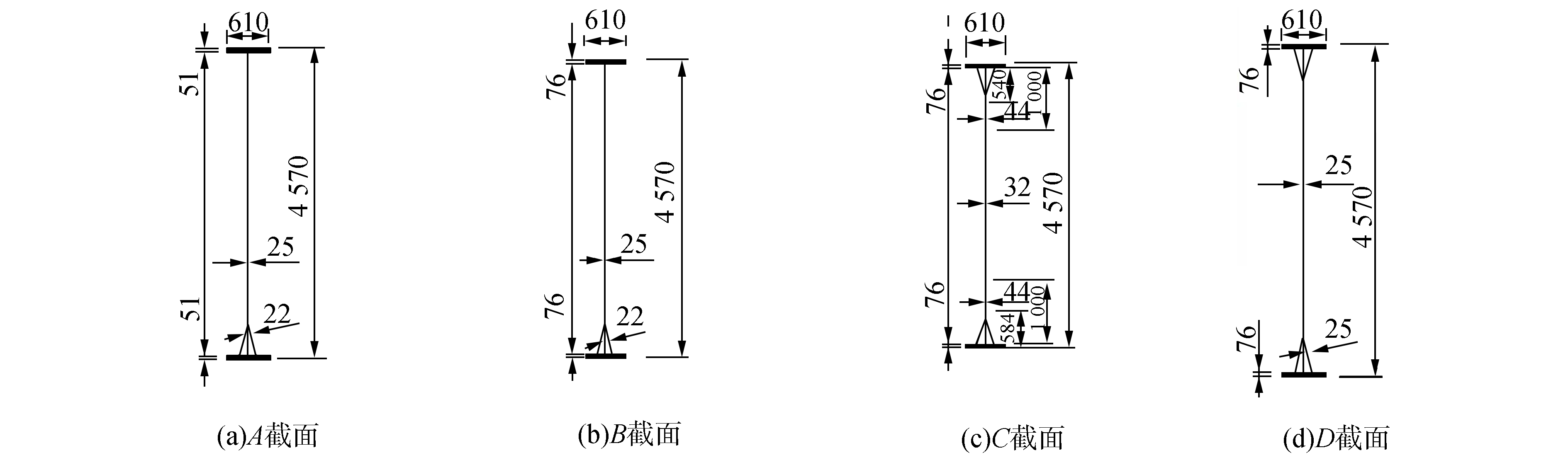
|
图 8 悬臂梁截面属性图 |
在设定钻井载荷作用时,根据钻台位置的变化制定许用钻井负荷图,可参照力学理论将悬臂梁结构简化成等效多跨梁,边界条件简化为简支约束,载荷简化为集中力和均布力形式,如图 9~11。
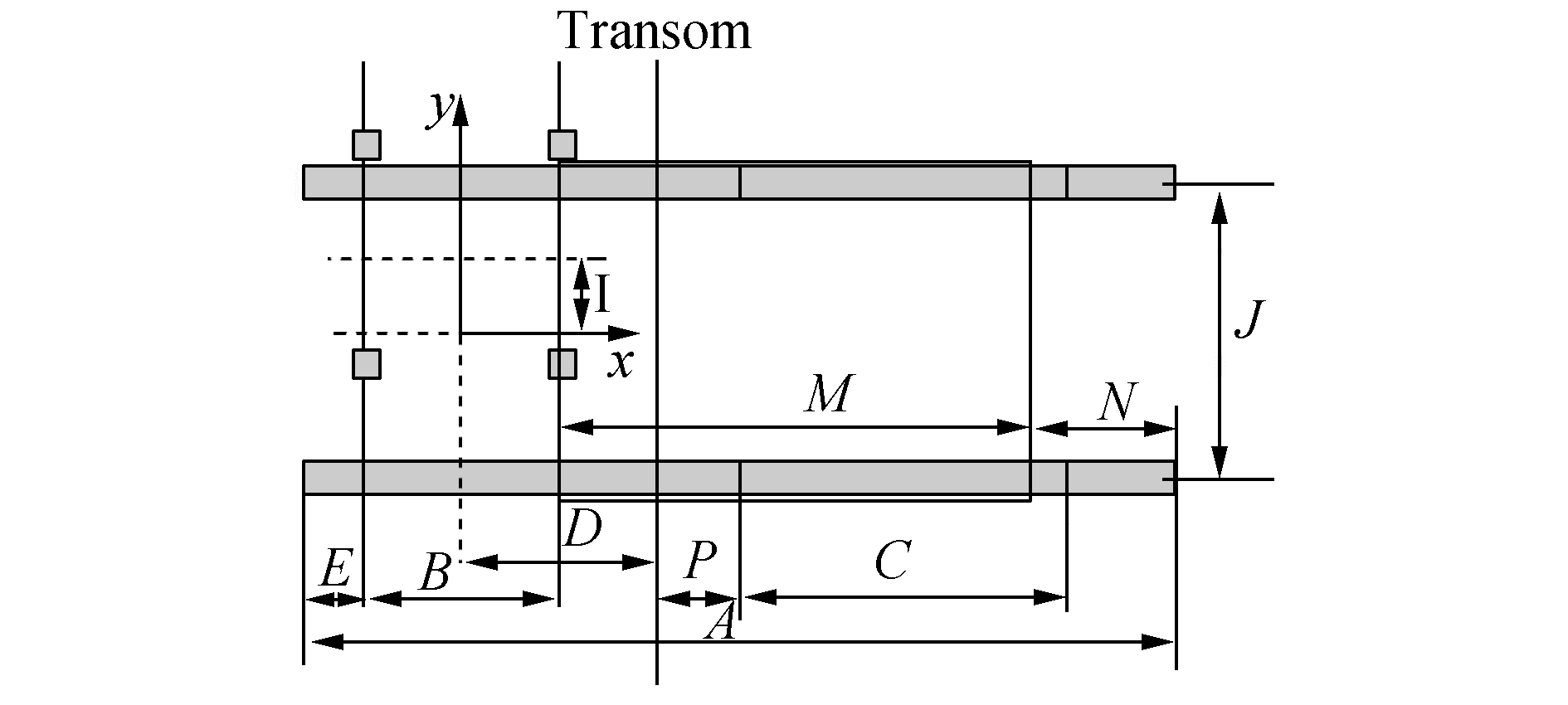
|
图 9 悬臂梁力学结构 |
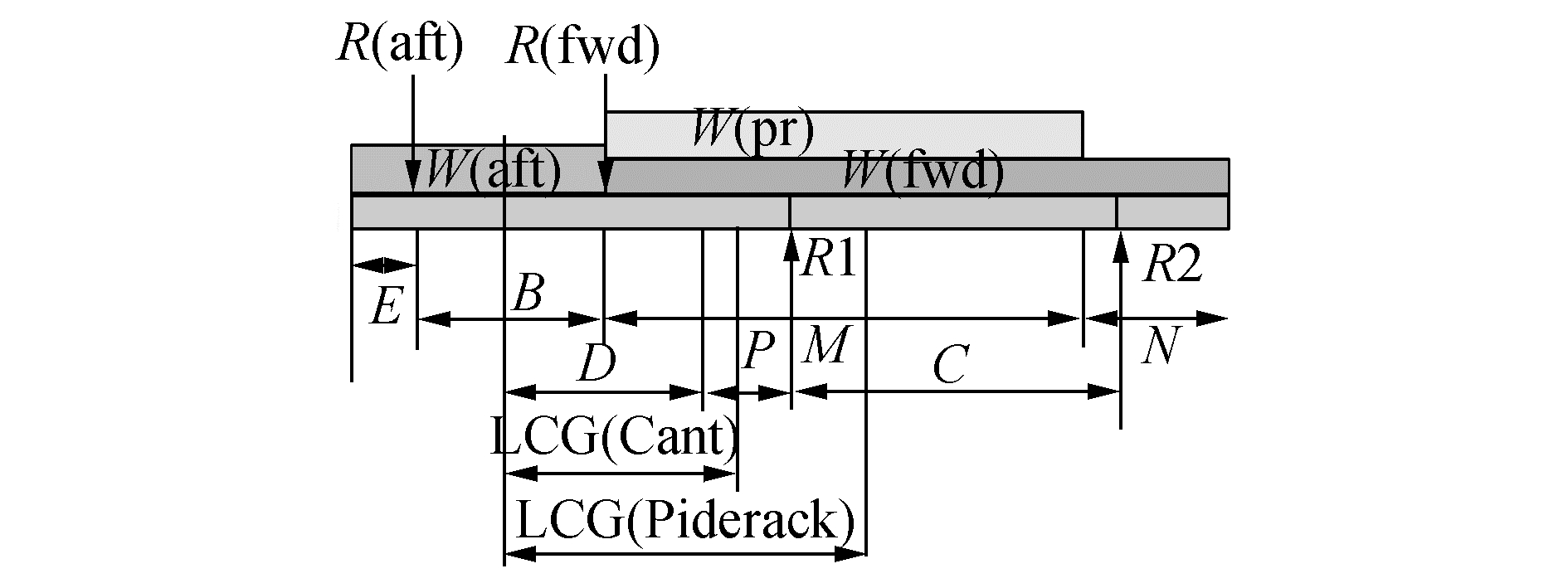
|
图 10 悬臂梁理论模型简化 |

|
图 11 悬臂梁设计尺寸示意 |
通过PCE软件,提取悬臂梁纵向主梁的剪力、弯矩及变形图,见图 12。从图 12中可以直观地得出悬臂梁主梁最大弯矩值和最大剪切力值,并且可得出最大值的所在区域。
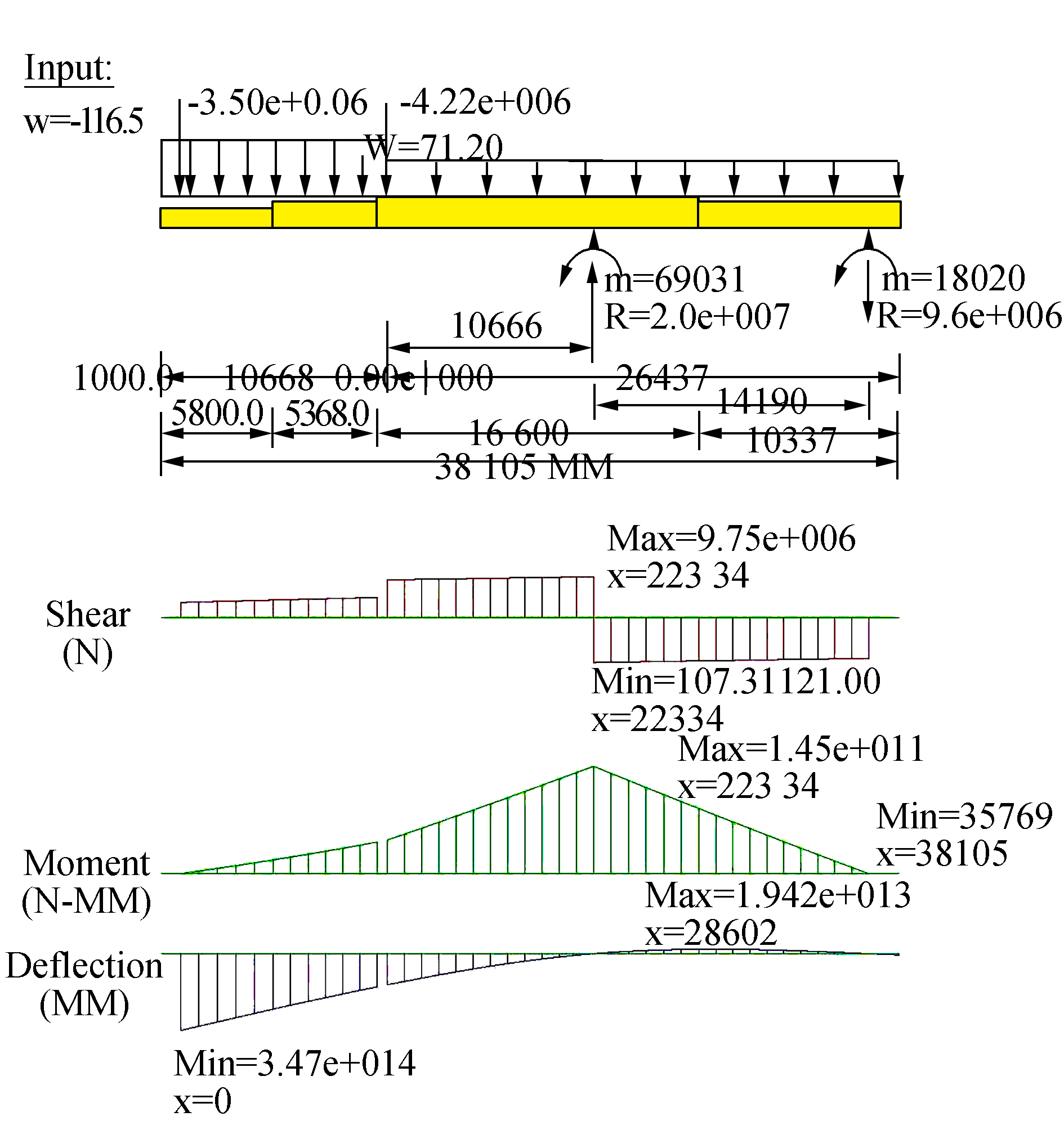
|
图 12 悬臂梁剪力、弯矩及变形图 |
综上所述,分别对正应力和剪切应力值进行提取,在剪切应力值较小的A区和B区调整截面积,在弯矩最大的C区增加转动惯量,增强抗弯能力,从而提高悬臂梁结构的有效强度利用率值。
参照规范中对自升式平台的系数要求和公式规范,整个设计结构板厚调整如下:
排管甲板:厚6 mm,纵向扶墙材L-75×75×6,材料为A-36;
横向大梁:1170×12W+300×12F,材料为EQ-47;
两纵向大梁腹板:厚度依次分别为22、25、22 mm,材料为EQ-47;
两纵向大梁面板:顶板厚度为45 mm,底板厚度为76 mm,材料为EQ-56;
上、下支座:前段为610×76,后段为610×45,材料为A-36;
其他构件材料均为A-36。
根据以上结构尺寸和材料属性,利用Abaqus6.10-1软件更新有限元模型,调整排管甲板、横向大梁及上下支座的板厚。整个结构重量从之前348.16 t,降低为321.25 t,减重26.91 t。详细板厚属性见图 13。

|
图 13 调整后结构板厚划分图 |
根据以上优化方案,调整悬臂梁结构的板厚,从新运行校核,得出应力云图。最大Mises应力值为490 MPa, 相对于优化前结构的最大Mises应力值474.926 MPa,有效提高了结构强度利用率,且仍旧满足ABS规范[15]中许用应力的要求,可认为,此设计能够满足悬臂梁正常工作要求,且符合规范各项要求。不同材质的最大结构应力值图,如图 14所示。

|
图 14 最大应力图谱 |
1) 文中进行了自升式平台悬臂梁工作方式的研究和对悬臂梁力学公式的推导,用有限元方法对悬臂梁结构进行了强度校核。
2) 利用数学模型法快速准确地对悬臂梁大应力区域定位,通过调整截面属性,优化了悬臂梁结构。
3) 再次利用有限元模型提取了结构的应力云图,参照美国船级社规范要求,完成了悬臂梁结构的优化设计及校核的规律性研究,确定了悬臂梁结构的安全可靠性设计。
| [1] |
钱亚林, 薄玉宝. 自升式悬臂梁钻井平台初探[J]. 上海造船, 2009(1): 15-18. ( 0) 0)
|
| [2] |
郑振豪, 卢永然, 徐少柯, 等. 某自升式平台结构性能分析与评估[J]. 船海工程, 2014, 43(6): 157-160. ( 0) 0)
|
| [3] |
高斌. 浅谈400英尺自升式钻井平台选型[J]. 科学中国人, 2013(3): 94-95. ( 0) 0)
|
| [4] |
朱启宪. 海洋平台结构可靠性的优化设计[J]. 中国海上油气(工程), 1991, 3(2): 1-10. ( 0) 0)
|
| [5] |
陈林. 钻井平台悬臂梁滑移动力分析[J]. 石油和化工设备, 2015(8): 29-31, 35. ( 0) 0)
|
| [6] |
樊敦秋, 董胜, 蒙占彬. 自升式钻井平台悬臂梁设计研究[J]. 中国造船, 2011, 52(S2): 138-145. ( 0) 0)
|
| [7] |
黄钦文, 陈大鹏, 叶甜春, 等. 基于微悬臂梁结构的生化传感器[J]. 电子工业专用设备, 2006, 35(1): 36-38. ( 0) 0)
|
| [8] |
赵建亭. 深水钻井船钻井系统设计研究[J]. 船舶与海洋工程, 2014(1): 1-7, 13. ( 0) 0)
|
| [9] |
刘祥建, 戴挺, 张佳宁, 等. 自升式平台悬臂梁结构分析方法的研究[C]//中国钢结构协会海洋钢结构分会2010年学术会议暨第六届理事会第三次会议. 洛阳, 2010: 103-108.
( 0) 0)
|
| [10] |
李昊. 自升式平台悬臂梁设计工具研究[D]. 大连. 大连理工大学, 2007: 76-79. http://cdmd.cnki.com.cn/Article/CDMD-10141-2008034815.htm
( 0) 0)
|
| [11] |
ABS. Rules for building and classing, mobile offshore drilling units, 2001 Part3-hull construction & equipment[R]. Houston, USA:ABS, 2005:58-62.
( 0) 0)
|
| [12] |
刘宇, 颜廷俊, 魏辽, 等. 海洋作业平台悬臂梁强度计算与试验分析研究[J]. 石油机械, 2012, 40(5): 53-56. ( 0) 0)
|
| [13] |
中国船级社. 海上移动平台入级规范[M]. 北京: 中国船级社, 2016: 45-57.
( 0) 0)
|
| [14] |
唐世振, 刘建军, 谢伟, 等. 海洋工程建造吊装计算优化分析[J]. 科技与企业, 2014(6): 324. ( 0) 0)
|
| [15] |
ABS.Guide for buckling and ultimate strength assessment for offshore structures[R].Houston, USA:ABS, 2004:65-72.
( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


