近几十年来,互联网技术和通信技术发展的十分迅速,图像和视频等信息被广泛应用于网络,由于图像和视频本身的数据冗余使得处理的数据量很大,给存储和传输带来很大的不便。因此,图像压缩技术便因此而产生。联合图像专家组(Joint Photographic Experts Group,JPEG)是由国际标准化组织(ISO)和国际电信联盟(ITU)联合组成的图像专家小组,该小组一直致力于静止图像压缩的标准化工作。JPEG标准是目前使用最为广泛的一种压缩标准,其中,80%左右的网站中所使用的图片均为JPEG/JPG格式[1-5]。
目前大多数研究者使用软件来对JPEG编码标准进行实现,但是软件实现的方法会使得实时性较差,并且需要运行在通用处理器之上。而硬件实现具有速度快、实时性好等特点,因此文中对JPEG算法的硬件实现进行研究。通过对JPEG算法的研究与分析,给出了JPEG系统的硬件实现架构,用Verilog HDL对JPEG编码器的关键模块进行了建模,并且对这些模块进行了仿真和验证,接着将这些模块按照JPEG压缩标准进行集成。为了验证JPEG编码器的正确性,利用MATLAB提取图像信息作为系统的激励,将系统的输出数据再利用MATLAB进行重建,将压缩后的图像与原图进行对比[6]。最后,对JPEG编码器进行了VLSI硬件实现。验证结果表明所设计的JPEG编码器满足应用需求。
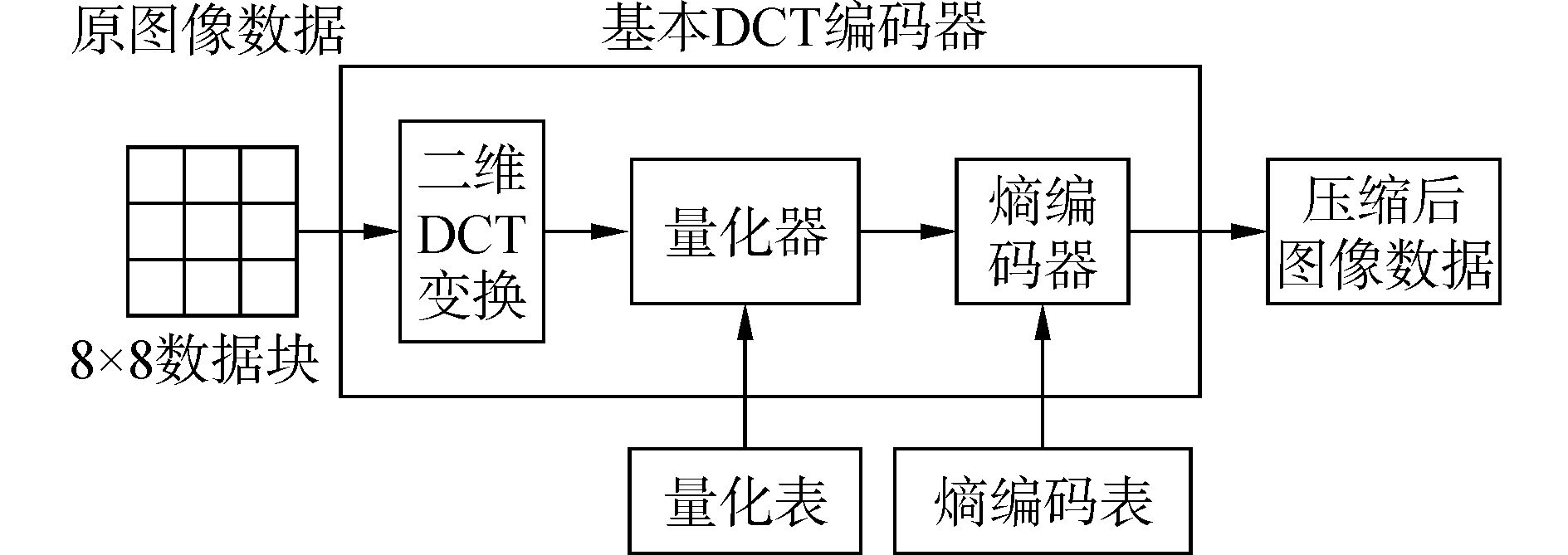
1 JPEG压缩算法的原理分析JPEG系统基本压缩编码处理框图如图 1所示,主要包括以下几个部分:首先,需要进行色域空间的转换,即将RGB分量转换为YCBCR分量;其次,对数据进行二维离散余弦变换(DCT),根据量化表对二维DCT(2D DCT)得到的结果进行量化;然后,将二维DCT运算之后输出的数据用Zigzag扫描编码,使用差分脉冲编码调制(differential pulse code modulation, DPCM)对直流(direct current,DC)系数进行编码,对交流(alternating current,AC)系数进行行程长度编码(run-length encoding, RLE);最后,将所得到的数据进行Huffman编码。
|
图 1 JPEG系统基本压缩编码处理框图 |
下文将对二维DCT变换、量化器和熵编码器这3个模块作重点的介绍。
2 二维DCT变换及其硬件实现 2.1 二维DCT变换JPEG编码中8×8块的二维离散余弦变换的公式如下:
| $ \begin{array}{*{20}{c}} {F\left( {u,v} \right) = \frac{1}{4}C\left( u \right)C\left( v \right) \cdot }\\ {\sum\limits_{x = 0}^7 {\sum\limits_{y = 0}^7 {f\left( {x,y} \right)\cos \left[ {\frac{{x\left( {2x + 1} \right)u}}{{16}}} \right]\cos \left[ {\frac{{x\left( {2y + 1} \right)u}}{{16}}} \right]} } } \end{array} $ | (1) |
根据式(1) 的特征,可以分解成两次一维变换:
| $ F\left( {u,v} \right) = \frac{1}{2}\sum\limits_{i = 0}^7 {c\left( u \right)Z\left( {i,v} \right)\cos \frac{{\left( {2i + 1} \right)u{\rm{\pi }}}}{{16}}} $ | (2) |
在式(2) 中,Z(i, v)的值为式(3):
| $ Z\left( {i,v} \right) = \frac{1}{2}\sum\limits_{j = 0}^7 {c\left( v \right)x\left( {i,j} \right)\cos \frac{{\left( {2j + 1} \right)v{\rm{\pi }}}}{{16}}} $ | (3) |
二维DCT的矩阵变换形式为
| $ \mathit{\boldsymbol{F}} = \mathit{\boldsymbol{CX}}{\mathit{\boldsymbol{C}}^{\rm{T}}} $ |
式中:C为带余弦基本函数的变换系数矩阵; CT为C的转置。可以得到:
| $ \mathit{\boldsymbol{F}} = \mathit{\boldsymbol{CX}}{\mathit{\boldsymbol{C}}^{\rm{T}}} = \mathit{\boldsymbol{C}}{\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{X}}^{\rm{T}}}} \right)^{\rm{T}}} $ | (4) |
根据式(4) 可知二维DCT将被分解为2步:第一步先计算XT的一维离散余弦变换;然后将中间结果进行转置并作为第二次变换的输入,再次进行一维DCT变换。
一维离散余弦变换的矩阵形式为
| $ \left[ {\begin{array}{*{20}{c}} {{Y_0}}\\ {{Y_1}}\\ {{Y_2}}\\ {{Y_3}}\\ {{Y_4}}\\ {{Y_5}}\\ {{Y_6}}\\ {{Y_7}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{C_0}}&{{C_0}}&{{C_0}}&{{C_0}}&{{C_0}}&{{C_0}}&{{C_0}}&{{C_0}}\\ {{C_1}}&{{C_3}}&{{C_5}}&{{C_7}}&{ - {C_7}}&{ - {C_5}}&{ - {C_3}}&{ - {C_1}}\\ {{C_2}}&{{C_6}}&{ - {C_6}}&{ - {C_2}}&{ - {C_2}}&{ - {C_6}}&{{C_6}}&{{C_2}}\\ {{C_3}}&{ - {C_7}}&{ - {C_1}}&{ - {C_5}}&{{C_5}}&{{C_1}}&{{C_7}}&{ - {C_3}}\\ {{C_4}}&{ - {C_4}}&{ - {C_4}}&{{C_4}}&{{C_4}}&{ - {C_4}}&{ - {C_4}}&{{C_4}}\\ {{C_5}}&{ - {C_1}}&{{C_7}}&{{C_3}}&{ - {C_3}}&{ - {C_7}}&{{C_1}}&{ - {C_5}}\\ {{C_6}}&{ - {C_2}}&{{C_2}}&{ - {C_6}}&{ - {C_6}}&{{C_2}}&{ - {C_2}}&{{C_6}}\\ {{C_7}}&{ - {C_5}}&{{C_3}}&{ - {C_1}}&{{C_1}}&{ - {C_3}}&{{C_5}}&{ - {C_7}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_0}}\\ {{x_1}}\\ {{x_2}}\\ {{x_3}}\\ {{x_4}}\\ {{x_5}}\\ {{x_6}}\\ {{x_7}} \end{array}} \right] $ | (5) |
通过观察与分析,矩阵C是具有对称性的,式(5) 可以进一步简化为
| $ \left[ {\begin{array}{*{20}{c}} {{Y_0}}\\ {{Y_2}}\\ {{Y_4}}\\ {{Y_6}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{C_0}}&{{C_0}}&{{C_0}}&{{C_0}}\\ {{C_2}}&{{C_6}}&{ - {C_6}}&{ - {C_2}}\\ {{C_4}}&{ - {C_4}}&{ - {C_4}}&{{C_4}}\\ {{C_6}}&{ - {C_2}}&{{C_2}}&{ - {C_6}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_0} + {x_7}}\\ {{x_1} + {x_6}}\\ {{x_2} + {x_5}}\\ {{x_3} + {x_4}} \end{array}} \right] $ | (6) |
| $ \left[ {\begin{array}{*{20}{c}} {{Y_1}}\\ {{Y_3}}\\ {{Y_5}}\\ {{Y_7}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{C_1}}&{{C_3}}&{{C_5}}&{{C_7}}\\ {{C_3}}&{ - {C_7}}&{ - {C_1}}&{ - {C_5}}\\ {{C_5}}&{ - {C_1}}&{ - {C_7}}&{{C_3}}\\ {{C_7}}&{ - {C_5}}&{{C_3}}&{ - {C_1}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_0} - {x_7}}\\ {{x_1} - {x_6}}\\ {{x_2} - {x_5}}\\ {{x_3} - {x_4}} \end{array}} \right] $ | (7) |
在式(5)~(7) 中,C0~C7为二维DCT变换的系数。
从以上分析可以看出,简化后的算法与简化之前的算法相比,加法次数不变,乘法次数由64次减少至32次,运算量减少了一半[7-9]。
2.2 二维DCT硬件架构实现二维DCT变换的总体架构如图 2所示,首先,将串行输入的数据进行串并转换,然后将8×8数据块中的每一行数据进行一维DCT变换,接着再将并行的一维DCT变换的输出数据转换为串行输出并存入到转置RAM当中。在经过转置并再次并串转换之后,对8×8的数据块的每一列进行一维DCT变换,最终得到的结果即为二维DCT变换值。

|
图 2 二维DCT变换的硬件架构 |
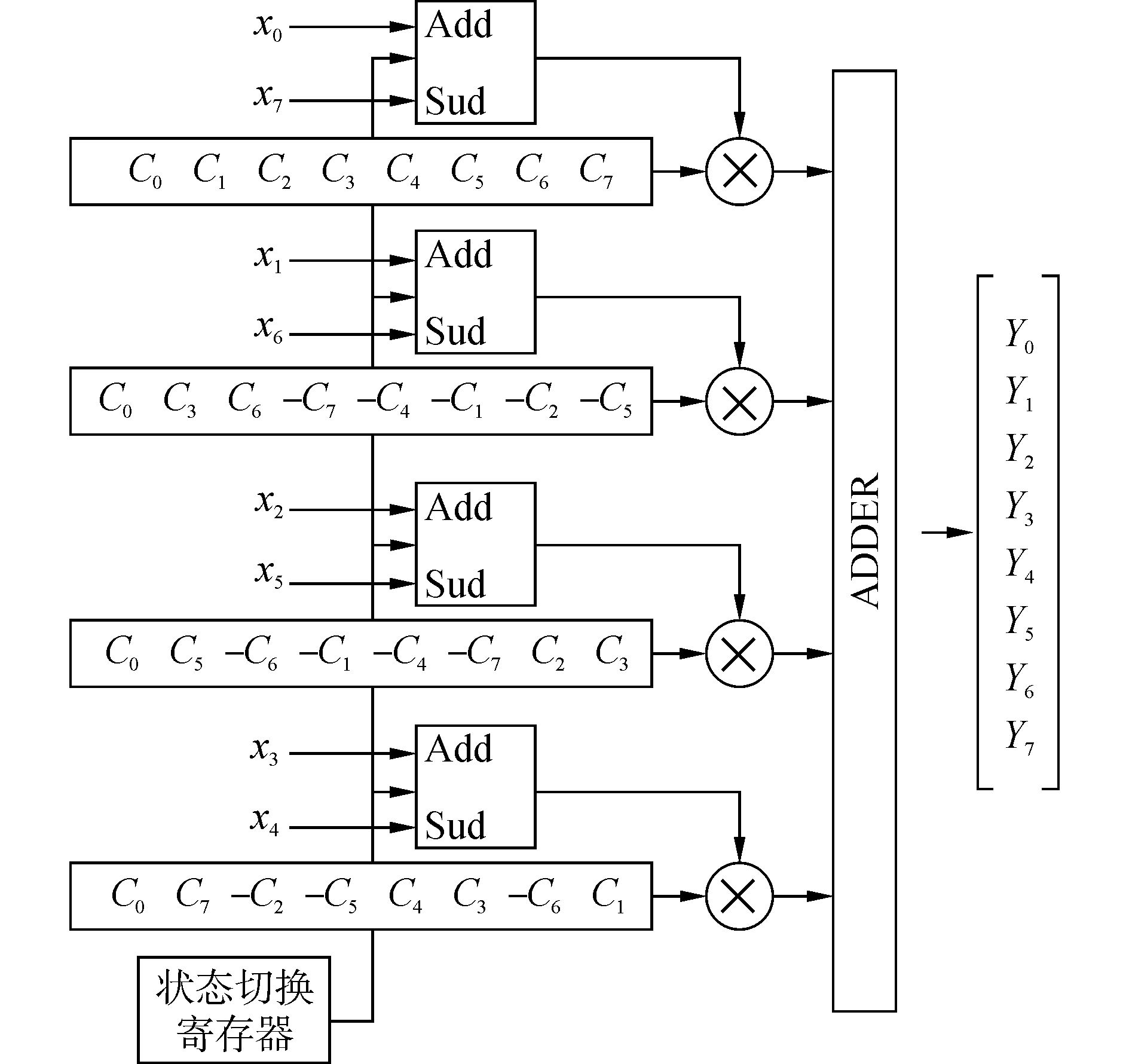
由于一维DCT的系数矩阵均为浮点数,但是在硬件系统中仅仅能够处理整型数据,因此,需要对其乘以一个固定的系数,将浮点数转换为整型数据。在文中,对DCT系数矩阵乘以16 384,将系数矩阵送入到DCT运算模块,运算完成之后,需要将数据再除以16 384,从而得出原有的DCT运算结果,但是硬件无法直接实现除法,考虑到被除数与2的关系,这里采用移位操作对数据进行整除,即右移14位。一维DCT的实现原理图如图 3所示。
|
图 3 一维DCT的硬件结构 |
在图 3中,x0~x7为输入,Y0~Y7为输出。首先,将输入的x0~x7利用移位寄存器进行串并转换,然后对状态切换寄存器的值进行判断,若值为1,则执行x0+x7、x1+x6、x2+x5、x3+x4;若值为0,则执行x0-x7、x1-x6、x2-x5、x3-x4。分别将DCT系数与x0+x7等运算结果按照式(6)、(7) 中的顺序做乘法运算,并将运算的结果相加,得到最终的Y0~Y7值。
基于以上的分析,编写相应的Verilog代码实现图 3所示的结构,接着从测试图像中提取一个8×8的矩阵数据,如式(8) 所示,矩阵中的数据均为十进制有符号数,将该组数据作为激励来测试该算法的正确性:
| $ \left[ {\begin{array}{*{20}{c}} {91}&{92}&{106}&{122}&{130}&{133}&{126}&{113}\\ {94}&{100}&{115}&{124}&{126}&{132}&{125}&{128}\\ {115}&{121}&{129}&{129}&{126}&{132}&{129}&{116}\\ {126}&{130}&{135}&{137}&{139}&{145}&{131}&{104}\\ {107}&{113}&{122}&{127}&{133}&{141}&{131}&{105}\\ {83}&{90}&{98}&{96}&{90}&{92}&{91}&{80}\\ {80}&{81}&{83}&{74}&{59}&{54}&{54}&{48}\\ {87}&{80}&{79}&{76}&{66}&{60}&{55}&{46} \end{array}} \right] $ | (8) |
为了方便JPEG的编码,需要将YCBCR中的Y信号减去128以使它转换到-128~127的范围内,因此在模块中,对所有的输入数据减去128然后再执行DCT变换。
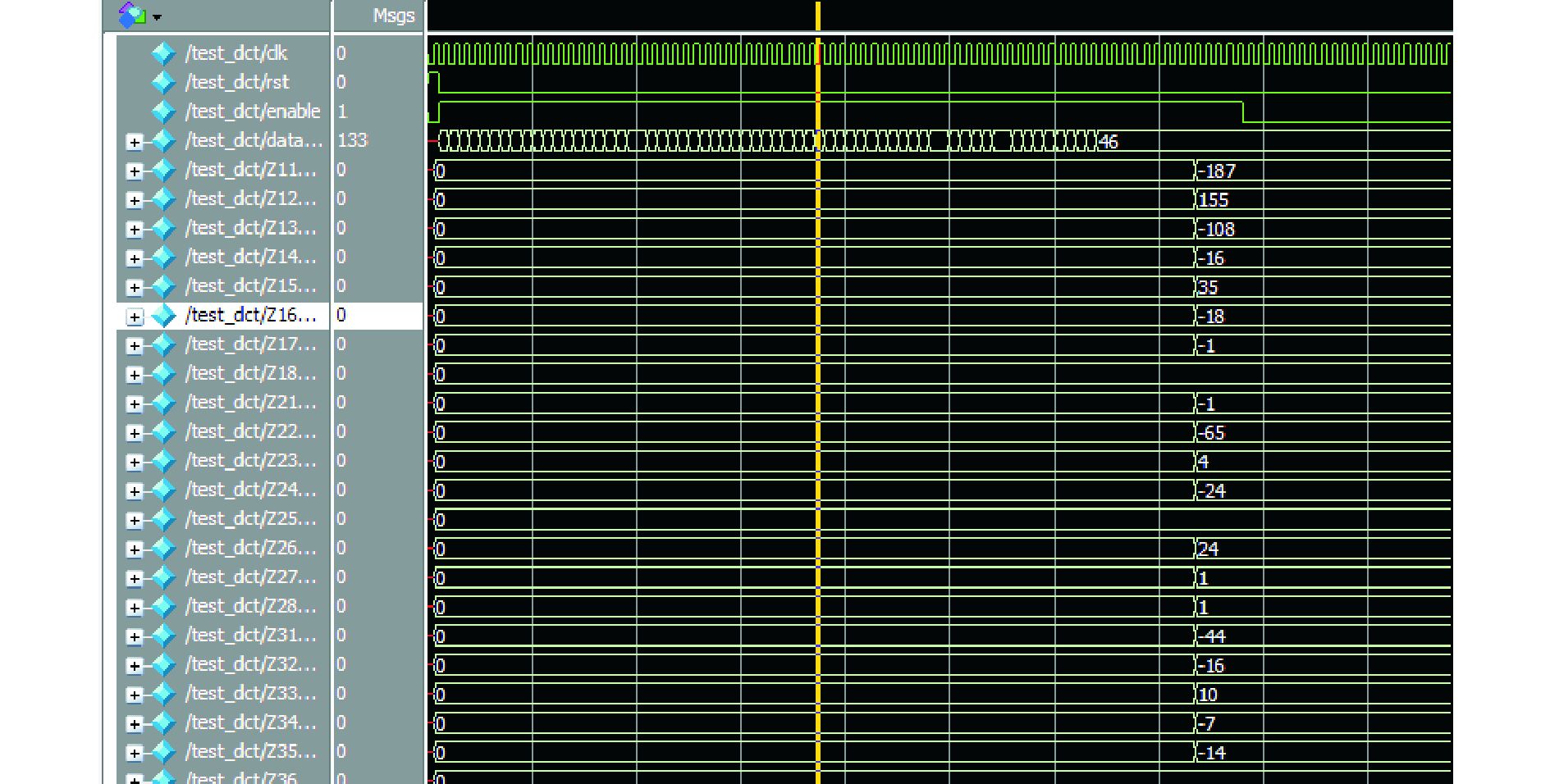
将式(8) 中的数据作为测试激励来对DCT模块进行测试。式(9) 是使用MATLAB进行DCT变换之后的结果,图 4为使用MODELSIM仿真的结果。将式(9) 中的数据与图 4中的数据进行对比,可知所设计的DCT模块具有较高的精度。
|
图 4 二维DCT模块的仿真波形 |
| $ \left[ {\begin{array}{*{20}{c}} { - 187.5}&{ - 0.77}&{ - 44.29}&{10.11}&{ - 17.25}&{13.62}&{0.22}&{ - 0.11}\\ {154.54}&{ - 64.68}&{ - 15.79}&{7.24}&{ - 0.5}&{ - 0.02}&{0.52}&{ - 0.32}\\ { - 107.67}&{4.19}&{10.5}&{ - 8.85}&{13.19}&{0.14}&{0.48}&{0.47}\\ { - 15.72}&{ - 23.74}&{ - 7.46}&{ - 0.02}&{0.19}&{ - 0.3}&{ - 0.32}&{0.6}\\ {33.5}&{ - 0.23}&{ - 13.56}&{18.47}&{ - 0.25}&{0.22}&{ - 0.07}&{ - 0.23}\\ { - 17.7}&{23.63}&{0.54}&{ - 0.02}&{ - 0.47}&{ - 0.48}&{0.23}&{ - 0.5}\\ { - 0.6}&{1.01}&{0.23}&{0.28}&{0.49}&{ - 0.45}&{0.25}&{ - 0.41}\\ {0.13}&{0.46}&{0.6}&{0.28}&{ - 0.61}&{0.00}&{0.09}&{0.18} \end{array}} \right] $ | (9) |
在图 4中,data_in为输入的信号,Z11-Z88为输出数据,在64个数据输入完成之后,再经过9个时钟周期即可得到64个二维DCT之后的系数,即总共所需的时钟周期为73个。从计算的结果可以看出,越靠近左上角的数据越大,而靠近右下角大部分数据为0,这个结果是由于人眼视觉对于高频信号不敏感。因此,低频信号被保留下来,而大多数高频信号变为0,节省了数据空间。
3 量化及熵编码 3.1 量化经过二维DCT后,接下来要对DCT系数矩阵进行量化。量化是压缩过程中一个非常重要的过程,是对DCT系数进行压缩的关键一步,方法是通过降低DCT系数的精度,去除掉图像中的冗余信息,达到压缩的目的,所以说量化是图像质量下降的主要原因。量化表的不同同时也会导致压缩比例的不同,可以自由选择量化表。式(10) 和式(11) 分别为色度量化矩阵和亮度量化矩阵。在进行量化时,令色度DCT系数矩阵除以色度量化矩阵,亮度DCT系数除以亮度量化矩阵。
| $ \left[ {\begin{array}{*{20}{c}} {17}&{18}&{24}&{47}&{99}&{99}&{99}&{99}\\ {18}&{21}&{26}&{99}&{99}&{99}&{99}&{99}\\ {24}&{26}&{56}&{99}&{99}&{99}&{99}&{99}\\ {47}&{66}&{99}&{99}&{99}&{99}&{99}&{99}\\ {99}&{99}&{99}&{99}&{99}&{99}&{99}&{99}\\ {99}&{99}&{99}&{99}&{99}&{99}&{99}&{99}\\ {99}&{99}&{99}&{99}&{99}&{99}&{99}&{99}\\ {99}&{99}&{99}&{99}&{99}&{99}&{99}&{99} \end{array}} \right] $ | (10) |
| $ \left[ {\begin{array}{*{20}{c}} {16}&{11}&{10}&{16}&{24}&{40}&{51}&{61}\\ {12}&{12}&{14}&{19}&{26}&{58}&{60}&{55}\\ {14}&{13}&{16}&{24}&{40}&{57}&{69}&{56}\\ {14}&{17}&{22}&{29}&{51}&{87}&{80}&{62}\\ {18}&{22}&{37}&{56}&{68}&{109}&{103}&{77}\\ {25}&{35}&{55}&{64}&{81}&{104}&{113}&{92}\\ {49}&{64}&{78}&{87}&{103}&{121}&{120}&{101}\\ {72}&{92}&{95}&{98}&{112}&{100}&{103}&{99} \end{array}} \right] $ | (11) |
量化后,要对数据进行熵编码,对于DC系数和交流系数,由于两者的性质不同,在编码的时候也要分开对待。对于相邻的8×8的模块,其相邻块之间的关联性很强,因此对于DC系数的编码采用了差值脉冲编码(DPCM),即对相邻块的DC系数之间的差值D=DCi-DCi-1进行编码,2个直接的DC系数均需要10 bit,而采用DPCM之后则仅仅需要10 bit和1 bit。对于其余63个AC系数,对这些数据进行零值行程的Huffman编码,这63个元素采用了Zig_Zag的排列方法,这样可以使AC系数的0值集中,便于压缩。熵编码可以分为两步进行。首先,需要将DC系数和AC系数转换为中间符号序列,然后再将这些符号赋以变长码字。DC系数的熵编码的中间格式由2个符号组成,符号1为尺寸(size),符号2为幅值(Diff), 尺寸表示幅值编码所需的比特数,而幅值表示DC差值的幅值,范围为[-211, 211-1]。AC系数熵编码的中间格式同样也由2个符号构成,符号1为行程和尺寸,符号2为幅值。对于DC系数和AC系数中的符号1采用Huffman表中的变长码编码(variable-length coding,VLC),符号2用变长整数(variable length integer,VLI)编码(补码)。Huffman表由JPEG压缩标准推荐指定。
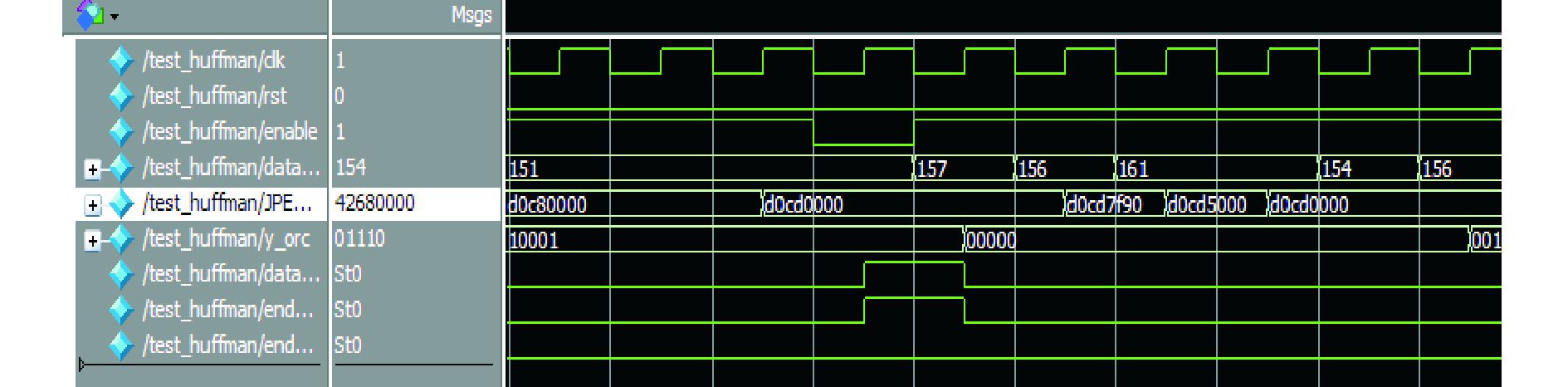
根据JPEG标准提供的Huffman表,编写程序实现量化以及熵编码模块,并对模块进行仿真,该模块的测试结果如图 5所示。
|
图 5 量化及熵编码模块的仿真波形 |
在图 5中,JPEG_bitstream是Huffman编码之后的32位数据,end_of_block_output当一个8×8的数据块输入完成之后,该信号置1。y_orc信号代表DC或AC系数Huffman编码之后有效数据所占位数的累加值。end_of_block_empty信号代表无任何有效的数据输出。当data_ready信号值为1时,JPEG_bitstream输出值为有效值。
| $ \left[ {\begin{array}{*{20}{c}} {16}&0&0&0&0&0&0&0\\ 1&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0 \end{array}} \right] $ | (12) |
式(12) 中的矩阵为经过二维DCT变换并量化之后的结果,将此矩阵作为测试信号来对熵编码模块进行测试,得到的仿真结果为D0CD0000,如图 5所示,与MATLAB仿真的结果是一致的。
4 JPEG编码器的测试与验证在上述的几个关键模块设计完成后,利用3个fifo接收熵编码输出的数据流。由于文中使用的图像采样格式为4:4:4,即每个Y块对应一个Cb块和Cr块,所以在组成图像数据流的时候,在每个Y块的码流后紧接着存放1个Cb块码流和Cr块码流,按照这个方式存储所有的JPEG数据流,这样就能够完成完整的JPEG编码器。在JPEG编码器完成之后,需要对其正确性以及压缩效果来进行验证。
首先,将源图像读取到MATLAB软件中,然后将图像的RGB色域的数据提取出来,并将数据写入到JPEG压缩系统的testbench文件中,对JPEG编码器添加激励进行测试,将最后得到的位数据流按照JFIF文件格式进行组织得到最终的图像。然后将JPG格式的图像解码还原成原格式,并与最初的图像进行比较。图 6为JPEG编码器测试的流程。
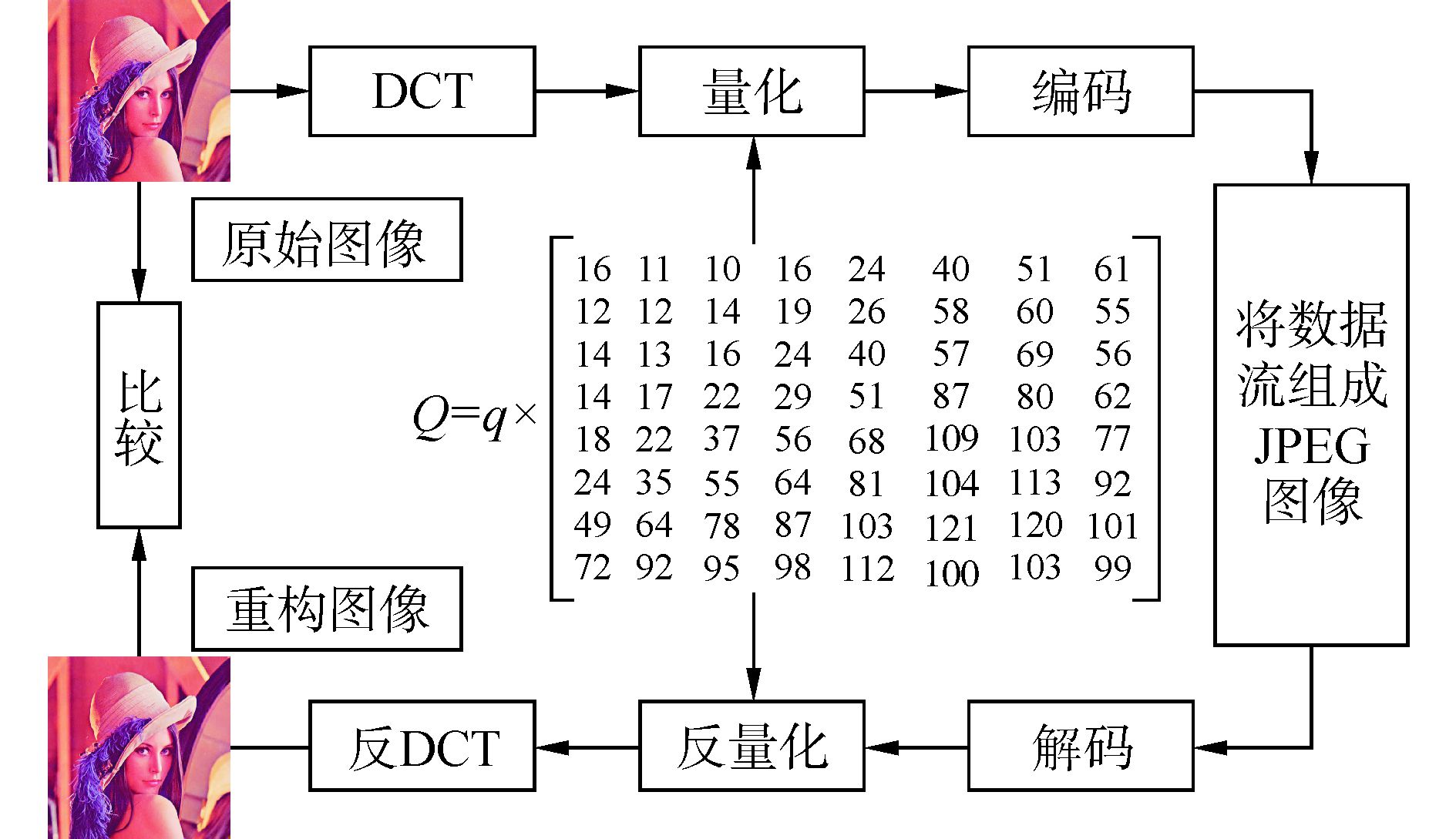
|
图 6 JPEG编码器测试流程 |
JPEG图像格式大体上可以分为2个大的部分:标记码和压缩数据。JPEG图像的每个标记都是由2个字节组成,其中前一个字节是固定在0xFF。每个标记之前还可以添加数目不限的OxFF填充字节。其中主要的几个标记如表 1所示[10-11]。
|
|
表 1 JPEG文件格式标记 |
使用MATLAB按照表 1中的JPEG格式将仿真后的数据进行重建,得到图 7中(b)、(d)和(f)图,其中Baboon图像的压缩比为12.2,Lena图像的压缩比为26.6,Peppers图像的压缩比为21.5。将JPG格式的图像再解码之后与原始图像进行比较,Baboon图像的峰值信噪比(peak signal to noise ratio,PSNR)为30.1 dB,Lena图像的PSNR为37.8 dB,Peppers图像的PSNR值为36.1 dB。从测试的结果可知,在相同的JPEG编码器下,对于不同的图像,压缩比不同。图 7中的测试图像在压缩之后在人类视觉系统下几乎感觉不到任何失真。从解码之后的PSNR值可以看出,图像具有较好的压缩效果。因此,文所设计的JPEG编码器可以正常工作,可以对图像起到压缩的作用。

|
图 7 压缩后与压缩前的图像 |
使用Synopsys公司的VCS软件来对整个系统进行仿真,仿真通过后,用Synopsys Design Compiler在SMIC 180 nm工艺下对设计进行综合,然后用Cadence SOC Encounter软件对综合后的门级网表进行布局布线,并且经过DRC和LVS验证。最后,在SMIC180 nm工艺下对系统进行综合并布局布线,工作在100 MHz下,芯片的功耗为460 mW,最终布局布线之后的面积为10.7 mm2。图 8为最终布局布线之后的版图。
|
图 8 JPEG编码器的版图 |
本文对JPEG压缩编码的基本原理进行详细的分析,用verilog实现了一种JPEG压缩编码器,成功地实现了对图像的压缩。
1) 重新设计了DCT模块的硬件架构,运算量得到了很大程度的简化。
2) 用MATLAB和Modelsim进行联合仿真,成功的对压缩之后的比特流进行了图像重建,与压缩之前的图像比较,有较好的PSNR值,图像失真较小。
3) 对RTL代码进行逻辑综合,并将电路进一步的进行VLSI实现,然后进行了DRC和LVS验证,完成了JPEG编码器的硬核设计。
本文所设计的硬件编码器采用并行计算的方式,与软件编码器相比具有良好的实时性,另外,该编码器也可以作为一个IP核应用到其他系统级芯片的设计之中。
| [1] |
肖迪, 谢沂均. 一种结合JPEG压缩编码的彩色图像加密算法[J]. 物理学报, 2013, 62(24): 67-77. ( 0) 0)
|
| [2] |
KAVITHA A, VARDHINI PAH. Efficient realization of jpeg encode for image compression on FPGA[J]. International journal of scientific engineering and technology research, 2015(4): 314-319. ( 0) 0)
|
| [3] |
YAGAIN H, DONAPATI S. Addressing the interoperability issues while using JPEG-XR[C]//International Symposium on Electronic System Design. IEEE, 2011:158-163.
( 0) 0)
|
| [4] |
胡广书. 数字信号处理、理论、算法与实现[M]. 北京: 清华大学出版社, 2012.
( 0) 0)
|
| [5] |
马媛媛, 杨峰, 信科, 等. 基于DCT的JPEG图像压缩的研究[J]. 计算机技术与发展, 2011, 21(8): 133-136. ( 0) 0)
|
| [6] |
彭益智, 霍家道, 徐伟. 一种基于TMS320C6678的JPEG编码算法并行实现方法[J]. 指挥控制与仿真, 2012, 34(1): 119-122. ( 0) 0)
|
| [7] |
CHEN T Y, LEI Q C. A fast algorithm for the multidimensional discrete cosine transform[J]. Journal of numerical methods & computer applications, 1986(2): 89-97. ( 0) 0)
|
| [8] |
靳刚, 庄奕琪, 刘锋. MPEG4编码器二维DCT变换的FPGA实现及优化[J]. 电路与系统学报, 2005, 10(4): 131-135. ( 0) 0)
|
| [9] |
山洪刚, 郑南宁, 杨国安, 等. 一种应用于8×8二维DCT/IDCT的高效结构[J]. 半导体技术, 2002, 27(6): 13-17. ( 0) 0)
|
| [10] |
RODRIGUES T A N. JPEG decoder implementation on FPGA using dynamic partial reconfiguration[EB/OL].[2016-04-06]. http://repositorio.ipl.pt/handle/10400.21/5375.
( 0) 0)
|
| [11] |
唐赛明. 基于FPGA的JPEG压缩编码的研究与实现[D]. 长沙: 湖南大学, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10532-2007161092.htm
( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


