出版日期: 2019-09-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20198204
2019 | Volumn23 | Number 5
上一篇  |  下一篇
技术方法 
多源数据融合的高时空分辨率植被指数生成
expand article info 杨军明1 , 吴昱2,3 , 魏永霞1,4 , 王斌1 , 汝晨1 , 马瑛瑛1 , 张奕1
1. 东北农业大学水利与土木工程学院，哈尔滨 150030
2. 东北林业大学林学院，哈尔滨 150040
3. 黑龙江农垦勘测设计研究院，哈尔滨 150090
4. 农业部农业水资源高效利用重点实验室，哈尔滨 150030
收稿日期: 2018-05-10; 预印本: 2018-08-17
基金项目: 国家重点研发计划(编号：2016YFC0400101)；国家自然科学基金(编号：51009026)；农业部农业水资源高效利用重点实验室开放课题资助项目(编号：2015002)
第一作者简介: 杨军明，1992年生，男，硕士研究生，研究方向为多源遥感数据融合及其农业应用。E-mail：julming@163.com
通信作者简介: 魏永霞，1964年生，女，教授，研究方向为农业水土资源高效利用与保护。E-mail：wyx0915@163.com

摘要

高时空分辨率的植被指数VI(Vegetation Index)数据是农业和生态研究的重要基础数据集，目前常用的VI数据的时空分辨率存在不可调和矛盾。考虑VI时序变化对数据融合的影响，提出一种新的VI数据时空融合模型VISTFM(Vegetation Index Spatial and Temporal Fusion Model)，VISTFM采用模糊C聚类算法，对存量时序VI数据按土地利用类型划分为若干子类，从高低分辨率影像中随土地覆被类的变化规律提取子类，结合低分辨率影像提取的土地覆被类变化规律融合生成高时空分辨率的VI数据。用常用的Landsat和MODIS数据验证该算法，测试表明，VISTFM能够较好的捕获VI的中间变化过程，与常用的基于线性混合模型的模型和时空自适应反射率融合模型及其改进模型相比，利用VISTFM获得的植被指数数据集具有更高的时空分辨率。

关键词

遥感, 植被指数, 数据融合, 时空分辨率, 模糊C聚类算法, 线性混合模型

A model for the fusion of multi-source data to generate high temporal and spatial resolution VI data
expand article info YANG Junming1 , WU Yu2,3 , WEI Yongxia1,4 , WANG Bin1 , RU Chen1 , MA Yingying1 , ZHANG Yi1
1.College of Water Conservancy and Architecture, Northeast Agricultural University, Harbin 150030, China
2.College of Forestry, Northeast Forestry University, Harbin 150040, China
3.Heilongjiang Agricultural Reclamation Survey and Research Institute, Harbin 150090, China
4.Key Laboratory of High Efficiency Utilization of Agricultural Water Resources in Ministry of Agriculture, Harbin 150030, China

Abstract

Vegetation Index (VI) data with high spatial and temporal resolution are highly important in the use of remote sensing technology to observe the earth. Owing to technological limitations, obtaining VI data that exhibits both high spatial and temporal resolution is impossible. The arrival of multi-source remote sensing data spatial and temporal fusion model enables the retrieval of data with high spatial and temporal resolution. The commonly used model does not have the ability to capture the intermediate change process of pixel value, and a certain regularity occurs in the change of the VI of the landmark. This study proposes a new multi-source data fusion model (FCMVISTFM) based on Fuzzy C-Mean algorithm (FCM). Making pixels that group together have similar VI values and law of VI changes throughout the period. FCMVISTFM uses FCM to divide land-cover types into certain categories based on multi-phase VI data, which are defined as subclasses of each land-cover class. Each land-cover class average value is calculated by using the linear unmixed model, and subclass average value is calculated by the law between land-cover class and subclass. The VI data are fused by Landsat8 OLI and MODIS data based on the assumption that the average VI value of subclass S is the same as the VI value of pixels that belong to subclass S. Results show that FCMVISTFM can achieve relatively high accuracy. The average values of correlation coefficient (R), RMSE, ERGAS, and variance are 0.9057, 0.0674, 1.9795, and 0.0045, respectively. With this level of accuracy, VI data can be used for vegetation research and observations of the earth. Commonly used line unmixed models, spatial and temporal adaptive reflectance fusion model (STARFM), and its improved models have the problem of uncertain ability to capture the intermediate change process of VI. Thus, FCMVISTFM is more accurate compared with STDFA and ESTARFM. FCMVISTFM is developed for obtaining high spatial and temporal resolution VI data, making it easier to capture the intermediate changes of VI, which can be applied where high spatial and temporal resolution VI data are needed. In this study, the accuracy of the multi-source data fusion model can be increased by the following aspects. (1) The models based on line unmixed model, regardless of pixel classes or subset S average value calculations, are based on the entire image. However, in the STARFM model and improved models based on STARFM, the data fusion based on high and low resolutions pixels in a certain window, cloud cover only affects the calculation of pixels near its coverage area. The acquisition of multiphase cloudless images is especially difficult when the study area is large. In this case, the STARFM model and improved models based on STARFM have more application advantages. (2) All of the multi-source remote sensing data fusion models are based on certain assumptions, though these assumptions are based on a certain theoretical and have certain rationality. Errors are mainly caused by assumptions. A complete model assumption is proposed as the main way to improve the accuracy of the multi-source remote sensing data fusion model. (3) The time sequence laws of the VI of various landmark are not disordered, but a certain regularity, such as the specific laws of the crop’s VI, occurs. If the multi-source remote sensing data fusion model is established based on these laws, then it can also improve the accuracy of fusion results to some extent.

Key words

remote sensing, Vegetation Index (VI), data fusion, temporal and spatial resolution, fuzzy c-means algorithm, linear unmixed model

1 引　言

植被指数VI(Vegetation Index)是在作物长势、植物生物量的研究中具有重要指示意义的数值(邱庆伦 等，2004)，是对植被生长发育状况简单、有效的度量参数(田庆久和闵祥军，1998；罗亚 等，2005)。VI被广泛地应用于农业、环境和生态系统等研究领域。利用遥感影像检测土地覆被类型、植被类型和环境变化特征时，往往不直接运用影像的地表反射率，而是通过运用VI达到研究目的。近几年，随着VI在植被检测等建模中的应用大幅度增加(Cerasoli 等，2016)，对高时空分辨率的VI需求也呈现不断增长态势。

受遥感技术和预算等限制，高时空分辨率的遥感影像很难获取(Wu 等，2016)，目前常用的遥感影像数据时间和空间分辨率存在不可调和的矛盾(蔡学良和崔远来，2009；邬明权 等，2010)，时间分辨率较高的影像数据空间分辨率较低，反之亦然。Landsat 等遥感卫星虽然空间分辨率较高，能够反应农田系统的复杂变化，但时间分辨率相对较低，容易受云和阴雨天气等的影响，造成作物检测的关键时期无卫星覆盖等现象。MODIS 等遥感卫星虽然时间分辨率较高，为1天，但空间分辨率相对较低。不适宜于种植结构复杂或者景观破碎、异质性较强的区域。为此，提出了多种多源遥感数据融合模型，这些模型以波段融合为主，在获取高时空分辨率的VI数据研究中发挥了积极作用(Liao 等，2016；石月婵 等，2015；Rao 等，2015)。

目前常用的多源遥感数据融合模型有两类，一类是基于线性混合模型的多源遥感数据融合模型，另一类是时空自适应反射率融合模型及其改进模型。线性混合模型的主要思想是从高分辨影像中提取丰度矩阵来定义子集S，然后利用线性混合模型，求解出低分辨率影像各时相子集S的平均反射率，进而融合生成高时空分辨率的影像。如Zhukov 等(1999)以目标像元一定范围内的像元为目标像元的子集S合成影像；邬明权 等(2012)以差值影像经过密度分割后的像元为子集S合成影像；Gevaer和García-Haro(2015)应用K-均值聚类算法对影像进行聚类，并以各个类别为子集S合成影像。此类方法忽略了各个子集的内部差异，认为各个子集的平均像元值与子集内部像元的像元值相近，且具有一致的时间演变特征。如果像元值随时间变化出现剧烈变化时，子集S平均值与子集内部像元值可能存在较大差异。如以作物VI为例，其时序VI曲线先增大后减小，中间变化过程复杂，以生育始末期的高分辨率VI来预测生育，可能产生较大误差。

Gao 等(2006)根据一定窗口内的像元之间的光谱相似性及空间相关性，提出了一种时空自适应反射率融合模型STARFM(Spatial and Temporal Adaptive Reflectance Fusion Model)，是目前最常用的遥感数据时空融合模型。研究人员不断对该模型进行了改进，如Hilker 等(2009)为降低基期影像选择不当对融合结果的影响，提出了一种新的算法来选择基期高分辨率影像。Zhu 等(2010)根据不同传感器系统之间存在误差等，提出了增强的时空自适应反射率融合模型ESTARFM(Enhanced Spatial and Temporal Adaptive Reflectance Fusion Model)；谢登峰 等(2016)应用降尺度数据代替重采样的MODIS数据，提出了结合像元分解和STARFM模型的遥感数据融合模型CDSTARFM(Combination of Downscaling Mixed Pixel Spatial and Temporal Adaptive Reflectance Fusion Model)。虽然这些模型从不同角度改进了STARFM模型，一定程度上提高了模型精度，但此类改进模型均建立在一定窗口内的相似像元与低分辨率像元平均值的比值为定值的假设基础上，当不同地物的像元值随时间变化差异较大时，该模型存在较大的不确定性。如草地和作物在作物生长发育初期的NDVI差异较小，以该时期的NDVI为基期影像来定义相似像元，这两类地物的像元可能被识别为相似像元。但与草地相比，作物的NDVI随时间变化剧烈，在作物生长发育茂盛的时期，作物NDVI大于草地，但融合计算结果可能与草地接近，与作物背离。

针对当VI随时间变化发生剧烈变化时，时空自适应类反射率融合模型可能产生较大误差；而且与像元反射率相比，VI时序变化有一定规律性。本文提出了一种基于模糊C聚类算法FCM(Fuzzy C-means Model)的VI数据时空融合方法(VISTFM)。

2 方法

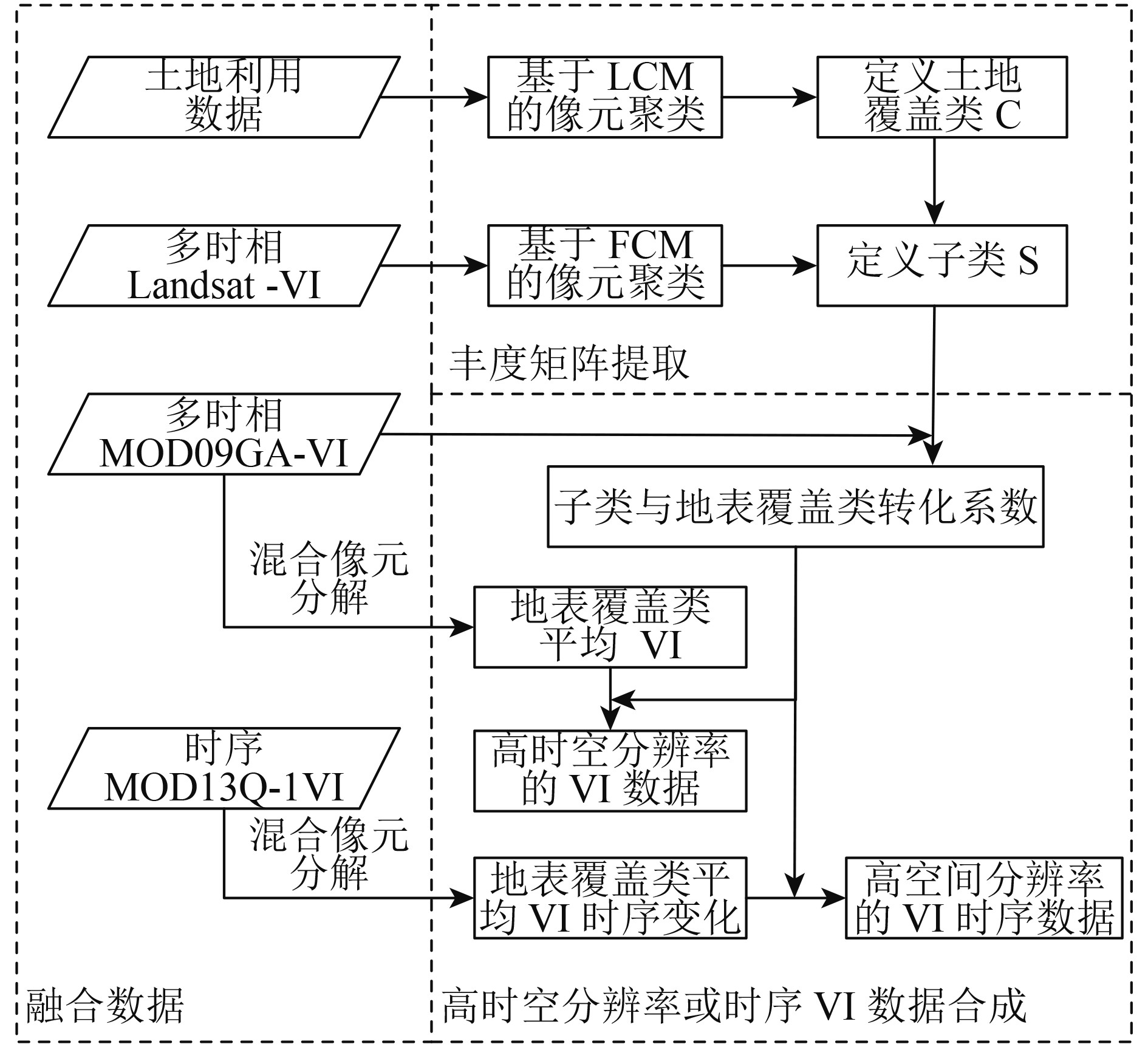
VISTFM针对每类高分辨率土地覆被类型数据，采用FCM，对多时相Landsat-VI数据进行分层聚类，定义为各高分辨率土地覆被类型的子类，使得同类像元具有不同时点VI相似，而且VI的时间变化特征相似的特征。假设子类中的像元具有相似的时点VI和相近的VI时间变化特征，进而融合生成高时空分辨率的VI数据集。计算流程如图1所示。该算法主要包括3个步骤：(1)像元聚类与计算类别平均VI；(2)计算子类与土地覆被类转化系数；(3)生成融合影像。


图 1 VISTFM流程图
Fig. 1 Flow chart of the VISTFM

2.1 像元聚类与类别定义

混合像元分解是高分辨率与低分辨率影像融合的关键(Gevaert和García-Haro，2015)。为进行数据融合，首先需要进行混合像元分解，按照线性混合模型的假设，混合像元(低分辨率像元)是其所包含的高分辨率端元的线性组合(式(1))。基于该假设，可认为混合像元VI为其所包含的高分辨率土地覆被类的线性组合(Wu 等，2016)。虽然每种高分辨率土地覆被类型有其独特的VI和VI变化特征，但每种土地覆被类型内部存在不同的地物类型，如农田内存在不同的作物，不透水层包括道路、建筑物等。不同的地物具有不同的VI和VI变化规律，故每种高分辨率土地覆被类型内部VI可能存在较大差异，且随时间的变化规律各异。

$VI_{\rm{L}}(k,t_i) = \sum\limits_{c = 1}^m {{{A}}_k(C,t_i)} \cdot \overline {VI}_{\rm{L}}(C,t_i) + \varepsilon (k,t_i)$ (1)

约束条件： $0 < {{A}}_k(C,t_i) < 1$ ； $\sum\limits_{c = 1}^m {{{A}}_k(C,t_i)} = 1$

$\begin{array}{l} \left[ \begin{gathered} VI_{\rm{L}}(1,t_i) \\ VI_{\rm{L}}(2,t_i) \\ \cdots \\ VI_{\rm{L}}(n,t_i) \\ \end{gathered} \right]{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{{A}}(1,1)}&{{{A}}(1,2)}& \cdots &{{{A}}(1,m)} \\ {{{A}}(2,1)}&{{{A}}(2,2)}& \cdots &{{{A}}(2,m)} \\ \cdots & \cdots & \cdots & \cdots \\ {{{A}}(n,1)}&{{{A}}(n,2)}& \cdots &{{{A}}(n,m)} \end{array}} \right]\cdot{\rm{}}\\\\ \;\;\quad\qquad\qquad\left[ \begin{gathered} \overline {VI}_{\rm{L}}(1,t_i) \\ \overline {VI}_{\rm{L}}(2,t_i) \\ \cdots \\ \overline {VI}_{\rm{L}}(m,t_i) \\ \end{gathered} \right] + \left[ \begin{gathered} \varepsilon (1,t_i) \\ \varepsilon (2,t_i) \\ \cdots \\ \varepsilon (n,t_i) \\ \end{gathered} \right]\end{array}$

式中， $VI_{\rm{L}}(k,t_i)$ 为 $t_i$ 时刻混合像元(低分辨率像元)k的VI(为方便区分，下标H表示高空间分辨率VI数据中获取的参数，本文特指Landsat数据，下标L表示低空间分辨率VI数据中获取的参数，本文特指MODIS数据)； ${{A}}_k$ 为混合像元k的丰度矩阵；C为像元k所包含的高分辨率土地覆被类型； $\overline {VI}_{\rm{L}}(k,t_i)$ 为低分辨率土地覆被类型C的平均VI，经MODIS数据混合像元分解求得； $\varepsilon (k,t_i)$ 为混合像元k计算的残差；m为类别数；n为混合像元数。

为解决不同土地覆被类型中不同地物的VI和VI变化规律各异的问题，对每种高分辨率土地覆被类型中的像元进行二次聚类，定义为土地覆被类型的子类。使得子类中的高分辨率像元具有相似的VI和VI变化。

FCM是一种软划分方法，借用模糊数学思想，用隶属度确定每个数据点所属子类，若用其对多维数据进行聚类，可使同类数据在各个维度均具有相对较好的相似性(Bezdek 等，1984；Ojeda-Magaña 等，2018)。若应用FCM对时序VI进行聚类，则可使得同类数据的VI在各个时相均有较好的相似性，即聚为一类的数据有相似的VI和VI变化规律。故借助可对多维数组进行聚类的FCM将每类土地覆被类划分成若干子类。

2.2 计算类别平均VI

从理论上讲，子类平均VI最精确的计算方法是从式(1)中经对MODIS影像混合像元分解求得。但受影像大气校正、几何校正等误差的影响。当子类数目过多时，经混合像元分解求得的子类平均VI可能存在较大误差。因此，假设低分辨率土地覆被类与其所包含的高分辨率子类的平均VI的比值 $k_{ij}$ 在一段时间内保持稳定。下面对该假设的合理性进行讨论。

从各类地物的VI曲线可以看出，其在一段时间内的变化基本为线性。因此，假设在一段时间内子类与土地覆被类的平均VI呈线性变化。基于该假设得到下式

$\overline {VI}_{\rm{L}}(C,t_i) - \overline {VI}_{\rm{L}}(C,t_j) = M\cdot(t_i - t_j)$ (2)
$\overline {VI}_{\rm{H}}(S,t_i) - \overline {VI}_{\rm{H}}(S,t_j) = N\cdot(t_i - t_j)$ (3)

式中，M, N分别为低分辨率土地覆被类与高分辨率子类的平均VI的变化率，一段时间内可当作定值； $\overline {VI}_{\rm{L}}(C,t_i)$ 、 $\overline {VI}_{\rm{L}}(C,t_j)$ 分别为 $t_i$ 、 $t_j$ 时刻低分辨率土地覆被类C的平均VI，从式(1)经MOD09GA- VI混合像元分解求得； $\overline {VI}_{\rm{H}}(S,t_i)$ 、 $\overline {VI}_{\rm{H}}(S,t_j)$ 为 $t_i$ 、 $t_j$ 时刻高分辨率子类S的平均VI，经Landsat 8-VI求得。

从两式的比值可以得到

$\frac{{\overline {VI}_{\rm{H}}(S,t_i,B) - \overline {VI}_{\rm{H}}(S,t_j,B)}}{{\overline {VI}_{\rm{L}}(C,t_i,B) - \overline {VI}_{\rm{L}}(C,t_j,B)}} = \frac{N}{M} = k_{ij}$ (4)

式中， $k_{ij}$ 为子类与土地覆被类型之间的转化系数。

从式(4)可以看出，当假设子类与土地覆被类型的平均VI在一段时间内呈线性变化时，子类与土地覆被类的平均VI的比值为定值，即子类与土地覆被类的比值在一段时间内保持稳定。

子类平均VI在一段时间内的变化可用下式表示

$\begin{gathered} \overline {VI}_{\rm{H}}(S,t_i) - \overline {VI}_{\rm{H}}(S,t_j) = \\ k_{ij}\cdot(\overline {VI}_{\rm{L}}(C,t_i) - \overline {VI}_{\rm{L}}(C,t_j)) \\ \end{gathered} $ (5)

虽然 $k_{ij}$ 在一段时间内保持稳定，但两景影像之间的 $k_{ij}$ 依然会发生变化。VISTFM中假设两景影像之间的 $k_{ij}$ 呈线性变化。即 $t_m$ 与 $t_n$ 之间的 $t_p$ 时刻高分辨率子类与低分辨率土地覆被类型的转化系数 $K_p$ 可通过下式求得

$K_p=K_m -\frac{{({{K}}_m - K_n)*(t_m - t_p)}}{{t_m - t_n}}$ (6)

式中， $K_m$ 、 $K_n$ 分别为 $t_m$ 、 $t_n$ 时刻的高分辨率子类与低分辨率土地覆被类之间的转化系数。

2.3 影像融合

因经过分层聚类的各个高分辨率子类内部高分辨率像元具有相似的VI和VI变化，故可假设高分辨率子类平均VI的变化与子类内部高分辨率像元VI的变化一致。基于该假设可以得到式(7)

$\begin{gathered} VI_{\rm{H}}({\rm{l}},t_m) - VI_{\rm{H}}({\rm{l}},t_p) = \\ \overline {VI}_{\rm{H}}(S,t_m) - \overline {VI}_{\rm{H}}(S,t_p) + \varepsilon ({\rm{l}},t_{mp}) \\ \end{gathered} $ (7)

式中， $VI_{\rm{H}}({\rm{l}},t_m)$ 为属于子类S的Landsat像元 ${\rm{l}}$ 在 $t_m$ 时刻的VI， $\varepsilon ({\rm{l}},t_{mp})$ 表示像元l计算的残差，在VISTFM中忽略不计。

结合式(5)可以得到 $t_p$ 时刻像元l的VI可通过下式求得

$\begin{gathered} VI_{\rm{H}}(l,t_p) = VI_{\rm{H}}({\rm{l}},t_m){\rm{ - }} \\ k_{mp}(\overline {VI}_{\rm{L}}(C,t_m) - \overline {VI}_{\rm{L}}(C,t_p)) \\ \end{gathered} $ (8)

$\overline {VI}_{\rm{L}}(C,t_m)$ 、 $\overline {VI}_{\rm{L}}(C,t_p)$ 可应用线性混合模型(式(1))经MODIS影像混合像元分解求得。可从式(8)求得任意时刻 $t_i$ (i=1,2,···)任意像元的VI。即可融合生成高时空分辨率的VI数据。

MOD13Q1为16日最大合成的VI数据产品，因进行了最大合成，所获得的数据产品基本无云覆盖，若经MOD13Q1混合像元分解求得 $\overline {VI}_{\rm{L}}(C,t_m)$ 、 $\overline {VI}_{\rm{L}}(C,t_p)$ 。则可合成高空间分辨率的时序VI数据。若经对无云覆盖的MOD09GA计算得到的日尺度VI数据进行混合像元分解求得 $\overline {VI}_{\rm{L}}(C,t_m)$ 、 $\overline {VI}_{\rm{L}}(C,t_p)$ ，则可合成日尺度的高空间分辨率VI数据。

3 算法测试

3.1 研究区概况

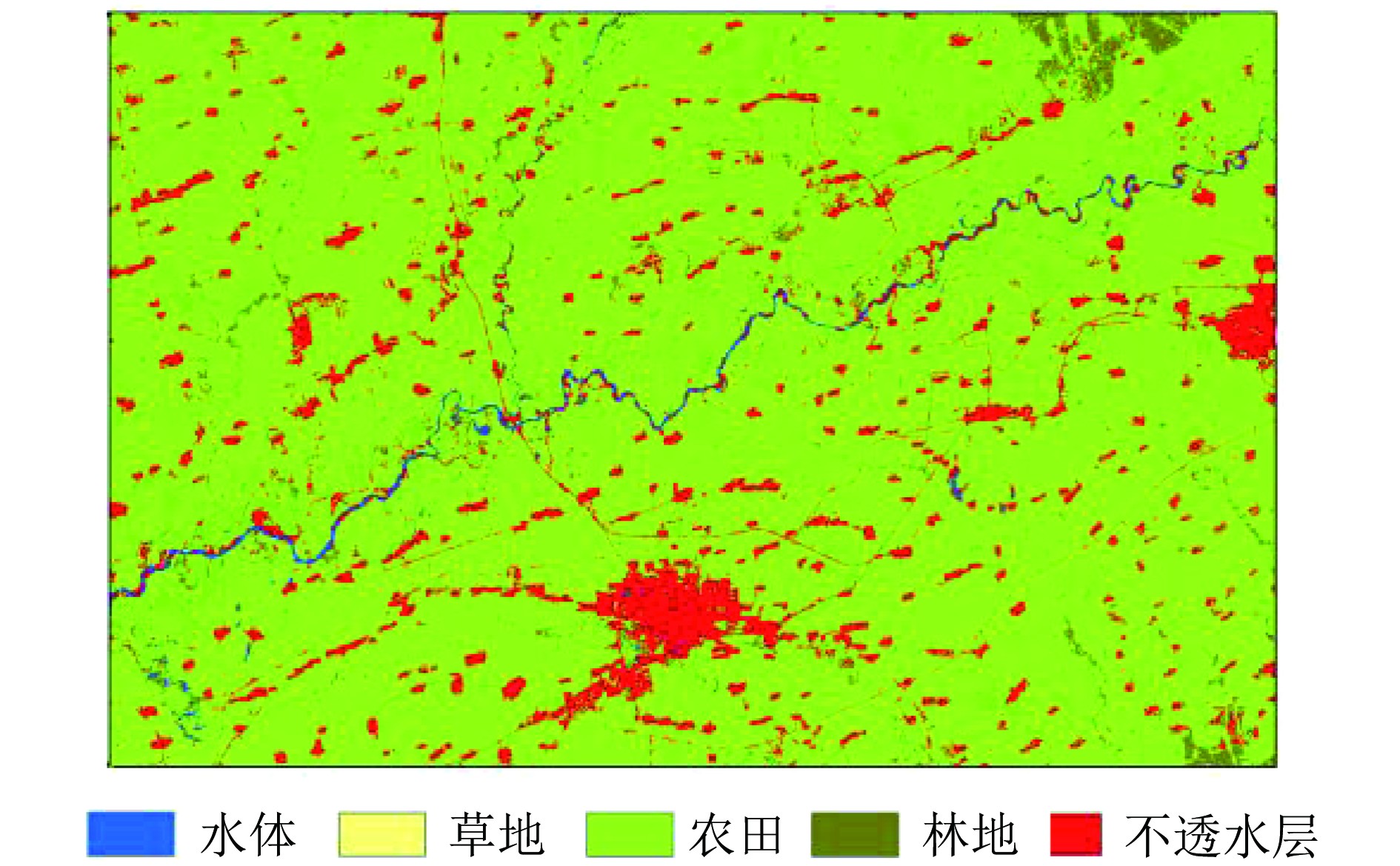
以黑龙江省绥化市和平灌区为研究区对VISTFM进行测试(图2)，其经度范围为46°51′7.83″E—47° 4′8.33″E，纬度范围为127°18′40.28″N—127°45′12.22″N。该区域的主要地物有农田、城镇、树林、水体和草地等。作物以水稻为主，且包含玉米、大豆等其他作物，水体、草地、城镇等地物分散且结构复杂，适合测试本算法。


图 2 研究区及土地利用状况
Fig. 2 The land cover type of study area

3.2 数据及其预处理

如表1所示，选择2017年可用的Landsat数据为数据源，其伽利略日为101、229、245、277；选择与Landsat数据日期接近日期(VI在短时间的变化很小，可以忽略，当Landsat数据所对应日期的MODIS数据不可用时，可选择与其接近日期的MODIS数据为数据源)的MOD09GA数据为数据源，其伽利略日分别为101、230、245、277；为融合生成高空间分辨率的时序VI数据，同时选择MODIS的三级产品MOD13Q1为数据源，其伽利略日如表1所示。所选影像数据质量较好，且无云覆盖或经过处理后无云覆盖，从USGS官网(https://earthexplorer.usgs.gov/[2018-05-10])获取。应用ENVI5.3 对Landsat 8 OLI影像经过辐射定标后用其提供的FLAASH大气校正模块进行大气校正。虽然Landsat 8 OLI已经经过几何校正，但为获得更高的精度，应用1∶10000的地形图对其进行几何校正，使得误差小于0.5个像元。

表 1 模型输入影像数据
Table 1 The image data for the model inputs

下载CSV 
影像数据 行列号 伽利略日
Landsat 8 OLI 117/027 101, 229, 245, 277
MOD09GA 25/04 101,230, 245, 277
MOD13Q1 25/04 113, 129, 145, 161, 177, 193, 209, 225, 241, 257, 273, 289

MOD09GA是经过几何校正和大气校正的二级产品，MOD013Q1是经过几何校正和大气校正的三级VI产品，提供16日最大合成的归一化植被指数NDVI(Normalized Differential Vegetation Index)和增强植被指数EVI(Enhanced Vegetation Index)产品。但均采用正弦坐标系统，利用MODIS批处理工具MRT(MODIS Reprojection Tool)将其转化与Landsat一致的坐标系统UTM-WGS84 52N，采用最近邻域法重采样成480 m×480 m，转化为tiff格式。

土地利用图的精度对融合结果具有重要的影响，为提高融合的精度，本文不采用下载的土地利用数据集。而是选择2015-09-13的Landsat 8 OLI影像采用支持向量机SVM(Support Vector Machine,)的方法将该区域的土地利用类型分成水体、草地、林地、农田和不透水层5类。

3.3 算法实现

以Landsat 8 OLI和MOD09GA为数据源计算得到高、低分辨率的NDVI和EVI数据后，应用研究区土地利用图定义高分辨率土地覆被类，以伽利略日为101、229、245和277的时相VI数据为模型输入，应用FCM以聚类数为10，加权指数为2.5，终止误差为0.0001，最大循环次数为100定义各土地覆被类的子类。然后根据第2节所示的方法来合成高时空分辨率的VI数据。并采用相关系数R，ERGAS，均方根误差RMSE和方差Variance对融合结果进行统计分析。

4 结果与分析

4.1 融合精度分析

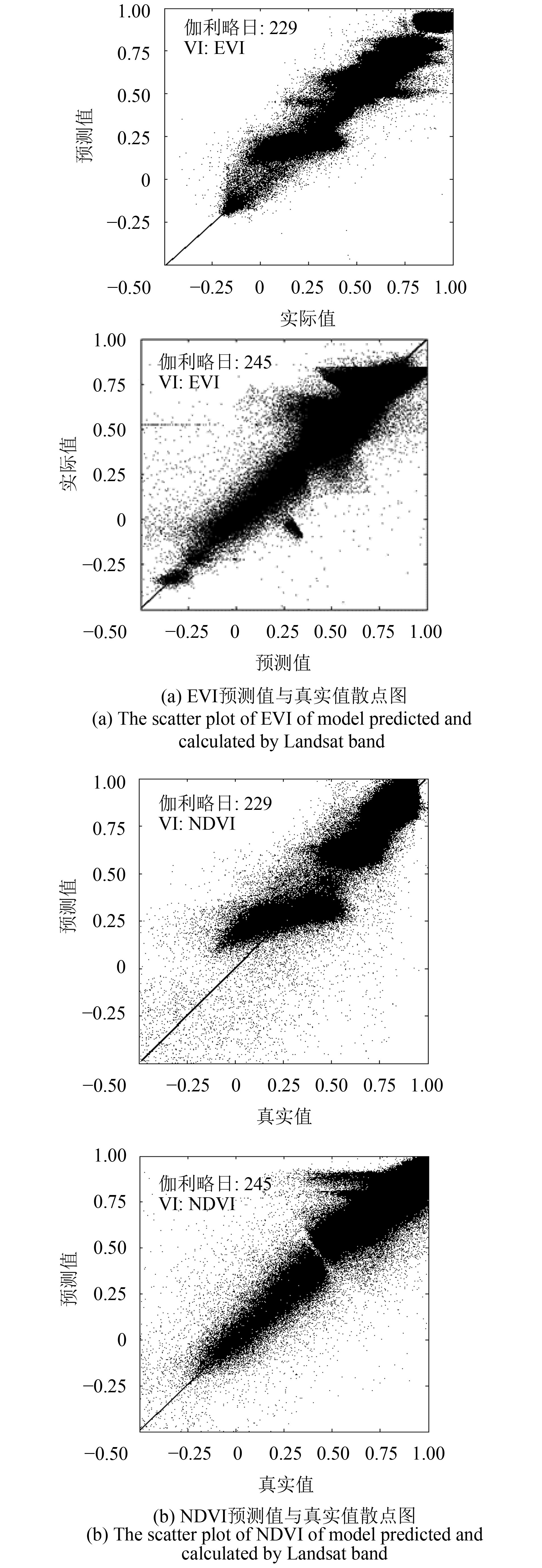
以表1所示的Landsat 8 OLI和MOD09GA计算得到的VI为数据源输入模型，融合生成伽利略日为229和245的两个时相的NDVI和EVI数据。两个时相Landsat数据计算得到的EVI与模型预测的EVI的散点图如图3(a)所示，两个时相Landsat数据计算得到的NDVI与模型预测的NDVI的散点图如图3(b)所示。从图3中可以看出，除少数点比较分散外，大多数的点都分布在直线y=x的两侧。


图 3 VI预测值与真实值散点图
Fig. 3 The scatter plot of VI of model predicted and calculated by Landsat band

融合生成的VI精度如表2所示，从表2中可以看出融合的精度相对较高，除伽利略日为245的时刻R为0.8744外，其他时刻的R均大于0.9。两个时相的NDVI和EVI的R、RMSE、ERGAS、Variance的均值分别为0.9057、0.0674、1.9795、0.0045。融合生成的影像各个土地覆被类的精度如表3所示，从表3中可以看出，基本所有的土地覆被类型都达到了相对较高的融合精度，该精度的VI数据基本可用于作物研究和地表观测等。

表 2 融合结果精度
Table 2 The Precision index of NDVI and EVI for the model VISTFM

下载CSV 
VI时相 R RMSE ERGAS Variance
NDVI229 0.9305 0.0607 1.7132 0.0037
NDVI245 0.9028 0.0721 1.9655 0.0052
EVI229 0.9154 0.0622 1.9547 0.0038
EVI245 0.8744 0.0748 2.2849 0.0055

表 3 VISTFM各土地覆被类融合精度
Table 3 The Precision index of each land cover type of VISTFM

下载CSV 
VI时相 覆被类型 R RMSE ERGAS Variance
EVI 229 水体 0.9435 0.0096 1.403 0.0055
不透水层 0.7605 0.0375 1.9396 0.0161
林地 0.7965 0.0102 0.816 0.0052
农田 0.7171 0.041 1.5849 0.0024
草地 0.8682 0.0243 1.0841 0.0035
EVI 245 水体 0.9576 0.0111 1.5052 0.0074
不透水层 0.7612 0.0468 2.2889 0.0251
林地 0.587 0.0153 0.986 0.0116
农田 0.8133 0.039 1.6499 0.0022
草地 0.6736 0.0391 1.4769 0.009
NDVI 229 水体 0.9175 0.0313 2.175 0.0589
不透水层 0.8454 0.0328 1.6177 0.0123
林地 0.8437 0.0113 0.6984 0.0063
农田 0.7139 0.0344 1.2683 0.0017
草地 0.6767 0.018 0.8834 0.0019
NDVI 245 水体 0.8927 0.0722 1.6082 0.0713
不透水层 0.9149 0.0306 1.6541 0.0107
林地 0.6301 0.0136 0.7462 0.0092
农田 0.7441 0.041 1.4808 0.0024
草地 0.5117 0.0349 1.2522 0.0072

4.2 与其他模型比较

如引言中所述，目前常用的多源遥感数据时空融合模型主要有基于线性混合模型的模型和STARFM及其改进模型两类，为检验VISTFM的精度，选择邬明权 等(2012)提出的遥感数据时空融合方法(STDFA)和Zhu 等(2010)对STARFM进行改进后提出的ESTARFM与本文中的模型进行比较。

STDFA融合精度如表4所示，结合表2中VISTFM的精度可以看出，与STDFA相比，VISTFM的精度更高，这是因为STDFA仅仅以始末两期影像为基期影像来提取丰度矩阵，当中间时刻(本文中伽利略日为229、245的时相)与始末两期影像的VI差异较大时，存在同一子集中的像元相似性较低的风险。

表 4 模型STDFA融合结果精度
Table 4 The Precision index of NDVI and EVI for the model STDFA

下载CSV 
VI时相 R RMSE ERGAS Variance
NDVI229 0.7155 0.1795 2.9439 0.0135
NDVI245 0.6962 0.1313 2.6517 0.0158
EVI229 0.7680 0.1222 2.7387 0.0097
EVI245 0.7652 0.1188 2.8795 0.0111

对于Landsat计算得到的NDVI，初始时刻至伽利略日为229、245的时相NDVI的变化与始末两期影像NDVI变化的相关系数仅为0.2506和0.2872。EVI变化的相关系数仅为0.1949和0.2824。这是因为VI的中间变化过程复杂，仅仅以始末两期影像为基期影像很难捕获VI复杂的中间变化过程。当中间时相的VI变化与始末两期相关性较低时，融合精度可能较低。

ESTARFM融合精度如表5所示，结合表2中VISTFM的精度可以看出，与ESTARFM相比，VISTFM具有更高的精度。这是因为VISTFM中假设一定窗口内的高分辨率相似像元平均VI与该窗口内的低分辨率像元平均VI的比值 $V_i$ 为定值，基于该假设融合生成高时空分辨率的VI数据。当VI变化剧烈时，比值 $V_i$ 存在发生较大变化的风险。

表 5 模型ESTARFM融合结果精度
Table 5 The Precision index of NDVI and EVI for the model ESTARFM

下载CSV 
VI时相 R RMSE ERGAS Variance
NDVI229 0.6769 0.2363 3.3832 0.0195
NDVI245 0.5036 0.1993 3.2818 0.0312
EVI229 0.5486 0.1773 3.3062 0.0179
EVI245 0.5431 0.1580 3.3379 0.0165

各个时相的NDVI和EVI的 $V_i$ 相关系数如表6和表7所示。因研究区以农田为主，伽利略日为229和245的时相同处于作物生长茂盛的时相，两个时相的NDVI及EVI的 $V_i$ 之间的相关系数相对较高。但因作物的NDVI及EVI经历了复杂的变化过程，部分中间时相的的 $V_i$ 与始末时刻 $V_i$ 的相关系数相对较低。

表 6 各个时相NDVI的 $V_i$ 之间的相关系数
Table 6 The correlation coefficients of NDVI of $V_i$ between each phase

下载CSV 
101 229 245 277
101 1
229 0.6596 1
245 0.4066 0.6450 1
277 0.7539 0.6809 0.5582 1

表 7 各个时相EVI的 $V_i$ 之间的相关系数
Table 7 The correlation coefficients of EVI of $V_i$ between each phase

下载CSV 
101 229 245 277
101 1
229 0.4289 1
245 0.2816 0.7909 1
277 0.5769 0.4251 0.4384 1

需要说明的是，虽然应用本文的测试数据对VISTFM的测试表明VISTFM的精度优于STDFA和ESTARFM，但本文测试数据有限，并不能说明所有的区域均存在VISTFM的精度优于STDFA和ESTARFM。

4.3 模型精度影响因素分析

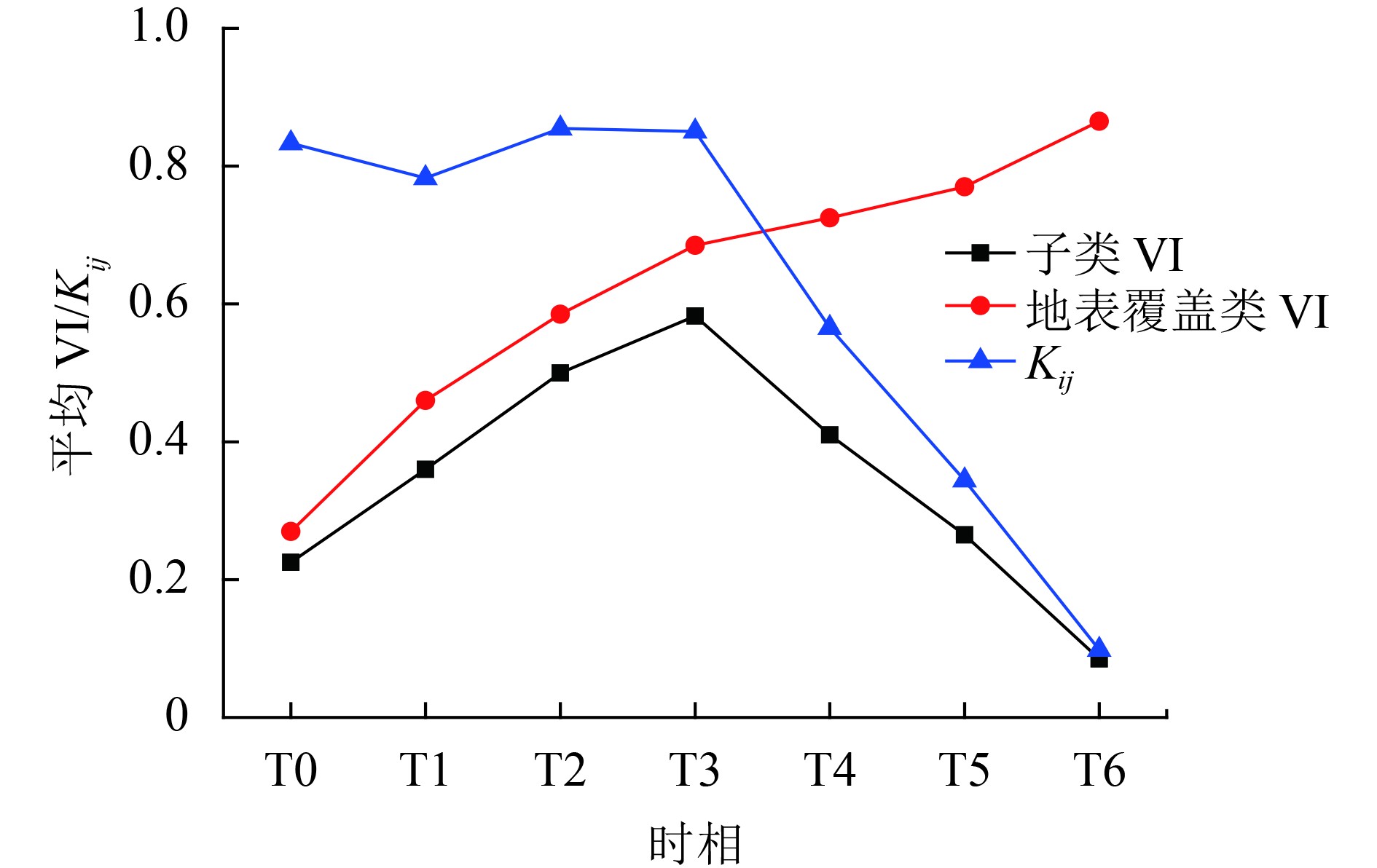
VISTFM是基于一定的模型假设建立的，各类地物的VI在一段时间内呈线性变化是本文的一个主要假设，据此来推导出各个高分辨率子类与其所属的低分辨率土地覆被类的平均VI的比值 $k_{ij}$ 在一段时间内保持稳定。 $k_{ij}$ 的准确预测是VISTFM的关键步骤，但当两景影像之间的某类地物的VI偏离其所属的土地覆被较大时，模型可能产生较大误差。

假设图4为某高分辨率子类及其所属的低分辨率土地覆被类VI的变化规律，子类在T0至T6时刻先增加后减小。土地覆被类在该时段呈增长趋势。从图中可以看出，以T0、T3、T6等3个时相基本能够精确的预测 $k_{ij}$ 的变化，但如果仅仅以T0，T6两个时期来预测 $k_{ij}$ 的变化，预测结果可能产生较大偏差。因此，当两景影像之间的VI变化过程较复杂，尤其是经历了抛物线式的变化过程时，VISTFM融合的精度可能相对较低。这说明该模型在选择输入数据时，应该选择包含主要地物VI曲线极值时相的影像数据为基期影像。


图 4 某子类及其所属的土地覆被类VI变化规律
Fig. 4 The variation of a subclass and its associated land cover class

子类与其内部像元VI及其变化相似是VISTFM的另一个主要假设。虽然经过聚类的像元具有一定的相似性，但依然存在一定的差异。为研究高分辨率子类像元内部差异对融合精度的影响，选择方差为子类内部像元差异的度量参数；RMSE为融合精度的度量参数，对两者之间的相关性进行分析。伽利略日为229、245时相的EVI和NDVI各个子类的方差和RMSE之间的相关系数分别为0.4033、0.6577、0.4682和0.5795，两者之间存在极显著的相关性。这说明子类内部像元的差异越大，融合生成的影像精度越低。FCM应用隶属度来确定各个像元所属的子类，如果可对隶属度求解函数进行改进，使得划分为一类的子类像元的差异变小，便可增加VISTFM的精度。

5 结　论

本文针对目前常用的多源遥感数据时空融合模型在融合高低分辨率的VI数据中存在的问题，基于FCM提出了一种新的多源遥感数据时空融合方法，该方法应用多时相VI对土地覆盖类型进行二次聚类来定义子类，使得子类中的像元具有相似的VI值和VI变化。基于子类中的VI与子类的平均VI的变化一致的假设来融合生成高时空分辨率的VI数据，与目前常用的多源遥感数据融合模型的对比表明该方法能够获得相对较高的精度。融合生成的VI数据的精度基本能够满足植被研究和对地观测等的目的。但本文对该算法的测试和评价数据有限，部分结论可能仅在有限数据上成立。

基于线性混合模型的多源遥感数据融合模型中，无论子集S的定义还是各个子集中的像元平均值的计算，均以整幅影像为基础。对于较小尺度的研究，多期无云覆盖的高分辨率影像数据的获取相对比较容易，但是随着研究区域的增大，无云覆盖的影像的获取难度逐渐增加。小区域的云覆盖对结果不会产生较大的影响，但当云覆盖区域较大时，融合误差可能较大。STARFM及其改进模型以一定窗口内的高低分辨率像元为基础来进行数据融合，云遮盖等仅会对其覆盖区域附近像元的计算产生影响。所以当区域较大，无云覆盖影像的获取相对较困难时，STARFM较有优势。

所有的多源遥感数据时空融合模型都是建立在一定的假设的基础上的，如本文的线性混合模型和子类与土地覆被类的变化为线性的假设。虽然这类假设都建立在一定的理论基础之上，具有一定的合理性，但都存在一定的误差，如植被覆盖下的像元非线性混合现象等。这些假设引起的误差是数据融合误差的主要来源，提出更加完善的模型假设条件是提高多源遥感数据融合模型的精度的主要途径。

各种地物的VI的变化并不是无序的，而是存在一定的规律性，如作物的VI的特定变化规律等。如果将多源遥感数据融合模型建立在这些规律的基础上，也可以一定程度提高融合结果的精度。本文采用分层聚类的方法将宏影像分成若干子类，使得每类子类具有相似的VI和VI变化。如果能够采用小波等方法从多时相影像中提取每个子类的时序变化规律，可用该规律来进行VI数据时空融合。

参考文献(References)

  • Bezdek J C, Ehrlich R and Full W. 1984. FCM: the fuzzy c-means clustering algorithm. Computers and Geosciences, 10 (2/3): 191–203. [DOI: 10.1016/0098-3004(84)90020-7]
  • Cai X L and Cui Y L. 2009. Crop planting structure extraction in irrigated areas from multi-sensor and multi-temporal remote sensing data. Transactions of the CSAE, 25 (8): 124–130. [DOI: 10.3969/j.issn.1002-6819.2009.08.023] ( 蔡学良, 崔远来. 2009. 基于异源多时相遥感数据提取灌区作物种植结构. 农业工程学报, 25 (8): 124–130. [DOI: 10.3969/j.issn.1002-6819.2009.08.023] )
  • Cerasoli S, Costa e Silva F and Silva J M N. 2016. Temporal dynamics of spectral bioindicators evidence biological and ecological differences among functional types in a cork oak open woodland. International Journal of Biometeorology, 60 (6): 813–825. [DOI: 10.1007/s00484-015-1075-x]
  • Gao F, Masek J, Schwaller M and Hall F. 2006. On the blending of the Landsat and MODIS surface reflectance: predicting daily Landsat surface reflectance. IEEE Transactions on Geoscience and Remote Sensing, 44 (8): 2207–2218. [DOI: 10.1109/tgrs.2006.872081]
  • Gevaert C M and García-Haro F J. 2015. A comparison of STARFM and an unmixing-based algorithm for Landsat and MODIS data fusion. Remote Sensing of Environment, 156 : 34–44. [DOI: 10.1016/j.rse.2014.09.012]
  • Hilker T, Wulder M A, Coops N C, Linke J, McDermid G, Masek J G and White J C. 2009. A new data fusion model for high spatial- and temporal-resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sensing of Environment, 113 (8): 1613–1627. [DOI: 10.1016/j.rse.2009.03.007]
  • Liao L M, Song J L, Wang J D, Xiao Z Q and Wang J. 2016. Bayesian method for building frequent Landsat-like NDVI datasets by integrating MODIS and Landsat NDVI. Remote Sensing, 8 (6): 452 [DOI: 10.3390/rs8060452]
  • Luo Y, Xu J H and Yue W Z. 2005. Research on vegetation indices based on the remote sensing images. Ecologic Science, 24 (1): 75–79. [DOI: 10.3969/j.issn.1008-8873.2005.01.021] ( 罗亚, 徐建华, 岳文泽. 2005. 基于遥感影像的植被指数研究方法述评. 生态科学, 24 (1): 75–79. [DOI: 10.3969/j.issn.1008-8873.2005.01.021] )
  • Ojeda-Magaña B, Quintanilla-Domínguez J, Ruelas R, Barba L G and Andina D. 2018. Improvement of the image sub-segmentation for identification and differentiation of atypical regions. International Journal of Pattern Recognition and Artificial Intelligence, 32 (1): 1860011 [DOI: 10.1142/s021800141860011x]
  • Qiu Q L, Zhao H Y, Guo J, Song F and Wu Y Z. 2004. The applying RS vegetation indexes in monitoring agricultural environment. Journal of Agricultural Mechanization Research (6): 215–217. [DOI: 10.13427/j.cnki.njyi.2004.06.081] ( 邱庆伦, 赵鸿燕, 郭剑, 宋福, 吴玉珍. 2004. 遥感植被指数在农业生态环境监测中的应用. 农机化研究 (6): 215–217. [DOI: 10.13427/j.cnki.njyi.2004.06.081] )
  • Rao Y H, Zhu X L, Chen J and Wang J M. 2015. An improved method for producing high spatial-resolution NDVI time series datasets with multi-temporal MODIS NDVI data and Landsat TM/ETM + images. Remote Sensing, 7 (6): 7865–7891. [DOI: 10.3390/rs70607865]
  • Shi Y C, Yang G J, Li X C, Song J, Wang J H and Wang J D. 2015. Intercomparison of the different fusion methods for generating high spatial-temporal resolution data. Journal of Infrared and Millimeter Waves, 34 (1): 92–99. [DOI: 10.3724/SP.J.1010.2015.00092] ( 石月婵, 杨贵军, 李鑫川, 宋健, 王纪华, 王锦地. 2015. 融合多源遥感数据生成高时空分辨率数据的方法对比. 红外与毫米波学报, 34 (1): 92–99. [DOI: 10.3724/SP.J.1010.2015.00092] )
  • Tian Q J and Min X J. 1998. Advances in study on vegetation indices. Advance in Earth Sciences, 13 (4): 327–333. [DOI: 10.3321/j.issn:1001-8166.1998.04.002] ( 田庆久, 闵祥军. 1998. 植被指数研究进展. 地球科学进展, 13 (4): 327–333. [DOI: 10.3321/j.issn:1001-8166.1998.04.002] )
  • Wu M Q, Niu Z and Wang C Y. 2010. Mapping paddy fields by using spatial and temporal remote sensing data fusion technology. Transactions of the CSAE, 26 (S2): 48–52. [DOI: 10.3969/j.issn.1002-6819.2010.z2.010] ( 邬明权, 牛铮, 王长耀. 2010. 利用遥感数据时空融合技术提取水稻种植面积. 农业工程学报, 26 (S2): 48–52. [DOI: 10.3969/j.issn.1002-6819.2010.z2.010] )
  • Wu M Q, Wang J, Niu Z, Zhao Y Q and Wang C Y. 2012. A model for spatial and temporal data fusion. Journal of Infrared and Millimeter Waves, 31 (1): 80–84. [DOI: 10.3724/SP.J.1010.2012.00080] ( 邬明权, 王洁, 牛铮, 赵永清, 王长耀. 2012. 融合MODIS与Landsat数据生成高时间分辨率Landsat数据. 红外与毫米波学报, 31 (1): 80–84. [DOI: 10.3724/SP.J.1010.2012.00080] )
  • Wu M Q, Wu C Y, Huang W J, Niu Z, Wang C Y, Li W and Hao P Y. 2016. An improved high spatial and temporal data fusion approach for combining Landsat and MODIS data to generate daily synthetic Landsat imagery. Information Fusion, 31 : 14–25. [DOI: 10.1016/j.inffus.2015.12.005]
  • Xie D F, Zhang J S, Sun P J, Pan Y Z, Yun Y and Yuan Z M Q. 2016. Remote sensing data fusion by combining STARFM and downscaling mixed pixel algorithm. Journal of Remote Sensing, 20 (1): 62–72. [DOI: 10.11834/jrs.20165058] ( 谢登峰, 张锦水, 孙佩军, 潘耀忠, 云雅, 袁周米琪. 2016. 结合像元分解和STARFM模型的遥感数据融合. 遥感学报, 20 (1): 62–72. [DOI: 10.11834/jrs.20165058] )
  • Zhu X L, Chen J, Gao F, Chen X H and Masek J G. 2010. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sensing of Environment, 114 (11): 2610–2623. [DOI: 10.1016/j.rse.2010.05.032]
  • Zhukov B, Oertel D, Lanzl F and Reinhackel G. 1999. Unmixing-based multisensor multiresolution image fusion. IEEE Transactions on Geoscience and Remote Sensing, 37 (3): 1212–1226. [DOI: 10.1109/36.763276]
数据专区
  • 目录 目录
  • 文章信息 文章信息
  • 引用格式 引用格式
  • 地图 地图
  • 评论 评论
  • 图 图
  • 表 表
  • 二维码 二维码
  • 参考文献 参考文献
  • 多媒体 多媒体