干涉合成孔径雷达InSAR(Interferometry Synthetic Aperture Radar)由于具备全天候、高精度、大区域成像、地形高程提取等优势，在地形测绘、地表形变检测、自然资源勘查、灾害监测、目标侦察等民用及军用领域具有非常重要的应用价值(Krieger 等，2010；Sato和Suzuki，2017)，已经成为目前发展迅速、极具潜力的遥感对地观测及测绘技术之一。InSAR图像配准是将含有相同场景或目标的合成孔径雷达SAR(Synthetic Aperture Radar)图像进行空间几何对准的过程，是InSAR数据处理中最基础及关键的一个步骤，也是InSAR技术问世以来其数据处理的研究热点之一。为了提高InSAR复图像对的相干性，保证干涉相位质量及地形高程反演精度，InSAR复图像的配准精度通常要达到亚像素级别，实际中一般要求其配准精度达到八分之一像素以上(丁赤飚 等，2017)。

针对InSAR复图像的幅度及相位特性，通常利用相似性匹配测度来确定图像偏移量，至今已提出了基于最大相干系数(丁赤飚 等，2017)、最大干涉频谱(Scheiber和Moreira，2000)、相位平均波动函数(Zou 等，2009)、相位最小二乘(Liao 等，2004)等相似性匹配准则下多种复图像配准算法。相对其他匹配准则方法，最大相干系数配准方法由于可采用快速傅里叶变换FFT(Fast Fourier Transform)实现，具有更高的运算效率，是实现InSAR复图像快速配准最常用的方法。为了达到亚像素级配准精度，FFT最大相干系数配准算法通常采用插值重采样技术，一般插值单元尺寸越小，配准精度就越高。另外，结合一些新理论及应用，近年来也提出了多种InSAR亚像素度配准方法。Guizar-Sicairos 等(2008)提出一种高效图像配准算法，主要利用FFT变换矩阵相乘特性，实现图像快速插值及亚像素偏移估计。Li和Zhang(2012)提出一种快速偏移估计方法，利用图像特征估计及最小均方割算法实现高精度InSAR配准。Natsuaki和Hirose(2013)利用SAR图像奇异点作为评判准则，提出一种基于明暗恢复形状的InSAR配准算法。Zhang 等(2016)提出了基于复相干函数的大场景InSAR配准方法，采用图像固定子块划分配准以实现大场景InSAR复图像配准。Chen 等(2016)针对剧烈畸变及非相干图像对情况，提出一种基于SAR图像几何特征点信息的InSAR图像配准方法。Gong 等(2014)基于尺度不变特征变换及最大互信息准则，提出一种粗至精SAR图像自动配准方法。Dellinger 等(2015)提出一种基于类尺度不变特征变换的SAR复图像配准算法，有效克服了SAR图像相干斑对配准的影响。Zhu 等(2016)提出一种基于图像多特征检测及树状网络匹配的高精度配准算法。薛海伟和冯大政(2016)提出了一种图像连续函数优化的精配准方法，利用拟牛顿法来优化代价函数估计亚像素偏移量。然而，上述高精度配准算法通常将InSAR复图像进行整体配准，如Guizar-Sicairos 等(2008)提出的快速配准算法等；或者利用固定分块配准估计出像素偏移，通过建立偏移模型进行精配准，如Zhang 等(2016)提出了基于复相干函数方法等。在大场景InSAR成像中，受系统和观测地物影响，不同图像区域像素失配往往不同且变化复杂。此时，传统配准方法可能存在局部配准精度下降、运算量大等问题。特别是，随着近几年来高分宽带InSAR成像系统的成功研制，大场景InSAR图像数据与日俱增，如何实现大场景InSAR复图像的高效高精度配准成为亟待解决的问题。

针对大场景InSAR复图像的高精度高效率配准问题，本文结合复图像相干系数的离散傅里叶变换DFT(Discrete Fourier Transform)特性，提出一种基于DFT模型的高效高精度配准方法，主要通过四叉树图像分块及矩阵相乘DFT快速插值配准，提升大场景InSAR复图像的配准精度和效率。相对于传统FFT最大相干系数配准方法，该方法在实现亚像素配准时具有更低的计算复杂度。仿真和星载实测InSAR复图像配准实验验证了算法的有效性，结果表明该方法具有较低的运算量及良好的配准精度。

假设 ${{{f}}_1}\left({x,y} \right)$ 和 ${{{f}}_2}\left({x,y} \right)$ 代表InSAR主副复图像，其维数为 $M \times N$ ，其中 $x = 1, \cdots,M$ 和 $y = 1, \cdots,N$ 表示距离向和方位向。对于搜索窗口 $P \times Q$ ，利用驻点滑窗计算得到 ${{{f}}_1}\left({x,y} \right)$ 和 ${{{f}}_2}\left({x,y} \right)$ 相干系数为(丁赤飚 等，2017)

$ {{r}}\left({x,y} \right) = \frac{{\sum\limits_{i = - {P / 2}}^{{P / 2}} {\sum\limits_{j = - {Q / 2}}^{{Q / 2}} {{{{f}}_1}\left({x + i,y + j} \right){{f}}_2^ * \left({x + i,y + j} \right)} } }}{{\sqrt {\sum\limits_{i = - {P / 2}}^{{P / 2}} {\sum\limits_{j = - {Q / 2}}^{{Q / 2}} {{{\left| {{{{f}}_1}\left({x + i,y + j} \right)} \right|}^2}} } } \sqrt {\sum\limits_{i = - {P / 2}}^{{P / 2}} {\sum\limits_{j = - {Q / 2}}^{{Q / 2}} {{{\left| {{{{f}}_2}\left({x + i,y + j} \right)} \right|}^2}} } } }} $

(1)

式中， $ * $ 表示共轭运算。最大相干配准算法基本思想是寻找 ${{r}}\left({x,y} \right)$ 最大值，该值即为 ${{{f}}_1}\left({x,y} \right)$ 和 ${{{f}}_2}\left({x,y} \right)$ 间的像素偏移量。

根据卷积函数特性，式(1)逐点滑窗得到的相干系数可转变为

$ {{r}}\left({x,y} \right) = IFFT\left({FFT\left({{{{f}}_1}\left({x,y} \right)} \right) \odot FFT{{\left({{{{f}}_{\rm{2}}}\left({x,y} \right)} \right)}^ * }} \right) $

(2)

式中， $FFT\left(\cdot \right)$ 表示FFT运算， $IFFT\left(\cdot \right)$ 表示逆FFT运算， $ \odot $ 表示点乘运算。对于相干系数计算，式(1)计算复杂度为 $O\left({MN{P^2}{Q^2}} \right)$ ，而式(2)采用FFT后计算复杂度仅为 $O\left({MN{{\log }_2}\left({MN} \right)} \right)$ ，其计算复杂度远小于式(1)。

对于InSAR复图像亚像素精配准，FFT配准方法的主要思路为：先采用频域补零方法对图像插值；再采用FFT方法计算相干系数 ${{r}}\left({x,y} \right)$ ；最后估计亚像素偏移量 $\left({\Delta x,\Delta y} \right)$ 并进行亚像素配准。

根据传统FFT精配准原理，为了达到 ${{\rm{1}} / k}$ 亚像素配准精度，需采用频域补零方法使 ${{{F}}_{\rm{1}}}\left({u,v} \right)$ 和 ${{{F}}_{\rm{2}}}\left({u,v} \right)$ 维数增大 $k$ 倍。在高分辨大场景InSAR成像中，图像 ${{{f}}_1}\left({x,y} \right)$ 和 ${{{f}}_2}\left({x,y} \right)$ 维数将达到数万及数十万的量级，此时传统FFT精配准方法将面临巨大的存储需求及运算量。例如，对大小为8192×8192的InSAR复图像进行0.1像素精度配准，则需对复图像进行 $k = 10$ 倍插值，将导致IFFT精配准处理的图像大小为81920×81920，计算复杂度约为 $O\left({MN{k^2}{{\log }_2}\left({MN{k^2}} \right)} \right)$ ，普通计算机内存难以存储、运算量大。为了减少计算机处理负担，传统FFT方法通常采用图像分块配准或偏移建模处理，目前常用方法是固定滑窗分块方法，然而固定分块配准同样面临计算复杂度大的问题。

另外，对于大场景InSAR观测成像，由于地距分辨率不均匀、观测地形起伏、基线状态不稳定、方位非直线运动等影响，通常其复图像中不同区域存在不同的像素偏移量及变化特性，直接利用传统FFT整体配准、固定分块配准方法或偏移建模方法难以实现大场景复图像的全局高精度配准。因此，为了提高大场景InSAR复图像的配准精度，需要更有效的处理方法对图像进行分块精配准处理。

DFT配准方法基本思想与传统FFT配准方法相似，区别为DFT方法可采用子区域插值及矩阵相乘DFT运算提高配准效率。假设InSAR复图像 ${{{f}}_1}\left({x,y} \right)$ 和 ${{{f}}_2}\left({x,y} \right)$ 间存在像素偏移 $\left({{x_0},{y_0}} \right)$ ，则其相干系数 ${{r}}\left({{x_0},{y_0}} \right)$ 可表示为

$ \begin{split} {{r}}\left({{x_0},{y_0}} \right) = &{{{f}}_1}\left({x,y} \right) \otimes {{f}}_2^ * \left({{x_0} - x,{y_0} - y} \right)= \\ & \sum\limits_{x,y} {{{{f}}_1}\left({x,y} \right){{f}}_2^ * \left({x - {x_0},y - {y_0}} \right)} =\\ & \sum\limits_{u,v} {{{{G}}_1}\left({u,v} \right){{G}}_2^ * \left({u,v} \right)\exp \left( {j2{\text{π}} \left({\frac{{u{x_{\rm{0}}}}}{M} + \frac{{v{y_0}}}{N}} \right)} \right)} \end{split} $

(3)

式中， ${{{G}}_1}\left({u,v} \right)$ 和 ${{{G}}_{\rm{2}}}\left({u,v} \right)$ 分别为 ${{{f}}_1}\left({x,y} \right)$ 和 ${{{f}}_2}\left({x,y} \right)$ 的DFT变换， $ \otimes $ 表示卷积符号。DFT配准通过求解 ${{{f}}_1}\left({x,y} \right)$ 和 ${{{f}}_2}\left({x,y} \right)$ 间最小均方根误差对偏移量 $\left({{x_0},{y_0}} \right)$ 进行估计(Guizar-Sicairos 等，2008)

$ \begin{split} \left({{{\hat x}_0},{{\hat y}_0}} \right) =& \mathop {\min }\limits_{{x_0},{y_0}} {\left\| {{{{f}}_1}\left({x,y} \right) - {{f}}_2 \left({x - {x_0},y - {y_0}} \right)} \right\|_2} \approx \\ & {\rm{1}} - \mathop {\max }\limits_{{x_0},{y_0}} \left| {{{r}}\left({{x_0},{y_0}} \right)} \right| \end{split} $

(4)

因此，DFT配准可等效于寻找主副图像的互相关 ${{r}}\left({x,y} \right)$ 最大位置 $\left({{x_0},{y_0}} \right)$ 。为了达到亚像素配准精度，DFT方法也需要对 ${{{f}}_1}\left({x,y} \right)$ 和 ${{{f}}_2}\left({x,y} \right)$ 进行 $k$ 倍插值后再求解 ${{r}}\left({{x_0},{y_0}} \right)$ 最大值。

为了提高复图像相干系数的计算效率，本文利用矩阵相乘DFT变换仅仅对感兴趣区域插值，减少了相干系数计算所需图像区域，从而提升算法运算效率。假设一维离散信号 ${{x}}\left(l \right) \in {\mathbb{C}^{N \times 1}}$ ，其DFT变换为 ${{u}}\left(l \right) = \left\langle {{{x}},{s_l}} \right\rangle = \sum\limits_{n = 0}^{N - 1} {{{x}}\left(n \right){{\rm{e}}^{ - j2{\text{π}} nl/N}}} $ ，其中 ${s_l}\left(n \right) = {{\rm{e}}^{ - j2{\text{π}} nl/N}}$ 。若令 ${{f}}\left(x \right) = {\left[ {{{x}}\left(0 \right), \cdots,{{x}}\left({N - 1} \right)} \right]^{\rm{T}}}$ ， ${{s}}\left(0 \right) = \left[ {{s_0}\left(0 \right), \ldots,{s_{N - 1}}\left(0 \right)} \right]$ ， ${{D}} = {\left[ {{{s}}\left(0 \right), \cdots,{{s}}\left({N - 1} \right)} \right]^{\rm{T}}}$ 表示DFT变换矩阵， ${{F}}\left(u \right) = {\left[ {{{u}}\left({\rm{0}} \right), \ldots,u{{}}\left({N - 1} \right)} \right]^{\rm{T}}}$ ，则1维信号DFT矩阵相乘形式表示为

$ {{F}}\left(u \right) = {\bf{D}}{{f}}\left(x \right) $

(5)

同理，对于一个2维信号 ${{f}}\left({x,y} \right) \in {\mathbb{C}^{M \times N}}$ ，其DFT矩阵相乘形式可表示为

$ {{F}}\left({u,v} \right) = {{{D}}_x}{{f}}\left({x,y} \right){{D}}_y^{\rm{T}} $

(6)

式中， ${{F}}\left({u,v} \right) \in {\mathbb{C}^{M \times N}}$ 为 ${{f}}\left({x,y} \right)$ 的DFT变换， ${{{D}}_x} \in {\mathbb{C}^{M \times M}}$ 为DFT列变换矩阵， ${{{D}}_y} \in {\mathbb{C}^{N \times N}}$ 为DFT行变换矩阵。

根据传统FFT配准方法，为使得 ${{{f}}_1}\left({x,y} \right)$ 和 ${{{f}}_2}\left({x,y} \right)$ 达到 ${{\rm{1}} / k}$ 亚像素配准精度，需对 ${{{F}}_1}\left({u,v} \right) \in {\mathbb{C}^{M \times N}}$ 进行 $\left({k - 1} \right)$ 倍零填充重采样 ${{\tilde{ F}}_1}\left({u,v} \right) = \left[ {{{{F}}_1}\left({u,v} \right),{\bf{0}}:{\bf{0}},{\bf{0}}} \right] \in $ ${\mathbb{C}^{kM \times kN}} $ ，同理对 ${{{F}}_{\rm{2}}}\left({u,v} \right)$ 进行 $\left({k - 1} \right)$ 倍插值。由于 ${{\tilde{ F}}_1}\left({u,v} \right)$ 含有大区域零元素子块，则可利用分块矩阵性质， ${{\tilde{ F}}_1}\left({u,v} \right)$ 的离散傅里叶逆变换IDFT(Inverse Discrete Fourier Transform)变换 ${{\tilde {{f}}}_{\rm{1}}}\left({x,y} \right)$ 可表示为

$ {\tilde {{f}}_{\rm{1}}}\left({x,y} \right) = {{{U}}_x}{{\tilde{ F}}_1}\left({u,v} \right){{{U}}_y} = {{{U}}_{x{\rm{s}}}}{{{F}}_1}\left({u,v} \right){{{U}}_{y{\rm s}}} $

(7)

式中， ${{{U}}_x} \in {\mathbb{C}^{kM \times kM}}$ 为IDFT列变换矩阵， ${{{U}}_y} \in {\mathbb{C}^{kN \times kN}}$ 为IDFT行变换矩阵， ${{{U}}_{x{\rm{s}}}} \in {\mathbb{C}^{M \times M}}$ 和 ${{{U}}_{x{\rm{s}}}} \in {\mathbb{C}^{N \times N}}$ 为 ${{{U}}_x}$ 和 ${{{U}}_y}$ 的子矩阵。从式(7)可知，矩阵乘法IDFT插值在精度上与传统FFT零填充重采样方法等效，但其不需将 ${{{F}}_1}\left({u,v} \right)$ 和 ${{{F}}_{\rm{2}}}\left({u,v} \right)$ 维数增大 $k$ 倍，仅改变DFT列变换矩阵 ${{{U}}_{x{\rm{s}}}}$ 和 ${{{U}}_{x{\rm{s}}}}$ ，从而减少 $k$ 倍插值重采样的计算机内存需求及运算时间。

若复图像 ${{{f}}_1}\left({x,y} \right)$ 和 ${{{f}}_2}\left({x,y} \right)$ 已实现像素级配准，此时 ${{r}}\left({{x_0},{y_0}} \right)$ 峰值中心为 $\left({0,0} \right)$ 。根据DFT插值特性，可在 $\left({0,0} \right)$ 附近选择 ${\rm{2}} \times {\rm{2}}$ 像素小区域进行 $k$ 倍插值重采样的矩阵乘法DFT配准，估计 ${{{f}}_1}\left({x,y} \right)$ 和 ${{{f}}_2}\left({x,y} \right)$ 的 ${{\rm{1}} / k}$ 亚像素偏移量。因此， $k$ 倍插值矩阵乘法DFT配准的计算复杂度仅为 $O\left({{\rm{2}}MNk} \right)$ ，远小于传统FFT配准方法计算复杂度 $O\left({MN{k^2}{{\log }_2}\left({MN{k^2}} \right)} \right)$ 。

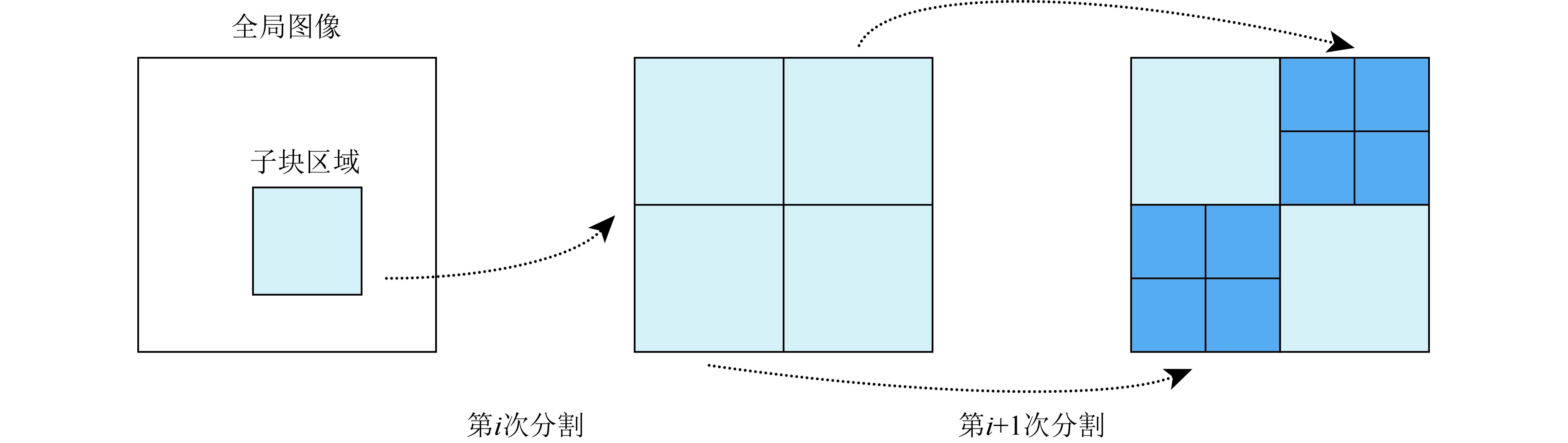
树结构是一种层迭形式数据结构，可将数据按层细分为多个类别，广泛应用于图像处理、空间数据索引的树形数据结构，且便于实现及并行计算。针对大场景InSAR复图像对中存在不同像素偏移及变化等问题，本文结合DFT高精度配准原理及四叉树结构特性，提出一种基于四叉树结构的迭代图像分块配准处理方法，通过子块内像素偏移指标作为判定条件，按照四叉树结构进行大场景InSAR图像迭代逐层分块配准，可减少分块数据并确保大场景图像不同区域的配准精度(图1)。若子块满足分块条件则继续四等分分块，否则该子块不再进行分块处理。

对于大场景InSAR复图像配准，为了达到 ${{\rm{1}} / k}$ $\left({k \geqslant {\rm{8}}} \right)$ 亚像素配准精度，本文四叉树迭代分块配准主要流程如下：

步骤1：粗分块。在 ${{{f}}_1}\left({x,y} \right)$ 和 ${{{f}}_2}\left({x,y} \right)$ 4个角上选定4个小子块 ${\Delta _l}$ ， $l = 1, \cdots,4$ ，块大小为 ${m_0} \times {m_0}$ ，采用3.1节 $k$ 倍插DFT配准方法估计每个子块亚像素偏移量 ${\alpha _l}$ ， $l = 1, \cdots,4$ ；利用 ${\alpha _l}$ 建立图像线性偏移模型，再利用相邻子块间 ${{\rm{1}} / k}$ 个像素偏移对主副图像进行分块，得到主副图像子块记为 ${{\bf{A}}_{1i}}$ 和 ${{\bf{A}}_{{\rm{2}}i}}$ ， $i = 1, \cdots,{M_0}$ ， ${M_0}$ 为子块总数。

步骤2：初始化迭代分块的初始参数。设置迭代判定阈值 ${\eta _{\rm{0}}}$ ，最小分块维数 ${n_0} \times {n_0}$ ，子块插值倍数 ${\rm{2}}k$ ，对每个子块 ${{\bf{A}}_{1i}}$ 和 ${{\bf{A}}_{{\rm{2}}i}}$ ， $i = 1, \cdots,{M_0}$ ，进行 $2k$ 倍插值DFT配准，得到亚像素配准结果 ${\bf{A}}_{1i}^{\left(0 \right)}$ 和 ${\bf{A}}_{{\rm{2}}i}^{\left(0 \right)}$ ， $i = 1, \cdots,{M_0}$ 。一般情况下，阈值 ${\eta _{\rm{0}}}$ 选择为0.1，最小分块维数 ${n_0} \times {n_0}$ 选择为16×16。

步骤3：四叉树迭代分块配准。对步骤2中所有子块 ${\bf{A}}_{1i}^{\left(0 \right)}$ 和 ${\bf{A}}_{{\rm{2}}i}^{\left(0 \right)}$ ， $i = 1, \cdots,{M_0}$ ，进行四叉树图像分割，基本原理是将 ${\bf{A}}_{1i}^{\left(0 \right)}$ 和 ${\bf{A}}_{{\rm{2}}i}^{\left(0 \right)}$ 等分为4个子区，对子区进行 ${\rm{2}}k$ 倍插值DFT配准并获取亚像素偏移量 ${\beta _i}$ ， $l = 1, \cdots,4$ ，逐块检查该子区偏移量，如果该子区中各分块的像素偏移量差异之和小于阈值，即满足 $\sum\limits_{1 \leqslant i,j \leqslant 4,i \ne j} {{{\left| {{\beta _i} - {\beta _j}} \right|} / {\rm{6}}}} < {\eta _{\rm{0}}}$ ，则该子区即不再继续四叉树分割，否则继续将该子区进行四叉树分割，再对其每一个子块进行四叉树分块配准，直到每个子块的偏移量差异之和小于阈值为止。

步骤4：合并各子块，得到最终 ${{{f}}_1}\left({x,y} \right)$ 和 ${{{f}}_2}\left({x,y} \right)$ 的 ${{\rm{1}} / k}$ 亚像素配准结果。

根据3.1节DFT配准原理及3.2节四叉树迭代分块处理方法，本文基于DFT模型的大场景InSAR高效高精度配准算法主要包含两个步骤：图像粗配准和迭代分块精配准，具体流程如下：

步骤1：图像粗配准。将 ${{{f}}_1}\left({x,y} \right)$ 和 ${{{f}}_2}\left({x,y} \right)$ 均匀分成 ${M_{\rm{1}}} \times {N_{\rm{1}}}$ 块，利用传统FFT配准方法进行像素级配准，得到粗配准后图像 ${{{g}}_1}\left({x,y} \right)$ 和 ${{{g}}_2}\left({x,y} \right)$ ；

步骤2：迭代分块精配准。对 ${{{g}}_1}\left({x,y} \right)$ 和 ${{{g}}_2}\left({x,y} \right)$ 进行粗分块，设置迭代分块初始参数，采用3.2节中四叉树迭代分块配准方法对每一个子块进行DFT亚像素精配准。

从算法流程可知，步骤1计算复杂度约为 $O\left({MN{{\log }_2}\left({{{MN} / {{M_{\rm{1}}}{N_1}}}} \right)} \right)$ ；步骤2中粗分块的计算复杂度约为 $O\left({{\rm{8}}m_0^2{{\log }_2}m_0 } \right)$ ，由于 $m_0 $ 通常很小，则该计算复杂度在整体算法运算中可忽略；步骤2中四叉树迭代分块配准每层的计算复杂度为 $O\left({{\rm{2}}MNk} \right)$ ，则迭代过程最小和最大计算复杂度分别为 $O\left({{\rm{2}}MNk} \right)$ 和 $O\left({{\rm{2}}MNk\log \left({{{MN} / {n_0^2}}} \right)} \right)$ 。对于传统FFT精配准方法， $k$ 倍插值整体配准的计算复杂度约为 $O\left({MN{k^2}{{\log }_2}\left({MN{k^2}} \right)} \right)$ ，而 $k$ 倍插值 ${M_{\rm{1}}} \times {N_{\rm{1}}}$ 分块配准的计算复杂度约为 $O\left({MN{k^2}{{\log }_2}\left({{{MN{k^2}} / {{M_{\rm{1}}}{N_1}}}} \right)} \right)$ 。对比可知，本文DFT模型配准算法与传统FFT运算效率差异主要体现在 $k$ 倍插值配准处理。相对于传统FFT整体及固定分块精配准方法，DFT模型配准算法运算效率最优可提高 $k{\log _2}\left({MN{k^2}} \right)$ 和 $k{\log _2}\left({{{MN{k^2}} / {{M_{\rm{1}}}{N_1}}}} \right)$ 倍，但随着四叉树迭代分块数增多，运算效率提升倍数降低。一般情况下，InSAR图像配准中经过3层四叉树分块即满足配准精度要求，此时最大计算复杂度约为 $O\left({{\rm{6}}MNk} \right)$ ，相对传统FFT配准方法仍大大提高了运算效率。

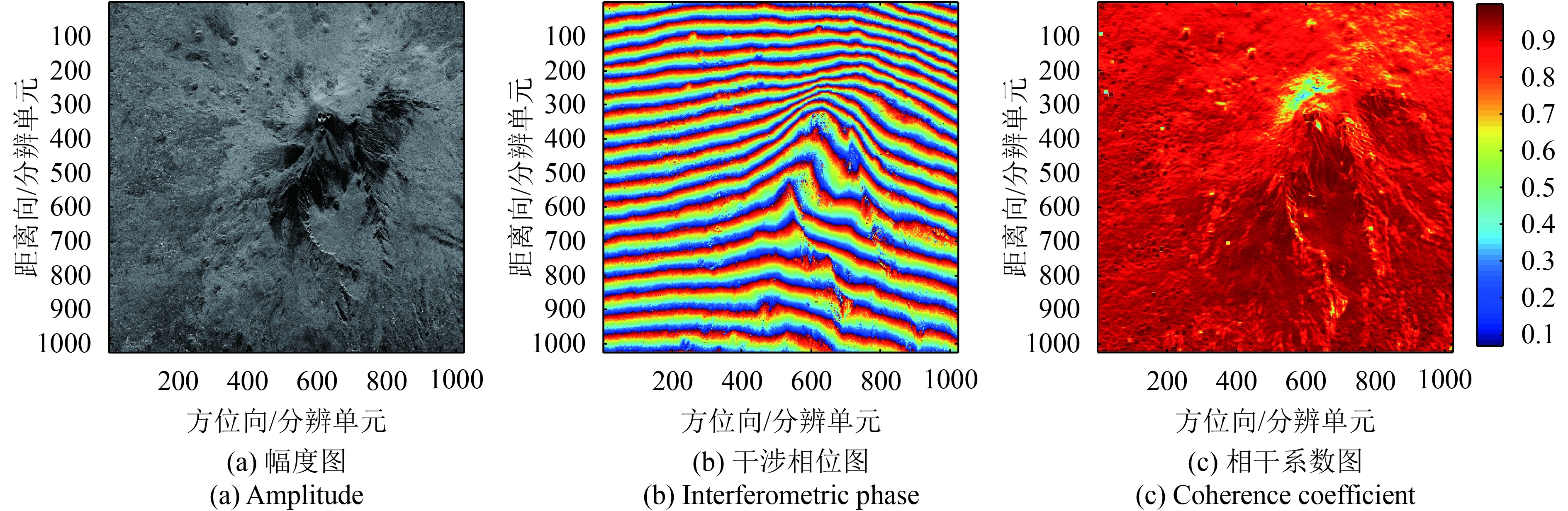
为了验证算法有效性，本节首先利用意大利Etna火山区域的ERS星载SAR图像及其地形高程图进行InSAR复图像仿真，得到的仿真InSAR主天线幅度及理想干涉相位图(图2)，图像大小为1024×1024。对主图像按照子块进行像素偏移从而产生副图像，当主副图像间存在固定常数、线性变化、二次项变化及随机分布等不同偏移时，对比传统FFT最大相干系数配准方法(简称FFT法)，分析本文配准方法的性能。其中，子块像素偏移方式是将主图像分成8×8均匀子块，不同子块间按照失配误差分布加入不同的像素偏移。仿真及配准处理中采用Matlab软件，计算机硬件条件：CPU为Intel Coreli7-6700(主频3.4 GHz)，内存为32 G，显卡为Nvidia GTX1080。实验中本文算法阈值 ${\eta _{\rm{0}}}$ 选择为0.1，最小分块维数 ${n_0} \times {n_0}$ 选择为16×16。

另外，为了进一步定性比较配准方法性能，本文利用配准后图像的干涉相位均方误差MSE(Mean Square Error)、干涉相位梯度均值、干涉相位残差点数及相干系数均值等指标进行评价。

干涉相位MSE定义为

${{\hat {{\phi}}} _{MSE}} = {{\sqrt {\sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {{{\left| {{{{\hat {{\phi}}} }_{m,n}} - {{{\phi}} _{m,n}}} \right|}^{\rm{2}}}} } } } {\Bigg/ }{\sqrt {\sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {{{\left| {{{{\phi}} _{m,n}}} \right|}^{\rm{2}}}} } } }}$

(8)

式中， ${\hat {{\phi}}} $ 表示配准后得到的InSAR干涉相位， ${{\phi}} $ 表示无失配误差时干涉相位。通常 ${{\hat {{\phi}}} _{MSE}}$ 越小表明图像配准后得到干涉相位误差小，则配准效果越好； ${{\hat {{\phi}}} _{MSE}}$ 越大表明干涉相位误差大，则配准效果越差。

干涉相位梯度均值定义为

${{\hat {{\phi}}} _\Delta } = {{\sum\limits_{n = {\rm{2}}}^N {\sum\limits_{m = {\rm{2}}}^M {\left( {\left| {{\Delta _x}\left({{{{\hat {{\phi}}} }_{m,n}}} \right)} \right| + \left| {{\Delta _y}\left({{{{\hat {{\phi}}} }_{m,n}}} \right)} \right|} \right)} } }{\Big/ } {\left({M - 1} \right)}}\left({N - 1} \right)$

(9)

式中， ${\Delta _x}\left({{{{\hat {{\phi}}} }_{m,n}}} \right) \!=\! {{\hat {{\phi}}} _{m,n}} - {{\hat {{\phi}}} _{m - 1,n}}$ 和 ${\Delta _y}\left({{{{\hat {{\phi}}} }_{m,n}}} \right) \!=\! {{\hat {{\phi}}} _{m,n}} - {{\hat {{\phi}}} _{m,n - 1}}$ 。一般情况下， ${{\hat {{\phi}}} _\Delta }$ 越小表明配准后得到的干涉相位质量越好，则进一步表明配准效果越好，反之亦然。

干涉相位残差点定义为

${Q_{m,n}} = \sum\limits_{i = 1}^4 {{\Delta _i}} = \left\{ {\begin{array}{*{20}{c}} 0&{\text{非残差点}}\\ { \pm 1}&{\text{残差点}} \end{array}} \right.$

(10)

${{\hat {{\phi}}} _{\rm{RES}}} = \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {{Q_{m,n}}} } $

(11)

式中，相位梯度 ${\Delta _1} = {{\hat {{\phi}}} _{m + 1,n}} - {{\hat {{\phi}}} _{m,n}}$ ， ${\Delta _2} = {{\hat {{\phi}}} _{m + 1,n + 1}} - $ ${{\hat {{\phi}}} _{m + 1,n}} $ ， ${\Delta _{\rm{3}}} = {{\hat {{\phi}}} _{m,n + 1}} - {{\hat {{\phi}}} _{m + 1,n + 1}}$ 和 ${\Delta _{\rm{4}}} = {{\hat {{\phi}}} _{m,n}} - {{\hat {{\phi}}} _{m,n{\rm{ + 1}}}}$ 。一般情况下，残差点数 ${{\hat {{\phi}}} _{\rm{RES}}}$ 越小则InSAR干涉相位越好，进一步说明图像配准效果越好。

相干系数均值定义为

${\gamma _{mean}} = {{\sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {\left| {{{\hat {{r}}}_{m,n}}} \right|} } }/ {MN}}$

(12)

式中，相干系数 ${\hat {{r}}_{m,n}}$ 可由式(1)计算得到。通常 ${\gamma _{\rm{mean}}}$ 值越大则配准效果越好， ${\gamma _{\rm{mean}}}$ 值越小则配准效果越差。

当仿真InSAR主副图像间存在 $\left({{\rm{1}}{\rm{.58}},{\rm{2}}{\rm{.25}}} \right)$ 固定常数、 $\left[ {{\rm{0,4}}} \right]$ 线性变化、 $\left[ {{\rm{0,3}}{\rm{.2}}} \right]$ 二次项变化、 $\left[ {0,2} \right]$ 区间随机均匀分布等像素偏移时，利用传统FFT整体配准法(简称FFT方法1)、FFT分块配准方法(简称FFT方法1)及本文方法进行亚像素配准，获得干涉相位(图3)，其中3种方法均采用10倍插值使得配准精度达到0.1像素，FFT分块配准方法中分块数为8×8。在干涉相位图方面，从图3可知，3种配准方法在主副图像整体偏移时得到的干涉相位图质量相当，均能良好实现主副InSAR复图像高精度配准；但当存在线性、二次项及随机分布像素偏移时，本文方法得到的干涉相位条纹清晰度明显优于FFT整体配准方法，略优于FFT分块配准方法。值得说明的是，因为实验中失配误差是按照图像子块加入，配准后相邻子块间边界无干涉相位，故干涉相位结果中存在块间边界条纹，在实际中失配误差通常是连续变化，配准后干涉相位不会出现此情况。另外，在运算效率方面，传统FFT整体配准方法和8×8分块配准法的平均用时分别为10.49 s和13.02 s，本文方法在整体、线性、二次项、随机偏移情况下的平均用时分别为0.24 s、0.67 s、1.98 s和2.13 s，可知本文方法的运算效率明显优于传统FFT整体配准方法及分块配准方法。

进一步定量对比本实验中3种配准方法的性能，表1给出了图3共3种配准方法所得到的干涉相位残差点数、相位均方误差、相位梯度均值、相干系数均值等评价指标计算结果，其中原始无失配主副图像的干涉相位残差点数为2136，相位梯度均值为0.733，相干系数均值为0.967。当主副复图像间存在亚像素整体偏移时，3种方法图像配准结果各性能指标差异很小，配准性能相当(表1)；当不同区域存在不同偏移量时，传统FFT整体配准方法失效，但本文方法得到的干涉相位残差点数、MSE、相干系数均值等指标均优于传统FFT固定分块配准方法，验证了本文方法的有效性。

为了进一步对比大场景图像时所提配准方法的运算效率，增大图2中原始仿真图像维数，且像素偏移情况与图3相同，配准算法均采用10倍插值，算法参数设置同图3，FFT分块配准方法采用8×8。表2给出不同图像大小情况下3种配准方法的平均运算时间，其中符号“—”表示计算机内存已溢出无法完成配准。传统FFT整体配准方法在图像维数为4096×4096时，计算机内存溢出无法实现配准(表2)；而本文方法平均运算时间明显小于传统FFT整体配准方法及8×8分块配准，通常运算效率可提高3倍以上。而且，图像对间偏移形式越简单，本文方法运算时间越少，其原因是偏移形式复杂时，本文方法自适应分块数就越多，各子块配准总的运算时间会增加。

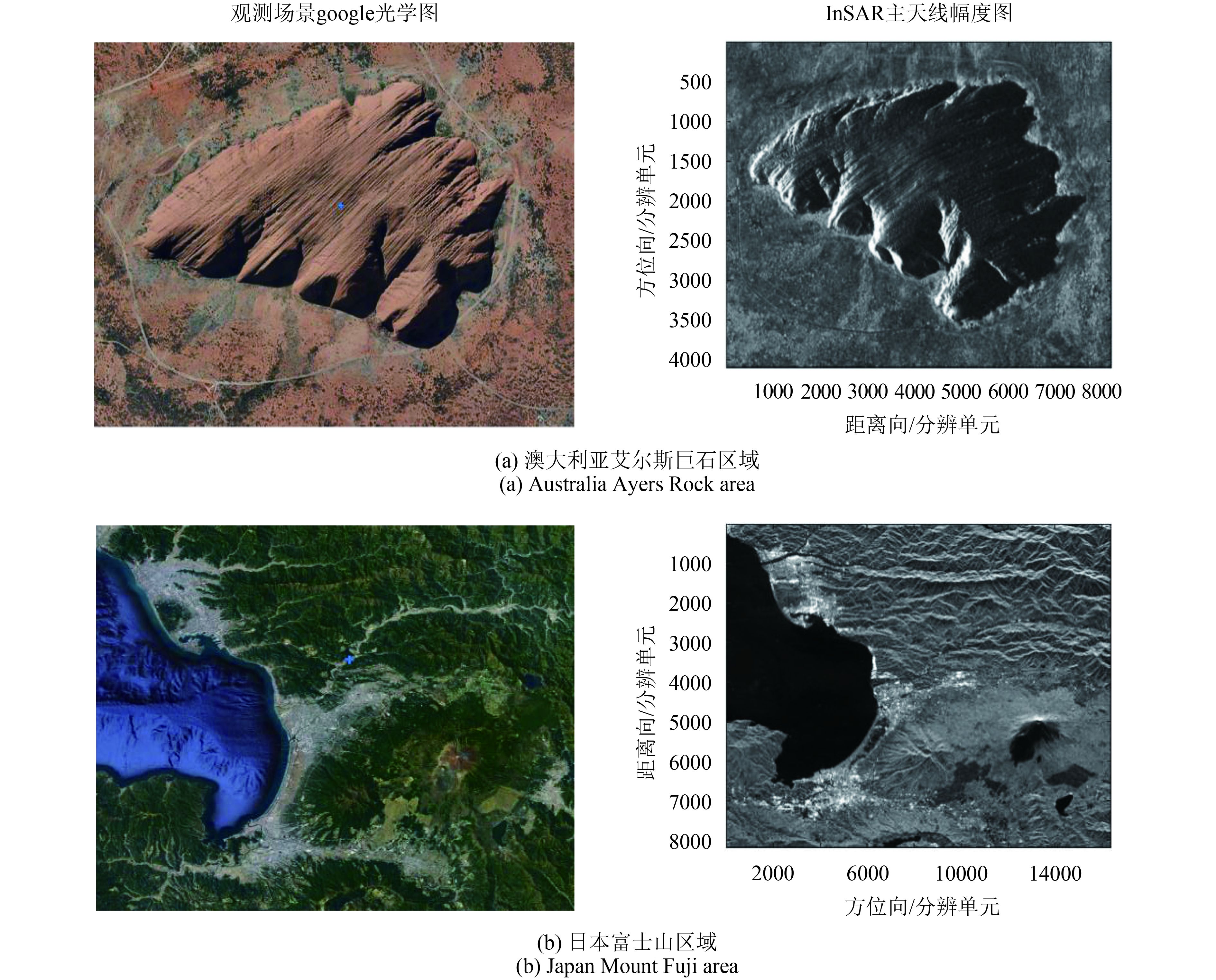
为了进一步验证配准算法有效性，本节利用星载InSAR实测复图像数据进行配准处理分析。图4分别为星载TerrSAR获取的澳大利亚艾尔斯巨石区域InSAR复图像数据、星载PALSAR获取的日本富士山区域InSAR复图像数据的google光学图及主天线幅度图。其中，艾尔斯巨石区域InSAR复图像大小为4096×8192，主要包括了陡变岩石山体、缓变地面等区域；日本富士山区域InSAR复图像大小8192×16384，主要包括了起伏山地、海面、城市等区域。因此，两组图像中存在一些低相干区域，如海面、阴影、山地等区域，此处难以得到干涉相位。实验中本文算法阈值 ${\eta _{\rm{0}}}$ 选择为0.1，最小分块维数 ${n_0} \times {n_0}$ 选择为32×32。

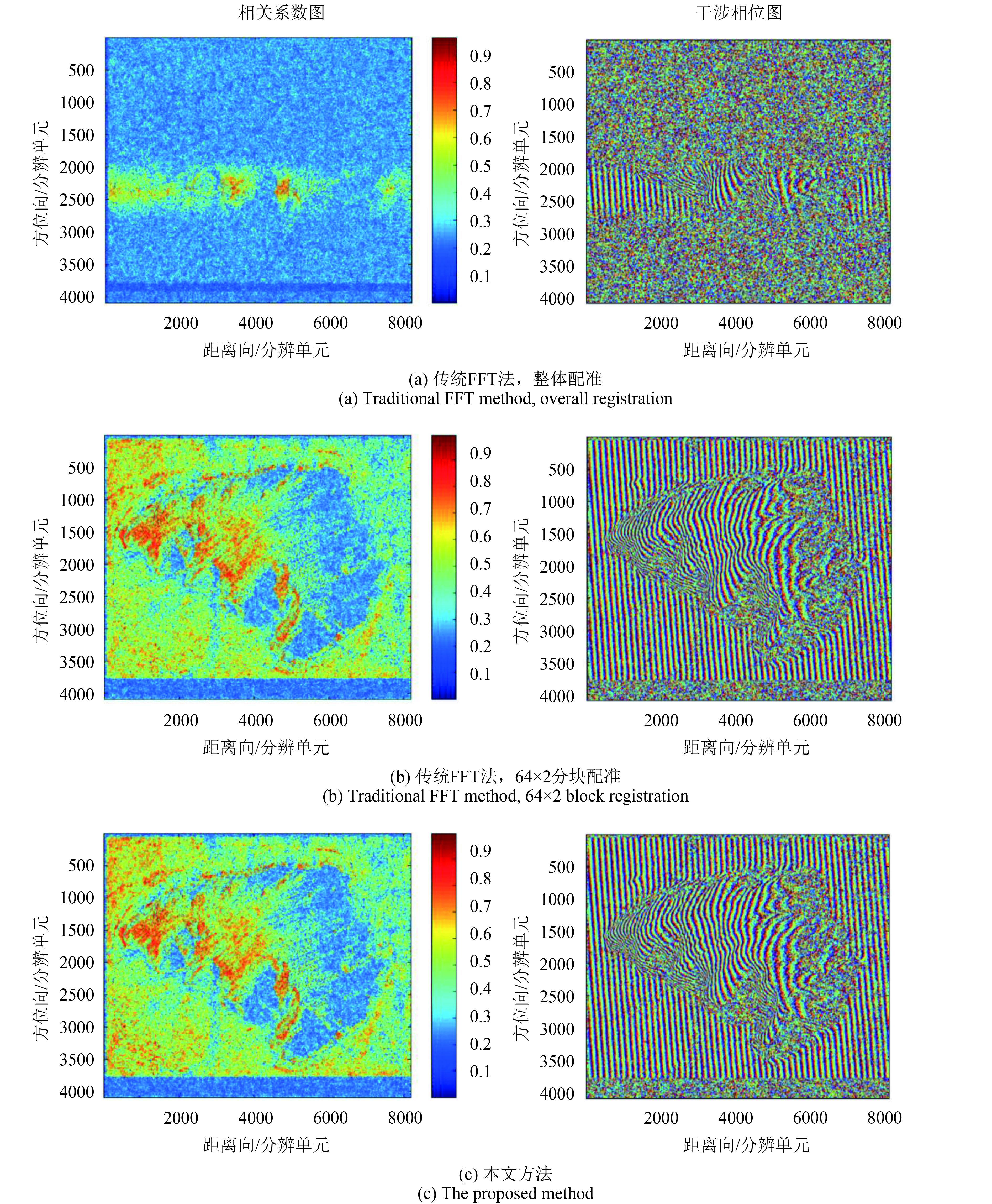
对于图4(a)的艾尔斯巨石区域InSAR复图像，图5给出了传统FFT配准方法和本文算法配准后得到的相干系数及干涉相位结果，其中图5(a) FFT方法采用整体像素级配准，图5(b)和(c)中采用10倍插值使得配准精度达到0.1像素级。从图5配准结果可知，图5(a)复图像整体配准时仅能获得方位向局部区域及对应所有距离向的干涉相位条纹，此区域相干系数较高，而无干涉相位区域相干系数很小，说明该InSAR图像中不同方位向像素偏移不同，而距离向像素偏移不大；图5(b)中FFT配准方法采用64×2分块处理，平均运行时间为844.67 s，而图5(c)中本文方法平均运行时间为52.84 s，但两种方法相干系数及干涉相位条纹基本相当。相对于图5(a)，传统FFT分块方法及本文方法均能获得全局图像的干涉相位，提升了主副图像配准的相干系数，而本文方法运算效率明显优于传统FFT分块处理，其运算效率提升了1个数量级，更有利于InSAR大场景图像配准快速处理。另外，本文方法与传统FFT相似，在低相干目标区域难以获得较好的干涉相位。

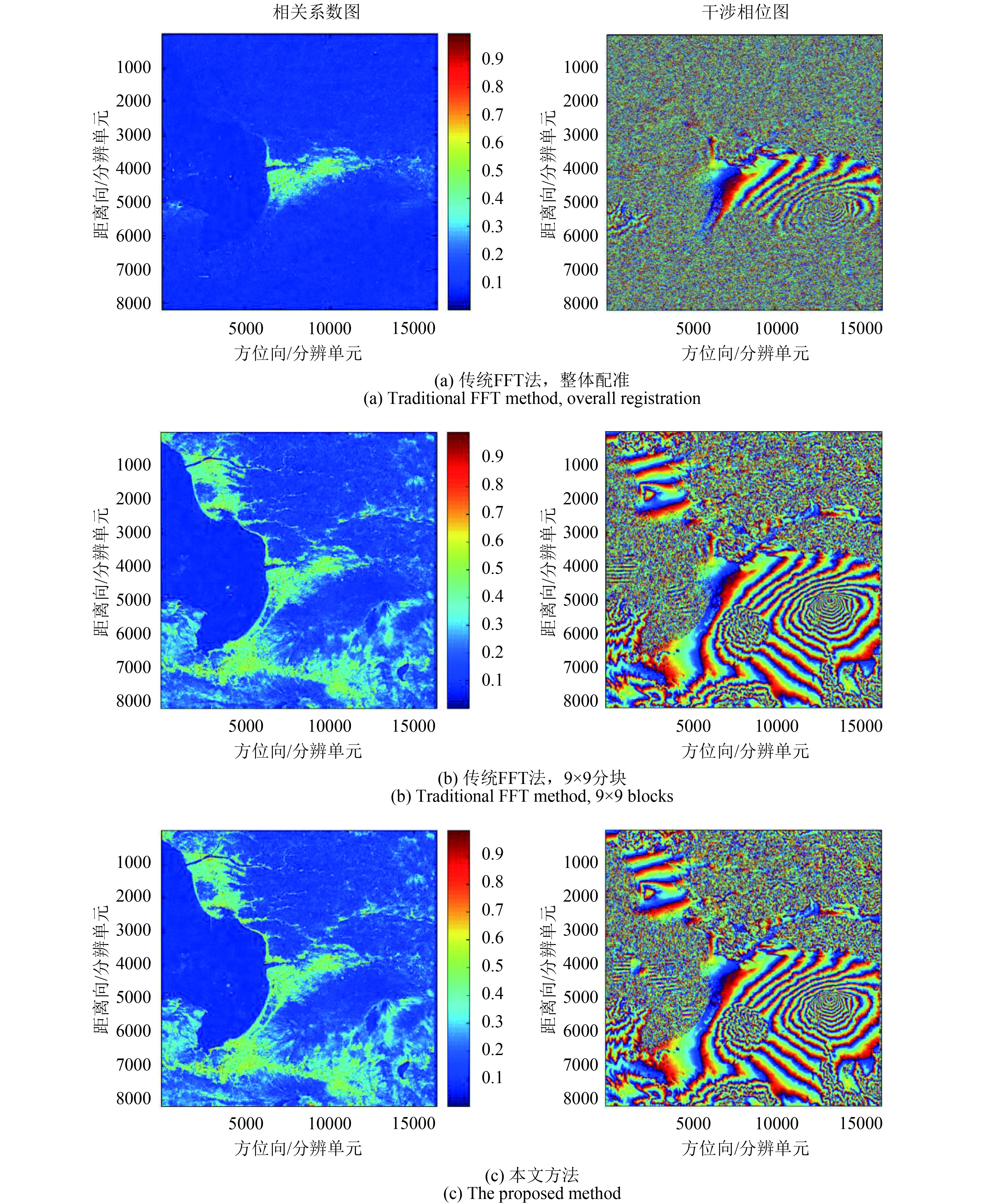
对于图4(b)的富士山区域InSAR复图像，图6给出了传统FFT配准方法和本文算法配准后得到的相干系数及干涉相位图，同样图6(a) FFT方法采用整体像素级配准，图6(b)和图6(c)中采用10倍插值使得配准精度达到0.1像素级，并且为了突出地形变化及相位条纹质量，图中干涉相位已完成相同平地效应去除及滤波处理。从图6可知，该InSAR主副图像在不同方位向和距离向区域均存在不同偏移量，整体配准不能获取全局图像的干涉相位；图6(b)中FFT配准方法采用9×9分块处理，平均运行时间为2018.72 s，可获得全局图像高相干区域的干涉相位；本文方法平均运行时间为59.88 s，获取的相干系数及干涉相位与FFT方法9×9分块配准处理基本相同，说明本文方法可实现高精度复图像配准，同时运算效率相对于传统FFT方法提升了近2个数量级，大大提高了InSAR图像配准运算效率。

为了对比实测数据实验中3种配准算法的性能，本文计算了图5和图6两组星载InSAR实测数据采用传统FFT方法及本文配准方法结果对应的干涉相位残差点数、干涉相位梯度均值及相干系数均值等性能指标(表3)，其中FFT方法1表示传统FFT方法整体配准，FFT方法2表示传统FFT方法分块配准。从表3可知，对于两组星载InSAR实测复图像，本文方法因采用DFT模型配准及四叉树分块处理，在干涉相位残差点数、干涉相位梯度均值及相干系数均值等性能指标均优于FFT方法1及FFT方法2。因此，相对于固定分块配准处理，实验中本文方法通过迭代四叉树分割处理可提高InSAR大场景图像局部区域的配准精度，进一步验证了本文方法在InSAR大场景复图像高精度配准的有效性。

大场景InSAR复图像对的像素失配误差形式往往较复杂，不同图像区域的失配量可能完全没有规律，传统FFT配准方法处理时会面临运算量大、局部区域配准精度不足等问题。针对此问题，本文提出了一种基于DFT模型的大场景InSAR高效高精度图像配准算法。该方法主要利用最小均方差准则构建InSAR复图像配准的DFT模型，采用四叉树自适应分块及DFT矩阵相乘快速重采样配准方法，实现大场景InSAR图像各子块区域的高效高精度亚像素配准。仿真和实测数据结果验证了算法的有效性，表明该方法相对传统FFT最大相干系数配准方法不仅可实现大场景InSAR复图像的亚像素级配准，还具有较高的运算效率，其运算效率通常可以提升3倍以上，且InSAR图像对间偏移形式复杂时运算时间会相应增加。后续可对算法中四叉树配准阈值进行研究，如采用自适应阈值或其他阈值指标，进一步提升算法的配准性能。