出版日期: 2019-07-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20197490
2019 | Volumn23 | Number 4
上一篇  |  下一篇
技术方法 
基准影像数据辅助遥感影像几何定位
expand article info 潘雪琛 , 姜挺 , 余岸竹 , 王鑫 , 张一
信息工程大学 地理空间信息学院，郑州 450052
收稿日期: 2017-11-27; 预印本: 2018-05-07
基金项目: 国家自然科学基金(编号：41471387，41301526)；地理信息工程国家重点实验室开放基金(编号：SKLGIE2015-M-3-1)
第一作者简介: 潘雪琛，1992年生，女，硕士研究生，研究方向为航天摄影测量。Email：xepp27@126.com

摘要

针对遥感卫星影像几何定位时实测控制数据不足的情况，提出利用影像范围内基准影像数据辅助定位提高精度的方法。由遥感影像匹配得到同名像点，利用高精度影像数据和高程数据获取物方平面和高程坐标后，将其视为精度较低的控制点参与区域网平差，从而实现在不额外增加实测控制条件的情况下提高定位精度。经过在国内外3个地区进行一系列试验，验证了方法的可行性和有效性，对提升线阵遥感影像几何定位精度效果显著。

关键词

遥感影像, 有理函数模型, 几何定位, 基准影像, 精度

Geo-positioning of remote sensing images with reference image
expand article info PAN Xuechen , JIANG Ting , YU Anzhu , WANG Xin , ZHANG Yi
Institute of Surveying and Mapping, Information Engineering University, Zhengzhou 450052, China

Abstract

Geometric positioning of satellite images, as one of the keys in producing geo-information products, plays an important role in development of national economic. In general, actual measured ground control data is necessary in geometric positioning of satellite images to correct systematic errors and then increase accuracy. However, the actual measured ground control data is high cost and difficult to obtained in some place. Considering lack of actual measured ground control data in some situations, a method of geometric positioning based on RFM with reference images to increase accuracy was proposed in this paper. The auxiliary control points extracted from high-precision images and digital elevation model (DEM) are used in geometric positioning based on RFM. Firstly, plenty of corresponding image points are matched from satellite images. The horizontal and elevation coordinates of the corresponding image points which named auxiliary control points are measured in high resolution reference images and elevation data and transformed into a unify coordinate system. Then, the auxiliary control points are used as ground control points with low accuracy in block adjustment without additional actual measured ground control data. Three kinds of satellite images including IKONOS images in Hobart, Australia, ZY-3 images in Sainte-Maxime, France, and TH-1 images in Dengfeng, China were used in the experiment in this paper, and the auxiliary control points named GE points were extracted from Google Earth data. The experiment divided into two parts, the first part was geometric positioning with the same amount of actual measured ground control points and GE points in the same position to analyze the accuracy of GE points, the result of which showing that there were systematic errors in both actual measured ground control points and GE points, the relation between two kinds of points depending on the quality of the satellite images. Another part of the experiment was block adjustment using GE points as ground control points and was designed in two cases, one was without actual measured ground control points and another was with few. It was found that the systematic errors were reduced and the accuracy were increased by proposed method in three experimental areas in both cases. Especially in the case without actual measured ground control points, the accuracy was increased obviously with plenty of GE points. Furthermore, the effect of the method was highly negatively correlated with the quality of the satellite images. The experimental result shows that the auxiliary control points extracted from reference images could be used as ground control points, proving the feasibility and availability of proposed method, which has good effect to increase accuracy of geometric positioning in the case without enough actual measured ground control data.

Key words

remote sensing images, RFM, stereo geo-positioning, reference images, accuracy

1 引　言

高分辨率遥感影像的高精度几何定位是制作地理信息成果的关键步骤。随着近几年对地观测技术的不断发展，利用遥感影像在全球范围内精确定位成为了可能(童旭东，2016)。在实际观测中，遥感影像的直接定位精度受到卫星位置误差、传感器姿态角观测精度及镜头畸变差等因素的影响和限制，定位精度的提高主要从定位模型和控制数据两方面入手(王涛 等，2013)。

通常情况下，进行遥感影像的高精度几何定位需要利用地面控制信息进行改正，而对于不易到达和测绘困难地区，实测控制点成本高且获取难度大。对此，国内外许多学者致力于研究如何在不额外增加实测控制数据的情况下提高遥感影像几何定位精度，并取得了大量的成果。随着新兴传感器的出现和地理信息数据的大量积累，极大促进了对于不同源数据的处理与应用(张祖勋和张永军，2012)，联合包括高精度影像数据(范冲和王雪平，2014；汪韬阳 等，2014；刘楚斌 等，2015)和已有高程数据(Goncalves，2008；刘楚斌 等，2016；张浩 等，2016；周平 等，2016；陈小卫 等，2016)的不同传感器数据辅助光学遥感影像定位作为一种新的思路引起了学者们的关注。

为了在实测控制点(以下称实测控制点)不足且不额外增加实测控制数据的情况下提高线阵卫星遥感影像几何定位精度，本文提出基准影像数据辅助定位方法。为验证方法的有效性，利用试验区域内已有影像数据成果和高程数据获取控制点(以下称辅助控制点)，并将其视为精度较低的控制点参与区域网平差，以提高定位精度。为验证方法的有效性，利用Google Earth获取的影像及DEM(Digital Elevation Model)数据分别在国内外3个地区进行试验，并取得了良好的效果。

2 基于RFM的区域网平差

有理函数模型RFM(Rational Function Model)是利用有理多项式建立影像像方与其对应的物方之间的数学映射关系，定义如下(刘军 等，2006；刘建辉 等，2014；郭文月 等，2017)

$ \left\{\begin{aligned} & {r_n} = \frac{{Nu{m_r}({X_n}, {Y_n}, {Z_n})}}{{De{n_r}({X_n}, {Y_n}, {Z_n})}} \\ & {c_n} = \frac{{Nu{m_c}({X_n}, {Y_n}, {Z_n})}}{{De{n_c}({X_n}, {Y_n}, {Z_n})}} \end{aligned} \right. $ (1)

式中， $Nu{m_r}({X_n}, {Y_n}, {Z_n})$ , $De{n_r}({X_n}, {Y_n}, {Z_n})$ , $Nu{m_c}({X_n}, {Y_n}, {Z_n})$ , $De{n_c}({X_n}, {Y_n}, {Z_n})$ 是最大次数为3的多项式，一般由卫星厂家以LINE_NUM_COEFF、LINE_DEN_COEFF、SAMPLE_NUM_COEFF、SAMPLE_DEN_COEFF的形式随遥感影像一同提供给用户。 $({X_n}, {Y_n}, {Z_n})$ 为标准化后的地面点空间坐标； $({r_n}, {c_n})$ 为标准化后的像点坐标。

RFM的参数是由严格成像模型拟合得来，其参数不具有实际物理意义，因此无法通过对误差源的具体分析来进行误差改正。目前应用最为广泛的方法是像方补偿方案，即通过在像方增加系统误差补偿模型的方式消除像点上的系统误差(Grodecki和Dial，2003)，形式如下

$ \left\{ \begin{aligned} & r + \Delta R = \frac{{Nu{m_r}({X_n}, {Y_n}, {Z_n})}}{{De{n_r}({X_n}, {Y_n}, {Z_n})}}{r_S} + {r_0} \\ & c + \Delta C = \frac{{Nu{m_c}({X_n}, {Y_n}, {Z_n})}}{{De{n_c}({X_n}, {Y_n}, {Z_n})}}{r_S} + {r_0} \end{aligned}\right. $ (2)

式中， $\left({R, C} \right)$ 为像点坐标； $\Delta R$ 和 $\Delta C$ 为像点坐标的系统误差改正项，可以表示为

$ \left\{ \begin{array}{l} \Delta R = {e_0} + {e_1}R + {e_2}C + {e_3}{R^2} + {e_4}{C^2} + \cdots \\ \Delta C = {f_0} + {f_1}R + {f_2}C + {f_3}{R^2} + {f_4}{C^2} + \cdots \end{array} \right. $ (3)

式中， $({e_0}, {e_1}, {e_2}, \cdots, {f_0}, {f_1}, {f_2}, \cdots)$ 为系统误差补偿模型参数。在实际应用时根据具体的卫星传感器类型和实测控制点的数量选择合适的参数。

对于覆盖同一区域的多幅遥感影像，系统误差往往具有相似性，因此通过建立数学模型，同时确定重叠区域内所有影像的误差参数，理论上更加严密(张永生 等，2004)。此时可列出如下误差方程

$ {{{V}}_1}={{AX}}-{{{L}}_1}\quad \quad {{{P}}_1} $ (4)

式中， ${{{V}}_1}$ 为像点行列坐标观测值残差向量；X= ${\left[ {{{{T}}^{\rm{T}}}\;{{{X}}_{\rm{G}}}^{\rm{T}}\;{{{X}}_{\rm{T}}}^{\rm{T}}} \right]^{\rm{T}} }$ ， ${{T}}$ 为系统误差补偿模型参数改正向量， ${{{X}}_{\rm{G}}}$ 为控制点地面坐标改正向量， ${{{X}}_{\rm{T}}}$ 为连接点地面坐标改正向量； ${{A}}{\rm{ = }}\left[ {{{C}}\;{{{A}}_{\rm{G}}}\;{{{A}}_{\rm{T}}}} \right]$ 为相应系数矩阵； ${{{L}}_1}$ 为观测值向量； ${{{P}}_1}$ 为对应权矩阵。

将辅助控制点作为精度较低的控制点参与平差，即要考虑控制点的地面坐标中含有误差的情况，则每个控制点还需要对地面坐标增设一组虚拟观测向量并赋予一定的权重，即

$ \left\{ {\begin{aligned} & {{v_X} = {X^0} + dX - {X_v}\qquad {P_X}} \\ & {{v_Y} = {Y^0} + dY - {Y_v}\qquad {P_Y}} \\ & {{v_Z} = {Z^0} + dZ - {Z_v}\qquad {P_Z}} \end{aligned}} \right. $ (5)

式中， $\left( {{v}_{x}},{{v}_{y}},{{v}_{z}} \right)$ 为虚拟观测值残差； $(dX, dY, dZ)$ 为控制点地面坐标改正项； $\left( {{X}^{0}},{{Y}^{0}},{{Z}^{0}} \right)$ 为控制点地面坐标观测值； $({X_v}, {Y_v}, {Z_v})$ 为控制点地面坐标虚拟观测量。

通常 ${X^0} = {X_v}$ ， ${Y^0} = {Y_v}$ ， ${Z^0} = {Z_v}$ 则虚拟误差方程写成矩阵形式为

$ {{{V}}_2}= {{B}}{{{X}}_{\rm{G}}}-{{{L}}_2}\quad \quad {{{P}}_2} $ (6)

式中， ${{{V}}_2}$ 为虚拟观测残差向量； ${{B}}$ 为相应的系数矩阵，一般为单位矩阵； ${{{L}}_2}$ 为虚拟观测向量，一般为零向量； ${{{P}}_2}$ 为对应的权矩阵。

将所列出的误差方程经过迭代求解和更新后得到补偿模型参数和连接点的地面坐标。

3 基准影像数据辅助下的遥感影像几何定位方法

本文提出的基准影像数据辅助下的遥感影像几何定位的基本思想是利用试验区域内已有基准影像数据和高程数据获取辅助控制点参与平差，从而实现在不额外增加实测控制数据的情况下提高遥感影像几何定位精度。

方法包括辅助控制点的获取、高程基准转换及参与平差3个方面。

3.1 辅助控制点的获取

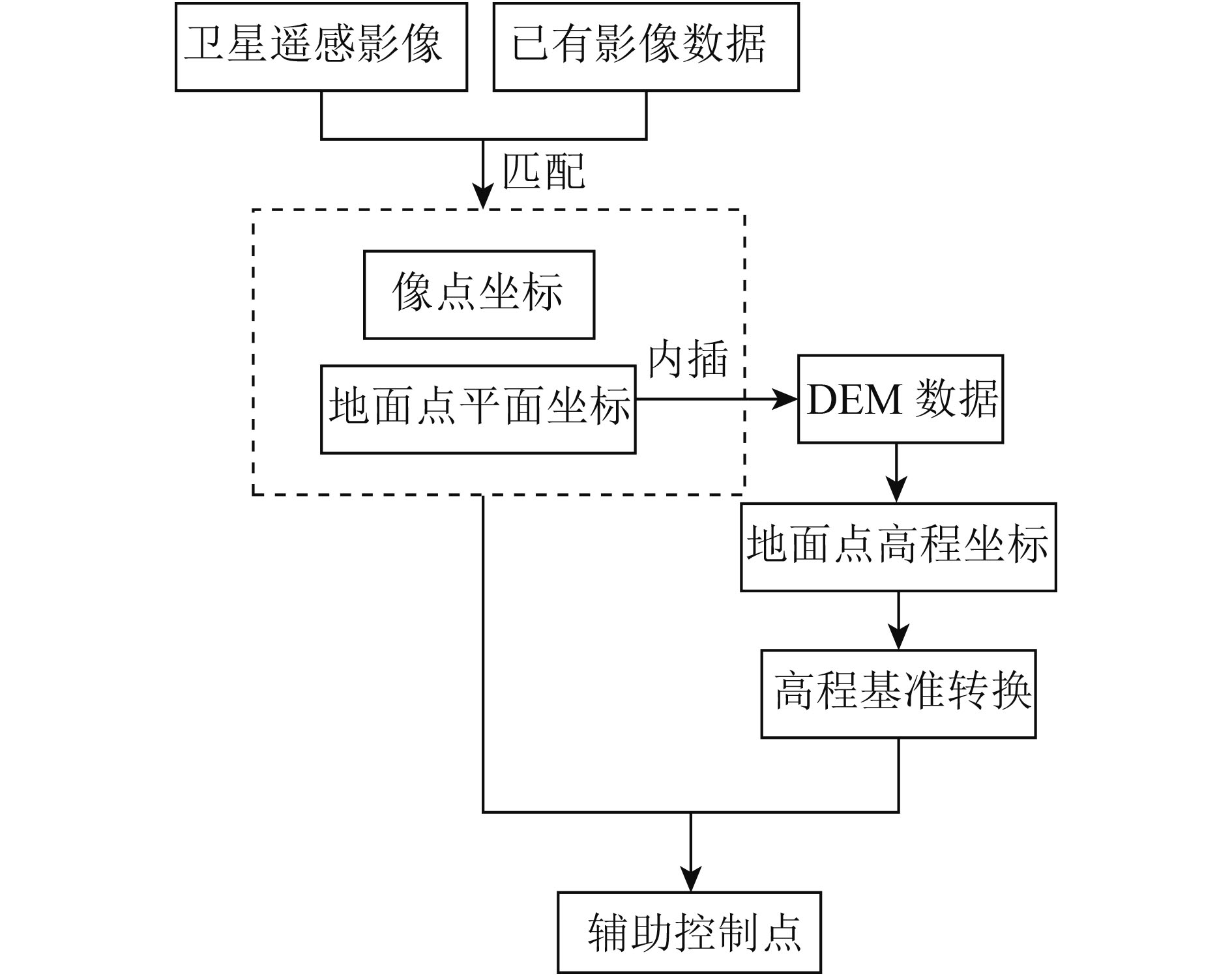
辅助控制点获取的基本方法是利用三线阵遥感影像通过匹配得到同名像点，与带有地面平面坐标的基准影像数据进行匹配得到相应地面点平面坐标，再在已有DEM数据中内插得到高程值，最后经高程基准转换统一坐标系。具体流程如图1。


图 1 辅助控制点的获取
Fig. 1 Obtaining additional control points

使用的基准影像数据为Google Earth提供的遥感影像，由其获得辅助控制点称为GE点，使用的DEM数据为Google Earth提供的高程数据。

Google Earth软件为用户提供全球范围内的多分辨率卫星影像，并携带有WGS-84坐标系下的平面坐标以及EGM96系统下的高程信息，可获得任意地面点的高精度坐标。目前软件可提供的全球影像为20级，最高空间分辨率为0.11 m左右，中国大陆可下载19级，最高空间分辨率为0.25 m左右；全球高程数据最高提供18级，采样间距为7 m左右。经验证Google Earth提供的数据平面精度可达1.80 m，高程精度达1.73 m(Mohammed 等，2013)。

3.2 高程基准转换

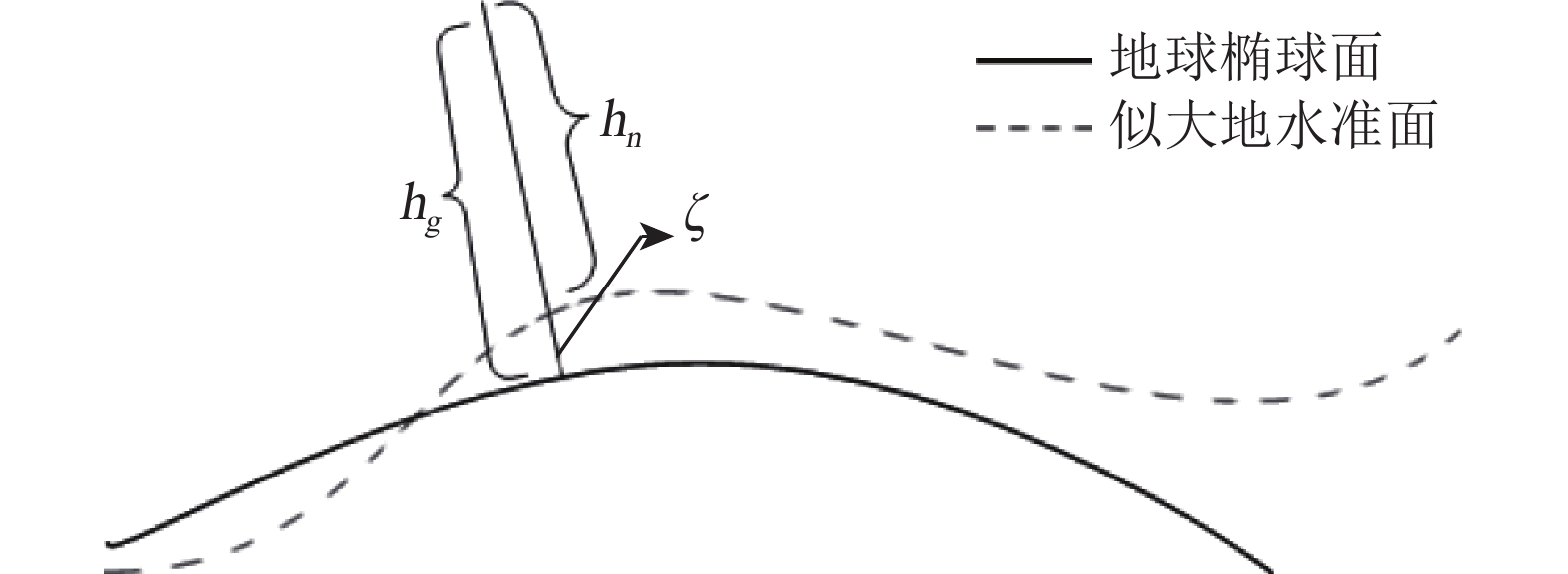
正常高即海拔高，指空间中某一点沿着过该点的正常重力线到似大地水准面的距离(吕志平和乔书波，2006)，而大地高是某一点相对于地球椭球的高程值(图2)，二者的关系可以表示为

$ {h_g} = {h_n} + \zeta $ (7)

式中， ${h_g}$ 为大地高， ${h_n}$ 为正常高， $\zeta $ 为高程异常值。


图 2 正常高和大地高之间的关系
Fig. 2 Relationship between normal height and geodetic height

遥感影像几何定位中高程坐标通常为大地高，而前述介绍的已有地理数据中的高程数据采用的是EGM96系统属于正常高系统，因此在获取辅助控制点后应先将其高程坐标转换到大地高系统下再用于辅助定位。

3.3 辅助控制点参与遥感影像区域网平差

得到辅助控制点并经过高程基准转换后便可将其视为精度较低的控制点参与区域网平差。在无实测控制点的方案中，所有实测控制点作为检查点进行精度评估；在稀少实测控制点的方案中，按照所设计的试验方案，部分实测控制点作为精度较高的控制点参与平差，其余为检查点，此时应考虑实测控制点和辅助控制点精度不同分别定权。

作为检查点的实测控制点不参与平差，在平差结束后利用求解得到的补偿模型参数经像方补偿后进行立体定位，再对所得的地面坐标与实测地面坐标比较计算定位精度。

具体平差流程如图3所示。


图 3 基准影像数据辅助区域网平差流程图
Fig. 3 Flowchart of block adjustment with reference images

4 试验与分析

在国内外3个试验区域设计了一系列的试验方案，分别对比研究在无实测控制点和布设稀少实测控制点的情况下，基准影像数据参与定位对于定位精度提升的效果。

4.1 试验数据

试验中的遥感影像数据采用IKONOS卫星获取的澳大利亚Hobart地区、资源三号卫星获取的法国Sainte-Maxime地区以及天绘一号卫星获取的河南登封地区3个试验区域的三视影像。

IKONOS卫星影像成像于2003年，空间分辨率为1 m，幅宽为11 km。影像范围内共有实测控制点34个，像方及物方坐标均由ISPRS(http://www.isprs.org/data/ikonos_hobart/default.aspx[2019-09-01])提供，像点量测精度约为0.7个像元；连接点个数为108个，由三视影像匹配得到；基准影像数据为Google Earth提供的空间分辨率为0.875 m的影像，在遥感影像上选取20个实测控制点，在基准影像上量测出相应地面坐标，获取20个GE点。高程数据由采样间距约为10 m的DEM数据内插得到。该区域遥感影像如图4所示，三角点为实测控制点，其中标红三角点为进行稀少实测控制点辅助时用到的中心及四角控制点；基准影像范围如图5所示，三角点为辅助控制点，其中标红三角点为进行辅助控制点精度验证时作为控制点使用的中心及四角控制点。


图 4 澳大利亚地区遥感影像及实测控制点分布
Fig. 4 Distribution of actual measured control points in the remote sensing image covering Hobart, Australia


图 5 澳大利亚地区GE点分布
Fig. 5 Distribution of GE points in the reference image covering Hobart, Australia

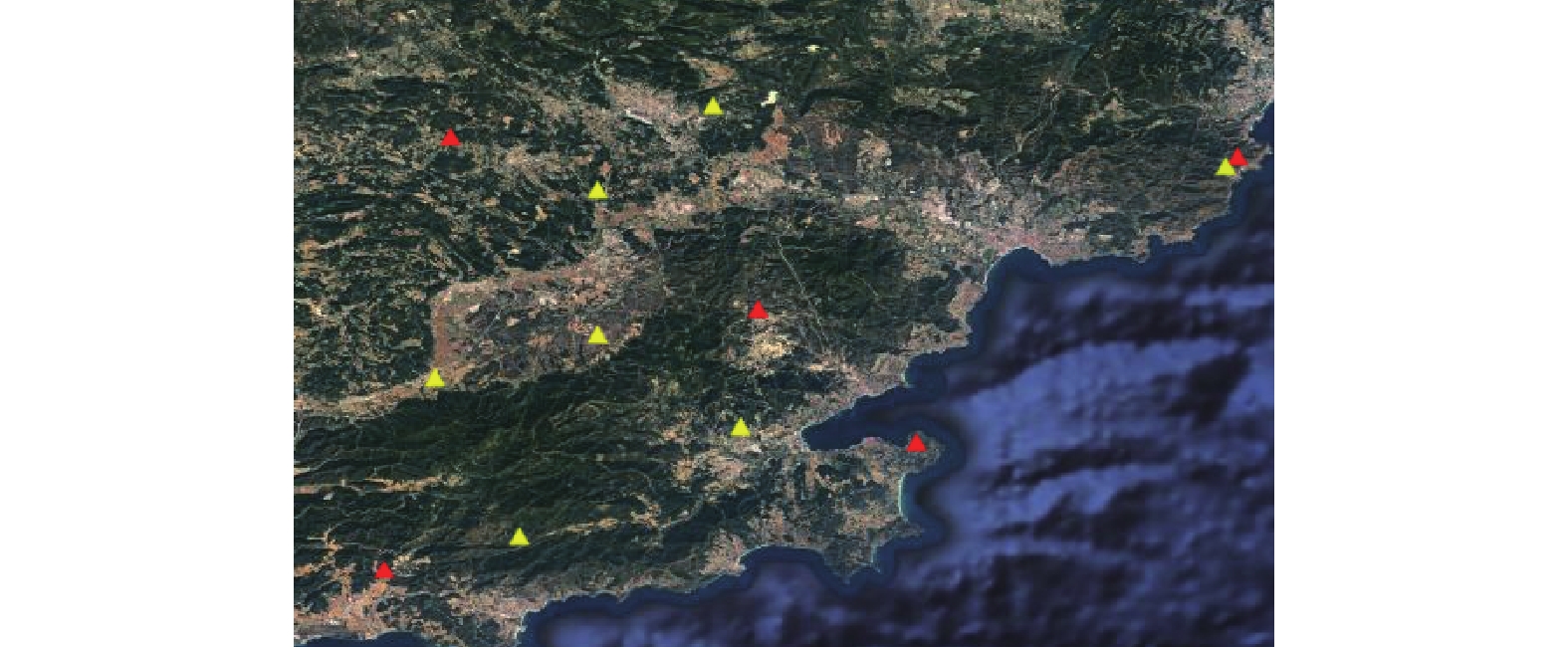
资源三号卫星影像数据成像于2014年，前后视空间分辨率为3.6 m，幅宽52 km，下视空间分辨率为2.1 m，幅宽51 km。影像范围内共有实测控制点12个，像方及物方坐标均由国际摄影测量与遥感协会ISPRS(International Society of Photogrammetry and Remote Sensing)(http://www.isprs.org/data/zy-3/data/reference-data/Default.aspx[2016-09-01])提供，像点量测精度约为0.5个像元；连接点个数为131个，由三视影像匹配得到；基准影像数据为Google Earth提供的空间分辨率为0.868 m的影像，在基准影像上量测出12个实测控制点相应的地面坐标，获取12个GE点，高程数据从Google Earth提供的采样间距约为10 m的DEM数据内插得到。该区域的遥感影像如图6所示，三角点为实测控制点，标红三角点为进行稀少实测控制点辅助时用到的中心及四角控制点；基准影像范围如图7所示，三角点为辅助控制点，其中标红三角点为进行辅助控制点精度验证时作为控制点使用的中心及四角控制点。


图 6 法国地区遥感影像及实测控制点分布
Fig. 6 Distribution of actual measured control points in the remote sensing image covering Sainte-Maxime, France


图 7 法国地区GE点分布
Fig. 7 Distribution of actual GE points in the reference image covering Sainte-Maxime, France

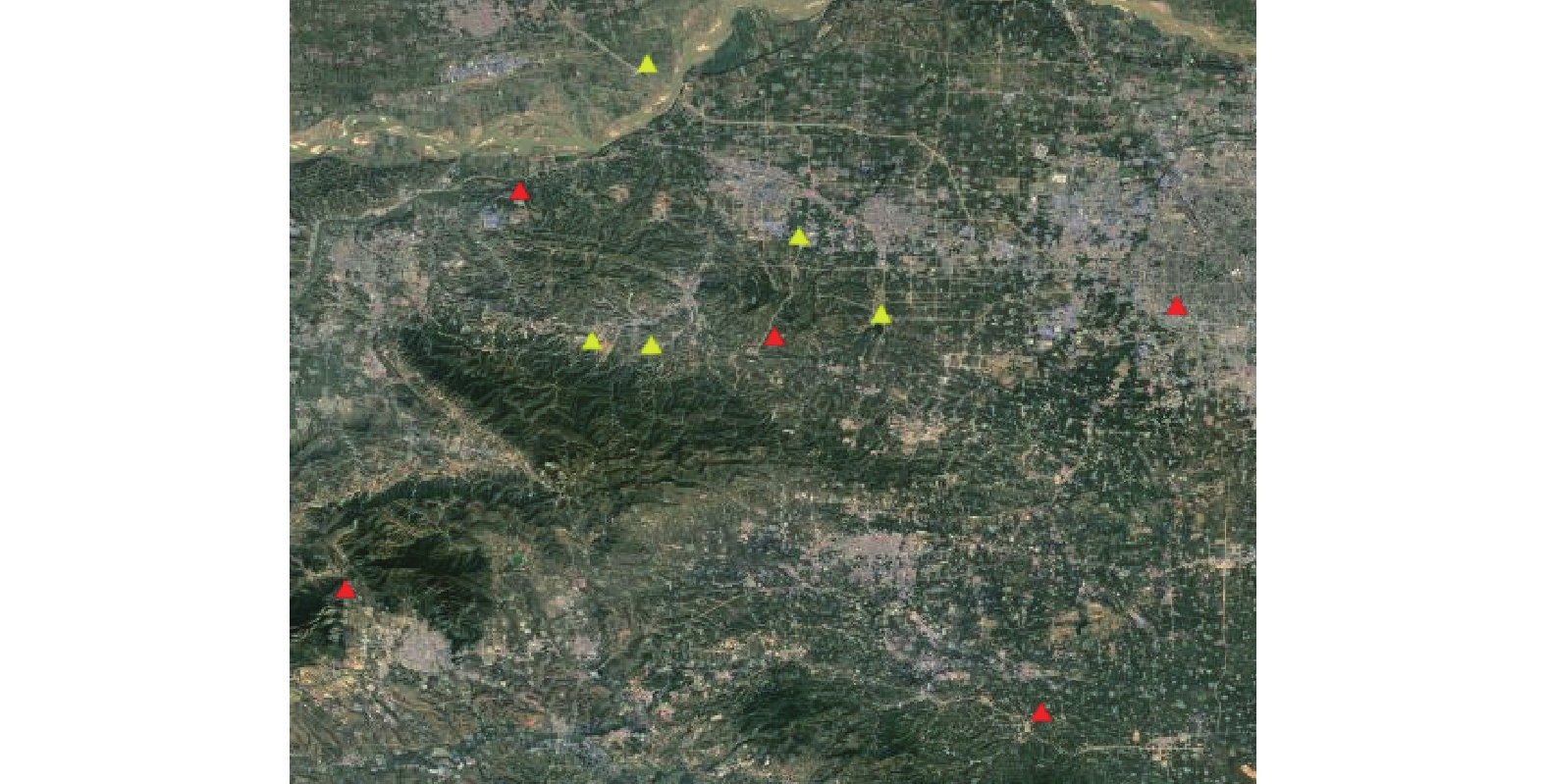
天绘一号卫星影像数据成像于2012年，空间分辨率为5 m，幅宽约为60 km。影像范围内共有实测控制点30个，物方坐标为野外GPS实测点，精度为分米级，像点坐标为手工量测，精度在一个像素左右；连接点个数为51个，由三视影像匹配得到；基准影像数据为Google Earth提供的空间分辨率为0.875 m的影像，在遥感影像上选取10个实测控制点，在基准影像上量测出相应地面坐标，获取10个GE点，高程数据从Google Earth提供的采样间距约为15 m的DEM数据内插得到。该区域遥感影像如图8所示，三角点为实测控制点，其中标红三角点为进行稀少实测控制点辅助时用到的中心及四角控制点；基准影像范围如图9所示，三角点为辅助控制点，其中标红三角点为进行辅助控制点精度验证时作为控制点使用的中心及四角控制点。


图 8 河南登封地区遥感影像及实测控制点分布
Fig. 8 Distribution of actual measured control points in the remote sensing image covering Dengfeng, China


图 9 河南登封地区GE点分布
Fig. 9 Distribution of actual GE points in the reference image covering Dengfeng, China

4.2 辅助控制点精度验证

3个试验区域中，基准影像范围均与遥感影像的范围相同，所获取的辅助控制点的像点坐标由遥感影像上的实测控制点选取获得，地面点坐标由基准影像数据和高程数据内插获得，因此本文在利用辅助控制点参与平差前，对3个试验区域实测控制点与辅助控制点的精度进行了研究。

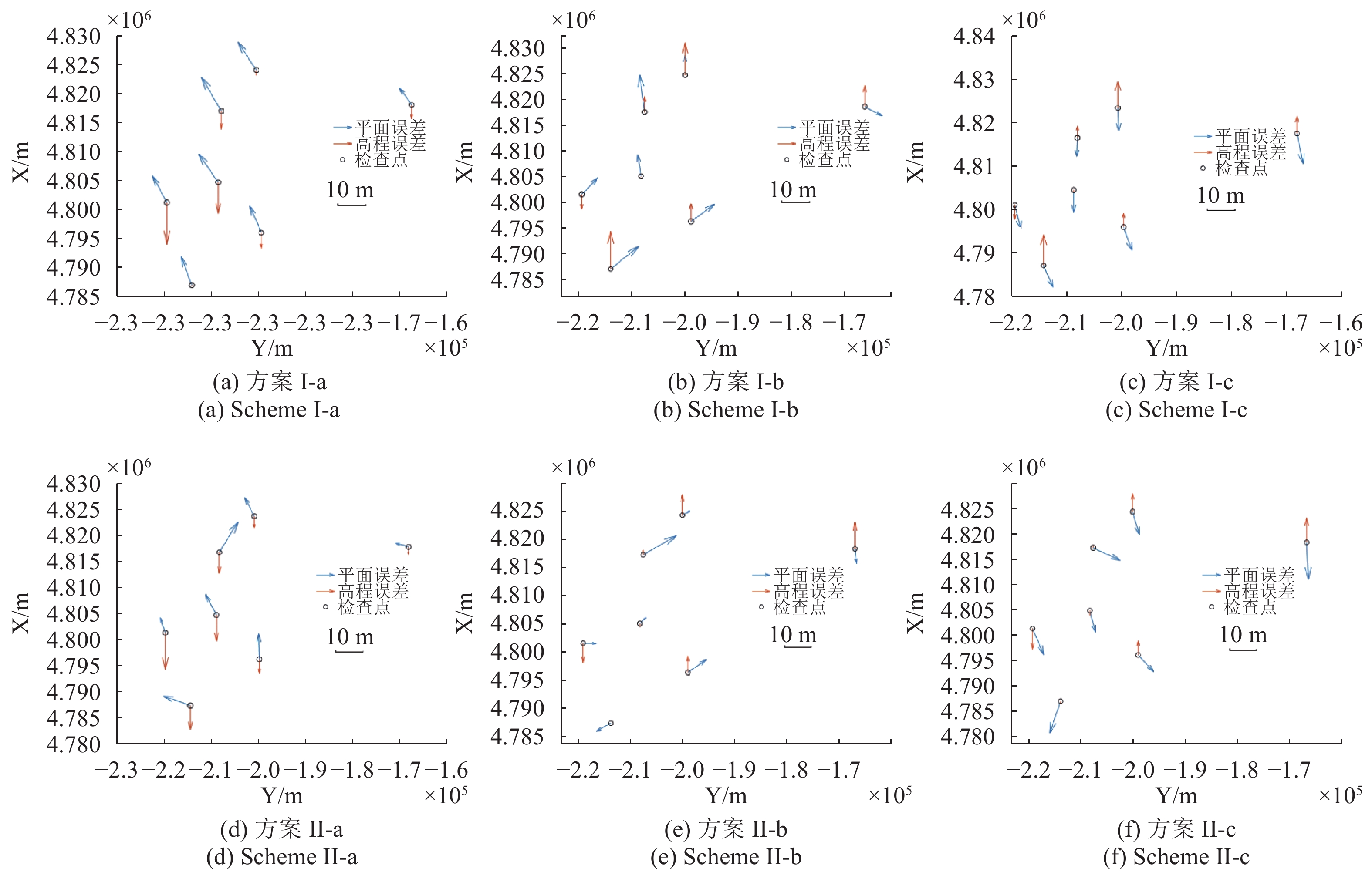
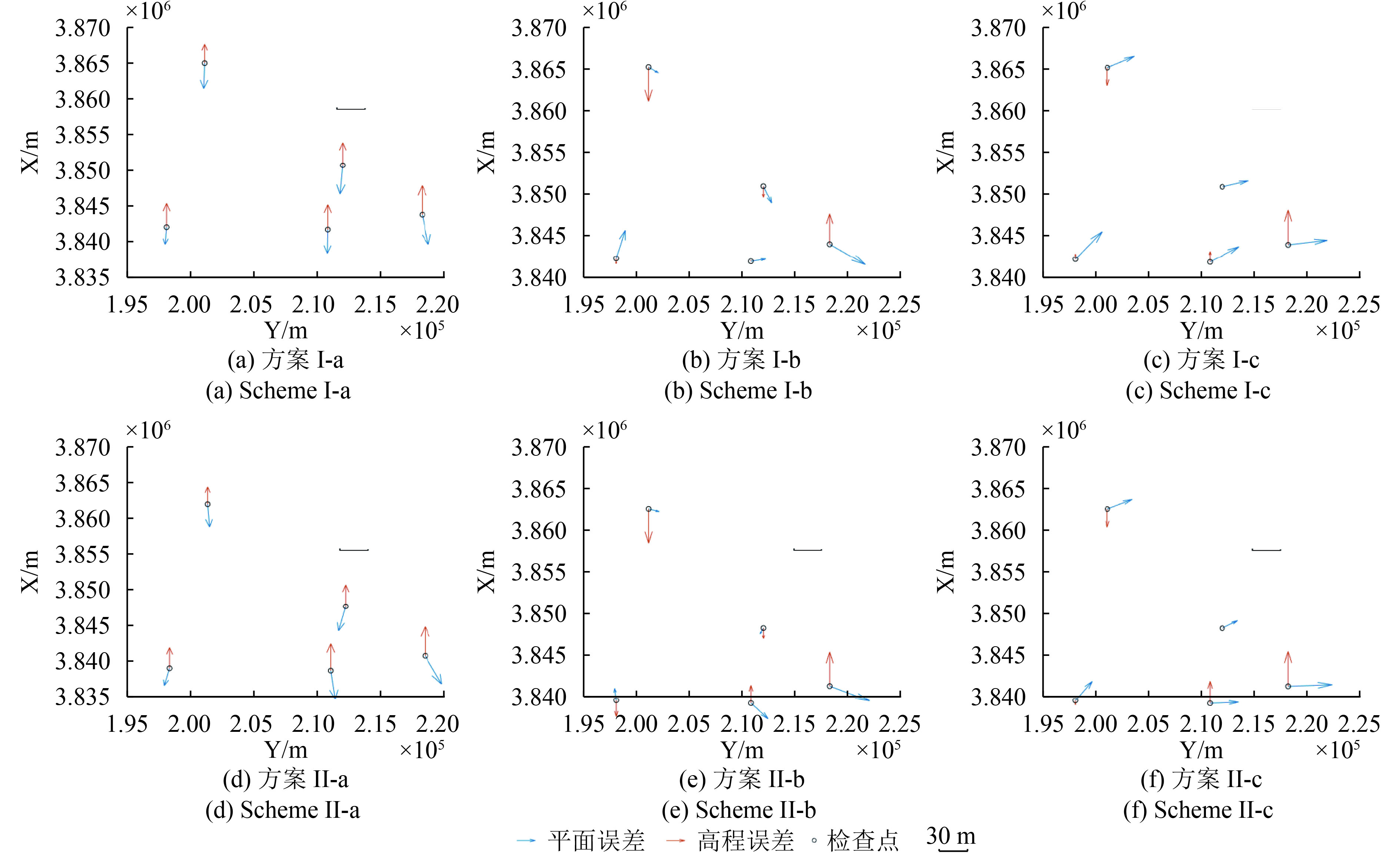
试验中控制点的布设方案分为无控制点、中心实测控制点、中心GE点、四角实测控制点、四角GE点，参与平差的两种控制点在遥感影像上的点位相对应。分别利用未参与定位的其余实测控制点和其余GE点作为检查点进行精度评价，得到的结果如表1—表3所示，无控制点及中心控制点方案的残差分布图如图10—图12所示。

表 1 澳大利亚Hobart地区实测控制点与GE点定位精度
Table 1 Positioning results of ground control points and GE points in Hobart

下载CSV 
试验方案 检查点 布点方案 控制点 最大误差/m 中误差/m
X Y Z X Y XY Z XYZ
Ⅰ-a 15个实测控制点 无 无 3.084 2.621 5.561 1.729 2.120 2.736 4.238 5.044
Ⅰ-b 中心布点 实测控制点 1.915 0.909 2.020 0.789 0.416 0.892 1.079 1.400
Ⅰ-c GE点 5.142 2.369 2.879 3.636 1.580 3.965 1.743 4.331
Ⅰ-d 四角布点 实测控制点 2.071 0.714 2.701 0.868 0.445 0.975 1.008 1.403
Ⅰ-e GE点 5.073 1.538 2.337 3.569 0.808 3.659 0.990 3.790
Ⅱ-a 15个GE点 无 无 8.533 4.534 8.862 5.157 3.487 6.226 4.506 7.685
Ⅱ-b 中心布点 实测控制点 6.619 2.387 5.188 3.316 1.404 3.601 1.764 4.010
Ⅱ-c GE点 3.392 1.173 6.180 1.136 0.556 1.265 2.257 2.587
Ⅱ-d 四角布点 实测控制点 6.463 2.627 4.507 3.170 1.629 3.564 1.700 3.949
Ⅱ-e GE点 3.461 1.758 4.871 1.132 0.856 1.419 1.701 2.215

表 2 法国Sainte-Maxime地区实测控制点与GE点定位精度
Table 2 Positioning results of ground control points and GE points in Sainte-Maxime, France

下载CSV 
试验方案 检查点 布点方案 控制点 最大误差/m 中误差/m
X Y Z X Y XY Z XYZ
Ⅰ-a 7个实测控制点 无 无 13.709 9.857 10.627 11.100 7.772 13.551 5.730 14.712
Ⅰ-b 中心布点 实测控制点 5.265 3.799 7.442 3.119 2.256 3.849 4.558 5.966
Ⅰ-c GE点 16.885 4.203 7.065 13.121 2.547 13.366 4.317 14.046
Ⅰ-d 四角布点 实测控制点 4.399 3.739 8.508 1.900 2.073 2.812 4.181 5.038
Ⅰ-e GE点 2.857 5.854 10.884 1.873 3.824 4.258 5.010 6.575
Ⅱ-a 7个GE点 无 无 16.545 31.086 11.657 10.649 13.927 17.532 7.082 18.908
Ⅱ-b 中心布点 实测控制点 8.101 40.258 5.357 4.761 16.013 16.706 3.225 17.014
Ⅱ-c GE点 21.891 40.666 5.005 15.075 16.219 22.143 3.100 22.359
Ⅱ-d 四角布点 实测控制点 9.405 39.328 6.215 4.958 15.581 16.351 4.238 16.891
Ⅱ-e GE点 5.943 36.259 8.544 3.849 14.783 15.276 4.613 15.957

表 3 河南登封地区实测控制点与GE点定位精度
Table 3 Positioning results of ground control points and GE points in Dengfeng, China

下载CSV 
试验方案 检查点 布点方案 控制点 最大误差/m 中误差/m
X Y Z X Y XY Z XYZ
Ⅰ-a 5个实测控制点 无 无 29.306 3.563 28.495 25.244 1.790 25.308 23.185 34.322
Ⅰ-b 中心布点 实测控制点 7.243 7.159 5.582 4.532 3.758 5.887 3.448 6.823
Ⅰ-c GE点 14.962 16.687 6.846 8.343 12.875 15.342 3.627 15.765
Ⅰ-d 四角布点 实测控制点 8.496 3.054 10.205 4.507 2.527 5.167 5.759 7.737
Ⅰ-e GE点 13.049 5.321 5.358 6.833 4.091 7.964 3.418 8.667
Ⅱ-a 5个GE点 无 无 31.128 10.363 29.805 26.938 5.405 27.475 23.661 36.259
Ⅱ-b 中心布点 实测控制点 6.996 13.960 6.341 5.119 7.023 8.690 4.528 9.799
Ⅱ-c GE点 13.165 23.487 8.156 6.985 14.988 16.535 4.787 17.215
Ⅱ-d 四角布点 实测控制点 6.699 9.146 11.515 4.648 5.436 7.152 6.697 9.798
Ⅱ-e GE点 11.295 7.858 6.453 5.688 5.941 8.225 4.505 9.378


图 10 澳大利亚Hobart地区GE点精度验证试验残差分布
Fig. 10 Error distribution of accuracy experimental results of GE points in Hobart, Australia


图 11 法国Sainte-Maxime地区GE点精度验证试验残差分布
Fig. 11 Error distribution of accuracy experimental results of GE points in Sainte-Maxime, France


图 12 河南登封地区GE点精度验证试验残差分布
Fig. 12 Error distribution of accuracy experimental results of GE points in Dengfeng, China

如图10—图12中(a)与(d)图所示，无控制点参与定位时，3组试验中实测控制点和GE点作为检查点得到的定位结果均存在明显系统误差，且残差分布相似，说明有理函数模型参数中携带系统误差，但使用两类控制点得到的定位精度不同，说明两类控制点自身也含有误差。3组试验中实测控制点作为检查点得到的整体定位精度均优于GE点，其中平面方向上精度差异十分明显。当有控制点参与定位时，系统误差均在不同程度上得到了削弱，但注意到表1—表3中试验方案Ⅰ-b与Ⅰ-d、Ⅱ-c与Ⅱ-e，在检查点同类控制点做控制时，实测控制点作为检查点得到的整体定位精度优于GE点。基本可以得到结论，3组试验区域中的实测控制点的精度均优于GE点。

对于3个测区中不同分辨率的遥感影像，实测控制点的刺点精度不同，与辅助控制点的精度关系也不同。从定位结果和残差分布中可以看出，对于影像分辨率较高的IKONOS卫星影像，以实测控制点做精度评价时，GE点参与定位后平面精度下降，该区域GE点的平面精度明显低于实测控制点；对于影像分辨率适中的“资源三号”卫星影像，以实测控制点做精度评价时，中心布点的GE点参与定位后平面精度略微提升，但同类的GE点做精度评价时平面精度反而大幅度下降，说明GE点平面精度的可靠性较低，中心GE点不能有效改善定位结果，但四角布点可获得与实测控制点接近的定位精度；对于影像分辨率较低的“天绘一号”卫星影像，以实测控制点做精度评价时，中心布点的GE点做控制得到的平面精度远不如实测控制点，但四角布点时定位精度的差异明显减小，高程精度甚至更高。

作者所在课题组使用试验区域的实测控制点作为精度评价标准，对本文的基准影像数据和高程数据相对于实测控制点的精度进行研究，得到的结论如下：对于Google Earth影像和高程数据，法国地区平面精度为5.454 m，高程精度为1.494 m，登封地区平面精度为3.575 m，高程精度为0.760 m，澳大利亚地区平面精度为6.162 m，高程精度为2.909 m。

4.3 试验方案

为了研究本文所提出的基准影像数据辅助定位对于定位精度的改善效果，将试验分为6个部分，具体试验方案为如表4所示。

表 4 基准影像数据辅助RFM区域网平差试验方案
Table 4 Experimental scheme for block adjustment of RFM with reference images

下载CSV 
方案 地面控制点数量 地面控制点分布 GE点参与
A 无控制点 无 无
B 无控制点 无 有
C 中心布点 无
D 中心布点 有
E 四角布点 无
F 四角布点 有

4.4 结果与分析

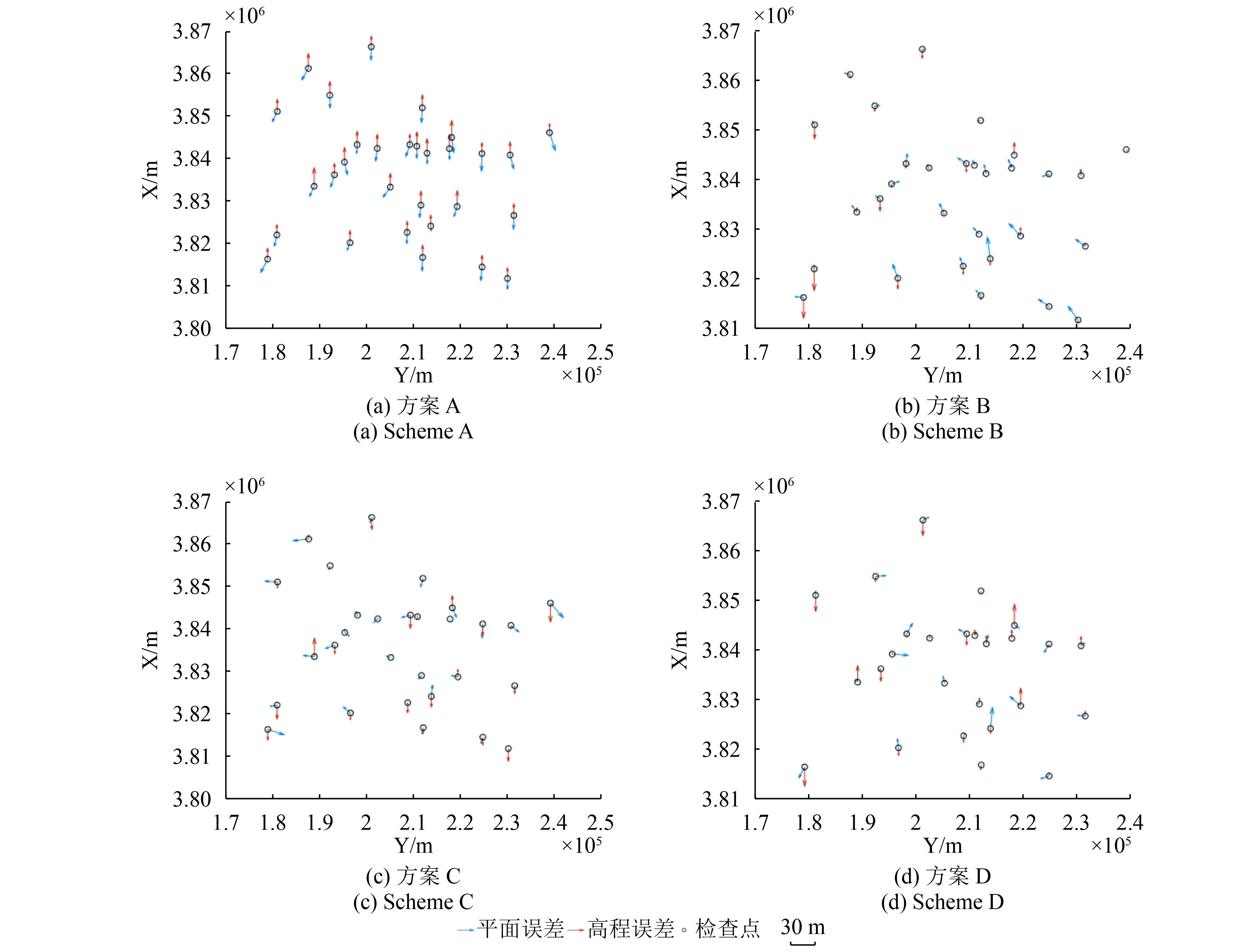
根据上述试验方案，利用相关数据在3个试验区域分别做了大量试验。表5—表7分别为3个试验区域定位结果，图13—图15分别为3个试验区域中直接定位及基准影像辅助定位方案的残差分布图。

表 5 澳大利亚Hobart地区基准影像数据辅助定位结果
Table 5 Positioning results with reference images in Hobart, Australia

下载CSV 
试验方案 实测控制点 检查点 补偿模型 辅助控制点 最大误差/m 中误差/m
X Y Z X Y XY Z XYZ
A 0 34 无 无 3.084 2.990 6.319 1.685 1.985 2.604 4.114 4.869
B 仿射变换 20 GE点 6.122 3.297 3.325 3.860 1.523 4.149 1.075 4.286
C 1 33 平移变换 无 1.893 1.765 5.340 0.780 0.605 0.987 1.774 2.030
D 20 GE点 2.087 2.069 4.205 0.887 0.611 1.077 1.196 1.609
E 4 30 仿射变换 无 2.122 1.891 3.212 0.707 0.674 0.977 1.178 1.530
F 20 GE点 1.620 1.519 3.206 0.711 0.576 0.915 1.020 1.370

表 6 法国Sainte-Maxime地区基准影像数据辅助定位结果
Table 6 Positioning results with reference images in Sainte-Maxime, France

下载CSV 
试验方案 实测控制点 检查点 补偿模型 辅助控制点 最大误差/m 中误差/m
X Y Z X Y XY Z XYZ
A 0 12 无 无 13.709 9.857 12.781 11.000 8.040 13.625 6.228 14.981
B 仿射变换 20 GE点 7.571 10.346 8.185 3.870 7.083 8.072 3.889 8.960
C 1 11 平移变换 无 5.265 3.798 7.666 3.074 1.969 3.650 5.141 6.306
D 20 GE点 5.277 3.771 6.808 3.083 1.968 3.657 4.658 5.922
E 4 8 仿射变换 无 4.318 3.476 8.520 2.024 1.797 2.707 4.056 4.876
F 20 GE点 4.286 3.434 8.481 2.014 1.763 2.676 3.938 4.761

表 7 河南登封地区基准影像数据辅助定位结果
Table 7 Positioning results with reference images in Dengfeng, China

下载CSV 
试验方案 实测控制点 检查点 补偿模型 辅助控制点 最大误差/m 中误差/m
X Y Z X Y XY Z XYZ
A 0 30 无 无 33.971 12.113 31.105 23.792 5.173 24.347 21.858 32.720
B 仿射变换 10 GE点 21.096 10.480 13.521 7.638 5.200 9.240 5.202 10.604
C 1 29 平移变换 无 13.727 13.922 9.122 5.736 6.019 8.315 4.505 9.457
D 10 GE点 13.658 13.825 8.060 5.706 5.977 8.263 3.934 9.152
E 4 26 仿射变换 无 14.088 10.312 11.029 4.711 3.745 6.018 4.568 7.556
F 10 GE点 14.247 10.139 7.992 4.725 3.690 5.995 3.875 7.138


图 13 澳大利亚Hobart地区几何定位残差分布
Fig. 13 Error distribution of positioning result in Hobart, Australia


图 15 河南登封地区几何定位残差分布
Fig. 15 Error distribution of positioning result in Dengfeng, China

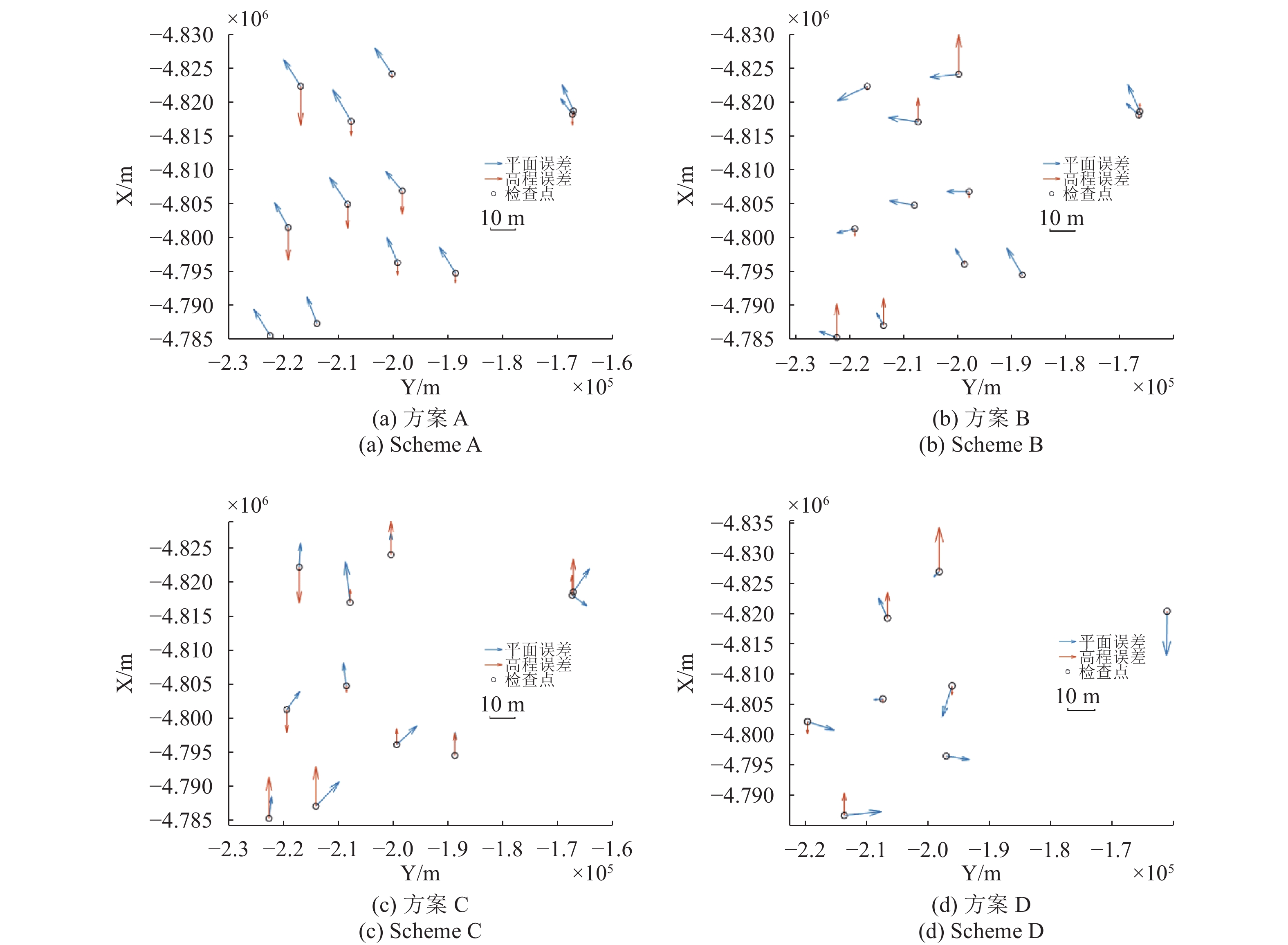
注意到图13(a)、图14(a)、图15(a)，3个地区无控情况下的定位结果中均存在明显的系统误差，有控制点参与后，系统误差得到了削弱。对比3个表中的试验A与试验B，整体来看，3个试验区域在仅用辅助控制点的情况下，几何定位精度都取得了不错的结果。对于法国Sainte-Maxime地区和河南登封地区，使用GE点对改善定位结果的效果十分明显。而对于澳大利亚Hobart地区，由于IKONOS影像质量高，直接定位已经得到了很好的定位精度，此时精度受限的GE点参与平差后虽高程精度提升，但平面精度反而下降，整体精度略有提高。


图 14 法国Sainte-Maxime地区几何定位残差分布
Fig. 14 Error distribution of positioning result in Sainte-Maxime, France

对比表5、表6、表7中试验C、E与试验D、F，3个试验区域在布设稀少实测控制点的情况下，基准影像数据参与平差后整体的定位精度得到了提升。对于法国Sainte-Maxime地区和河南登封地区，平面精度没有明显的变化，高程精度提升效果较明显，相比无控定位时定位精度的大幅度提高，随着布设的实测控制点增多，精度较低的辅助控制点对定位精度的影响逐渐减弱；对于澳大利亚Hobart地区，布设一个实测控制点时，GE点参与平差后同样是平面精度下降、高程精度提高，整体精度略有提高；而布设4个实测控制点时，实测控制点对定位已经起到了很好的控制作用，在此基础上以低权值参与平差的GE点使得平面精度和高程精度小幅度得到了改善。

由上述可知，在无实测控制点和布设稀少实测控制点情况下，本文提出的基准影像数据辅助定位可在不同程度改善定位结果。尤其在卫星影像质量较低的无实测控制点定位中效果明显。

5 结　论

为实现在实测控制点不足且不额外增加实测控制条件的情况下提高线阵遥感影像几何定位精度，本文提出利用基准影像数据及已有高程数据辅助定位方法。通过对国内外3个试验区域的试验，证明本文方法可以在缺少实测控制条件的情况下提高遥感影像几何定位精度，尤其对于无实测控制点时效果明显，验证了方法的可行性和有效性。在试验中也发现了一些待改进的问题，如对于影像质量较好、直接定位精度较高的遥感影像，自身精度较低的辅助控制点参与平差后对于定位精度的提升有限。另外，如何在定位过程中发现、剔除粗差也是亟待研究的问题。

参考文献(References)

  • Chen X W, Zhang B M, Zhang T G, Guo H T and Cen M Y. 2016. Public DEM-assisted positioning method for Chinese satellite imagery without ground control points. Acta Geodaetica et Cartographica Sinica, 45 (11): 1361–1370. [DOI: 10.11947/j.AGCS.2016.20160317] ( 陈小卫, 张保明, 张同刚, 郭海涛, 岑敏仪. 2016. 公开DEM辅助无地面控制点国产卫星影像定位方法. 测绘学报, 45 (11): 1361–1370. [DOI: 10.11947/j.AGCS.2016.20160317] )
  • Fan C and Wang X P. 2014. Geolocation of optical satellite image based on TerraSAR-X image. Geomatics and Spatial Information Technology, 37 (8): 1–4. [DOI: 10.1137/0717073] ( 范冲, 王雪平. 2014. 基于TerraSAR-X影像的光学遥感影像地理定位研究综述. 测绘与空间地理信息, 37 (8): 1–4. [DOI: 10.1137/0717073] )
  • Goncalves J A. 2008. Orientation and DEM extraction from ALOS-PRISM images using the SRTM-DEM as ground control//The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Beijing: ISPRS: 1177-1182
  • Grodecki J and Dial G. 2003. Block adjustment of high-resolution satellite images described by rational polynomials. Photogrammetric Engineering and Remote Sensing, 69(1): 59-68 [DOI: 10.14318/PERS.69.159]
  • Guo W Y, Yu A Z, Liu H Y, Jiang T and Wei X P. 2017. Regularized total least squares used in remote sensing image positioning of optical line array. Optics and Precision Engineering, 25 (1): 236–244. [DOI: 10.3788/OPE.20172501.0236] ( 郭文月, 余岸竹, 刘海砚, 姜挺, 魏祥坡. 2017. 正则化总体最小二乘用于光学线阵遥感影像定位. 光学精密工程, 25 (1): 236–244. [DOI: 10.3788/OPE.20172501.0236] )
  • Liu C B, Fan D Z, Lei R and Dai H T. 2016. RPC model block adjustment with SRTM. Geomatics and Spatial Information Technology, 39 (1): 9–12. [DOI: 10.3969/j.issn.1672-5867.2016.01.003] ( 刘楚斌, 范大昭, 雷蓉, 戴海涛. 2016. SRTM辅助下的RPC模型区域网平差. 测绘与空间地理信息, 39 (1): 9–12. [DOI: 10.3969/j.issn.1672-5867.2016.01.003] )
  • Liu C B, Zhang Y S, Fan D Z and Lei R. 2015. Research on the geometrical positioning evaluation of ZY-3 satellite at abroad. Bulletin of Surveying and Mapping, (9): 6-8, 27 (刘楚斌, 张永生, 范大昭, 雷蓉. 2015. 资源三号卫星境外高精度定位方法研究. 测绘通报, (9): 6-8, 27 [DOI: 10.13474/j.cnki.11-2246.2015.0266])
  • Liu J, Zhang Y S and Wang D H. 2006. Precise positioning of high spatial resolution satellite images based on RPC models. Acta Geodaetica et Cartographica Sinica, 35 (1): 30–34. [DOI: 10.3321/j.issn:1001-1595.2006.01.007] ( 刘军, 张永生, 王冬红. 2006. 基于RPC模型的高分辨率卫星影像精确定位. 测绘学报, 35 (1): 30–34. [DOI: 10.3321/j.issn:1001-1595.2006.01.007] )
  • Liu J H, Jiang T, Li Y J and Li H P. 2014. Verification and analysis of positioning accuracy of RPC model of TH-1 three-line imagery. Engineering of Surveying and Mapping, 23 (11): 25–29. [DOI: 10.3969/j.issn.1006-7949.2014.11.006] ( 刘建辉, 姜挺, 李延杰, 李厚朴. 2014. 天绘一号卫星三线阵影像RPC模型定位精度验证与分析. 测绘工程, 23 (11): 25–29. [DOI: 10.3969/j.issn.1006-7949.2014.11.006] )
  • Lv Z P and Qiao S B. 2010. Foundation of Geodesy. Beijing: Survey and Mapping Press (吕志平, 乔书波. 2010. 大地测量学基础. 北京: 测绘出版社)
  • Mohammed N Z, Ghazi A and Mustaf H E. 2013. Positional accuracy testing of Google earth. International Journal of Multidisciplinary Science and Engineering, 4 (6): 6–9.
  • Tong X D. 2016. Development of China high-resolution earth observation system. Journal of Remote Sensing, 20 (5): 775–780. [DOI: 10.11834/jrs.20166302] ( 童旭东. 2016. 中国高分辨率对地观测系统重大专项建设进展. 遥感学报, 20 (5): 775–780. [DOI: 10.11834/jrs.20166302] )
  • Wang T, Zhang Y, Zhang Y S and Pan S L. 2013. Construction and validation of rigorous imaging model for high-resolution remote sensing satellites. Journal of Remote Sensing, 17 (5): 1087–1102. [DOI: 10.11834/jrs.20132224] ( 王涛, 张艳, 张永生, 潘申林. 2013. 高分辨率遥感卫星传感器严格成像模型的建立及验证. 遥感学报, 17 (5): 1087–1102. [DOI: 10.11834/jrs.20132224] )
  • Wang T Y, Zhang G, Li D R, Jiang W S, Tang X M and Liu X L. 2014. Comparison between plane and stereo block adjustment for ZY-3 satellite images. Acta Geodaetica et Cartographica Sinica, 43 (4): 389–395, 403. [DOI: 10.13485/j.cnki.11-2089.2014.0058] ( 汪韬阳, 张过, 李德仁, 江万寿, 唐新明, 刘学林. 2014. 资源三号测绘卫星影像平面和立体区域网平差比较. 测绘学报, 43 (4): 389–395, 403. [DOI: 10.13485/j.cnki.11-2089.2014.0058] )
  • Zhang H, Zhang G, Jiang Y H and Wang T Y. 2016. A SRTM-DEM-controlled ortho-rectification method for optical satellite remote sensing stereo images. Acta Geodaetica et Cartographica Sinica, 45 (3): 326–331, 378. ( 张浩, 张过, 蒋永华, 汪韬阳. 2016. 以SRTM-DEM为控制的光学卫星遥感立体影像正射纠正. 测绘学报, 45 (3): 326–331, 378. )
  • Zhang Y S, Liu J and Gong D C. 2004. Application of High-Resolution Remote Sensing Satellites. Beijing: Science Press (张永生, 刘军, 巩丹超. 2004. 高分辨率遥感卫星应用. 北京: 科学出版社)
  • Zhang Z X and Zhang Y J. 2012. Building geospatial information of China with domestic satellite imagery. Journal of Geomatics, 37 (5): 7–9. [DOI: 10.14188/j.2095-6045.2012.05.008] ( 张祖勋, 张永军. 2012. 利用国产卫星影像构建我国地理空间信息. 测绘地理信息, 37 (5): 7–9. [DOI: 10.14188/j.2095-6045.2012.05.008] )
  • Zhou P, Tang X M, Cao N, Wang X, Li G Y and Zhang H. 2016. SRTM-aided stereo image block adjustment without ground control points. Acta Geodaetica et Cartographica Sinica, 45 (11): 1318–1327. [DOI: 10.11947/j.AGCS.2016.20160219] ( 周平, 唐新民, 曹宁, 王霞, 李国元, 张恒. 2016. SRTM约束的无地面控制立体影像区域网平差. 测绘学报, 45 (11): 1318–1327. [DOI: 10.11947/j.AGCS.2016.20160219] )
数据专区
  • 目录 目录
  • 文章信息 文章信息
  • 引用格式 引用格式
  • 地图 地图
  • 评论 评论
  • 图 图
  • 表 表
  • 二维码 二维码
  • 参考文献 参考文献
  • 多媒体 多媒体