Abstract

With the development of spectral imaging technique and its data processing technology, anomaly detection using hyperspectral data has become a popular topic. Anomaly detection refers to the search for sparse pixels of unknown spectral signals in hyperspectral imagery. Given that the anomaly detection is unsupervised, providing a priori information is necessary. Thus, anomaly detection has a strong practicality. Considering the lack of spatial correlation and low normal distribution adaptation, the traditional RX algorithm has an inaccurate background estimation. Thus, this algorithm is unsuitable for detecting hyperspectral data. In this study, a saliency weighted RX algorithm is proposed on the basis of the local neighborhood spectra of an image. When the human eye observes an image, the first object that is viewed is frequently the most significant. The significance of the saliency detection algorithm is to identify this goal. The saliency map is a 2D image of the same size as the original image to represent the significance of the corresponding pixel in the original image. In this algorithm, the image background modeling based on probability density is improved by introducing a saliency analysis method. Afterward, the spectral saliency map is established, and the mean vector and covariance matrix of the RX algorithm are redefined. Saliency weighted RX algorithm provides different weights to optimize the background estimation. Anomaly detection experiments are conducted using synthetic and real hyperspectral data. Synthetic data experimental results show that, for each target, the number of anomalies detected using the saliency weighted RX algorithm is more than that of the traditional algorithms, and the saliency weighted RX algorithm can detect anomalies with abundance below 0.1. By contrast, traditional algorithms cannot detect these anomalies. Moreover, the false alarm pixels of the traditional algorithms are distributed in various positions, whereas the saliency weighted RX algorithm concentrates on an area called a false alarm area. This area can be removed effectively by morphological filtering. Real data experimental results show that the saliency weighted RX algorithm corresponds to the largest AUC value and has the optimal detection results. The traditional RX algorithm assumes that the background model follows a multivariate Gaussian distribution and does not perform well in hyperspectral imagery. The method of saliency analysis in the field of computer vision can be effectively analyzed in the spatial domain. This phenomenon compensates for the shortcomings of the RX algorithm to ignore spatial correlation, thus detecting the anomalies synchronized in the spatial and spectral domains. The saliency weighted RX algorithm uses a saliency analysis method to provide the background and anomaly pixels with a different weight, thereby improving the adaptability of the background model. Through the experiment of synthetic and real data, the saliency weighted algorithm can improve the detection probability while reducing the false alarm rate in comparison with the traditional RX algorithm and has a certain anti-noise ability.

Key words

anomaly detection, saliency, RX algorithm, hyperspectral image processing

1 引　言

高光谱图像是由成像光谱仪获得的具有二维空间信息与一维光谱信息的一种图像数据立方体。高光谱图像能同时提供目标的辐射、几何、光谱信息，且具有图像光谱分辨率高、图谱合一、光谱通道多的特点，能在目标检测与识别上发挥巨大的优势(童庆禧等，2006)。传统的遥感图像目标检测需要很高的空间分辨率，当空间分辨率不足时，目标很难被检测到。高光谱图像目标检测就是利用光谱信息进行识别，不需要很高的空间分辨率。光谱特征能够反应目标本质属性，从而利用光谱特征进行目标探测更加可靠(高昆等，2015；童庆禧等，2016)。

高光谱图像目标检测主要分为两种：有先验信息的目标特征匹配识别与无先验信息的异常目标检测。异常目标检测指的是在高光谱图像中搜索未知光谱信号的稀疏像素(赵春晖等，2016)。异常点的定义没有统一标准，通常认为异常点是光谱特征与周围像素的光谱特征有明显区别且以低概率出现的像素点(Chang 等，2015)。由于异常点检测是非监督的，不需要提供先验信息，因此具有很强的实用性。

最早的异常点检测算法是由Reed和Yu提出的RX算法(Reed和Yu，1990；Yu 等，1993)。RX算法的假设条件是背景服从多元高斯分布，是在一个简化的条件下构造的似然比算子。RX算法有两点不足：(1)背景信息往往很复杂，服从多元高斯分布的这种假设不能完全而真实的描述实际场景的情况；(2)当用均值向量和协方差矩阵作为背景特征来估计背景信息时，RX算法会带入异常点和噪声的信息，造成背景估计的不准确。MRX算法和NRX算法作为RX算法的两种简单变体，对RX算子做了改进，对某些特殊情况有不错的检测效果(Chang和Chiang，2002)。UTD-RXD算法与RX算法类似，这种算法认为不应该给探测器中添加先验信息，它使用单位向量作为输入信号(Ashton和Schaum，1998)。LRX算法采用局部信息估计RX算法中的均值向量，能提高背景模型估计的准确性(Guo 等，2014；Liu和Chang，2013；Molero 等，2013)。Weighted-RX算法通过给不同的背景样本赋予不同的权重，减少了异常点信号和噪声信号对背景估计的影响，让背景正态适应度更高，提高了算法性能(Guo 等，2014)。

RX，MRX，NRX，UTD-RX这些算法的背景估计都不够精确，正态适应度低。LRX算法虽然通过局部采样提高了背景估计的准确性，但仍无法避免RX算法的缺点。Weighted-RX算法虽然使用了基于概率密度的权重对背景进行建模，增加了背景分布的正态适应度，但这个权重不能最好的区分异常点与背景信息，且同时突出了噪声，使得误检率变高。

为了解决上述问题，本文引入图像显著性分析的方法，提出了一种基于显著性图的Saliency Weighted-RX算法。人眼在观察一幅图像时，第一眼看到的目标往往是最显著的，显著性检测算法的意义就是识别这一目标。最早对显著性图的定义来自Itti等(1998)，他们提出了一个基于神经网络结构的视觉关注系统，用亮度、彩色和方向特征来定义显著性图。传统显著性检测的目的是提取出图像、视频中最吸引人注意的显著部分，并利用一张显著性图(灰度图)来表示各个像素点的显著程度(李君浩和刘志，2015)。显著性图是一幅尺寸与原始图像相同的二维图像，用来表示原始图像中对应像素点的显著性。Saliency Weighted-RX算法通过建立光谱显著性权重图，能在更好的区分异常点和背景像素的同时有效避免将噪声信号检测为异常点信号，从而提高了检测效果。

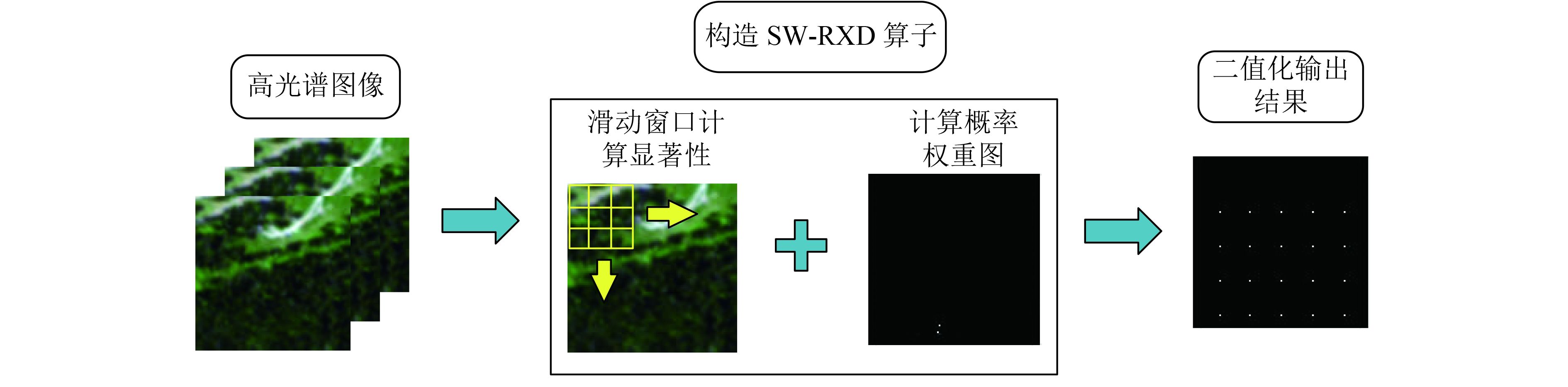
首先对待处理的高光谱数据进行预处理，以待检测像元为中心设置局部处理窗口，计算显著性图和光谱显著性权重，最后重新定义RX算法中的均值向量和协方差矩阵，计算新的SW-RXD异常点检测算子(图1)。利用本文提出的SW-RX算法和RX，MRX，LRX，UTD-RX，W-RX这5种对比算法分别对合成的高光谱数据和真实高光谱数据进行实验，并对比检测结果。

图 1 SW-RX算法流程图

Fig. 1 Flowchart of SW-RX algorithm

2 异常点检测算法理论

2.1 传统的RX算法

RX算法是由Reed和Yu(1990)提出的一种高光谱异常点检测算法。该算法可认为是广义似然比检测(GLRT)衍生出的一种具有恒虚警率(CFAR)的异常点探测器，通常被认为是高光谱异常点检测中的一个基准算法(Stellman 等，2000；张兵，2016)。

RX算法的异常检测算子如下

${\delta _{\rm{RXD}}}({{r}}) ={({{r}} - {{{\mu}} _{\rm{b}}})^{\rm{T}}}{{{C}}_{\rm{b}}}^{ - 1}({{r}} - {{{\mu}} _{\rm{b}}})$

(1)

式中，r是一个像素点的光谱曲线，μ_b是背景估计的均值，C_b是背景估计的协方差矩阵。

${{{\mu }}_{\rm{b}}} =\frac{1}{N}\sum\limits_{i =1}^N {{{{r}}_i}} $

(2)

${{{C}}_{\rm{b}}} =\frac{1}{N}\sum\limits_{i =1}^N {({{{r}}_i} - {{{\mu}} _{\rm{b}}}){{({{{r}}_i} - {{{\mu}} _{\rm{b}}})}^{\rm{T}}}} $

(3)

式中，N为像素点数。

2.2 显著性图的定义

显著性目标检测在图像处理和计算机视觉中有着广泛的应用，如图像压缩、分割、缩放等。通过引入基于视觉感知的图像显著性分析方法，本文对图像像素的概率密度权重进行了重新定义，使其具有区分不同目标的能力。在高光谱图像中，像素点之间的差异通常指像素点对应光谱的差异，当一个像素点的光谱信息与邻域像素点的光谱信息差异很大时，可以认为该像素点具有区域显著性。因此，本文选择图像局部邻域光谱的距离来定义显著性。

定义p_i，i∈(1，n)来表示局部窗口中任意一个像素的光谱曲线，其中n为像素点的个数。p_i=[p_i1，p_i2， $ \cdots $ ，p_iM]^T，为一个M行的列向量，M为这个高光谱数据的波段数。定p_j为局部窗口的中心像素点，p_j=[p_j1，p_j2， $ \cdots $ ，p_jM]^T。定义d_Spectrum(p_i，p_j)为光谱i和j之间的距离，当对于窗口中的所有i，d_Spectrum(p_i，p_j)都很大时，则局部窗口的中心像素点j是显著的。

在光谱距离表达方面，常用的光谱距离有绝对距离d_Abs、光谱角距离d_Ang、欧氏距离d_Euc，其计算公式分别如下

${d_{\rm{Abs}}}({{{p}}_i}, {{{p}}_j}) =\sum\limits_{k =1}^M {\left| {{p_{ik}} - {p_{jk}}} \right|} $

(4)

${d_{{\rm{Ang}}}}({{{p}}_i}, {{{p}}_j}) =\arccos \left({\displaystyle\frac{{\displaystyle\sum\limits_{k =1}^M {{p_{ik}}{p_{jk}}} }}{{\sqrt {\displaystyle\sum\limits_{k =1}^M {p_{ik}^2} \displaystyle\sum\limits_{k =1}^M {p_{jk}^2} } }}} \right)$

(5)

${d_{{\rm{Euc}}}}({{{p}}_i}, {{{p}}_j}) =\sqrt {\sum\limits_{k =1}^M {{{({p_{ik}} - {p_{jk}})}^2}} } $

(6)

定义d_Position(p_i，p_j)为局部窗口任意一像素点i和局部窗口的中心像素点j在窗口中位置信息之间的欧氏距离。显著性d_Saliency (p_i，p_j)定义如下

${d_{{\rm{Saliency}}}}({{p}_i}, {{p}_j}) =\frac{{{d_{{\rm{Spectrum}}}}({{{p}}_i}, {{{p}}_j})}}{{1 + c \cdot {d_{{\rm{Position}}}}({{{p}}_i}, {{{p}}_j})}}$

(7)

式中，c为尺度参数，用来调整显著性中光谱距离和位置距离的比重。分母中的1是为了避免分母为零(Goferman 等，2012)。

由式(7)可知，当分子d_Spectrum(p_i，p_j)很大而分母d_Position(p_i，p_j)很小时，表示局部窗口的中心像素点j和像素点i的空间距离很近但光谱差异很大，此时通过式(7)对应计算出的d_Saliency (p_i，p_j)很大，由此认为局部窗口的中心像素点j相对于局部窗口任意一像素点i的显著性很强。因此，随着d_Saliency (p_i，p_j)越大，局部窗口的中心像素点j相对于局部窗口任意一像素点i的显著性逐渐增强。当局部窗口的中心像素点j相对于局部窗口所有的像素点i的显著性都很强时，局部窗口的中心像素点j在这个窗口中为异常点。相反，当分子d_Spectrum(p_i，p_j)很小而分母d_Position(p_i，p_j)很大时，表示局部窗口中心像素点j和像素点i虽然空间距离很远，但其光谱差异很小，由此说明此时局部窗口的中心像素点j与周围领域像素点相似，则像素点j更可能为背景像素，对应的显著性很弱，计算出的d_Saliency (p_i，p_j)也很小。

通过计算局部窗口的中心像素点j相对于局部窗口所有像素点i的显著性来定义图像的显著性图。定义d_{Saliency_eva}为局部窗口的中心像素点j相对于局部窗口所有像素点i显著性的平均值，d_{Saliency_eva}的计算方法如式(8)

${d_{{\rm{Saliency\_eva}}}} =\displaystyle\frac{{\displaystyle\sum\limits_{i =1}^N {{d_{{\rm{Saliency}}}}} }}{{Num - 1}}$

(8)

式中，Num为窗口中显著性取值非零的像素点的个数，这样能保证窗口边界补0时显著性d_{Saliency_eva}的准确性。分母为Num–1是考虑到局部窗口所有像素点i也包括局部窗口的中心像素点j，即d_Saliency (p_i，p_j)=0，所以减去一个像素点样本。

通过滑动窗口遍历整幅图像，计算出各窗口中心像元的d_{Saliency_eva}，组成这幅图像的显著性图S。

2.3 加权的RX算法

为了保留背景信号并且减少非背景信号，Guo等(2014)中提到一种加权的RX算法，即W-RX算法，该算法通过给不同的背景像素赋予不同的权重来减少异常点对背景模型估计的影响、提升对协方差矩阵的估计。W-RX算法给与背景像素相似的像素点一个更高的权重，与背景像素相差很远的像素点一个很低的权重。权重的计算过程如式(9)

${{p}}(r|{H_0}) =\frac{1}{{{(2{\text{π}})}^{M/2}}{{{C}}_{\rm{b}}^{1/2}}}{e^{ - \displaystyle\frac{1}{2}{{({{r}} - {{{\mu}} _{\rm{b}}})}^{\rm{T}}}{{{C}}_{\rm{b}}}^{ - 1}({{r}} - {{{\mu}} _{\rm{b}}})}}$

(9)

式中，M表示图像的波段数。p(r|H₀)是一个被探测到的像素点为背景像素的概率。用式(10)标准化p(r|H₀)

$P({r_k}|{H_0}) =p({r_k}|{H_0})/\displaystyle\sum\limits_{i =1}^N {p({r_i}|{H_0})} $

(10)

式中，N是像素点数，k是当前计算的像素点，k=1，2， $ \cdots $ ，N。P(r_k|H₀)是每个像素标准化之后对应的权重。

3 基于显著性分析的加权RX异常点检测算法(SW-RX)

3.1 算法原理

SW-RX算法用显著性图中的显著特性定义一个权值，这个权值对背景像素和异常点是不同的，从而在背景模型估计时减少异常点和噪声的影响，使背景模型的正态适应性更好。

基于显著性分析的权重P_SW(r_k|H₀)计算过程如式(11)

${{{P}}_{\rm{SW}}}({r_k}|{H_0}) =\frac{{P({r_k}|{H_0})}}{{\exp (1/{d_k})}}$

(11)

式中，d_k为像素点k对应的显著性d_{Saliency_eva}。由式(11)对基于概率的权重和基于显著性图的权重进行融合，exp(1/d_k)是基于显著性d_{Saliency_eva}计算出的光谱显著性权重，光谱显著性权重扩大了显著性d_{Saliency_eva}的值域，使各像素点显著性的区分度更大。用光谱显著性权重优化基于概率的权重，使在新的权重P_SW(r_k|H₀)作用下的背景模型正态适应度更好。

新的均值向量μ_SW和协方差矩阵C_SW定义如式(12)、(13)

${{{\mu}} _{\rm{SW}}} =\sum\limits_{i =1}^N {{{{P}}_{\rm{SW}}}({{{r}}_i}|{H_0}){{{r}}_i}} $

(12)

${{{C}}_{\rm{SW}}} =\sum\limits_{i =1}^N {{{{P}}_{\rm{SW}}}({{{r}}_i}|{H_0})({{{r}}_i} - {{{\mu}} _{\rm{SW}}}){{({{{r}}_i} - {{{\mu}} _{\rm{SW}}})}^{\rm{T}}}} $

(13)

SW-RX检测算子定义如式(14)

${\delta _{\rm{SW - RXD}}}({{r}}) ={({{r}} - {{{\mu}} _{\rm{SW}}})^{\rm{T}}}{{{C}}_{\rm{SW}}}^{ - 1}({{r}} - {{{\mu}} _{\rm{SW}}})$

(14)

3.2 算法伪代码及复杂度分析

SW-RX算法的伪代码如下

输入：

X={row，col，spec}，X为高光谱图像，row、col为图像的行和列数，spec为波段数

窗口大小 (2×w+1)×(2×w+1)

参数c值

显著性图获取过程：

for i=1，2， $ \cdots $ ，row×col

进行图像扩展，在原始图像上、下、左、右4个边缘各补上 $w$ 行的0，新的高光谱图像X_expand={row+2w，col+2w，spec}

取一个子窗口Win={2×w+1，2×w+1，spec}

根据式(7)计算第i个窗口中心像素点的显著性

根据式(8)计算显著性的平均值

End

得到显著性图S={row，col}

显著性权重计算过程：

根据式(9)、(10)计算基于概率的权重P(r_k|H₀)

根据式(11)计算融合的权重P_SW(r_k|H₀)

SW-RX检测算子计算过程：

根据式(12)、(13)计算新的均值向量μ_SW和协方差矩阵C_SW

根据式(14)计算SW-RX检测算子

算法的复杂度主要取决于所包含乘法项的个数(Zhao 等，2016)。为了更加直观的分析SW-RX算法的复杂度，分析执行一次像元检测SW-RX算法中两项计算成分μ_SW和C_SW的复杂度。假设P_SW(r_k|H₀)的复杂度为O(N)，根据式(12)、(13)，μ_SW的复杂度为O(MN)，C_SW的复杂度为O(M³N³)。

4 实验结果与分析

实验采用一组模拟合成的高光谱数据和两组真实的高光谱数据进行仿真，来评估RX、MRX、UTD-RX、LRX、W-RX和SW-RX共6种算法的检测性能。

为了能够量化的评价算法的优劣，通常使用接收机操作特征曲线(ROC)来评价一个目标探测算法的性能。ROC曲线建立了检测过程中取不同的阈值时，检测概率(PD)和虚警率(FAR)的一一对应关系。

$PD =\frac{{{N_{\rm{d}}}}}{{{N_{\rm{t}}}}}$

(15)

$FAR =\frac{{{N_{\rm{f}}}}}{{{N_{\rm{b}}}}}$

(16)

式中，PD为检测概率，其中N_d为检测到的目标像素个数，N_t为图像中所有目标像素个数；FAR为虚警率，其中N_f为探测时虚警目标像素个数，N_b为图像中所有背景像素个数。ROC曲线分别以检测概率PD和虚警率 $FAR$ 为纵轴和横轴，曲线下方区域面积(AUC)越大表示算法检测性能越好。

4.1 实验数据介绍

4.1.1 合成高光谱数据介绍

近年来国际上通用一种模拟合成高光谱数据进行试验仿真的方法。利用目标植入的方法来合成一组适合于做异常点检测的高光谱数据，能可控的验证算法的优劣(Yuan 等，2015)。

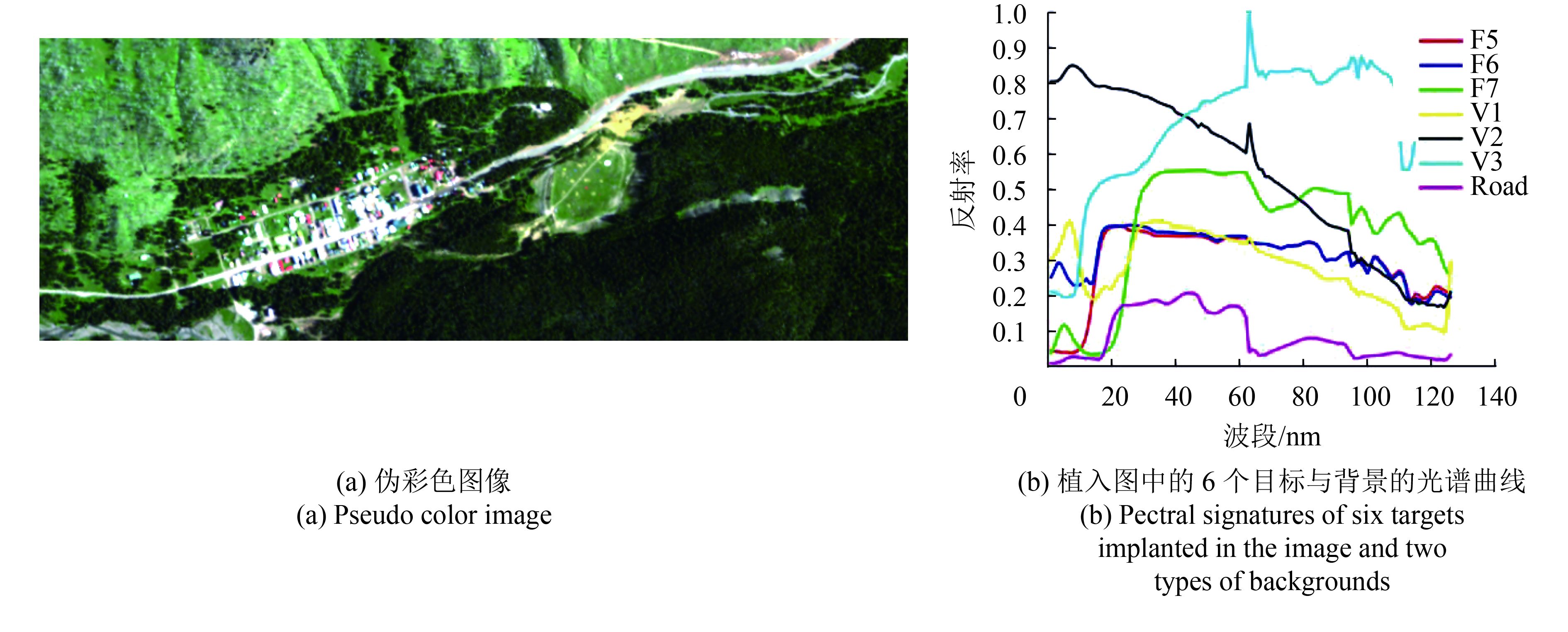
实验采用Hymap Cook City of Montana高光谱数据，每幅图有280×800个像素，126个波段，空间分辨率为3 m。待合成的异常点是从RIT(Rochester Institute of Technology)所提供的target detection blind-test scenes中得到的6种不同目标的光谱曲线，分别为V1(1993年雪佛兰汽车)，V2(1997年丰田汽车)，V3(1985年斯巴鲁汽车)，F5(褐色尼龙布)，F6(灰色尼龙布)，F7(绿色棉布)，如图2所示。

图 2 Hymap 蒙大拿库克城高光谱图像

Fig. 2 Hymap hyperspectral image over Cook City. Montana

假设需要得到的包含异常点的高光谱数据为a，背景为b，待合成目标为t，k是一个可变的丰度值，通过让目标t和背景b以不同的丰度值k来混合，构成实验需要的合成数据(Khazai 等，2011；Xu 等，2016)。植入异常光谱的线性混合模型如下

$a =k \cdot t + (1 - k) \cdot b$

(17)

由式(13)可以看出，目标a为亚像元，并且随着丰度值k比例的减小，a的光谱与背景的相似度越大。本实验中，选择一块背景为植被，空间分辨率为100×100像素的区域植入异常目标。分别植入4行5列共20个目标，每个目标的丰度值k从左至右、从上至下是一个差值为0.02的等差数列，即k的最大值为左上角的0.4，最小值为右下角的0.02。

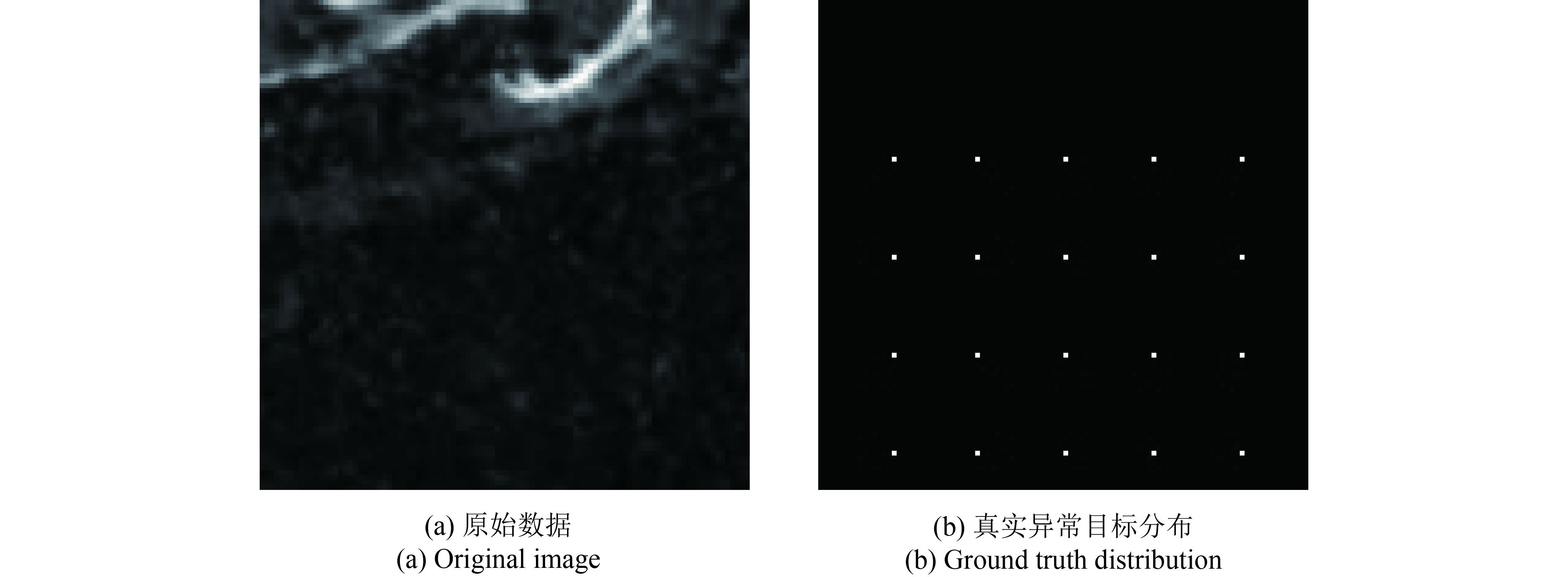
原始数据和其对应的真实异常目标分布如图3所示。

图 3 模拟高光谱数据

Fig. 3 Synthetic hyperspectral data

4.1.2 真实高光谱数据介绍

实验采用的第一组真实高光谱数据是AVIRIS美国圣地亚哥机场高光谱数据中的一部分，去除水汽吸收和噪声较明显的谱段后剩下189个波段，选取图像空间分辨率为100 $ \times $ 100像素，其中包含38个异常目标(Zhao 等，2014)。原始图像及其真实目标分布如图4所示。

图 4 圣地亚哥高光谱数据

Fig. 4 Sandiego hyperspectral data

第2个真实高光谱数据是AVIRIS美国世贸中心高光谱数据中的一部分，选取图像空间分辨率为200 $ \times $ 200像素，共有224个波段。原始图像及其真实目标分布如图5所示。

图 5 世贸中心高光谱数据

Fig. 5 WTC hyperspectral data

4.2 SW-RX算法相关参数确定

4.2.1 光谱距离的选取

在第2节SW-RX算法的构成中，定义d_Spectrum(p_i，p_j)为某种光谱距离，实验选取绝对距离、光谱角距离、欧氏距离这3种常用的距离进行比较。实验目标为V1、V2、V3、F5、F6、F7这6个不同的异常目标，窗口大小为7×7，参数c取1到5。由于篇幅原因，不再列出每一种情况的ROC曲线，选用ROC曲线的曲线下方面积AUC来表示算法的优劣，AUC面积越大，算法效果越好(表1)。

表 1 SW-RX算法在不同距离下的实验结果
Table 1 The experimental results for different distances in SW-RX algorithm

下载CSV

目标	距离	C=1	C=2	C=3	C=4	C=5
V1	绝对距离	0.9677	0.9683	0.9689	0.9695	0.9703
	光谱角距离	0.9700	0.9697	0.9667	0.9441	0.9715
	欧氏距离	0.9759	0.9817	0.9861	0.9878	0.9870
V2	绝对距离	0.9728	0.9737	0.9741	0.9742	0.9743
	光谱角距离	0.9793	0.9733	0.9221	0.9071	0.8806
	欧氏距离	0.9794	0.9853	0.9836	0.9822	0.9801
V3	绝对距离	0.9812	0.9813	0.9814	0.9815	0.9817
	光谱角距离	0.9823	0.9763	0.9712	0.9682	0.9781
	欧氏距离	0.9850	0.9889	0.9891	0.9911	0.9893
F5	绝对距离	0.9917	0.9919	0.9921	0.9922	0.9926
	光谱角距离	0.9984	0.9979	0.9960	0.9948	0.9932
	欧氏距离	0.9973	0.9992	0.9995	0.9993	0.9992
F6	绝对距离	0.9804	0.9811	0.9818	0.9824	0.9834
	光谱角距离	0.9920	0.9912	0.9887	0.9857	0.9769
	欧氏距离	0.9923	0.9974	0.9978	0.9978	0.9978
F7	绝对距离	0.9759	0.9757	0.9758	0.9764	0.9773
	光谱角距离	0.9891	0.9910	0.9832	0.9883	0.9853
	欧氏距离	0.9863	0.9910	0.9890	0.9886	0.9891

观察表1的每一列，93%的样本在SW-RX算法选择欧氏距离时算法的AUC值最大，即检测效果最好；仅有7%的样本在选择光谱角距离时检测效果最好。观察表1的每一行，不同的c值会对算法的AUC面积产生细微的影响。实验证明欧氏距离为SW-RX算法中相对最优的光谱距离。

4.2.2 窗口大小的选取

实验选取3×3、5×5、7×7、9×9这4种窗口进行比较。实验目标为V1、V2、V3、F5、F6、F7这6个不同的异常目标，光谱距离选择欧氏距离，参数c取1到30。由于篇幅原因，对于一个目标的一种窗口，给出的AUC值为c取1到30时总共30个AUC面积的平均值(表2)。

表 2 SW-RX算法在不同窗口大小下的实验结果
Table 2 The experimental results for different window size in SW-RX algorithm

下载CSV

目标	窗口
目标	3 $ \times $ 3	5 $ \times $ 5	7 $ \times $ 7	9 $ \times $ 9
V1	0.9836	0.9885	0.9853	0.8634
V2	0.9840	0.9874	0.9856	0.9540
V3	0.9436	0.9914	0.9646	0.9476
F5	0.9986	0.9989	0.9680	0.9867
F6	0.9957	0.9984	0.9979	0.9905
F7	0.9950	0.9941	0.9459	0.8921

由表2可知，对于不同的6种异常目标，有5种目标在SW-RX算法中的局部窗口取5×5的情况下AUC值最大，即算法检测效果最好；仅有1种目标在窗口取3×3的情况下检测效果最好。实验证明5×5的窗口为SW-RX算法中局部窗口大小的最优选择

4.2.3 参数c值的选取

实验选取参数c的大小为1到30。实验目标为V1、V2、V3、F5、F6、F7这6个不同的异常目标，光谱距离为欧氏距离，局部窗口大小为5×5(图6)。

图 6 SW-RX算法在不同参数c取值情况下的实验结果

Fig. 6 The experimental results for different c values in SW-RX algorithm.

图6中红色曲线mean代表的是6种异常目标的平均值，观察红色的曲线可以看到c=17时为极大值点，即c=17时SW-RX算法对于6种异常目标的平均AUC值最大，检测效果最好。实验证明c=17为SW-RX算法中c值的最优选择。

4.3 合成高光谱数据实验结果

实验选取目标为V1、V2、V3、F5、F6、F7这6个不同的异常目标，SW-RX算法的光谱距离为欧氏距离，窗局部口大小为5×5，参数c的取值为17。图8为SW-RX算法和另外5种对比算法选取阈值为0.9980并二值化分割后的实验结果，阈值取0.9980是因为总共10000个像素中有20个位异常点像素(图7)。

图 7 对于植入目标为V1，V2，V3，F5，F6，F7的模拟数据不同算法的实验结果

Fig. 7 Detection result provided by different algorithms on the synthetic data with implanted targets V1, V2, V3, F5, F6, F7

图 8 对于植入目标为V1，V2，V3，F5，F6，F7的模拟数据不同算法的ROC曲线

Fig. 8 ROC curves provided by different algorithms on the synthetic data with implanted targets V1, V2, V3, F5, F6, F7

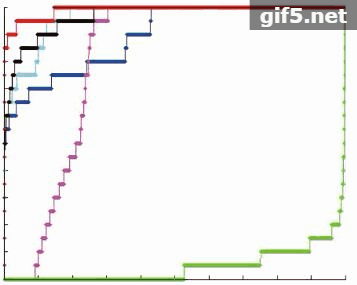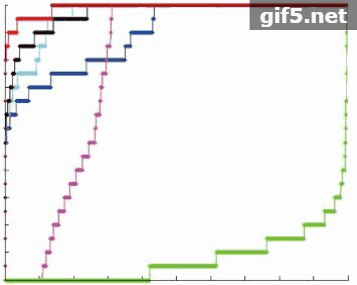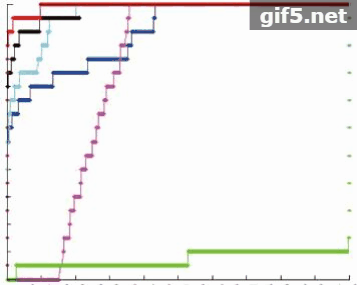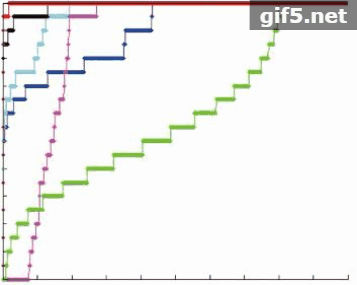
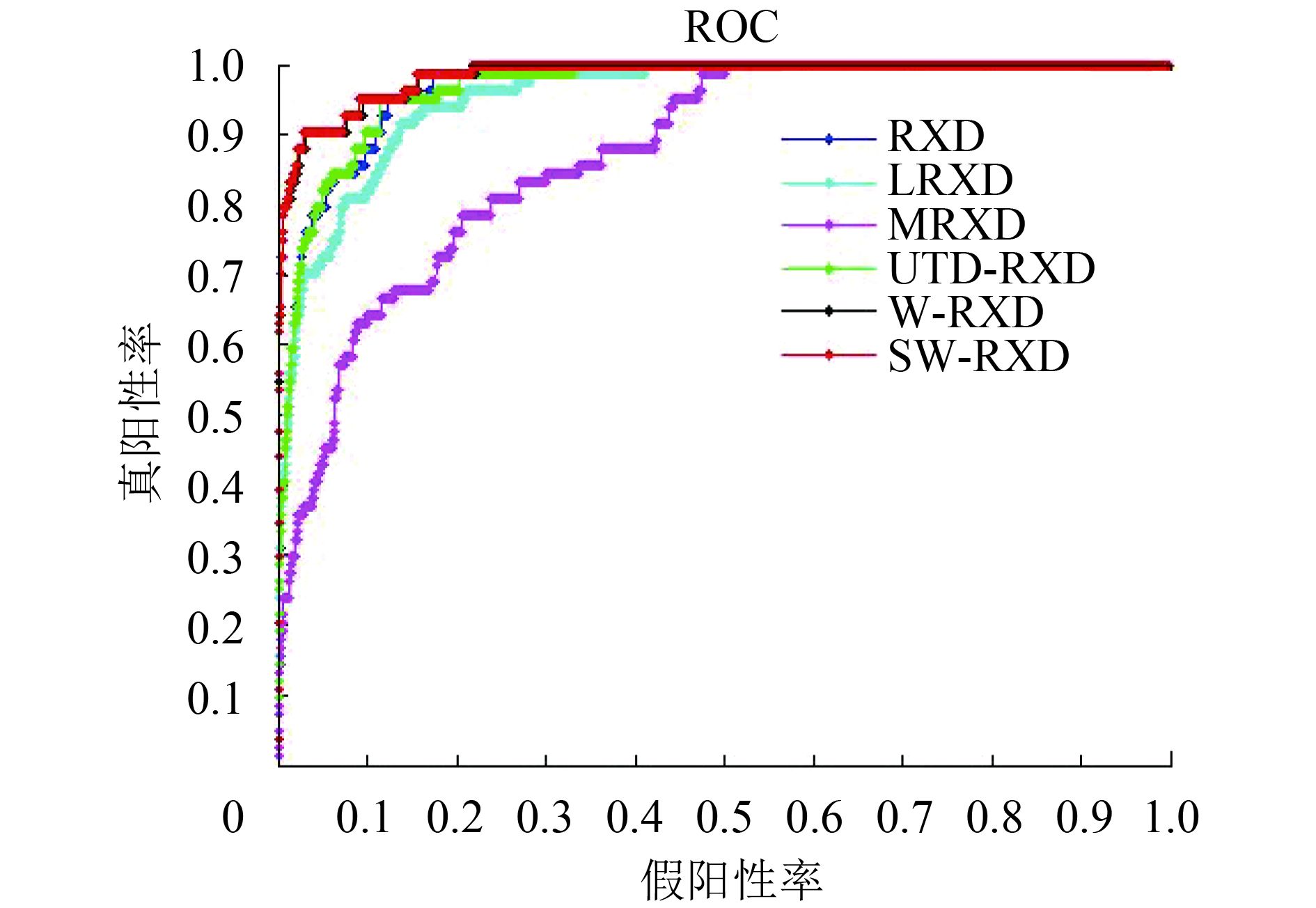
图7显示了SW-RX算法和5种对比算法对于不同的6个目标在同一实验条件下的异常检测阈值分割结果图。对于每一个目标，SW-RX算法检测到的异常点个数都要比W-RX算法多3—5个，比另外4种对比算法多5个以上。且SW-RX算法能探测到丰度值为0.1以下的异常点，其他5种对比算法均不能探测到。同时可以观察到传统算法的误检点分散分布在不同的位置，而SW-RX算法的误检点集中在某一个区域，可以称其为一个误检区域，这种误检区域相比误检点可以更好的用形态学滤波的方法消除。

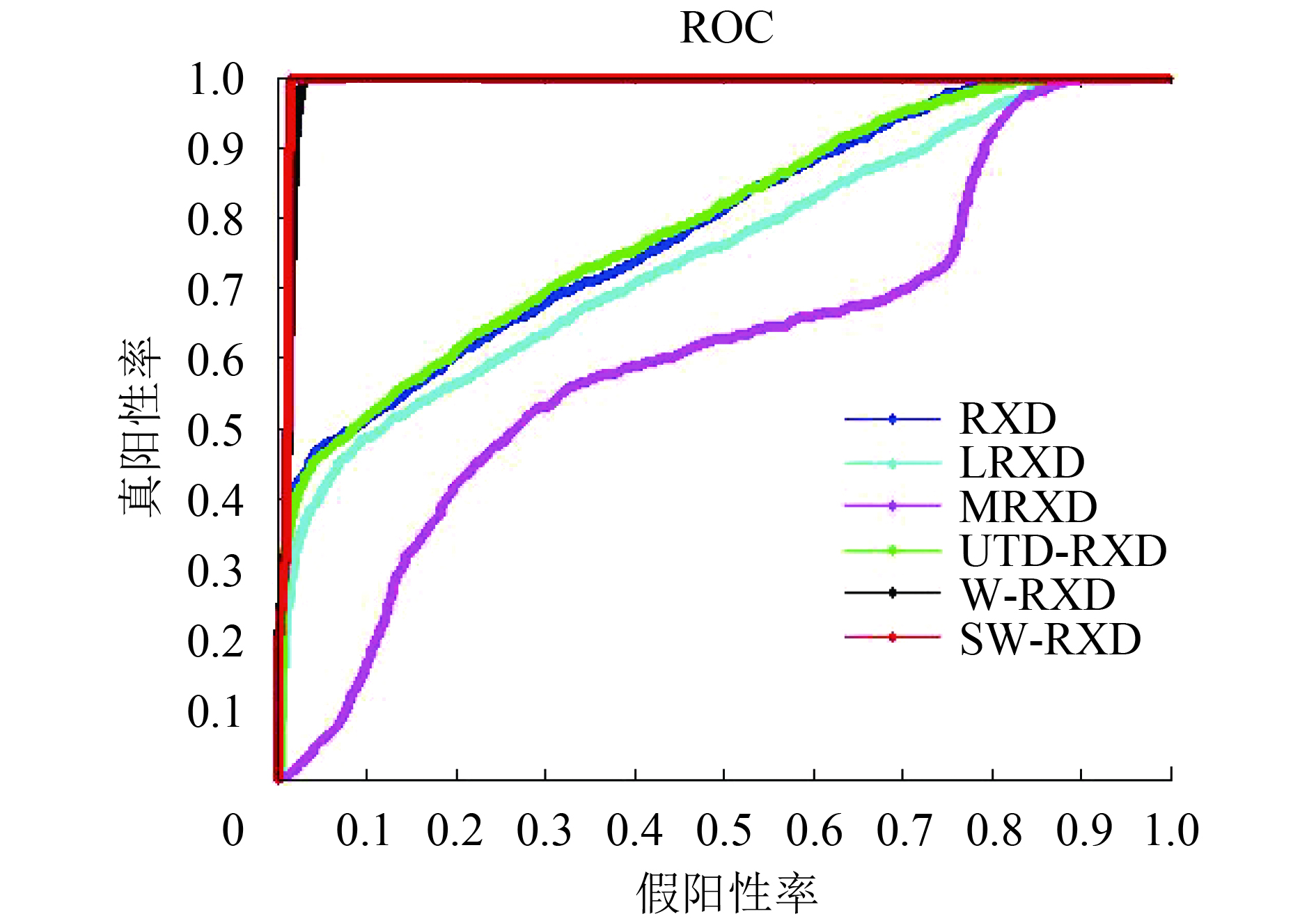
图8为6个不同的目标实验结果对应的ROC曲线。

表3为SW-RX算法和5种对比算法对于6个不同的目标实验结果ROC曲线对应的曲线下方区域的面积AUC值。

表 3 模拟高光谱数据实验结果的曲线下方面积
Table 3 AUC for the detection results on synthetic hyperspectral data

下载CSV

目标	算法	AUC	算法	AUC	算法	AUC
V1	RXD	0.8954	MRXD	0.8038	W-RXD	0.9669
	LRXD	0.9642	UTD-RXD	0.0468	SW-RXD	0.9902
V2	RXD	0.8957	MRXD	0.7700	W-RXD	0.9705
	LRXD	0.9643	UTD-RXD	0.0762	SW-RXD	0.9905
V3	RXD	0.8962	MRXD	0.7449	W-RXD	0.9807
	LRXD	0.9642	UTD-RXD	0.0723	SW-RXD	0.9940
F5	RXD	0.8974	MRXD	0.8554	W-RXD	0.9910
	LRXD	0.9647	UTD-RXD	0.5818	SW-RXD	0.9990
F6	RXD	0.8977	MRXD	0.8405	W-RXD	0.9787
	LRXD	0.9644	UTD-RXD	0.5077	SW-RXD	0.9989
F7	RXD	0.8972	MRXD	0.8483	W-RXD	0.9780
	LRXD	0.9645	UTD-RXD	0.4511	SW-RXD	0.9964

从表3可以看出，对于所有的目标，SW-RX算法ROC曲线下方区域面积AUC值都大于其他5种算法，即对于6组合成的高光谱异常目标数据，SW-RX算法相比5种对比算法具有最好的检测效果。

4.4 真实高光谱数据实验结果

4.4.1 圣地亚哥数据实验结果

实验选用SW-RX算法的光谱距离为欧氏距离，局部窗口大小为5×5，参数c的取值为17。图9为SW-RX算法和另外5种算法选取阈值为0.9700并二值化分割后的实验结果。

图 9 圣地亚哥高光谱图像不同算法的实验结果

Fig. 9 Detection results provided by different algorithms on sandiego hyperspectral data

本次实验采用的数据中共有38个异常目标，每个异常目标由多个像素构成，若算法能检测到属于某个异常目标的像素，则称该算法能检测到这个异常目标。图9中可以看出，RX、LRX、MRX和UTD-RX算法具有较高的虚警率。W-RX算法能检测到34个异常目标，而SW-RX算法能检测到36个，是6个算法中最多的，且虚警点最少。对应的ROC曲线如图10。

图 10 圣地亚哥高光谱数据实验结果的ROC曲线

Fig. 10 ROC curves corresponding to the detection results on sandiego hyperspectral image

曲线下方面积AUC如表4。由表4可以看出SW-RX算法对应的AUC最大，具有最好的检测效果。

表 4 圣地亚哥高光谱数据实验结果的曲线下方面积
Table 4 AUC for the detection results on sandiego hyperspectral data

下载CSV

算法	RXD	LRXD	MRXD	UTD-RXD	W-RXD	SW-RXD
AUC	0.7844	0.7464	0.0685	0.7896	0.9885	0.9904

4.4.2 世贸中心数据实验结果

实验选用SW-RX算法的光谱距离为欧氏距离，局部窗口大小为5×5，参数c的取值为17。图11为SW-RX算法和另外5种算法选取阈值为0.9979并二值化后的实验结果，阈值取0.9979是因为总共40000个像素中有84个位异常点像素。

图 11 世贸中心高光谱图像不同算法的实验结果

Fig. 11 Detection results provided by different algorithms on WTC hyperspectral data

对应的ROC曲线如图12。

图 12 世贸中心高光谱数据实验结果的ROC曲线

Fig. 12 ROC curves corresponding to the detection results on WTC hyperspectral image

曲线下方面积AUC如表5。由表5可以看出SW-RX算法对应的AUC最大，具有最好的检测效果。

表 5 世贸中心高光谱数据实验结果的曲线下方面积
Table 5 AUC for the detection results on WTC hyperspectral data

下载CSV

算法	RXD	LRXD	MRXD	UTD-RXD	W-RXD	SW-RXD
AUC	0.9674	0.9551	0.8729	0.9678	0.9845	0.9852

在上述两组真实高光谱图像中的实验结果中，LRX算法的AUC值都不如RX算法，这是因为这两组数据的异常目标都是多像素的，即一个异常目标由多个像素点组成。在这两组实验数据中，全局RX算法在面对多像素的异常目标时的检测效果要优于局部LRX算法，局部LRX算法对上一节中单像素的异常目标检测效果更好。

4.4.3 抗噪能力分析实验

实验选用数据为世贸中心高光谱数据，分别手动添加信噪比分别为5 db、10 db、20 db、30 db、40 db、50 db的高斯噪声。SW-RX算法的光谱距离为欧氏距离，局部窗口大小为5×5，参数c的取值为17。表6为在不同信噪比的高斯噪声干扰下，SW-RX算法和5种对比算法的AUC面积。

表 6 不同信噪比噪声干扰下实验结果的曲线下方面积
Table 6 AUC for the detection results interfered by different SNR noise

下载CSV

噪声/db	5	10	20	30	40	50
AUC	0.9783	0.9792	0.9816	0.9834	0.9848	0.9850

由表6可以看出，通过加入不同分贝的高斯噪声，SW-RX检测算子的检测能力随之下降，但噪声对检测效果的影响在1%以下，因此SW-RXD算子具有一定的抗噪能力。

4.4.4 算法计算时间分析实验

实验选用合成数据、圣地亚哥数据和世贸中心数据在同一硬件配置的计算机上，对6种算法所需的计算时间进行比较。实验采用的计算机硬件配置如下，处理器型号为Intel Core i7，主频为2.6 GHz，内存为8 G，仿真实验平台为Matlab2014a版本。表7给出了6种算法在3组数据实验中所用的时间。

表 7 6种算法的计算时间
Table 7 Computing time of six algorithms

下载CSV

算法	RXD	LRXD	MRXD	UTD-RXD	W-RXD	SW-RXD
合成数据运行时间/s	1.013	126.328	1.277	1.008	1.272	90.015
圣地亚哥数据运行时间/s	1.141	185.064	1.233	1.094	1.378	90.347
世贸中心数据运行时间/s	2.298	2933.062	2.763	2.420	3.723	2396.691

由表7可以看出，由于要利用子窗口进行循环计算，LRXD和SW-RXD算法的计算速度相对较慢。

5 结　论

本文提出了一种基于显著性分析加权的RX算法，利用合成高光谱数据和真实高光谱数据进行异常点检测实验并将该算法与传统算法的实验结果相对比，得出以下结论：

传统的RX算法假设背景模型服从一个多元高斯分布，RX算法直接应用在高光谱数据中效果并不好。SW-RX算法通过显著性分析给背景像素和异常点像素一个不同的权值，使背景模型的正态适应性更好。通过合成数据和真实数据的对比试验，相比于传统的RX算法，SW-RX算法能在提高检测概率的同时降低虚警率，具有更好的检测效果，且有一定的抗噪能力。

计算机视觉中显著性分析的方法能有效的在空间域进行分析，这弥补了RX算法忽略空间相关性的缺点，使得异常点的检测在空间域和光谱域同步进行。

SW-RX算法由于要循环计算显著性图，该算法的计算复杂度比传统RX算法大。下一步工作将考虑引入DSP加速，对SW-RX算法进行并行化处理，加快计算速度。

参考文献(References)

Ashton E A and Schaum A. 1998. Algorithms for the detection of sub-pixel targets in multispectral imagery. Photogrammetric Engineering and Remote Sensing, 64 (7): 723–731.

Chang C I and Chiang S S. 2002. Anomaly detection and classification for hyperspectral imagery. IEEE Transactions on Geoscience and Remote Sensing, 40 (6): 1314–1325. [DOI: 10.1109/TGRS.2002.800280]

Chang C I, Li Y, Hobbs M C, Schultz R C and Liu W M. 2015. Progressive band processing of anomaly detection in hyperspectral imagery. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 8 (7): 3558–3571. [DOI: 10.1109/JSTARS.2015.2415782]

Gao K, Liu Y, Wang L J, Zhu Z Y and Cheng H B. 2015. A hyperspectral imagery anomaly detection algorithm based on gauss-Markov model. Spectroscopy and Spectral Analysis, 35 (10): 2846–2850. [DOI: 10.3964/j.issn.1000-0593(2015)10-2846-05] ( 高昆, 刘莹, 王丽静, 朱振宇, 程灏波. 2015. 基于高斯马尔科夫模型的高光谱异常目标检测算法研究. 光谱学与光谱分析, 35 (10): 2846–2850. [DOI: 10.3964/j.issn.1000-0593(2015)10-2846-05] )

Goferman S, Zelnik-Manor L, Tal A. 2012. Context-aware saliency detection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 34 (10): 1915–1926. [DOI: 10.1109/TPAMI.2011.272]

Guo Q D, Zhang B, Qiong R, Gao L R, Li J and Plaza A. 2014. Weighted-RXD and linear filter-based RXD: improving background statistics estimation for anomaly detection in hyperspectral imagery. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7 (6): 2351–2366. [DOI: 10.1109/JSTARS.2014.2302446]

Itti L, Koch C, Niebur E. 1998. A model of saliency-based visual attention for rapid scene analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence, 20 (11): 1254–1259. [DOI: 10.1109/34.730558]

Khazai S, Homayouni S, Safari A and Mojaradi B. 2011. Anomaly detection in hyperspectral images based on an adaptive support vector method. IEEE Geoscience and Remote Sensing Letters, 8 (4): 646–650. [DOI: 10.1109/LGRS.2010.2098842]

Li J H and Liu Z. 2015. Object detection based on visual saliency map and objectness. Journal of Computer Applications, 35 (12): 3560–3564. [DOI: 10.11772/j.issn.1001-9081.2015.12.3560] ( 李君浩, 刘志. 2015. 基于视觉显著性图与似物性的对象检测. 计算机应用, 35 (12): 3560–3564. [DOI: 10.11772/j.issn.1001-9081.2015.12.3560] )

Liu W M and Chang C I. 2013. Multiple-window anomaly detection for hyperspectral imagery. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 6 (2): 644–658. [DOI: 10.1109/JSTARS.2013.2239959]

Molero J M, Garzón E M, García I and Plaza A. 2013. Analysis and optimizations of global and local versions of the RX algorithm for anomaly detection in hyperspectral data. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 6 (2): 801–814. [DOI: 10.1109/JSTARS.2013.2238609]

Reed I S and Yu X. 1990. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Transactions on Acoustics, Speech, and Signal Processing, 38 (10): 1760–1770. [DOI: 10.1109/29.60107]

Stellman C M, Hazel G G, Bucholtz F, Michalowicz J V, Stocker A D and Schaaf W. 2000. Real-time hyperspectral detection and cuing. Optical Engineering, 39 (7): 1928–1935. [DOI: 10.1117/1.602577]

Tong Q X, Zhang B and Zheng L F. 2006. Hyperspectral Remote Sensing: Principle, Technology and Application. Beijing: Higher Education Press: 40–47 (童庆禧, 张兵, 郑兰芬. 2006. 高光谱遥感: 原理、技术与应用. 北京: 高等教育出版社: 40–47)

Tong Q X, Zhang B and Zhang L F. 2016. Current progress of hyperspectral remote sensing in China. Journal of Remote Sensing, 20 (5): 689–707. [DOI: 10.11834/jrs.20166264] ( 童庆禧, 张兵, 张立福. 2016. 中国高光谱遥感的前沿进展. 遥感学报, 20 (5): 689–707. [DOI: 10.11834/jrs.20166264] )

Xu Y, Wu Z B, Li J, Plaza A and Wei Z H. 2016. Anomaly detection in hyperspectral images based on low-rank and sparse representation. IEEE Transactions on Geoscience and Remote Sensing, 54 (4): 1990–2000. [DOI: 10.1109/TGRS.2015.2493201]

Yu X, Reed I S and Stocker A D. 1993. Comparative performance analysis of adaptive multispectral detectors. IEEE Transactions on Signal Processing, 41 (8): 2639–2656. [DOI: 10.1109/78.229895]

Yuan Y, Wang Q and Zhu G K. 2015. Fast hyperspectral anomaly detection via high-order 2-D crossing filter. IEEE Transactions on Geoscience and Remote Sensing, 53 (2): 620–630. [DOI: 10.1109/TGRS.2014.2326654]

Zhang B. 2016. Advancement of hyperspectral image processing and information extraction. Journal of Remote Sensing, 20 (5): 1062–1090. [DOI: 10.11834/jrs.20166179] ( 张兵. 2016. 高光谱图像处理与信息提取前沿. 遥感学报, 20 (5): 1062–1090. [DOI: 10.11834/jrs.20166179] )

Zhao C H, Wang L G and Qi B. 2016. Hyperspectral Remote Sensing Images Processing Methods and Applications. Beijing: Publishing House of Electronics Industry: 261–271 (赵春晖, 王立国, 齐滨. 2016. 高光谱遥感图像处理方法及应用. 北京: 电子工业出版社: 261–271)

Zhao C H, Yao X F. 2016. Local kernel RX algorithm-based hyperspectral real-time detection. Journal of Infrared and Millimeter Waves, 35 (6): 708–714. [DOI: 10.11972/j.issn.1001-9014.2016.06.013] ( 赵春晖, 姚淅峰. 2016. 基于局部核RX算法的高光谱实时检测. 红外与毫米波学报, 35 (6): 708–714. [DOI: 10.11972/j.issn.1001-9014.2016.06.013] )

Zhao R, Du B and Zhang L P. 2014. A robust nonlinear hyperspectral anomaly detection approach. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7 (4): 1227–1234. [DOI: 10.1109/JSTARS.2014.2311995]

摘要

关键词

Abstract

Key words

1 引　言

2 异常点检测算法理论

2.1 传统的RX算法

2.2 显著性图的定义

2.3 加权的RX算法

3 基于显著性分析的加权RX异常点检测算法(SW-RX)

3.1 算法原理

3.2 算法伪代码及复杂度分析

4 实验结果与分析