出版日期: 2019-05-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20197510
2019 | Volumn23 | Number 3
上一篇 | 下一篇

技术方法

高光谱图像滚动引导递归滤波与地物分类

崔宾阁 , 吴亚男 , 钟勇 , 钟利伟 , 路燕

山东科技大学计算机科学与工程学院，青岛 266590

收稿日期: 2017-11-30; 预印本: 2018-04-17

基金项目: 国家重点研发计划(编号：2017YFC1405600)；国家青年科学基金(编号：41406200)；山东省自然科学基金(编号：ZR2014DQ030)

第一作者简介: 崔宾阁，1979年生，男，副教授，研究方向为高光谱遥感的理论和应用。E-mail：cuibinge@qq.com

通信作者简介: 路燕，1975年生，女，副教授，研究方向为智能信息处理。E-mail：luyan@sdust.edu.cn

摘要

高光谱图像类内光谱变化较大，“同物异谱”现象普遍存在。利用原始地物光谱特征进行分类精度较低而且分类结果图中存在“椒盐现象”。为了获得好的分类结果，必须充分利用高光谱图像的光谱信息和空间信息，减少类内的光谱变化，并扩大类别间的光谱差异。为此，提出一种滚动引导递归滤波的高光谱图像光谱—空间分类方法。首先，利用主成分分析对高光谱图像进行降维；然后，利用高斯滤波对输入图像进行模糊化，消除图像中的噪声和小尺度结构；接下来，将模糊化后的图像作为引导图像，对输入图像进行边缘保持递归滤波，输出结果作为新的引导图像，重复迭代这个过程直至大尺度边缘被恢复；最后，利用提取的特征波段和支持向量机对高光谱图像进行分类。在两个真实高光谱数据集上进行了分类实验，结果表明本文方法的分类精度优于其他的高光谱图像分类方法。在训练样本极少的情况下，本文方法也能获得较高的分类精度。

关键词

高光谱图像分类, 滚动引导递归滤波, 特征提取, 主成分分析

Hyperspectral image rolling guidance recursive filtering and classification

CUI Binge , WU Yanan , ZHONG Yong , ZHONG Liwei , LU Yan

College of Computer Science and Engineering, Shandong University of Science and Technology, Qingdao 266590, China

Abstract

Hyperspectral images have relatively large changes in intra-class spectra, and the " same material, different spectra” phenomena are widespread. Moreover, classification accuracy is low when only the original spectral features are considered, and the " pepper and salt phenomenon” can be observed in the classification result map. In the attempt to improve the classification result, the spectral and spatial information of a hyperspectral image needs to be fully utilized to reduce the spectral changes within the class and expand the spectral difference between classes. Thus, in this study, we propose a spectral–spatial hyperspectral image classification method with rolling guidance recursive filtering. First, principal component analysis (PCA) is used to reduce the dimension of the hyperspectral image, in which the main components with large amounts of information are maintained for the input image of the next step. Second, the Gaussian filter is adopted to blur the input image and eliminate the small-scale structure. Third, recursive filtering is performed on the input image to preserve the edge of the image, in which the guidance image is the blurred image, and then the output result is treated as the new guidance image. The process is repeated iteratively until the large-scale edge is restored. Finally, the extracted feature bands of the hyperspectral image are used for classification by a support vector machine. Indian Pines and University of Pavia datasets were initially used to verify the effectiveness of the proposed rolling guidance recursive filtering (RGRF) method. As shown by the homogeneous regions in Figs. 5 and 6, the noise phenomenon is severe when the extracting feature of PCA is used, whereas the noise is effectively removed when rolling guidance filtering (RGF) and RGRF are utilized. However, at the strong edges, the boundary is blurred and irregular and the spatial smoothness is excessive for RGF. By contrast, the boundary is clear and the strong edges are protected for RGRF. Then, the proposed method is compared with related classification methods by using two real hyperspectral image datasets. The comparative results in Tables 1 and 2 indicate that RGRF can improve classification accuracy more effectively than the other methods. Subsequently, McMemar test was performed to analyze the statistical significance and verify the comparative results. As shown in Tables 3 and 4, the correlations of RGRF with the other methods are statistically significant, and the values exceed p>1.96. The McMemar values inTables 3 and 4 increase with the decrease in number of samples, which indicates that the advantages of using RGRF becomes more obvious in the case of fewer samples. This study presents an improved edge-preserving filtering method named RGRF. Compared with the other filtering methods, RGRF can maintain the edge structures of land covers and eliminate the texture and noise information within these land covers. RGRF effectively uses the recursive filtering method instead of the bilateral filtering method (i.e., of the RGF method) in each iteration. In this manner, the continuous spreading of texture and noise information across the strong edges is avoided. Moreover, considering that image quality is significantly improved after RGRF filtering, the classification accuracy of the hyperspectral image is also greatly enhanced. Classification experiments were performed on two real hyperspectral datasets. The results indicate that the classification accuracy of RGRF is superior to the other hyperspectral image classification methods. Moreover, RGRF can achieve higher classification accuracy when only few training samples are used.

Key words

hyperspectral image classification, rolling guidance recursive filtering, feature extraction, principal component analysis

1 引　言

成像光谱仪获取的地表图像含有丰富的空间、光谱和辐射多重信息。通过高光谱图像的光谱空间、特征空间和图像空间等多个空间对目标进行探测和识别，可以大大提高地物分类的可靠性与稳定性。因此，在过去几十年中高光谱图像广泛应用到环境监测(Pontius 等，2008)、海洋监测(van Ruitenbeek 等，2006)、矿物识别(Baldwin 等，1990)以及精准农业(Boggs 等，2003)等领域中。

高光谱图像波段数目众多，但用于图像分类的训练样本通常难于获取，模型复杂度和样本的数量严重不匹配，存在所谓的休斯现象(Hughes，1968)。为了解决这一问题，国内外研究人员通常采用特征选择和特征提取两种方式进行降维。特征选择是指从给定的特征集合中选取有效区分目标的最小特征子集，它主要使用特定的评价准则和搜索算法实现波段选择，典型方法包括Relief算法(Amjady 等，2010)、顺序后向选择法SBS(Peng 等，2014)、ReliefF算法(Spolaôr 等，2014)、基于动态信息的特征选择算法(Wang，2015)、基于最小冗余最大相关方法mRMR(Sakar 等，2012)等。与特征选择不同的是，特征提取将原始特征空间映射到新的特征空间中，是一种特征变换方法。典型方法包括主成分分析法PCA(Prasad和Bruce，2008)、线性判别分析法LDA(Altman 等，1994)、核主成分分析法KPCA(Fauvel 等，2009)以及基于流形学习的方法如等度量映射IsoMap (Balasubramanian 等，2002)、局部线性嵌入LLE(Donoho和Grimes，2003)和拉普拉斯特征映射LE(Chen 等，2010)等。

由于高光谱图像波段狭窄，每个通道接收的光能量较低，因此相对于宽波段的多光谱图像来说，高光谱图像的信噪比通常较低，部分波段噪声严重。此外，光照条件、地物地形和混合像元等问题都会不同程度地引入噪声。这些噪声会同时存在于光谱域和空间域中，导致高光谱图像分类图呈现“椒盐现象”，严重影响了高光谱遥感图像的应用能力。为了消除图像和分类结果图中存在的噪声，人们提出了多种滤波方法，如均值滤波、中值滤波、高斯滤波、边缘保持滤波等。其中，边缘保持滤波方法(Edge-Preserving Filter)能在消除图像噪声的同时保持地物边缘结构清晰而非模糊化，因此近年来已成为图像处理领域的一个热点主题。典型边缘保持滤波方法包括双边滤波(Paris 等，2009)、引导滤波(Palumbo 等，2010)、域变换递归滤波(Gastal和Oliveira，2011)、各向异性扩散(Wang 等，2010)等。部分滤波方法已经被应用于高光谱图像的预处理或分类后处理，取得了良好的降噪效果(Kang 等，2014a；Kang 等，2014b；崔宾阁等，2017)。然而，对于图像中具有强边缘的小分辨率图案(纹理或细节区域的梯度大小同样足够高)，边缘保持滤波器会很自然地将它们保留下来，这与只将不同地物类型之间的强边缘保留下来的初衷是不一致的。

滚动引导滤波RGF(Rolling Guidance Filter)是一种改进的基于尺度理论(Lindeberg，1994)的边缘保持滤波方法(Zhang 等，2014)。它的设计目标是消除图像中的小尺度结构，保留大尺度结构。尺度大小可以由用户根据图像内容定义。RGF方法基本能够满足人们对消除地物内部纹理/细节特征，同时保持地物之间边缘的需求。然而，由于RGF采用的基础滤波方法是双边滤波器，不可避免地存在信息跨越强边缘继续传播的可能。

为了在强边缘处停止信息传播，本文提出了在RGF方法中将双边滤波器替换为递归滤波器的RF(Recursive Filter)特征提取方法，简称为RGRF(Rolling Guidance Recursive Filter)。首先，对高光谱图像使用主成份分析PCA(Principle Component Analysis)进行降维；然后，使用本文提出的滚动引导图像的递归滤波RGRF(Rolling Guidance image Recursive Filter)方法对降维后的高光谱图像进行边缘保持滤波操作；最后使用支持向量机SVM(Gualtieri和Cromp，1999)对高光谱图像进行分类。实验结果表明，在训练样本稀少情况下，本文方法能够显著改善高光谱图像的分类精度。

2 常用的滤波方法

在现有的边缘保持滤波方法中，有许多在实际场景中产生好的效果的方法，例如双边滤波、引导滤波、域变换递归滤波、滚动引导滤波等。本节主要介绍与论文工作相关的两个滤波方法，递归滤波和滚动引导滤波。

2.1 递归滤波

Gastal等(2011)提出的递归滤波方法首先建立了一个在从五维空间(二维平面坐标加三颜色通道)到一维空间(实线)的等距域变换，其中等距域变换是指对于二维图像流形曲面上的任意两个点，它们之间的测地线距离在映射到一维空间后保持不变。域变换操作可以容易地扩展到多光谱图像或高光谱图像处理。经过域变换后，可以利用一维边缘保持滤波方法(如递归滤波器)在线性时间内完成对图像的滤波处理。域变换递归滤波不仅能够对图像进行高质量的边缘保持滤波，而且可以实现对图像的实时处理。

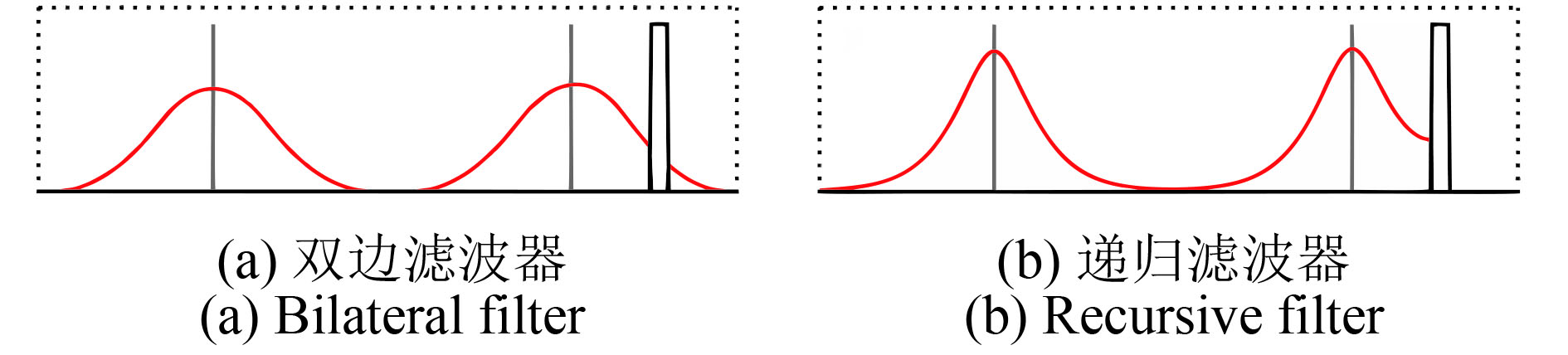
图1中给出了双边滤波BF(Bilateral Filter)和递归滤波RF(Recursive Filter)在均匀区域和强边缘处的脉冲响应(Gastal和Oliveira，2011)。可以看出，BF具有高斯脉冲响应，而RF具有指数脉冲响应；BF在强边缘另一侧像元仍然有较小的权重，RF在强边缘另一侧像元权重为零，从而阻止了不同地物间的光谱信息传播过程。

图 1 双边滤波和递归滤波脉冲响应的对比

Fig. 1 Comparison of impulse response between bilateral filter and recursive filter

域变换递归滤波首先将输入信号 ${{I}}$ 转换到变换域 ${\Omega _\omega }$ 中，对于一个离散的输入信号 ${{I}}[n] = {{I}}({x_n})$ ，其滤波结果可以在变换域中定义如下

${{J}}[n] = (1 - {a^d}){{I}}[n] + {a^d}{{J}}[n - 1]$

(1)

式中， ${{J}}[n]$ 是滤波结果， $n$ 是递归滤波的次数， $a \in [0, 1]$ 是反馈系数，并且 $a = \exp(- {{\sqrt 2 }/{\sigma _s}})$ 。 $d = ct({x_n}) - ct({x_{n - 1}})$ ，是变换域 ${\Omega _\omega }$ 中相邻样本点 ${x_n}$ 和 ${x_{n - 1}}$ 之间的距离。变换函数 $ct(u)$ 定义如下

$ ct\left(u \right) = \int_0^u {1 + \frac{{{\sigma _s}}}{{{\sigma _r}}}} \left| {{{I}}'\left(x \right)} \right|{\rm{d}}x, u \in {\Omega _\omega } $

(2)

式中， ${{I}}'(x)$ 是输入信号 ${{I}}(x)$ 的导数， ${\sigma _s}$ 和 ${\sigma _r}$ 分别用于控制空间和光谱的权重。随着 $d$ 增大， ${a^d}$ 将趋向于0，从而使得信息传播链终止，进而起到边缘保持的作用。

2.2 滚动引导滤波

Zhang等(2014)利用高斯滤波器对图像进行滤波，发现小尺度结构被完全消除了，而大尺度结构虽然被模糊化，但并没有被消除，其边缘仍然是可见的。人们仍然可以意识到大尺度结构的存在而不需要去参照输入图像。基于这一观察，Zhang等(2014)提出了一种尺度感知的边缘保持滤波器，即滚动引导滤波。该滤波器的执行分为两步：(1)小尺度结构消除；(2)大尺度结构边缘恢复。第1步可以使用高斯滤波器进行滤波，使得图像处处模糊；第2步是利用第1步的输出作为引导图像，对原始输入图像进行边缘保持滤波；输出图像将作为新的引导图像，对原始输入图像进行下一轮滤波；重复这个过程，直到强边缘恢复。在这个过程中，输入图像总是相同的，持续更新的是引导图像。

首先对输入图像使用高斯函数进行滤波，公式如下

$G = \frac{1}{{{K_p}}}\sum\limits_{q \in {{N}}\left(p \right)} {\exp \left(- \displaystyle\frac{{{{\left\| {p - q} \right\|}^2}}}{{2\sigma _s^2}}\right)} \cdot I(q)$

(3)

式中， ${{I}}$ 是输入图像， $p$ 和 $q$ 是像素的索引坐标， ${K_p} = \displaystyle\sum\limits_{q \in {{N}}(p)} {\exp\left(- \displaystyle\frac{{{{\left\| {p - q} \right\|}^2}}}{{2\sigma _s^2}}\right)} $ 是正则化参数， ${{N}}(p)$ 是关于 $p$ 的邻域像素集合， ${\sigma _s}$ 是空间标准差， ${{G}}$ 是高斯滤波结果。

在每一轮迭代过程中，使用联合双边滤波生成新的引导图像

$ {{{J}}^{t + 1}}(p) \!=\! \frac{1}{{{K_p}}}\!\!\sum\limits_{q \in {{N}}(p)} {\exp \left(- \frac{{{{\left\| {p - q} \right\|}^2}}}{{2\sigma _s^2}}\! -\! \frac{{{{\left\| {{{{J}}^t}(p) \!-\! {{{J}}^t}(q)} \right\|}^2}}}{{2\sigma _r^2}}\right)} \cdot {{I}}(q) $

(4)

式中， ${{{J}}^{t + 1}}$ 是第 $t$ 次迭代后的输出图像。 ${\sigma _s}$ 和 ${\sigma _r}$ 分别是空间标准差和光谱标准差，用于控制空间和光谱的权重。当 ${\sigma _s}$ 越大时，滤波器在空间域的宽度越大，平滑效果越明显；当 ${\sigma _r}$ 越大时，对同等光谱差异的像素平滑作用就越大，边缘保持效果越差。这两个参数的最优值可以通过实验获得。 ${K_p}$ 是用于正则化的参数，其定义如下

${K_p} = \sum\limits_{q \in {{N}}(p)} {\exp \left(- \frac{{{{\left\| {p - q} \right\|}^2}}}{{2\sigma _s^2}} - \frac{{{{\left\| {{{{J}}^t}(p) - {{{J}}^t}(q)} \right\|}^2}}}{{2\sigma _r^2}}\right)} $

(5)

迭代开始时 $t = 0$ ， ${{{J}}^0} = {{G}}$ ，即高斯滤波的输出图像。经过多轮迭代后，最后一轮迭代的滤波结果将作为图像分类的输入图像。

3 提出的方法

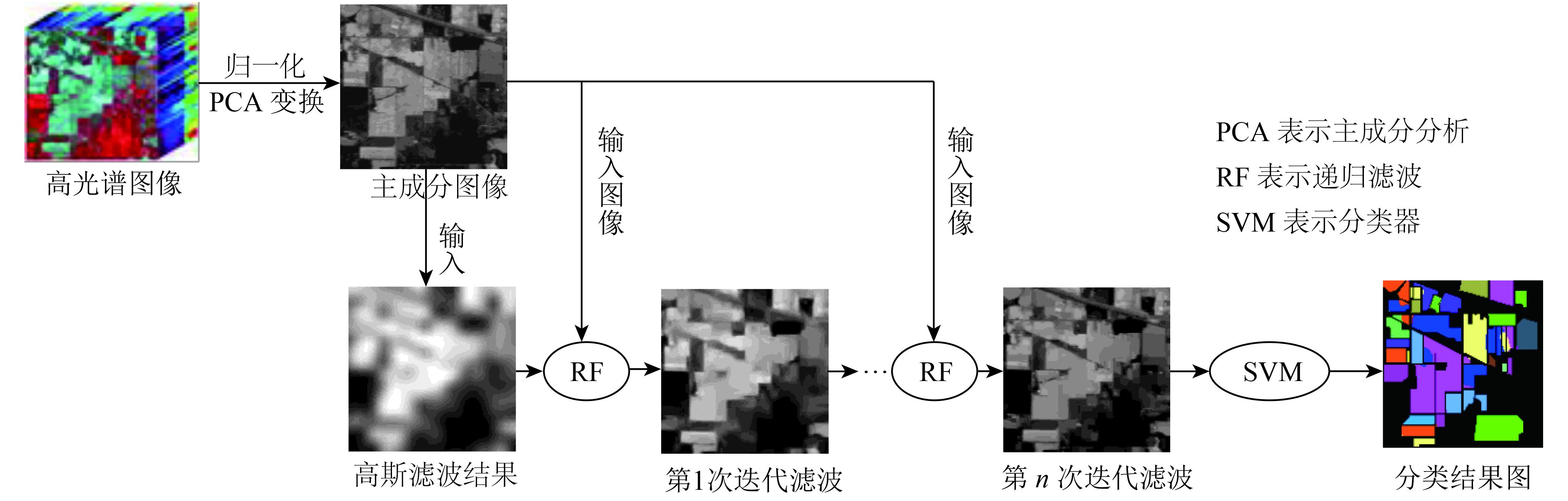
本文提出的高光谱图像滤波和分类方法可分为4步(图2)：(1)将高光谱图像进行归一化处理；(2)使用主成分分析法对高光谱图像进行降维；(3)对每一个主成分图像迭代地进行递归滤波处理，前一次递归滤波的输出图像作为后一次递归滤波的引导图像，通过多次迭代消除主成分图像中细小的纹理结构并保留强边缘；(4)利用支持向量机SVM对最后一次滤波后的图像进行分类。

图 2 滚动引导递归滤波的高光谱图像分类方法示意图

Fig. 2 Schematic of the proposed RGRF-based classification method

(1)图像归一化：高光谱图像记录的数值是地物辐亮度，而不是反射率，因此必须要对高光谱图像各个波段进行归一化处理，否则将会导致算法收敛速度变慢且不一定能够收敛到最小值附近。归一化计算公式如下所示

${{X}} = \frac{{{{I}} - {{{I}}_m}}}{{{{{I}}_M} - {{{I}}_m}}}$

(6)

式中， ${{I}}$ 和 ${{X}}$ 分别是输入图像和归一化后的图像。 ${{{I}}_m}$ 和 ${{{I}}_M}$ 分别是图像中每一波段的最小值和最大值。通过归一化操作，高光谱图像各个波段的光谱值都在[0，1]范围之内。

(2)PCA变换：高光谱图像波段众多，信息冗余较大且部分波段的噪声严重。为了缓解“休斯现象”，本文利用PCA变换对高光谱图像进行降维，同时消除图像中的高斯噪声。

对于归一化的图像 ${{X}} \in {{{R}}^{L \times N}}$ ，其中 $L$ 是波段数目， $N$ 是像元数目，将 ${{X}}$ 的每一行进行零均值化，然后计算其协方差矩阵 ${{\Sigma}} = \displaystyle\frac{{{{X}}{{{X}}^{\rm{T}}}}}{N}$ ，最后对协方差矩阵进行特征值分解，将所有特征值和对应的特征向量按降序排列。根据累计方差贡献率，计算需要保留的特征向量数目，公式如下

$l = \mathop {\arg \min }\limits_l = \displaystyle\frac{{\sum\limits_{i = 1}^l {{\lambda _i}} }}{{\sum\limits_{i = 1}^L {{\lambda _i}} }} \geqslant Th$

(7)

式中， ${\lambda _i}$ 是第 $i$ 个特征值，对应的特征向量为 ${{{\xi}} _{{i}}}$ 。阈值 $Th$ 用来控制降维后的图像保留原图像信息量的比例，通常设置为99%或以上即可。

将前 $l$ 个特征向量组成矩阵 ${{W}} = \{ {{{\xi}} _1}, {{{\xi}} _2}, \cdots, {{{\xi}} _l}\} $ 。将图像 ${{X}}$ 向矩阵 ${{W}}$ 投影，得到降维到 $l$ 维后的图像

$ {{Y}} = {{{W}}^{\rm{T}}}{{X}} $

(8)

(3)滚动引导递归滤波：首先利用高斯滤波器对降维后的图像 ${{Y}}$ 进行滤波，生成初始的引导图像 ${{G}}$ ；然后，对图像 ${{Y}}$ 进行迭代的递归边缘保持滤波，最终得到内部均一、边缘清晰的高光谱特征图像。与标准递归滤波方法不同，在计算变换域 ${\Omega _\omega }$ 中相邻样本点 ${x_n}$ 和 ${x_{n - 1}}$ 之间的距离时，需要对公式(2)中变换函数 $ct(u)$ 的定义修改如下

$ct(u) = \int_0^u 1 + \displaystyle\frac{{{\sigma _s}}}{{{\sigma _r}}}|{{{J}}'_t}(x)|{\rm{d}}x, u \in {\Omega _\omega }$

(9)

式中， ${{{J}}_t}$ 是第 $t$ 次迭代时的输出图像，它被用作第 $t + 1$ 次迭代时的引导图像，初始时 ${{{J}}_0} = {{G}}$ 。滚动引导递归滤波算法的实现过程如下

输入：图像 ${{Y}}$ ，空间和光谱标准差 ${\sigma _s}$ ， ${\sigma _r}$ ，最大迭代次数 $T$ ，循环计数器 $t$ 。

输出：滤波后的图像 ${{J}}$

1. 高斯滤波： ${{G}} = Gauss({{Y}}, {\sigma _s})$ ，其中 $Guass( \cdot )$ 是高斯滤波函数，由式(3)计算得出，获得初始引导图像 ${{G}}$ ；

2. 初始化循环计数器 $t = 0$ ，初始引导图像 ${{J}} = {{G}}$ 。

3. For t = 1∶T

4. 对输入图像进行边缘保持递归滤波，并更新引导图像： ${{J}} = RF({{Y}}, {{J}}, {\sigma _s}, {\sigma _r})$ 。 $RF(\cdot )$ 是递归滤波函数，由式(1)和式(9)计算得出。滤波后的输出作为新的引导图像。

5. End

6. 输出最终滤波图像 ${{J}}$ ，算法结束。

(4)分类：SVM是一个广泛应用的分类器，在分类精度方面要优于大多数其他的分类器，所以本文使用SVM分类器对降维和滤波后的特征图像进行分类，获得最终的分类结果并输出。

4 实验与讨论

4.1 实验数据集

(1) Indian Pines数据集：利用机载可见光/红外成像光谱仪(AVIRIS)获取的来自美国印第安纳州西北部Indian Pines农业试验场的高光谱图像。主要地物类型包括玉米、大豆、苜蓿、小麦、燕麦、草、树等，部分地物还进行了细分，比如玉米分为免耕法、少耕法和传统耕作法3种类型，总共16种地物。图像空间分辨率为20 m，220个波段，光谱范围为400—2500 nm。20个水吸收严重的波段(104—108，150—163，200)从数据集删除，最后得到200个波段。Indian Pines图像很多波段噪声严重。图3给出了Indian Pines 3波段(第50、27和17波段)假彩色图和地面真值图。

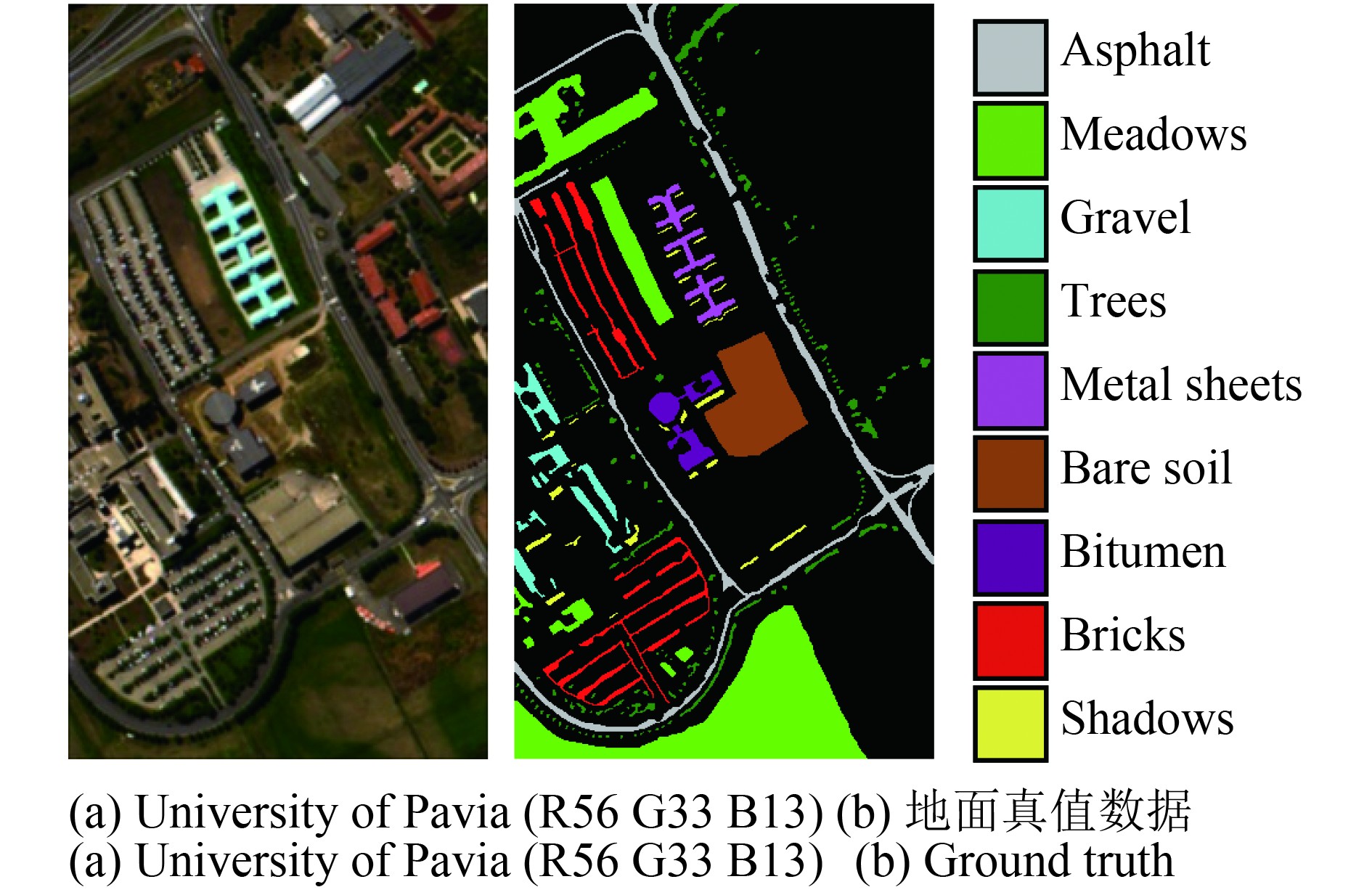
(2) University of Pavia数据集：利用反射光学系统成像光谱仪(ROSIS-03)获取的来自帕维亚大学的高光谱图像。主要地物类型包括柏油马路、草地、砂砾、树、金属板、裸露土壤、沥青屋顶、砖地和阴影，总共9种地物。图像空间分辨率为1.3 m，103个波段，光谱范围为430—860 nm。图4给出了University of Pavia 3波段(第56、33和13波段)假彩色图和地面真值图。

图 3 Indian Pines数据集

Fig. 3 Indian Pines data set

图 4 University of Pavia数据集

Fig. 4 University of Pavia data set

4.2 实验

为了验证RGRF分类方法的有效性，本文使用RGRF和其他分类方法作对比试验。由于RGRF是基于PCA和RGF改进后的分类方法，因此提出的方法与PCA和RGF方法进行比较，SVM作为经典基准分类方法进行比较。RGRF提出了一种新的边缘保持滤波方法，因此与文献中滤波后分类精度较高的边缘保持滤波方法，如SnEPF(Cui 等，2017)、IFRF(Kang 等，2014a)、EPF (Kang 等，2014b)方法进行对比。最后，由于RGRF方法是基于光谱空间信息的分类方法，广义组合核GCK(Li 等，2013)分类方法也作为本文的一种对比方法。

其中，PCA方法是先用PCA降维，然后再调用SVM分类；EPF方法是基于双边滤波，使用PCA变换生成的第一主成分为引导图像。这些方法中涉及的实验参数分别使用文献中默认的参数。本文使用两个高光谱数据集来验证RGRF方法的优越性。为了减少训练样本的随机性选择给实验结果带来的影响，每个方法都是采用不同的训练样本实验30次，最后得到的精度是这30次实验结果的均值。

实验分别在Indian Pines和University of Pavia 数据集上执行，图5和图6分别展示了两个数据集上的PCA、RGF以及RGRF所提取的特征对比图。从图5可以观察到：在同质区域中，图5(a)的噪声现象非常严重，而图5(b)和图5(c)能有效的去除噪点；在强边缘处，图5(b)的边界划分模糊和不规整，图5(c)的边界划分很清晰。从图6中的红色和黄色方框内可以看出，对于强边缘划分，RGRF方法优于RGF方法，能够更好地保持地物边缘，与图5(a)中的PCA第一主成分图像非常接近；蓝色方框内是一小片裸露的土壤，可以看出图5(a)中地物纹理现象明显，图5(b)和图5(c)都取得了较好的平滑效果，但图5(c)的平滑结果更合理。在图5和图6中RGF存在过度的空间平滑现象，而RGRF对强边缘区域进行了保护，验证了递归滤波可以在强边缘处阻止不同地物间的光谱信息传播。

图 5 不同特征提取方法的比较

Fig. 5 Comparison of the different feature extraction methods

图 6 不同分类方法在 University of Pavia特征提取对比图

Fig. 6 Comparison of different classification methods in University of Pavia feature extraction

第1个实验在India Pines高光谱图像上进行。在这个实验里，每个类别中随机选取总样本数的1%—5%作为训练样本。表1给出了不同训练样本数目下不同分类方法的总体精度(OA)、平均精度(AA)和Kappa系数。从表1可以看出，即使使用的训练样本数目较少，本文方法也可取得较高的分类精度。当训练样本数为总样本数的1%时，RGRF方法总体精度达到79.66%，相比较于SVM的总体精度提高了31.89%，高于RGF方法16.9%，与IFRF方法相比RGRF方法高出12.56%。在训练样本数为总样本数的2%时，RGRF方法的Kappa系数高出RGF方法20.18%。随着训练样本数目增加，RGRF方法的分类精度与其他方法的分类精度的差距逐渐减少(表1)。当训练样本数为总样本数的5%时，IFRF方法总体分类精度达到94.31%，仅仅低于RGRF方法1.6%，同样RGF方法总体分类精度与RGRF方法的精度差距缩小到了6.31%。总之，RGRF方法在不同数量训练样本的情况下，都可以获得好的分类表现，当然训练样本越多越有利于分类精度提高，而其他方法在训练样本较少时分类精度较差。图7展示了训练样本数占总样本数5%时某一次实验的分类效果图，因而其分类精度与表1中的平均分类精度稍有差异。可以看出，RGRF方法的分类结果更接近于地面真值图。

表 1 Indian Pines高光谱图像不同方法分类精度
Table 1 Classification accuracy of different methods in Indian Pines hyperspectral image

下载CSV

分类方法		训练样本数
分类方法		1%	2%	3%	4%	5%
SVM	OA	47.77	61.42	67.41	71.62	74.22
	AA	49.45	60.10	65.05	69.07	71.79
	Kappa	41.29	56.46	63.19	67.83	70.77
PCA	OA	47.20	56.69	61.57	67.00	68.72
	AA	51.49	59.04	63.25	67.69	70.24
	Kappa	40.70	51.38	56.74	62.66	64.58
EPF	OA	64.29	77.32	82.12	85.57	88.05
	AA	67.89	78.39	83.37	85.88	88.84
	Kappa	59.79	74.28	79.74	83.57	86.39
SnEPF	OA	68.36	81.44	87.36	90.81	93.00
	AA	68.42	79.01	84.00	88.27	95.69
	Kappa	64.64	79.08	85.67	89.54	95.21
GCK	OA	71.99	83.63	88.75	90.90	92.43
	AA	80.30	89.29	92.38	93.82	94.71
	Kappa	68.52	81.49	87.21	89.64	91.36
IFRF	OA	67.10	83.51	89.60	92.43	94.31
	AA	68.55	79.61	86.34	90.32	93.14
	Kappa	62.86	81.30	88.17	91.37	93.49
RGF	OA	62.76	69.85	76.63	88.10	89.62
	AA	63.14	74.42	78.15	82.88	84.61
	Kappa	57.71	65.98	73.51	86.45	88.18
RGRF	OA	79.66	87.84	92.25	94.21	95.91
	AA	80.53	86.20	90.32	93.38	95.26
	Kappa	76.95	86.16	91.15	93.37	95.31

图 7 不同方法的Indian Pines图像分类结果图

Fig. 7 Indian Pines image classification results obtained by different methods

第2个实验在University of Pavia高光谱图像上进行，在这个实验中，由于图像的总体样本数量较多，所以在选取样本的时，每个类别的训练样本数占总体样本比例较小，表2中给出了0.2%、0.4%、0.6%、0.8%和1%的训练样本的总体精度(OA)，平均精度(AA)和Kappa系数以及各个类别的精度。可以看出，当训练样本数为总样本数的0.4%时，RGRF方法的总体精度达到了91.82%，与SVM方法和IFRF方法的总体精度相比分别高出了21.51%和7.45%，而RGF方法的总体精度是84.42%。图8为训练样本数占总样本数0.4%时某一次实验的分类效果图，可以看出RGRF方法对边界区域实现了更为精确的分类。

表 2 University of Pavia高光谱图像不同方法分类精度
Table 2 Classification accuracy of different methods in University of Pavia hyperspectral image

下载CSV

分类方法		训练样本数
分类方法		0.2%	0.4%	0.6%	0.8%	1%
SVM	OA	63.15	70.31	74.88	78.61	80.35
	AA	65.48	71.48	75.27	77.48	78.88
	Kappa	54.08	62.82	68.26	72.73	74.85
PCA	OA	64.58	70.26	75.31	76.74	78.48
	AA	64.74	70.35	74.02	75.16	76.58
	Kappa	55.22	62.72	68.57	70.42	72.48
EPF	OA	71.62	78.65	86.42	88.54	90.49
	AA	74.36	81.22	86.48	88.09	89.80
	Kappa	64.21	73.16	82.57	85.24	87.71
SnEPF	OA	85.47	91.18	94.35	95.61	96.70
	AA	86.22	89.70	92.69	94.46	95.55
	Kappa	81.49	88.58	92.62	94.24	95.65
GCK	OA	78.51	83.28	87.21	88.65	90.35
	AA	82.33	87.48	90.05	91.24	92.28
	Kappa	72.29	78.46	83.38	85.21	87.38
IFRF	OA	74.73	84.37	89.04	91.35	92.99
	AA	69.16	80.45	84.26	86.91	89.06
	Kappa	67.59	79.89	85.69	88.66	90.77
RGF	OA	76.49	84.42	88.41	90.34	92.33
	AA	76.13	80.56	83.10	84.70	86.36
	Kappa	70.04	79.94	84.92	87.39	89.91
RGRF	OA	86.27	91.82	94.56	95.94	97.61
	AA	87.27	90.09	93.06	95.21	97.10
	Kappa	81.97	89.32	92.53	94.65	96.84

图 8 不同方法的Pavia图像分类结果图

Fig. 8 Pavia image classification results obtained by different methods

为了验证RGRF分类方法的有效性，本文采用遥感图像分类中常用的McMemar检验(Foody，2004)进行统计显著性分析，该方法是基于标准正态检验公式，其公式表达如下

${{\textit{z}}_{\rm{ab}}} = \frac{{{f_{\rm{ab}}} - {f_{\rm{ba}}}}}{{\sqrt {{f_{\rm{ab}}} - {f_{\rm{ba}}}} }}$

(10)

式中， ${f_{\rm{ab}}}$ 表示分类方法a分类正确且分类方法b分类错误的像元数； ${f_{\rm{ba}}}$ 则是分类方法b分类正确且分类方法a分类错误的像元数。在高光谱遥感图像分类中，一般使用5%的显著性门限为标准。此外，当 $|{{\textit{z}}_{\rm{ab}}}| > 1.96$ 时，表明这两种分类方法的精度具有统计显著性差异； ${{\textit{z}}_{\rm{ab}}} > 0$ 时，表明方法a的分类精度优于方法b。

RGRF方法与其他方法在Indian Pines图像不同样本的McMemar显著性分析结果如表3所示。表3是以RGRF方法作为方法a，其他为方法b。在测试样本数为总样本数1%的情况下，以IFRF分类方法为例，代入式(10)进行计算，得到McMemar值是24.19，而以SnEPF为方法b时，McMemar值是12.72，因此RGRF方法优于IFRF和SnEPF。从表中可以看出，RGRF方法和其他对比方法的显著性检验结果大于零，且远大于1.96，这表明RGRF方法相对于其他对比方法具有显著性统计学意义，这是由算法本身的优势造成的而与随机样本造成的差异无关。

表 3 Indian Pines图像不同分类方法McMemar对比
Table 3 Comparison of McMemar values for different classification methods in Indian Pines image

下载CSV

分类方法	训练样本数
分类方法	1%	2%	3%	4%	5%
SVM	67.60	55.71	54.04	52.12	50.34
PCA	52.08	51.18	49.88	49.02	47.38
EPF	48.67	39.00	35.23	32.63	31.49
SnEPF	12.44	12.72	12.15	11.52	11.61
GCK	15.12	14.69	14.25	14.11	13.89
IFRF	24.19	17.94	13.33	10.32	9.49
RGF	42.73	33.21	30.74	29.11	25.58

表4则是RGRF方法与其他方法在University of Pavia图像不同样本的McMemar显著性分析结果。表中展示了训练样本数占总样本数0.2%、0.4%、0.6%、0.8%和1%时的McMemar值，同样以IFRF和SnEPF作为方法b为例分别代入式(10)，当样本数是0.2%时得到的McMemar值分别为47.93和18.91，所以RGRF方法在第2幅图像同样优于IFRF和SnEPF方法。从数据中也可以得出RGRF相对于其他对比方法具有显著性统计学意义。

表 4 University of Pavia图像不同方法McMemar对比
Table 4 Comparison of McMemar values for different classification methods in University of Pavia image

下载CSV

分类方法	训练样本数
分类方法	0.2%	0.4%	0.6%	0.8%	1%
SVM	86.61	84.66	83.34	79.17	76.02
PCA	84.50	82.47	80.24	79.81	76.73
EPF	65.08	57.88	50.77	45.01	40.31
SnEPF	18.91	17.98	13.13	12.74	10.68
GCK	61.96	59.19	44.72	45.69	44.33
IFRF	47.93	41.96	35.88	33.71	31.76
RGF	68.12	66.26	55.08	50.08	44.72

需要注意的是，表3和表4中的McMemar值随着样本的减少而增加，这表明RGRF方法在样本越少的情况下，优势越明显，进一步证明了RGRF方法适用于样本较少时的高光谱图像分类。

4.3 参数设置

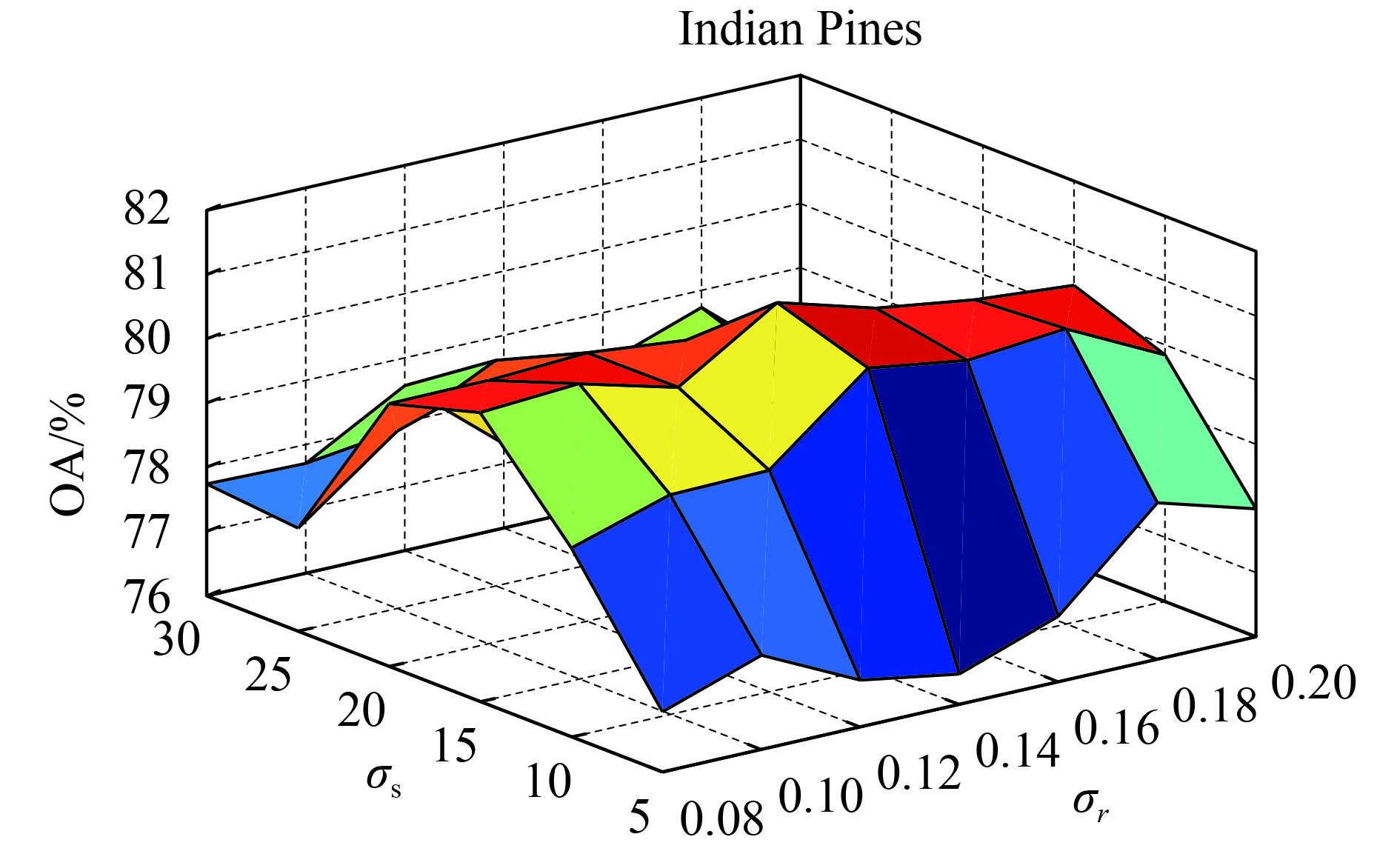
不同的参数设置会对RGRF方法的分类精度产生一定的影响。图9展示了对于Indian Pines图像，当空间标准差 ${\sigma _{\rm{s}}}$ 和光谱标准差 ${\sigma _{\rm{r}}}$ 变化时，RGRF方法的总体精度(OA)的变化，取训练样本数为总体样本数的1%。从图9中可以看出，当 ${\sigma _{\rm{s}}}$ 值非常小时，由于特征提取过程中仅考虑非常有限的局部空间信息，因而最终的分类精度不高；当 ${\sigma _{\rm{s}}}$ 值非常大时，则会滤波掉有用边缘，造成图像平滑过度，而RGRF方法的OA精度也呈现了明显下降趋势。 ${\sigma _{\rm{r}}}$ 值变化对最终的分类精度影响不大。根据观察，在Indian Pines图像上，当 ${\sigma _{\rm{s}}}$ 和 ${\sigma _{\rm{r}}}$ 的值分别为15和0.14时，RGRF方法的总体精度取得了最优值。

为了展示迭代次数对RGRF方法的影响，分别在Indian Pines图像和University of Pavia图像上，使用RGRF方法做了多次迭代的滤波实验，其表现结果如图10和图11所示。可以看出，两幅图像在高斯滤波后的图像被模糊化，但随着迭代次数的增加，较强的边缘在逐步恢复，同时图像内部的噪声和细小的纹理结构被消除，如图10与图11中(c)、(d)和(e)所示。

图 9 Indian Pines图像不同的 ${\sigma _{\rm{s}}}$ 和 ${\sigma _{\rm{r}}}$ 值对分类精度的影响

Fig. 9 The influence of different ${\sigma _{\rm{s}}}$ and ${\sigma _{\rm{r}}}$ values on classification accuracy of Indian Pines data set

图 10 使用RGRF方法在Indian Pines图像不同迭代次数的结果图

Fig. 10 The result graph of different iterations using the RGRF filtering in Indian Pines image

图 11 使用RGRF在University of Pavia图像不同迭代次数的结果图

Fig. 11 The result graph using the rolling guided recursive filtering of different iterations in University of Pavia image

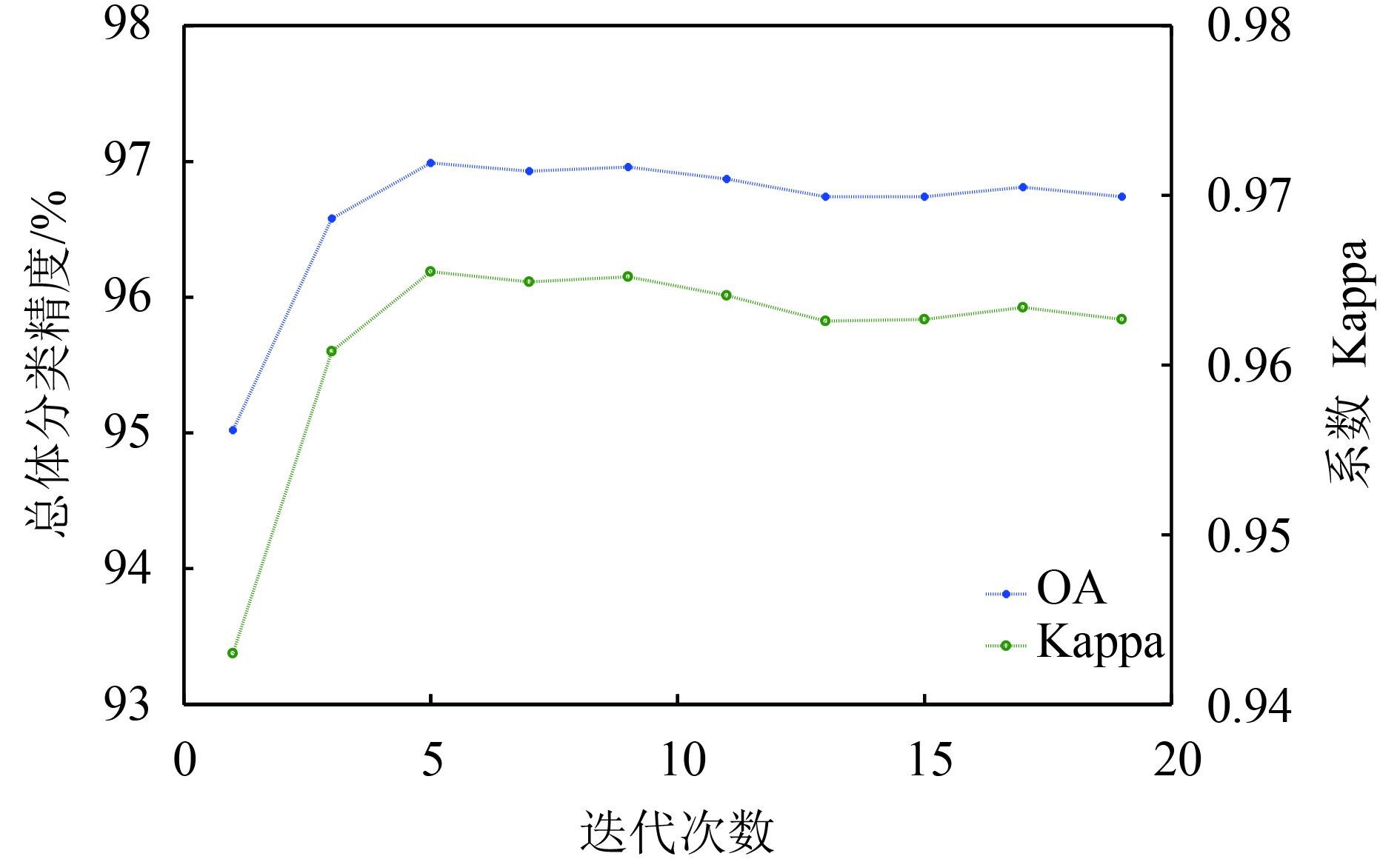
图12展示了当训练样本数为5%时，Indian Pines图像在不同迭代次数下总体分类精度与Kappa系数的变化图。可以看出，随着迭代次数的增加，总体分类精度(OA)和Kappa系数都实现大幅度上升。当迭代次数达到5时，精度达到最高，约为97%。随着迭代次数进一步增加，精度的变化较为平稳。考虑到迭代所需的时间代价，本文默认设置的迭代次数为5。

图 12 不同迭代次数在Indian Pines数据集的总体分类精度与Kappa系数

Fig. 12 Overall accuracy and Kappa with different iteration times on Indian Pines data set

4.4 讨论

本文提出的滚动引导递归滤波RGRF方法是受滚动引导滤波RGF方法启发，并在此基础上进行改进得到的方法。与RGF方法相比，RGRF方法主要有两点不同：(1)RGRF方法在滤波之前使用了PCA方法对图像进行了降维，这一方面可以有效地消除高光谱图像中存在的噪声，另一方面可以缓解分类“休斯”现象，同时降低滤波和分类处理的计算量；(2)RGRF方法使用域变换递归滤波方法替换RGF方法中采用的双边滤波方法，原因为双边滤波器在强边缘处具有高斯脉冲响应，而递归滤波器在强边缘处具有指数脉冲响应，从而阻止了光谱信息跨越强边缘继续传播，有效地保护了强边缘。由于这两个原因，使得RGRF方法在图像滤波结果和分类精度上较RGF方法有显著提升。

5 结　论

本文提出了一种新的高光谱遥感图像分类方法RGRF。该方法利用尺度空间理论，在滤波过程中能够控制细节的级别，从而实现小尺度结构消除、大尺度结构保留的目标；利用基于测地线距离的等距域变换和递归滤波的指数衰减特性，阻止了信号跨越强边缘传播，从而能够产生比RGF方法更清晰的边缘。在两个真实高光谱数据集上实验表明，不管是分类精度还是可视化分类结果的效果图，RGRF方法都是最优的，在样本稀少情况下优势尤为明显。

本文方法还有其他几个优点：(1)使用PCA对高光谱图像降维，不仅可以减少图像噪声，而且能够大幅降低边缘保持滤波和图像分类操作的时间；(2)只需要少量迭代就可以获得好的滤波结果和分类精度。由于每次迭代可以在线性时间内完成，RGRF方法在执行时间上是非常高效的，从而能够满足高光谱图像实时处理和分类的需求。

下一步的研究内容：目前边缘保持滤波方法大多是利用PCA变换后第一主成分作为引导图像对原始图像进行滤波，边缘位置和边缘强弱的判定是依靠第一主成分图像梯度的变化。实际上，现有的边缘检测算法也可以得到边缘的位置和强弱信息，因此下一步将研究如何将边缘检测算法(黄秋燕等，2014)提取的边缘信息结合到边缘保持滤波方法中，获得更好的滤波图像，从而有利于图像分类精度进一步提高。

参考文献(References)

Altman E I, Marco G and Varetto F. 1994. Corporate distress diagnosis: comparisons using linear discriminant analysis and neural networks (the Italian experience). Journal of Banking and Finance, 18 (3): 505–529. [DOI: 10.1016/0378-4266(94)90007-8]

Amjady N, Daraeepour A and Keynia F. 2010. Day-ahead electricity price forecasting by modified relief algorithm and hybrid neural network. IET Generation, Transmission and Distribution, 4 (3): 432–444. [DOI: 10.1049/iet-gtd.2009.0297]

Balasubramanian M, Schwartz E L, Tenenbaum J B, de Silva V and Langford J C. 2002. The isomap algorithm and topological stability. Science, 295 (5552): 7 [DOI: 10.1126/science.295.5552.7a]

Baldwin J L, Bateman R M and Wheatley C L. 1990. Application of a neural network to the problem of mineral identification from well logs. The Log Analyst, 31 (5): 279–293.

Boggs J L, Tsegaye D T, Coleman T L, Reddy K C and Fahsi A. 2003. Relationship between hyperspectral reflectance, soil nitrate-nitrogen, cotton leaf chlorophyll, and cotton yield: a step toward precision agriculture. Journal of Sustainable Agriculture, 22 (3): 5–16. [DOI: 10.1300/J064v22n03_03]

Chen C, Zhang L J, Bu J J, Wang C and Chen W. 2010. Constrained Laplacian Eigenmap for dimensionality reduction. Neurocomputing, 73 (4/6): 951–958. [DOI: 10.1016/j.neucom.2009.08.021]

Cui B G, Ma X D, Xie X Y, Ren G B and Ma Y. 2017. Classification of visible and infrared hyperspectral images based on image segmentation and edge-preserving filtering. Infrared Physics and Technology, 81 : 79–88. [DOI: 10.1016/j.infrared.2016.12.010]

Cui B G, Ma X D and Xie X Y. 2017. Hyperspectral image de-noising and classification with small training samples. Journal of Remote Sensing, 21 (5): 728–738. [DOI: 10.11834/jrs.20176239] ( 崔宾阁, 马秀丹, 谢小云. 2017. 小样本的高光谱图像降噪与分类. 遥感学报, 21 (5): 728–738. [DOI: 10.11834/jrs.20176239] )

Donoho D L and Grimes C. 2003. Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data. Proceedings of the National Academy of Sciences of the United States of America, 100 (10): 5591–5596. [DOI: 10.1073/pnas.1031596100]

Fauvel M, Chanussot J and Benediktsson J A. 2009. Kernel principal component analysis for the classification of hyperspectral remote sensing data over urban areas. EURASIP Journal on Advances in Signal Processing, 2009 : 783194 [DOI: 10.1155/2009/783194]

Foody G M. 2004. Thematic map comparison. Photogrammetric Engineering and Remote Sensing, 70 (5): 627–633. [DOI: 10.14358/PERS.70.5.627]

Gastal E S L and Oliveira M M. 2011. Domain transform for edge-aware image and video processing. ACM Transactions on Graphics, 30 (4): 69 [DOI: 10.1145/2010324.1964964]

Gualtieri J A and Cromp R F. 1999. Support vector machines for hyperspectral remote sensing classification//Proceedings of the SPIE 3584, 27th AIPR Workshop: Advances in Computer-Assisted Recognition. Washington, DC, United States: SPIE [DOI: 10.1117/12.339824]

Huang Q Y, Xiao P F, Feng X Z and Wang Y. 2014. Edge detection from high resolution remote sensing image combining phase congruency with total variation model. Journal of Image and Graphics, 19 (3): 439–446. ( 黄秋燕, 肖鹏峰, 冯学智, 王玥. 2014. 结合相位一致与全变差模型的高分辨率遥感图像边缘检测. 中国图象图形学报, 19 (3): 439–446. )

Hughes G. 1968. On the mean accuracy of statistical pattern recognizers. IEEE Transactions on Information Theory, 14 (1): 55–63. [DOI: 10.1109/TIT.1968.1054102]

Kang X D, Li S T and Benediktsson J A. 2014a. Feature extraction of hyperspectral images with image fusion and recursive filtering. IEEE Transactions on Geoscience and Remote Sensing, 52 (6): 3742–3752. [DOI: 10.1109/TGRS.2013.2275613]

Kang X D, Li S T and Benediktsson J A. 2014b. Spectral–spatial hyperspectral image classification with edge-preserving filtering. IEEE Transactions on Geoscience and Remote Sensing, 52 (5): 2666–2677. [DOI: 10.1109/TGRS.2013.2264508]

Li J, Marpu P R, Plaza A, Bioucas-Dias J M and Benediktsson J A. 2013. Generalized composite kernel framework for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 51 (9): 4816–4829. [DOI: 10.1109/TGRS.2012.2230268]

Lindeberg T. 1994. Scale-space theory: a basic tool for analyzing structures at different scales. Journal of Applied Statistics, 21 (1/2): 225–270. [DOI: 10.1080/757582976]

Palumbo N F, Harrison G A, Blauwkamp R A and Marquart J K. 2010. Guidance filter fundamentals. Johns Hopkins Apl Technical Digest, 29 (1): 60–70.

Paris S, Kornprobst P and Tumblin J. 2009. Bilateral Filtering. Hanover, MA, USA: Now Publishers Inc.: 1911–1938

Peng H Y, Jiang C F, Fang X and Liu J S. 2014. Variable selection for Fisher linear discriminant analysis using the modified sequential backward selection algorithm for the microarray data. Applied Mathematics and Computation, 238 : 132–140. [DOI: 10.1016/j.amc.2014.03.141]

Pontius J, Martin M, Plourde L and Hallett R. 2008. Ash decline assessment in emerald ash borer-infested regions: a test of tree-level, hyperspectral technologies. Remote Sensing of Environment, 112 (5): 2665–2676. [DOI: 10.1016/j.rse.2007.12.011]

Prasad S and Bruce L M. 2008. Limitations of principal components analysis for hyperspectral target recognition. IEEE Geoscience and Remote Sensing Letters, 5 (4): 625–629. [DOI: 10.1109/LGRS.2008.2001282]

Sakar C O, Kursun O and Gurgen F. 2012. A feature selection method based on kernel canonical correlation analysis and the minimum Redundancy-Maximum Relevance filter method . Expert Systems with Applications, 39 (3): 3432–3437. [DOI: 10.1016/j.eswa.2011.09.031]

Spolaôr N, Cherman E A, Monard M C and Lee H D. 2014. ReliefF for multi-label feature selection//Proceedings of 2013 Brazilian Conference on Intelligent Systems. Fortaleza, Brazil: IEEE [DOI: 10.1109/BRACIS.2013.10]

van Ruitenbeek F J A, Debba P, van der Meer F D, Cudahy T, van der Meijde M and Hale M. 2006. Mapping white micas and their absorption wavelengths using hyperspectral band ratios. Remote Sensing of Environment, 102 (3/4): 211–222. [DOI: 10.1016/j.rse.2006.02.012]

Wang L P. 2015. Feature selection algorithm based on conditional dynamic mutual information. International Journal on Smart Sensing and Intelligent Systems, 8 (1): 316–337. [DOI: 10.21307/ijssis-2017-761]

Wang Y, Niu R Q and Yu X. 2010. Anisotropic diffusion for hyperspectral imagery enhancement. IEEE Sensors Journal, 10 (3): 469–477. [DOI: 10.1109/JSEN.2009.2037800]

Zhang Q, Shen X Y, Xu L and Jia J Y. 2014. Rolling Guidance Filter//Proceedings of the 13th European Conference on Computer Vision. Zurich, Switzerland: Springer: 815–830 [DOI: 10.1007/978-3-319-10578-9_53]

摘要

关键词

Abstract

Key words

1 引 言

2 常用的滤波方法

2.1 递归滤波

2.2 滚动引导滤波

3 提出的方法

4 实验与讨论

4.1 实验数据集

4.2 实验

4.3 参数设置

4.4 讨论

5 结 论

参考文献(References)

1 引　言

5 结　论