|
收稿日期: 2017-09-03; 优先数字出版日期: 2018-01-01
基金项目: 国家自然科学基金(编号:41371492);国家重点研发计划项目(编号:2017YFB0503003);广西自然科学基金重点项目(编号:2016JJD110017)
第一作者简介: 赵海盟,1980年生,男,副教授,研究方向为无人机遥感、偏振仪器、卫星导航、嵌入式系统设计。E-mail:zhaohaimeng@163.com
通信作者简介: 晏磊,1956年生,男,教授,研究方向为偏振与无人机仿生遥感、高分辨率成像与遥感定标、仿生导航。E-mail:lyan@pku.edu.cn
中图分类号: TP701
文献标识码: A
|
摘要
在光学遥感中,水的强烈镜面反射性和角度选择性使探测器饱和或反射率过低而难以提取有效信息,雪的强反射性和表面敏感性使传感器难以直接探测,植被指数在不同反射强度下的敏感性对经典植被监测方法的精度和有效性提出挑战。偏振手段可大大提高水、雪和植被的遥感识别能力。本文利用地物遥感偏振光效应的高信息—背景反差比滤波特性,解决光学遥感中水、雪的不可测量问题,以及破除植被强光反射条件下无法精细监测的瓶颈。本文从偏振高信息—背景反差比滤波特性理论出发,通过实验证明偏振手段可有效提升水的信息—背景反差比、剥离70%以上的太阳耀光,为强反射特性下的积雪遥感提供必要方法,并最高降低78%的植被监测误差。本文首次推导证明了偏振探测高信息—背景反差比滤波特性机理,在理论指导和实验深化引导下解决了光学遥感中水、雪因探测器饱和而无法测量的问题,并破除了强反射条件下植被无法精细监测的瓶颈。
关键词
偏振, 信息—背景反差比, 滤波特性, 水, 雪, 植被
Abstract
In optical remote sensing, the strong specular reflectivity and angle selectivity of water lead to detector saturation or to very low reflectivity for extracting effective information. The strong reflection characteristics and surface sensitivity of the snow limit the capability of the sensor to detect directly. Thus, water and snow are problems of passive remote sensing. The sensitivity of vegetation index under different reflection intensities in high-resolution quantitative remote sensing also challenges the accuracy and effectiveness of classical vegetation monitoring methods. This study aims to solve the bottleneck of water and snow that cannot be measured by optical remote sensing. This study uses the fourth law of remote sensing polarization effect, that is, high information–background ratio filtering characteristics. The polarization information can be obtained by adding the polarizer to the sensor in any direction. The Fessenkov method can be used to calculate the Degree Of Polarization (DOP) according to the data of different polarization angles and thus provide a new solution to the abovementioned remote sensing problems. The polarizing method can effectively enhance the information of the water-background ratio, which strips more than 70% of the glitter, provides the necessary method for the remote sensing of snow, and reduce up to 78% of error in vegetation monitoring. The mechanism of high-information-background ratio filtering is proved for the first time. Under the theoretical guidance and deepening of the experiment, the problems that water and snow can hardly be measured, and the bottleneck that vegetation cannot be accurately measured under strong reflection are solved.
Key words
polarization, information-background ratio, filter characteristics, water, snow, vegetation
1 引 言
中国的海洋战略对于海藻、赤潮、水体富营养化等环境问题以及利用雪粒子化学成分进行区域污染及演化分析、冰川消融溯源、雪灾监测等的高分辨率遥感探测需求迫在眉睫。但目前,光学遥感对地观测主要应用于地物电磁波辐射能量适中的条件。对于辐射强度过强的目标,如冰雪区域、耀斑、部分叶片的镜面反射,遥感信号过强会导致探测器饱和(罗杨洁 等,2006);在遥感信息暗目标表达方面,探测器又会因探测到的信号过弱而无法对地物进行有效反演识别(吴太夏 等,2010)。
偏振是与光强、频率、相位并列的遥感电磁波的4大基本属性之一。波的振动方向对于传播方向的不对称性称为偏振,是横波特有的现象(晏磊,2014)。针对上述光学遥感存在的问题,偏振遥感具有“强光弱化”、“弱光强化”的特点,可以有效分析地表过强和过弱反射的特征,从而提升遥感数据的利用率和遥感反演的精度。前人通过对地表水、土、岩和植被4大对象的研究,探索出地物偏振遥感的5大规律,高信号—背景反差比滤波特性就是其中之一。
本文首先介绍了偏振光谱数据处理和高信息—背景反差比滤波特性的基本原理,其次分别从卫星和地面测量两个角度将该特性应用于水体卫星遥感监测和水面天空光及太阳耀光的剥离,然后通过分析不同粒径和不同污染程度积雪的偏振光谱和空间分布证明了偏振探测应用于积雪遥感的必要性,并基于此特性分析了将偏振手段应用于植被遥感监测相对于传统植被指数方法的优势。
2 基本原理与方法
2.1 地物偏振光谱数据处理原理
斯托克斯(Stokes)四参量法可以描述光波的强度和所有偏振态。I、Q、U、V 4个参量都是光强的时间平均值,分别表示偏振光强度、水平方向的线偏振光分量、45°方向的线偏振光分量和右旋圆偏振光分量,组成一个4维数学矢量,因此最少需要4个方程才能解出一个目标待测点的完整的Stokes参数。当入射光通过一个理想起偏器时,与参考方向成θ角的理想起偏器的米勒矩阵为Mp,则出射光的Stokes参数Sout为
| ${{S}_{{\rm{out}}}} = \left[ \begin{array}{l}{I'}\\{Q'}\\{U'}\\{V'}\end{array} \right] = {{M}_{\rm{p}}}\left[ \begin{array}{l}I\\Q\\U\\V\end{array} \right]$ | (1) |
式中,I、Q、U、V和I′、Q′、U′、V′分别表示入射光经过理想起偏器前后Stokes参数中的4个分量值。在目前的偏振遥感测量中,认为Stokes参量的第4个分量值很小(吴太夏,2010),故在一般情况下忽略不计,则可得出透射光强度Iout的表达式为
| ${I_{{\rm{out}}}} = {S_0} = \frac{1}{2}\left( {{S_0} + {\rm{cos}}2 q \cdot {S_1} + {\rm{sin}}2 q \cdot {S_2}} \right)$ | (2) |
式中,S0、S1、S2分别为Stokes矢量的I、Q、U3个参量。这样就可以通过在0°,60°,120° 3个偏振方向上的测量值I(0°)、I(60°)、I(120°),得到3个独立的方程,从而推演出待测目标的偏振信息,即Fessenkov方法(晏磊,2014):
| $\left\{ {\begin{aligned}& {I = \displaystyle\frac{2}{3}\left( {I\left( {0^\circ } \right) + I\left( {60^\circ } \right) + I\left( {120^\circ } \right)} \right)}\\& {Q = \displaystyle\frac{2}{3}\left( {2I\left( {0^\circ } \right) - I\left( {60^\circ } \right) - I\left( {120^\circ } \right)} \right)}\\& {U = \displaystyle\frac{2}{{\sqrt 3 }}\left( {I\left( {60^\circ } \right) - I\left( {120^\circ } \right)} \right)}\end{aligned}} \right.$ | (3) |
这种测量方法只用一个线偏振片,旋转3个方位角,即可得出Stokes参量I、Q、U的值,这种测量方法也目前偏振遥感最常用的方法。
则入射光的偏振度为
| $P = \frac{{\sqrt {{Q^2} + {U^2} + {V^2}} }}{I} \approx \frac{{\sqrt {{Q^2} + {U^2}} }}{I}$ | (4) |
入射光的偏振方位角为
| $q = \frac{1}{2}{\rm{arctan}}\left( {U/Q} \right)$ | (5) |
综上,将0°,60°,120° 3个偏振方向上的光谱测量值分别代入公式进行运算,即可得到对应的Stokes参数、偏振度和偏振角。
2.2 偏振光反射信息-背景高反差比原理
偏振具有“强光弱化”、“弱光强化”的特性。传感器探测到的偏振度为
| $\rho = \frac{{{r_{{\rm{sp}}}}}}{{{r_{\rm{s}}} + \left( {1 - {r_{\rm{s}}}} \right)\omega \rho }}$ | (6) |
式中,rsp为偏振反射率,可以认为是光谱不变量;rs表示光在物体表面直接反射的概率,ωρ表示光进入物体内部向上散射的概率,ω表示物体的单次散射反照率,ρ表示光在物体内部向上散射的概率。因此,物体的反射率(分母值)与偏振度ρ表现为负相关关系,从而实现了用偏振度表征地物时“强光弱化”、“弱光强化”的特性。
这一特性可以直接提高遥感研究中的信息—背景反差比。所谓信息—背景反差比即为目标物和背景之间的反射率比值,并用γr表示。假设目标m1和背景m2的反射率在可见光近红外波段内十分接近,则反射率rm1和rm2的信息—背景反差比为
| ${\gamma _{\rm{r}}} = \frac{{{r_{m1}}}}{{{r_{m2}}}} = \frac{{{r_{{\rm{s}},m1}} + \left( {1 - {r_{{\rm{s}},m1}}} \right){\omega _{m1}}{\gamma _{m1}}}}{{{r_{{\rm{s}},m2}} + \left( {1 - {r_{{\rm{s}},m2}}} \right){\omega _{m2}}{\gamma _{m2}}}} \approx 1.0$ | (7) |
在这种情况下,目标m1和背景m2的反射率差异很小,很难区分目标和背景。依据式(4)计算偏振度之后,二者偏振度的信息—背景反差比γp为
| ${\gamma _{\rm{p}}} = \frac{{{p_{m1}}}}{{{p_{m2}}}} = \frac{{{r_{{\rm{sp}},m1}}}}{{{r_{{\rm{sp}},m2}}}}\frac{{{r_{{\rm{s}},m2}} + \left( {1 - {r_{{\rm{s}},m2}}} \right){\omega _{m2}}{\gamma _{m2}}}}{{{r_{{\rm{s}},m1}} + \left( {1 - {r_{{\rm{s}},m1}}} \right){\omega _{m1}}{\gamma _{m1}}}} \approx \frac{{{r_{{\rm{sp}},m1}}}}{{{r_{{\rm{sp}},m2}}}}$ | (8) |
由于偏振反射率对物体表面粗糙度十分敏感,rsp, m1和rsp, m2比值会比对应反射率比值1.0大或小很多,即尽管在反射率上目标和背景的差异小,但是在偏振反射率上,差异却很大,有时甚至会达到数倍的关系,这也就增大了信号—背景反差比。
2.3 水表天空光和太阳耀光剥离原理
太阳耀光是在太阳光入射的镜面反射方向上观测到强烈的天空光。天空光与太阳耀光是影响水色遥感图像质量的关键因素。利用光的偏振特性剥离太阳耀光的物理基础是菲涅尔反射折射公式。设空气与水的折射率分别为n1和n2。光从大气入射,在气水界面上会发生反射和折射。将入射的自然光分解成振动方向相互垂直和振幅相等的两个独立分量,一个为振动面平行于入射面的线偏振光(简称为平行分量或P分量),另一个为振动面垂直于入射面的线偏振光(简称为垂直分量或S分量),则菲涅尔反射折射公式为
| ${r_{\rm{s}}} = \frac{{E_{1{\rm{s}}}'}}{{{E_{1{\rm{s}}}}}} = - \frac{{\sin ({i_1} - {i_2})}}{{\sin ({i_1} + {i_2})}}$ | (9) |
| ${r_{\rm{p}}} = \frac{{E_{1{\rm{p}}}'}}{{{E_{1{\rm{p}}}}}} = \frac{{\tan ({i_1} - {i_2})}}{{\tan ({i_1} + {i_2})}}$ | (10) |
| ${t_{\rm{s}}} = \frac{{E_{2{\rm{s}}}'}}{{{E_{1{\rm{s}}}}}} = \frac{{2\cos {i_1}\sin {i_2}}}{{\sin ({i_1} + {i_2})}}$ | (11) |
| ${t_{\rm{p}}} = \frac{{E_{2{\rm{p}}}'}}{{{E_{1{\rm{p}}}}}} = \frac{{2\cos {i_1}\sin {i_2}}}{{\sin ({i_1} + {i_2})\cos ({i_1} - {i_2})}}$ | (12) |
式中,E1、E′1和E2表示入射光、反射光和折射光的光矢量;i1和i2分别为入射角和折射角;rp和rs分别为P分量和S分量的振幅反射比;tp和ts分别为P分量和S分量的振幅透射比。
由式(9)—(12)可知当偏振片透光轴与入射面平行且入射光以布儒斯特角入射即i1+i2=π/2时,rp=0,反射光全为S分量,如果此时在传感器前加一个偏振片,其透光轴与光的入射平面平行(即为0°偏振,透光轴与光的入射平面垂直时称90°偏振),那么S分量的线偏振光将完全无法通过偏振片进入传感器,此时由传感器得到的将是带有水体内部信息的离水辐射能量,太阳耀光全部剥离。
当i1+i2≠π/2时,由菲涅尔反射折射公式可知,反射光中的P分量与部分S分量可重新合称为自然光,而剩余的部分S分量则仍然是线偏振光。这时,水面反射光为自然光和线偏振光组成的部分偏振光。设部分偏振光中自然光强In,线偏振光为Il,则水面反射光I0可以表示为
| ${I_0} = {I_{\rm{n}}} + {I_{\rm{l}}}$ | (13) |
设水中散射出的光强度为Ii,则传感器接收到的总的光强度I为
| $I = {I_0} + {I_{\rm{i}}} = {I_{\rm{n}}} + {I_{\rm{l}}} + {I_{\rm{i}}}$ | (14) |
在此,假设水中散射出的光看做自然光,由于自然光通过偏振片后的光强减半,所以90°偏振方向上,光强的计算方法为
| ${I_{{{90}^ \circ }}} = \frac{1}{2}{I_{\rm{n}}} + {I_{\rm{l}}} + \frac{1}{2}{I_{\rm{i}}}$ | (15) |
0°偏振方向上,光强的计算方法为
| ${I_{{0^ \circ }}} = \frac{1}{2}{I_{\rm{n}}} + \frac{1}{2}{I_{\rm{i}}}$ | (16) |
由(15)、(16)式有
| ${I_{\rm{l}}} = {I_{{{90^ \circ}}}}- {I_{{0^ \circ}}} = {I_{\rm{s}}} - {I_{\rm{p}}}$ | (17) |
式中,Is为水面反射光的S分量光;Ip为水面反射光P分量光。由于光强与振幅的平方成正比,又由于入射光为自然光,所以E1s=E1p,从而有
| $\frac{{{I_{\rm{s}}}}}{{{I_{\rm{p}}}}} = \displaystyle\frac{{|{r_{\rm{s}}}{|^2}}}{{|{r_{\rm{p}}}{|^2}}} = \displaystyle\frac{{{{\left| {\displaystyle\frac{{E{'_{1{\rm{s}}}}}}{{{E_{1{\rm{s}}}}}}} \right|}^2}}}{{{{\left| {\displaystyle\frac{{E{'_{1{\rm{p}}}}}}{{{E_{1{\rm{p}}}}}}} \right|}^2}}} = {\left( {\frac{{\cos ({i_1} - {i_2})}}{{\cos ({i_1} + {i_2})}}} \right)^2}$ | (18) |
设水面反射光的偏振度为P,则由偏振度的定义可得:
| $\begin{aligned}P & = \frac{{{I_{\rm{l}}}}}{{{I_0}}} = \frac{{{I_{\rm{s}}} - {I_{\rm{p}}}}}{{{I_{\rm{s}}} + {I_{\rm{p}}}}} =\\ & \displaystyle\frac{{{{\cos }^2}({i_1} - {i_2}) - {{\cos }^2}({i_1} + {i_2})}}{{{{\cos }^2}({i_1} - {i_2}) + {{\cos }^2}({i_1} + {i_2})}} = \frac{{{I_{{{90}^ \circ}}} - {I_{{0^ \circ}}}}}{{{I_{{0^ \circ}}}}}\end{aligned}$ | (19) |
则水面反射光强为
| ${I_0} = \frac{{{{\cos }^2}({i_1} - {i_2}) + {{\cos }^2}({i_1} + {i_2})}}{{{{\cos }^2}({i_1} - {i_2}) - {{\cos }^2}({i_1} + {i_2})}}({I_{{{90}^ \circ}}} - {I_{{0^ \circ}}})$ | (20) |
由于n1sini1=n2sini2,所以当光线的入射角i1已知时,就可以计算出折射角i2的大小。
综上所述,以任意观测角度观测时,通过对0°偏振和90°偏振的测量,就可以计算得到水表反射光,进而在总能量中减去这部分能量,就可以消除水表反射光对离水辐亮度测量的影响。
2.4 偏振植被遥感监测原理
在植被遥感中,当传感器接收到的能量信号过弱或过强时都会严重影响植被反演精度。接收到的反射信号过强时可能会使传感器信号饱和,而信号过弱又会干扰植被的识别。植被指数VIs(Vegetation Indexes, )能够很好的反映出植物的生物物理性质,但由于同时获取植被高光谱、高空间分辨率影像的限制,会忽略强反射或阴影条件下进行植被检测、反演的误差分析(Zhang 等,2011)。可见,植被遥感的定量化必须考虑到过强、过弱反射。基于地基偏振高光谱成像系统FISS-P,可以在获得地物偏振高光谱信息的同时获得高空间分辨率的影像,从而可以获得在阴影或强反射区域的植被的单个像元偏振光谱信息,以研究植被在反射过强或过弱条件下的偏振特性及其滤波作用。本研究实验采用0°,60°及120°的偏振片进行Stokes参量测量,即式(3)所示方法计算。
对于0°、60°和120°偏振方位角获取的反射强度适中的植被光强I(0°)、I(60°)和I(120°),当植被反射过强或过弱时,此时探测器获取的光强为kI(0°)、kI(60°)和kI(120°),系数k为植被反射强度变化时引起的探测器接收的光强(能量)的变化。根据Fessenkov方法求解Stokes参量原理,则反射过强或过暗条件下对应的计算公式如下(Schott,2009;曹汉军 等,2002):
| $\left\{ {\begin{aligned}& {I' = \displaystyle\frac{2}{3}\left( {kI\left( {0^\circ } \right) + kI\left( {60^\circ } \right) + kI\left( {120^\circ } \right)} \right)}\\& {Q' = \displaystyle\frac{2}{3}\left( {2kI\left( {0^\circ } \right) - kI\left( {60^\circ } \right) - kI\left( {120^\circ } \right)} \right)}\\& {U' = \displaystyle\frac{2}{{\sqrt 3 }}\left( {kI\left( {60^\circ } \right) - kI\left( {120^\circ } \right)} \right)}\end{aligned}} \right.$ | (21) |
式中,I′、Q′、U′和I、Q、U分别代表则植被在过强或过暗照度条件和正常照度条件下的Stokes参量。则过强或过暗条件下线偏振度DoLP′为
| $\begin{aligned}DoL{P'} = & \frac{{\sqrt {Q{'^2} + U{'^2}} }}{{I'}} = \frac{{\sqrt {{{\left( {kQ} \right)}^2} + {{\left( {kU} \right)}^2}} }}{{{{\left( {kI} \right)}^2}}} = \\& \frac{{\sqrt {{Q^2} + {U^2}} }}{{{I^2}}} = DoLP\end{aligned}$ | (22) |
可以看出,同一探测物体在不同照度条件下具有相同线偏振度,由于偏振具有高信息-背景反差比滤波特性,被探测物体的线偏振度并不会因为反射过强或过弱而产生干扰,即不同物体的偏振反射特征主要由物体的本质类别决定。
2.5 实验偏振探测仪器
用于偏振机理验证的地基多角度偏振光谱仪及成像设备与航空航天偏振遥感探测器相互促进,取得了巨大发展。在国内,中科院长春光学精密机械研究所1998年研制的多角度偏振反射光谱测量仪较早的应用于地物偏振机理的研究(吴太夏,2006),在此基础上,东北师范大学研制开发了室内大型多角度偏振高光谱测量装置(孙仲秋,2013)。中科院安徽光学精密机械研究所李新等人(2008)设计的多角度测量系统可以实现室外多角度测量。在国外,芬兰大地测量研究所的Suomalainen等人(2009a, 2009b)利用FIGIFIGO多角度偏振光谱仪对地物进行偏振特性研究,并不断对仪器进行改进优化,配合地物偏振反演模型的需要。本文关于雪的多角度偏振特性就是基于该仪器进行探测的(图1(a))。
本团队自主研制的仪器实现了对本文中水和植被的多角度偏振观测。李俊生等人(2013)自行设计并制作了一套手持式多角度水面光谱测量杆(图1(b)),能够控制光谱仪探头角度,配合ASD光谱仪及偏振探头,从而实现对水面的多角度偏振探测。Zhang等人(2011)和Tong等人(2014)研制的地基高光谱偏振成像仪FISS-P(图1(c))可以同时获取地物高空间、高光谱分辨率偏振影像,为本文利用偏振手段进行植被遥感监测提供了前提。
3 实验验证与分析
3.1 偏振探测高信息—背景反差比滤波特性卫星遥感数据验证
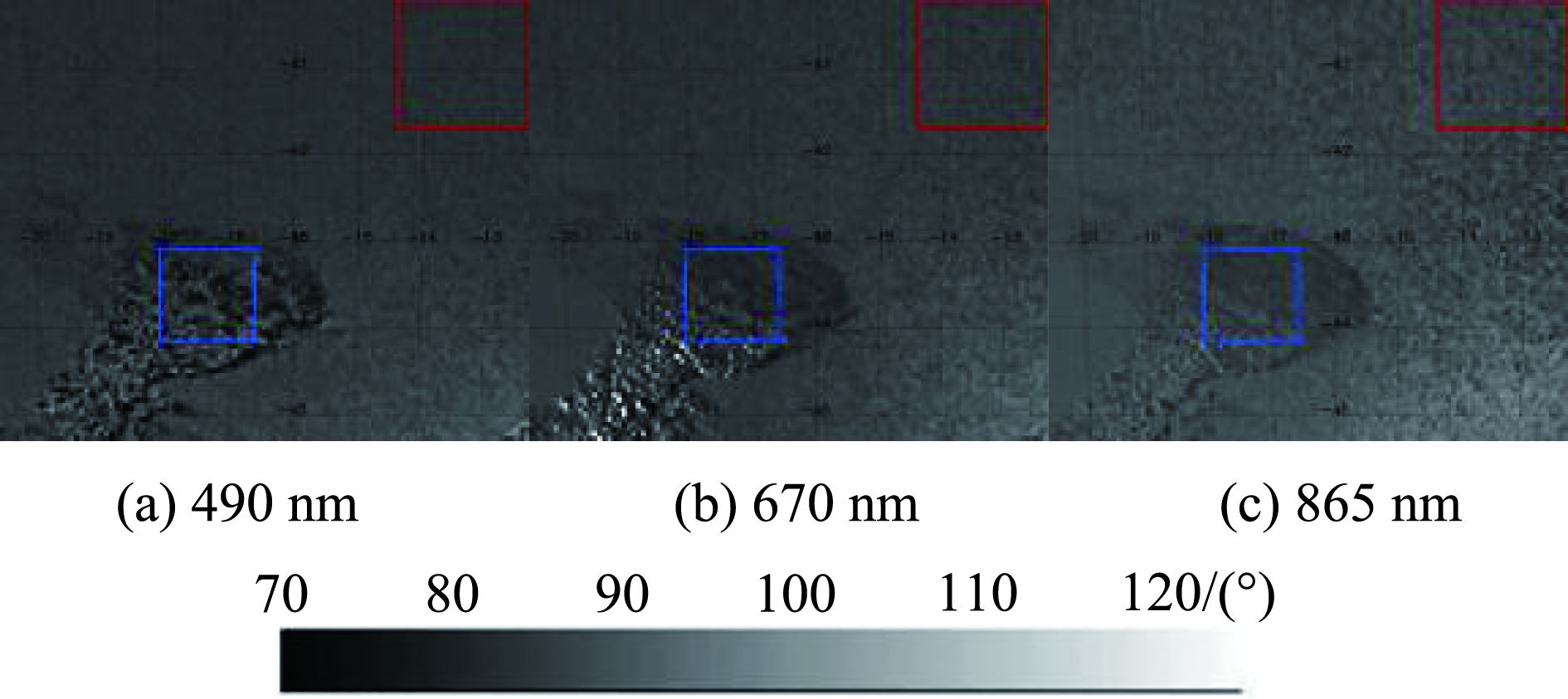
偏振的高信息—背景比滤波特性的原理为低反射率地物的遥感提供了一条重要的观测手段。为了验证星载多角度偏振遥感器对水体识别与反演的优势,对比PARASOL卫星数据中截取的2008年11月29日位于大西洋某海域的无偏和偏振卫星图像(吴太夏 等,2010)。图2(a)、(b)、(c)分别对应490 nm、670 nm和865 nm的反射强度图像。图2中白色区域为云,黑色区域为海水。图3所示的是对应波长的偏振度图像。
水体探测中,海水作为目标信号时,云作为背景信号。从图3中可以看出,各波长对应的偏振度图像的水体部分亮度都高于强度图像的水体部分亮度,而云的亮度则远低于强度图像。表1将图1和图2的图像中的红框区域(水体)和蓝框区域(云)的亮度的平均值进行统计,并计算了二者的信息—背景比。信息—背景比定义为方框内水的亮度平均值与云的亮度平均值的比值。可以看出,在背景信号很强的条件下,偏振度图像将目标信号由强度图像中的弱信号变为偏振度图像中的强信号,而将背景信号则变为相对较弱的信号,各波段的信息—背景比分别提升了8.14倍、41.67倍和55.50倍。490 nm由于大气偏振、水体吸收等因素的影响而倍数较小,但总体上水体偏振度图像的信息—背景比要远大于其反射率强度图像。该效应有利于通过亮度分割等手段进行水体影像的识别与分类,以提高遥感解译与反演精度。
表 1 水体偏振度与强度图像的平均亮度值及信息-背景反差比
Table 1 The average brightness and information-background ratio of water’s DOP and intensity images
| 波段 | ||||
| 490 nm | 670 nm | 865 nm | ||
| 反射率图像 | 水 | 14.07 | 3.47 | 1.97 |
| 云 | 97.77 | 102.22 | 107.37 | |
| 信息–背景比 | 0.14 | 0.03 | 0.02 | |
| 偏振度图像 | 水 | 57.25 | 62.51 | 72.49 |
| 云 | 50.31 | 50.16 | 65.16 | |
| 信息–背景比 | 1.14 | 1.25 | 1.11 | |
3.2 水表天空光与太阳耀光偏振剥离实验验证
利用偏振片可以不同程度地剥离天空光,从而大幅提高目标信号—背景反差比。如图4,当偏振片旋转到某一角度时,表面反射强光通过偏振片滤除为弱反射信号,水下目标很好地展现出来,成为强反射信号,从而大幅提升了信号—背景比(晏磊,2014)。
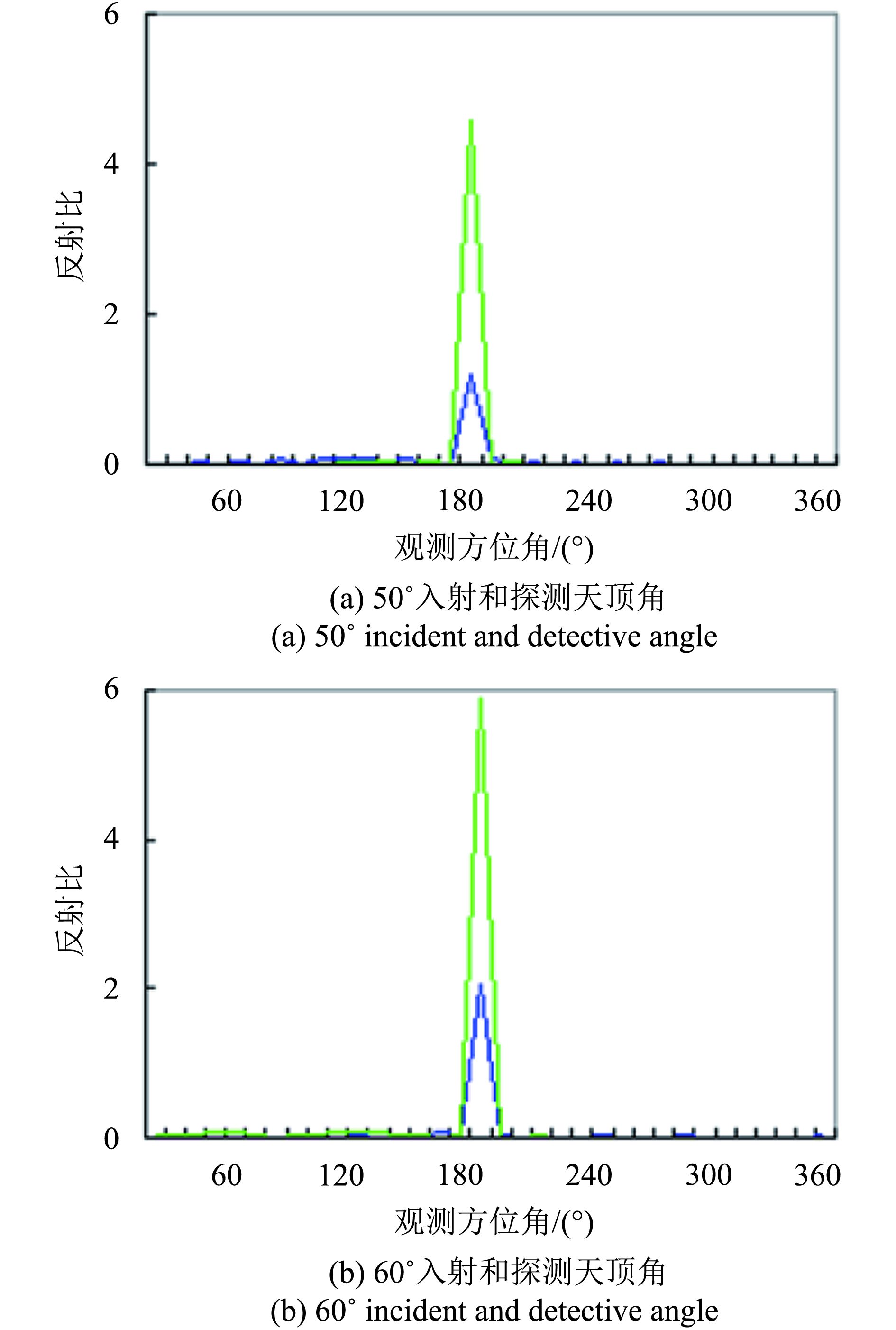
为了验证偏振测量剥离太阳耀光的效果,利用偏振光谱测量仪对水体的镜面反射进行实验。图5、图6所示的分别为纯净水体在入射角为53°、50°、60°时在波段为670—690 nm,方位角为0°—360°时相应探测角时的0度偏振、二向性反射(不配偏振镜头所测数据)的反射比波谱曲线,横坐标为方位角,纵坐标为相对方向反射比。
从图5可以看出发现,当光线入射角为布儒斯特角(53°)时,水体反射光为偏振化方向垂直于入射面的完全偏振光,此时传感器前偏振器的偏振方位角为0°,被偏振器完全吸收,理论上全部剥离了太阳耀光,剥离效率达到90%以上。但0°偏振反射比还有一定的反射峰,并不是理论上的零值,这跟实验中有一定的杂光干扰以及布儒斯特角的角度控制的精度有一定的关系,由于仪器角度定位的精度只能精确到度,而纯净水体的布儒斯特角应为53.1°,该突出部分应该是由非偏振光的影响而形成。
从图6(a)和(b)可以看出,入射角为50°、60°,即不是布儒斯特角的时候,相应探测角上0°偏振反射比的值仍然大大小于无偏时反射比的值,图6(a)的0°偏振反射比的值为1.192,无偏反射比的值为4.571,其剥离效率为73.92%;图6(b) 的0°偏振反射比的值为2.036,无偏反射比的值为5.871,其剥离效率为65.32%。这说明了越接近布儒斯特角,其剥离效果越佳。其原因是越接近布儒斯特角,反射光中的自然光成分逐渐减少,偏振光成分逐渐增多;水体反射光中的偏振光部分理论上可完全剥离(罗杨洁 等,2006,2007)。
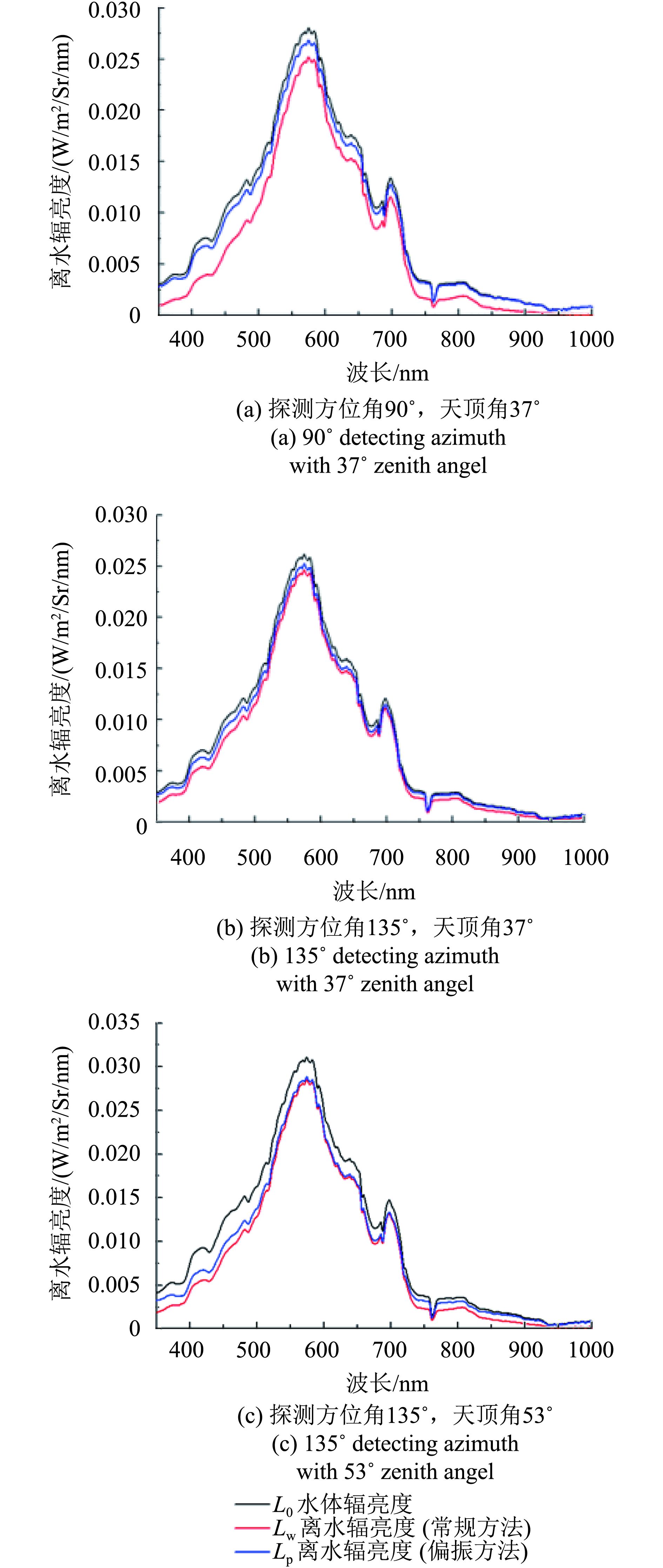
传统的水表天空光反射剥离的方法是水面以上法(李铜基 等,2001),即测量入射天空光的辐亮度Lsky,通过菲涅尔公式计算得到的水表反射率r计算得到水表反射的天空光辐亮度r·Lsky,然后从测量得到的辐亮度L中减去该辐亮度,即可得到离水辐亮度Lw。
为了验证偏振测量剥离天空光的效果,将偏振测量得到的离水辐亮度与常规测量辐亮度计算得到的离水辐亮度进行对比。如图7所示。为了不受水表镜面反射影响,规定观测方位与入射方位夹角为90°—135°(唐军武,1999)。从图7中可以看出,全部3个观测角度测量的偏振光谱都可以起到剥离天空光的作用,其中偏振剥离天空光最好的观测角度是135°探测方位角和53°探测天顶角,这与菲涅尔反射折射定律是一致的(申茜 等,2016)。
相比于常规的离水辐射提取方式,利用偏振探测去除天空光反射从而提取离水辐射存在诸多优势。对于实验过程,传统方式需要不断调整观测方向,同时或先后测量某个方向的水体辐亮度以及对称方向的天空光;而偏振探测在任意观测几何下只需要旋转偏振片探测0°和90°偏振方向上的能量即可获得天空光反射能量,这既简化了实验流程又减小了不断调整仪器所带来的误差和时间上的不确定性。从上述结果来看,相对于传统方法,利用偏振方法剥离天空光存在其适用条件,即布儒斯特角附近观测时效果达到最佳。
3.3 雪的偏振高信息—背景反射比滤波特性实验验证
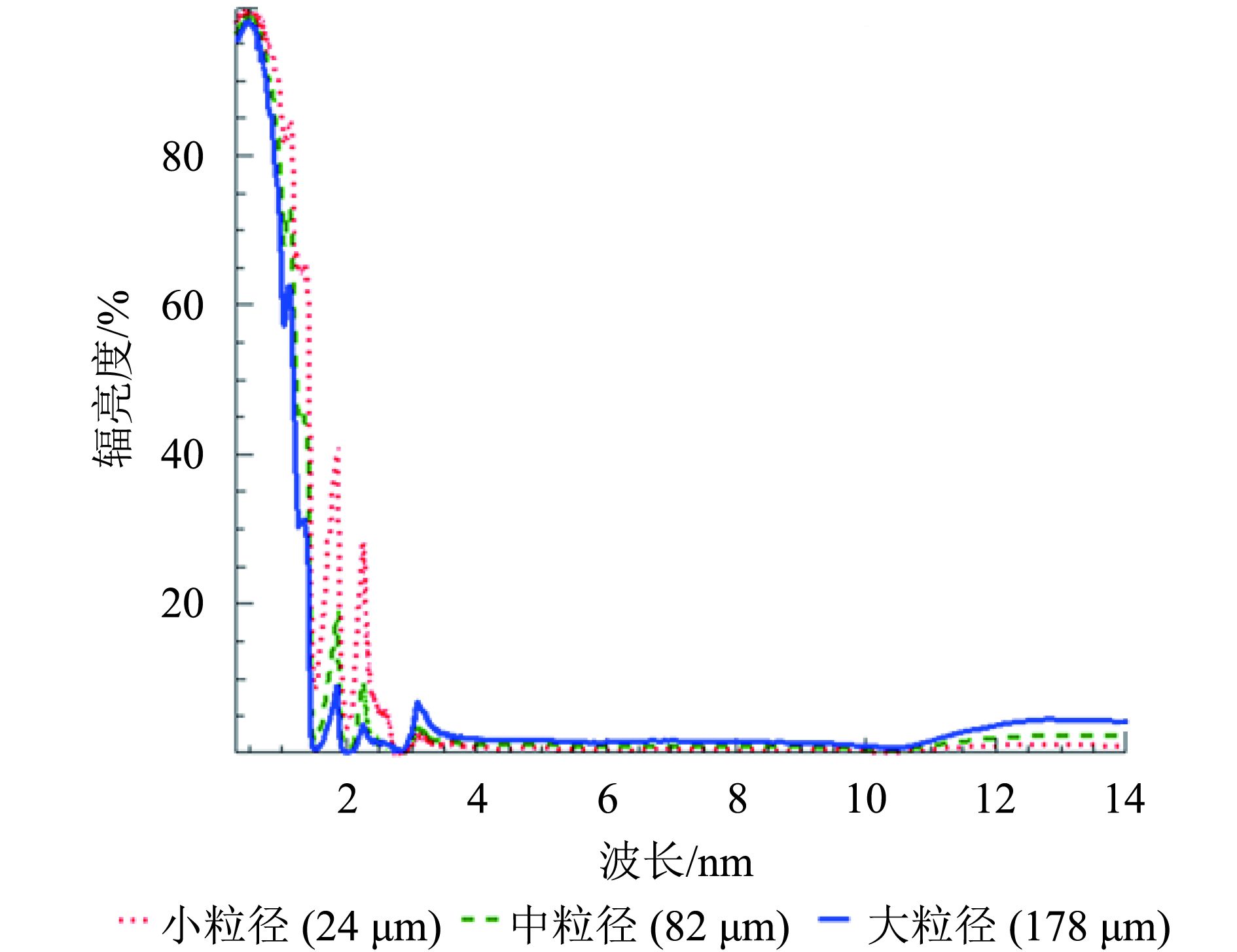
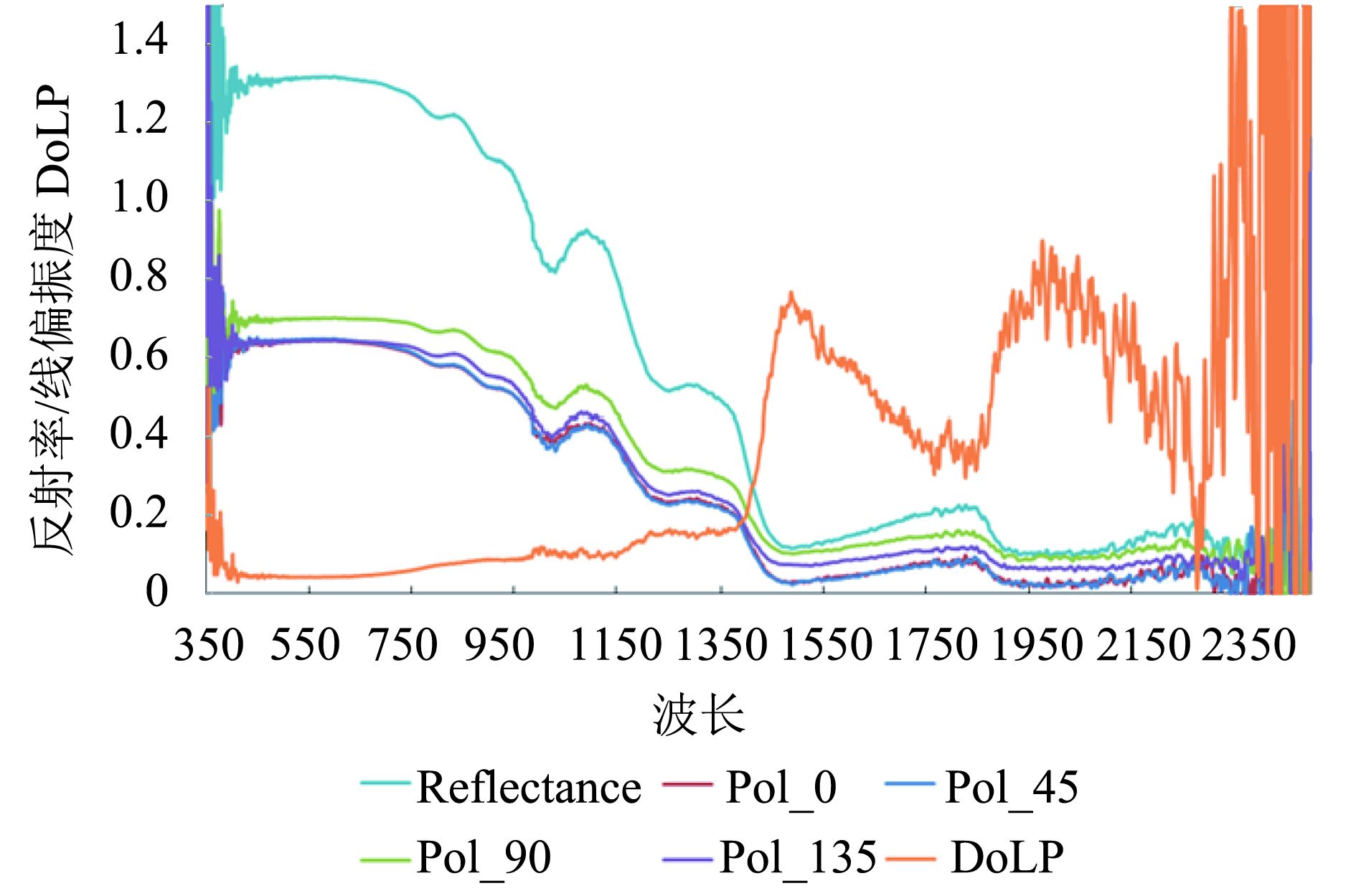
为了验证雪的高信息—背景反差比偏振滤波特性,图8展示了细颗粒(粒径24 μm)、中等颗粒(粒径82 μm)和粗颗粒(粒径178 μm)3种粒径的积雪光谱数据。可以看出,积雪在可见光波段有很强的反射率,达到95%以上,在0.6 μm附近达到峰值。积雪的粒径大小对反射光谱有一定的影响,随着积雪粒径的增加,反射率减小。
分析不同粒径积雪的光谱特性发现,在可见光和近红外波段范围内,不同粒径的积雪均表现出很强的反射率。芬兰大地测量研究所研制的多角度偏振光谱仪FIGIFIGO可以测量积雪在2π。空间范围内获取被测物体多偏振方位角的高光谱信息,进而获取Stokes参量和线偏振度(DoLP),分析积雪的双向偏振反射特性。图9的数据来源于芬兰大地测量所的地物反射光谱库(FGI reflectance library),从图9中可以看出,总反射在可见光和近红外波段有极强的反射能量,部分波段的反射值大于1,很容易使探测器能量饱和,有较大误差,且近红外波段的总反射强度低于可见光波段。当反射信号通过不同偏振方位角的偏振片后,能量有所减小,强度减少为总反射强度的一半左右,不易使探测器能量饱和。但不同偏振方位角下的反射强度在不同波段与总反射具有相近的变化趋势,即不影响积雪在不同波段的光谱变化规律。分析400—1000 nm的反射率与线偏振度的关系,发现对于线偏振度,其值与总反射(反射率)在不同波段表现出相反的变化趋势,呈负相关,利用二次曲线拟合,R2为0.9611,具有很好的拟合精度,起到很好的滤波作用。即在积雪遥感观测时可以利用偏振度信息对常规非偏振反射进行补充,在总反射过强的时候线偏振度值较小,而总反射过弱的时候线偏振度值较大,有助于积雪遥感观测的精度提高。
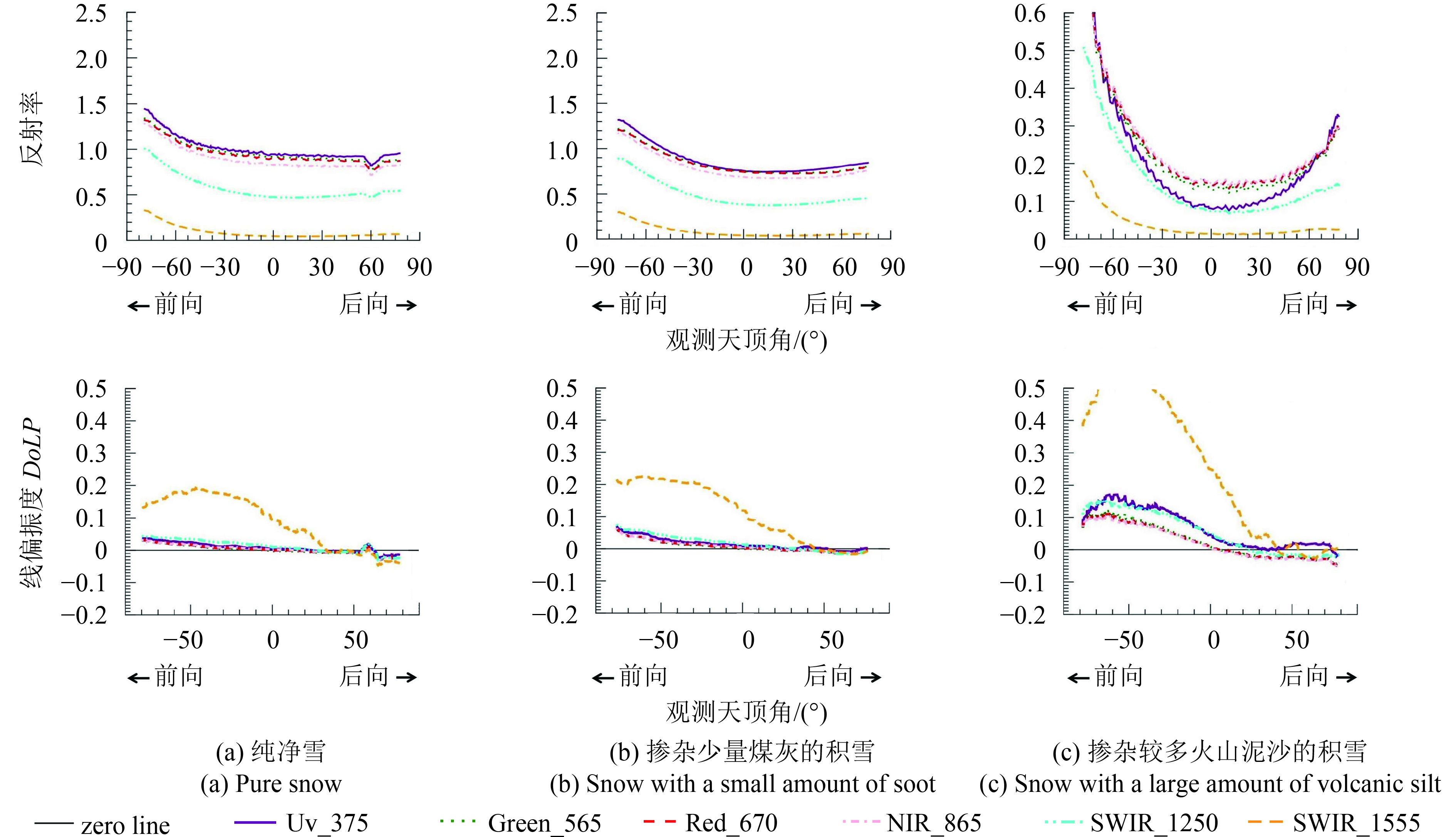
此外利用偏振可以进行雪的污染监测。污染程度会影响雪的偏振二向分布特性,图10是太阳天顶角为62°时不同污染程度下雪的反射率、线偏振度在主平面上的二向空间分布。污染程度不同即纯净积雪、掺杂少量煤灰的积雪以及掺杂较多火山泥沙的积雪。不同污染程度下,雪的线偏振度随观测相位角的增大而增大,而反射率则呈现不同的特征。从图10中可以看出,少量灰尘不会显著改变雪的偏振反射特征,但反射率已经使传感器饱和;而大量灰尘使雪色变深,在空间内减小了反射率的同时增大了偏振度。灰尘颗粒在日光下将雪在其周围融化并在其中下沉,疏水的轻质分子会附着在灰尘颗粒表面从而增大了其偏振效应。因此当传感器未进行光学定标时可以利用偏振来推断雪的污染程度。
3.4 偏振植被遥感监测实验验证
为了验证2.5节中植被偏振度滤波特性的理论,以线偏振度作为指标进行植被遥感监测,并分析其相对于用NDVI进行植被监测的传统方法的优势。
本实验选取的目标植被位于中国科学院奥运村科技园区,实验当日天空晴朗,白色圆板为定标白板。由于叶片的不同取向及相互交错的影响,植被处于不同的反射状态,即反射强度适中区域(vegetation with general reflection),反射强度过强区域(vegetation with strong reflection)和反射强度过弱(阴影)区域(vegetation with shadow)。图11即为相对配准和兴趣区域选取后,在555 nm不同偏振方位角下探测得到的目标植被的偏振高光谱影像。
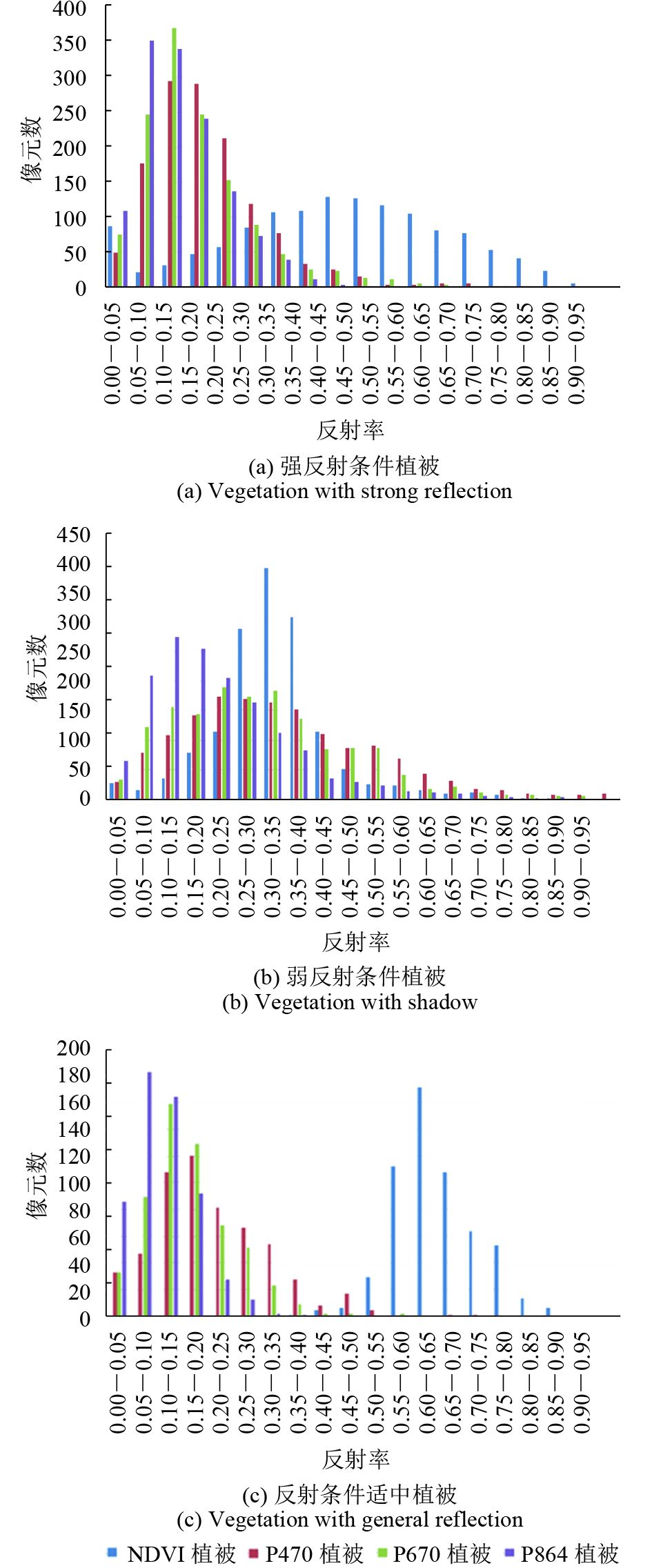
归一化差分植被指数NDVI(Normalized Difference Vegetation Index)广泛应用于卫星遥感数据反演和植被监测中,在照度条件适中的情况下可以对植被密集度进行有效监测,但在反射过强或过弱条件下表现为NDVI值较低,从而低估植被的实际密度。偏振度是表征偏振态变化的一个重要参量,利用配准好的不同偏振方位角的植被偏振影像可以计算偏振度。图12显示了在反射强度过强、过弱和适中条件下,植被NDVI和不同波段DoLP的值域的分布。从图12中可以看出,在正常反射强度条件下,NDVI值主要集中在0.55—0.7,符合实际情况,即植被密集;而在反射过强或过弱时,NDVI值分别集中在0.25—0.6和0.25—0.4,均明显小于正常反射条件值,即此时利用NDVI指数会低估植被密集度。与植被的NDVI相比,DoLP值较低,主要范围为0—0.35,但对于不同波段的DoLP,在不同反射强度条件下表现为近似相同的分布。相比于NDVI,强反射条件下利用DoLP识别植被具有较高的精度。对于阴影区域,DoLP的直方图相比于反射条件适中的区域的直方图有一个较小的向右平移。
表2统计了对于强反射区域、反射强度适中区域和弱反射(阴影)区域的植被,其NDVI与各波段DoLP的中位数值。以反射强度适中区域的NDVI和DoLP值为标准,可以看到,强反射条件引起的植被NDVI中位数值的相对误差为31.3%,而引起的植被DoLP中位数值在不同波段的相对误差分别为10.5%(470 nm)、6.7%(670 nm)和33.3%(864 nm)。DoLP的相对误差在蓝光和红光等植被较强吸收波段的误差降到最低(<10%)。相比于NDVI,利用DoLP进行植被监测在植被的强吸收波段误差可降低78%。偏振很大程度上来源于单次散射,强反射区域探测到的光大多为单次散射光,而阴影区域却进行了多次散射,因此对于阴影带来的影响,植被NDVI和DoLP均有较大误差。
表 2 研究区域不同反射强度条件下植被不同参数的统计数据
Table 2 Statistical data of various parameters in various intensity conditions of reflection in ROI
| 参数 | 反射适中 | 强反射 | 弱反射 |
| NDVI | 0.64 | 0.44 | 0.32 |
| DoLP(470 nm) | 0.19 | 0.17 | 0.31 |
| DoLP(670 nm) | 0.15 | 0.14 | 0.30 |
| DoLP(864 nm) | 0.10 | 0.13 | 0.23 |
通过地基偏振光谱实验数据处理与分析,偏振反射的滤波特征应用于植被遥感能够有效的提高精度。同时,偏振信息作为电磁波的固有属性,增加了遥感观测的信息维度,因而为高分辨率植被遥感监测以及定量化反演的精度提升提供了新的途径。
4 结 论
由上述实验验证可以得知,将偏振探测应用于水、雪和植被遥感,较各自的常规探测而言具有很大优势。对于水体遥感,偏振度影像得到的水体像元亮度较反射率影像水体像元亮度可提高一到两个数量级,从而使图像的信息—背景反差比提升数10倍,这为反射率极低的水体或其他地物的遥感探测提供了观测手段;在特定观测角度附近,偏振手段剥离水面太阳耀光的效率最高可达90%以上,偏振离水辐射提取剥离天空光的效率可达常规水平,且偏振探测流程简洁并有效减小了系统误差。
对于雪的遥感探测,偏振高信息—背景反差比滤波特性和偏振度“强光弱化”特性减小了探测器过饱和的可能性,为不同粒径及不同污染程度的积雪遥感探测提高精度。但积雪遥感定量化依然是后续遥感研究亟待解决的问题,需要将偏振普遍物理学规律,如菲涅尔定律,引入遥感观测并进行地学分析,总结不同观测几何下的积雪偏振分布规律。因此后续研究将构建基于偏振滤波特点的积雪二向偏振分布模型。
对于植被,本文对比分析了以偏振度为指标进行植被密集度监测相对于传统植被指数方法的优势。以偏振度作为定量指标进行植被监测,可将常规方法中由于植被过强或过弱反射带来的误差降低至10%以内,使植被密集度的遥感监测精度提升70%以上,从而破解了强反射条件下利用NDVI无法有效监测植被的瓶颈。此外,利用多角度偏振卫星数据进行全球范围内植被偏振反射率二向分布模型的研究,建立偏振特性与植被生化含量之间的定量关系,并将偏振探测应用于高分辨率植被定量遥感的高精度修正,成为植被偏振遥感的发展趋势。
参考文献(References)
-
Cao H J, Qiao Y L, Yang W F, Wang L Y, Hong J, Luo R Z and Yuan Y K. 2002. Characterization and analysis of the polarization images in remote sensing. Chinese Journal of Quantum Electronics, 19 (4): 373–378. [DOI: 10.3969/j.issn.1007-5461.2002.04.020] ( 曹汉军, 乔延利, 杨伟锋, 王乐意, 洪津, 罗睿智, 原育凯. 2002. 偏振遥感图像特性表征及分析. 量子电子学报, 19 (4): 373–378. [DOI: 10.3969/j.issn.1007-5461.2002.04.020] )
-
Li J S, Zhang B, Shen Q, Zhang H, Zhang F F and Wang Q. 2013. Analysis of directional reflectance properties of Lake Taihu using multi-angle measurements. Spectroscopy and Spectral Analysis, 33 (9): 2506–2511. [DOI: 10.3964/j.issn.1000-0593(2013)09-2506-06] ( 李俊生, 张兵, 申茜, 张浩, 张方方, 王桥. 2013. 太湖水面多角度遥感反射率光谱测量与方向特性分析. 光谱学与光谱分析, 33 (9): 2506–2511. [DOI: 10.3964/j.issn.1000-0593(2013)09-2506-06] )
-
Li T J, Tang J W, Chen Q L and Ren H Q. 2001. A method for measuring water-leaving radiance using photometer. Journal of Tropical Oceanography, 20 (4): 56–60. [DOI: 10.3969/j.issn.1009-5470.2001.04.009] ( 李铜基, 唐军武, 陈清莲, 任洪啟. 2001. 光谱仪测量离水辐射亮度的方法. 热带海洋学报, 20 (4): 56–60. [DOI: 10.3969/j.issn.1009-5470.2001.04.009] )
-
Li X, Zheng X B, Xun L N, Liu J J and Rong Z G. 2008. Realization of field BRDF acquisition by multiangular measurement system. Opto-Electronic Engineering, 35 (1): 66–70. [DOI: 10.3969/j.issn.1003-501X.2008.01.014] ( 李新, 郑小兵, 寻丽娜, 刘京晶, 戎志国. 2008. 多角度测量系统实现室外BRDF测量. 光电工程, 35 (1): 66–70. [DOI: 10.3969/j.issn.1003-501X.2008.01.014] )
-
Luo Y J, Zhao Y S, Hu X L and Wu T X. 2006. Polarization and sun glitter’s peeling-off of multi-angle remote sensing. Optical Technique, 32 (2): 205–208. [DOI: 10.3321/j.issn:1002-1582.2006.02.033] ( 罗杨洁, 赵云升, 胡新礼, 吴太夏. 2006. 偏振与多角度遥感中的太阳耀光剥离. 光学技术, 32 (2): 205–208. [DOI: 10.3321/j.issn:1002-1582.2006.02.033] )
-
Luo Y J, Zhao Y S, Wu T X and Zhao L L. 2007. Study and application in multi-angle polarization characters of water’s specular reflectance. Science in China, 37 (3): 411–416. [DOI: 10.3321/j.issn:1006-9267.2007.03.015] ( 罗杨洁, 赵云升, 吴太夏, 赵丽丽. 2007. 水体镜面反射的多角度偏振特性研究及应用. 中国科学 D辑: 地球科学, 37 (3): 411–416. [DOI: 10.3321/j.issn:1006-9267.2007.03.015] )
-
Schott J R. 2009. Fundamentals of Polarimetric Remote Sensing. Bellingham, Washington: SPIE Press
-
Shen Q, Li J S, Zhang B, Wu Y H, Zou L and Wu T X. 2016. Analyzing spectral characteristics of water involving in-situ multiangle polarized reflectance and extraction of water-leaving radiance. Spectroscopy and Spectral Analysis, 36 (10): 3269–3273. [DOI: 10.3964/j.issn.1000-0593(2016)10-3269-05] ( 申茜, 李俊生, 张兵, 吴艳红, 邹雷, 吴太夏. 2016. 水面原位多角度偏振反射率光谱特性分析与离水辐射提取. 光谱学与光谱分析, 36 (10): 3269–3273. [DOI: 10.3964/j.issn.1000-0593(2016)10-3269-05] )
-
Sun Z Q. 2013. The Study of the Polarized Factors of Snow Surfaces and Its Relationship with Snow Properties. Changchun: Northeast Normal University (孙仲秋. 2013. 积雪表面偏振特性及其与积雪性质之间关系研究. 长春: 东北师范大学)
-
Suomalainen J, Hakala T, Peltoniemi J and Puttonen E. 2009a. Polarised multiangular reflectance measurements using the finnish geodetic institute field goniospectrometer. Sensors, 9 (5): 389–3907. [DOI: 10.3390/s90503891]
-
Suomalainen J, Hakala T, Puttonen E and Peltoniemi J. 2009b. Polarised bidirectional reflectance factor measurements from vegetated land surfaces. Journal of Quantitative Spectroscopy and Radiative Transfer, 110 (12): 1044–1056. [DOI: 10.1016/j.jqsrt.2009.02.017]
-
Tang J W. 1999. The Simulation of Marine Optical Properties and Color Sensing Model. Beijing: Institute of Remote Sensing Application, Chinese Academy of Sciences (唐军武. 1999. 海洋光学特性模拟与遥感模型. 北京: 中国科学院遥感应用技术研究所)
-
Tong Q X, Xue Y Q and Zhang L F. 2014. Progress in Hyperspectral remote sensing science and technology in China over the past three decades. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7 (1): 70–91. [DOI: 10.1109/JSTARS.2013.2267204]
-
Wu T X. 2006. Quantitative Relationship Between Multi-Angle Polarized Reflectance and BRDF. Changchun: Northeast Normal University (吴太夏. 2006. 偏振方向反射与二向性反射定量关系研究. 长春: 东北师范大学)
-
Wu T X. 2010. Study on the Land Objects Charactreristics and the Separation Method for the Effect between Objects and Atmosphere in Polarization Remote Sensing. Beijing: Peking University (吴太夏. 2010. 偏振遥感中的地物性质及地–气分离方法研究. 北京: 北京大学)
-
Wu T X, Yan L, Xiang Y, Zhao Y S and Chen W. 2010. The multi-angle polarization spectral character of water and its applications in water color remote sensing. Spectroscopy and Spectral Analysis, 30 (2): 448–452. [DOI: 10.3964/j.issn.1000-0593(2010)02-0448-05] ( 吴太夏, 晏磊, 相云, 赵云升, 陈伟. 2010. 水体的多角度偏振波谱特性及其在水色遥感中应用. 光谱学与光谱分析, 30 (2): 448–452. [DOI: 10.3964/j.issn.1000-0593(2010)02-0448-05] )
-
Yan L. 2014. Polarization Remote Sensing Physics. Beijing: Science Press (晏磊. 2014. 偏振遥感物理. 北京: 科学出版社)
-
Zhang L F, Huang C P, Wu T X, Zhang F Z and Tong Q X. 2011. Laboratory calibration of a field imaging spectrometer system. Sensors, 11 (3): 2408–2425. [DOI: 10.3390/s110302408]