|
收稿日期: 2017-03-16
基金项目: 上海市科学技术委员会科研计划项目(编号:14590502200,17DZ1204900)
第一作者简介: 曹斌,1992年生,男,硕士研究生,研究方向为海洋遥感测绘。E-mail:caobinalonzo@sina.com
通信作者简介: 朱述龙,1964年生,男,教授,研究方向为卫星遥感应用。E-mail:zhushulong668@sina.com
中图分类号: P236
文献标识码: A
|
摘要
主要研究利用高分辨率WorldView-2卫星影像和双介质立体摄影测量方法进行浅海地形测绘的可行性,同时解决双介质立体摄影测量精定位算法(即折射改正算法)适用性差的问题。首先依据通用的双介质物像几何关系,提出了一种普适的双介质立体摄影测量折射改正算法;然后以海南省三沙市甘泉岛、珊瑚岛周围浅海区域为试验场,利用两个地区的WorldView-2立体影像,运用双介质立体摄影测量方法进行了浅海地形测绘试验。试验成功提取到了两个地区浅海海底的数字高程模型(DEM)。其中,甘泉岛地区的浅海DEM精度达到2.08 m(剔除其中的高程异常点后的结果)。研究表明:提出的折射改正算法,无论“空中同名光线延长线是否相交”都是适用的,且能改善浅海地形测绘精度。在水体清澈、无海浪情况下,利用相应的WorldView-2立体影像和双介质立体摄影测量方法进行浅海地形测绘是可行的。
关键词
WorldView影像, 双介质立体摄影测量, 精定位, 折射改正, 浅海地形, 测量精度
Abstract
Two-media satellite stereophotogrammetry, a combination of high-resolution satellite stereo images and two-media stereophotogrammetry, is a potential and promising method for shallow seafloor surveying, especially in areas far from the mainland. This study focuses on this method and its possible application in shallow seafloor surveying. The study has two objectives. The first is to solve the problem of poor applicability of an existing accurate positioning algorithm (i.e., refraction correction algorithm) in two-media stereophotogrammetry. The second is to explore the feasibility of shallow seafloor surveying using WorldView-2 stereo images and two-media stereophotogrammetry. First, a universal algorithm is presented for refraction correction based on the general geometry of two-media stereophotogrammetry. Two cases are considered in the algorithm, namely, the intersection and non-intersection of the corresponding two aerial straight rays of an underwater object. The positional relationship between the transitional point and other important relevant points in two-media stereophotogrammetry is also considered. Three experiments are performed to verify the feasibility of shallow seafloor surveying using two-media satellite stereophotogrammetry and the performance of the proposed refraction correction algorithm. The first experiment uses two-media stereophotogrammetry to assess whether a Digital Elevation Model (DEM) of shallow seafloor can be derived and determine how it is derived from WorldView-2 images. The second experiment assesses the accuracy of the DEM. (Note that quantitative accuracy assessment is not carried out for the Shanhu Island area because of the lack of reference data). The third experiment demonstrates the performance of the proposed refraction correction algorithm by comparing it with the results of Murase’s algorithm, which is a typical method. Two groups of WorldView-2 stereo images are used in these experiments, which show the Ganquan and Shanhu Island areas in Shansha City, Hainan Province. Results show that the DEMs of the two areas are successfully derived from the stereo images using the proposed method. For the Ganquan Island area, the DEM obtained by our refraction correction algorithm has an accuracy of 2.08 m, while the DEM obtained by Murase’s algorithm has an accuracy of 2.31 m. Previous practice suggests that the DEM accuracy of 2.08 m is satisfactory for satellite photogrammetry. These experiments show that an eligible DEM of shallow seafloor can be derived from WorldView-2 images by using two-media stereophotogrammetry, and its accuracy can be slightly improved by using our proposed refraction correction algorithm. In conclusion, the proposed refraction correction algorithm is generally applicable because it is suitable for both two-media stereophotogrammetric cases, specifically, the intersection and non-intersection of corresponding two aerial straight rays of an underwater object point. Deriving a DEM of shallow seafloor from WorldView-2 images using the method of two-media stereophotogrammetry is feasible.
Key words
WorldView-2 image, two-media stereophotogrammetry, accurate positioning, refraction correction, shallow seafloor, surveying accuracy
1 引 言
利用高分辨率商业遥感卫星(如WorldView-2、3、4)拍摄的浅海区域立体影像,运用双介质摄影测量方法获取浅海海底地形信息,是海洋测绘方法之一。但从目前掌握到的资料来看,基于卫星立体影像的双介质摄影测量研究和浅海测绘应用还很少,仅有曹彬才等人(2016)对其进行了初步研究和试验,其可行性还需进一步验证。
在双介质摄影测量中,水下目标(包括水中目标和水底目标)的定位方法有两种。一是利用立体影像上的同名像点,直接按照双介质物像折线关系模型交会得到水下目标点的3维大地坐标(王有年 等,1988;常本义,1991;单杰,1993;周高伟 等,2015;Shan,1994;Telem和Filin,2013)。二是利用立体影像上的同名像点,先按照单介质物像直线关系模型(或其近似模型)联立求解出虚拟的水中点位(以下称为“过渡点”)的3维大地坐标,再按照光线在空气和水中的折线传播规律,对过渡点的3维大地坐标进行折射改正,进而得到水下目标点的3维大地坐标(Fryer和Kniest,1985;Westaway 等,2000,2001;Butler 等,2002;Murase 等,2008;Georgopoulos和Agrafiotis,2012;Maas,2015)。由于卫星影像大都仅提供像点与地面点的直线关系模型(或其近似模型),因此基于卫星立体影像的双介质摄影测量一般采用第2种方法。
在第2种方法中,折射改正是影响测量精度的主要环节之一。现有折射改正算法都存在明显的缺陷,它们都回避了空中同名直线光线延长线不相交情况对折射改正的影响,有些仅按空中同名直线光线延长线相交时的几何关系对过渡点的大地坐标进行折射改正(Murase 等,2008;曹彬才 等,2016),有些仅按单像几何关系对过渡点的大地坐标进行折射改正(Fryer和Kniest,1985;Westaway 等,2000, 2001;Butler 等,2002;Georgopoulos和Agrafiotis,2012;Maas,2015),其不合理性及造成的测量误差是显而易见的。
以高分辨率卫星影像为资料,运用双介质摄影测量方法进行浅海地形测绘,既有折射改正等理论问题亟待解决,也有可行性等需要验证。为此,在前期研究的基础上(曹彬才 等,2016),继续以海南省三沙市甘泉岛、珊瑚岛周围浅海区域为试验场,利用两个地区的WorldView-2立体影像,系统性地开展了卫星影像双介质摄影测量在浅海地形测绘中的试验研究。其中,重点解决了折射改正算法存在的问题,试验验证了WorldView-2影像与双介质摄影测量方法相结合获取浅海海底DEM的可行性,取得了预期效果。
2 WorldView-2影像特点与海底特征粗定位方法
WorldView-2是美国DigitalGlobe公司拥有的高分辨率商业遥感卫星(DigitalGlobe,2013)。该星搭载了推扫式相机,相机焦平面采用了图1所示的线阵探测器(DigitalGlobe,2010),飞行过程中能同时获取全色和多光谱两种影像,经处理后分别形成0.5 m全色和2 m多光谱影像产品(如表1所示)。星上安装的高性能控制力矩陀螺,使卫星具备敏捷的姿态控制能力,能够按需调整卫星姿态来获取立体影像(包括全色立体和多光谱立体两种)。从质量上看,WorldView-2全色立体影像和多光谱立体影像都能满足摄影测量的需要。
表 1 WorldView-2影像的有关信息
Table 1 Some related information of WorldView-2 images
| 波段名称 | 波段范围/μm | 分辨率/m | 立体情况 | ||
| 全色(PAN) | 450—800 | 0.5 | 有全色和多光谱两种立体影像产品供用户选择 | ||
| 多光谱
(MS) |
MS1 | 近红外波段1 | 770—895 | 2.0 | |
| 红色波段 | 630—690 | ||||
| 绿色波段 | 510—580 | ||||
| 蓝色波段 | 450—510 | ||||
| MS2 | 海岸波段 | 400—450 | |||
| 黄色波段 | 585—625 | ||||
| 红色边缘波段 | 705—745 | ||||
| 近红外波段2 | 860—1040 | ||||
由于WorldView-2搭载的推扫式相机采用了图1所示的拼接型线阵探测器,它由多个短线阵探测器沿垂直于飞行方向的焦平面中心线两侧交错排列而成,所以WorldView-2影像(包括全色和多光谱)是由每个短线阵探测器分别成像后经过拼接处理得到的,用户拿到的影像产品已不是严格意义上的原始影像,所以无法建立严格的物像关系模型。为此,WorldView-2提供了有理函数模型RFM(Rational Function Model)以及相应的有理多项式系数RPCs(Rational Polynomial Coefficients)和坐标归一化参数作为近似的地面目标定位模型(DigitalGlobe,2014)。该模型为单介质物像关系模型(即物、像均位于大气层一种介质中),并且考虑了光学相机镜头畸变、光行差、大气折射的影响。其表达式如下
| $\left\{ {\begin{array}{*{20}{c}} {r = \frac{{\displaystyle\sum\limits_{i = 0}^{{m_i}} {\displaystyle\sum\limits_{j = 0}^{{m_j}} {\displaystyle\sum\limits_{k = 0}^{{m_k}} {{a_{ijk}}{X^i}{Y^j}{Z^k}} } } }}{{\displaystyle\sum\limits_{i = 0}^{{m_i}} {\displaystyle\sum\limits_{j = 0}^{{m_j}} {\displaystyle\sum\limits_{k = 0}^{{m_k}} {{b_{ijk}}{X^i}{Y^j}{Z^k}} } } }}} \\ {c = \frac{{\displaystyle\sum\limits_{i = 0}^{{m_i}} {\displaystyle\sum\limits_{j = 0}^{{m_j}} {\displaystyle\sum\limits_{k = 0}^{{m_k}} {{c_{ijk}}{X^i}{Y^j}{Z^k}} } } }}{{\displaystyle\sum\limits_{i = 0}^{{m_i}} {\displaystyle\sum\limits_{j = 0}^{{m_j}} {\displaystyle\sum\limits_{k = 0}^{{m_k}} {{d_{ijk}}{X^i}{Y^j}{Z^k}} } } }}} \end{array}} \right.$ | (1) |
式中,
为了能够运用最小二乘法求解地面点的大地坐标
| $\left\{ {\begin{array}{*{20}{c}} {{v_r} = \displaystyle\frac{{\partial r}}{{\partial X}}\Delta X + \displaystyle\frac{{\partial r}}{{\partial Y}}\Delta Y + \displaystyle\frac{{\partial r}}{{\partial Z}}\Delta Z - (r - \hat r)} \\ {{v_c} = \displaystyle\frac{{\partial c}}{{\partial X}}\Delta X + \displaystyle\frac{{\partial c}}{{\partial Y}}\Delta Y + \displaystyle\frac{{\partial c}}{{\partial Z}}\Delta Z - (c - \hat c)} \end{array}} \right.$ | (2) |
式中,
对于立体影像上陆地范围内的每对同名特征点,依据式(2)可以列出4个误差方程式,再运用最小二乘法就能求得对应地面点的大地坐标。但是,如果该点为海底特征点,则按照上述方法得到的大地坐标只是该点对应的“过渡点”的大地坐标。由于该坐标确定了海底特征点的概略位置,所以这一步又称为海底特征点的“粗定位”。
3 依据双介质立体摄影测量点位关系的海底特征精定位算法
对于海底特征点,按照上一节方法得到其“过渡点”的大地坐标后,还需要通过折射改正修正为该点本身的大地坐标,这一步称为“精定位”。
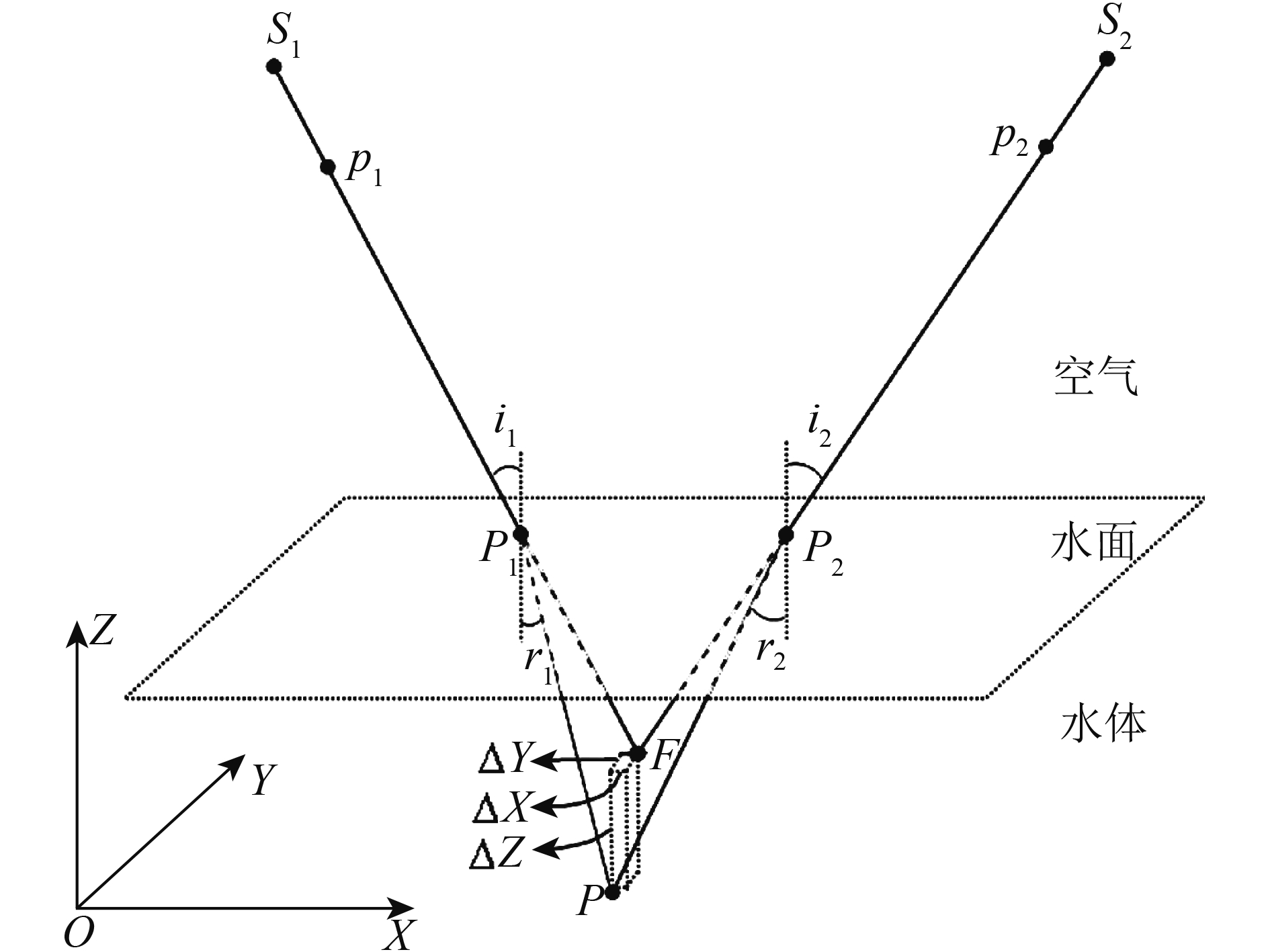
如图2所示,在双介质立体成像情况下,海底特征点
Murase等人(2008)和曹彬才等人(2016)研究表明:过渡点
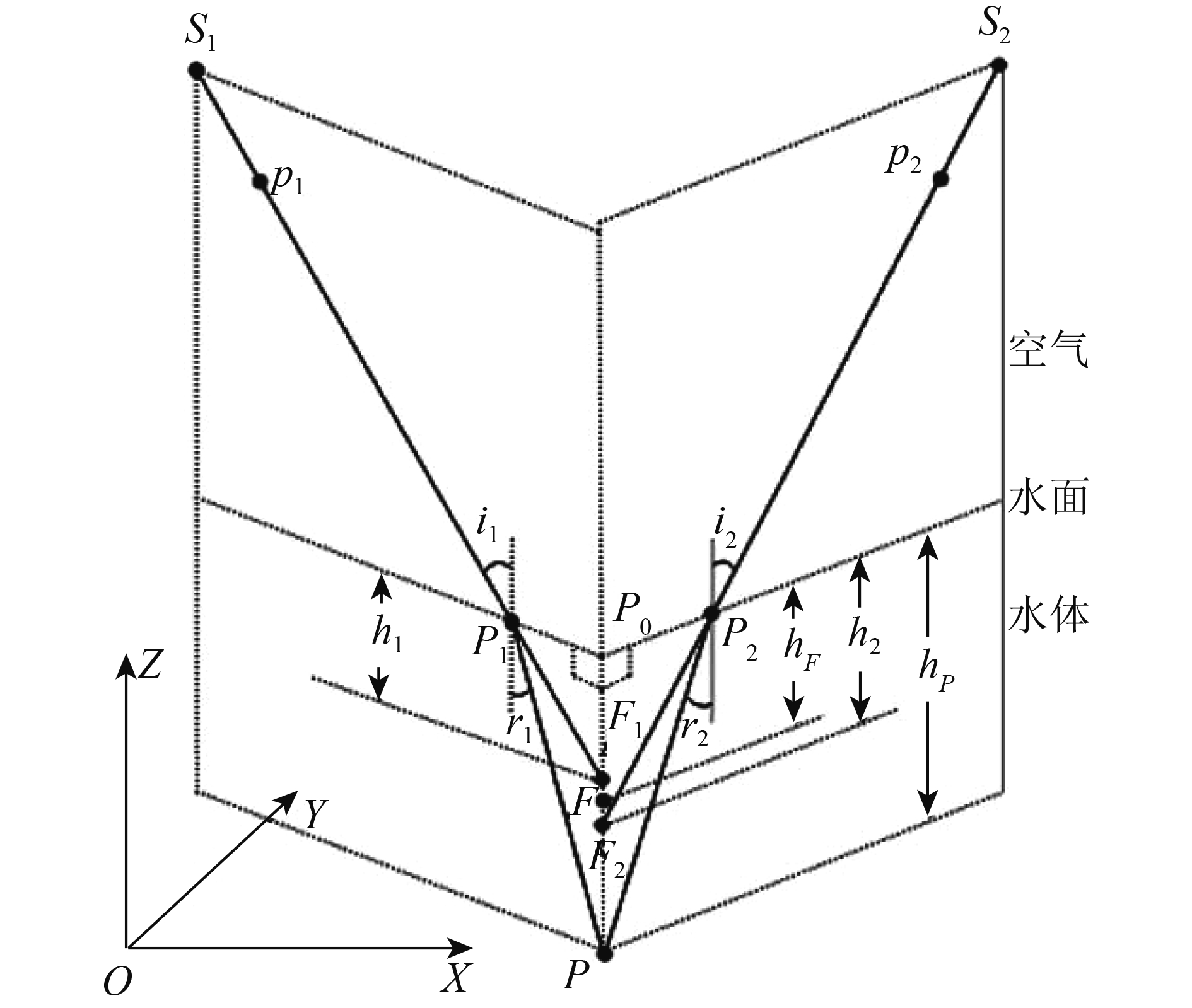
如前所述,在空中同名光线延长线不相交情况下,按照相交时的几何关系或者按照单像几何关系进行高程折射改正,都是不合理的。深入研究双介质物像几何关系后发现(图3):在
在图3中,摄影测量观测视线的入射角
| ${r_1} = \arcsin \left({{{\left({\sin {i_1}} \right)} / n}} \right)$ | (3) |
| ${r_2} = \arcsin \left({{{\left({\sin {i_2}} \right)} / n}} \right)$ | (4) |
式中,
设过渡点
| ${h_F} = {Z_ {\rm{W}}} - {Z_F}$ | (5) |
设
| $ {h_P} = \frac{{ {h_1} \cdot \operatorname{tg} {i_1}}}{{\operatorname{tg} {r_1}}}$ | (6) |
同理由图3中的
| $ {h_P} = \frac{{ {h_2} \cdot \operatorname{tg} {i_2}}}{{\operatorname{tg} {r_2}}}$ | (7) |
用
| $ {h_P} \approx \frac{{ {h_F} \cdot \operatorname{tg} {i_1}}}{{\operatorname{tg} {r_1}}}$ | (8) |
同理用
| $ {h_P} \approx \frac{{ {h_F} \cdot \operatorname{tg} {i_2}}}{{\operatorname{tg} {r_2}}}$ | (9) |
由于
| ${h_P} \approx \frac{{{h_F}}}{2} \cdot \left({\frac{{ \operatorname{tg} {i_1}}}{{\operatorname{tg} {r_1}}} + \frac{{ \operatorname{tg} {i_2}}}{{\operatorname{tg} {r_2}}}} \right)$ | (10) |
所以
| $\left\{ \begin{gathered} {X_P} = {X_F} \hfill \\ {Y_P} = {Y_F} \hfill \\ {Z_P} = {Z_ {\rm{W}}} - {h_P} \hfill \\ \end{gathered} \right.$ | (11) |
式(10)和式(11)就是在求出摄影测量交会点
该算法适用于空中同名光线延长线不相交和相交两种情况,比现有方法适用面更广。另外,该算法是依据双介质立体摄影测量点位关系推导出来的,同时顾及了“
4 运用双介质立体摄影测量方法获取浅海海底DEM的流程
以WorldView-2立体影像为资料,运用双介质摄影测量方法获取浅海海底DEM(含同步获取陆地DEM)的步骤和流程如下:
(1)准备数据,包括测区的WorldView-2立体影像及其观测参数和定位模型参数。
(2)消除太阳耀斑。运用Hedley算法(Hedley 等,2005)对受太阳耀斑影响的WorldView-2影像进行处理,剔除影像上的太阳耀斑现象。
(3)提取水陆分界线,确定水域和陆地的范围。运用种子点区域生长算法(朱述龙 等,2013)提取WorldView-2影像上的水陆分界线,进而确定水域和陆地的范围,以便后续对水域和陆地区域实施不同的处理。
(4)匹配确定同名特征点并计算对应点的大地坐标。首先运用稳健的SIFT特征匹配算法(Lowe,1999,2004),在WorldView-2立体影像上寻找同名特征点(包括海底和陆地特征点);然后按第二节的定位原理计算每对同名特征点的大地坐标(若为同名陆地特征点,则该坐标就是对应地面点的大地坐标;若为同名海底特征点,则该坐标是过渡点的大地坐标)。
(5)获取水面的高程值。以水陆分界线数据和上一步得到的陆地特征点的大地坐标为基础,直接找出或内插出水陆分界线上各点的大地坐标,取其中准确性最好的水陆分界点的高程作为水面的高程值。
(6)水陆分开处理,分别得到陆地和浅海海底的数字高程模型DEM。对于陆地区域,以(4)计算得到的地面点的大地坐标为基础,直接内插得到规则格网的陆地DEM。对于浅海区域,先对(4)计算得到的过渡点的高程进行折射改正,再以折射改正后的结果为基础内插得到规则格网的浅海海底DEM。
(7)分别对陆地和浅海海底的数字高程模型DEM进行精度评价。
5 试验与分析
为了验证高分辨率卫星影像与双介质摄影测量方法相结合用于浅海地形测绘的可行性,检验所提折射改正算法的性能,首先按本文算法和技术流程开发了双介质立体摄影测量软件(以下简称“软件”),然后选择海南省三沙市甘泉岛、珊瑚岛周围浅海区域作为试验场,以两个地区的WorldView-2立体影像为资料,运用该软件进行了浅海海底DEM测绘、精度评价、折射改正性能比较3项试验。
试验区WorldView-2多光谱立体影像为同轨立体影像,其基本信息如表2所示。考虑到WorldView-2多光谱蓝、绿波段影像上的浅海海底纹理特征比其他波段(包括全色)更清晰、更容易辨识(曹斌 等,2016,2017a),实际使用的是WorldView-2多光谱红、绿、蓝波段合成影像。为节省篇幅,文中仅给出了局部立体影像,如图4所示。
表 2 试验区WorldView-2立体影像的基本信息
Table 2 Basic information of WorldView-2 images of experimental areas
| 地点 | 立体像对 | 第1行成像时间
(北京时间) |
观测视线的入射角/(°) | 太阳耀斑
影响情况 |
定位模型参数 | 验证数据 | ||
| 最小 | 最大 | 平均 | ||||||
| 甘泉岛 | 左 | 2014-04-02(11:32:15) | 4.8 | 5.1 | 4.9 | 严重 | 包含在对应RPC00B
文件中 |
2013年1月19日的SHOALS-3000测量数据 |
| 右 | 2014-04-02(11:33:31) | 31.7 | 31.9 | 31.8 | 无 | |||
| 珊瑚岛 | 左 | 2014-04-02(11:31:59) | 10.4 | 10.7 | 10.6 | 严重 | 包含在对应RPC00B
文件中 |
Navionics海图数据,生产时间不详 |
| 右 | 2014-04-02(11:33:18) | 27.5 | 27.7 | 27.6 | 无 | |||
5.1 浅海海底DEM生成试验
本试验重点检验利用WorldView-2立体影像和双介质立体摄影测量方法能否生成浅海海底DEM以及如何生成浅海海底DEM。下面介绍主要环节的试验情况并给出试验结果。
(1)太阳耀斑消除。首先运用软件的“耀斑消除模块”,对有严重太阳耀斑的两地左影像进行了处理(两地右影像均无太阳耀斑,参见图4)。为了观察处理效果,从处理前后的图像上取出局部进行放大,结果如图5所示。
比较图5(a)与(b)以及图5(c)与(d)可以看出:剔除太阳耀斑前的影像,有明显的波纹,这些波纹压盖和模糊了海底特征,使得浅海海底特征的识别变得更加困难;而剔除太阳耀斑后的影像,浅海海底特征和浅海海床轮廓清晰可见,为后续特征点检测和同名像点匹配创造了有利条件。
(2)水陆分界线提取和水陆范围确定。仔细观察试验卫星影像可以发现:在没有太阳耀斑(或剔除了太阳耀斑)的图像上,岛屿与海水之间都有一个高亮度、色调均匀的环状滩涂区域。因此,选择该区域内的点作为“种子点”,运用软件的“边界线检测模块”提取环状滩涂区域的外边界作为岛屿与海水的分界线,该闭合分界线内部(含分界线)即为陆地区域、外部即为水域。
由于种子点代表性、环状滩涂区域内其他像元与种子点一致性判断标准对提取结果有很大影响,而且很难一次性精准确定,所以采用“尝试法”来获得最佳的水陆分界线。具体做法是:利用软件的“边界线检查模块”,将提取到的水陆分界线与相应影像进行叠置显示,在此基础上目视检查水陆分界线与相应影像特征的吻合情况;若发现两者不一致,则重新选择“种子点”并调整阈值(该阈值用于判断环状滩涂区域内其他像元与种子点是否一致),直至获得准确的水陆分界线为止。图6(a)、(b)分别为甘泉岛和珊瑚岛的最终水陆分界线(为节省篇幅,未按对应影像绘出),它们是以最佳种子点和最佳阈值为基础得到的。
(3)同名特征点匹配和对应点大地坐标计算。同名特征点匹配试验中,由于左、右图像均为WorldView-2同轨影像,获取时间非常接近,剔除太阳耀斑后图像质量也基本一致,所以匹配结果主要取决于匹配算法。软件采用的是SIFT特征匹配算法(取自OpenCV算法库),它由SIFT特征提取和SIFT特征矢量匹配两部分构成。其中,SIFT特征提取算法的参数有:原始分辨率影像高斯滤波系数
试验中,使用不同参数进行了SIFT特征匹配,并观察不同参数对同名特征点数量和位置的影响。结果表明:参数差异对同名特征点数量影响较大,对匹配到的同名特征点位置影响不大。为了尽可能多地得到同名特征点,用
在得到同名特征点(包括海底和陆地的同名特征点)以后,我们接着运用软件的“地面坐标计算模块”计算得到了每个特征点的大地坐标(对于陆地特征点,该坐标就是对应地面点的大地坐标;但对海底特征点,该坐标仅是过渡点的大地坐标)。
(4)浅海海底和岛屿的DEM生成。由于表2仅给出了整幅图像的最小、最大和平均入射角,而像元的入射角是不知道的,需要先计算出来才能进行海底特征点的折射改正。WorldView-2影像属于线阵推扫图像,同一行(飞行方向)各像元的入射角是一样的,不同行各像元的入射角则不同。根据这一特点,采用下列公式计算每个像元的入射角(图8)。
| $i = \frac{{ d}}{w} \cdot {i_0} + \frac{{ w - d}}{w} \cdot {i_{\rm{n}}}$ | (12) |
式中,
折射改正时还必须已知海水的折射率。研究表明(周高伟 等,2015):海水折射率随海水温度、海水盐度、光的波长等变化而变化,但海水折射率误差导致的双介质水深测量误差仅为实测水深的百分之几,可以忽略不计。因此,在综合考虑试验区地理位置、成像时间、海水平均温度等多种因素的基础上,选用20ºC时水的折射率作为海水折射率,即取
按上述步骤分别得到水陆分界线、每个特征点的大地坐标、每个特征点像元的入射角以及海水折射率以后,接着运用软件的“DEM生成模块”生成了浅海海底和岛屿的DEM,结果如图9所示。试验中,水面高程由软件自动得到。为了大致判断DEM的准确度和可靠性,将DEM和相应影像进行了目视比对,发现两者所呈现的地形形态特征基本一致,由此可以初步断定生成的DEM是正确的。
5.2 DEM精度评价试验
精度评价的方法是:用测区已有测量成果作为基准数据,将本文方法生成的DEM与测区基准数据进行比较分析,并根据分析结果对DEM质量做出评价。
对于甘泉岛地区,收集到了SHOALS-3000激光测深数据(Optech,2006;Kuus 等,2008)(如图10(a)所示)。该数据是2013年1月19日获取的,虽然与试验所用的WorldView-2影像拍摄日期(2014年4月2日)相差一段时间,但两者水陆分界线(即影像中的水边线与激光测量数据数中的“零值线”)的形状和大小几乎一致,即两者的水面高程几乎一致。由于甘泉岛地区有精度高、一致性好的SHOALS-3000数据作为参考基准,所以我们对甘泉岛周围浅海海底DEM精度进行了定量评价。
对于珊瑚岛地区,只收集到了Navionics海图数据(数据网址:http://www.navionics.com/en/[2017-03-16]),如图10(b)所示。该海图数据生产日期不详,图上陆地和水域范围与试验所用WorldView-2影像呈现的情况差异较大,而且该海图分辨率较低,很难准确找到明显的地形特征进行精度试验,所以我们仅用Navionics数据对珊瑚岛周围浅海海底DEM精度进行了定性评价。
(1)甘泉岛周围浅海海底DEM精度的定量评价。首先将本文方法得到的DEM(图9(a))与高精度SHOALS-3000数据(图10(a))进行配准,然后用SHOALS-3000数据作为参考基准,按式(13)计算DEM的均方根误差(RMSE),结果如表3所示。
| ${\rm{RMSE}} = \sqrt {\frac{{\displaystyle\sum\limits_{i = 1}^n {{{(Z_i^{(1)} - Z_i^{(2)})}^2}} }}{n}} $ | (13) |
式中,
从表3可以看出:本文方法测出了0—19 m水深范围内的浅海海底DEM,该水深范围内所有测量点的均方根误差为3.12 m(表3右侧倒数第2项),但不同水深范围的均方根误差有所不同。
从表3还可以看出:0—4 m水深范围内的均方根误差明显异常。主要原因是:水深0—4 m区域离岸较近,海浪拍岸带来的杂质较多,提取到的特征点可能是水中杂质点而非海底特征点;水中杂质会改变光线传播方向和传播路径,导致海底特征点产生像移;SHOALS-3000的测深能力为2—50 m,水深2 m以内的机载激光测深数据也不准。
为避免异常情况对精度评价的影响,最终用4—19 m水深范围内的均方根误差作为DEM的精度,其值为2.08(表3右侧倒数第1项)。
表 3 本文方法得到的甘泉岛周围浅海海底DEM精度
Table 3 DEM accuracy of Ganquan Island area derived by our method
| /m | ||||
| 水深范围 | RMSE | 水深范围 | RMSE | |
| 0—1 | 5.11 | 11—12 | 1.75 | |
| 1—2 | 4.33 | 12—13 | 1.64 | |
| 2—3 | 3.47 | 13—14 | 1.65 | |
| 3—4 | 3.05 | 14—15 | 2.12 | |
| 4—5 | 2.02 | 15—16 | 2.36 | |
| 5—6 | 2.48 | 16—17 | 2.29 | |
| 6—7 | 2.49 | 17—18 | 2.76 | |
| 7—8 | 2.12 | 18—19 | 2.66 | |
| 8—9 | 2.13 | 0—19 | 3.12 | |
| 9—10 | 1.80 | 4—19 | 2.08 | |
| 10—11 | 2.12 | |||
(2)珊瑚岛周围浅海海底DEM精度的定性评价。首先以本文方法得到的数字高程模型DEM为基础,提取珊瑚岛周围浅海海底的地形特征(图11(a)),再将其叠置到Navionics海图上(图11(b)),然后通过目视判读分析来检验本文方法得到的DEM的准确性。
由于珊瑚岛周围浅海海底地形中间部分比较平坦,本文重点检查了边缘部分两种数据的吻合情况。通过目视判读比较可以发现:本文方法得到的地形特征与海图呈现的地形基本吻合,尤其在叠置图中箭头所指位置(图11(b))吻合得比较好。鉴于浅海海底地形具有长期稳定性,两种数据呈现的地形特征能够吻合得较好,也从一个侧面说明了本文方法生成的DEM是正确的。
5.3 折射改正算法性能比较试验
为了验证本文折射改正算法的性能,将本文算法的结果与最有代表性的Murase算法(Murase 等,2008)的结果进行了比较。两种方法均以甘泉岛地区的WorldView-2立体影像为资料,两种方法的双介质立体摄影测量处理过程也完全相同,只是过渡点折射改正时使用的公式不同。
从表2可以看出:对于甘泉岛地区WorldView-2立体影像,左、右图像观测视线的入射角相差很大(左图像平均入射角为4.9°,右图像平均入射角为31.8°),该立体影像同名像点对应的空中同名光线延长线一般是不相交的。此时,若按Murase算法进行折射改正(即按空中同名光线延长线相交情况进行折射改正),其不合理性及导致的误差是显而易见的;而按本文算法进行折射改正才是合理的。表4给出了本文算法和Murase算法得到的DEM的均方根误差(均以SHOALS-3000数据为参考基准)。
表 4 两种方法得到的甘泉岛周围浅海海底DEM精度
Table 4 The DEM accuracy of Ganquan Island area derived by different methods
| /m | |||
| 方法 | RMSE
(水深0—19 m) |
RMSE
(水深4—19 m) |
备注 |
| 本文方法 | 3.12 | 2.08 | 两种方法的双介质立体摄影测量处理过程完全相同,只是物方坐标折射改正时使用的公式不同。 |
| Murase方法 | 3.13 | 2.31 | |
从表4可以看出:对于0—19 m水深范围内所有测量点,两种方法的均方根误差几乎相同;但剔除水深0—4 m的异常区域后,本文方法的均方根误差为2.08 m,优于Murase方法的2.31 m。这说明:在空中同名光线延长线不相交情况下,本文折射改正算法对提高测量精度有一定作用。
6 结 论
本文主要工作有两项:一是针对双介质立体摄影测量精定位算法(即折射改正算法)适用性差的问题,提出了一种普适的双介质立体摄影测量折射改正算法。二是通过试验初步验证了利用WorldView-2影像和双介质立体摄影测量方法获取浅海海底DEM的可行性。主要成果和重要结论如下:
(1)提出的折射改正算法,无论“空中同名光线延长线是否相交”都是适用的,它克服了原有折射改正算法仅适用“空中同名光线延长线相交”一种情况的局限性,具有普适性。
(2)提出的折射改正算法,是依据通用的双介质立体摄影测量点位关系推导出来的,在近似过程中顾及了“
(3)对于水体清澈、无海浪的浅海区域,利用对应的WorldView-2立体影像、运用双介质立体摄影测量方法获取浅海海底DEM是可行的。试验表明:在剔除水深0—4 m范围内的高程异常点以后,浅海海底DEM测量精度达到2.08 m(指高程测量精度,平面精度理论上优于高程精度)。
需要指出的是:本文方法获取的水深是相对成像时刻海水面的瞬时水深,得到的浅海海底高程包含了潮汐的影响。由于缺少试验区的潮汐数据,本文未对水深和高程进行潮汐改正。若利用本文方法获得的浅海海底DEM进行海图制图,则必须想方设法对DEM的高程进行潮汐改正,并将其统一到海图的高程基准面上。
另外,本文的折射改正算法,虽然理论上更具合理性,但仍然是近似的。下一步将利用更严密的物方坐标折射改正算法(曹斌 等,2017b)进行更多的双介质立体摄影测量和浅海海底地形测绘试验,进一步验证利用卫星影像获取浅海海底地形的可行性。
参考文献(References)
-
Butler J, Lane S, Chandler J and Porfiri E. 2002. Through-water close range digital photogrammetry in flume and field environments. Photogrammetric Record, 17 (99): 419–439. [DOI: 10.1111/0031-868X.00196]
-
Cao B, Qiu Z G and Cao B C. 2016. Comparison among four inverse algorithms of water depth. Journal of Geomatics Science and Technology, 33 (4): 388–393. [DOI: 10.3969/j.issn.1673-6338.2016.04.012] ( 曹斌, 邱振戈, 曹彬才. 2016. 四种遥感浅海水深反演算法的比较. 测绘科学技术学报, 33 (4): 388–393. [DOI: 10.3969/j.issn.1673-6338.2016.04.012] )
-
Cao B, Qiu Z G, Zhu S L and Cao B C. 2017. Improvement of BP-ANN based algorithm for estimating water depth from satellite imagery. Bulletin of Surveying and Mapping (2): 40–44. [DOI: 10.13474/j.cnki.11-2246.2017.0045] ( 曹斌, 邱振戈, 朱述龙, 曹彬才. 2017. BP神经网络遥感水深反演算法的改进. 测绘通报 (2): 40–44. [DOI: 10.13474/j.cnki.11-2246.2017.0045] )
-
Cao B, Zhu S L, Qiu Z G and Cao B C. 2017. More rigorous correction of refraction effects in two-media stereophoto grammetry. Acta Geodaetica et Cartographica Sinica, 46 (9): 1182–1192. [DOI: 10.11947/j.AGCS.2017.20170119] ( 曹斌,朱述龙,邱振戈,曹彬才. 2017. 一种更严密的双介质立体摄影测量折射改正算法. 测绘学报, 46 (9): 1182–1192. [DOI: 10.11947/j.AGCS.2017.20170119] )
-
Cao B C, Qiu Z G, Zhu S L, Tu X R, Cao F and Cao B. 2016. Shallow water bathymetry through two-medium photogrammetry using high resolution satellite imagery. Acta Geodaetica et Cartographica Sinica, 45 (8): 952–963. [DOI: 10.11947/j.AGCS.2016.20150583] ( 曹彬才, 邱振戈, 朱述龙, 涂辛茹, 曹芳, 曹斌. 2016. 高分辨率卫星立体双介质浅水水深测量方法. 测绘学报, 45 (8): 952–963. [DOI: 10.11947/j.AGCS.2016.20150583] )
-
Chang B Y. 1991. Basic formulas of two-media photogrammetry. Acta Geodaetica et Cartographica Sinica, 20 (4): 288–294. ( 常本义. 1991. 双介质摄影测量基本公式. 测绘学报, 20 (4): 288–294. )
-
DigitalGlobe. 2010. Radiometric Use of WorldView-2 Imagery. https://dg-cms-uploads-production.s3.amazonaws.com/uploads/document/file/104/Radiometric_Use_of_WorldView-2_Imagery.pdf [2017-03-10]
-
DigitalGlobe. 2013. WorldView-2 Overview. http://content.satimagingcorp.com.s3.amazonaws.com/static/satellite-sensor-specification/WorldView-2-PDF-Download.pdf[2017-03-10]
-
DigitalGlobe. 2014. Imagery Support Data (ISD) Documentation. https://dg-cms-uploads-production.s3.amazonaws.com/uploads/document/file/106/ISD_External.pdf [2017-03-10]
-
Fryer J G and Kniest H T. 1985. Errors in depth determination caused by waves in through-water photogrammetry. The Photogrammetric Record, 11 (66): 745–753. [DOI: 10.1111/j.1477-9730.1985.tb01326.x]
-
Georgopoulos A and Agrafiotis P. 2012. Documentation of a submerged monument using improved two media techniques//Proceedings of the 2012 18th International Conference on Virtual Systems and Multimedia. Milan, Italy: IEEE: 2012: 173–180 [DOI: 10.1109/VSMM.2012.6365922]
-
Hedley J D, Harborne A R and Mumby P J. 2005. Technical note: simple and robust removal of sun glint for mapping shallow-water benthos. International Journal of Remote Sensing, 26 (10): 2107–2112. [DOI: 10.1080/01431160500034086]
-
Kuus P, Clarke J H, and Brucker S. 2008. SHOALS3000 surveying above dense fields of aquatic vegetation–quantifying and identifying bottom tracking issues//Proceedings of the Canadian Hydrographic Conference and National Surveyors Conference. [s.n.]: Victoria, BC
-
Lowe D G. 1999. Object recognition from local scale-invariant features//Proceeding of the 7th International Conference on Computer Vision. Kerkyra, Greece: IEEE: 1150–1157 [DOI: 10.1109/ICCV.1999.790410]
-
Lowe D G. 2004. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision, 60 (2): 91–110. [DOI: 10.1023/B:VISI.0000029664.99615.94]
-
Maas H G. 2015. A modular geometric model for underwater photogrammetry. ISPRS - International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, XL-5/W5: 139–141 [DOI: 10.5194/isprsarchives-XL-5-W5-139-2015]
-
Murase T, Tanaka M, Tani T, Miyashita Y, Ohkawa N, Ishiguro S, Suzuki Y, Kayanne H and Yamano H. 2008. A photogrammetric correction procedure for light refraction effects at a two-medium boundary. Photogrammetric Engineering and Remote Sensing, 74 (9): 1129–1136. [DOI: 10.14358/PERS.74.9.1129]
-
Optech. 2006. SHOALS-3000 Product Brochure. [2017-03-10]. http://pdf.directindustry.com/pdf/optech/shoals-3000-product-brochure/25132-53146.html
-
Shan J. 1993. Relative orientation for two-media photogrammetry. Journal of the PLA Institute of Surveying and Mapping (3): 38–44. ( 单杰. 1993. 双介质摄影测量的相对定向. 解放军测绘学院学报 (3): 38–44. )
-
Shan J. 1994. Relative orientation for two-media photogrammetry. The Photogrammetric Record, 14 (84): 993–999. [DOI: 10.1111/j.1477-9730.1994.tb00299.x]
-
Telem G and Filin S. 2013. Photogrammetric modeling of the relative orientation in underwater environments. ISPRS Journal of Photogrammetry and Remote Sensing, 86 : 150–156. [DOI: 10.1016/j.isprsjprs.2013.10.001]
-
Wang Y N, Han L and Wang Y. 1988. Experimental research of underwater close-range photogrammetry. Acta Geodaetica et Cartographica Sinica, 17 (3): 217–224. ( 王有年, 韩玲, 王云. 1988. 水下近景摄影测量试验研究. 测绘学报, 17 (3): 217–224. )
-
Westaway R M, Lane S N and Hicks D M. 2000. The development of an automated correction procedure for digital photogrammetry for the study of wide, shallow, gravel-bed rivers. Earth Surface Processes and Landforms, 25 (2): 209–226. [DOI: 10.1002/(SICI)1096-9837(200002)25:2<209::AID-ESP84>3.0.CO;2-Z]
-
Westaway R M, Lane S N and Hicks D M. 2001. Remote sensing of clear-water, shallow, gravel-bed rivers using digital photogrammetry. Photogrammetric Engineering and Remote Sensing, 67 (11): 1271–1281.
-
Zhou G W, Li Y C, Ren Y X, Sheng L, Ye D M, Fan F Y and Bai J. 2015. Research of two-media underwater reefs depth measurement experiment based on low-altitude UAV. Acta Geodaetica et Cartographica Sinica, 44 (5): 548–554, 562. [DOI: 10.11947/j.AGCS.2015.20140259] ( 周高伟, 李英成, 任延旭, 盛琳, 叶冬梅, 范凤云, 白洁. 2015. 低空无人机双介质水下礁盘深度测量试验与分析. 测绘学报, 44 (5): 548–554, 562. [DOI: 10.11947/j.AGCS.2015.20140259] )
-
Zhu S L, Meng W C and Zhu B S. 2013. Irregular water boundary extraction using GVF Snake. Journal of Remote Sensing, 17 (4): 742–758. [DOI: 10.11834/jrs.20132179] ( 朱述龙, 孟伟灿, 朱宝山. 2013. 运用GVF Snake算法提取水域的不规则边界. 遥感学报, 17 (4): 742–758. [DOI: 10.11834/jrs.20132179] )