|
收稿日期: 2017-06-02
基金项目: 国家自然科学基金(编号:41401479);高分辨率对地观测系统重大专项(编号:E03071112)
第一作者简介: 李楠,1992年生,女,博士研究生,研究方向为农业遥感。E-mail:lena@mail.bnu.edu.cn
通信作者简介: 朱秀芳,1982年生,女,副教授,研究方向为农业遥感。E-mail:zhuxiufang@bnu.edu.cn
中图分类号: TP751
文献标识码: A
|
摘要
SVM分类器的参数设定对分类精度有着显著的影响,针对现有人工智能算法优化参数易陷入局部最优的现状,提出了一种基于人工蜂群算法改进SVM参数的遥感分类方法(ABC-SVM)。该方法模仿蜜蜂采蜜的行为,以训练样本的交叉验证精度代表蜜源的丰富程度,通过蜂群的分工协作搜索出最优蜜源(即SVM分类器最优参数),最终利用参数优化后的SVM分类器实现遥感影像的分类。本文先后比较了3种人工智能算法(包括人工蜂群算法优化的SVM(ABC-SVM)、遗传算法GA(Genetic Algorithm)优化的SVM(GA-SVM)、粒子群算法PSO(Practical Swarm Optimization)优化的SVM(PSO-SVM))在UCI标准数据集上的分类精度和效率,以及3种人工智能算法优化的SVM算法与未经优化参数的SVM算法在遥感影像上分类的差异。结果显示:(1)在利用UCI数据集测试3种人工智能算法优化的SVM算法的结果中,ABC-SVM显示出更高的分类精度、更高的适应度和更快的收敛速度;(2)在利用遥感影像验证4种分类算法精度的结果中,人工智能算法优化后的SVM比未经参数优化的SVM算法的分类精度更高;其中,ABC-SVM分类精度最高,分别比遗传算法、粒子群算法的结果高1.67%、1.50%。
关键词
人工蜂群算法, 支持向量机SVM, 遥感影像, 分类
Abstract
In the applications of a Support Vector Machine (SVM) classifier in solving classification problems, setting model parameters significantly influence the classification result, which causes a necessity for optimizing the key factors (cost and kernel parameters) in the SVM classifier to obtain the optimal classification results. Artificial Intelligence (AI) methods, which provide solutions for the parameter optimization problem of the SVM classifier, have emerged in recent years with the rapid advancement of the AI technology. However, these methods can easily trap the local optimal solution during the optimization process. An Artificial Bee Colony (ABC) algorithm exerts advantages, such as fast convergence and uneasiness of falling into a local optimum. Therefore, this study is aimed at introducing the ABC algorithm into optimizing the key parameters of the SVM classifier, thereby attempting to achieve a high precision in remote sensing image classification. The ABC algorithm imitates the behavior of honey bees in searching for the optimal parameters (also referred as the nectar) in the SVM classifier. The quality of the parameters is continuously validated using a threefold cross-validation accuracy of the training samples until The quality of parameters reaches the maximum accuracy. Then, the SVM with the optimized parameters are applied to classify the remote sensing images. First, three types of SVM classifier, namely, SVM optimized by an ABC algorithm (ABC-SVM), SVM optimized by a genetic algorithm (GA-SVM), and SVM optimized by a particle swarm algorithm (PSO-SVM), were compared when classifying five standard UCI datasets to verify the classification accuracy and efficiency of the ABC-SVM. The operation efficiency of the three AI algorithms was compared in the classification experiment based on the same UCI dataset, during which the training time and convergence curve of the three algorithms were recorded. Results showed that the ABC-SVM method has the highest classification accuracy, which is 6.55% and 6.07% higher than that of the GA-SVM and PSO-SVM algorithms, respectively. In terms of the efficiency of the three AI algorithms, the GA-SVM and PSO-SVM undergo minimal training time in the classification experiments of the five datasets. However, their global searching capability is inefficient, and the convergence rates are slow. The ABC-SVM undergoes the longest operation time among the three AI algorithms, but its fitness value is the highest and the convergence rate the fastest. Then, classification accuracies were evaluated based on a remote sensing image in the test area (Landsat-8 OLI image in Huairou area, Beijing), in which the SVMs were optimized by the three AI algorithms, and the original SVMs were compared. Results showed that the ABC-SVM method has the highest classification accuracy, which is 10.50% higher than that of the original SVM classification algorithm and is 1.67% and 1.50% higher than those of the other two AI algorithms (GA-SVM and PSO-SVM, correspondingly). The conclusions are listed as follows: (1) The ABC-SVM shows the highest classification accuracy among the results of the three types of AI optimized using the SVM algorithm when classifying the UCI datasets. The average classification accuracy of the five datasets is 6.55% and 6.07% higher than that of the GA-SVM and PSO-SVM, respectively. In addition, ABC-SVM has the fastest convergence among the three AI methods and shows a complex trapping local optimum. (2) The results of using the remote sensing image to verify the accuracy of the four classification algorithms show that the average accuracy of the SVM optimized by the three AI algorithms is 9.45% higher than the original SVM algorithm. Among these AI algorithms, the classification accuracy is 1. 67% and 1.50% higher in the ABC-SVM than in the GA-SVM and PSO-SVM, respectively.
Key words
artificial bee colony algorithm, Support Vector Machine (SVM), remote sensing image, classification
1 引 言
随着遥感技术的发展和影像信息源的丰富,遥感影像在不同领域得到了广泛应用。通常,在应用之前需要对影像进行分类操作,使其转换为能够识别的、有意义的信息。因此,遥感图像分类不仅是遥感数据处理的基础,也是关键环节(Wilkinson,2005)。目前运用较多的遥感影像分类方法为基于统计分析的模式识别方法,例如最大似然法、最小距离法,ISODATA法、K-Means法等。这些方法基于样本的分布是遵循正态分布的,但是对于遥感影像,这种假设往往不成立,因此对于地表复杂的情况,分类精度受到的影响较大(贾坤 等,2011)。而由Vapnik等人(1995)提出支持向量机SVM(Support Vector Machine)方法则不需要对数据做出正态分布的假设,该方法是一种建立在统计学习理论的结构风险最小化原则之上的机器学习方法,在解决小样本、非线性以及高维数据分类问题中具有突出优势,因而更适用于复杂地表环境下的分类问题。Roli和Fumera(2001)利用SVM进行遥感影像分类,结果优于神经网络法和K-NN算法。骆剑承等人(2002)利用SVM对影像进行了特征信息提取,并获得了较高的分类精度。张锦水等人(2006)利用光谱、纹理、结构等多元复合信息,对高分辨率IKONOS影像进行分类,结果优于最大似然法。
虽然SVM遥感分类方法能够降低非线性地物造成的混分、漏分现象,提高分类精度,然而在实际应用中存在参数选择的问题。有研究表明,模型参数的设置对分类结果有显著影响(Chapelle 等,2002),若想获取最优分类结果,必须对模型中关键因子进行优化。因此,参数优化方法一直以来是SVM研究领域中备受关注的问题。
最为传统的SVM优化算法是格网搜索算法(Hsu 等,2003),虽然具有获取全局最优参数的能力,但需要遍历解空间中的可行解,算法耗时长、效率低,只适用于极小的范围内的搜索。近年来,人工智能科学飞速发展,涌现出许多优秀的算法,人工智能算法作为启发式算法,不用遍历解空间的每一个位置,为解决SVM参数最优化问题提供了省时、高效的新方案。目前,已有学者将人工智能算法应用到了SVM参数优化中,如遗传算法GA (Genetic Algorithm)(刘胜和李妍妍,2007)、蚁群算法(Zhang 等,2010)、粒子群算法PSO (Particle Swarm Optimization)(Lu 等,2009),但实践表明,上述方法在寻优过程中容易陷入局部最优解,无法取得最优分类结果。人工蜂群算法ABC (Artificial Bee Colony Algorithm) (Karaboga,2005)是继遗传算法、粒子群算法、蚁群算法之后的一种新的群体智能算法,具有鲁棒性强、不易陷入局部最优的特点(Karaboga和Basturk,2008),近年来在参数优化(Akay和Karaboga,2012)、图像处理(Benala 等,2009;肖永豪和余卫宇,2010)、通信工程(Taşpņar 等,2011;刘俊霞 等,2013)、数据挖掘(Karaboga和Ozturk,2011)和电力系统(Linh和Anh,2010)等领域得到了广泛应用。
针对现有人工智能算法优化SVM参数的缺陷,本文尝试将人工蜂群算法引入SVM关键参数优化研究,先以加州大学欧文分校机器学习资源库中的标准数据集(通常简称为UCI(University of California, Irvine)数据集)评估3种人工智能算法(蜂群算法、遗传算法、粒子群算法)优化SVM的分类精度和效率,再以怀柔地区的Landsat 8遥感影像作为实例进行分类,并与ENVI中默认参数的SVM(下文称未经参数优化的SVM)及其他两种人工智能算法(遗传算法、粒子群算法)优化的SVM的分类精度进行对比。
2 研究方法
2.1 人工蜂群算法
人工蜂群算法由Karaboga(2005)提出,该算法是通过模仿蜜蜂群体搜索蜂巢附近优质蜜源的行为抽象而成(江铭炎和袁东风,2014)。
人工蜂群算法的基本思想为:首先,随机初始化一些可行解;然后,通过迭代、邻域搜索的策略向更优质的解靠近,从而得到最优解。寻优的过程基于蜂群的两种基本行为模型(为优质食物源招揽蜜蜂和放弃某个质量较低的食物源)来实现(Karaboga 等,2014)。具体过程为:首先,由采蜜蜂种群在解空间中随机生成可行解(可行解个数与采蜜蜂个数相同),并展开邻域搜索;然后,共享这些解的信息给等候的跟随蜂。跟随蜂种群通过观察采蜜蜂分享的信息,依据解的优质程度选择将要跟随的可行解(解越优质被选中的概率越高),并在其附近展开邻域搜索。在采蜜蜂和跟随蜂搜索的过程中,当一个可行解在邻域搜索一定次数后其质量依旧没有提升,说明该可行解附近缺乏优质解(表示该蜜源已完全开采),蜜蜂则会放弃该解,转变为侦查蜂,随机寻找解空间内的新解,该机制能够避免运算陷入局部最优。
采蜜蜂种群和跟随蜂种群各完成一次邻域搜索看作一次循环,当达到设定的最大迭代次数时,蜂群停止搜索,此时得到的即为最优解。
2.2 支持向量机
SVM算法的基本原理即通过构造最优分割超平面,实现训练样本分类。给定一训练样本集为
| $\begin{array}{l}\mathop {\min }\limits_{{{\omega }},{{b}}} \displaystyle\frac{1}{2}{\left\| {{\omega }} \right\|^2}\\{\rm{s}}.{\rm{t}}.\;\;\;{y_i}\left( {{{{\omega }}^{\rm{T}}}{{{x}}_i} + b} \right) \geqslant 1, \;\;i = 1,2, \cdots ,L\end{array}$ | (1) |
式中,ω和b是超平面的法向量和位移项,Rn为n维样本空间。
对式(1)使用拉格朗日乘子法可以得到其“对偶问题”(dual problem)为
| $\begin{array}{l}\mathop {\max }\limits_\alpha \displaystyle\sum\limits_{i = 1}^L {{\alpha _i} - \frac{1}{2}\sum\limits_{i = 1}^L {\sum\limits_{j = 1}^L {{\alpha _i}} } } {\alpha _j}{y_i}{y_j}\left( {{{{x}}_i}^{\rm{T}},{{{x}}_j}} \right)\\{\rm{s}}.{\rm{t}}.\;\;\;\displaystyle\sum\limits_{i = 1}^L {{y_i}{\alpha _i}} = 0,\;\;{\alpha _i} \geqslant 0,\;\;i = 1,2, \cdots ,L\end{array}$ | (2) |
式中,
针对线性不可分的状况,可将样本从原始空间映射到更高维度的特征空间中,使其转化为线性可分问题。如果原始空间是有限维,总能通过核函数找到一个高维特征空间使得样本线性可分,此时对于超出最优分类边界的样本点,引入松弛因子ξi来控制其成为支持向量的伸缩性,由此凸二次规划的对偶问题转化为
| $\begin{array}{l}\mathop {\max }\limits_\alpha \displaystyle\sum\limits_{i = 1}^L {{\alpha _i} - } \frac{1}{2}\sum\limits_{i = 1}^L {\sum\limits_{j = 1}^L {{y_i}{y_i}{\alpha _i}{\alpha _j}\left( {{{\left( {\phi \left( {{{{x}}_i}} \right)} \right)}^{\rm{T}}} \cdot \phi \left( {{{{x}}_j}} \right)} \right)} } \\{\rm{s}}.{\rm{t}}.\;\;\;\displaystyle\sum\limits_{i = 1}^L {{y_i}{\alpha _i}} = 0,\;\;0 \leqslant {\alpha _i} \leqslant C,\;\;i = 1,2, \cdots ,L\end{array}$ | (3) |
式中,C为惩罚参数,
| $f\left( x \right) = {\rm{sgn}}\left( {\sum\limits_{i = 1}^L {{\alpha _i}{y_i}K\left( {{{{x}}_{i,}}{{{x}}_j}} \right) + b} } \right)$ | (4) |
常见的SVM核函数主要有多项式核函数、高斯核函数、sigmoid核函数、拉普拉斯核函数等。已有研究表明,高斯核函数更适用于土地覆被的分类(Kavzoglu和Colkesen,2009),因此本文选择高斯核函数作为分类模型中的核函数,其数学形式为
| $K\left( {{{{x}}_{i,}}{{{x}}_j}} \right) = \exp \left( {\frac{{{{\left\| {{{{x}}_i} - {{{x}}_j}} \right\|}^2}}}{{2{\sigma ^2}}}} \right)$ | (5) |
式中,σ为核参数。
2.3 人工蜂群算法的SVM参数优化
对于SVM分类器而言,选定核函数后,分类器的性能仅与判别函数中的惩罚参数C以及核函数中的核参数σ相关。因此本文将ABC算法的优化目标设定为选择最优参数组合(C, σ)。ABC-SVM的遥感影像分类本质上即基于训练样本的人工蜂群算法最优参数提取,使用最优参数的支持向量机实现对遥感影像的分类。基于ABC算法的参数挖掘技术路线如图1所示。
算法所涉及符号的含义如下:SN、Ne和Nu分别代表蜜蜂的总个数、采蜜蜂以及跟随蜂的个数;D为个体向量维度;个体搜索空间为S=RD;最大迭代次数和每个参数组合的最大搜索次数分别为maxCycle和Limit。一般定义采蜜和观察蜂的数量相等,即
2.3.1 ABC-SVM适应度函数
在ABC-SVM的分类中将可行的参数组合看作可行解,适应度大小即参数组合质量的好坏,最优解对应最优参数组合。
适应度函数用来衡量参数组合的优劣,它决定了参数的搜索方向,本文采用训练样本的3折交叉验证精度(Stone,1974)作为适应度函数值。具体做法是:将原始训练样本均分为3个子集,依次抽选一个子集作为测试样本,剩余的2个子集作为新的训练样本,共得到3个模型,以3个模型得到的平均精度作为适应度值。该方法有效避免了过拟合和欠拟合现象,得到的结果更为可信。
2.3.2 人工蜂群算法挖掘SVM最优参数过程
本节对应图1中的核心程序部分,是ABC-SVM中的利用人工蜂群算法进行SVM最优参数挖掘的过程。根据蜂群算法的思想(Karaboga,2005),SVM参数挖掘步骤如下:
首先,初始化采蜜蜂种群,即在解空间中随机搜索、生成Ne个可行的SVM参数组合。用X=
| $X_i^j = X_{\min }^j + rand\left( {0,1} \right)\left( {X_{\max }^j - X_{\min }^j} \right)$ | (6) |
式中,
初始化结束后,采蜜蜂在其所在位置附近寻找新的蜜源,并采用贪婪选择,在新、旧参数组合中选取适应度更高的保留给下一代种群,以实现对参数进行优化。对于第n次循环,采蜜蜂在当前位置附近邻域搜索新的位置的公式为
| $V_i^j = X_i^j + \varphi _i^j\left( {X_i^j - X_k^j} \right)$ | (7) |
式中,
当采蜜蜂优化结束后,跟随蜂依照采蜜蜂的适应度大小,以一定的概率选择一个采蜜蜂,并依照其对应的参数组合展开邻域搜索,公式同式(7)。具体的概率计算公式为
| $P\left( {{X_i}} \right) = \frac{{fit\left( {{X_i}} \right)}}{{\displaystyle\sum\limits_{m = 1}^{{N_{\rm{e}}}} {fit\left( {{X_m}} \right)} }}$ | (8) |
式中,
当采蜜蜂和跟随蜂的优化结束后,需要检查是否有蜜蜂对应的参数组合最大搜索次数Limit,即经过次迭代后解仍未更新。对于搜索次数超限的解,该蜜蜂将放弃旧解,并转换为侦察蜂随机在解空间中随机寻找新解,公式同式(6)。
在检查过是否有解的搜索次数超限后,视作一次完整的迭代。每次迭代都需要记录目前的最高适应度值和所对应的参数组合。最后,若迭代次数没有超过最大迭代次数maxCycle,算法从采蜜蜂邻域搜索起继续循环,直至达到最大迭代次数,此时的最优解即为SVM的最优参数组合。
3 数据和实验设计
3.1 数据
3.1.1 UCI数据集
本文选取5组UCI标准数据集(Blake和Merz,1998)以对比3种人工智能算法优化SVM参数的分类性能,5组数据的具体信息如表1所示。本文选取的这5组数据中兼具了属性维度高和属性维度低的情况,对3种算法分类性能的评价更为客观。每组数据集都被划分为用于参数挖掘的训练样本和用于精度验证的验证样本。
表 1 UCI数据集
Table 1 UCI Dataset
| 编号 | 数据集 | 类别数 | 实例数 | 属性个数 |
| 1 | Ionosphere | 2 | 351 | 34 |
| 2 | Vehicle | 4 | 846 | 18 |
| 3 | Wine | 3 | 178 | 13 |
| 4 | Iris | 3 | 150 | 4 |
| 5 | Seeds | 3 | 210 | 7 |
3.2 精度验证
对UCI数据集的精度评价是利用训练后的模型对验证样本分类,以正确分类个数与验证样本总量的比值作为验证结果,即总体精度。
对遥感影像的分类精度则采取混淆矩阵的方式。评价指标包括总体精度、Kappa系数、用户精度和制图精度。具体的验证过程为:首先,使用优化后的SVM模型对整幅遥感影像分类;然后,利用ENVI软件中的混淆矩阵功能,生成验证样本对分类结果的混淆矩阵。
3.3 实验设计
在Matlab 2015b平台中编程实现训练样本数据的最优参数挖掘,支持向量机采用LibSVM模型(Chang和Lin,2011),遗传算法采用谢菲尔德大学的遗传算法工具箱(Chipperfield 等,1994)。经反复实验,分别设定蜂群初始化参数如下:蜜蜂种群规模为20,最大搜索次数Limit为10,最大迭代次数maxCycle依据数据复杂程度设定(初始设定为50代),SVM的参数C和σ的取值范围分别为[1, 100]和[0.1, 1000]
(1)实验1旨在对比3种人工智能算法优化的SVM算法的分类精度和效率。实验共采用5组UCI标准数据集,在对每组数据分类试验中,首先,将属性值分别归一化到[0, 1];然后,将数据分为训练集和测试集,寻找训练集交叉验证精度最高的参数组合;最后,以优选参数组合的SVM模型对测试集分类并计算分类精度。每个数据集做10次实验,取平均精度,并记录平均运行时间和收敛曲线。
(2)实验2是评估ABC-SVM方法提高遥感数据分类精度的能力。分别采用3种智能优化的SVM(人工蜂群算法优化的SVM(ABC-SVM)、遗传算法GA(Genetic Algorithm)优化的SVM(GA-SVM)、粒子群算法PSO(Practical Swarm Optimization)优化的SVM(PSO-SVM))以及未经参数优化的SVM对试验区的遥感影像进行分类及精度评价。3种人工智能算法优化SVM遥感影像分类操作与实验1类似,首先,将训练样本和遥感影像的各波段值进行归一化处理;然后,利用人工智能算法寻找训练样本交叉验证精度最高的参数组合;最后,以优选参数组合的SVM模型对遥感影像进行分类并计算测试样本的分类精度。
4 实验结果
4.1 实验1:UCI数据集分类实验
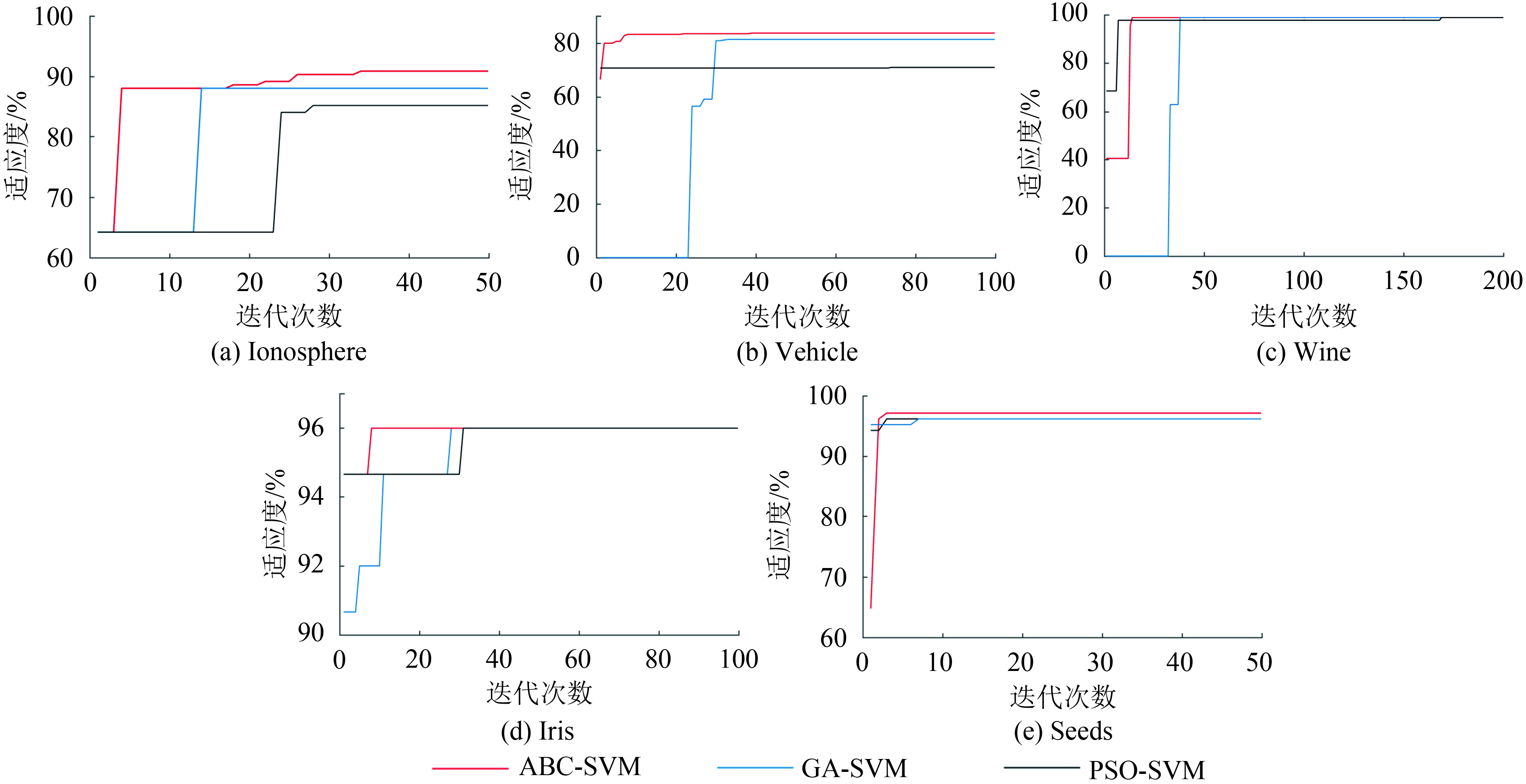
针对5个UCI标准数据集的分类结果,不论数据属性是高维度还是低维度,ABC-SVM都展现出了更强的寻优能力(表2)。此外,ABC-SVM对Ionosphere、Seeds、Vehicle和Wine这4个数据集的精度标准差也优于其他两种方法,说明ABC-SVM算法不仅在寻优能力上更强,而且算法的稳定性也优于其余两者。而在3种人工智能算法的运行时间上,GA-SVM的速度是三者中最快的,而ABC-SVM也表现出了较好的收敛性,运行时间仅次于GA-SVM,随着类别数与属性数增加,其时间开销增幅也处于中间位置,且保持着相对较高的分类精度,充分显示了该算法的稳定性。除了Iris,ABC-SVM算法在4个数据集上都体现出了更高的适应度和更快的收敛速度(图3),即ABC-SVM在解空间中总能收敛于适应度更高的解,不易陷入局部最优。
表 2 3种人工智能算法分类精度与运行时间
Table 2 Classification accuracy and running time of three artificial intelligent algorithm
| 数据集 | 方法 | 最大精度/% | 精度平均值/% | 精度标准差/% | 平均运行时间/s |
| Ionosphere | ABC-SVM | 95.43 | 95.03 | 0.63 | 3.05 |
| GA-SVM | 95.43 | 78.86 | 14.39 | 2.96 | |
| PSO-SVM | 96.00 | 78.69 | 14.22 | 3.39 | |
| Vehicle | ABC-SVM | 82.51 | 82.18 | 0.19 | 37.95 |
| GA-SVM | 70.45 | 70.36 | 0.12 | 32.50 | |
| PSO-SVM | 73.76 | 72.53 | 1.76 | 45.59 | |
| Wine | ABC-SVM | 98.88 | 97.98 | 0.45 | 3.92 |
| GA-SVM | 97.75 | 96.18 | 1.15 | 3.59 | |
| PSO-SVM | 96.63 | 93.93 | 2.02 | 4.14 | |
| Iris | ABC-SVM | 97.33 | 94.00 | 1.81 | 1.31 |
| GA-SVM | 96.00 | 95.60 | 0.61 | 1.19 | |
| PSO-SVM | 97.33 | 95.87 | 0.72 | 1.43 | |
| Seeds | ABC-SVM | 88.57 | 86.19 | 1.77 | 2.22 |
| GA-SVM | 83.81 | 81.62 | 1.21 | 2.20 | |
| PSO-SVM | 87.62 | 84.00 | 2.82 | 2.31 |
4.2 实验2:遥感影像分类实验
4种算法(ABC-SVM、GA-SVM、PSO-SVM、SVM)遥感分类实验的精度验证结果见表3,分类结果见图4。首先对4种方法分类结果进行大致比较,发现未经参数优化的SVM的分类结果(图4(d))比较综合,与其他几种方法相比缺乏细节。对局部进行放大处理后(图5),发现未经参数优化的SVM(图5(e))对混杂在裸地和耕地中的林地无法很好地识别,易将光谱信息较弱的耕地分类成裸地。再观察表3的分类精度,其中林地与耕地制图精度较低,分别为和66.88%和72.09%,这一结果也为目视观察的结果提供了佐证。在人工智能算法优化的SVM分类图中,能够明显发现,GA-SVM(图5(c))与PSO-SVM(图5(d))将影像左上角的一些实际为林地的像元分类成了居民地。而ABC-SVM(图5(b))算法在林地部分却少有混杂类别,能够将其完整的提取出来。结合表3,GA-SVM与PSO-SVM的总精度分别为82.17%和82.33%,林地的精度在两种算法中均为最低,存在将其错分为居民地的现象。
4种算法中ABC-SVM的总精度最高,达到83.83%,Kappa系数为0.79,对比智能优化的SVM分类结果,其优势在于林地的提取,而与未经参数优化的SVM分类算法比较,其优势在于对裸地和耕地正确识别。
表 3 分类精度表
Table 3 Classification accuracy table
| ABC-SVM | GA-SVM | PSO-SVM | SVM | ||||||||
| 用户精度 | 制图精度 | 用户精度 | 制图精度 | 用户精度 | 制图精度 | 用户精度 | 制图精度 | ||||
| 林地 | 94.31 | 73.89 | 93.10 | 68.79 | 93.10 | 68.79 | 96.33 | 66.88 | |||
| 居民地 | 94.44 | 85.96 | 78.11 | 88.20 | 78.89 | 88.20 | 99.08 | 60.67 | |||
| 耕地 | 72.73 | 80.62 | 78.95 | 81.40 | 78.36 | 81.40 | 65.96 | 72.09 | |||
| 裸地 | 73.25 | 96.64 | 80.74 | 91.60 | 80.88 | 92.44 | 52.95 | 98.32 | |||
| 水体 | 100 | 88.24 | 93.33 | 82.35 | 93.33 | 82.35 | 85.00 | 100 | |||
| 总体精度 | 83.83 | 82.17 | 82.33 | 73.33 | |||||||
| Kappa | 0.79 | 0.76 | 0.77 | 0.66 | |||||||
5 讨 论
相较于改进的SVM算法,未经参数优化的SVM算法在地表情况复杂的情况下,图面缺乏细节,对地物的区分状况较差,其精度比3种优化算法的平均精度低9.45%。这是由于ENVI软件自带的SVM分类算法中核参数和惩罚参数虽然可以根据用户需求进行定义,但在缺乏参数优选之下,用户只能主观的设定参数或选择默认值,而在选定核函数后,支持向量机的核参数和惩罚参数对于其分类性能具有重要影响,不同分类影像需根据其自身特质选择合适的参数组合,仅使用默认参数进行分类往往无法达到理想的精度。
在改进的SVM算法中,3种人工智能算法的改进方式有许多相似之处。首先,都是通过随机初始化的种群来构造最初的可行解;然后,都以训练样本的三折交叉试验精度为评价指标,遵循各自的算法机理调整种群的可行解在解空间中的位置,经数次演化后最终得到最优参数组合。导致精度差异的原因在于优化算法的演化机制不同。遗传算法通过染色体的选择、交叉、变异实现进化,由于初始化的染色体编码是随机生成的,含有大量离最优解距离很远的个体,而这种机制能够迅速剔除上述个体,因此能够获得较快的搜索速度(曾建潮 等,2004),GA-SVM在本文中的分类速度优于ABC-SVM,并且在对5组UCI数据集的分类实验中,是3种算法中时间标准差最低的,表现出了良好的稳定性,但是需要指出的是,从收敛曲线(图3)来看,遗传算法存在全局搜索能力不足的问题,往往容易陷入局部最优解。粒子群算法则是通过调整方向和速度实现优化,每个粒子不仅记忆自己的历史最优位置,并且吸收全局最优粒子的位置信息,由此保证了整个种群的进化方向是保持一致的,一方面能够保证较高的分类精度,但另一方面带来了容易陷入局部最优的问题(江铭炎和袁东风,2014)(图3)。蜂群算法是通彼此合作共享信息来改变蜜源位置达到寻优的目的,它与遗传算法和粒子群算法最大的不同在于每次迭代都能够实现局部和全局寻优,因此避免了早熟现象,不容易陷入局部最优,虽然时间开销略高,但其收敛速度快,分类精度更高,ABC-SVM在对5组UCI数据集的分类平均比GA、PSO高6.31%,这种较强的寻优能力也同样表现在对遥感影像的分类中,其分类精度比未经参数优化的SVM高10.50%,比其余两种算法平均高1.56%。
6 结 论
本文将人工蜂群算法应用于SVM的惩罚参数C和核参数σ的挖掘中,构造了ABC-SVM遥感分类方法,并通过UCI数据集和遥感影像分类实验对ABC-SVM的分类效率和精度进行评价。根据结果分析,本文提出的ABC-SVM遥感分类方法改进了未经参数优化的SVM方法,相比其他人工智能算法(GA、PSO)优化的SVM有更高的精度和更快的收敛速度,具有一定的推广应用价值。
本文研究发现,ABC-SVM优化的参数的范围设置比较关键,一方面参数范围设置过大会对算法效率产负面影响,另一方面参数范围设置过小却有可能无法获取全局最优参数,仅得到局部最优值。因此,在未来的研究中,可改进参数范围,以达到保证精度与提高算法效率的目的。此外,一些学者(Huang和Wang,2006;Ranaee 等,2010)提出利用人工智能算法优选高维数据的特征子集实现降级冗余信息的干扰,提高算法分类精度,这种方式集成了支持向量机对高维数据分类的优势(Cortes和Vapnik,1995),又克服了高维数据特征冗余的缺陷,能够显著提升算法精度。高光谱遥感数据实质上也是高维数据的一种,尚处于研究和发展阶段,结合本文现有的研究成果和前人的研究基础,未来将尝试将ABC-SVM引入高光谱遥感数据的分类,实现对高光谱数据的特征选择和SVM的参数优化,通过两者联合优化以期提高高光谱数据处理的自动化和智能化水平。
参考文献(References)
-
Akay B and Karaboga D. 2012. A modified artificial bee colony algorithm for real-parameter optimization. Information Sciences, 192 : 120–142. [DOI: 10.1016/j.ins.2010.07.015]
-
Benala T R, Villa S H, Jampala S D and Konathala B. 2009. A novel approach to image edge enhancement using artificial bee colony optimization algorithm for hybridized smoothening filters//Proceedings of World Congress on Nature and Biologically Inspired Computing. Coimbatore, India: IEEE: 1071–1076 [DOI: 10.1109/NABIC.2009.5393866]
-
Blake C and Merz C J. 1998. UCI machine learning repository[EB/OL]. http://www.ics.uci.edu/~mlearn/MLRepository.html [2017-06-02])
-
Chang C C and Lin J C. 2011. LIBSVM: a library for support vector machines. ACM Transactions on Intelligent Systems and Technology, 2 (3): 27 [DOI: 10.1145/1961189.1961199]
-
Chapelle O, Vapnik V, Bousquet O and Mukherjee S. 2002. Choosing multiple parameters for support vector machines. Machine Learning, 46 (1/3): 131–159. [DOI: 10.1023/A:1012450327387]
-
Chipperfield A J, Fleming P J and Fonseca C M. 1994. Genetic algorithm tools for control systems engineering//Proceedings of Adaptive Computing in Engineering Design and Control. Plymouth, UK: Plymouth Engineering Design Centre: 128–133.
-
Cortes C and Vapnik V. 1995. Support-vector networks. Machine Learning, 20 (3): 273–297. [DOI: 10.1007/BF00994018]
-
Hsu C W, Chang C C and Lin C J. 2003. A Practical Guide to Support Vector Classification. Taipei, China: National Taiwan University.
-
Huang C L and Wang C J. 2006. A GA-based feature selection and parameters optimizationfor support vector machines. Expert Systems with Applications, 31 (2): 231–240. [DOI: 10.1016/j.eswa.2005.09.024]
-
Jia K, Li Q Z, Tian Y C and Wu B F. 2011. A review of classification methods of remote sensing imagery. Spectroscopy and Spectral Analysis, 31 (10): 2618–2623. [DOI: 10.3964/j.issn.1000-0593(2011)10-2618-06] ( 贾坤, 李强子, 田亦陈, 吴炳方. 2011. 遥感影像分类方法研究进展. 光谱学与光谱分析, 31 (10): 2618–2623. [DOI: 10.3964/j.issn.1000-0593(2011)10-2618-06] )
-
Jiang M Y and Yuan D F. 2014. Artificial Bee Colony Algorithm and its Application. Beijing: Science Press (江铭炎, 袁东风. 2014. 人工蜂群算法及其应用. 北京: 科学出版社)
-
Karaboga D. 2005. An Idea Based on Honey Bee Swarm for Numerical Optimization. Kayseri, Turkey: Erciyes University, Engineering Faculty
-
Karaboga D and Basturk B. 2008. On the performance of artificial bee colony (ABC) algorithm. Applied Soft Computing, 8 (1): 687–697. [DOI: 10.1016/j.asoc.2007.05.007]
-
Karaboga D, Gorkemli B, Ozturk C and Karaboga N. 2014. A comprehensive survey: artificial bee colony (ABC) algorithm and applications. Artificial Intelligence Review, 42 (1): 21–57. [DOI: 10.1007/s10462-012-9328-0]
-
Karaboga D and Ozturk C. 2011. A novel clustering approach: artificial bee colony (ABC) algorithm. Applied Soft Computing, 11 (1): 652–657. [DOI: 10.1016/j.asoc.2009.12.025]
-
Kavzoglu T and Colkesen I. 2009. A kernel functions analysis for support vector machines for land cover classification. International Journal of Applied Earth Observation and Geoinformation, 11 (5): 352–359. [DOI: 10.1016/j.jag.2009.06.002]
-
Linh N T and Anh N Q. 2010. Application artificial bee colony algorithm (ABC) for reconfiguring distribution network//Proceedings of the 2nd International Conference on Computer Modeling and Simulation. Sanya, China: IEEE: 102–106 [DOI: 10.1109/ICCMS.2010.306]
-
Liu J X, Jia Z H, Qin X Z, Chang C and Wang H. 2013. Applications in channel assignment based on improved artificial bee colony algorithm. Computer Engineering and Applications, 49 (7): 119–122. [DOI: 10.3778/j.issn.1002-8331.1108-0257] ( 刘俊霞, 贾振红, 覃锡忠, 常春, 王浩. 2013. 改进人工蜂群算法在信道分配上的应用. 计算机工程与应用, 49 (7): 119–122. [DOI: 10.3778/j.issn.1002-8331.1108-0257] )
-
Liu S and Li Y Y. 2007. Parameter selection algorithm for support vector machines based on adaptive genetic algorithm. Journal of Harbin Engineering University, 28 (4): 398–402. [DOI: 10.3969/j.issn.1006-7043.2007.04.007] ( 刘胜, 李妍妍. 2007. 自适应GA-SVM参数选择算法研究. 哈尔滨工程大学学报, 28 (4): 398–402. [DOI: 10.3969/j.issn.1006-7043.2007.04.007] )
-
Lu N, Zhou J Z, He Y Y and Liu Y. 2009. Particle swarm optimization for parameter optimization of support vector machine model//Proceedings of the 2nd International Conference on Intelligent Computation Technology and Automation. Changsha, China: IEEE: 283–286 [DOI: 10.1109/ICICTA.2009.76]
-
Luo J C, Zhou C H, Liang Y and Ma J H. 2002. Support vector machine for spatial feature extraction and classification of remotely sensed imagery. Journal of Remote Sensing, 6 (1): 50–55. [DOI: 10.11834/jrs.20020110] ( 骆剑承, 周成虎, 梁怡, 马江洪. 2002. 支撑向量机及其遥感影像空间特征提取和分类的应用研究. 遥感学报, 6 (1): 50–55. [DOI: 10.11834/jrs.20020110] )
-
Ranaee V, Ebrahimzadeh A and Ghaderi R. 2010. Application of the PSO–SVM model for recognition of control chart patterns. ISA Transactions, 49 (4): 577–586. [DOI: 10.1016/j.isatra.2010.06.005]
-
Roli F and Fumera G. 2001. Support vector machines for remote sensing image classification//Processing of SPIE 4170, Image and Signal Processing for Remote Sensing VI. Barcelona, Spain: SPIE: 160–166 [DOI: 10.1117/12.413892]
-
Stone M. 1974. Cross-validatory choice and assessment of statistical predictions. Journal of the Royal Statistical Society. Series B (Methodological), 36 (2): 111–147. [DOI: 10.2307/2984809]
-
Taşpņar N, Karaboğa D, Yıldırım M and Akay B. 2011. Partial transmit sequences based on artificial bee colony algorithm for peak-to-average power ratio reduction in multicarrier code division multiple access systems. IET Communications, 5 (8): 1155–1162. [DOI: 10.1049/iet-com.2010.0379]
-
Wilkinson G G. 2005. Results and implications of a study of fifteen years of satellite image classification experiments. IEEE Transactions on Geoscience and Remote Sensing, 43 (3): 433–440. [DOI: 10.1109/TGRS.2004.837325]
-
Xiao Y H and Yu W Y. 2010. Bee colony algorithm for image edge detection. Application Research of Computers, 27 (7): 2748–2750. [DOI: 10.3969/j.issn.1001-3695.2010.07.098] ( 肖永豪, 余卫宇. 2010. 基于蜂群算法的图像边缘检测. 计算机应用研究, 27 (7): 2748–2750. [DOI: 10.3969/j.issn.1001-3695.2010.07.098] )
-
Zeng J C, Jie J and Cui Z H. 2004. Particle Swarm Optimization. Beijing: Science Press (曾建潮, 介婧, 崔志华. 2004. 微粒群算法. 北京: 科学出版社)
-
Zhang J S, He C Y, Pan Y Z and Li J. 2006. The high spatial resolution RS image classification based on SVM method with the multi-source data. Journal of Remote Sensing, 10 (1): 49–57. [DOI: 10.11834/jrs.20060108] ( 张锦水, 何春阳, 潘耀忠, 李京. 2006. 基于SVM的多源信息复合的高空间分辨率遥感数据分类研究. 遥感学报, 10 (1): 49–57. [DOI: 10.11834/jrs.20060108] )
-
Zhang X L, Chen X F and He Z J. 2010. An ACO-based algorithm for parameter optimization of support vector machines. Expert Systems with Applications, 37 (9): 6618–6628. [DOI: 10.1016/j.eswa.2010.03.067]