出版日期: 2018-05-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20187152
2018 | Volumn22 | Number 3
上一篇  |  下一篇
技术方法 
激光雷达回波模型辅助的坡地森林冠层高度反演
expand article info 汪垚1,2 , 倪文俭1 , 张志玉1 , 刘见礼1,2 , 于浩洋1,3 , 张大凤1,2
1. 中国科学院遥感与数字地球研究所 遥感科学国家重点实验室，北京 100101
2. 中国科学院大学，北京 100049
3. 北京师范大学信息科学与技术学院，北京 100875
收稿日期: 2017-05-15
基金项目: 国家重点研发计划(编号：2017YFA0603002)；国家重点基础研究发展计划(973计划)(编号：2013CB733401, 2013CB733404)；国家自然科学基金(编号：41371357, 41301395, 41471311)
第一作者简介: 汪垚(1993—　)，男，硕士研究生，研究方向为森林遥感。E-mail：wangyao@radi.ac.cn
通讯作者简介: 倪文俭(1982—　)，男，研究员，研究方向为森林遥感机理模型发展及基于多源遥感数据的森林植被碳储量及其动态变化监测。E-mail：niwj@radi.ac.cn
中图分类号: TP79
文献标识码: A

摘要

大光斑激光雷达数据已广泛应用于森林冠层高度提取，但通常仅限于地形坡度小于20°的平缓地区。在地形坡度大于20°的陡峭山区, 地形引起的波形展宽使得地面回波和植被回波信息混合在一起，给森林冠层高度提取带来巨大挑战。本文利用激光雷达回波模型和地形信息，提出了一种模型辅助的坡地森林冠层高度反演算法。该方法以激光雷达回波信号截止点为参考，定义了波形高度指数H50和H75，使用激光雷达回波模型与已知地形信息模拟裸地的激光雷达回波，将裸地回波信号截止点与森林激光雷达回波信号截止点对齐，利用裸地回波计算常用的波形相对高度指数RH50和RH75，对森林冠层高度进行反演。并与高斯波形分解法和波形参数法的反演结果进行了比较。研究结果表明：(1)利用所提取的波形指数RH50和RH75对胸高断面积加权平均高(Lorey’s height)进行了估算，在坡度小于20°时，高斯波形分解法、波形参数法和模型辅助法的估算结果与实测值线性拟合的相关系数(R2)分别为0.70，0.78和0.98，对应的均方根误差(RMSE)分别为2.90 m, 2.48 m和0.60 m, 模型辅助法略优于其他两种方法；(2)在坡度大于20°时，高斯波形分解法、波形参数法和模型辅助法的R2分别为0.14，0.28和0.97，相应的RMSE分别为4.93 m, 4.53 m和0.81 m, 模型辅助法明显优于其他两种方法；(3)在0°—40°时，模型辅助法对Lorey’s height估算结果与实测值的R2为0.97，RMSE为0.80 m。本研究提出的模型辅助法具有更好的地形适应性，在0°—40°的坡度范围内具备对坡地森林冠层高度反演的潜力。

关键词

激光雷达, 地形, 波形展宽, GLAS, 森林冠层高度

Retrieval of forest canopy heights by using large-footprint waveform data assisted by the LiDAR model over hillsides
expand article info WANG Yao1,2 , NI Wenjian1 , ZHANG Zhiyu1 , LIU Jianli1,2 , YU Haoyang1,3 , ZHANG Dafeng1,2
1.State Key Laboratory of Remote Sensing Science, Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China
2.University of Chinese Academy of Sciences, Beijing 100049, China
3.School of Information Science and Technology, Beijing Normal University, Beijing 100875, China

Abstract

Full waveform data of large-footprint LiDAR are widely used to retrieve global or regional forest canopy heights. However, most studies have focused on forests on relatively flat terrains where the slope is smaller than 20°. Estimating the canopy height of hillside forest stands over mountainous areas with large relief remains a challenge. A model-assisted method is proposed to estimate canopy heights of hillside forest stands by using LiDAR waveforms and overcome the effect of terrains. The adaptability of the method in 0° to 40° is evaluated. We propose a new method and redefine the height index. First, the LiDAR waveform of bare ground is simulated according to given terrain slopes. Second, the LiDAR waveforms of a forest stand and bare ground are aligned according to their signal ending points. Finally, the heights of quarter energy points (i.e., H50 and H75) of the LiDAR waveform of forests are defined relative to the signal ending points, and the heights of quarter energy points (i.e., Hg50 and Hg75) of the LiDAR waveform of bare ground are defined relative to the signal ending points. The relative height indices (i.e., RH50 and RH75) of the forest LiDAR waveform are defined as the difference in the corresponding index of the simulated waveform of forest and bare ground, namely, RH50=H50 − Hg50 and RH75=H75 − Hg75. The newly defined RH50 and RH75 are used to estimate forest canopy heights. The model-assisted method is validated within 0° to 40° terrain slopes and compared with Gaussian decomposition and edge-extent methods. (1) Within the 0° to 20° terrain slopes, the accuracies of estimating forest canopy heights using Gaussian decomposition, edge-extent, and proposed model-assisted methods are R2=0.70, 0.78, and 0.98 and root-mean-square error (RMSE)=2.90 m, 2.48 m, and 0.60 m, respectively. The performance of the proposed method is slightly better than that of the two other methods. (2) Within the 22° to 40° terrain slopes, the accuracies of estimating forest canopy heights using Gaussian decomposition, edge-extent, and proposed model-assisted methods are R2=0.14, 0.28, and 0.97 and RMSE=4.93 m, 4.53 m, and 0.81 m, respectively. The proposed model-assisted method is superior to the two other methods. (3) The estimation accuracy of the model-assisted method within the 0° to 40° terrain slopes is R2=0.97 and RMSE=0.80 m. This model can overcome the effect of the terrain and maintain high accuracy. The method will be further validated using spaceborne LiDAR data in future research. The proposed method can correct the effect of slope over hillsides, and the relative height indices extracted by this method are insensitive to terrain slopes. The proposed method shows a potential for use in the accurate estimation of forest canopy heights over hillsides.

Key words

LiDAR, terrain, waveform broadened, GLAS, forest canopy height

1 引　言

森林是陆地生态系统的重要组成部分，森林储存了45%的陆地碳，贡献了50%的陆地净初级生产(Field和Raupach，2004)。森林生物量作为森林生态系统的基础数量特征和森林生态系统性质、状态的重要指示特征，是研究许多林业问题和生态问题的基础，也是森林生态系统碳储量的重要数据来源和全球碳循环的重要组成部分，因此开展森林生物量的精确估算和评估具有重要意义。

传统的森林参数测定需要外业实地测量, 且仅能获得一些点上的数据，很难及时地获取区域或大范围有空间分布信息的森林参数。遥感方法可快速、准确、无破坏地对森林参数或生物量从林分到区域等不同空间尺度进行估算，对生态系统进行宏观监测。早期基于多光谱遥感数据的生物量反演研究较多，但不同区域的反演精度差异较大，生物量反演的饱和点较低(Dubayah和Drake，2000)。激光雷达LiDAR(Light Detection And Ranging)，即激光探测与测距，它是一种主动式遥感技术。激光雷达遥感获得的高精度森林垂直结构，可以克服生物量饱和问题，能够大大地提高森林生物量的估测精度，从而更好地计算森林的碳储量(Drake 等，2002)。常用的激光雷达主要有两类：记录少量回波的小光斑激光雷达与记录完整波形数据的大光斑激光雷达(Wulder 等，2012)。小光斑激光雷达可利用高密度的激光点云进行精确的单木尺度上的高度、胸高断面积等估测工作。大光斑激光雷达主要利用回波波形特征反演脚印内森林的垂直结构与生物量参数，利用首次回波与末次回波估算森林冠层高度(Harding 等，2001)。通过冠层高度指标的计算，估算地上森林生物量(Pang 等，2008；Sun 等，2011, 2008)。

受数据获取成本的限制，机载激光雷达难以用于大范围制图(Cao 等，2014)。星载大光斑激光雷达广泛用于全球或区域的森林冠层高度的反演(Hayashi 等，2013；Popescu 等，2011)。搭载在冰云和陆地高程卫星ICESat(the Ice，Cloud and land Elevation Satellite)上的地学激光测高系统GLAS (Geoscience Laser Altimeter System)提供的完整波形数据，可以估算平坦地面的森林冠层高度(Duong 等，2008；Enßle 等，2014；Wang 等，2013)。但是，在地形起伏较大的区域, 地形引起的波形展宽使得光斑内的森林冠层信息和地面反射信息混杂在一起，给森林冠层高度提取带来很大挑战。

针对不同地形坡度和地表粗糙度，利用大光斑激光雷达数据反演森林冠层高度方法主要分为3类，即高斯波形分解法，波形参数法和物理模型方法。

大光斑激光雷达回波波形通常呈现由地面和物体的反射引起的多个能量峰值的特征。在平坦地区，最后一个峰值一般是地面的响应。高斯波形分解法首先确定信号起始位置和信号截止位置，然后通过高斯拟合将信号起止之间的波形分解为多个高斯波形，将最后一个高斯波形为地面回波，以该波形的中心高程作为地面高程，计算各种波形相对高度指数(Duong 等，2008；Rosette 等，2009, 2008；Sun 等，2008)。高斯分解法在平坦地区效果较好。但是，在山区，复杂地形造成波形展宽，使得地面回波的波形与植被的回波混合，为分解地面高程带来困难。最低峰可能对应的是光斑内的小树或者小的地形特征，并不代表光斑内的集中地形高度。

地形引起的波形展宽在波形长度，波形前沿和波形后沿长度等波形参数上均有体现，因此研究人员提出了基于波形参数法的冠层高度反演算法(Chen，2010；Hilbert和Schmullius，2012；Lefsky 等，2005, 2007；Pang 等，2011)。但是，模型参数不稳定，在不同植被类型和不同地形条件下，需要重新进行统计回归拟合。

Lee等人(2011)提出了一个基于森林冠层几何光学和辐射传输模型的物理方法。他们的模型量化了地形表面坡度对森林冠层高度反演的影响，但是该模型基于相似植被结构均匀分布，精度相对于波形参数法较低。Allouis等人(2012)提出了一个基于波形建模的地形纠正方法用于反演森林冠层高度，考虑了坡度对高度提取的影响。Nie等人(2015)基于Allouis等人(2012)的方法，考虑了坡度等因素提出了新的地形纠正方法，减少了森林冠层高度的估算误差。

在坡度小于20°情况下，现有的3类方法可以通过纠正地形的影响提高森林冠层高度的反演精度。但是在坡度大于20°情况下，反演森林冠层高度仍具有很大的挑战(Enßle 等，2014；Hilbert和Schmullius，2012；Wang 等，2014；Xing 等，2010；Yang 等，2011)。

随着地形由平坦向陡峭过度，波形展宽使地面回波波峰逐渐变弱，为地面回波位置的确定带来困难，进而影响到波形相对高度参数(如RH50，RH75等)的提取, 从而影响森林冠层高度参数的反演。本研究尝试发展一种模型辅助的坡地森林冠层高度反演算法，称为“模型辅助法”。该算法的核心思路是利用地形信息和激光雷达波形模型，模拟给定地形条件下的裸地回波，将模拟裸地回波的信号截止位置与待反演波形的信号截止位置对齐，以对齐后的模拟裸地回波的峰值位置作为待反演波形的地面参考位置，提取波形相对高度指数，进行森林冠层高度参数反演。

2 研究数据

 

目前ICESat/GLAS是常用的星载大光斑激光雷达数据，但其数据获取时间介于2003年—2009年，已经停止工作8年，难以获得与之相对应的地面调查数据，且已有的历史地面调查数据多在平坦地形条件下获取，无法满足本研究需求。在此，本文主要使用森林激光雷达回波模型的模拟数据进行分析。所采用的模型是Sun和Ranson(2000)所发展的激光雷达回波模型。

激光回波波形是由发射脉冲、激光光斑内的森林3维场景和地表特性共同决定。激光发射脉冲由波长、脉冲宽度、脉冲能量、光斑尺寸和记录回波脉冲的时间间隔等参数定义；森林3维场景由包括激光光斑内每株树的位置、高度、树种、树冠大小和形状、冠层的反射率等参数描述；地表特性由反射率、坡度、坡向等参数描述。激光发射脉冲参数可以根据所模拟激光雷达系统设定，地表特性可以根据地形数据或模拟需求来设定，而3维森林场景不能任意设定，因为单木的大小分布需要满足一定的生态学生长规律。本文采用森林动态生长模型(ZELIG)模拟的3维森林场景来驱动激光雷达回波模型。

ZELIG是一种基于单木的森林动态模拟模型(Smith和Urban，1988)，它通过模拟单木的萌发、生长、竞争和死亡等过程，模拟不同林龄的3维森林场景。模型主要由两个大的模块构成：环境对森林生长的影响因子模块和植被生理因子模块。其中环境影响因子模块由光因子限制方程、土壤肥力限制方程、土壤水分限制方程和温度限制方程4个小模块构成，植被生理因子模块由林木更新模型、林木生长模型和林木死亡模型3个小模块构成。因为ZELIG模型模拟每棵树生长状态是具有一定的随机特征，因此本研究进行了10次重复模拟，以提高所模拟的3维森林结构的可靠性。本研究所采用的ZELIG模型驱动参数在美国Howland研究区进行了本地化(Ranson 等，2001)。模拟生长时间0—200年，每5年输出一次3维森林场景；区域北纬45.2°、西经68.7°，海拔100 m，模拟林分大小30×30 m2；模拟主要树种冷杉、白桦、落叶松、红皮云杉和铁杉(表1)。

表 1 ZELIG模型参数
Table 1 Driving parameters of ZELIG model

下载CSV 
树种 Amax/a Dmax/cm Hmax/cm DDmin DDmax Light Drt Nutri
冷杉 200 50 1500 250 2404 1 1 3
白桦 140 100 2500 700 2500 4 3 3
落叶松 335 75 2500 280 2660 5 3 3
红皮云杉 300 100 3000 500 2580 2 2 3
铁杉 650 150 3500 1324 3100 1 2 3
　注：Amax、Dmax、Hmax分别为树种的最大寿命、最大胸径和最大树高；DDmin和DDmax分别为树种自然分布条件下所需的>5°的最小和最大有效积温；Light是树种的耐阴性等级，ZELIG模型分5个级别的耐阴性指标，其中1表示非常耐阴，5表示非常喜阳；Drt是树种的耐旱等级，ZELIG分5个耐旱等级，其中1表示喜湿，5表示非常耐旱；Nutri是树种的肥力等级，ZELIG分3个肥力等级，1为喜肥，3为耐贫瘠。

鉴于灌木、草地的高度较小，其分布接近于地面，空间异质性远小于乔木层，对于波形展宽的影响较小，因此，本文没有考虑灌木、草地对回波信号的影响，仅对森林乔木进行了模拟(Carabajal和Harding, 2005, 2006；Pagnutti和Ryan，2009)。

本文采用的激光雷达传感器参数参照搭载在冰、云和陆地高程卫星上的地学激光测高系统GLAS，脚印大小为70 m，所用的入射脉冲为高斯脉冲, 持续时间是4 ns。光斑边缘激光能量减弱到中心的e–2。波形数据记录间隔是1 ns(即15 cm)，所用波长为1064 nm(池泓，2011)。树冠在该波长的反射率为0.55，透过率是0.3，地面反射率为0.20(Sun和Ranson，2000)。ZELIG共模拟了400个森林场景(40个林龄组×10次重复)；每个森林场景模拟了以2°为间隔，坡度从0°—40°的森林回波波形数据，因此共模拟了8400条激光雷达回波数据。

3 森林冠层高度反演方法

本文采用3种方法进行森林冠层高度的反演，包括 “高斯分解法”、“波形参数法”和本文所发展的“模型辅助法”，并对它们的反演结果进行比较。使用胸高断面积加权平均高(Lorey’s height)作为森林冠层高度的描述指标。

3.1 高斯分解法

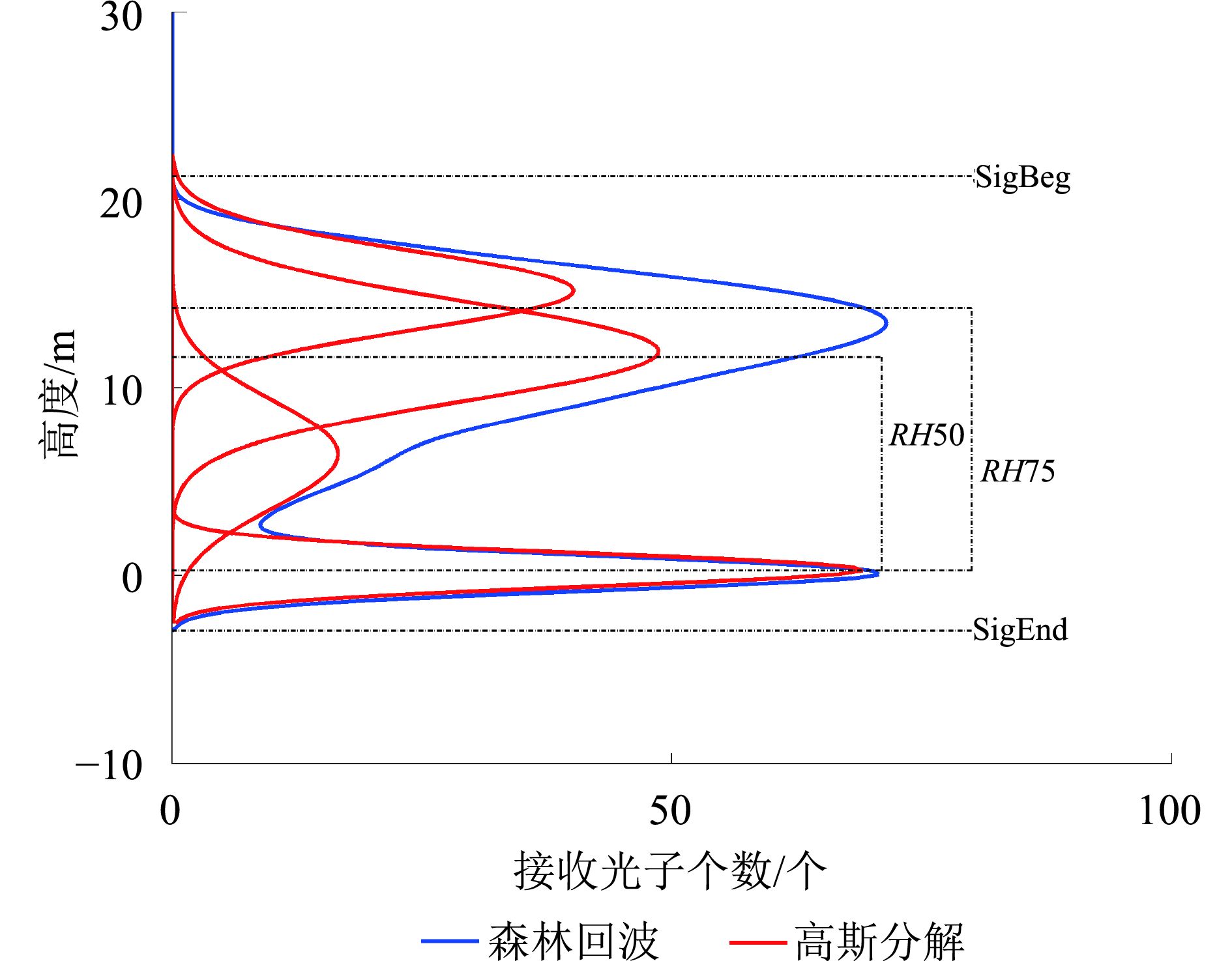
现有研究表明，森林冠层高度与激光雷达回波波形相对高度指数之间存在明显的线性相关性，常用的波形相对高度指数是回波波形能量四分位高度指数RH25、RH50、RH75和RH100(Lee等，2011)。Sun等人(2008) 分别采用了RH25、RH50、RH75和RH100对GLAS提取的高度进行了验证，发现RH50和RH75相关系数R2较好，分别为0.77和0.82。Sun等人(2011) 采用RH25、RH50、RH75和RH100进行生物量反演，相关系数R2仅为0.32，采用RH50和RH75进行生物量反演，相关系数R2明显提高，为0.70。因此本文采用RH50和RH75(图1)，RH50和RH75分别定义为激光雷达回波波形能量50%位置和75%的位置相对于地面回波波峰位置的高度。


图 1 高斯分解波形
Fig. 1 Gaussian decomposition of LiDAR waveform

回波波形能量四分位高度指数的计算需要首先获取地面回波位置。在地面回波较弱的情况下，对回波波形进行高斯分解，得到多个高斯波形，将最后一个高斯波形作为地面回波，其回波峰值位置点为地面位置(图1)，然后求得森林回波的四分位高度指数(Duong 等，2008；Sun 等，2008)。本文首先分析高斯分解法得到的RH50、RH75对地形坡度的敏感性，进而构建基于RH50与RH75的线性回归模型，对森林冠层高度进行反演，所采用的模型如式(1)(2)(3)

$h = {a_1} + {a_2} \times RH{\rm{50}}$ (1)
$h = {a_1} + {a_2} \times RH{\rm{75}}$ (2)
$h = {a_1} + {a_2} \times RH{\rm{50}} + {a_{\rm{3}}} \times RH{\rm{75}}$ (3)

式中，h为冠层高度，单位为m；a1、a2、a3为拟合系数；RH50、RH75为波形相对高度指数，单位为m。

3.2 波形参数法

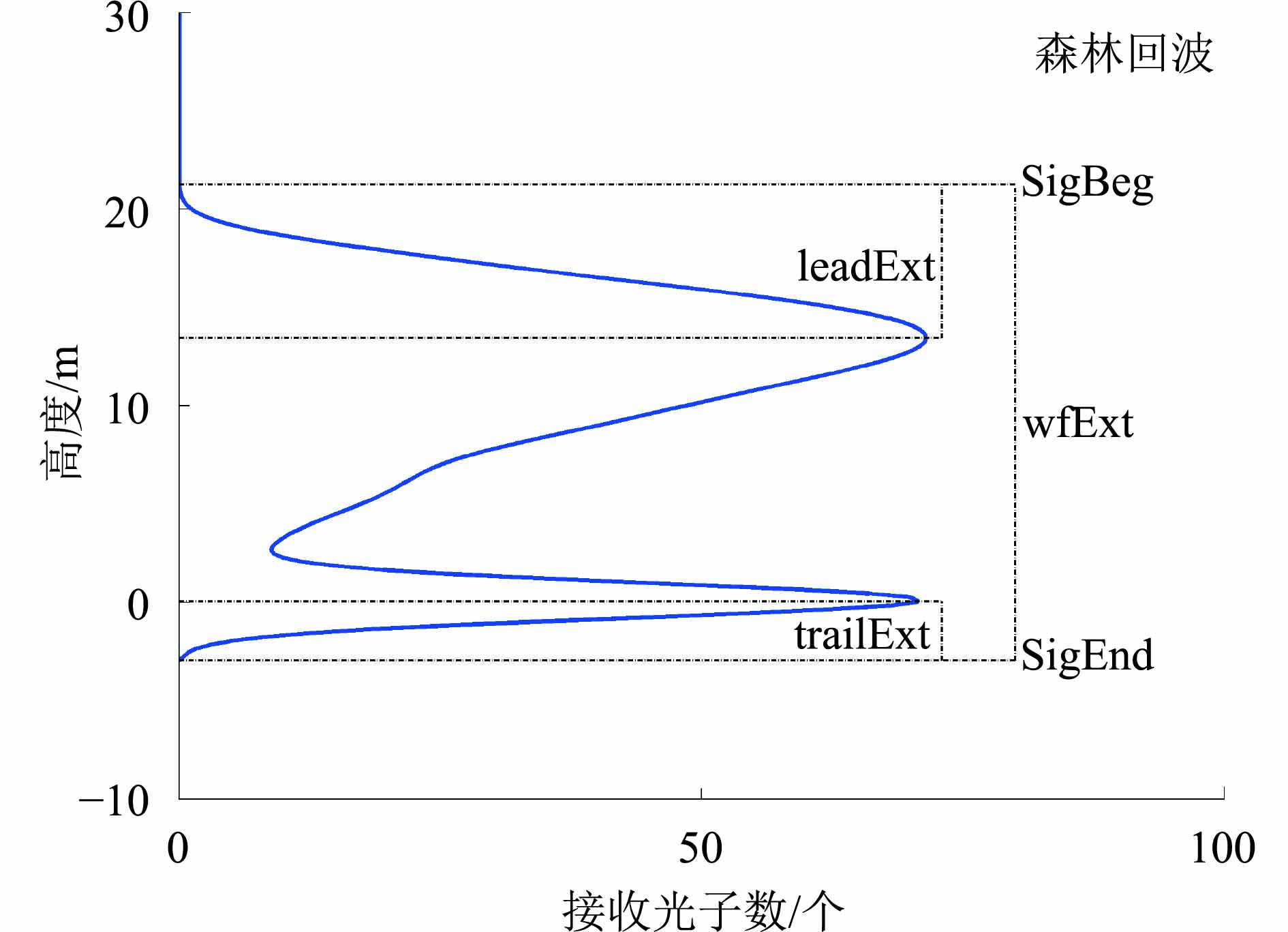
Lefsky等人(2007)提出了“Edge-extent线性模型”，即基于回波波形前沿长度、后沿长度和波形长度的森林冠层高度反演模型。波形参数的定义如图2所示，波形长度wfExt(Waveform Extent)定义为激光雷达回波信号起始位置(SigBeg)与截止位置(SigEnd)之间的垂直距离；回波波形前沿长度leadExt(Leading Edge Extent) 定义为信号起始点与最上端第一个反射峰半能量的垂直距离；回波波形后沿长度trailExt(Trailing Edge Extent)定义为信号结束点与最上端反射峰半能量的垂直距离(Lefsky 等，2007)。Pang等人(2008)在Lefsky等人(2007)方法的基础上使用“Edge-extent非线性模型”来估计冠幅加权平均高。本文分别采用Edge-extent线性模型和Edge-extent非线性模型对森林冠层高度进行反演，所采用的反演模型形式如式(4)(5)

$h = {a_1} \times {\rm{wfExt}} - {a_2} \times (\rm{leadExt + trailExt})$ (4)
$h = {a_1} \times {\rm{wfExt}} - {({a_2} \times (\rm{leadExt + trailExt}))^{a3}}$ (5)

式中，h为冠层高度，单位为m；a1、a2、a3为拟合系数；wfExt为波形垂直高度，leadExt为回波波形前沿长度，trailExt为回波波形后沿长度，单位为m。


图 2 波形参数定义示意图
Fig. 2 Schematic definitions of waveform parameters

3.3 模型辅助法

目前已有3套全球的高程数据集，包括由NASA JPL利用C波段雷达干涉数据生产的全球SRTM (Shuttle Radar Topography Mission)数字高程产品；由日本经济贸易产业省和美国国家航空航天局(NASA)联合开发的，基于ASTER立体观测数据生产的全球数字高程模型(ASTER GDEM)；由日本宇航研究开发机构基于ALOS/PRISM立体观测数据生产的全球AW3D30产品。这些数据为波形展宽研究提供了已知的地形信息。

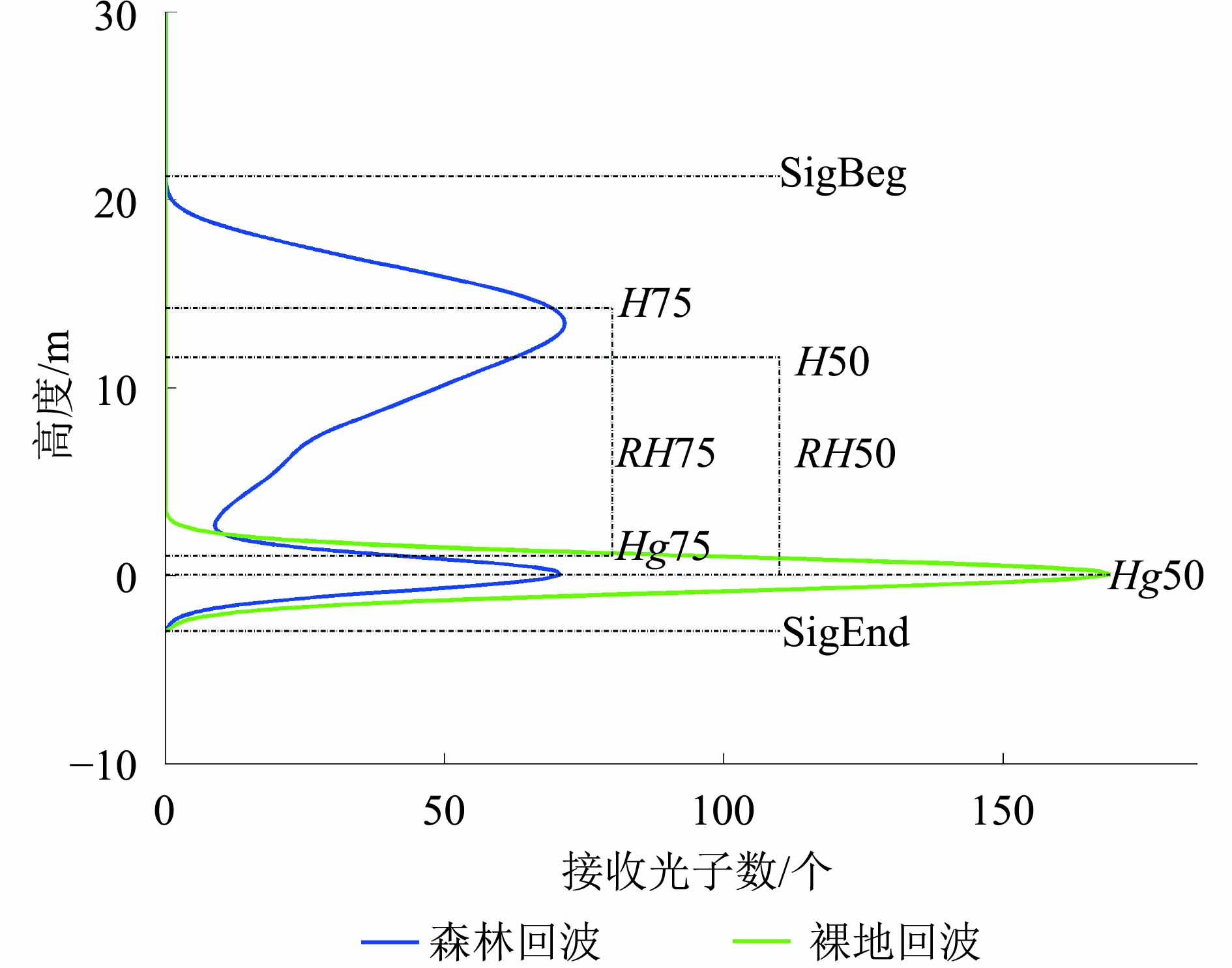
现有的回波波形能量四分位高度指数计算严重依赖地面回波峰值位置的确定，当森林郁闭度较高或地形较陡使得地面回波较弱时，会给这些参数的提取带来困难。传统的高度指数计算方法是以地面回波波峰点进行对齐，求得相对高度指数，地面回波波峰点以下的波形也有展宽的现象，但是传统的波形高度指数并没有考虑这一部分影响，因此对地形的纠正并没有达到很好的效果。本文采取了背景均值加上3倍的标准差为阈值来确定信号的开始与结束位置(Sun等，2008；池泓，2011)，利用激光雷达回波信号截止点作为参考，考虑了地面回波波峰以下的波形展宽，对波形高度指数进行重新定义。如图3所示，蓝色曲线为森林激光雷达回波波形，H50和H75分别定义为激光雷达回波波形能量50%位置和75%的位置到信号截止点的距离。利用地形坡度信息和激光雷达回波模型对裸露地表的回波进行模拟，将模拟的裸露地表回波波形与森林回波波形的信号截止点对齐，如图3所示的绿色曲线，相应地，Hg50和Hg75分别为模拟的裸地回波波形能量50%位置和75%位置相对于回波信号截止位置的高度。森林回波波形四分位相对高度指数分别定义为：RH50=H50—Hg50，RH75=H75—Hg75。采用与“高斯分解法”相同的模型进行森林冠层高度反演，如式(1)(2)(3)所示。


图 3 波形相对高度指数定义示意图
Fig. 3 Schematic definitions of relative height indexes

4 结果与分析

4.1 森林场景与激光雷达回波模拟结果

表2以5年、50年、150年和200年的林分为例，给出了使用ZELIG模型模拟3维森林场景的株密度、胸高断面积加权平均高和最大树高等统计信息。

表 2 林分生长情况统计
Table 2 Characteristics of forest stands

下载CSV 
林龄/a 株密度/(株/ha) Lorey’s H/m 最大高/m
5 4011 2.87 4.00
50 7266 6.37 10.00
150 1377 15.84 20.00
200 1177 20.40 24.00

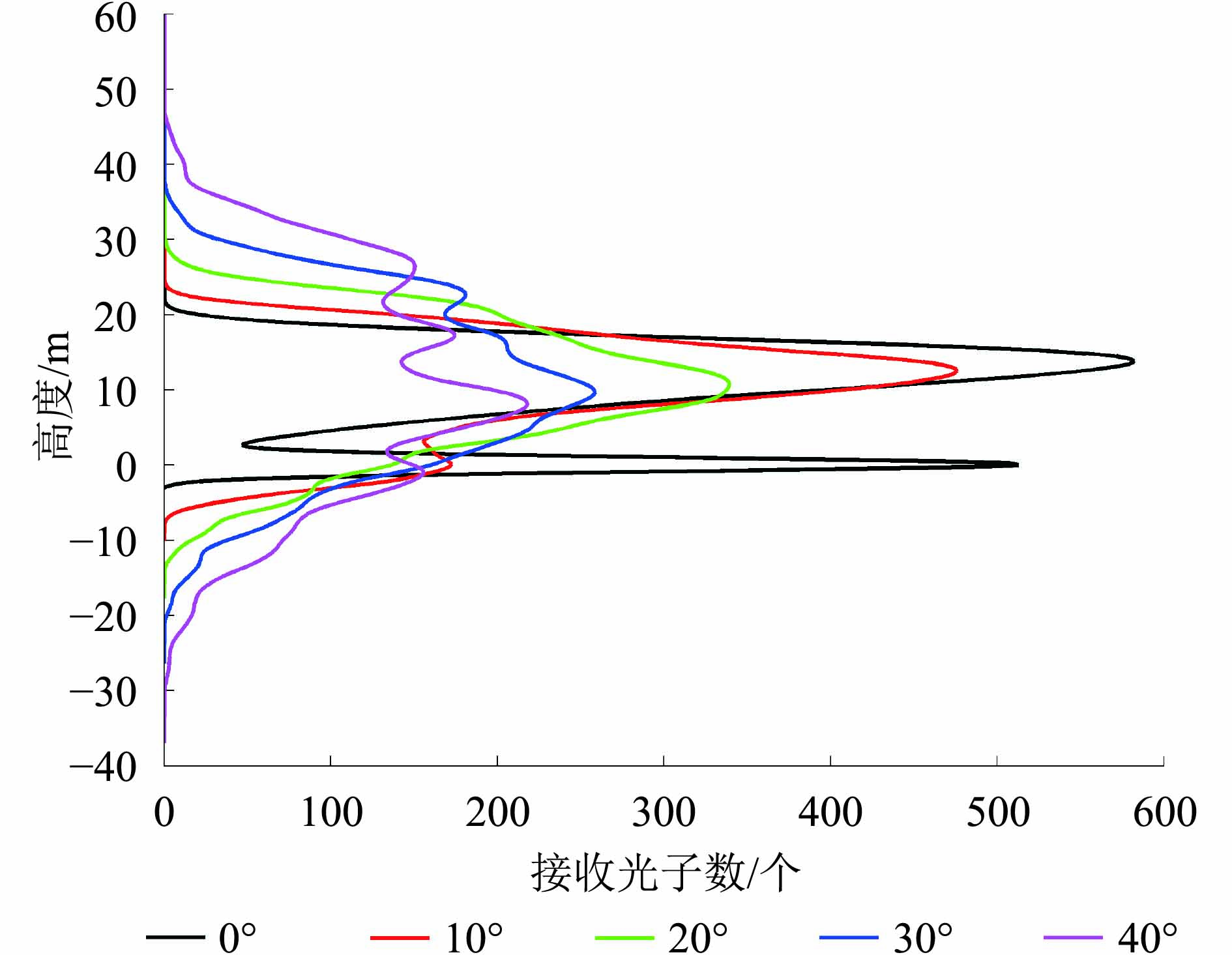
图4展示了以表2所示的林龄为150年林分构建的3维森林场景模拟的不同地形条件下的激光雷达回波波形。可以看出，在坡度为0°的情况下，回波呈现典型的双峰结构特征，上面的回波来自森林冠层, 下面的回波来自地面。随着坡度的增大，坡度对大光斑激光雷达波形影响较为明显，地面回波和树冠回波都有展宽，波形长度也随之增加，同时地面的波峰和植被的波峰值都降低，森林冠层波峰逐渐与地面波峰发生混叠。可见，模拟数据较好地再现了地形对回波波形的展宽作用。


图 4 地形坡度对大光斑激光雷达回波的影响模拟
Fig. 4 Simulated LiDAR waveforms on different terrain slope

4.2 波形高度指数对地形敏感性分析

激光雷达回波波形指数对地形的敏感性分析是发展具备一定地形适应性的森林冠层高度反演算法的基础。波形指数对地形的敏感性越低，表明它们受地形的影响越小。

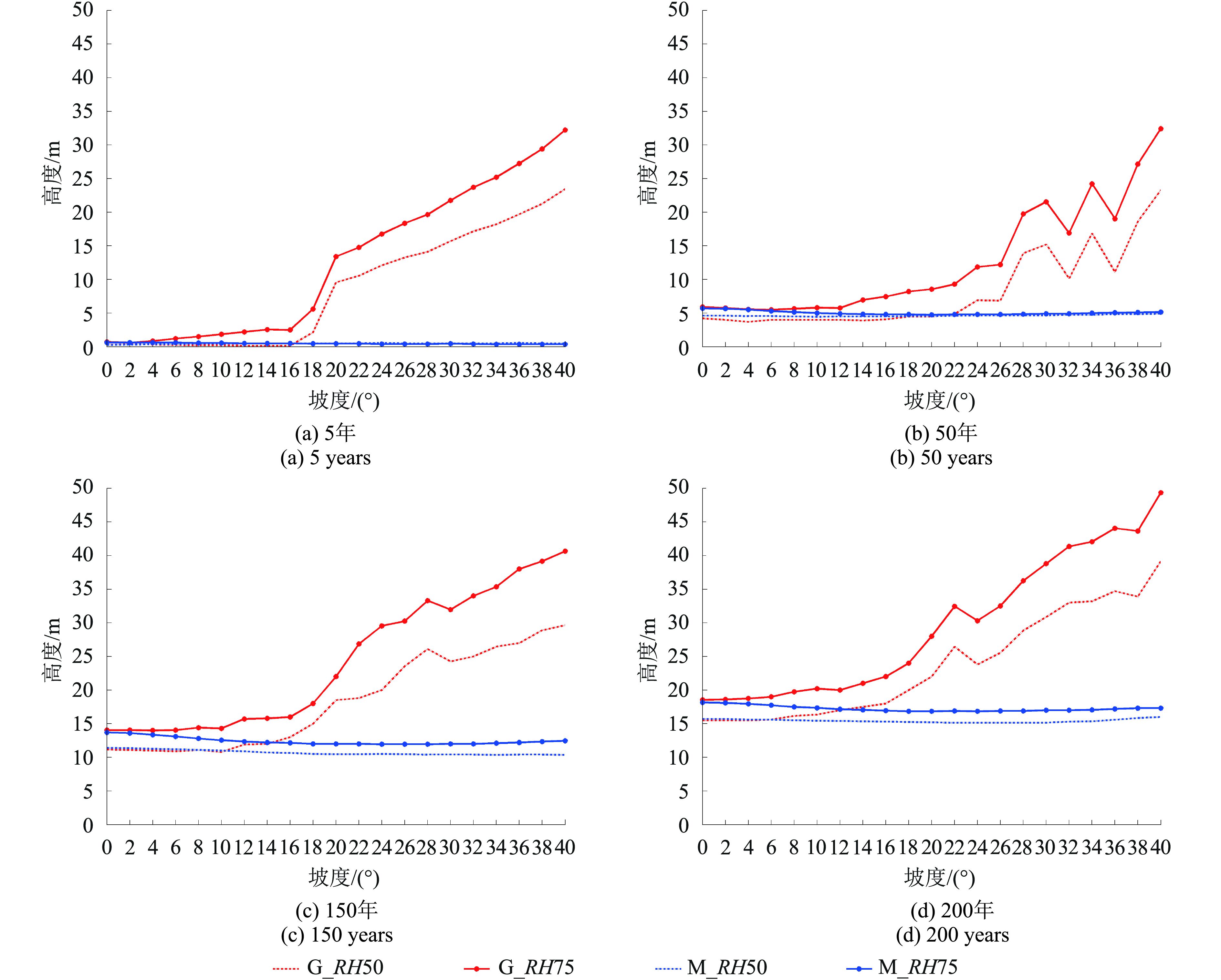
图5展示了基于“高斯分解法”和“模型辅助法”计算的RH50和RH75对坡度的敏感性。图5(a)—(d)分别是利用林龄为5年、50年、150年和200年的3维森林场景模拟的结果。每个图内红色虚线(G_RH50)和实线(G_RH75)分别代表相同森林场景不同坡度情况下，使用“高斯分解法”计算得到的RH50和RH75随坡度的变化，蓝色虚线(M_RH50)和实线(M_RH75)分别代表使用“模型辅助法”计算得到的RH50和RH75随坡度的变化。


图 5 不同年龄的林分中RH50和RH75对坡度的敏感性分析
Fig. 5 Sensitivity analysis of RH50 and RH75 to terrain slope of forest stand with different age

从图5可以看出，在坡度小于16°时，高斯分解法得到的RH50和RH75受地形坡度影响较小，存在轻微的上升趋势，坡度介于16°—20°时，上升趋势比较明显，说明随着坡度上升，高斯分解法找到地面回波位置精度较低；当坡度大于20°时，高斯分解法得到的RH50和RH75随着坡度上下波动变化明显，总的趋势是随着坡度线性上升，因为此时高斯分解法不能准确地找到地面回波波峰点，会将矮小的植被回波作为地面回波。“模型辅助方法”提取的RH50和RH75，随坡度的变化呈现近似水平直线的特征，在0—40°，波动范围在1 m之内，表明“模型辅助方法”提取的RH50和RH75受地形坡度影响较小，对地形是适应性明显优于“高斯分解法”。

4.3 森林冠层高度反演结果

在构建森林冠层高度反演模型时，将8400条激光雷达回波数据按坡度分为两组，0°—20°为一组(共21个角度值)，包含了4400条激光雷达回波数据；22°—40°(共20个角度值)为一组，包含了4000条激光雷达回波数据。0°—20°，采用其中的2200条数据作为训练数据来进行建立模型，剩下的2200个数据验证模型精度，22°—40°，采用其中的2000个数据来进行建立模型，剩下的2000个数据验证模型精度。通过线性回归，得到模型中的各个系数a1，a2，a3，并采用相关系数R2，均方根误差RMSE评价构建模型的精度。

表3给出了森林冠层高度反演模型的构建情况。在0°—20°范围内，高斯分解法采用RH75和RH50计算冠层高度的相关系数为0.69，RMSE为2.90 m，比单一使用RH50或RH75精度略高。波形参数法中，Edge-extent线性模型和Edge-extent非线性模型具有相似的结果，相关系数为0.76，RMSE为2.54 m，略优于高斯分解法。模型辅助法无论单独使用RH50或RH75建模，还是RH50和RH75共同建模，相关系数R2都达到0.98，RMSE最大为0.74 m，明显高于高斯分解法和波形参数法，RH50和RH75共同构建模型略微提高了模型精度，效果最好。

表 3 模型分析
Table 3 Analysis of model

下载CSV 
坡度 方法 模型 R2 RMSE/m
0°—20° 高斯分解法 h=5.46+0.69×RH50 0.68 2.92
h=4.59+0.59×RH75 0.67 2.99
h=5.45+0.69×RH50+0.005×RH75 0.69 2.9
波形参数法 h=0.75×wfExt–0.48×(leadExt+trailExt) 0.76 2.54
h=0.75×wfExt–(0.47×(leadExt+trailExt))1.008 0.76 2.54
模型辅助法 h=0.73+1.35×RH50 0.98 0.57
h=0.90+1.15×RH75 0.98 0.74
h=0.73+1.30×RH50+0.04×RH75 0.99 0.56
22°—40° 高斯分解法 h=7.98+0.19×RH50 0.11 5.02
h=6.62+0.19×RH75 0.12 4.98
h=4.55–0.41×RH50+0.57×RH75 0.14 4.93
波形参数法 h=0.25×wfExt–0.09×(leadExt+trailExt) 0.27 4.54
h=0.26×wfExt–(0.11×(leadExt+trailExt))0.89 0.28 4.54
模型辅助法 h=0.49+1.40×RH50 0.97 0.93
h=0.90+1.26×RH75 0.97 0.92
h=0.61+0.70×RH50+0.64×RH75 0.98 0.8
0°—40° 模型辅助法 h=0.68+1.36×RH50 0.98 0.75
h=0.93+1.20×RH75 0.97 0.94
h=0.69+1×RH50+0.32×RH75 0.98 0.72

在坡度介于22°—40°内，高斯分解法和波形参数法对森林冠层高度的估算的建模精度明显低于坡度在0°—20°内的情况。高斯分解法构建的模型最大相关系数R2仅仅为0.14，RMSE最小为4.93 m，因为随着坡度的增大，地形的影响越来越严重，高斯分解找到地面回波准确性大大降低；波形参数法中，Edge-extent线性模型和Edge-extent非线性模型仍具有相似的结果，波形参数法最大R2为0.28，RMSE最小为4.54 m，波形参数法只能消除小部分坡度带来的展宽影响。模型辅助法保持着良好的结果，RH50和RH75共同建模，相关系数R2为0.98，RMSE为0.80 m。

通过两组坡度模型来看，无论坡度在0°—20°，还是在22°—40°的坡度范围内，模型辅助法的建模精度都较高，对坡度不敏感，因此，在0°—40°的坡度范围内，使用8400条激光雷达回波数据中的4200条数据对模型辅助法的结果进行统一建模。结果如表3所示，发现模型辅助法在0°—40°范围内，仍具有较高的建模精度，RH50和RH75共同建模，相关系数R2为0.98，RMSE为0.80 m。

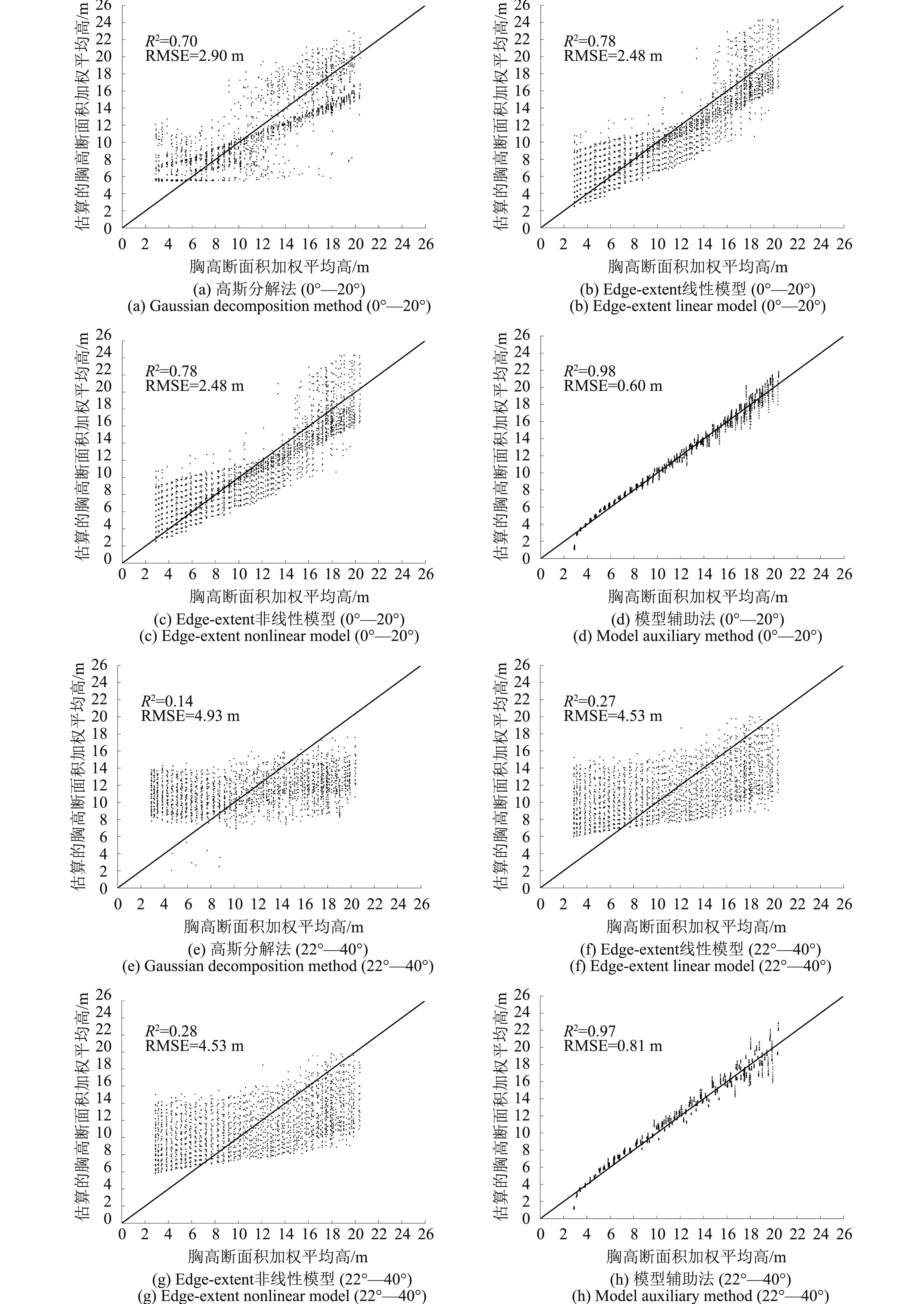
图6展示了对表3中的各种冠层高度估算模型的验证结果。考虑到联合使用RH50和RH75的建模精度高于单独使用它们的建模精度，图6只展示了对联合使用RH50和RH75建模的验证结果。


图 6 胸高断面积加权平均高反演模型验证
Fig. 6 Validation of different models for the estimation of Lorey’s height using LiDAR waveform

图6(a)、(b)、(c)、(d)给出了在0°—20°范围内的模型验证结果，图6(e)、(f)、(g)、(h)给出了在22°—40°范围内的模型验证结果。

从图6可以看出，在0°—20°地形条件下，模型验证精度与建模精度相似，高斯分解法精度最低，R2=0.7，RMSE为2.9 m；波形参数法的线性模型与非线性模型结果相似，比高斯分解法略有提高，R2=0.78，RMSE为2.48 m；模型辅助法的结果精度明显高于高斯分解法和波形参数法，R2=0.98，RMSE为0.6 m；在22°—40°的地形条件下，这个现象更加明显，高斯分解法的森林冠层高度估算精度更低，R2仅为0.14，RMSE为4.93 m。波形参数法虽然比高斯分解法略有改进，但R2仅为0.27，RMSE为4.53 m。相比之下，模型辅助法的森林冠层高度估算精度在两个地形坡度范围内变化不大，都给出了最高的反演精度。

从图6可以看出，高斯分解法和波形参数法反演结果的波动范围较大，尤其在地形坡度大于20°的情况下。同一个实测的Lorey’s Height对应着一系列反演结果，这是由于地形引起的波形展宽造成的。如图5所示，同一个森林场景，由于高斯分解法和波形参数法不能完全克服地形展宽的影响，不同坡度条件下的反演结果不同。

从图6可以看出，在小于20°时，高斯分解法可以近似找到地面回波峰值，但在地形坡度大于20°后，地面回波和植被回波混合在一起，高斯分解法不易得到地面回波峰值点。虽然波形参数法试图利用波形自身的信息如波形前沿长度、后沿长度来消除坡度的影响，但结果表明，波形参数法的反演结果仍受地形影响，特别是地形坡度较大的情况下。坡度影响造成波形的展宽，坡度带来波形长度的变化并不能被前沿长度和后沿长度完全去除。Edge-extent线性模型和Edge-extent非线性模型并不能完全消除坡度带来的前沿展宽、后沿展宽和波形的长度变化。

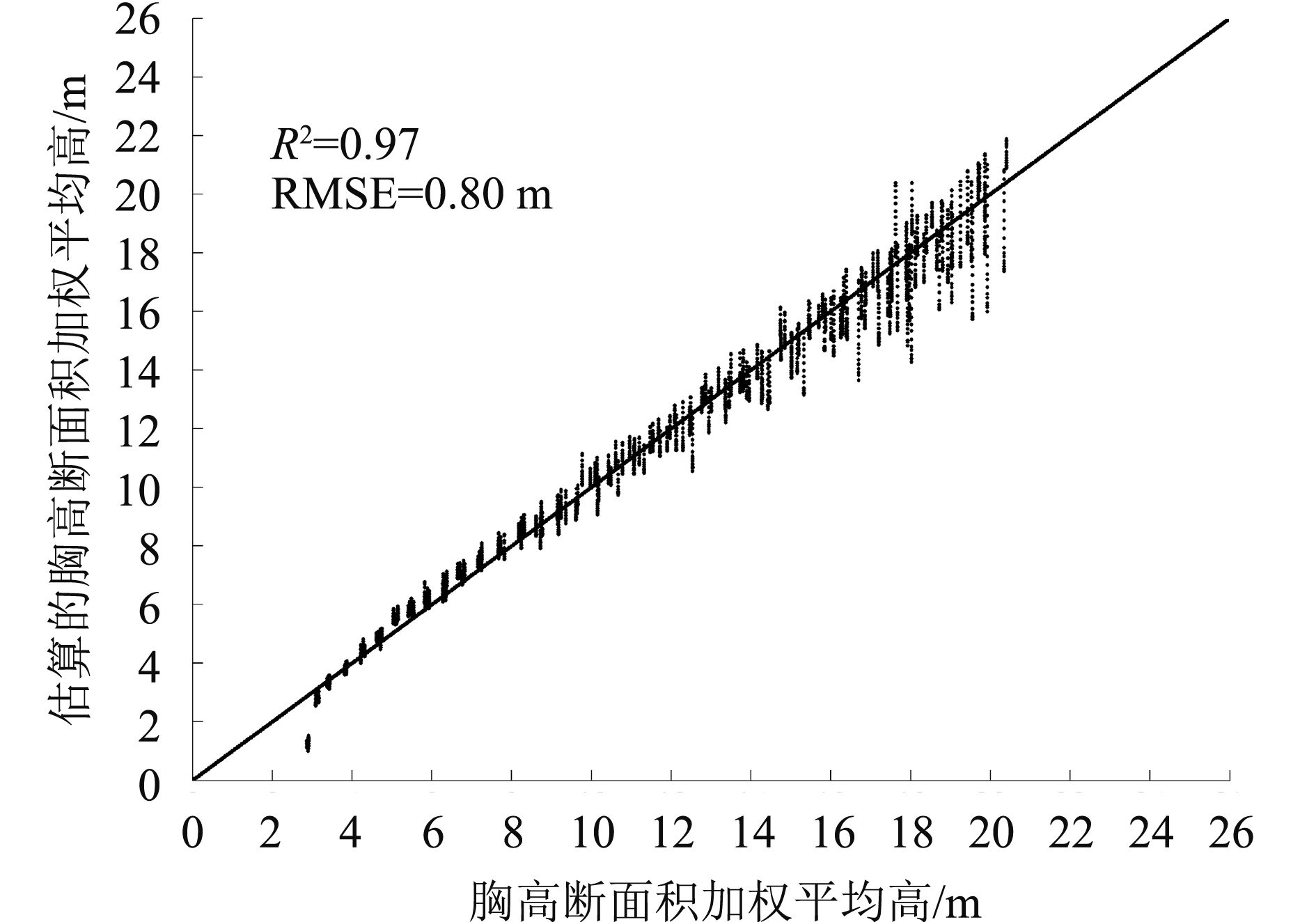
从图6(d)和图6(h)可以看出，模型辅助方法受坡度影响较小，反演结果没有出现随地形变宽的情况，表明模型辅助法具备良好的地形适应性，与图5展示的结果一致。利用本文重新定义的RH50和RH75可以较好地反演森林冠层高度。图7展示了0°—40°范围内统一建模的模型验证情况。模型辅助法对森林冠层高度的估算精度R2=0.97，RMSE=0.8 m。


图 7 胸高断面积加权平均高反演模型验证(0°—40°)
Fig. 7 Validation the estimation of Lorey’s height using LiDAR waveform (0°—40°)

5 结　论

本研究提出了一种基于已知地形信息和激光雷达回波模型的坡地森林冠层高度反演方法。该方法以激光雷达回波信号截止点为参考，定义了波形高度指数H50和H75，使用激光雷达回波模型与已知地形信息模拟裸地的激光雷达回波，将裸地回波信号截止点与森林激光雷达回波信号截止点对齐，利用裸地回波计算常用的波形相对高度指数RH50和RH75，分析了相对高度指数对坡度的敏感性，构建了模型辅助的森林冠层高度反演模型，在0°—40°地形坡度范围内，对模型的适用性进行了分析评价，并与常用的高斯波形分解法和波形参数法的反演结果进行了比较，得到以下结论：

(1)采用森林动态生长模型(ZELIG)模拟的3维森林场景来驱动激光雷达回波模型，分析不同地形条件下的激光雷达回波波形，模拟数据较好地再现了地形对回波波形的展宽作用。

(2)高斯分解法在坡度小于20°时，可以近似找到地面回波位置，利用得到的RH50和RH75能高精度的反演森林冠层高度；在坡度大于20°，受坡度影响大，高斯分解法不能准确地找到地面回波波峰点，反演结果精度较低。

(3)波形参数法在坡度小于20°时，可以在一定程度上克服地形影响，但当坡度大于20°时，求得的森林冠层高度波动大，精度较低。

(4) 模型辅助法，在0°—40°坡度内可以很好地反演森林冠层高度，受坡度的影响较小；模型辅助的方法可以克服较大坡度的影响，比其他两种方法更适合山区森林冠层高度反演。

本文提出的模型辅助法可以精确地反演森林冠层高度，但是该分析数据是基于模拟的森林回波波形数据。下一步将采用真实的星载激光雷达波形数据(如GEDI)对所提出的模型辅助法验证。

志 谢 本文所使用的激光雷达回波模型由美国马里兰大学孙国清教授提供，孙国清教授在论文成文过程中给了很多宝贵的建议，在此表示感谢。

参考文献(References)

  • Allouis T, Durrieu S and Couteron P. 2012. A new method for incorporating hillslope effects to improve canopy-height estimates from large-footprint lidar waveforms. IEEE Geoscience and Remote Sensing Letters, 9 (4): 730–734. [DOI: 10.1109/LGRS.2011.2179635]
  • Cao L, Coops N C, Hermosilla T, Innes J, Dai J S and She G H. 2014. Using small-footprint discrete and full-waveform airborne LiDAR metrics to estimate total biomass and biomass components in subtropical forests. Remote Sensing, 6 (8): 7110–7135. [DOI: 10.3390/rs6087110]
  • Carabajal C C and Harding D J. 2005. ICESat validation of SRTM C-band digital elevation models. Geophysical Research Letters, 32 (22): L22S01 [DOI: 10.1029/2005gl023957]
  • Carabajal C C and Harding D J. 2006. SRTM C-band and ICESat laser altimetry elevation comparisons as a function of tree cover and relief. Photogrammetric Engineering and Remote Sensing, 72 (3): 287–298. [DOI: 10.14358/PERS.72.3.287]
  • Chen Q. 2010. Retrieving vegetation height of forests and woodlands over mountainous areas in the Pacific Coast region using satellite laser altimetry. Remote Sensing of Environment, 114 (7): 1610–1627. [DOI: 10.1016/j.rse.2010.02.016]
  • Chi H. 2011. Research on Forest Aboveground Biomass Estimation in China Based on ICESat/GLAS and MODIS Data. Beijing: Institute of Remote Sensing Applications Chinese Academy Sciences (池泓. 2011. 基于ICESat/GLAS和MODIS数据的中国森林地上生物量估算研究. 北京: 中国科学院遥感应用研究所)
  • Drake J B, Dubayah R O, Clark D B, Knox R G, Blair J B, Hofton M A, Chazdon R L, Weishampel J F and Prince S. 2002. Estimation of tropical forest structural characteristics using large-footprint lidar. Remote Sensing of Environment, 79 (2/3): 305–319. [DOI: 10.1016/s0034-4257(01)00281-4]
  • Dubayah R O and Drake J B. 2000. Lidar remote sensing for forestry. Journal of Forestry, 98 (6): 44–46.
  • Duong V H, Lindenbergh R, Pfeifer N and Vosselman G. 2008. Single and two epoch analysis of ICESat full waveform data over forested areas. International Journal of Remote Sensing, 29 (5): 1453–1473. [DOI: 10.1080/01431160701736372]
  • Enßle F, Heinzel J and Koch B. 2014. Accuracy of vegetation height and terrain elevation derived from ICESat/GLAS in forested areas. International Journal of Applied Earth Observation and Geoinformation, 31 : 37–44. [DOI: 10.1016/j.jag.2014.02.009]
  • Field C B and Raupach M R. 2004. The Global Carbon Cycle: Integrating Humans, Climate, and the Natural World. Washington: Island Press
  • Harding D J, Lefsky M A, Parker G G and Blair J B. 2001. Laser altimeter canopy height profiles: methods and validation for closed-canopy, broadleaf forests. Remote Sensing of Environment, 76 (3): 283–297. [DOI: 10.1016/S0034-4257(00)00210-8]
  • Hayashi M, Saigusa N, Oguma H and Yamagata Y. 2013. Forest canopy height estimation using ICESat/GLAS data and error factor analysis in Hokkaido, Japan. ISPRS Journal of Photogrammetry and Remote Sensing, 81 : 12–18. [DOI: 10.1016/j.isprsjprs.2013.04.004]
  • Hilbert C and Schmullius C. 2012. Influence of surface topography on ICESat/GLAS forest height estimation and waveform shape. Remote Sensing, 4 (8): 2210–1125. [DOI: 10.3390/rs4082210]
  • Lee S, Ni-Meister W, Yang W Z and Chen Q. 2011. Physically based vertical vegetation structure retrieval from ICESat data: validation using LVIS in White Mountain National Forest, New Hampshire, USA. Remote Sensing of Environment, 115 (11): 2776–2785. [DOI: 10.1016/j.rse.2010.08.026]
  • Lefsky M A, Harding D J, Keller M, Cohen W B, Carabajal C C, Del Bom Espirito-Santo F, Hunter M O and De Oliveira Jr R. 2005. Estimates of forest canopy height and aboveground biomass using ICESat. Geophysical Research Letters, 32 (22): L22S02 [DOI: 10.1029/2005GL023971]
  • Lefsky M A, Keller M, Pang Y, De Camargo P B and Hunter M O. 2007. Revised method for forest canopy height estimation from geoscience laser altimeter system waveforms. Journal of Applied Remote Sensing, 1 (1): 013537 [DOI: 10.1117/1.2795724]
  • Nie S, Wang C, Zeng H C, Xi X H and Xia S B. 2015. A revised terrain correction method for forest canopy height estimation using ICESat/GLAS data. ISPRS Journal of Photogrammetry and Remote Sensing, 108 : 183–190. [DOI: 10.1016/j.isprsjprs.2015.07.008]
  • Pagnutti M and Ryan R E. 2009. Automated DEM validation using ICESat GLAS data//Proceedings of ASPRS/MAPPS 2009 Fall Conference. San Antonio, Texas: ASPRS
  • Pang Y, Lefsky M, Andersen H E, Miller M E and Sherrill K. 2008. Validation of the ICEsat vegetation product using crown-area-weighted mean height derived using crown delineation with discrete return lidar data. Canadian Journal of Remote Sensing, 34 (S2): S471–S484. [DOI: 10.5589/m08-074]
  • Pang Y, Lefsky M, Sun G Q and Ranson J. 2011. Impact of footprint diameter and off-nadir pointing on the precision of canopy height estimates from spaceborne lidar. Remote Sensing of Environment, 115 (11): 2798–2809. [DOI: 10.1016/j.rse.2010.08.025]
  • Popescu S C, Zhao K G, Neuenschwander A and Lin C. 2011. Satellite lidar vs. small footprint airborne lidar: comparing the accuracy of aboveground biomass estimates and forest structure metrics at footprint level. Remote Sensing of Environment, 115 (11): 2786–2797. [DOI: 10.1016/j.rse.2011.01.026]
  • Ranson K J, Sun G, Knox R G, Levine E R, Weishampel J F and Fifer S T. 2001. Northern forest ecosystem dynamics using coupled models and remote sensing. Remote Sensing of Environment, 75 (2): 291–302. [DOI: 10.1016/s0034-4257(00)00174-7]
  • Rosette J A, North P R J, Suárez J C and Armston J D. 2009. A comparison of biophysical parameter retrieval for forestry using airborne and satellite LiDAR. International Journal of Remote Sensing, 30 (19): 5229–5237. [DOI: 10.1080/01431160903022944]
  • Rosette J A B, North P R J and Suárez J C. 2008. Vegetation height estimates for a mixed temperate forest using satellite laser altimetry. International Journal of Remote Sensing, 29 (5): 1475–1493. [DOI: 10.1080/01431160701736380]
  • Smith T M and Urban D L. 1988. Scale and resolution of forest structural pattern. Vegetatio, 74 (2/3): 143–150. [DOI: 10.1007/BF00044739]
  • Sun G, Ranson K J, Kimes D S, Blair J B and Kovacs K. 2008. Forest vertical structure from GLAS: an evaluation using LVIS and SRTM data. Remote Sensing of Environment, 112 (1): 107–117. [DOI: 10.1016/j.rse.2006.09.036]
  • Sun G Q and Ranson K J. 2000. Modeling lidar returns from forest canopies. IEEE Transactions on Geoscience and Remote Sensing, 38 (6): 2617–2626. [DOI: 10.1109/36.885208]
  • Sun G Q, Ranson K J, Guo Z, Zhang Z, Montesano P and Kimes D. 2011. Forest biomass mapping from lidar and radar synergies. Remote Sensing of Environment, 115 (11): 2906–2916. [DOI: 10.1016/j.rse.2011.03.021]
  • Wang C, Tang F X, Li L W, Li G C, Cheng F and Xi X H. 2013. Wavelet analysis for ICESat/GLAS waveform decomposition and its application in average tree height estimation. IEEE Geoscience and Remote Sensing Letters, 10 (1): 115–119. [DOI: 10.1109/lgrs.2012.2194692]
  • Wang X Y, Huang H B, Gong P, Liu C X, Li C C and Li W Y. 2014. Forest canopy height extraction in rugged areas with ICESat/GLAS data. IEEE Transactions on Geoscience and Remote Sensing, 52 (8): 4650–4657. [DOI: 10.1109/tgrs.2013.2283272]
  • Wulder M A, White J C, Nelson R F, Næsset E, Ørka H O, Coops N C, Hilker T, Bater C W and Gobakken T. 2012. Lidar sampling for large-area forest characterization: a review. Remote Sensing of Environment, 121 : 196–209. [DOI: 10.1016/j.rse.2012.02.001]
  • Xing Y Q, De Gier A, Zhang J J and Wang L H. 2010. An improved method for estimating forest canopy height using ICESat-GLAS full waveform data over sloping terrain: a case study in Changbai mountains, China. International Journal of Applied Earth Observation and Geoinformation, 12 (5): 385–392. [DOI: 10.1016/j.jag.2010.04.010]
  • Yang W Z, Ni-Meister W and Lee S. 2011. Assessment of the impacts of surface topography, off-nadir pointing and vegetation structure on vegetation lidar waveforms using an extended geometric optical and radiative transfer model. Remote Sensing of Environment, 115 (11): 2810–2822. [DOI: 10.1016/j.rse.2010.02.021]
数据专区
  • 目录 目录
  • 文章信息 文章信息
  • 引用格式 引用格式
  • 地图 地图
  • 评论 评论
  • 图 图
  • 表 表
  • 二维码 二维码
  • 参考文献 参考文献
  • 多媒体 多媒体