出版日期: 2018-05-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20187076
2018 | Volumn22 | Number 3
上一篇  |  下一篇
技术方法 
激光雷达和点云切片算法结合的森林有效叶面积指数估算
expand article info 路璐 , 郑光 , 马利霞
南京大学 国际地球系统科学研究所，南京 210023
收稿日期: 2017-04-05
基金项目: 国家自然科学基金(编号：41771374)；空基科研星工程先期攻关项目
第一作者简介: 路璐(1993—　)，女，硕士研究生，研究方向为激光雷达林业应用。E-mail：lulu9349@163.com
通讯作者简介: 郑光(1982—　)，男，副教授，研究方向为植被结构参数的激光雷达反演和森林生物量遥感反演等。E-mail：zhengguang@nju.edu.cn
中图分类号: TP79
文献标识码: A

摘要

叶面积指数(LAI)是定量模拟和刻画植被冠层结构、生理过程以及研究森林生态系统碳水循环中物质和能量交换的重要生物物理参数之一。定量分析林冠元素的3维空间分布是准确估算森林叶面积指数的重要基础和关键步骤。本文利用地面激光雷达扫描系统(TLS)，获取了不同树种、密度、年龄和空间分布的森林3维点云数据，利用“径向半球点云切片”和“点云法向量重建”算法分别计算森林的角度孔隙率和消光系数，进而得到森林冠层的有效叶面积指数。通过与利用传统光学仪器得到的结果比较发现：单站半球式激光雷达扫描得到森林样方尺度的结果与LAI-2200和数字半球摄影观测所得结果的相关性分别为R2=0.7084(N=9，p<0.01)和0.7409(N=14，p<0.01)。通过角度分辨率(LBA)和角度孔隙率(AGF)的敏感性分析，建议径向半球切片算法的角度分辨率应参考中心单站TLS半球式扫描所设置的采样间距。本文所采用的径向半球切片算法可以有效地利用单站半球式扫描所获取的3维点云进行森林冠层有效叶面积指数的定量估算。

关键词

叶面积指数, 地基激光雷达, 角度孔隙率, 消光系数, 叶倾角

Combining point cloud slicing and terrestrial laser scanning data to retrieve an effective leaf area index
expand article info LU Lu , ZHENG Guang , MA Lixia
International Institute for Earth System Science, Nanjing University, Nanjing 210023, China

Abstract

Leaf Area Index (LAI) is one of the most important forest canopy biophysical parameters and plays a key role in many forest biophysical processes and energy and matter exchange among forest–soil–atmosphere. Terrestrial laser scanning (TLS)-based Point Cloud Data (PCD) implicitly contain three-dimensional forest structural information. PCD can be used to quantitatively characterize the structural information of forests from a three-dimensional perspective and provides a high spatial resolution. Consequently, PCD provides highly detailed information about forests and enable the retrieval of forest parameters. In this study, we retrieved the canopy effective leaf area index (LAIe) by using TLS and validated the TLS-based results through field-based measurements. Three-dimensional PCD were acquired with a single- or multiple-location experimental setup in all forest plots. All PCD were clipped into a circular plot with a radius of 30 m. An algorithm called " radial hemispherical point cloud slicing (RHPCS)” was utilized to process the original PCD to retrieve the " Angular Gap Fraction (AGF)” and extinction coefficients by dividing the hemispherical volume into many " trapezoid voxels.” A " gap” voxel is an empty or a foliage voxel depending on the number of points within it. By reconstructing the normal vector of a point within a certain neighbor region, we computed the leaf mean inclination angle and obtained the canopy extinction coefficient by using Campbell’s algorithm. We calculated the LAIe of each forest plot on the basis of Beer’s law by dividing a hemisphere PCD into 9° intervals in the inclination direction. Ten annulus hemispherical regions were obtained. Each region had an azimuthal angle ranging from 0° to 360° and a 9° inclination angle range. Then, we computed the AGF, extinction coefficient, and LAIe of each hemispherical region. We obtain the LAIe of the entire plot by computing the means of the LAIe of 10 hemispherical regions. Results showed that the TLS-based LAIe captured 70.84% (N=9, p<0.01) and 74.09% (N=14, p<0.01) of the variations in LAI-2200 and Digital Hemispherical Plotography (DHP), respectively. We conducted a sensitivity analysis of laser beam angle in AGF estimation and discovered that the AGF of RHPCS should be determined based on a user-predefined laser sampling space and is affected by the characteristic size of foliage elements of a forest canopy. We also analyzed the effect of the number of neighboring points on LAIe calculation. The optimal number of neighboring points was 12 in this study, and we suggest that the number of neighboring points be based on leaf curvature when reconstructing a normal vector. Comparison of TLS-based LAIe with the LAIe results of LAI-2200 and DHP showed that calculating the LAIe of forest plots by combining TLS-based PCD with the RHPCS algorithm is feasible and suitable for forests with different densities and ages. The TLS-based LAIe estimation approach presents considerable importance in quantitatively characterizing forest canopy structural parameters from a 3D perspective.

Key words

leaf area index, terrestrial LiDAR, angular gap fraction, extinction coefficient, leaf inclination

1 引　言

叶面积指数(LAI)的定义是单位水平地表面积上所有绿色叶片表面积的一半(Chen和Black，1992)，是植被冠层结构最重要的生物物理参数之一，也是控制植被蒸腾作用(Chen 等，2005；Cleugh 等，2007；Jongschaap，2006)、光合作用(Duchemin 等，2006)、呼吸作用、碳循环(Soegaard，1999)等许多生物物理过程的重要参数(Chen和Cihlar，1996)。LAI可以表征植被冠层的太阳辐射能量吸收能力，是大多数生态系统生产力模型和全球气候、水文、生物地球化学和生态学模型的关键参数(Myneni 等，2002)；它还可以作为森林生长效率的指标，用来反映森林抵抗昆虫攻击的能力和昆虫灾害之间的关系(Waring和Pitman，1985)。对LAI的长期监测有利于掌握森林生态系统生物量、生产力的动态变化(Asner 等，2003；Lee和Kwon，2006)和气候对生态系统的影响(Asner 等，1998；Hyvönen 等，2007)。因此，准确估算LAI对于分析碳循环，进而研究全球变暖等全球变化具有重要的意义。但是由于叶片的聚集效应等因素使得观测真实LAI较为困难，因此很多研究都使用有效叶面积指数(LAIe)来表征植被叶面积情况(Black 等，1991；Chen 等，1991)。

叶面积指数的测定方法主要有直接测量法和间接测量法。直接测量法主要是手动测量，包括破坏性采样、凋落物收集(Neumann 等，1989)、点采样法(Wilson，1965)等。但因直接测量法耗时耗力，限制了它的应用。间接测量法因其可适用于大区域并且成本较低，获得了较大的发展和应用(Chen 等，1997)。间接测量法主要包括遥感影像和使用光学仪器等。具有较大孔隙的非均质植被的叶面积指数可以通过适当平均局部孔隙率，如探测太阳直射光束的传输来测量(Lang和Xiang，1986)。具体的方法是：将太阳直射光束当作探针，对一个十倍于叶片特征宽度的水平路径上太阳直射光束与叶片的接触数取平均值，然后取该平均值的对数。这样得到的许多路径的对数的平均值与叶面积指数呈线性相关关系，并且比整个路径上太阳直射光束与叶片接触数的平均值更加精确。一些研究通过卫星遥感数据反演大范围LAI (Chen和Cihlar，1996)。骆社周等人(2012)利用TM遥感数据估算西藏林芝区域高山松的LAI；Chen和Cihlar(1996)使用陆地卫星TM影像来反演加拿大北部针叶林的LAI。但是由于背景的光学特性在不同的空间和季节上存在变化，导致估算的LAI不准确。利用光学仪器估测LAI主要是基于贝尔定律(Hirose，2005)，根据消光系数和孔隙率来估算植被的LAIe，如鱼眼相机和LAI-2200。数码相机加鱼眼镜头的数字半球摄影技术是间接获取植被LAIe较为常用的一种方法(Chen 等，1991)，它是通过使用广角镜头在森林冠层下方向上拍照来获得植被冠层图像，通过区分天空和冠层估算孔隙率，进而估计LAI。LAI-2200因为不需要后期的图像处理而被认为是鱼眼摄影的便捷方式(Chen 等，1997)。TRAC (Chen和Cihlar，1995)是设计用来定量刻画森林植被聚集度指数，进而计算植被冠层孔隙大小和叶面积指数等参数的一种光学仪器。在利用上述3种光学仪器估算植被LAI时，鱼眼摄影和LAI-2200要求在散射光条件下进行，TRAC需要在晴天观测。此外，鱼眼照片的曝光和分辨率都会影响之后计算的孔隙率等参数，进而影响LAIe的估算。

传统基于光学仪器的方法只能从2维角度描述冠层结构参数。随着技术和研究的深入，3维技术手段得到充分发展。Rakocevic等人(2000)发展了一种使用电磁式3维数字化仪评估白色苜蓿冠层3维几何结构的方法，通过使用数字化仪记录的数据和特殊的软件可以重建冠层结构，进而计算冠层叶面积指数。但是该方法是针对于小型冠层(如草地)的研究，并不能适用于森林植被LAI的研究。Disney等人(2006)通过构建针叶林冠层的详细3维结构，使利用冠层散射模型对森林冠层辐射响应进行描述成为可能，进而探索冠层结构对LAI、生物量和冠层覆盖等生物物理参数的影响。但是由于该方法计算能力的限制，对于复杂冠层的构建还无法实现。

具有3维制图能力的激光雷达技术的出现为反演森林冠层结构提供了一种新的技术手段，可详细刻画森林冠层的水平和垂直信息(Lim 等，2003)。常用的激光雷达有航空激光雷达(ALS)和地基激光雷达(TLS)。激光雷达扫描系统通过发射激光对目标进行扫描，以获得目标的3维点云数据。点云数据信息通常可以用如下形式表示：

$P(x , y , {\textit{z}} , I , \cdots , R , G , B , NIR)$

式中，(x，y，z)是点的几何信息，通常为笛卡儿坐标系，I是点的强度信息，(R，G，B，NIR)是点的红、绿、蓝以及近红外波段的光谱信息。

地基激光雷达扫描系统由于其获得的高密度点云数据，可更加精确反演冠层结构参数，包括森林冠层孔隙率(Danson 等，2007；Hancock 等，2014)、叶面积指数(Hosoi和Omasa，2006；Ilangakoon 等，2015；Moorthy 等，2008；Olsoy 等，2016；Zheng 等，2013)、植被面积指数(Takeda 等，2008)、胸径(Henning和Radtke，2006；Moskal和Zheng，2012；Strahler 等，2008；Tansey 等，2009；刘鲁霞 等，2014)、地上生物量(Greaves 等，2015；Hauglin 等，2013；Kankare 等，2013；Olsoy 等，2014)等。Hosoi和Omasa(2006)利用点云数据建立单木水平上基于体元的3维模型，通过切片方式计算植被的叶面积密度和叶面积指数。但是由于切片和利用激光雷达测量时层与层之间边缘的差异，会影响叶面积密度估算的精度，并且该方法还未应用于大型森林植被。孔隙率是使用贝尔定律计算植被有效叶面积指数的必要参数之一。Danson等人(2007)将TLS点云数据投影到半球形的单位圆上，然后计算森林孔隙率。Hancock等人(2014)使用射线跟踪法将植被的点云数据转换为半球形的黑(冠层)白(孔隙)两色图像，进而计算森林植被孔隙率。上述方法虽然使用TLS点云数据计算森林孔隙率，但是没有利用点云数据的3维优势。由TLS获得的点云数据包含了森林冠层详细的几何信息，因此可以用来从3维的角度计算孔隙率(Zheng 等，2016)。本文使用“径向半球切片算法”(Zheng 等，2016)对TLS获得的森林点云数据进行体元化处理求得不同天顶角方向孔隙率进而计算冠层LAIe，具体的研究目标是：

(1) 基于地面激光雷达所获取的点云数据(包括叶片、树枝以及树干)，从3维角度利用“径向半球切片算法”估算森林样方的角度孔隙率(AGF)、消光系数和有效叶面积指数；

(2) 研究该方法在不同密度和树龄森林样方的适用性以及对估算结果与传统光学仪器所得到的结果进行对比研究。

2 数据和方法

2.1 研究区

实验研究区一位于江苏省南京市溧水区白马镇的白马国家农业科技园区(31°35′18.44″N，119°11′19.46″E)。园区内植被类型丰富，有针叶林、阔叶林等。园内大部分森林样方为人工种植，有少许自然林。本文选取的实验样地分布在园区内的9处地方，选取的植被具有不同的树种(栾树、海棠、樱桃、杨树、松柏等)、密度(1000 棵/ha、4000 棵/ha、10000 棵/ha等)以及树高(2 m、11 m、20 m等)等，LAIe主要分布范围为1—3。

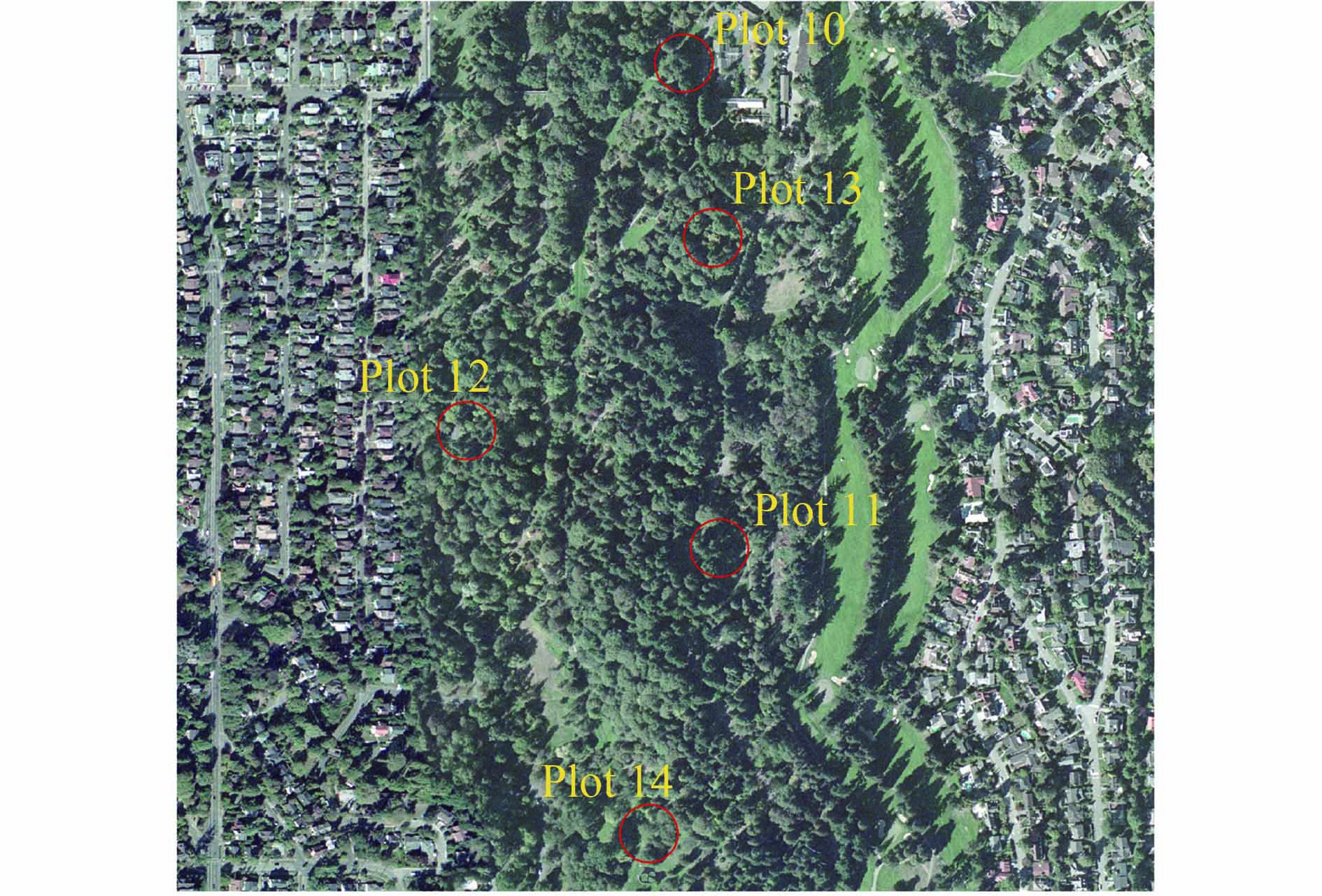
实验研究区二位于美国华盛顿植物园WPA (Washington Park Arboretum)，其紧邻华盛顿湖，处于西雅图市中心西侧，华盛顿大学的南方。植物园内覆盖有4600余种植被，20000多棵树木、灌木以及藤本植物等。本文选取了植物园内的5个样地，包含了不同的树种，LAIe主要范围是2—4。选取两个实验研究区，使得实验及数据具有一定的全面性、准确性。

2.2 数　据

2.2.1 点云数据

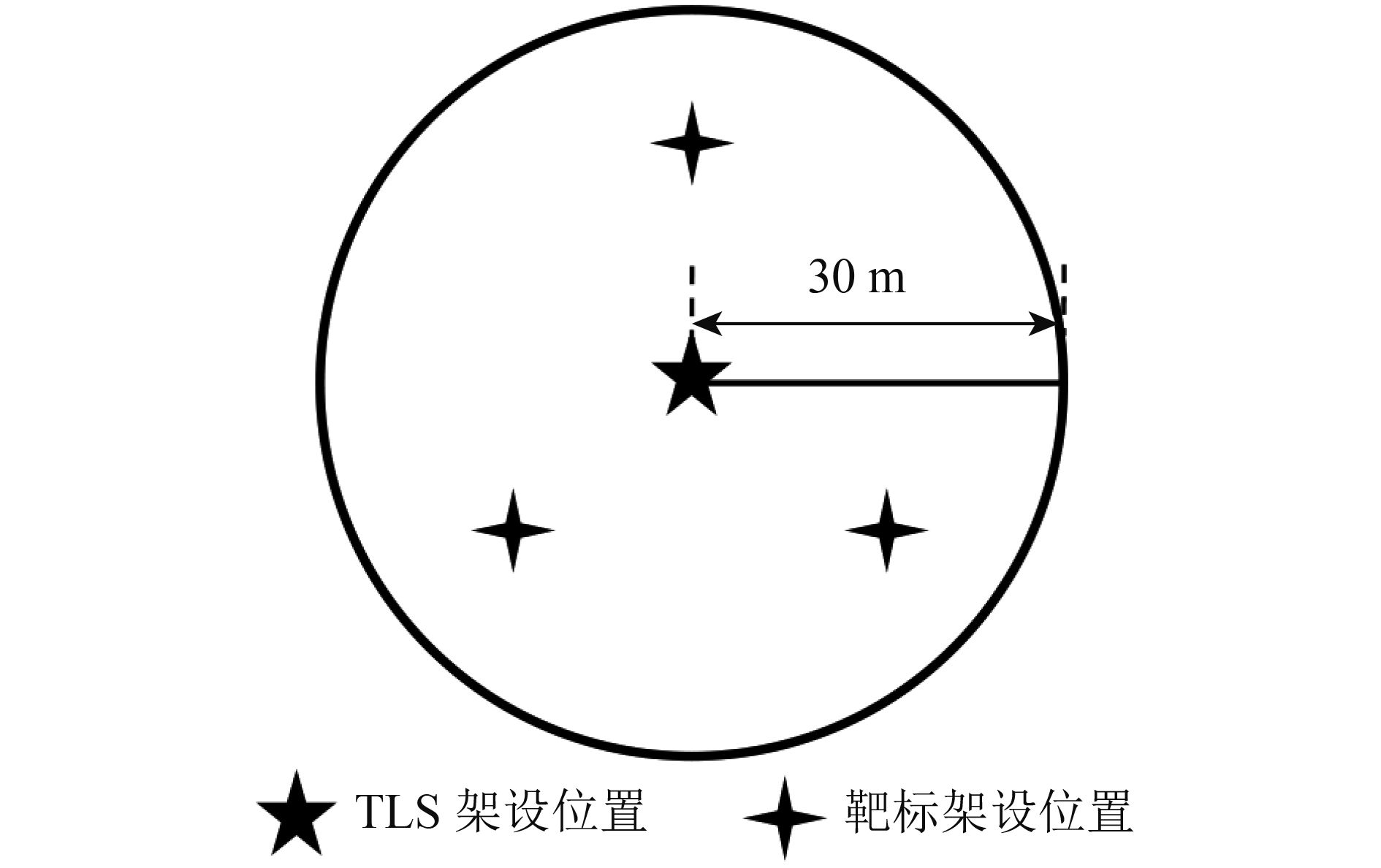
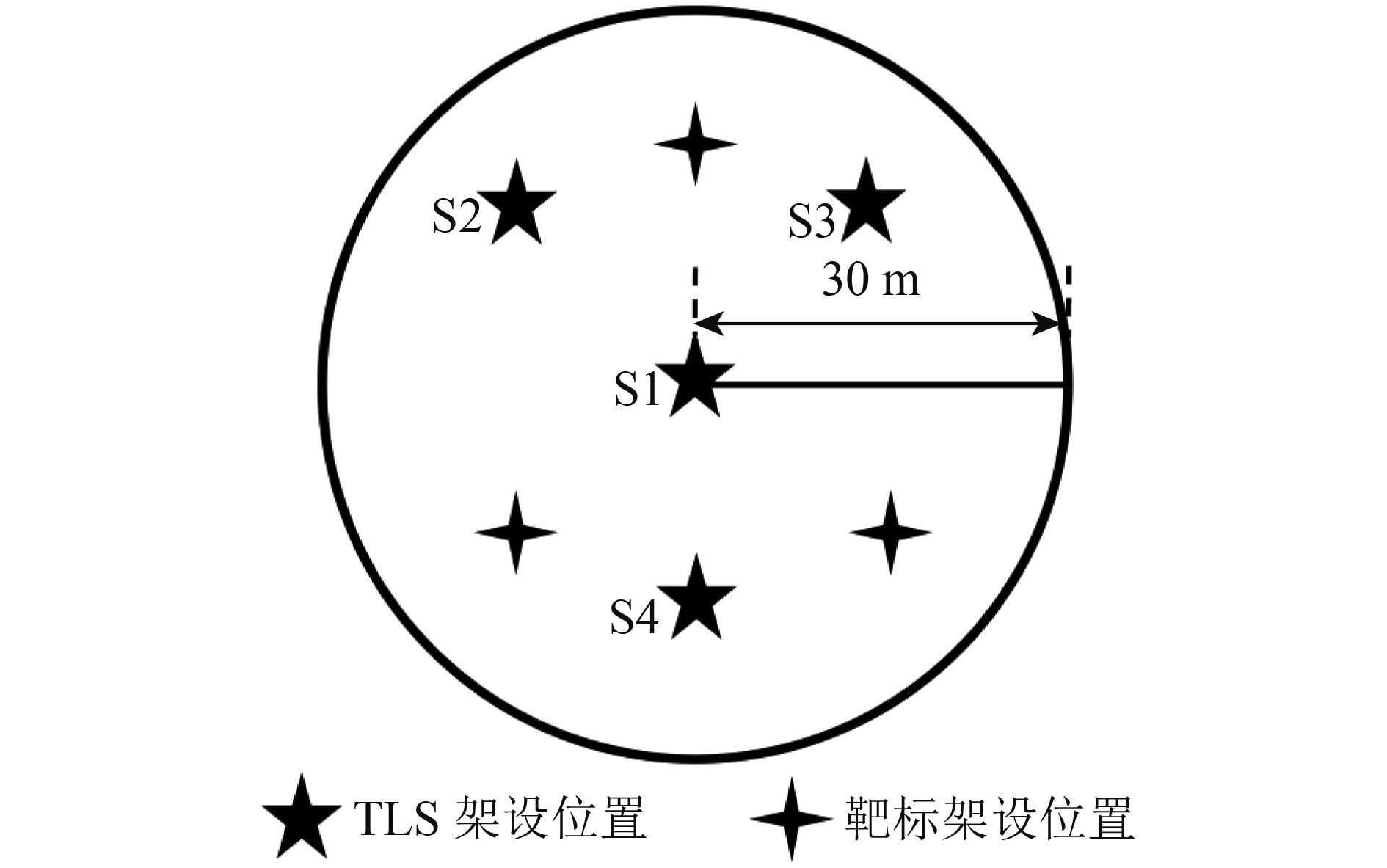
在样方中心位置架设地面激光雷达扫描仪(Leica ScanStation C10)(详细参数见表1)对植被样方进行单站扫描以获取样地的点云数据(图1)。对于样地7、样地8和样地9均选择了4个不同的位置架设激光雷达扫描仪对植被样方进行扫描，4站所选位置包括1站样地中心位置(S1)和3站样地周围位置(S2、S3、S4)，3站形成三角形，S1处于三角形中心(图2)，获得了4站点云数据。白马基地的9个实验样地的无人机航拍图(图3)，华盛顿植物园5个样地的航拍图(图4)。

表 1 3维激光扫描仪Leica ScanStation C10 参数
Table 1 Characteristic of Leica ScanStation C10

下载CSV 
参数 数值
扫描速率 50000点/s
视场角 水平：360° 垂直：270°
光斑大小 4.5 mm(全宽半高基准) 7 mm(高斯基准)
波长 532 nm(绿光)
测距范围 300 m@90%反射率134 m@18%反照率


图 1 激光扫描仪架设位置图(样地1—6、10—14)
Fig. 1 Schematic diagrams showing TLS experimental setup for forest plots 1—6 and plots 10—14


图 2 样地7、样地8和样地9激光扫描仪架设位置
Fig. 2 Schematic diagrams showing TLS experimental setup for forest plot7, plot8, and plot9


图 3 白马基地9个样地无人机航拍图
Fig. 3 Unmanned Aerial Vehicle-based photos of 9 forest plots in Baima site


图 4 华盛顿植物园5个样地航拍图
Fig. 4 Aerial photo of 5 plots in WPA

2.2.2 手动测量数据

在实验样地架设扫描仪的位置用鱼眼相机拍摄样地的鱼眼照片，用于计算样地的叶面积指数。具体的方法是：在多云或阴天的天气条件下，在实验样地架设TLS仪器的位置，距离地面约30 cm处，将鱼眼相机调至曝光模式，竖直向上拍摄样地的鱼眼照片，进而对冠层图像处理获得样地的孔隙率等参数，最终得到样地的叶面积指数。另外使用LAI-2200在傍晚时分测量了白马样地的叶面积指数，用于实验结果的对比。此外，在架设仪器中心位置用手持GPS记录其经纬度，作为该样地的中心经纬度。14个实验样地的中心经纬度及设置的采样间距如表2所示。采样间距为在距扫描仪的某一距离处，相邻两束激光束的距离，主要根据样地的树种以及叶片的特征尺度而确定，并参考了样地植被的密度，由此可以计算得到激光雷达在数据获取时所采用的扫描角分辨率。

在样地用皮卷尺在离地约1.3 m处测量每棵树的胸径，并取其平均值作为该样地树的平均胸径；选取每棵树树干上最低的树枝处测量枝下高，以其平均值作为该样地的平均枝下高；因样地树木种植均匀整齐分布，所以在样地均匀选取树木，用皮卷尺测量相邻两棵树的间距，取其平均值作为树间距；树高以及冠幅采用目视测量法进行记录；样地密度根据一定面积内树的棵数对样地密度进行计算。样地测量的参数信息见表3。

表 2 实验样地采样间距
Table 2 Sampling spacing of TLS data for each forest plot

下载CSV 
样地编号 经度/(°E) 纬度/(°N) 采样间距
Plot1 119.173657 31.607647 1 cm @ 5 m
Plot2 119.172680 31.610165 1 cm @ 10 m
Plot3 119.172798 31.610068 1 cm @ 10 m
Plot4 119.167192 31.610263 1 cm @ 15 m
Plot5 119.167785 31.610103 1 cm @ 10 m
Plot6 114.169123 31.611908 1 cm @ 10 m
Plot7 119.169038 31.611902 1 cm @ 10 m
Plot8 119.155422 31.610303 1 cm @ 10 m
Plot9 119.168747 31.611155 1 cm @ 10 m
Plot10 –122.295442 47.639509 5 cm @ 15 m
Plot11 –122.294831 47.636206 5 cm @ 15 m
Plot12 –122.298244 47.637105 5 cm @ 15 m
Plot13 –122.295011 47.638246 5 cm @ 15 m
Plot14 –122.295765 47.634409 5 cm @ 15 m

表 3 样地参数信息表
Table 3 Parameters information of forest plots

下载CSV 
样地号 树种(英文名/拉丁名) 胸径/cm 枝下高/m 树间距/m 树高/m 冠幅/m 样地密度/(棵/ha)
Plot1 栾树(Goldenrain/Koelreuteria paniculata Laxm)
乌桕(Sapium sebiferum/Sapium sebiferum (L.) Roxb.) 		8.0 1.5 4.0 4.0 2.5 1000
Plot2 海棠(Cherry-apple tree/Begonia evansiana) 4.0 1.4 1.0 3.0 1.3 10000
Plot3 樱桃(Cherry/Cerasus pseudocerasus G. Don) 2.5 0.6 1.3 2.0 0.7 4000
Plot4 青钱柳(Cyclocarya paliurus/Cyclocarya paliurus) 5.0 2.0 3.0 4.0 0.7 1000
Plot5 圆柏(China Savin/Sabina Chinensis (L.) Ant.) 5.0 0.3 1.5 3.5 1.0 4000
Plot6 枫香(Sweetgum/Liquidambar formosana) 7.5 1.5 3.5 4.0 2.0 1000
Plot7 湿地松(Slash Pine/Pinus Elliottii) 18.0 4.0 2.5 11.0 2.5 2000
Plot8 大杨树(Aspen/Populus L.) 20.0 4.5 3.0 20.0 5.0 1000
Plot9 小杨树(Aspen/Populus L.) 7.5 1.0 3.0 4.5 3.0 2000
Plot10 杜鹃(Sims Azalea/Rhododendron) 18 1.8 3.0 8.0 7.2 400
Plot11 山梨(Sorb/Pyrus ussuriensis maxim) 10.9 2.0 4.0 8.9 8.1 400
Plot12 大叶枫(Bigleaf Maple/Acer macrophyllum) 22 2.5 5.5 13.1 8.7 500
Plot13 鸡爪枫(Japanese maple/Acer palmatum) 38 4.2 6.0 20.1 9.6 500
Plot14 杨树(Aspen/Populus L.) 23 2.8 3.2 10.2 8.4 400

2.3 研究方法

本文计算样地植被有效叶面积指数主要利用了贝尔定律(Hirose，2005)。利用贝尔定律计算有效叶面积指数主要有两个参数，一个是孔隙率，一个是消光系数。本文使用“径向半球切片算法”对利用TLS获得的点云数据进行体元化处理，得到样地的角度孔隙率，再利用最小二乘法，通过重建点的法向量得到叶片的倾角分布，进而计算消光系数。

2.3.1 森林样方角度孔隙率

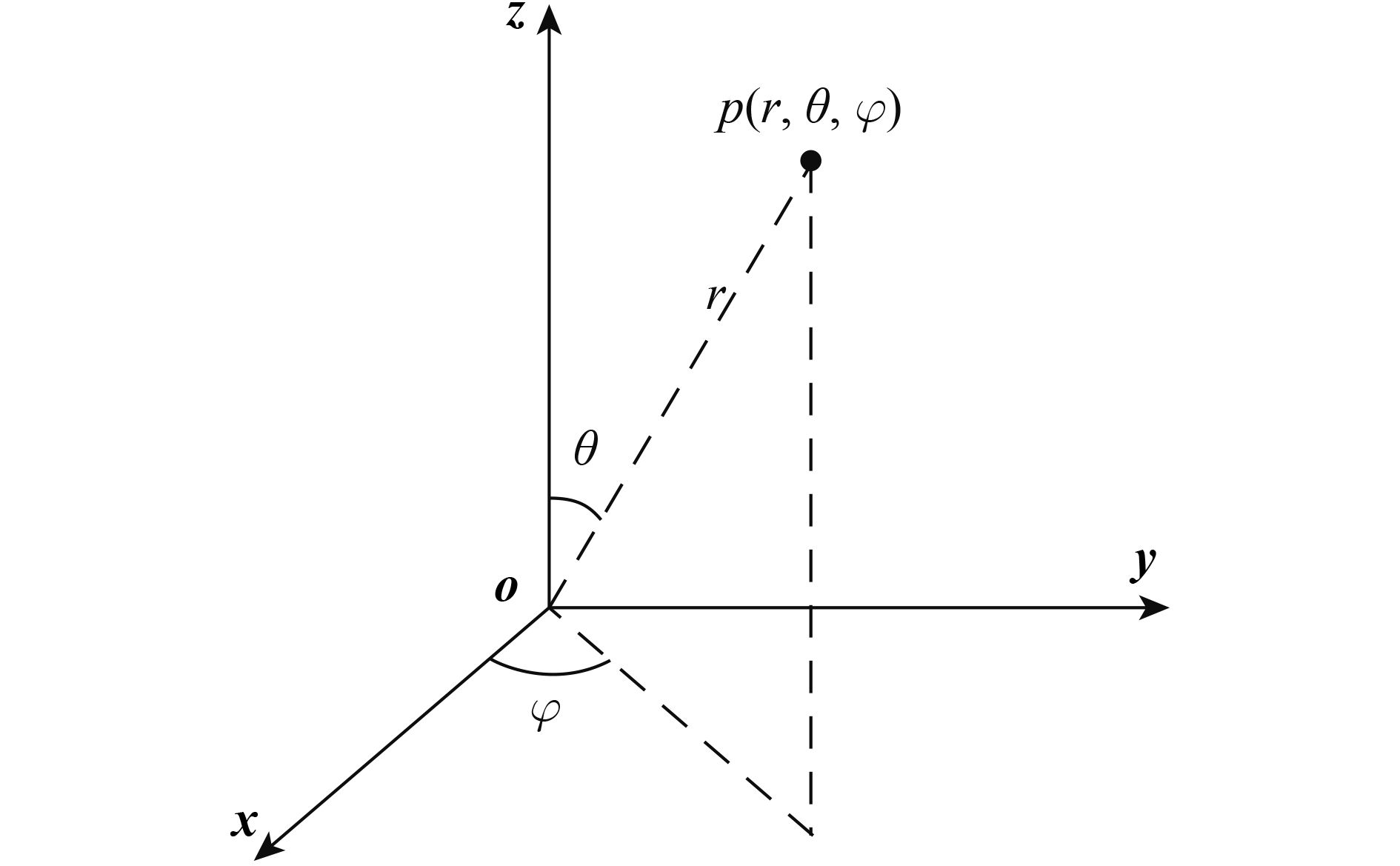
角度孔隙率(AGF)被定义为部分或全部半球空间内，未被植被遮挡范围的百分比(Zheng 等，2016)。径向半球切片算法主要是在半球空间对点云数据进行切片，也就是从半径方向和角度方向(天顶角、方位角)将半球体分成一个个近似于梯形体的不同大小的体元。每个体元的大小是由切片时设置的半径分辨率(RSL)以及角度分辨率(LBA)共同决定。半径分辨率是两个环形半球面半径的差值，角度分辨率通过敏感性分析发现与采样间距相关。TLS获取的点云数据是笛卡尔坐标系，首先需要将其转为球坐标系，即半径(r)、天顶角(θ)和方位角(φ)，如图5所示。


图 5 点云数据坐标系转换示意图
Fig. 5 Diagrams showing the spherical and Cartesian coordinate systems of a point in 3-D domain

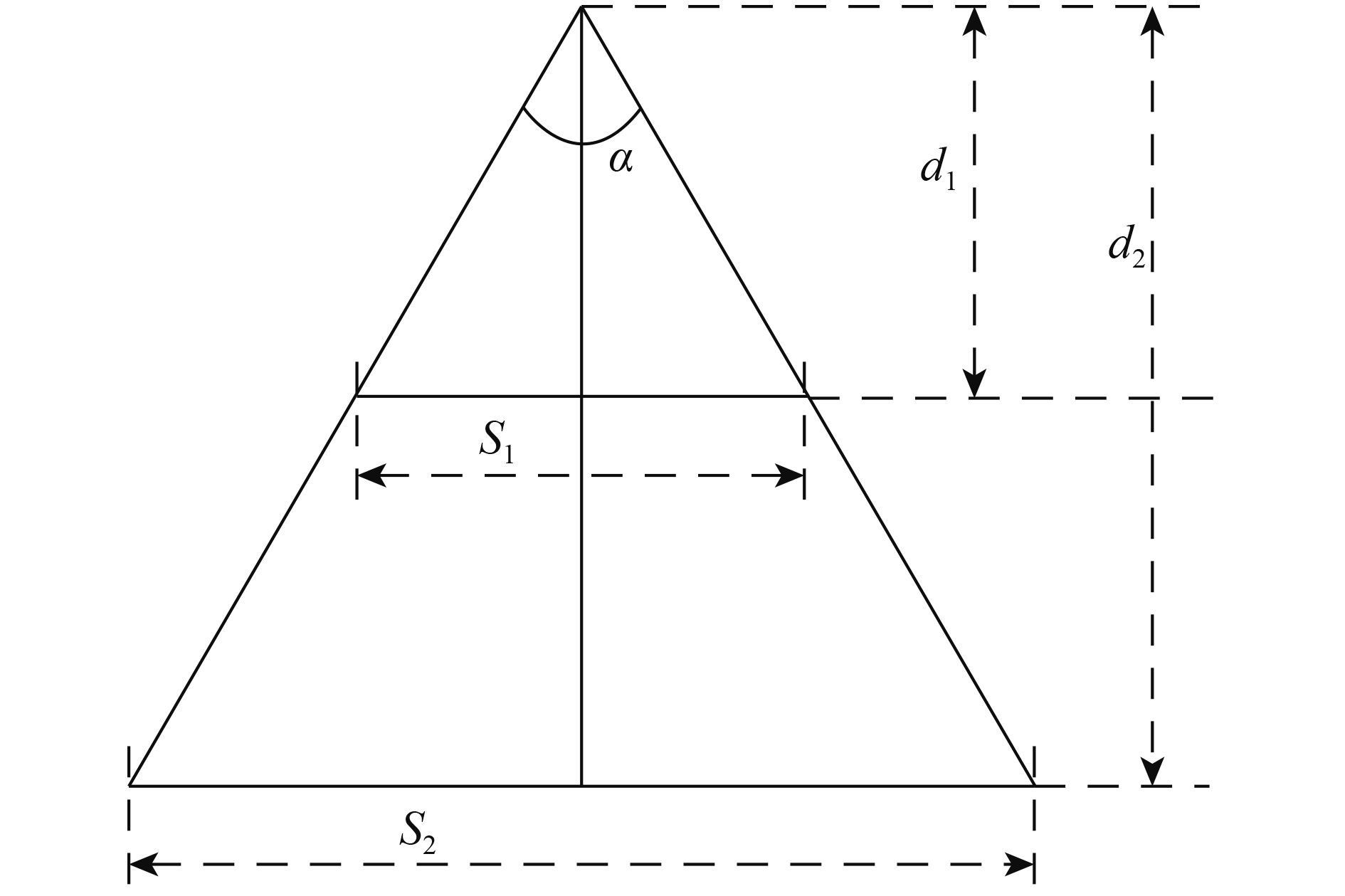
通过敏感性分析，对于角度分辨率的设置建议如下：采样间距S和目标与扫描仪的距离d的关系如图6所示。d1和d2分别是扫描仪与目标物之间的距离，S1和S2分别是距离d1和d2处对应的采样间距。通过敏感性分析发现LBA的设置需参考α，α为相邻两束激光的夹角，即扫描角分辨率，由式(1)确定

$\tan \left( {\frac{\alpha }{2}} \right) = \left( {\frac{{\displaystyle\frac{{{S_1}}}{2}}}{{{d_1}}}} \right)$ (1)

通过设置LBA，方位角被分为360°/LBA，天顶角被分为90°/LBA。半径分辨率为自定义设置。经过以上步骤之后就将半球体分为一个个梯形体元。

本文通过径向半球切片算法，按照9°的天顶角间隔，将点云数据分为10个同心环，通过计算每个环内“空”体元数，也就是不包含点云数据的体元数，占该环内总体元数的比例，就可以计算出每个环的角度孔隙率。


图 6 采样间距和与扫描仪距离的关系
Fig. 6 The relationship between the distance away from TLS scanner and sampling spaces

2.3.2 森林样方消光系数

消光系数是由入射太阳光方向和叶片方向分布函数共同决定(Campbell，1986)，本文使用式(2)(Wang 等，2007)计算消光系数

$K\left( {\theta ,\phi } \right) = \frac{{G\left( {\theta ,\phi } \right)}}{{\cos \left( \theta \right)}}$ (2)

式中，θ是光束的天顶角，ϕ是光束的方位角， $G\left( {\theta ,\phi } \right)$ 是叶片面积的投影。

在该实验中，将TLS发出的激光束看做入射太阳光束，而由TLS获得的3维点云数据包含的精确的距离和高度信息(Zheng和Moskal，2012)可用于估算植被元素方向分布。使用最小二乘法，通过重建每个点在其邻域内的法向量(Hoppe 等，1992)，再在邻域内构建黎曼图，选择最小生成树的法向量作为该点的法向量，以此方法来获得叶片的倾角分布，进而计算消光系数，具体方法如下：

(1) 将整个点云数据记为点集S，重建法向量的点记为pi(xi，yi，zi)，则pi的n邻域点集记为Sp，Sp包含点p1、p2、p3、…、pn，在Sp点集内重建点pi的切平面T(pi)，进而得到单位法向量ni。T(pi)可以由Sp的几何中心Oi表示，Oi由式(3)计算

${{{O}}_i} = \frac{1}{n}\sum\limits_{i{\rm{ = }}1}^n {{{{p}}_i}} $ (3)

Oi的单位法向量记为ni。根据叶片大小、点云密度确定临近点个数的范围，通过基于不同临近点个数的TLS点云数据LAIe计算结果与LAI-2200和鱼眼照片结果的比较，确定最优的临近点个数。

(2) 计算点集Sp的协方差矩阵：

${{M}} = \frac{1}{{{n}}}\sum\limits_{i{\rm{ = }}1}^{{n}} {\left( {{{{p}}_i} - {{{O}}_i}} \right)} {\left( {{{{p}}_i} - {{{O}}_i}} \right)^{\rm{T}}}$ (4)

得到协方差矩阵M的特征向量v1、v2、v3以及对应的特征值λ1、λ2、λ3。点pi的法向量是3个特征值中最小的特征值所对应的特征向量。比如，如果λ1≥λ2≥λ3，那么点pi的法向量就是v3或者–v3。

(3) 法向量的方向具有不确定性，可以通过建立点邻域的黎曼图，并且选择具有最小生成树的法向量来作为该点的法向量(Alliez 等，2016)，并以该法向量的倾角的余角作为该点的倾角。

计算出倾角之后可得到G值，进而利用式(2)计算消光系数。对于G值，使用下面的公式(Fuchs 等，1984)计算：

$G = \cos \left( {\overline {{\theta _L}} } \right)$ (5)

式中， ${\overline {{\theta _L}} }$ 是平均叶倾角。

按照9°的天顶角间隔将半球形空间分为10个同心环，依据上述方法计算出每个环内的点的倾角，以此来表征叶片倾角，然后计算每个环的G值，进而得到每个环的消光系数。

2.3.3 森林样方有效叶面积指数

根据前两个部分计算得到的角度孔隙率和消光系数，利用贝尔定律(Hirose，2005)来估算森林冠层的有效叶面积指数：

$\ln \left( {P\left( \theta \right)} \right) = - G\left( \theta \right){L_{\rm{e}}}/\cos \left( \theta \right)$ (6)

式中，θ是天顶角，Le是有效叶面积指数，P(θ)和–G(θ)/cos(θ)分别是天顶角为θ时的角度孔隙率和消光系数。

假设利用径向半球切片算法将半球空间分为n个同心环，那么样地的有效叶面积指数利用式(7)计算：

$\begin{aligned}{L_{\rm{e}}} = & \left( {{L_{{\rm{e}}1}}\left( {{\theta _1}} \right) + {L_{{\rm{e}}2}}\left( {{\theta _2}} \right) + \cdots + {L_{{\rm{e}}n}}\left( {{\theta _n}} \right)} \right)/n = \\ & - (\cos {\theta _1} \cdot \frac{{\ln P\left( {{\theta _1}} \right)}}{{G\left( {{\theta _1}} \right)}} + \cos {\theta _2} \cdot \frac{{\ln P\left( {{\theta _2}} \right)}}{{G\left( {{\theta _2}} \right)}} + \cdots + \\ & \cos {\theta _n} \cdot \frac{{\ln P\left( {{\theta _n}} \right)}}{{G\left( {{\theta _n}} \right)}})/n\end{aligned}$ (7)

式中，Le是森林样方的有效叶面积指数，Le1、Le2、 $ \cdots $ 、Len分别是n个环的有效叶面积指数，θ1、θ2、 $ \cdots $ 、θn分别是n个环的天顶角。

3 结　果

在本文中，根据上述方法利用TLS点云数据计算样地LAIe。按照9°的天顶角间隔，将半球样地空间分成10个同心环，并计算每个环的角度孔隙率和消光系数，进而得到每个环的LAIe，再取10个值的平均值，得到整个样地的LAIe。

3.1 森林样方角度孔隙率的计算结果

根据敏感性分析，角度分辨率设置的最优值应该参考扫描时设置的采样间距。首先由14个样地的采样间距(表2)，根据式(1)计算每个样地半球空间内点云数据在进行体元化时分割天顶角和方位角的角度分辨率，如表4所示，样地1的LBA是0.12°，样地4的LBA是0.04°，样地2、样地3、样地5至样地9的LBA均为0.06°，样地10至样地14的LBA均为0.2°。

表 4 样地角度分辨率
Table 4 LBA of 9 plots

下载CSV 
样地编号 角度分辨率/(°)
Plot1 0.12
Plot2 0.06
Plot3 0.06
Plot4 0.04
Plot5 0.06
Plot6 0.06
Plot7 0.06
Plot8 0.06
Plot9 0.06
Plot10 0.2
Plot11 0.2
Plot12 0.2
Plot13 0.2
Plot14 0.2

将半径分辨率自定义为30 m，是由于实际样地大小为30 m×30 m，并且由于鱼眼照片无法有效地区别森林在半径方向林冠密度的变化，因此取范围相同的点云数据以及设置半径分辨率为30 m便于对计算结果进行比较分析。根据计算得到的角度分辨率，以及设置的半径分辨率，对半球空间内的点云数据利用径向半球切片算法进行切片和体元化，计算每个环内的“空”体元数和总体元数，进而计算每个环的角度孔隙率。14个样地角度孔隙率计算结果选取了Plot9为代表(表5)。由表5可以看出，不同天顶角范围计算出来的角度孔隙率不同，呈现天顶角越大，角度孔隙率越小的趋势，并且角度孔隙率的最大值为0.95，最小值为0.15。

表 5 Plot9有效叶面积指数计算结果
Table 5 The LAIe results for forest Plot9 in Baima site

下载CSV 
子样地天顶角/(°) 角度分辨率/(°) 角度孔隙率 平均叶倾角/(°) 光束天顶角/(°) 消光系数 LAIe 样地LAIe
0—9 0.06 0.95 66.00 4.5 0.41 0.12 0.99
9—18 0.06 0.79 66.71 13.5 0.41 0.57
18—27 0.06 0.58 67.20 22.5 0.42 1.28
27—36 0.06 0.53 66.85 31.5 0.46 1.38
36—45 0.06 0.51 66.61 40.5 0.52 1.30
45—54 0.06 0.40 66.17 49.5 0.62 1.47
54—63 0.06 0.33 65.19 58.5 0.80 1.38
63—72 0.06 0.30 65.44 67.5 1.09 1.11
72—81 0.06 0.24 66.90 76.5 1.68 0.86
81—90 0.06 0.15 70.73 85.5 4.21 0.46

3.2 森林样方消光系数的计算结果

计算某点法向量时，根据叶片的大小以及点云密度，确定临近点个数的范围是6—18个。取临近点个数的步长为3，分别计算基于不同临近点个数的点云数据的LAIe，最终发现临近点个数为12个时，基于TLS计算的LAIe与基于LAI-2200和鱼眼照片的计算结果的相关性最好。因此，重建点的法向量时，其邻域选取12个临近点。通过重建点的法向量进而得到每个环的平均叶倾角。选取Plot9为代表，10个环的平均叶倾角如表5所示，倾角范围为65°—71°。

计算得出每个环的平均叶倾角后，利用Fuchs的算法(Fuchs 等，1984)计算每个环的G值，再利用Nilson的算法(Wang 等，2007)计算每个环的消光系数。其中，10个环光束天顶角取值如表5所示。那么，Plot9每个环的消光系数计算结果如表5所示，最小值是0.41，最大值是4.21。

3.3 森林样方有效叶面积指数的计算结果

根据径向半球切片算法和点云法向量重建的方法利用点云数据分别计算得到10个环的角度孔隙率和消光系数，由贝尔定律计算出每个环的LAIe，然后取10个环的LAIe的平均值作为样地的LAIe。14个样地的LAIe计算结果如表5和表6所示。由表6可以看出，LAIe最小的是样地3，值为0.28，LAIe最大的是样地7，值为4.78。

表 6 有效叶面积指数计算结果
Table 6 The LAIe results for forest plots

下载CSV 
样地编号 LAIe
Plot1 0.49
Plot2 0.49
Plot3 0.28
Plot4 0.31
Plot5 1.31
Plot6 1.39
Plot7 4.78
Plot8 2.04
Plot9 0.73
Plot10 3.65
Plot11 3.24
Plot12 2.50
Plot13 3.34
Plot14 2.44

对于样地7、样地8和样地9，均在样地选取了4个不同位置对森林植被进行了扫描(图2)，获取了4站TLS点云数据。表6所示样地7的LAIe、样地8的LAIe以及样地9的LAIe均为4站单站点云数据计算结果的平均值。表7所示为利用样地7的4站单站TLS点云数据分别计算得到的LAIe，表8所示为利用样地8的4站单站TLS点云数据分别计算得到的LAIe，表9所示为基于样地9的4站单站TLS点云数据计算的植被LAIe。由表7可以看出，由中心站点S1的TLS点云数据计算得到的LAIe最大，值为5.51，由S2站点和S4站点点云数据计算得到的LAIe与S1站点相近，分别为5.03和5.01，而由S3站点的点云数据计算得到的LAIe为3.58，与其他3个站点的计算结果相差较大。由表8可以看出，由中心站点S1的点云数据计算得到的LAIe最大，值为2.24，由S3站点的点云数据计算得到的LAIe最小，值为1.60，由S2站点和S3站点点云数据计算得到的LAIe与S1站点相近，分别为2.14和2.19。由表9可以看出，中心站点S1数据计算的LAIe为0.99，S3站点计算的LAIe最大，为1.13，与中心站点的结果相近，S2计算的LAIe最小，为0.19，与其余站点计算结果相差较大。

表 7 Plot7有效叶面积指数计算结果
Table 7 The LAIe results for forest Plot7

下载CSV 
站点编号 LAIe
S1 5.51
S2 5.03
S3 3.58
S4 5.01

表 8 Plot8有效叶面积指数计算结果
Table 8 The LAIe results for forest Plot8

下载CSV 
站点编号 LAIe
S1 2.24
S2 2.14
S3 2.19
S4 1.60


图 7 基于TLS的有效叶面积指数计算结果与实测有效叶面积指数的对比图
Fig. 7 Comparison of TLS- and field-based LAIe results

表 9 Plot9有效叶面积指数计算结果
Table 9 The LAIe results for forest Plot9

下载CSV 
站点编号 LAIe
S1 0.99
S2 0.19
S3 1.13
S4 0.60

3.4 基于TLS计算的LAIe与实测LAIe的对比

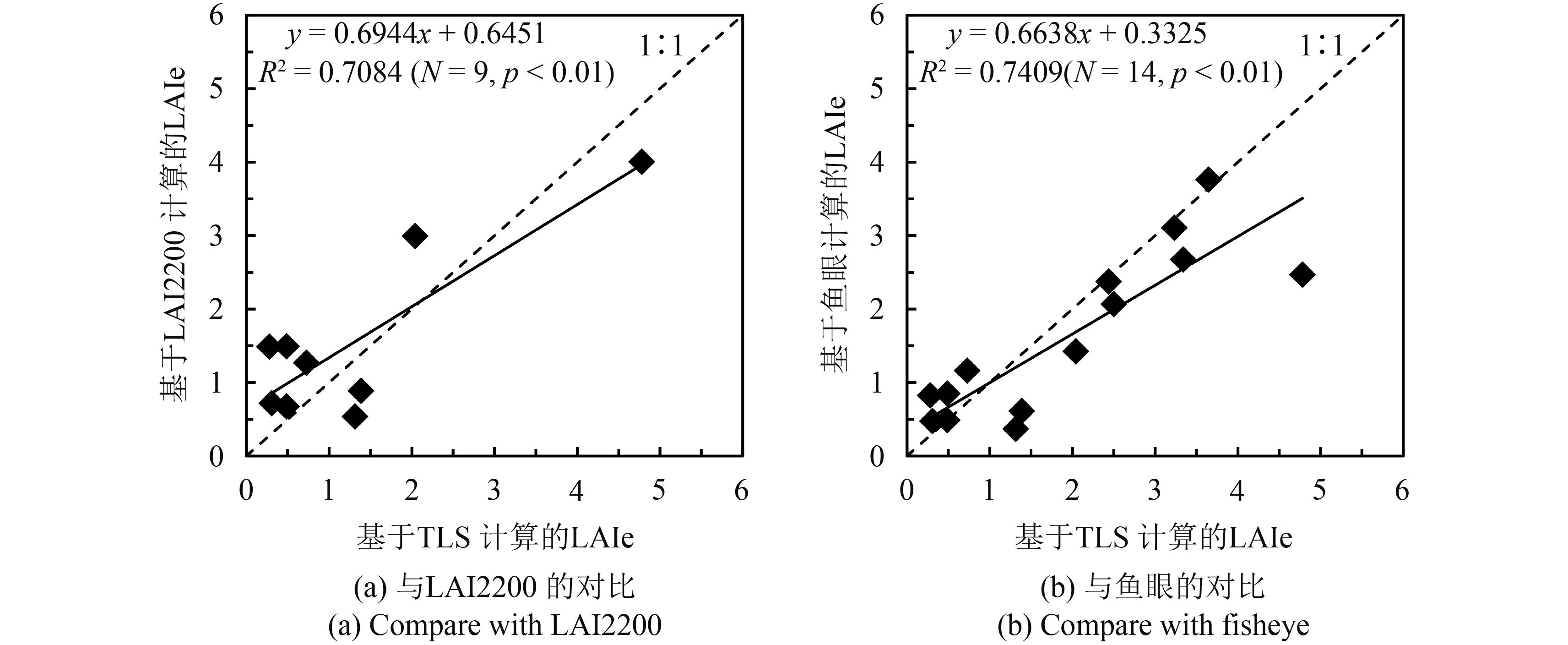
图7(a)所示为利用TLS点云数据计算得到的白马基地9个样地的LAIe与基于LAI-2200的LAIe测量结果的对比图，R2达到0.7084(N=9，p<0.01)；图7(b)所示为利用TLS点云数据计算得到的白马基地和植物园的14个样地的LAIe和使用DHP软件(Leblanc，2004)处理鱼眼照片得到的LAIe的对比图，R2达到了0.7409(N=14，p<0.01)。由图7可以看出，LAIe较小时，基于TLS计算的LAIe小于基于LAI-2200和鱼眼照片计算的LAIe，LAIe较大时，基于TLS计算的LAIe大于基于LAI-2200和鱼眼照片计算的LAIe。其中，图7(a)存在不符合该规律的站点。

4 讨　论

本文利用地面激光雷达获取的单站点云数据计算14个森林样方的有效叶面积指数，并通过与LAI-2200和鱼眼相机的实测结果的对比，证实地基激光雷达获取的点云数据结合径向半球点云切片算法对于计算植被有效叶面积指数具有一定的准确性，并且对于不同密度和树龄的森林样方均具有适用性。

4.1 角度分辨率对计算样方角度孔隙率的影响

本文使用径向半球切片算法计算森林样方的角度孔隙率。在对半球空间内的点云数据体元化时，在方位角方向和天顶角方向影响梯形体元数目的角度分辨率对于计算角度孔隙率具有一定的影响。这是因为在计算角度孔隙率时，是利用“空”体元数与总体元数的比值来计算的。在体元化时，若角度分辨率设置不同，则体元化后的总体元数会不同，并且“空”体元数也会发生变化。当“空”体元数与总体元数变化不一致时，就会导致角度孔隙率发生变化。因此，在对点云数据进行体元化时，角度分辨率就具有重要的作用，也直接影响到LAIe的计算精度(Zheng 等，2016)。

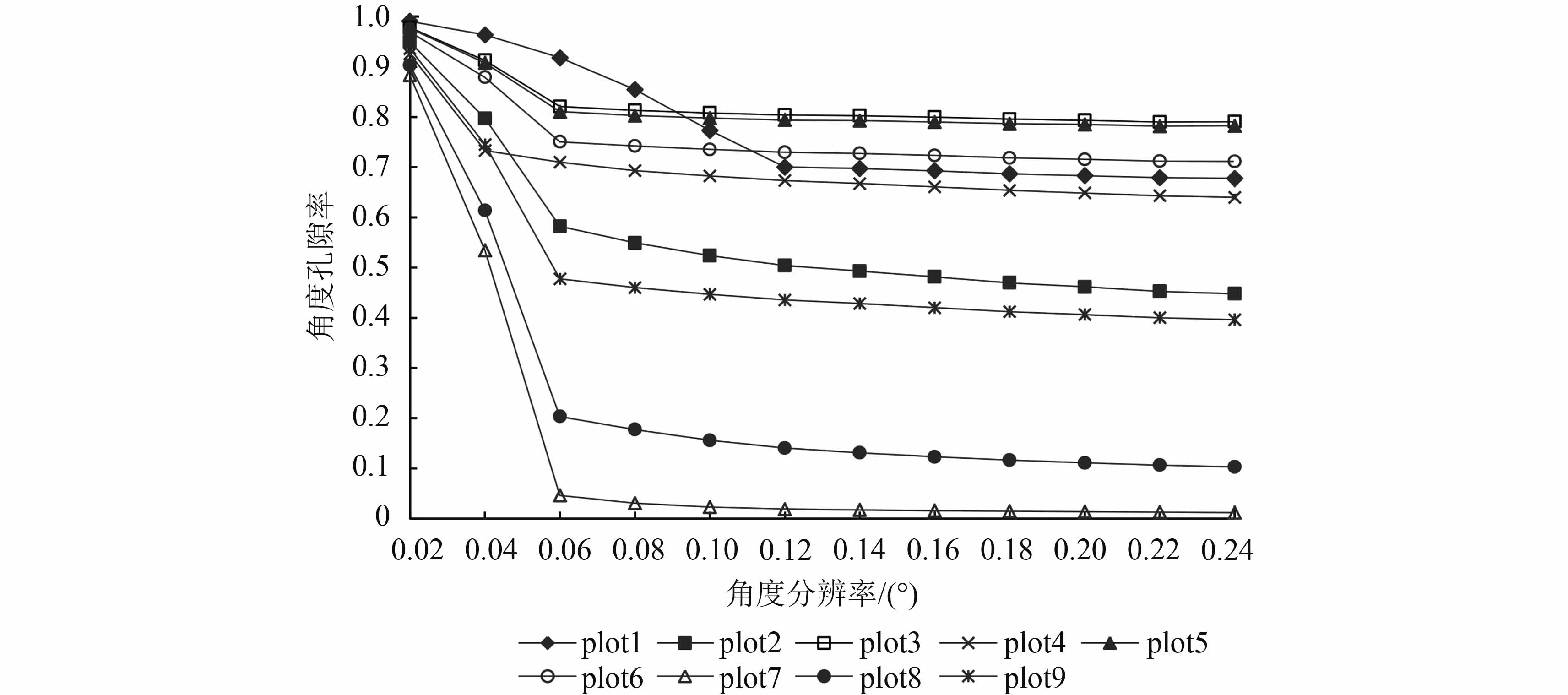
对白马基地的9个样地计算了当角度分辨率分别为0.02°、0.04°、0.06°、0.08°、0.10°、0.12°、0.14°、0.16°、0.18°、0.20°、0.22°、0.24°时的角度孔隙率，以进一步详细说明角度分辨率对计算角度孔隙率的影响(图8)。由图8可以看出，样地1的角度孔隙率在角度分辨率为0.02°—0.12°时呈下降趋势，在0.12°—0.24°时趋于平缓；样地4在角度分辨率为0.02°—0.04°时呈下降趋势，在0.04°—0.24°时呈现平缓趋势；而样地2、样地3、样地5、样地6、样地7、样地8、样地9均在角度分辨率为0.02°—0.06°时呈现下降趋势，在0.06°—0.24°时趋于平缓。9个样地的角度孔隙率均随着角度分辨率的降低在快速减少之后呈现一个相对平缓的趋势，并且角度孔隙率在之后所示范围内的变化均小于0.1。对于样地1来说，角度分辨率0.12°接近于利用TLS对森林进行扫描时参考的样地叶片特征尺度；0.04°接近于扫描样地4时参考的样地叶片特征尺度；0.06°接近于扫描样地2、样地3、样地5、样地6、样地7、样地8、样地9时参考的样地叶片特征尺度。当角度分辨率高于扫描角分辨率时，因为激光点云密度不够而使得计算的角度孔隙率偏大，因此，高于扫描角分辨率的角度分辨率不适合作为体元化时设置的角度分辨率；随着设置的角度分辨率逐渐降低，直至与扫描角分辨率相近时，计算得到的角度孔隙率趋于平稳，因为采样间距的设置主要是根据样地的树种以及叶片的特征尺度而确定的，因此利用与扫描角分辨率相近的角度分辨率对半球空间内的点云数据进行体元化，最能刻画样地植被的叶片特征；当设置的角度分辨率继续降低，逐渐低于扫描角分辨率时，计算得到的角度孔隙率并没有发生显著的变化。因此，利用TLS点云数据使用径向半球切片算法计算森林LAIe时，TLS扫描森林植被时根据叶片特征尺度所设置的采样间距是切片时设置的角度分辨率的最优参考值。

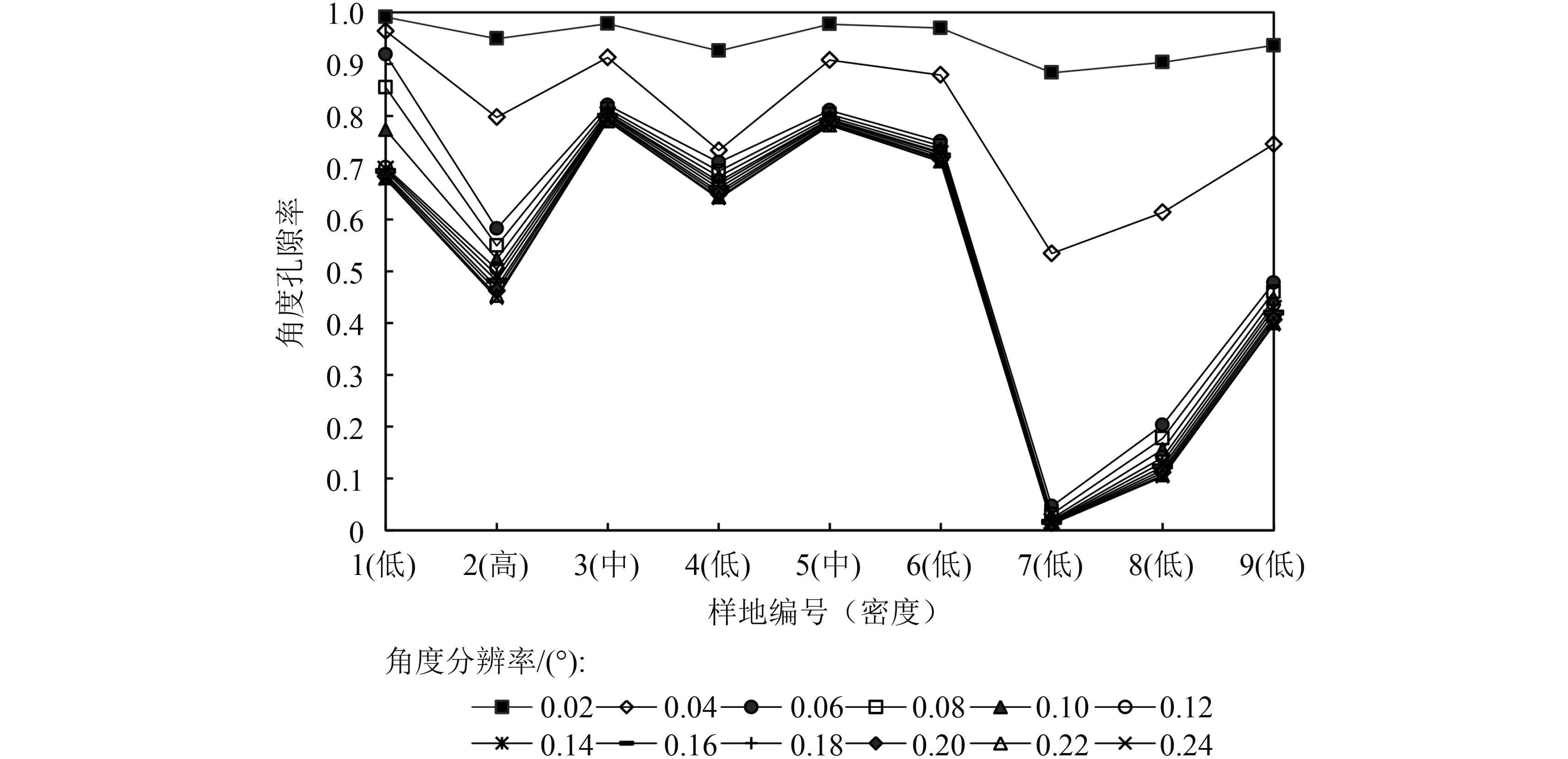
将9个样地按照高密度(Plot2)、中密度(Plot3、Plot5)、低密度(Plot1、Plot4、Plot 6、Plot7、Plot8、Plot9)分为3个等级，3个密度等级的森林样方的角度孔隙率随角度分辨率的变化趋势如图9所示。由图9可以看出，不同密度等级的森林样方的角度孔隙率随着角度分辨率从0.02°—0.24°的增加而减少。高密度样地2的角度孔隙率在角度分辨率为0.02°—0.06°时极速减少，在0.06°—0.24°趋于缓慢；中密度样地3和样地5的角度孔隙率在角度分辨率为0.02°—0.06°时快速减少，在0.06°—0.24°呈现聚集趋势；低密度样地1的角度孔隙率在角度分辨率为0.02°—0.12°时呈现下降趋势，在0.12°—0.24°趋于聚集；低密度样地4的角度孔隙率在角度分辨率为0.02°—0.04°时大幅度减少，在0.04°—0.24°时减少幅度甚微；低密度样地6、样地7、样地8、样地9的角度孔隙率在角度分辨率为0.02°—0.06°时快速减少，在0.06°—0.24°时趋于聚集，下降甚少。综上所述，我们可以得出，不同密度的森林样方的角度孔隙率随着角度分辨率的变化具有相同的变化趋势，即当角度分辨率达到在体元化时的预设值之后，角度孔隙率的变化趋于平稳，证明径向半球切片算法对于不同密度的森林样方具有良好的适用性。


图 8 9个样地角度孔隙率随0.02°—0.24°角度分辨率的变化图
Fig. 8 Diagram showing the AGF variations with the LBA ranging from 0.02°—0.24° for 9 different forest plots in Baima site


图 9 不同密度森林样地的角度孔隙率随0.02°—0.24°角度分辨率的变化图
Fig. 9 Diagram showing the AGF variations with LBA ranging from 0.02°—0.24° for forest plots with high, medium, and low densities in Baima site

4.2 临近点个数对计算样方有效叶面积指数的影响

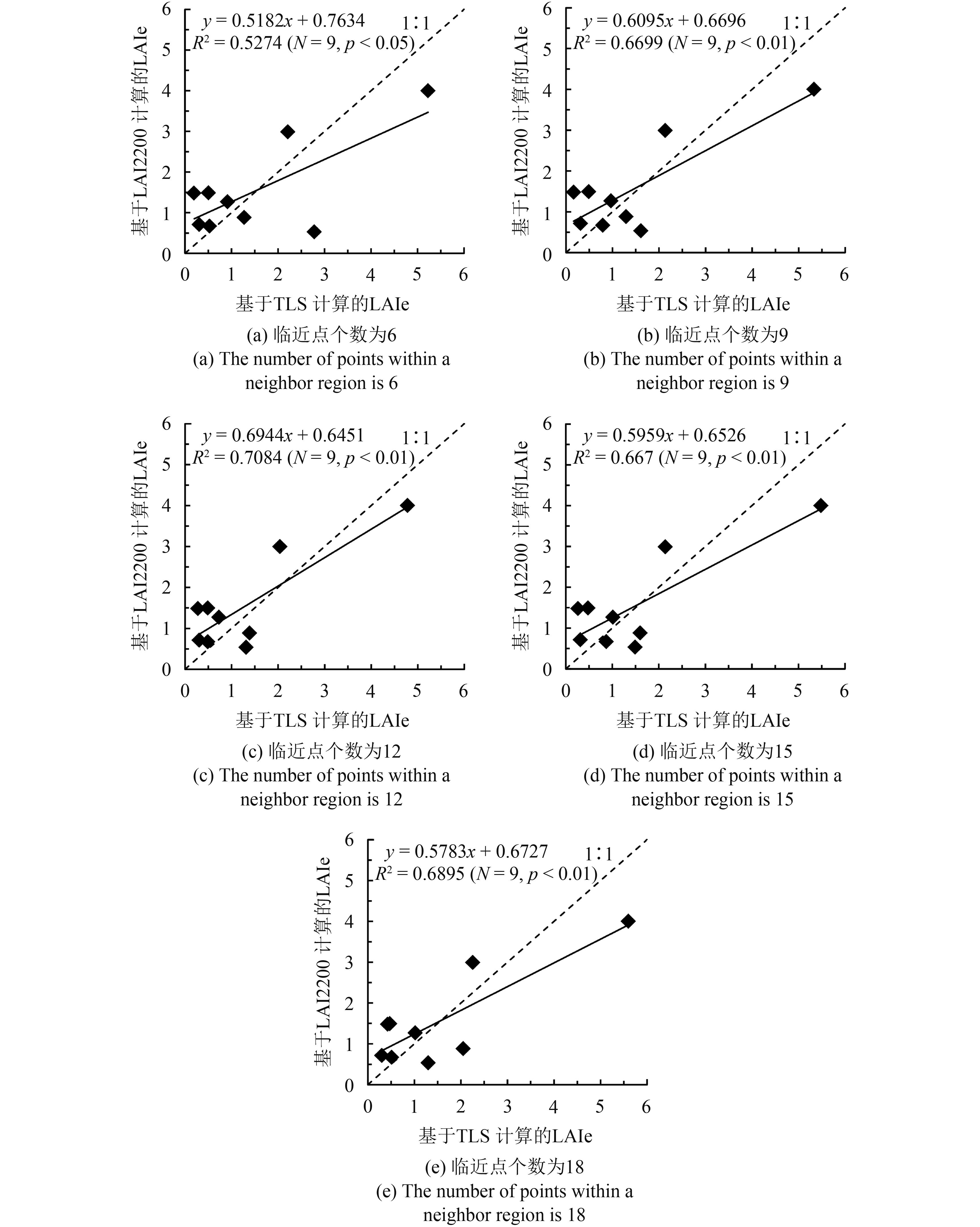
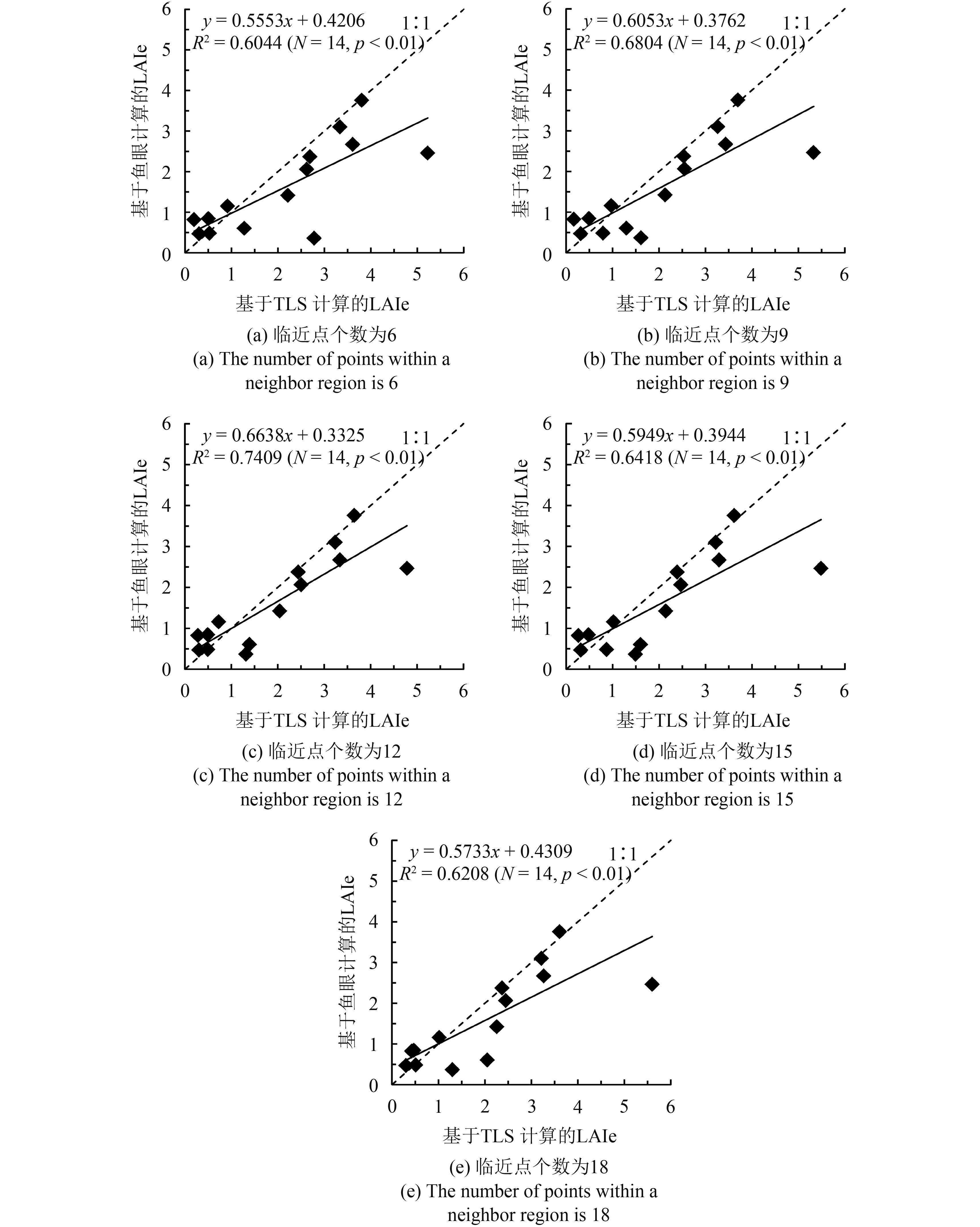
本文使用了点云法向量重建的方法来获得点的平均倾角，并由此来表征叶片倾角。在重建某点法向量时，选择该点领域中临近点的个数对于法向量的重建结果具有一定的影响。在实验计算中，选取了6个、9个、12个、15个以及18个临近点，分别重建了点的法向量，进而计算了各个样地的LAIe，并与基于LAI-2200和鱼眼计算的LAIe分别进行了对比，如图10和图11所示。当临近点为6个、9个、12个、15个和18个时，基于TLS计算的白马基地9个样地的LAIe与LAI-2200测得的LAIe对比显示，R2分别为0.5274、0.6699、0.7084、0.667、0.6895。基于TLS计算的白马基地和植物园的14个样地LAIe与鱼眼相片计算的LAIe对比显示，在临近点个数分别为6个、9个、12个、15个和18个时，R2分别为0.6044、0.6804、0.7409、0.6418、0.6208。通过与LAI-2200实测结果的对比发现，在临近点个数为12个时，基于TLS计算得到的LAIe相比较临近点个数为6个、9个、15个和18个时更为准确；与鱼眼照片计算结果的对比发现，在临近点个数为12个时，基于TLS数据计算得到的LAIe相比较临近点个数为6个、9个、15个和18个时更为准确。由此可见，临近点个数对利用TLS点云数据计算森林样方LAIe具有一定的影响，并且对于本文的样方来说，选择的临近点个数应为12个。

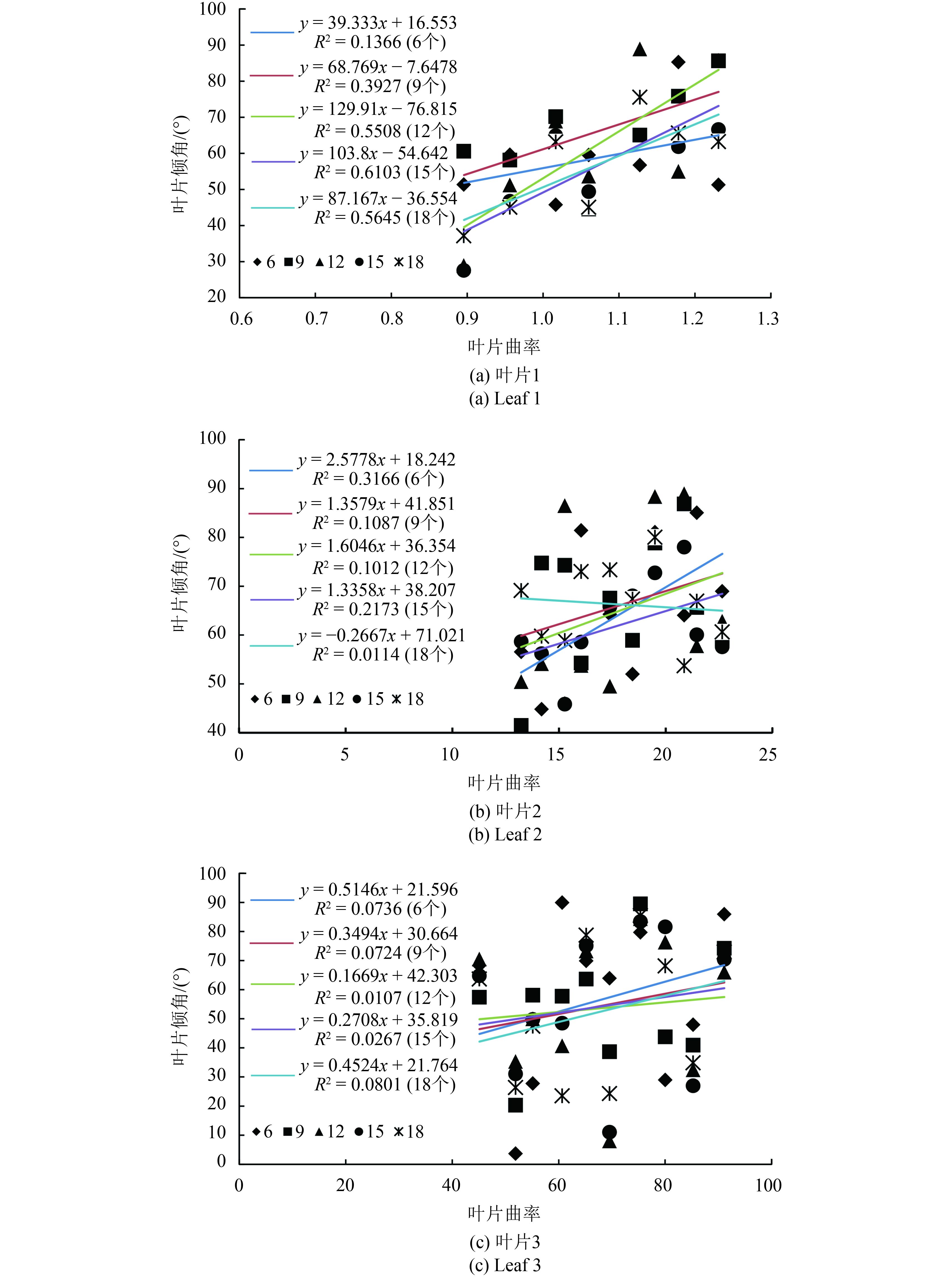
需要注意的是，在重建点的法向量时，应根据叶片的曲率来选择重建法向量时临近点的个数。我们在样地3的点云数据中目视选取3片不同曲率的叶片，使用CloudCompare软件计算叶片的高斯曲率。然后在每个叶片上选取8—10个点，根据文章中重建点的法向量的方法分别计算每个点在临近点个数为6个、9个、12个、15个和18个时的法向量，得到法向量的倾角和方位角。最后，我们选取法向量的倾角为代表，对不同临近点个数得到的点的法向量的倾角和叶片在该点处的曲率进行相关性分析，如图12所示。由图12可知，图12(a)所示叶片1曲率范围为0.8—1.3，图12(b)所示叶片2曲率范围为13—23，图12(c)所示叶片3曲率范围为45—95。由图12(a)可见，当叶片曲率较小时，临近点个数从6个增加到18个时，计算得到的点的法向量的倾角与叶片在该点处的曲率的相关性有所提高，且在临近点个数从12个增加到18个时，相关性相近，因此，在叶片曲率较小时，临近点个数在一定范围内的增加，对于重建点的法向量的结果影响不大；图12(b)叶片2的曲率大于图12(a)叶片1的曲率，图12(c)叶片3的曲率大于图12(b)叶片2的曲率，随着临近点个数的增加，叶片2和叶片3的点的法向量的倾角与该点处曲率的相关性整体均呈现下降的趋势，叶片3的点在临近点个数为18个时的法向量的倾角与该点处的曲率的相关性最高，由此可见，随着叶片曲率的增加，临近点个数对重建法向量的结果具有重要影响，临近点个数的增加会使重建结果整体变差，因此，叶片曲率较大时，选择的临近点的个数就应该减少，以减小叶片曲率对重建法向量结果的影响。


图 10 基于TLS计算的有效叶面积指数与LAI-2200实测有效叶面积指数的对比
Fig. 10 Comparison of TLS-based LAIe results and LAI-2200 measurement LAIe results


图 11 基于TLS的有效叶面积指数计算结果与鱼眼实测有效叶面积指数的对比
Fig. 11 Comparison of TLS-based LAIe results and Fisheye measurement LAIe results


图 12 叶片曲率与临近点个数的相关性分析图
Fig. 12 Correlation Analysis between leaf curvature and the number of neighboring points

4.3 扫描站点对计算样方有效叶面积指数的影响

利用样地7的S1、S2和S4的3个单站站点计算得到的LAIe结果相近，分别为5.51、5.03、5.01，由S3单站站点计算得到的LAIe为3.58，与S1、S2和S4站点的LAIe计算结果相差较大。样地8的S1、S2、S3的3站单站点云数据计算的LAIe结果相近，分别为2.24、2.14、2.19，S4单站点云数据计算得到的LAIe为1.6，与其余3站结果相差较大。样地9的S1、S3站数据计算的LAIe相近，分别为0.99和1.13，S4站数据计算的LAIe与S1和S3的结果差距较小，但S2站计算结果与其余3站的结果相差较大。首先，样地7和样地8的3站单站点云数据计算的LAIe相近，证明了利用TLS获取的点云数据使用径向半球切片算法和重建点的法向量的方法计算森林样方有效叶面积指数的可行性以及计算结果具有一定的准确性。其次，样地7的S3单站点云数据和样地8的S4单站点云数据的LAIe计算结果与其他3个站点计算结果的差异是由于在样地7的S3站点、样地8的S4站点的位置靠近森林植被边缘，导致没有获取到完整的森林样方的点云数据。对于样地9，由图3的样地航拍图可以看出，样地9的植被分布与样地7和样地8相比不均匀，导致基于各个站点数据计算得到的植被LAIe差距较大。当站点选择在样地中心附近时，植被分布较为均匀，且可以获取到较为完整的森林植被的点云数据，当站点选择的位置靠近样方边缘时，由于样地外没有植被覆盖，且植被较为稀疏，不能很好的获取完整的样地植被点云数据，导致计算结果出现差异。因此，在植被样地选择扫描站点时，在条件允许的情况下，样地的中心点作为能够获取完整样地植被信息的最佳位置，是首选也是必选的站点之一。除此之外，还应该选择样地的其他位置进行多站扫描，以检验利用中心站点点云数据计算得到的LAIe的准确性，并取多站计算结果的平均值作为该样地的LAIe，以获得较为准确的森林植被的LAIe。

4.4 利用TLS与LAI-2200和鱼眼获取数据的对比

将利用TLS获取的点云数据计算得到的LAIe与基于LAI-2200和鱼眼相片计算得到的LAIe对比，显示了利用点云数据使用径向半球切片算法计算森林植被有效叶面积指数的准确性。对于图7所示的基于TLS计算的LAIe存在“LAIe较小时，基于TLS计算的LAIe小于基于LAI-2200和鱼眼照片计算的LAIe，LAIe较大时，基于TLS计算的LAIe大于基于LAI-2200和鱼眼照片计算的LAIe”的规律，认为，相比较LAI-2200及鱼眼照片，TLS可以从3维的角度获取植被点云数据，提供了更为详细及准确的3维植被结构信息，并且由于激光具有一定的穿透力，可以获得部分被距离扫描仪较近的植被所遮挡的植被信息，而鱼眼照片和LAI-2200则无法获得，所以对于LAIe较大的样地植被而言，TLS获得的植被信息更为完整，因此在LAIe较大的样地，基于TLS计算的LAIe大于鱼眼照片计算的LAIe。其次，在计算角度孔隙率时，将TLS获得的点云数据裁剪为半径为30 m的半球形样方，使计算使用的数据只限于此，没有30 m之外的植被等无关信息的干扰。而利用鱼眼相机获得的照片以及LAI-2200实测的LAIe，是可见范围内所有植被等物体的信息，不仅包括了30 m之内的植被信息，也包括了30 m之外的植被等信息，因此在LAIe较小的样地，利用鱼眼照片计算得到的样地植被的LAIe就会大于基于TLS计算的LAIe。第三，利用鱼眼相机拍摄照片时需要调至曝光模式，且要求在阴天的天气条件下进行拍摄。LAI-2200对光照条件的要求很高，需要避免直射太阳光，尽量在日出或日落时测量，并且在使用时，操作者也可能会对测量结果产生影响。而利用TLS获取植被3维点云数据时就无需这些条件，不仅不受光照等条件的限制，而且在晚上也可以进行扫描，获取数据。图7(a)中存在基于TLS计算的LAIe与LAI-2200实测值的对比不符合“LAIe较小时，基于TLS计算的LAIe小于基于LAI-2200计算的LAIe”这一规律的站点。该站点为样地8，结合图3中样地8的航拍图以及表8中4站单站数据计算的LAIe可以发现，植被密度在样地中心较大且植被分布较为均匀，在样地边缘植被密度较小且分布并不均匀，使用LAI-2200对植被进行测量与使用TLS扫描仪获取植被点云数据的时间不同，可能会导致测量选取的位置有所偏差，并且LAI-2200实测数据在测量时可能受到外界因素影响，导致测量值偏高。虽然TLS获取数据不受光照等条件的影响，但是，风对获取的点云数据的质量有很大的影响，在利用TLS采集数据时应注意避免并减小风对森林植被的影响。

5 结　论

本文利用地面激光雷达扫描系统获取的森林植被的点云数据，并结合径向半球切片算法、点云法向量重建等方法计算植被的有效叶面积指数。通过与LAI-2200和鱼眼的LAIe实测结果的对比分析，利用TLS点云数据以及径向半球切片算法计算森林植被的有效叶面积指数具有可行性、准确性，并且适用于不同密度和树龄的森林。

TLS点云数据的获取不会对植被造成破坏，并且能够获得植被详细的3维结构信息。本文采用的径向半球切片算法从3维角度出发，充分利用植被点云数据的3维结构信息，对于发展3维角度的叶面积指数的计算方法、提高叶面积指数的计算精度具有重要的意义。同时，对于利用点云数据计算其他植被结构参数具有积极的推动作用，进而促进激光雷达技术在林业研究上的应用。

本研究的下一步目标是利用TLS数据在生长季连续对森林植被冠层3维结构进行观测，探讨激光雷达技术动态监测森林冠层3维结构变化的能力及其在定量森林生态遥感中的应用。

志 谢 此次地面激光雷达数据在野外的获取得到了南京林业大学白马实验基地的大力支持，野外数据采集得到了张乾、徐麒等同学的帮助，在此表示感谢！

参考文献(References)

  • Alliez P, Saboret L and Guennebaud G. 2016. Surface reconstruction from point sets. CGAL User and Reference Manual, 4: 1. http://doc.cgal.org/latest/Surface_reconstruction_points_3/index.html [2016-11-01]
  • Asner G P, Braswell B H, Schimel D S and Wessman C A. 1998. Ecological research needs from multiangle remote sensing data. Remote Sensing of Environment, 63 (2): 155–165. [DOI: 10.1016/s0034-4257(97)00139-9]
  • Asner G P, Scurlock J M O and Hicke J A. 2003. Global synthesis of leaf area index observations: implications for ecological and remote sensing studies. Global Ecology and Biogeography, 12 (3): 191–205. [DOI: 10.1046/j.1466-822X.2003.00026.x]
  • Black T A, Chen J M, Lee X H and Sagar R M. 1991. Characteristics of shortwave and longwave irradiances under a douglas-fir forest stand. Canadian Journal of Forest Research, 21 (7): 1020–1028. [DOI: 10.1139/x91-140]
  • Campbell G S. 1986. Extinction coefficients for radiation in plant canopies calculated using an ellipsoidal inclination angle distribution. Agricultural and Forest Meteorology, 36 (4): 317–321. [DOI: 10.1016/0168-1923(86)90010-9]
  • Chen J M and Black T A. 1992. Defining leaf area index for non-flat leaves. Plant, Cell and Environment, 15 (4): 421–429. [DOI: 10.1111/j.1365-3040.1992.tb00992.x]
  • Chen J M, Black T A and Adams R S. 1991. Evaluation of hemispherical photography for determining plant area index and geometry of a forest stand. Agricultural and Forest Meteorology, 56 (1/2): 129–143. [DOI: 10.1016/0168-1923(91)90108-3]
  • Chen J M, Chen X Y, Ju W M and Geng X Y. 2005. Distributed hydrological model for mapping evapotranspiration using remote sensing inputs. Journal of Hydrology, 305 (1/4): 15–39. [DOI: 10.1016/j.jhydrol.2004.08.029]
  • Chen J M and Cihlar J. 1995. Quantifying the effect of canopy architecture on optical measurements of leaf area index using two gap size analysis methods. IEEE Transactions on Geoscience and Remote Sensing, 33 (3): 777–787. [DOI: 10.1109/36.387593]
  • Chen J M and Cihlar J. 1996. Retrieving leaf area index of boreal conifer forests using landsat TM images. Remote Sensing of Environment, 55 (2): 153–162. [DOI: 10.1016/0034-4257(95)00195-6]
  • Chen J M, Rich P M, Gower S T, Norman J M and Plummer S. 1997. Leaf area index of boreal forests: theory, techniques, and measurements. Journal of Geophysical Research: Atmospheres, 102 (D24): 29429–29443. [DOI: 10.1029/97jd01107]
  • Cleugh H A, Leuning R, Mu Q Z and Running S W. 2007. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sensing of Environment, 106 (3): 285–304. [DOI: 10.1016/j.rse.2006.07.007]
  • Danson F M, Hetherington D, Morsdorf F, Koetz B and Allgower B. 2007. Forest canopy gap fraction from terrestrial laser scanning. IEEE Geoscience and Remote Sensing Letters, 4 (1): 157–160. [DOI: 10.1109/lgrs.2006.887064]
  • Disney M, Lewis P and Saich P. 2006. 3D modelling of forest canopy structure for remote sensing simulations in the optical and microwave domains. Remote Sensing of Environment, 100 (1): 114–132. [DOI: 10.1016/j.rse.2005.10.003]
  • Duchemin B, Hadria R, Erraki S, Boulet G, Maisongrande P, Chehbouni A, Escadafal R, Ezzahar J, Hoedjes J C B, Kharrou M H, Khabba S, Mougenot B, Olioso A, Rodriguez J C and Simonneaux V. 2006. Monitoring wheat phenology and irrigation in Central Morocco: on the use of relationships between evapotranspiration, crops coefficients, leaf area index and remotely-sensed vegetation indices. Agricultural Water Management, 79 (1): 1–27. [DOI: 10.1016/j.agwat.2005.02.013]
  • Fuchs M, Asrar G, Kanemasu E T and Hipps L E. 1984. Leaf area estimates from measurements of photosynthetically active radiation in wheat canopies. Agricultural and Forest Meteorology, 32 (1): 13–22. [DOI: 10.1016/0168-1923(84)90024-8]
  • Greaves H E, Vierling L A, Eitel J U H, Boelman N T, Magney T S, Prager C M and Griffin K L. 2015. Estimating aboveground biomass and leaf area of low-stature Arctic shrubs with terrestrial LiDAR. Remote Sensing of Environment, 164 : 26–35. [DOI: 10.1016/j.rse.2015.02.023]
  • Hancock S, Essery R, Reid T, Carle J, Baxter R, Rutter N and Huntley B. 2014. Characterising forest gap fraction with terrestrial lidar and photography: an examination of relative limitations. Agricultural and Forest Meteorology, 189-190 : 105–114. [DOI: 10.1016/j.agrformet.2014.01.012]
  • Hauglin M, Astrup R, Gobakken T and Næsset E. 2013. Estimating single-tree branch biomass of Norway spruce with terrestrial laser scanning using voxel-based and crown dimension features. Scandinavian Journal of Forest Research, 28 (5): 456–469. [DOI: 10.1080/02827581.2013.777772]
  • Henning J G and Radtke P J. 2006. Detailed stem measurements of standing trees from ground-based scanning lidar. Forest Science, 52 (1): 67–80.
  • Hirose T. 2005. Development of the Monsi-Saeki theory on canopy structure and function. Annals of Botany, 95 (3): 483–494. [DOI: 10.1093/aob/mci047]
  • Hoppe H, DeRose T, Duchamp T, McDonald J and Stuetzle W. 1992. Surface reconstruction from unorganized points. ACM SIGGRAPH Computer Graphics, 26 (2): 71–78. [DOI: 10.1145/133994.134011]
  • Hosoi F and Omasa K. 2006. Voxel-based 3-D modeling of individual trees for estimating leaf area density using high-resolution portable scanning lidar. IEEE Transactions on Geoscience and Remote Sensing, 44 (12): 3610–3618. [DOI: 10.1109/tgrs.2006.881743]
  • Hyvönen R, Ågren G I, Linder S, Persson T, Cotrufo M F, Ekblad A, Freeman M, Grelle A, Janssens I A, Jarvis P G, Kellomäki S, Lindroth A, Loustau D, Lundmark T, Norby R J, Oren R, Pilegaard K, Ryan M G, Sigurdsson B D, Strömgren M, van Oijen M and Wallin G. 2007. The likely impact of elevated [CO2], nitrogen deposition, increased temperature and management on carbon sequestration in temperate and boreal forest ecosystems: a literature review . New Phytologist, 173 (3): 463–480. [DOI: 10.1111/j.1469-8137.2007.01967.x]
  • Ilangakoon N T, Gorsevski P V and Milas A S. 2015. Estimating leaf area index by Bayesian Linear Regression using terrestrial LiDAR, LAI-2200 plant canopy analyzer, and landsat TM spectral indices. Canadian Journal of Remote Sensing, 41 (4): 315–333. [DOI: 10.1080/07038992.2015.1102629]
  • Jongschaap R E E. 2006. Run-time calibration of simulation models by integrating remote sensing estimates of leaf area index and canopy nitrogen. European Journal of Agronomy, 24 (4): 316–324. [DOI: 10.1016/j.eja.2005.10.009]
  • Kankare V, Holopainen M, Vastaranta M, Puttonen E, Yu X W, Hyyppä J, Vaaja M, Hyyppä H and Alho P. 2013. Individual tree biomass estimation using terrestrial laser scanning. ISPRS Journal of Photogrammetry and Remote Sensing, 75 : 64–75. [DOI: 10.1016/j.isprsjprs.2012.10.003]
  • Lang A R G and Xiang Y Q. 1986. Estimation of leaf area index from transmission of direct sunlight in discontinuous canopies. Agricultural and Forest Meteorology, 37 (3): 229–243. [DOI: 10.1016/0168-1923(86)90033-X]
  • Leblanc S G. 2004. Digital Hemispherical Photography Manual, Draft Version 1.0. Ottawa: Canada Centre for Remote Sensing, Natural Resources Canada: 25
  • Lee D K and Kwon K C. 2006. Biomass and annual net production of Quercus mongolica stands in Pyungchang and Jecheon areas . Journal of Korean Forestry Society, 95 (3): 309–315.
  • Lim K, Treitz P, Wulder M, St-Onge B and Flood M. 2003. LiDAR remote sensing of forest structure. Progress in Physical Geography, 27 (1): 88–106. [DOI: 10.1191/0309133303pp360ra]
  • Liu L X, Pang Y, Li Z Y, Xu G C, Li D and Zheng G. 2014. Retrieving structural parameters of individual tree through terrestrial laser scanning data. Journal of Remote Sensing, 18 (2): 365–377. [DOI: 10.11834/jrs.20143091] ( 刘鲁霞, 庞勇, 李增元, 徐光彩, 李丹, 郑光. 2014. 用地基激光雷达提取单木结构参数——以白皮松为例. 遥感学报, 18 (2): 365–377. [DOI: 10.11834/jrs.20143091] )
  • Luo S Z, Cheng F, Wang F J, Xi X H and Wang C. 2012. Leaf area index inversion based on TM in Linzhi, Tibet. Remote Sensing Technology and Application, 27 (5): 740–745. [DOI: 10.11873/j.issn.1004-0323.2012.5.740] ( 骆社周, 程峰, 王方建, 习晓环, 王成. 2012. 基于TM遥感数据的西藏林芝地区叶面积指数反演. 遥感技术与应用, 27 (5): 740–745. [DOI: 10.11873/j.issn.1004-0323.2012.5.740] )
  • Moorthy I, Miller J R, Hu B X, Chen J and Li Q M. 2008. Retrieving crown leaf area index from an individual tree using ground-based lidar data. Canadian Journal of Remote Sensing, 34 (3): 320–332. [DOI: 10.5589/m08-027]
  • Moskal L M and Zheng G. 2012. Retrieving forest inventory variables with terrestrial laser scanning (TLS) in urban heterogeneous forest. Remote Sensing, 4 (1): 1–20. [DOI: 10.3390/rs4010001]
  • Myneni R B, Hoffman S, Knyazikhin Y, Privette J L, Glassy J, Tian Y, Wang Y, Song X, Zhang Y, Smith G R, Lotsch A, Friedl M, Morisette J T, Votava P, Nemani R R and Running S W. 2002. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sensing of Environment, 83 (1/2): 214–231. [DOI: 10.1016/s0034-4257(02)00074-3]
  • Neumann H H, Den Hartog G and Shaw R H. 1989. Leaf area measurements based on hemispheric photographs and leaf-litter collection in a deciduous forest during autumn leaf-fall. Agricultural and Forest Meteorology, 45 (3/4): 325–345. [DOI: 10.1016/0168-1923(89)90052-x]
  • Olsoy P J, Glenn N F, Clark P E and Derryberry D R. 2014. Aboveground total and green biomass of dryland shrub derived from terrestrial laser scanning. ISPRS Journal of Photogrammetry and Remote Sensing, 88 : 166–173. [DOI: 10.1016/j.isprsjprs.2013.12.006]
  • Olsoy P J, Mitchell J J, Levia D F, Clark P E and Glenn N F. 2016. Estimation of big sagebrush leaf area index with terrestrial laser scanning. Ecological Indicators, 61 : 815–821. [DOI: 10.1016/j.ecolind.2015.10.034]
  • Rakocevic M, Sinoquet H, Christophe A and Varlet-Grancher C. 2000. Assessing the geometric structure of a white clover (Trifolium repens L.) canopy using 3-D digitising . Annals of Botany, 86 (3): 519–526. [DOI: 10.1006/anbo.2000.1209]
  • Soegaard H. 1999. Fluxes of carbon dioxide, water vapour and sensible heat in a boreal agricultural area of Sweden-scaled from canopy to landscape level. Agricultural and Forest Meteorology, 98-99 : 463–478. [DOI: 10.1016/s0168-1923(99)00116-1]
  • Strahler A H, Jupp D L B, Woodcock C E, Schaaf C B, Yao T, Zhao F, Yang X Y, Lovell J, Culvenor D, Newnham G, Ni-Miester W and Boykin-Morris W. 2008. Retrieval of forest structural parameters using a ground-based lidar instrument (Echidna®) . Canadian Journal of Remote Sensing, 34 (2): S426–S440. [DOI: 10.5589/m08-046]
  • Takeda T, Oguma H, Sano T, Yone Y and Fujinuma Y. 2008. Estimating the plant area density of a Japanese larch (Larix kaempferi Sarg.) plantation using a ground-based laser scanner . Agricultural and Forest Meteorology, 148 (3): 428–438. [DOI: 10.1016/j.agrformet.2007.10.004]
  • Tansey K, Selmes N, Anstee A, Tate N J and Denniss A. 2009. Estimating tree and stand variables in a Corsican Pine woodland from terrestrial laser scanner data. International Journal of Remote Sensing, 30 (19): 5195–5209. [DOI: 10.1080/01431160902882587]
  • Wang W M, Li Z L and Su H B. 2007. Comparison of leaf angle distribution functions: effects on extinction coefficient and fraction of sunlit foliage. Agricultural and Forest Meteorology, 143 (1/2): 106–122. [DOI: 10.1016/j.agrformet.2006.12.003]
  • Waring R H and Pitman G B. 1985. Modifying lodgepole pine stands to change susceptibility to mountain pine beetle attack. Ecology, 66 (3): 889–897. [DOI: 10.2307/1940551]
  • Wilson J W. 1965. Stand structure and light penetration. I. Analysis by point quadrats. Journal of Applied Ecology, 2 (2): 383–390. [DOI: 10.2307/2401487]
  • Zheng G, Ma L X, He W, Eitel J U H, Moskal L M and Zhang Z Y. 2016. Assessing the contribution of woody materials to forest angular gap fraction and effective leaf area index using terrestrial laser scanning data. IEEE Transactions on Geoscience and Remote Sensing, 54 (3): 1475–1487. [DOI: 10.1109/tgrs.2015.2481492]
  • Zheng G and Moskal L M. 2012. Leaf orientation retrieval from terrestrial laser scanning (TLS) data. IEEE Transactions on Geoscience and Remote Sensing, 50 (10): 3970–3979. [DOI: 10.1109/tgrs.2012.2188533]
  • Zheng G, Moskal L M and Kim S H. 2013. Retrieval of effective leaf area index in heterogeneous forests with terrestrial laser scanning. IEEE Transactions on Geoscience and Remote Sensing, 51 (2): 777–786. [DOI: 10.1109/tgrs.2012.2205003]
数据专区
  • 目录 目录
  • 文章信息 文章信息
  • 引用格式 引用格式
  • 地图 地图
  • 评论 评论
  • 图 图
  • 表 表
  • 二维码 二维码
  • 参考文献 参考文献
  • 多媒体 多媒体