|
收稿日期: 2017-09-13
基金项目: 国家自然科学基金(编号: 41571432)
第一作者简介: 李烁(1990— ),男,博士研究生,研究方向为数字摄影测量和数字图像处理。E-mail:chxyls@163.com
中图分类号: P237
文献标识码: A
|
摘要
针对Mask匀光法对低通滤波器及其尺寸参数依赖的问题,提出一种变分Mask自适应匀光算法。根据影像自身的先验信息,结合Mask数学模型构造变分能量函数,分别利用各向异性和各向同性全变分正则项约束理想影像和背景影像,采用分裂Bregman方法交替迭代求解,可同时获取最优化背景影像和理想影像。利用3幅光照不均匀的遥感影像进行实验并与3种不同滤波尺寸的Mask匀光法进行了比较,本文方法在目视效果和定量评价指标上均呈现明显的优势,在消除亮度不均的同时能够保持影像的纹理和细节信息。
关键词
影像匀光, 变分Mask, 亮度不均, 背景影像, 分裂Bregman
Abstract
The illumination of a captured remote sensing image may be unevenly distributed because of the influences of sensors and external factors, such as light and fog. Uneven illumination degrades the quality of an image and causes interference in the subsequent processing (e.g., image interpretation, image classification, and image mosaicking). The process of correcting uneven illumination is called image dodging, which is of great practical significance and application value. Current methods focus on how to obtain the illumination distribution within an image and compensate for the different parts of the image in different degrees. The mask dodging method is widely used for remote sensing images. The background is generated by a low-pass filter to simulate the illumination distribution and subtracted from the original image to obtain the ideal image with even illumination. Estimation of the background image is a key step in the mask dodging method and directly affects the resulting image, which depends on the low-pass filter and its dimension parameter. Automatic selection of the dimension parameter is a problem in the mask dodging method. However, no suitable solution to the problem exists, and manual adjustment is usually required in practical applications. An adaptive dodging method based on a variational mask is proposed in this study to resolve the poor universality of the mask dodging method. A variational energy function is constructed according to the prior information of the image itself and the mathematical model of the mask dodging method. L1 and L2 norms are adopted to constrain the texture and detail of the ideal image and the smoothness of the background image, respectively. Estimation of the background image is transformed into an optimal solution of the variational energy function. Solving the problem directly is often difficult because the variational function contains two norms. The split Bregman method is used to decompose the variational function into three subproblems, which are solved by alternate iteration, to simplify the calculation. Optimal background and ideal images are then obtained simultaneously. Two groups of experiments are conducted on three remote sensing images to verify the effectiveness of the proposed method. Compared with mask dodging methods with three different dimension parameters, the proposed method performs better in visual evaluation and quantitative measurements. The proposed method can effectively eliminate uneven illumination while maintaining the textures and details of the remote sensing images.
Key words
image dodging, variational Mask, uneven illumination, background image, split Bregman
1 引 言
影像匀光是指消除影像内部不均匀光照现象(王密和潘俊,2004)的处理过程,使影像能够更好地反映地表的真实情况,不仅可以提高影像的目视效果,还有利于影像的后续处理和应用,如影像判读和数字正射影像图制作。因此,影像匀光已经成为遥感影像处理中的一个重要问题。
现有的匀光方法主要分为两大类,一类是空间域方法,如自适应模板法(Zhang 等,2003)、背景拟合法(郑军 等,2003)和均值方差法(朱述龙 等,2011);另一类是频率域方法,如Mask匀光法(王密和潘俊,2004)、Retinex匀光法(Jiang 等,2015)、同态滤波法(Fan和Zhang,2011)和小波变换法(张振 等,2009)。其中,Mask匀光法是一种常用的遥感影像匀光方法,采用高斯低通滤波器模拟影像的亮度分布作为背景影像,再将原始光照不均匀影像与获得的背景影像做相减运算,然后再进行对比度拉伸,增强影像细节反差,达到匀光的目的。以此为基础,孙明伟(2009)提出比值匀光法,即获取背景影像后,执行相除操作代替相减操作,旨在同时调整影像的亮度分布问题和反差分布问题。Zhang和Zou(2011)综合利用差值法和比值法,构造了新的数学模型。张振等人(2010)提出了反差一致性的Mask匀光算法,使用非线性模型消除反差不均匀现象,使影像整体反差一致。为了更准确的模拟光照变化,姚芳等人(2013)采用分块策略,不同影像块采用不同的滤波器尺寸来获取背景影像。袁修孝等人(2014)采用扩张吞噬算法优化背景影像,消除灰度剧烈变化区域边缘对背景影像的影响。但是这些方法本质上都是利用低通滤波生成背景影像,生成结果比较依赖滤波器的设计及其尺寸参数的选择,通用性较差。而理想影像是在求解背景影像的基础上计算出来的,结果依赖于背景影像的估计,因此获取的理想影像不一定最优。
变分方法是一种研究泛函极大值和极小值的数学方法,通过构造一个能够反映变量自身固有性质的变分能量函数,并以输出该函数的最大值或最小值为目标,从而获得最优变量估计值。近年来变分方法快速发展,广泛应用于图像处理领域,如影像复原(郭从洲 等,2016)和影像去噪(霍丽君 等,2017)。
为了能够自适应获取最优背景影像和理想影像,本文在Mask匀光法的基础上,提出一种变分Mask自适应匀光方法。分别利用各向异性和各向同性全变分正则项对理想图像和背景图像进行约束,运用分裂Bregman方法交替迭代求解背景影像和理想影像,可克服Mask匀光法对滤波器及其尺寸参数的依赖的缺点。
2 基本原理
2.1 Mask匀光原理
Mask匀光法又称模糊正像匀光法,最初是针对光学像片的晒印提出来的(李德仁 等,2006)。根据Mask匀光原理,光照不均匀的数字遥感影像可以用如下数学模型进行描述
| ${{I'}}\left({x, y} \right) = {{I}}\left({x, y} \right) + {{B}}\left({x, y} \right)$ | (1) |
式中,
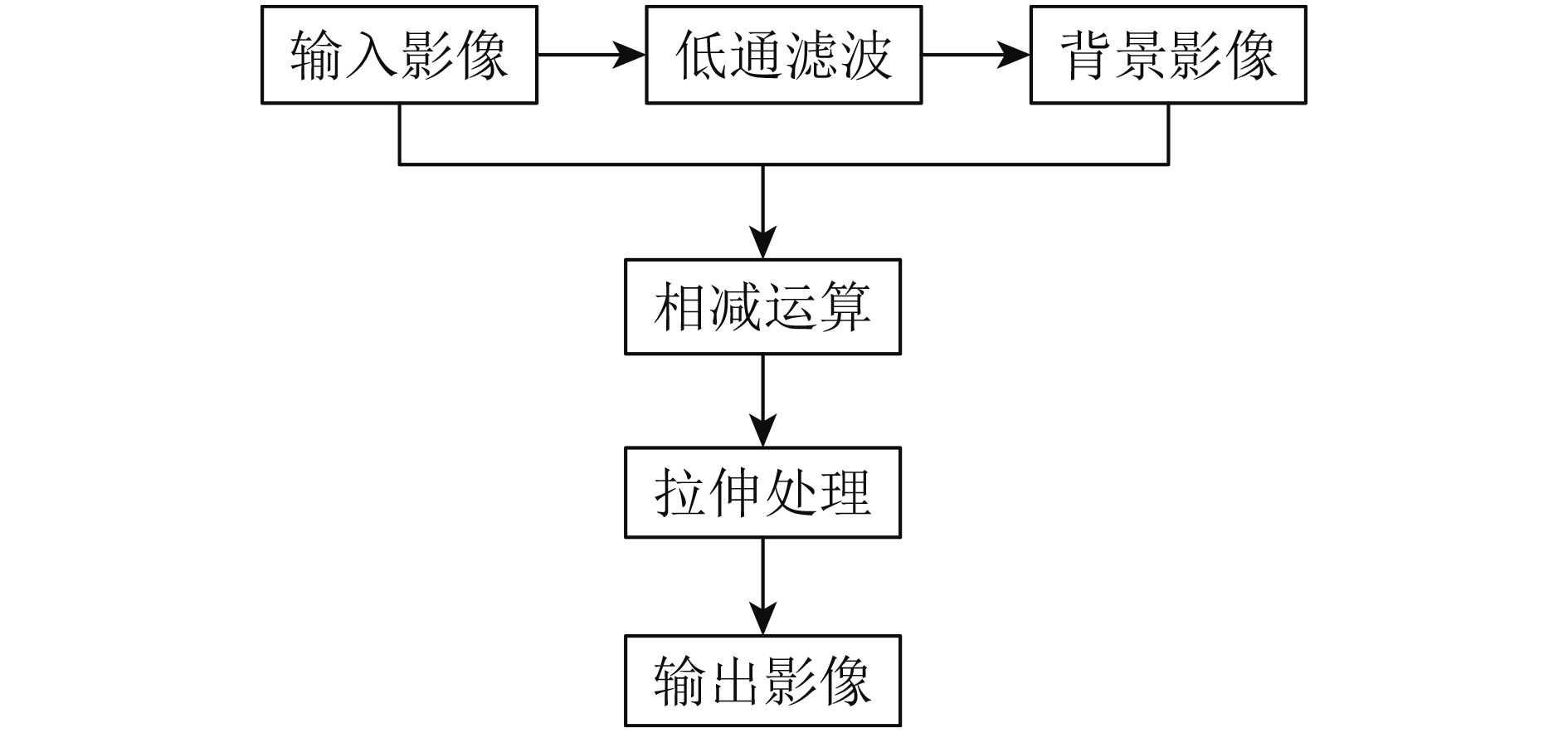
根据式(1),光照不均匀的影像可以看成是光照均匀的理想影像与背景影像相叠加的结果。如果能够很好地模拟出背景影像,将其从原始影像中减去,然后再对相减结果进行拉伸处理,增大影像的细节反差,即可得到均匀光照的理想影像,达到影像匀光的目的,流程图如图1。
背景影像的估计是Mask匀光法中的关键步骤,直接影响最终的匀光效果。传统Mask匀光法采用低通滤波的方法获取影像的低频信息作为背景影像,选取合适滤波器及其尺寸参数非常重要。由于高斯滤波器可以在空间域和频率域达到最佳(王密和潘俊,2004),一般选用高斯低通滤波器来生成背景影像。高斯低通滤波器的数学公式为
| ${{H}}(u, v) = {{\rm{e}}^{ - {{{D}}^2}(u, v)/2{\sigma ^2}}}$ | (2) |
式中,
尺寸参数
2.2 变分Mask匀光方法
Mask匀光法的本质是在已知原始影像的基础上求解背景影像和理想影像,是一个病态反问题,可以采用变分正则化的方法求解。通过分析背景影像和理想影像自身的性质,提出以下假设:
(1) 背景影像
(2) 理想影像
(3) 为了保证变量的物理意义,对
基于上述3个假设,构造变分能量函数如下
| $\mathop {\arg \min }\limits_{{I}, {B}} \frac{1}{2}\left\| {{{I}} + {{B}} - {{I'}}} \right\|_2^2 + {{\textit{λ}}_1}\left\| {\nabla {{I}}} \right\|_1^{} + {{\textit{λ}}_2}\left\| {\nabla {{B}}} \right\|_2^2$ | (3) |
式中,
背景影像的估计问题转化为变分能量函数的最优解问题,由于变分函数中包含两种范数,直接求解往往比较困难。为了简化计算,本文采用专门用于求解含有TV(Total Variation)先验或者
| $\begin{array}{l}\mathop {\arg \min }\limits_{{{I}}, {{B}}, {{{b}}_1}, {{{b}}_2}, {{{c}}_1}, {{{c}}_2}}\displaystyle \frac{1}{2}\left\| {{{B}} + {{I}} - {{I'}}} \right\|_2^2 + {{\textit{λ}} _1}{\left\| {\left({{{{b}}_1}, {{{b}}_2}} \right)} \right\|_1} + {{\textit{λ}} _2}{\left\| {\left({{{{c}}_1}, {{{c}}_2}} \right)} \right\|_2}\\{\kern 1pt} \;\;\;\;{\rm{s}}.{\rm{t}}.\;\;\;{{{b}}_1} = {\nabla _x}{{I}}, {{{b}}_2} = {\nabla _y}{{I}}, {{{c}}_1} = {\nabla _x}{{B}}, {{{c}}_2} = {\nabla _y}{{B}}\end{array}$ | (4) |
式中,
| ${\left\| {\left({{{{b}}_1}, {{{b}}_2}} \right)} \right\|_1} = \sum\limits_{i, j} {(|{{{b}}_{1(i, j)}}| + |{{{b}}_{2(i, j)}}|)} $ | (5) |
| ${\left\| {\left({{{{c}}_1}, {{{c}}_2}} \right)} \right\|_2} = \sum\limits_{i, j} {\sqrt {{{c}}_{1(i, j)}^2 + {{c}}_{2(i, j)}^2} } $ | (6) |
添加4个二次惩罚函数项,可将上式由约束优化问题转化为无约束问题
| $\begin{array}{l}\left( {{{{I}}^{k + 1}},{{{B}}^{k + 1}},{{{b}}_1}^{k + 1},{{{b}}_2}^{k + 1},{{{c}}_1}^{k + 1},{{{c}}_2}^{k + 1}} \right) = \\\mathop {\arg \min }\limits_{{{I}},{{B}},{{{b}}_1},{{{b}}_2},{{{c}}_1},{{{c}}_2}} \displaystyle\frac{1}{2}\left\| {{{B}} + {{I}} - {{I}}'} \right\|_2^2 + {{\textit{λ}} _1}{\left\| {\left( {{{{b}}_1},{{{b}}_2}} \right)} \right\|_1} + {{\textit{λ}} _2}{\left\| {\left( {{{{c}}_1},{{{c}}_2}} \right)} \right\|_2} +\\{\kern 1pt} \;\;\;\;\; \displaystyle\frac{{{\gamma _1}}}{2}\left( {\left\| {{{{b}}_1} - {\nabla _x}{{I}} - {{t}}_1^k} \right\|_2^2 + \left\| {{{{b}}_2} - {\nabla _y}{{I}} - {{t}}_2^k} \right\|_2^2} \right) +\\\;\;\;\;\; \displaystyle\frac{{{\gamma _2}}}{2}\left( {\left\| {{{{c}}_1} - {\nabla _x}{{B}} - {{s}}_1^k} \right\|_2^2 + \left\| {{{{c}}_2} - {\nabla _y}{{B}} - {{s}}_2^k} \right\|_2^2} \right)\end{array}$ | (7) |
| ${{t}}_1^{k + 1} = {{t}}_1^k + {\nabla _x}{{{I}}^{k + 1}} - {{b}}_1^{k + 1}$ | (8) |
| ${{t}}_2^{k + 1} = {{t}}_2^k + {\nabla _y}{{{I}}^{k + 1}} - {{b}}_2^{k + 1}$ | (9) |
| ${{s}}_1^{k + 1} = {{s}}_1^k + {\nabla _x}{{{B}}^{k + 1}} - {{c}}_1^{k + 1}$ | (10) |
| ${{s}}_2^{k + 1} = {{s}}_2^k + {\nabla _y}{{{B}}^{k + 1}} - {{c}}_2^{k + 1}$ | (11) |
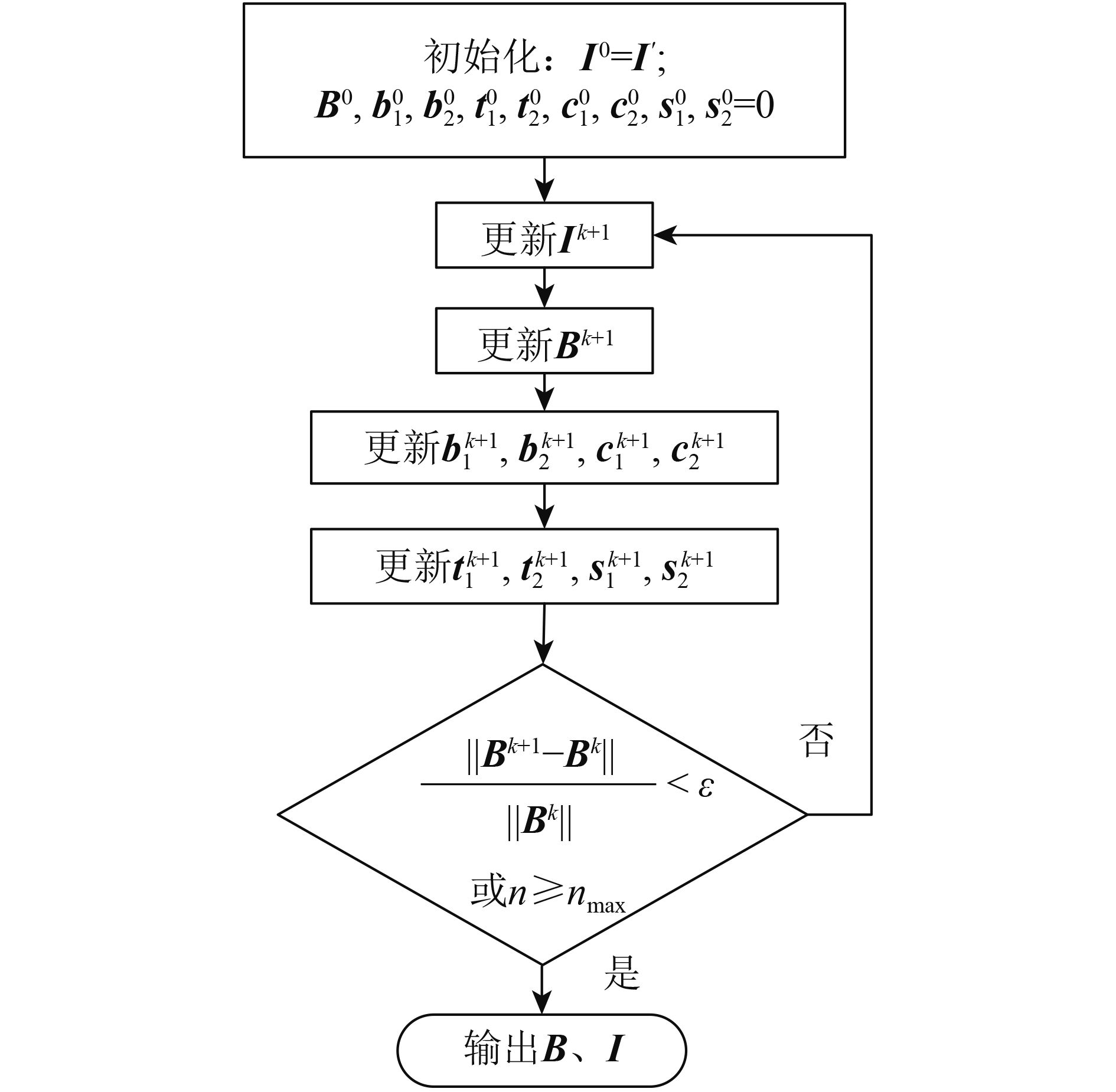
为了计算上述最小化问题,本文采用交替迭代方法,将变分模型的求解分解为3个子问题
(1) 理想影像
| $\begin{aligned} {{{I}}^{k + 1}} = & \mathop {\arg \min }\limits_{{I}} \frac{1}{2}\left\| {{{B}} + {{I}} - {{I'}}} \right\|_2^2 + \\ & \frac{{{\gamma _1}}}{2}\left({\left\| {{{{b}}_1} - {\nabla _x}{{I}} - {{t}}_1^k} \right\|_2^2 + \left\| {{{{b}}_2} - {\nabla _y}{{I}} - {{t}}_2^k} \right\|_2^2} \right) \end{aligned} $ | (12) |
对上式求导,得
| $\begin{array}{l}\left({{{{B}}^k} + {{{I}}^{k + 1}} - {{I'}}} \right) + {\gamma _1}{\nabla ^{\rm{T}}}\nabla {{{r}}^{k + 1}} + \\\quad\quad {\gamma _1}\left({\nabla _x^{\rm{T}}\left({{{t}}_1^k - {{b}}_1^k} \right) + \nabla _y^{\rm{T}}\left({{{t}}_2^k - {{b}}_2^k} \right)} \right) = 0\end{array}$ | (13) |
整理,得
| ${{{I}}^{k + 1}} = \frac{{{{I'}} - {{{B}}^{k + 1}} + {\gamma _1}\left({\nabla _x^{\rm{T}}\left({{{b}}_1^k - {{t}}_1^k} \right) + \nabla _y^{\rm{T}}\left({{{b}}_2^k - {{t}}_2^k} \right)} \right)}}{{{{E}} - {\gamma _1}\Delta }}$ | (14) |
式中,
(2) 背景影像
| $\begin{aligned} {{{B}}^{k + 1}} = & \mathop {\arg \min }\limits_{{B}} \frac{1}{2}\left\| {{{B}} + {{I}} - {{I'}}} \right\|_2^2 \hfill + \\ &\frac{{{\gamma _2}}}{2}\left({\left\| {{{{c}}_1} - {\nabla _x}{{B}} - {{s}}_1^k} \right\|_2^2 + \left\| {{{{c}}_2} - {\nabla _y}{{B}} - {{s}}_2^k} \right\|_2^2} \right) \hfill \\ \end{aligned} $ | (15) |
对上式求导,得
| $\begin{array}{l}\left({{{{I}}^k} + {{{B}}^{k + 1}} - {{I'}}} \right) + {\gamma _2}{\nabla ^{\rm{T}}}\nabla {{{B}}^{k + 1}} + \\{\kern 1pt} \;\;\;\;\;\;\;{\gamma _2}\left({\nabla _x^{\rm{T}}\left({{{s}}_1^k - {{c}}_1^k} \right) + \nabla _y^{\rm{T}}\left({{{s}}_2^k - {{c}}_2^k} \right)} \right) = 0\end{array}$ | (16) |
整理,得
| ${{{B}}^{k + 1}} = \frac{{{{I'}} - {{{I}}^k} + {\gamma _2}\left({\nabla _x^{\rm{T}}\left({{{c}}_1^k - {{s}}_1^k} \right) + \nabla _y^{\rm{T}}\left({{{c}}_2^k - {{s}}_2^k} \right)} \right)}}{{{{E}} - {\gamma _2}\Delta }}$ | (17) |
(3) 辅助变量最优化子问题
| $\begin{array}{l} \left({{{b}}_1^{k + 1}, {{b}}_2^{k + 1}} \right) = \mathop {\arg \min }\limits_{{{{b}}_1}, {{{b}}_2}} {{\textit{λ}} _1}{\left\| {\left({{{{b}}_1}, {{{b}}_2}} \right)} \right\|_1} + \\ \quad \displaystyle\frac{{{\gamma _1}}}{2}\left\| {{{{b}}_1} - {\nabla _x}{{{r}}^{k + 1}} - {{t}}_1^k} \right\|_2^2 + \frac{{{\gamma _1}}}{2}\left\| {{{{b}}_2} - {\nabla _y}{{{r}}^{k + 1}} - {{t}}_2^k} \right\|_2^2 \\ \end{array} $ | (18) |
| $\begin{gathered} \left({{{c}}_1^{k + 1}, {{c}}_2^{k + 1}} \right) = \mathop {\arg \min }\limits_{{{{c}}_1}, {{{c}}_2}} {{\textit{λ}} _2}{\left\| {\left({{{{c}}_1}, {{{c}}_2}} \right)} \right\|_2} + \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\gamma _2}}}{2}\left\| {{{{c}}_1} - {\nabla _x}{{{B}}^{k + 1}} - {{s}}_1^k} \right\|_2^2 + \frac{{{\gamma _2}}}{2}\left\| {{{{c}}_2} - {\nabla _y}{{{B}}^{k + 1}} - {{s}}_2^k} \right\|_2^2 \hfill \\ \end{gathered} $ | (19) |
通过迭代收缩算法,可以得到式(18)、(19)的近似解
| ${{b}}_1^{k + 1} = \frac{{{\nabla _x}{{{I}}^{k + 1}} + {{t}}_1^k}}{\big|{{{\nabla _x}{{{I}}^{k + 1}} + {{t}}_1^k}}\big|}\max \left\{ {\big|{{{\nabla _x}{{{I}}^{k + 1}} + {{t}}_1^k}}\big| - \frac{{{{\textit{λ}} _1}}}{{{\gamma _1}}}, 0} \right\}$ | (20) |
| ${{b}}_2^{k + 1} = \frac{{{\nabla _y}{{{I}}^{k + 1}} + {{t}}_2^k}}{\big|{{{\nabla _y}{{{I}}^{k + 1}} + {{t}}_2^k}}\big|}\max \left\{ {\big|{{{\nabla _y}{{{I}}^{k + 1}} + {{t}}_2^k}}\big| - \frac{{{{\textit{λ}} _1}}}{{{\gamma _1}}}, 0} \right\}$ | (21) |
| ${{c}}_1^{k + 1} = \frac{{{\nabla _x}{{{B}}^{k + 1}} + {{s}}_1^k}}{{{{{W}}^k}}}\max \left\{ {{{{W}}^k} - \frac{{{{\textit{λ}} _2}}}{{{\gamma _2}}}, 0} \right\}$ | (22) |
| ${{c}}_2^{k + 1} = \frac{{{\nabla _y}{{{B}}^{k + 1}} + {{s}}_2^k}}{{{{{W}}^k}}}\max \left\{ {{{{W}}^k} - \frac{{{{\textit{λ}} _2}}}{{{\gamma _2}}}, 0} \right\}$ | (23) |
式中,
| ${{{W}}^k} = \sqrt {{{\left({{\nabla _x}{{{B}}^{k + 1}} + {{s}}_1^k} \right)}^2} + {{\left({{\nabla _y}{{{B}}^{k + 1}} + {{s}}_2^k} \right)}^2}} $ | (24) |
当残差
3 实验与分析
为了客观真实地验证本文方法的有效性,分别在3幅遥感影像上进行匀光实验,并从目视效果和定量评价参数两方面与Mask匀光法进行比较。实验平台为Intel Core i5 CPU、8G内存的PC机,编程语言为Matlab。
本文方法需要设置4个参数,其中
3.1 视觉评价
3幅原始影像分别为3种不同类型的亮度不均匀影像(图3)。图3(a)为典型的虚光效应影像,影像中间亮,四周暗,图3(b)为局部过曝影像,图3(c)为存在水域亮斑的影像。分别利用本文方法和3种不同尺寸参数(
对比图4(a)—(c)和图6(a)—(c),可以看出,当滤波器尺寸
此外,Mask匀光法的匀光结果四周产生了光晕(图6(e))。这是由于在频率域进行高斯低通滤波会出现边界效应,导致估计的背景影像边缘的灰度值偏低,从而相减运算得到的匀光结果边缘的灰度值偏高,即光晕现象。滤波器尺寸
相比而言,本文方法对3幅遥感影像的处理结果都比较理想。估计的背影影像中纹理信息较少,较好反映了光照变化。匀光结果亮度均匀,既抑制了过曝区域又增强了低亮度区域,并且未出现光晕和偏色现象,体现了明显的优势。
3.2 定量评价
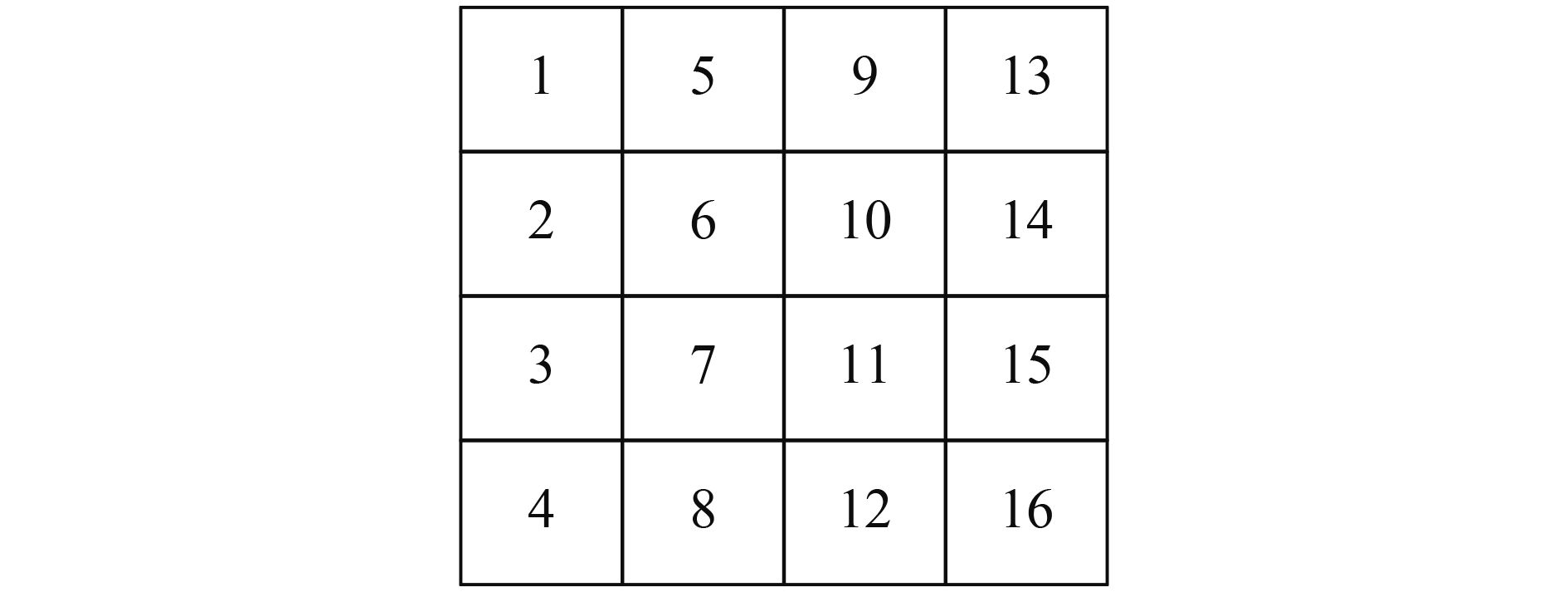
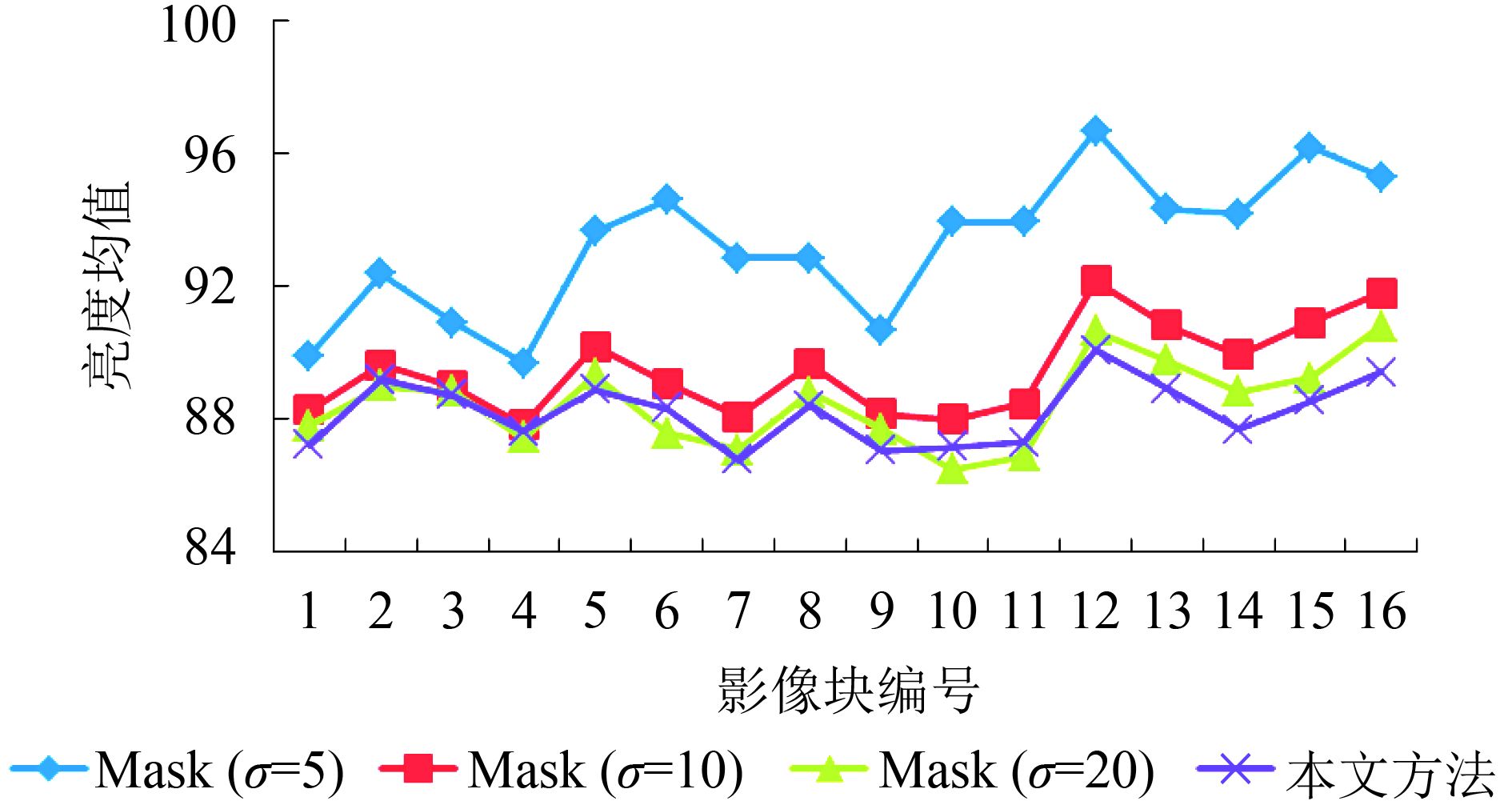
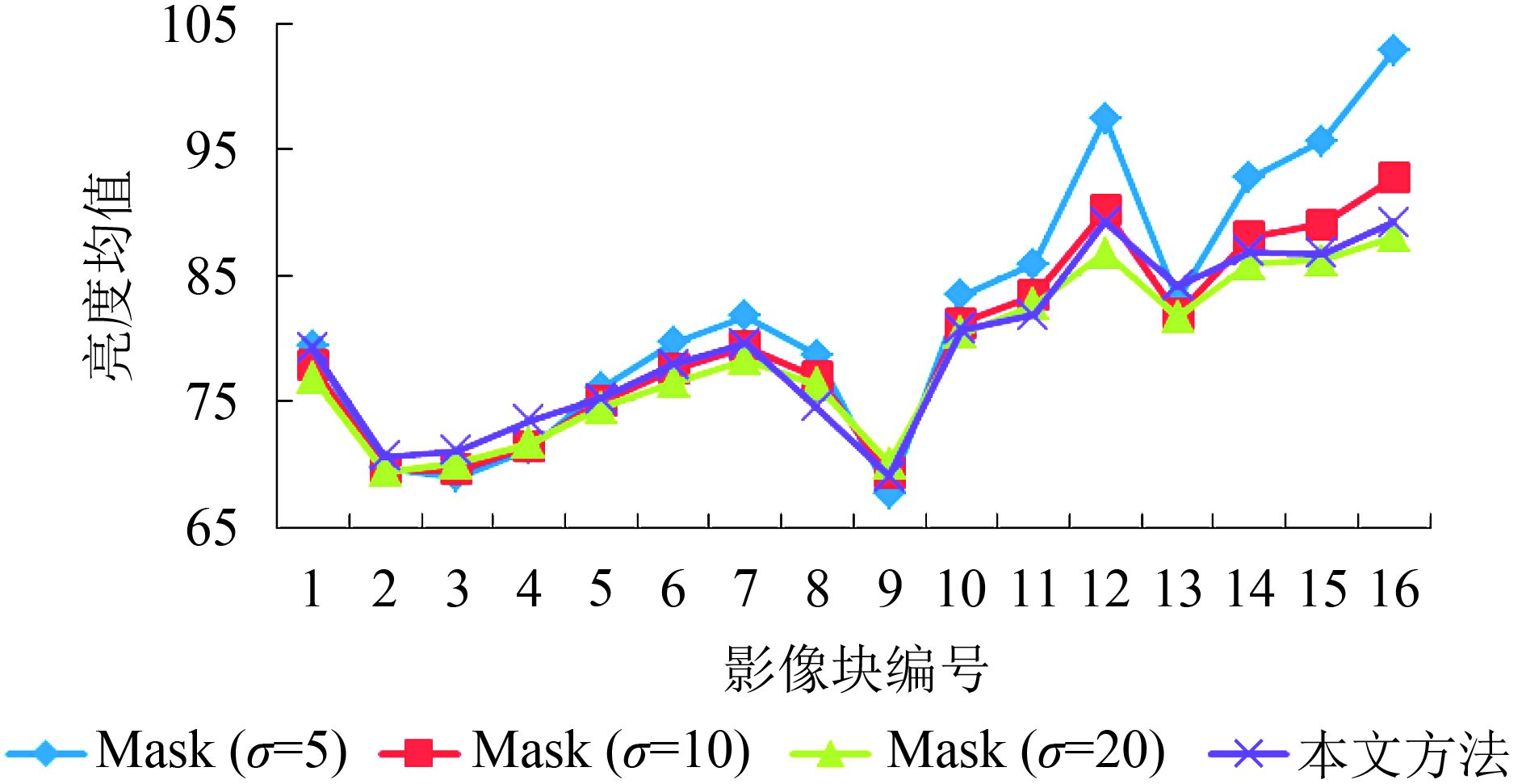
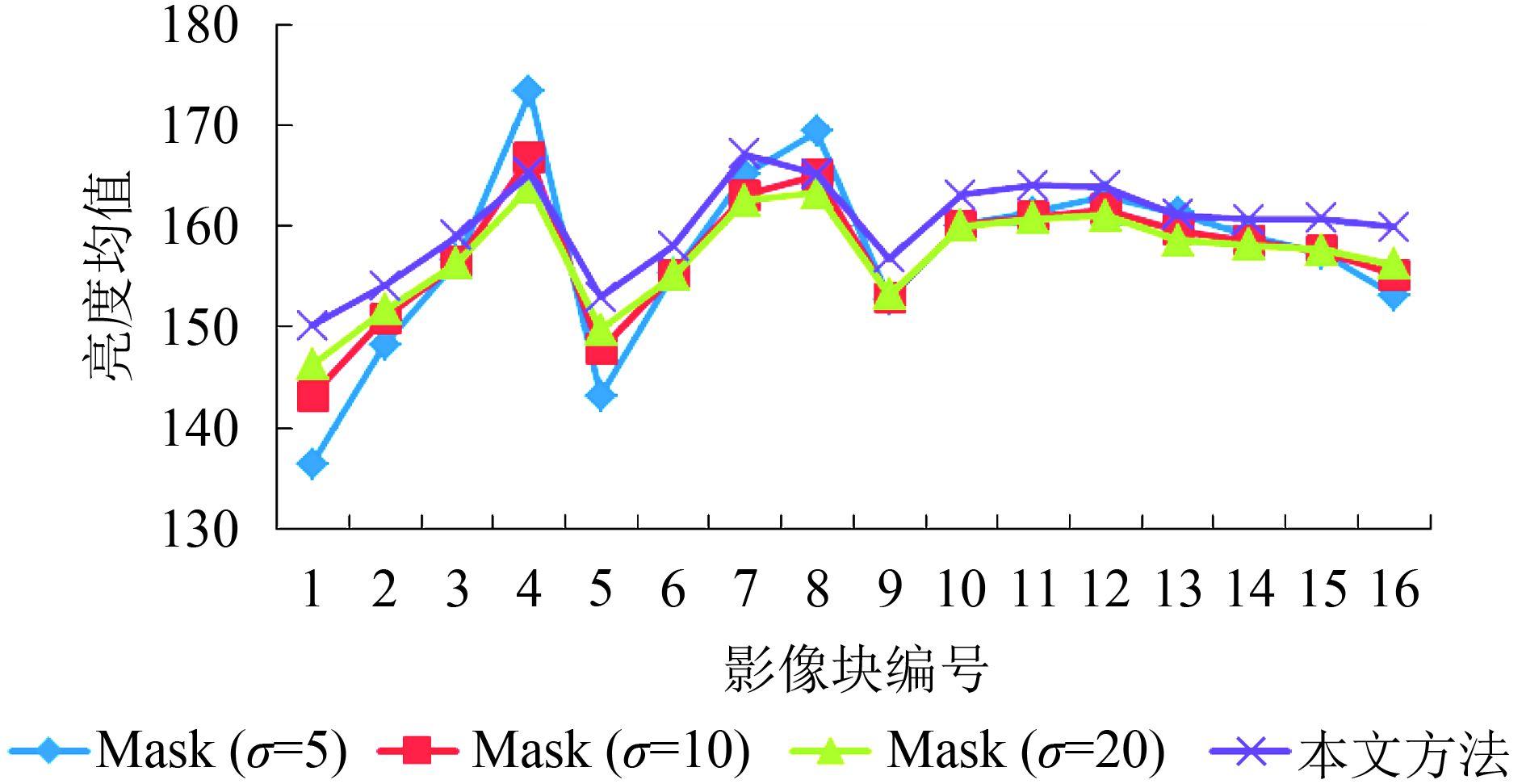
为了对比匀光影像内部光照分布的均匀性,将各匀光影像分成
为了对匀光影像进行定量评价,统计信息熵、清晰度、平均对比度和块标准差等影像质量评价参数(表1—表3)。信息熵、清晰度、平均对比度为经典的无参考影像质量评价参数,可以反映影像的纹理和细节信息。块标准差是16个影像块亮度均值的标准差,反映了16个亮度均值的离散程度,即影像内部亮度分布的均匀程度。
由图8—图10可以看出,滤波器尺寸
由上可知,滤波器尺寸
表 1 影像Ⅰ匀光结果的质量评价参数
Table 1 The quality parameters of dodging results of image Ⅰ
| 评价参数 | Mask(
|
Mask(
|
Mask(
|
本文方法 |
| 信息熵 | 6.81 | 6.69 | 6.56 | 6.81 |
| 清晰度 | 11.36 | 11.35 | 11.32 | 11.30 |
| 平均对比度 | 29.25 | 26.99 | 24.49 | 27.40 |
| 块标准差 | 2.10 | 1.38 | 1.30 | 0.97 |
表 2 影像Ⅱ匀光结果的质量评价参数
Table 2 The quality parameters of dodging results of image Ⅱ
| 评价参数 | Mask(
|
Mask(
|
Mask(
|
本文方法 |
| 信息熵 | 7.51 | 7.42 | 7.29 | 7.48 |
| 清晰度 | 22.76 | 22.85 | 22.79 | 22.63 |
| 平均对比度 | 49.66 | 45.97 | 40.54 | 48.39 |
| 块标准差 | 10.63 | 7.65 | 6.33 | 6.64 |
表 3 影像Ⅲ匀光结果的质量评价参数
Table 3 The quality parameters of dodging results of image Ⅲ
| 评价参数 | Mask(
|
Mask(
|
Mask(
|
本文方法 |
| 信息熵 | 6.92 | 6.79 | 6.67 | 6.91 |
| 清晰度 | 19.41 | 19.46 | 19.49 | 19.43 |
| 平均对比度 | 30.75 | 28.11 | 25.93 | 30.41 |
| 块标准差 | 9.31 | 6.28 | 4.99 | 4.79 |
4 结 论
本文将变分方法引入到遥感影像匀光中,提出一种变分Mask自适应匀光算法,将背景影像的估计问题转化为变分能量模型的最优解问题,通过交替迭代优化的方法自适应求解最优背景和理想影像,克服了传统Mask匀光法对滤波器及其尺寸参数的依赖,提高了算法的通用性。实验结果表明,本文方法对多种类型的光照不均影像都能够有效的校正,并且不会丢失纹理和细节信息,较好地保持影像的颜色和对比度,在视觉效果和定量评价指标上均优于传统Mask匀光法,是一种有效且通用的遥感影像匀光方法,具有较强的实用性。
本文方法可以有效地解决遥感影像中亮度不均现问题,但是没有考虑反差一致性,需要进一步优化模型。另外本文方法需要迭代求解,效率低于传统Mask匀光法,后续需要考虑如何提高运算效率的问题。
参考文献(References)
-
Chen C and Xu G L. 2016. A new linearized split Bregman iterative algorithm for image reconstruction in sparse-view X-ray computed tomography. Computers and Mathematics with Applications, 71 (8): 1537–1559. [DOI: 10.1016/j.camwa.2016.01.003]
-
Fan C N and Zhang F Y. 2011. Homomorphic filtering based illumination normalization method for face recognition. Pattern Recognition Letters, 32 (10): 1468–1479. [DOI: 10.1016/j.patrec.2011.03.023]
-
Guo C Z, Shi W J, Qin Z Y and Geng Z X. 2016. Non-convex sparsity regularization for wave back restoration of space object images. Optics and Precision Engineering, 24 (4): 902–912. [DOI: 10.3788/OPE.20162404.0902] ( 郭从洲, 时文俊, 秦志远, 耿则勋. 2016. 空间目标图像的非凸稀疏正则化波后复原. 光学精密工程, 24 (4): 902–912. [DOI: 10.3788/OPE.20162404.0902] )
-
Huo L J, He B and Zhou D B. 2017. A destriping method with multi-scale variational model for remote sensing image. Optics and Precision Engineering, 25 (1): 198–207. [DOI: 10.3788/OPE.20172501.0198] ( 霍丽君, 何斌, 周达标. 2017. 遥感图像条带噪声的多尺度变分模型去除. 光学精密工程, 25 (1): 198–207. [DOI: 10.3788/OPE.20172501.0198] )
-
Jiang B, Woodell G A and Jobson D J. 2015. Novel multi-scale Retinex with color restoration on graphics processing unit. Journal of Real-Time Image Processing, 10 (2): 239–253. [DOI: 10.1007/s11554-014-0399-9]
-
Kimmel R, Elad M, Shaked D, Keshet R and Sobel I. 2003. A variational framework for retinex. International Journal of Computer Vision, 52 (1): 7–23. [DOI: 10.1023/A:1022314423998]
-
Li D R, Wang M and Pan J. 2006. Auto-dodging processing and its application for optical RS images. Geomatics and Information Science of Wuhan University, 31 (9): 753–756. [DOI: 10.3321/j.issn.1671-8860.2006.09.001] ( 李德仁, 王密, 潘俊. 2006. 光学遥感影像的自动匀光处理及应用. 武汉大学学报(信息科学版), 31 (9): 753–756. [DOI: 10.3321/j.issn.1671-8860.2006.09.001] )
-
Li H F, Shen H F, Zhang L P and Li P X. 2010. An uneven illumination correction method based on variational Retinex for remote sensing image. Acta Geodaetica et Cartographica Sinica, 39 (6): 585–591. ( 李慧芳, 沈焕锋, 张良培, 李平湘. 2010. 一种基于变分Retinex的遥感影像不均匀性校正方法. 测绘学报, 39 (6): 585–591. )
-
Sun M W. 2009. Research on key technology of automatic and fast DOM generation. Wuhan: Wuhan University (孙明伟. 2009. 正射影像全自动快速制作关键技术研究. 武汉: 武汉大学)
-
Tang S, Gong W G and Zhong J H. 2013. Sparsity and smoothing multi-regularization constraints for blind image deblurring. Journal of Software, 24 (5): 1143–1154. [DOI: 10.3724/SP.J.1001.2013.04256] ( 唐述, 龚卫国, 仲建华. 2013. 稀疏平滑特性的多正则化约束图像盲复原方法. 软件学报, 24 (5): 1143–1154. [DOI: 10.3724/SP.J.1001.2013.04256] )
-
Wang M and Pan J. 2004. A method of removing the uneven illumination for digital aerial image. Journal of Image and Graphics, 9 (6): 744–748. [DOI: 10.3969/j.issn.1006-8961.2004.06.016] ( 王密, 潘俊. 2004. 一种数字航空影像的匀光方法. 中国图象图形学报, 9 (6): 744–748. [DOI: 10.3969/j.issn.1006-8961.2004.06.016] )
-
Yao F, Wan Y C and Hu H. 2013. Research on the improved image dodging algorithm based on Mask technique. Remote Sensing Information, 28 (3): 8–13. [DOI: 10.3969/j.issn.1000-3177.2013.03.002] ( 姚芳, 万幼川, 胡晗. 2013. 基于Mask原理的改进匀光算法研究. 遥感信息, 28 (3): 8–13. [DOI: 10.3969/j.issn.1000-3177.2013.03.002] )
-
Yuan X X, Han Y T and Fang Y. 2014. Improved Mask dodging algorithm for aerial imagery. Journal of Remote Sensing, 18 (3): 630–641. [DOI: 10.11834/jrs.20143295] ( 袁修孝, 韩宇韬, 方毅. 2014. 改进的航摄影像Mask匀光算法. 遥感学报, 18 (3): 630–641. [DOI: 10.11834/jrs.20143295] )
-
Zhang Z, Zhu B S and Zhu S L. 2010. An improved MASK dodging method based on contrast consistency processing. Journal of Geomatics Science and Technology, 27 (1): 54–56. [DOI: 10.3969/j.issn.1673-6338.2010.01.014] ( 张振, 朱宝山, 朱述龙. 2010. 反差一致性改进的MASK匀光算法. 测绘科学技术学报, 27 (1): 54–56. [DOI: 10.3969/j.issn.1673-6338.2010.01.014] )
-
Zhang Z, Zhu B S, Zhu S L and Cao W. 2009. Improved MASK dodging method based on wavelet. Journal of Remote Sensing, 13 (6): 1074–1081. [DOI: 10.11834/jrs.20090607] ( 张振, 朱宝山, 朱述龙, 曹闻. 2009. 小波变换改进的MASK匀光算法. 遥感学报, 13 (6): 1074–1081. [DOI: 10.11834/jrs.20090607] )
-
Zhang Z X, Li Z J, Zhang J Q and Zheng L. 2003. Use discrete chromatic space to tune the image tone in a color image mosaic//Proceedings of the Third International Symposium on Multispectral Image Processing and Pattern Recognition. Beijing: SPIE [DOI: 10.1117/12.538550]
-
Zhang Z X and Zou S B. 2011. An improved algorithm of Mask image dodging for aerial image// Proceedings of MIPPR 2011: Remote Sensing Image Processing, Geographic Information Systems and Other Applications. Guilin: SPIE [DOI: 10.1117/12.901869]
-
Zheng J, Xu C G, Xiao D G, Li H and Huang H. 2003. The technique of digit image’s illumination uneven elimination. Transactions of Beijing Institute of Technology, 23 (3): 285–289. [DOI: 10.3969/j.issn.1001-0645.2003.03.006] ( 郑军, 徐春广, 肖定国, 理华, 黄卉. 2003. 数字图像中照度不均匀校正技术研究. 北京理工大学学报, 23 (3): 285–289. [DOI: 10.3969/j.issn.1001-0645.2003.03.006] )
-
Zhu S L, Zhang Z, Zhu B S and Cao W. 2011. Experimental comparison among five algorithms of brightness and contrast homogenization. Journal of Remote Sensing, 15 (1): 111–122. [DOI: 10.11834/jrs.20110109] ( 朱述龙, 张振, 朱宝山, 曹闻. 2011. 遥感影像亮度和反差分布不均匀性校正算法的效果比较. 遥感学报, 15 (1): 111–122. [DOI: 10.11834/jrs.20110109] )