出版日期: 2017-11-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20176493
2017 | Volumn21 | Number 6
上一篇 | 下一篇

面向属性空间分布特征的空间聚类

朱杰 , 孙毅中 , 李吉龙

1. 南京师范大学虚拟地理环境教育部重点实验室，南京 210023

2. 江苏省地理信息资源开发与利用协同创新中心，南京 210023

收稿日期: 2016-12-26; 优先数字出版日期: 2017-11-01

基金项目: 国家自然科学基金(编号：41671392)；公安部科技强警基础工作专项项目(编号：2015GABJC39)

第一作者简介: 朱杰(1989—　)，男，博士研究生，研究方向为空间数据表达与挖掘。E-mail：Chu_Je@163.com

通讯作者简介: 孙毅中(1957—　)，男，教授，研究方向为城市空间数据挖掘。E-mail：sunyizhong_cz@163.com

中图分类号: P208

文献标识码: A

摘要

空间聚类应当同时满足空间位置邻近和属性相似，在此背景下，为满足空间邻近实体之间趋势性和不均匀性的属性聚类需求，提出一种基于图论和信息熵的空间聚类算法。该算法主要是在Delaunay三角网空间位置聚类基础上，通过引入信息熵，采用多元相似性度量方法以解决二元关系在属性聚类中的缺陷，同时基于“等概率最大熵”原则提出了一种局部参数度量方法，用于表达邻近目标间属性分布的局部变化信息。将本文方法与多约束聚类方法和DDBSC聚类方法进行对比分析，结果表明：(1)在属性空间分布不均的情况下，本文方法的聚类精度要高于多约束方法和DDBSC方法，尤其是当属性空间分布不均程度不断扩大时，DDBSC和多约束算法会将空间簇内的实体误判为噪声；(2)在对异常值的敏感性问题上，3类方法都能识别出异常值的位置，但DDBSC和多约束算法对异常值具有一定的敏感性，聚类结果会掩盖属性分布的趋势性，本文方法受异常值影响很小。通过模拟实验和实际算例可以发现，在保证空间邻近的基础上本文方法具有如下优势：第一，能反映实体属性在空间分布中的趋势性特征；第二，能满足属性空间分布不均匀；第三，对异常值具有良好的稳健性。

关键词

空间聚类, Delaunay三角网, 信息熵, 趋势性, 不均匀性

Spatial clustering method considering spatial distribution feature in the attribute domain

ZHU Jie , SUN Yizhong , LI Jilong

1.Key Laboratory of Virtual Geographic Environment of Ministry of Education, Nanjing Normal University, Nanjing 210023, China

2.Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China

Abstract

Spatial clustering is important for spatial data mining and spatial analysis. Spatial objects in the same cluster should be similar in the spatial and attribute domains. Tendency and heterogeneity are important characteristics of geographic phenomena. Currently, most spatial clustering algorithms only consider either tendency or heterogeneity, failing to obtain satisfied clustering results. To overcome these limitations, a spatial clustering method based on graph theory and information entropy is developed in this work. The proposed algorithm involves two main steps: construct spatial proximity relationships and cluster spatial objects with similar attributes. Delaunay triangulation with edge length constraints is first employed to construct spatial proximity relationships among objects. To obtain satisfactory results in spatial clustering with attribute similarity, the information entropy is introduced to overcome the defects of similarity measure with binary relation, which can reflect the clustering tendency of geographical phenomena. Furthermore, a local parameter measurement method based on the principle of " equal probability maximum entropy” is designed to adapt to the local change information of attribute distribution. The performance of the proposed algorithm was evaluated experimentally by comparing the leading state-of-the-art alternatives: DDBSC and multi-constraint algorithms. Results showed that our method outperformed the two other algorithms as attributes are unevenly distributed in space. The sensitivity analysis of these algorithms showed that our method was the least sensitive to outliers. The effectiveness and practicability of the proposed algorithm were validated using simulated and real spatial datasets. Two experiments were performed to illustrate the three advantages of our algorithm: (1) It can reflect the tendency of the entity attribute in the spatial distribution. (2) It can meet the requirement that attributes are unevenly distributed in space. (3) It can discover clusters with arbitrary shape and is robust to outliers.

Key words

spatial clustering, Delaunay triangulation, information entropy, tendency, heterogeneity

1 引　言

空间聚类是地理空间数据挖掘与知识发现的重要技术手段，其能够发现空间实体自然的空间集聚模式，对于揭示空间实体的分布规律和空间结构特征具有重要的作用。进一步，结合空间实体属性在空间上的分布与差异对于解释复杂的地理现象具有重要意义(邓敏等，2011)。目前空间聚类技术已广泛应用于地图综合(Ai和van Oosterom，2002；武芳等，2008)、城市规划(Hong和O’Sullivan，2012；焦利民等，2015)、图像处理(贺辉等，2016)、气候变化(Birant和Kut，2007；石岩等，2013)等研究领域。

国内外学者对空间聚类方法做了大量的研究，可分为两种形式：一种是只顾及空间位置的聚类方法；另一种是兼顾空间位置和属性特征的聚类方法。基于空间位置聚类方法主要是通过解决实体空间位置分布的不规则性包括噪声问题(Ahuja，1982)、空间密度分布不均问题(Kang 等，1997；Eldershaw和Hegland，1997)和簇间边问题(Estivill-Castro和Lee，2002；Zhong 等，2010)等，以此获取实体的空间邻近关系，现有方法主要包括划分法(MacQueen，1967)、层次法(Zhang 等，1996)、基于密度的方法(Ester 等，1996)和基于图论的方法(Estivill-Castro和Lee，2002)等。兼顾空间位置和属性特征的聚类方法在聚类过程中顾及了实体的空间邻近性和属性相似性，目前主要有3类方法：(1)双重距离聚类方法(Sander 等，1998；Birant和Kut，2007；李光强等，2008)将空间距离和属性距离作为聚类变量分开来考虑，聚类过程中两种距离要同时满足聚类要求才能划分到同一个簇中。这类算法所涉及对象之间的相似性度量均为二元关系(单个实体与单个实体)，国内外已有研究(Slonim 等，2005；Bai 等，2012)表明二元相似关系在复杂数据中难以获取有意义的结构，就地理要素而言，在局部区域内会出现邻近要素之间区分度很小的情况，二元相似关系在面对这种局部特征时本身所具有的传递性会导致属性值之间的差异在聚类过程不断传播积累，造成最终的聚类结果无法准确地反映地理要素在空间分布中的过渡性；(2)一体化法(Mundur 等，2006；邓敏等，2010；焦利民等，2011)将空间坐标和属性数据加权融合构造距离函数，再结合特定的空间聚类算法进行聚类，本质是将空间位置和属性特征纳入统一的空间距离测度。由于空间位置和属性特征存在不可比性，对空间距离度量进行属性扩展或对属性距离进行空间扩展存在一定的人为任意性；(3)空间位置上的属性相似性聚类方法(Lin 等，2005；刘启亮等，2011；Liu 等，2012；石岩等，2012)首先考虑实体的空间邻近性，然后加入属性约束，可以适应不同用途的空间聚类应用且可操作性更强。但此类方法在聚类过程中采用了固定的阈值如刘启亮等人(2011)和Liu等人(2012)将属性阈值设为最邻近实体非空间属性差异的平均值，这种设置方法在属性空间分布均匀的情况能够很好地揭示空间对象的分布规律，但是不能满足属性分布不均匀的情况，有可能将局部相似的对象划入到噪声簇中或划入其他聚类簇中，导致聚类精度降低。针对目前兼顾空间位置和属性特征的聚类方法存在的问题，本文将信息熵引入到空间聚类算法中。

2 方　法

提出的空间聚类方法分为两个步骤：第一，空间位置聚类，得到实体间的空间邻近关系；第二，在此基础上进一步顾及属性聚类，得到最终聚类结果。

2.1 基于空间实体位置的聚类

实体间空间邻近关系的构建是空间位置聚类的关键问题，许多聚类算法需要输入人为参数和先验知识如密度阈值，聚类的数目，数据分布模式的假设，核密度窗口大小等，这种带有参数的方法难以适应空间实体分布的不规则性且效率较低。Delaunay三角网是空间相似性表达的一种有效工具，不需要任何参数设置，参数信息完全包含在三角网中，这有利于减少人为产生的误差，提高聚类效率。为适应空间实体分布的不规则性，本文首先采用一种顾及全局和局部信息的动态筛选准则(Estivill-Castro和Lee，2002)对Delaunay三角网施加整体边长约束，具体表达如下。

定义1 　整体边长约束：给定一个空间数据集D，其包含的对象生成的Delaunay三角网表示为DT。针对任一对象P，与其直接相连的对象表示为DN(P)，Longedge表示与P连接的所有边的整体边长约束，表示为

$Longedge = Loca{l_ - }Mea{n_ - }Length\left( P \right) + Global\_SD$

(1)

$Loca{l_ - }Mea{n_ - }Length\left( P \right) = \frac{1}{{d\left( P \right)}}\mathop \sum \limits_{i = 1}^{d\left( P \right)} \left| {{e_i}} \right|$

(2)

$Loca{l_ - }SD\left( P \right) = \sqrt {\frac{{\mathop \sum \limits_{i = 1}^{d\left( P \right)} {{\left( {Loca{l_ - }Mea{n_ - }Length\left( P \right) - \left| {{e_i}} \right|} \right)}^2}}}{{d\left( P \right)}}} $

(3)

$Global\_SD = \frac{1}{N}\mathop \sum \limits_{i = 1}^N Loca{l_ - }SD\left( P \right)$

(4)

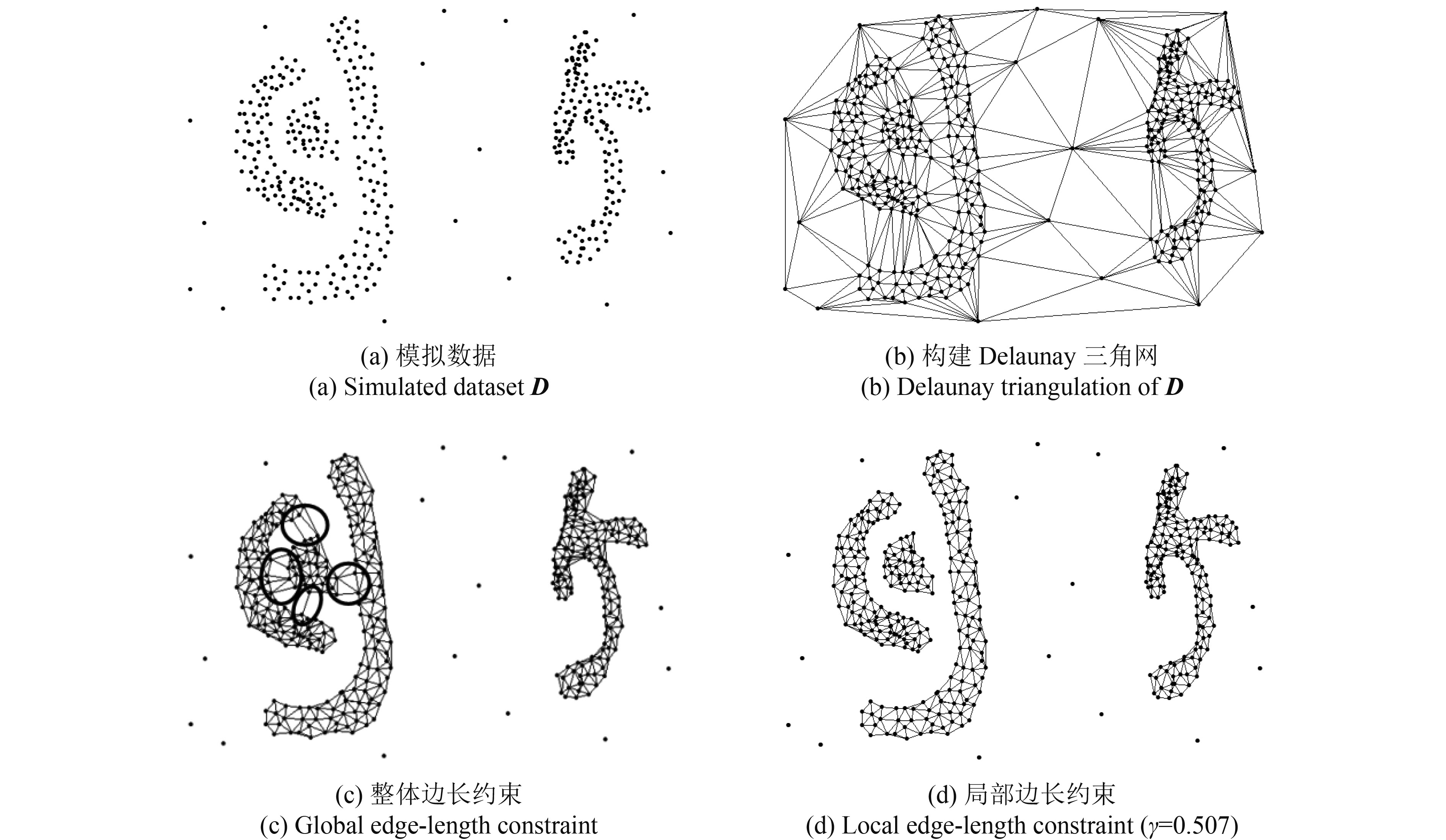
式中， $Loca{l_ - }Mea{n_ - }Length\left( P \right)$ 表示点P的邻域内所有边长的均值； $Loca{l_ - }SD\left( P \right)$ 表示点P邻域内所有边长的标准差； $Global\_SD$ 表示DT所有对象 $Loca{l_ - }SD\left( {{P_i}} \right)$ 的平均值；d(P)表示点P直接邻近对象的个数；|e_i|表示点P邻域内的边长；N表示平面点集数目。

如果网内任一对象P与DN(P)相连的边长长度大于Longedge，则将其删除。整体边长约束能够适应发现任意形状、不同密度的空间簇(图1(c))，但无法解决簇间的“颈”问题(图1(c)黑色圆圈所示)，需要进一步施加局部边长约束。

由图1可以看出，簇间的“颈”通常位于空间聚类簇的边界处，边界点邻域内连线长短不一，梯度变化较大。基于此，采用一个相对参数来量化这种特征，即通过判断点的松散度来探测簇间的“颈”。

定义2 　点的松散度：给定一个平面点集D，由点集生成的Delaunay三角网表示为DT。针对DT内任一点实体P，F(P)表示点实体P的松散度，表示为

$F\left( P \right) = Loca{l_ - }SD\left( P \right)/Loca{l_ - }Mea{n_ - }Length\left( P \right)$

(5)

式中，F(P)是一个相对参数，表示对象P邻域内的紧凑程度，F(P)越小该邻域越紧凑。

由定义2可知F(P)值越小说明该对象邻域内边长梯度变化小。很明显，聚类簇内的点由于邻域内边长变化较小，其F(P)值较小，相反，聚类簇边界点F(P)值较大。因此，针对DT内任一点实体P，聚类簇边界点的松散度可以表示为

${Sets} = \left\{ {F\left( P \right){\rm{|}}F\left( P \right) > \gamma } \right\}$

(6)

式中，Sets表示聚类簇边界点的松散度集合；γ表示松散度阈值，采用Liu和Sourina(2004)的启发式方法可确定γ。通过集合Sets可以找到聚类簇的边界点，删除这些边界点之间的连线以此获取局部边长约束结果(图1(d))。

图 1 基于Delaunay三角网空间位置聚类过程

Fig. 1 Different stages of spatial clustering

通过上述过程对Delaunay三角网施加多层次的边长约束能够满足实体空间位置分布的不规则性，探测不同空间簇之间的边界获取若干相似的簇以此达到空间位置的聚类。

2.2 基于信息熵度量的属性聚类

信息熵(Shannon，1948)可以用来测量一个系统的有序程度，熵值越大说明系统中的数据越无序；熵值越小说明系统中的数据越有序。如果将信息熵应用到聚类中，根据聚类的判断准则，同一聚类簇中数据越相似越好，而数据越有序。因此，基于信息熵的聚类要求应使得聚类后类内熵尽可能小，类间熵尽可能大。然而，具体如何聚类以及采用何种聚类准则仍然是个问题。目前基于信息熵聚类的主流做法是将原始数据集分配到K个聚类簇中，找出使得整个分配的总信息熵最小的那种分配组合。这个过程中信息熵实际上是对聚类结果进行处理以达到改善聚类效果的目的，聚类过程仍然以一些经典聚类算法为主(Li 等，2004；周悦来，2011；郭新辰等，2015；李凯和曹喆，2016)。本文受最大熵理论启发，从信息熵相对变化的角度来看待聚类过程，提出了一种基于信息熵度量的属性聚类方法，具体表达如下。

定义3 　属性熵: 属性熵: 设有 $n\left( {n \geqslant 2} \right)$ 个空间对象的聚类簇 ${X} = \left\{ {{x_1},{x_2}, \cdots, {x_n}} \right\}$ ，空间对象的属性集合为 ${A} = \left\{ {{A_1},{A_2}, \cdots ,{A_{\textit{z}}}} \right\}$ ，X在属性A_j上的取值记为矩阵 ${{R}_{{A_j}}} = {\left( {{r_i}} \right)_{n \times 1}}$ ，此时定义任一对象 ${x_k} \in {X}$ 在属性A_j的属性概率为P_k，即

${P_k} = \frac{{{r_k}}}{{\sum\limits_{i = 1}^n {{r_i}} }}$

(7)

显然，P_k具有归一性，相当于某事件的概率，于是X在属性A_j的属性熵H( $ {M_{{A_j}}} $ )表示为

$H\left( {{M_{{A_j}}}} \right) = - \mathop \sum \limits_{i = 1}^n {P_i}{\log _2}{P_i}$

(8)

由最大熵原理(张继国和Singh，2012)可知，当对所有i=1, 2, …, n，P_i为相同值时，H( $ {M_{{A_j}}} $ )会达到最大值，称为信息的“等概率最大熵”原则。换言之，某一聚类簇中对象属性值相差越小，信息熵值也就越高；反之，对象属性值差异性越大，熵值也就越低。根据聚类的判断准则，同一聚类簇中的数据越相似越好，因此聚类过程中应尽量遵循“等概率最大熵”原则，确保样本数据划分到最相似的聚类簇中，具体参数化过程见2.3.1节。

如果属性集合A中各个属性独立不相关，那么该聚类簇的信息熵值即为每个属性的信息熵的和，表示为

$H\left( M \right) = {W_{{A_1}}}H\left( {{M_{{A_1}}}} \right) + {W_{{A_2}}}H\left( {{M_{{A_2}}}} \right) + \cdots + {W_{{A_{\textit{z}}}}}H\left( {{M_{{A_{\textit{z}}}}}} \right)$

(9)

式中， $ {M_{{A_{\textit{z}}}}} $ 表示第z个属性值的权重， ${W_{{A_1}}} + {W_{{A_2}}} + \cdots +$ $ {W_{{A_{\textit{z}}}}} = 1$ 。

定义4 　直接邻居：空间位置聚类后获得Sub_DT空间邻近图，针对任一对象P，存在一个对象 $Q \in DN\left( P \right)$ ，则Q是P的直接邻居。直接邻居表达了某个实体的一阶邻域对象。

定义5 　间接邻居：在Sub_DT空间邻近图中，如果存在一个对象链 ${P_1},{P_2}, \cdots ,{P_{n - 1}}$ ，P_n满足P_n仅属于DN(P_n-1)，P_m属于 $\left\{ {DN\left( {{P_{m - 1}}} \right)\mathop \cap \nolimits {DN\left( {{P_{m + 1}}} \right)},1 < m < n} \right\}$ ，P₂仅属于DN(P₁)，那么 ${P_3},{P_4}, \cdots ,{P_n}$ 是P₁的间接邻居。间接邻居表达了某个实体的多阶邻近对象。

定义6 　信息熵度量:在Sub_DT空间邻近图中，对象x₁与x₂互为直接邻居关系，其在某个属性A_j′上的取值分别为a₁、a₂，那么定义两个对象之间的信息熵相似度为

$S\left( {{x_1},{x_2}} \right) = {H_{{x_1}{x_2}}}\left( {{M_r}} \right)$

(10)

${H_{{x_1}{x_2}}}\left( {{M_{A_j'}}} \right){\rm{ = - }}\sum\limits_{i = 1}^2 {{P_i}} {\log _{\rm{2}}}{{{P}}_{{i}}},{{{P}}_{{k}}}{\rm{ = }}\frac{{{{{a}}_{{k}}}}}{{\sum\limits_{i = 1}^2 {{a_i}} }}$

(11)

式中， ${a_k} \in \left\{ {{a_1},{a_2}} \right\}$ ，如果对象x₁和x₂的属性向量是集合 ${A}' = \left\{ {A{'_1},A{'_2}, \cdots, A{'_{\textit{z}}}} \right\}$ ，那么两个对象之间的信息熵相似度可以定义为

$\begin{aligned}S\left( {{x_1},{x_2}} \right) = & {W_{A{'_1}}}{H_{{x_1}{x_2}}}\left( {{M_{A{'_1}}}} \right) + {W_{A{'_2}}}{H_{{x_1}{x_2}}}\left( {{M_{A{'_2}}}} \right) + \\ &\cdots +{W_{A{'_{\textit{z}}}}}{H_{{x_1}{x_2}}}\left( {{M_{A{'_{\textit{z}}}}}} \right)\end{aligned}$

(12)

${H_{{x_1}{x_2}}}\left( {{M_{A_{\textit{z}}'}}} \right) = - \sum\limits_{i = 1}^2 {{P_i}} {\log _2}{P_i},{P_k} = \frac{{{a_{k{\textit{z}}}}}}{{\sum\limits_{i = 1}^2 {{a_{i{\textit{z}}}}} }}$

(13)

式中，a_iz表示对象x₁与x₂在属性A_z′上的取值；式(10)和(12)所给出的对象之间的相似性度量为二元关系，当聚类对象数量只有两个时，式(10)和(12)是可行的，但聚类对象大于2时，在空间聚类中二元相似关系有可能无法准确反映地理要素在空间分布的趋势性特征，具体表现为同一聚类簇中出现属性差异较大的现象，因此，当判断对象是否属于同一个类时，需要更多的对象参与到相似性度量中。

若存在一个对象v，其加入到一个聚类簇B(簇中实体数量≥2)中的可能性要取决于对象v与聚类簇B中所有对象的相似度。设对象v的属性为q_v，聚类簇B中对象的属性为 $\left\{ {{q_1},{q_2}, \cdots ,{q_m}} \right\}$ ，则对象v与聚类簇B的相似性表示为

$S\left( {v,B} \right) = {H_{vB}}\left( {{M_q}} \right)$

(14)

${H_{vB}}\left( {{M_q}} \right) = - \mathop \sum \limits_{i = 1}^{m + 1} {P_i}{\log _2}{P_i},{P_k} = \frac{{{q_k}}}{{\sum\limits_{i = 1}^{m + 1} {{q_i}} }}$

(15)

式中， ${q_k} \in \left\{ {{q_1},{q_2}, \cdots ,{q_m},{q_v}} \right\}$ 。同样，如果对象的属性是多维的，可以根据式(14)进行扩展。

定义7 　邻域属性熵：在Sub_DT空间邻近图中，针对任一对象P，其直接邻居包括自身表示为Sub_DN(P)，则空间对象P的邻域属性熵为

$Hnear\left( P \right) = \frac{{{H_{S\!ub\_DN\left( P \right)}}\left( M \right)}}{{\left\| {S\!ub\_DN\left( P \right)} \right\|}}$

(16)

式中， ${H_{S\!ub\_DN\left( P \right)}}\left( M \right)$ 表示P与直接邻居集合之间的相似性，可由式(14)计算得出； $\left\| {S\!ub\_DN\left( P \right)} \right\|$ 表示Sub_DN(P)的个数。 ${H_{S\!ub\_DN\left( P \right)}}\left( M \right)$ 能够比较比较量纲不同或者平均值差别较大的两组数据(成员数量相同)的离散度，其值越大说明Sub_DN(P)内对象属性差异越小，信息熵的单调性决定了 ${H_{S\!ub\_DN\left( P \right)}}\left( M \right)$ 在比较两组数量不同的数据时可能是失效的。因此，提出邻域属性熵的概念，其是一个相对参数，数值越大说明对象P与直接邻居对象间属性差异度越小。

定义8 　聚类中心：在Sub_DT空间邻近图中，Cluster_Point表示聚类中心点，表示为

$Cluster\_Point\left( P \right) = max\left( {Hnear\left( P \right)} \right)$

(17)

通常很多方法没有考虑到聚类结果的唯一性，聚类中心的定义用来选取属性差异最小的区域开始聚类，每次凝聚实体时，也是按照实体邻域属性熵最大原则进行，可以保证聚类结果的有序性。计算所有对象Hnear(P)值，按照降序排列，取最大值作为聚类中心点。聚类中心不是固定的，当一个聚类簇形成时，在所有未被聚类的对象中，按照上述定义重新选择中心点。

定义9 　聚类簇：在Sub_DT空间邻近图中，选取聚类中心，对其直接邻居和间接邻居的邻域属性熵按照降序排列，采用广度优先遍历方法(严蔚敏和吴伟民，2007)依次访问该聚类中心的直接邻居和间接邻居并进行信息熵度量，访问顺序按照实体的邻域属性熵从大到小依次进行，将符合相似性阈值(详见2.3.1节)的所有对象进行合并，一个聚类簇形成。

定义10 　噪声：聚类簇全部形成后，给定一个对象P，如果P不属于任何簇，P被认定为噪声。

2.3 算法分析与描述

2.3.1 属性聚类阈值分析

由定义3和定义6可知聚类簇中属性值差异越小，H(M)值越高，那么当每个对象的属性值都相等，H(M)取得最大值记为H_max(M)，此时聚类簇内达到了最大相似性。为确保聚类过程中遵循“等概率最大熵”原则，给出了具体的参数化过程：对于任一对象P，如果它与已知对象或者聚类簇相似时，根据信息熵的单调性可知，加入P的聚类簇信息熵与最大信息熵差异小；如果P与已知对象或者聚类簇差异性较大时，加入P的聚类簇信息熵与最大信息熵差异也越大，本文引入θ这个参数量化对象x与已知对象或者聚类簇之间的相似性，具体表达如下

$\theta = \frac{{H\left( {{M'}} \right)}}{{{H_{{\rm{max}}}}\left( {{M'}} \right)}}$

(18)

式中， $H\left( {M'} \right)$ 表示增加对象x后聚类簇的信息熵， ${H_{{\rm{max}}}}\left( {{M'}} \right)$ 表示增加对象x后聚类簇的最大信息熵。全局参数聚类实质上假设了空间实体分布的均匀性，有可能将局部相似的对象划入到噪声簇中或者其他簇中，导致聚类精度降低。θ是一个相对率的概念能够描述对象间的相对变化信息，可以同时满足属性空间分布不均匀和均匀两种情况。显然θ∈[0, 1]，θ值越大，对象P与已知对象或者聚类簇之间的相似性越大。

为了保证参数θ能够自动地适应不同的聚类需求，本文引入了PBM指数(Pakhira等，2004)来确定参数θ的取值。PBM指数作为一个相对评价指标能够满足紧密性与分离性的聚类准则，该指数越大则得到的聚类结果越可靠，其具体表示为

${\rm{PBM}} = {\left( {\frac{1}{{{N_c}}}\frac{{{E_1}}}{{{E_{{N_c}}}}}{D_{{N_c}}}} \right)^2}$

(19)

${E_{{N_c}}} = \mathop \sum \limits_{i = 1}^{{N_c}} {E_i},{E_i} = \mathop \sum \limits_{j = 1}^{{N_i}} \|{x_j} - {v_i}\|,{D_{{N_c}}} = \mathop \sum \limits_{i,j = 1}^{{N_c}} {\rm{max}}\left(\| {{v_i} - {v_j}}\| \right)$

(20)

式中，N_c表示簇的数量；N_i表示簇C_i中实体数量；v_i表示簇i的质心；E_i表示簇C_i的内部距离(簇内所有空间对象到其质心的距离之和)；E₁表示数据集只分为一类的聚类内部距离； $ {E_{{N_c}}} $ 表示数据集分为N_c个簇的聚类内部距离； $ {D_{{N_c}}} $ 表示空间簇间的分离度，其随着N_c增大而增大，最大值为数据集中最远两个簇的质心距离。

2.3.2 算法描述

本文提出的空间聚类方法主要包含两个主要步骤：

第一，构建空间邻近关系，对所有空间对象构建Delaunay三角网，对三角网施加边长约束，删除不一致边；

第二，基于信息熵度量的属性聚类，在空间邻近关系的基础上进行属性聚类，具体过程如下：

(1)计算每个对象的邻域属性熵，并对Delaunay三角网内所有对象的邻域属性熵值按照降序排列；

(2)选取邻域属性熵最大值作为初始聚类中心；

(3)按照广度优先遍历方法搜索该对象的直接邻居，将符合θ值的对象聚类合并，并标识为已聚类；

(4)循环步骤2和步骤3，依次搜寻该对象的间接邻居，向外不断扩散，将符合阈值的对象加入到簇中，直到没有新对象加入，一个聚类簇即形成；

(5)对于未被标识聚类的对象，迭代步骤2—4，遍历完所有对象，聚类结束，没有被标识到任何一类簇的对象视为噪声。

3 实例验证

为了验证本文方法的有效性与可行性，共设计了两组实验。实验1采用了一组模拟数据；实验2采用756个气象站点的海拔高度数据，并将本文方法与双重距离(DDBSC)聚类算法(李光强等，2008)和多约束聚类算法(刘启亮等，2011)进行比较。

3.1 模拟实验

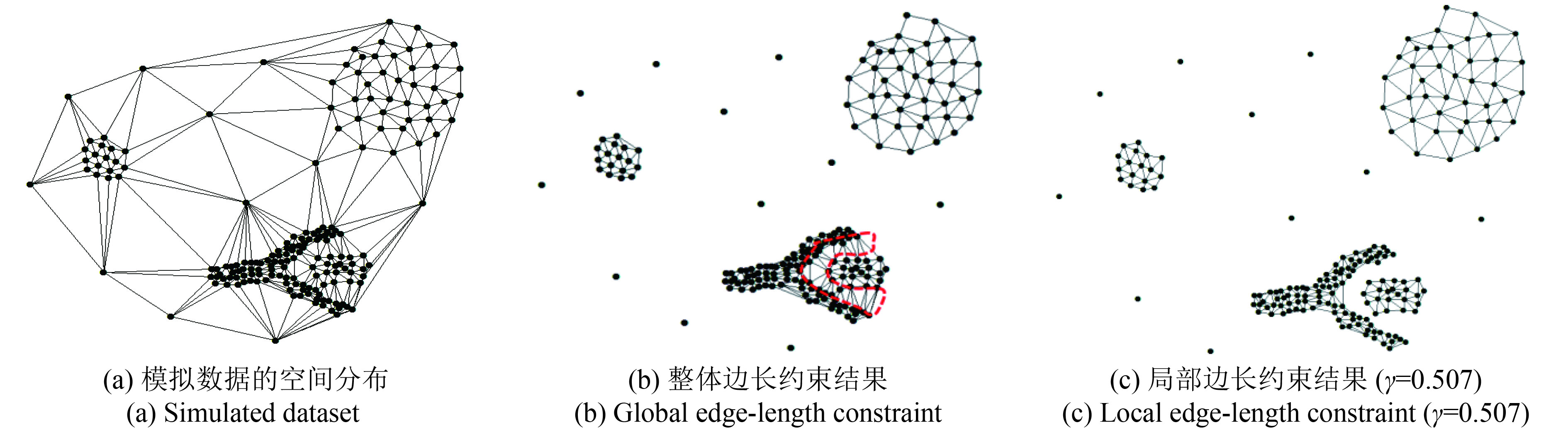
模拟数据是在Ester等人(1996)的2维模拟数据库的基础上进一步添加了1维专题属性，其中图2(a)是模拟数据的空间分布，模拟数据包含了空间密度不同、形状各异的空间簇，采用整体边长约束对三角网过滤，结果显示Delaunay三角网内还会存在簇间边问题(图2(b)红色虚线范围)，需要进一步施加局部边长约束获取最终的空间位置聚类结果(如图2(c)所示)。

图 2 模拟数据空间位置聚类过程

Fig. 2 Spatial clustering in simulated dataset

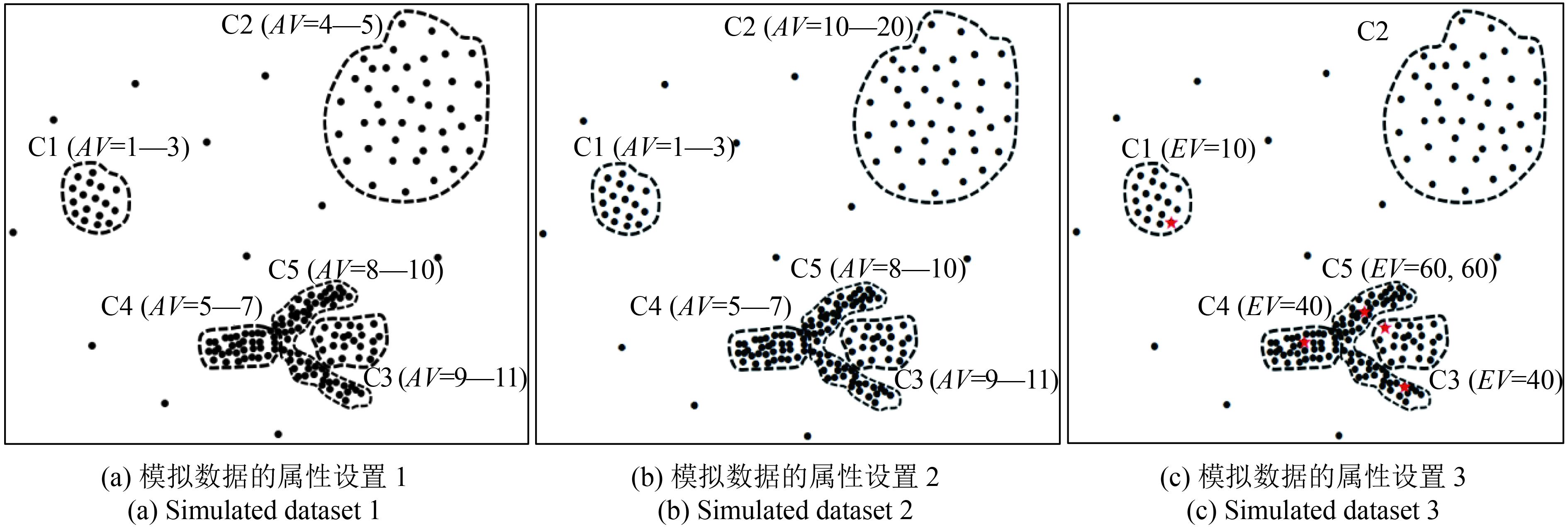
在图2(c)的聚类结果上对模拟数据添加1维属性值(图3)，AV表示属性的取值范围，为避免聚类结果出现偶然性，对每个数据点随机生成20次数值，取其均值作为最终的属性值，共预设了5个空间簇(C1—C5)。

图 3 模拟数据的属性设置

Fig. 3 Attribute settings of simulated dataset

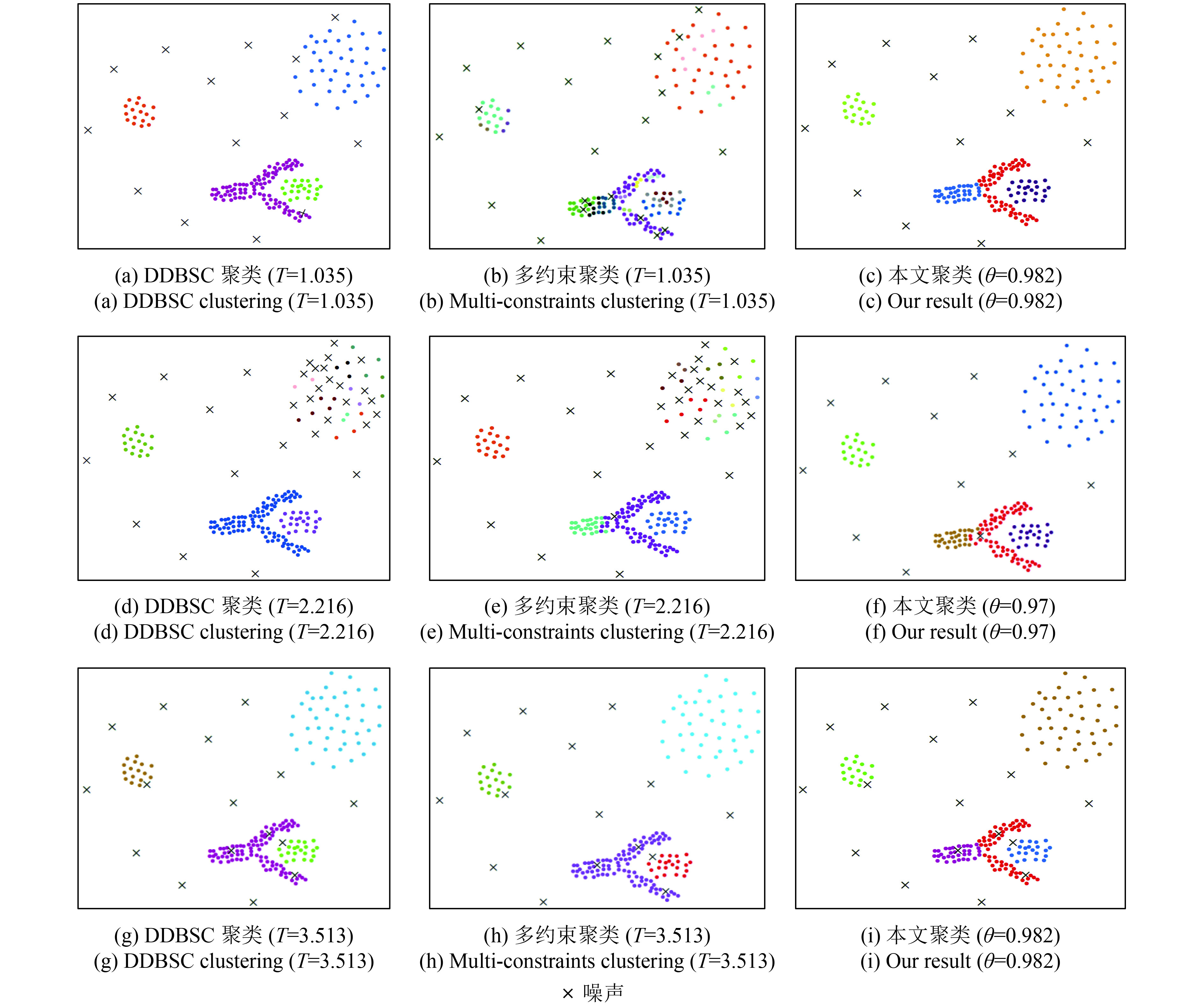
图3(a)中各个空间簇的属性上存在差异且属性空间分布不均(C2内部属性差异区别于其他簇)，采用多约束聚类方法、DDBSC算法和本文方法分别进行属性聚类，结果如图4所示。可以发现：(1)本文方法准确识别了预设的空间簇(图4(c))；(2)DDBSC聚类过程中采用的是二元相似关系，二元关系的传递性会掩盖属性空间分布的过渡性，其结果将C4和C5识别为一个空间簇(图4(a))；(3)多约束聚类方法虽然采用了一种类似K-means(MacQueen，1967)的相似性策略即单个实体与聚类集合间的相似性，但全局距离阈值难以满足属性分布不均匀的情况，可能会导致局部区域会产生多个空间簇(如图4(b)中C3被分解为3个)，整个聚类结果产生了17个空间簇。进一步探讨全局参数的局限性，将C2的属性范围扩大到10—20(图3(b))，聚类结果出现了另一种现象：DDBSC和多约束算法将C2内的多个实体误判为噪声(图4(d)—(e))，而本文方法能够准确识别预设的空间簇(图4(f))。

图 4 不同方法的聚类结果对比

Fig. 4 Comparison of the clustering results using different methods

图3(c)在图3(a)的基础上设置了5个异常值(★表示)来检验3类算法的敏感性，EV表示异常数值。从聚类结果看出3类方法都准备识别出异常值的位置，但DDBSC(图4(g))和多约束算法(图4(h))对异常值具有一定的敏感性，这导致C4和C5被误判为一个空间簇，掩盖了属性分布的趋势性，本文算法表现出一定的稳健性，能够识别出预设的空间簇(图4(i))。

3.2 实验二

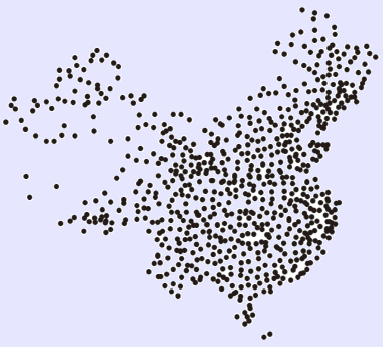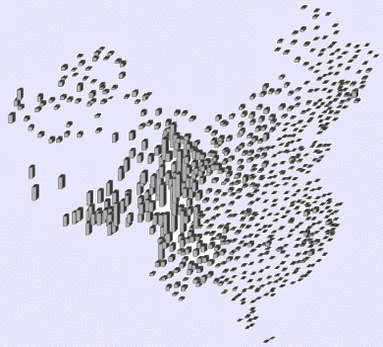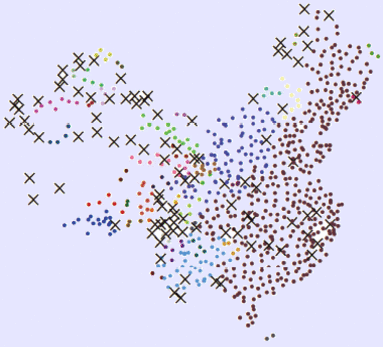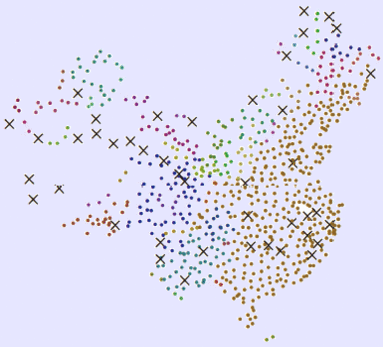
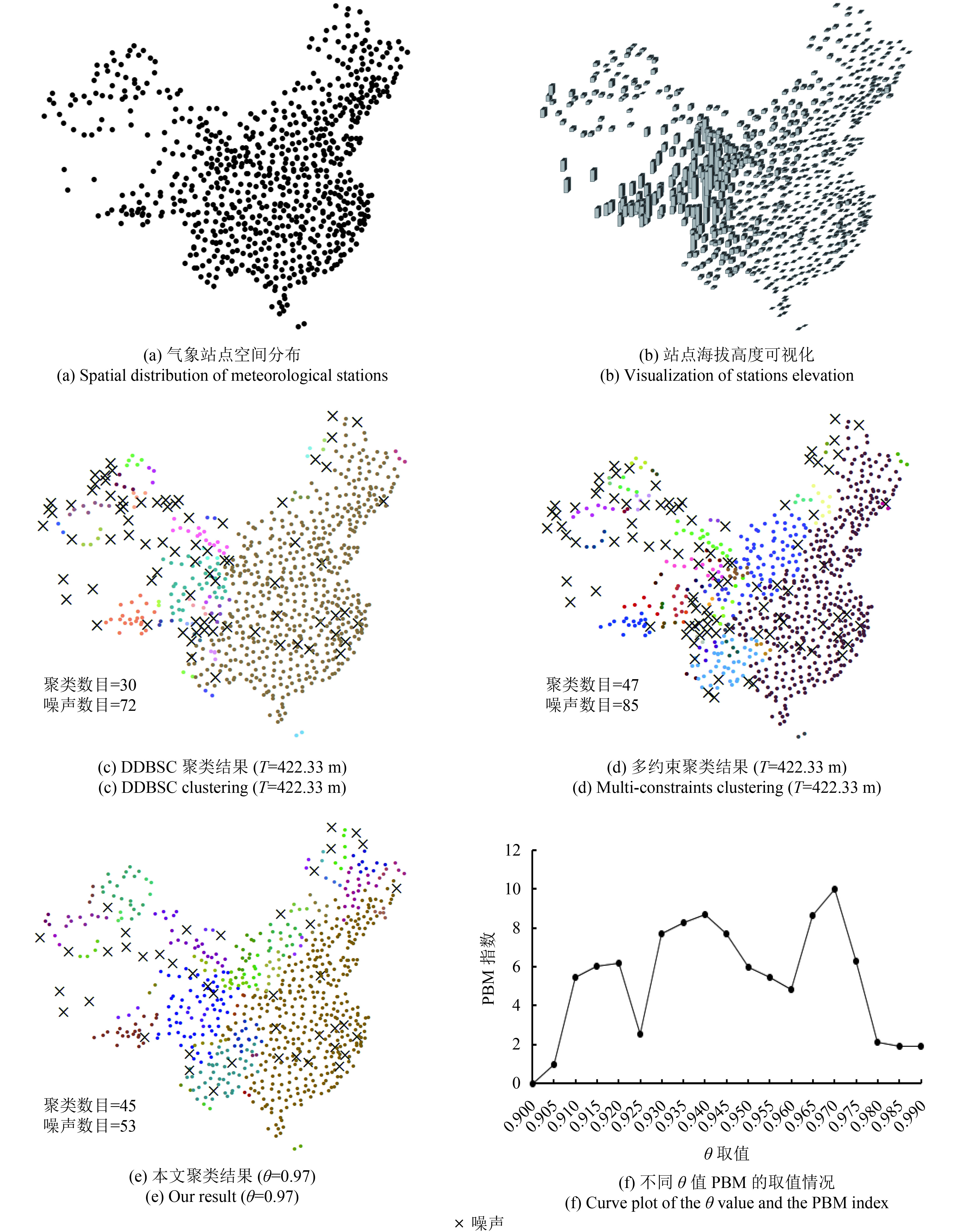
实际应用选用了中国大陆地区756个气象站点的海拔高度数据，图5(a)显示了气象站点的空间分布，图5(b)可视化表达了各气象站点的海拔高度，可见地势西高东低，呈阶梯状分布，海拔高度存在差异且空间分布不均。在空间位置聚类结果的基础上分别采用DDBSC方法、多约束方法与本文方法进行属性(海拔高度)聚类，结果如图5(c)—(e)所示。可以发现：(1)DDBSC聚类方法将东部平原地区海拔高度与内蒙古高原、云贵高原地区划分为一类，这明显是不合理的；(2)多约束聚类结果虽然在一定程度上能够识别平原地区与高原地区，但在地形的第二阶梯和第三阶梯产生了大量的噪声，如青藏高原地区、准噶尔盆地地区，难以从整体上反映中国地形的阶梯变化特征，主要还是因为全局阈值无法适应非均匀的情况；(3)本文方法能够较准确反映图5(b)的海拔分布趋势，包括识别一些明显的局部“热点”，如横断山脉一带的高海拔聚集区；图5(f)给出了不同θ值PBM的取值情况，当θ=0.90时PBM值开始变化，这是因为θ在区间(0, 0.90]内空间位置聚类结果即为属性聚类结果，PBM取值是一样的，当θ=0.97时PBM值最大，得到最终的聚类结果。

图 5 实际结果对比分析

Fig. 5 Comparison of the clustering results using different methods

4 结　语

空间聚类分析的作用不仅在于发现空间实体自然的空间集聚模式，还需结合空间实体的属性空间分布规律对复杂的地理现象进行解释。趋势性和非均匀性是属性空间分布的两个重要特性，已有空间聚类算法往往不能兼顾二者，从而导致空间聚类结果存在一定的误差，降低空间聚类的质量。为此，本文利用信息熵解决了以上两个关键问题。趋势性问题的解决体现在信息熵的多元相似性度量弥补了二元关系相似性度量中误差积累传播的缺陷，使聚类结果能够准确地反映地理要素在空间分布中的过渡性；而非均匀性问题的解决体现在信息熵中“等概率最大熵”原则为属性聚类过程提供了一种相对参考，由此设计的相对阈值可以实现属性非均匀性的空间聚类。通过模拟实验和实际数据验证，以及与相关空间聚类算法进行比较得出以下结论：(1)本文算法可以保证空间簇内实体不仅空间毗邻，且属性相近；(2)算法能发现任意形状的空间簇，且对异常值具有良好的稳健性；(3)算法具有自适应性，可以处理属性空间分布不均、邻近空间簇中实体间专题属性差异性较小等复杂情况下的聚类。

然而本文还存在若干问题：(1)本文对聚类结果的评价主要依赖先验知识，需研究空间聚类结果的有效性评价方法；(2)信息熵的计算最开始并不是针对地理数据的，而地理数据的复杂多样性应该在信息熵聚类中得到体现，后期还需拓展应用范围尤其是多个属性数据共同影响的地理现象；(3)在实际应用中不同属性的尺度度量值(定名、等级、比率、差异量)各异，如何计算多维属性特征的信息熵同样是需要考虑的问题。

参考文献(References)

Ahuja N. 1982. Dot pattern processing using Voronoineighborhoods. IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-4 (3): 336–343. [DOI: 10.1109/TPAMI.1982.4767255]

Ai T H and van Oosterom P. 2002. GAP-Tree extensions based on skeletons//Richardson DE and van Oosterom P, eds.Advances in Spatial Data Handling. Berlin Heidelberg: Springer: 501–513 [DOI: 10.1007/978-3-642-56094-1_37]

Bai X, Zhao Y B and Luo S W. 2012. Normalized joint mutual information measure for ground truth based segmentation evaluation. IEICE Transactions on Information and Systems, E95.D (10): 2581–2584. [DOI: 10.1587/transinf.E95.D.2581]

Birant D and Kut A. 2007. ST-DBSCAN: an algorithm for clustering spatial-temporal data. Data and Knowledge Engineering, 60 (1): 208–221. [DOI: 10.1016/j.datak.2006.01.013]

Deng M, Liu Q L, Li G Q and Cheng T. 2010. Field-theory based spatial clustering method. Journal of Remote Sensing, 14 (4): 694–709. [DOI: 10.11834/jrs.20100406] ( 邓敏, 刘启亮, 李光强, 程涛. 2010. 基于场论的空间聚类算法. 遥感学报, 14 (4): 694–709. [DOI: 10.11834/jrs.20100406] )

Deng M, Liu Q L, Li G Q and Huang J B. 2011.Spatial Clustering Analysis and Its Application. Beijing: Science Press: 2–5 (邓敏, 刘启亮, 李光强, 黄健柏. 2011. 空间聚类分析及应用. 北京: 科学出版社: 2–5)

Eldershaw C and Hegland M. 1997. Cluster analysis using triangulation//NoyeB J, TeubnerM D and GillA W, eds.Computational Techniques and Applications: CTAC97. Singapore: World Scientific: 201–208

Ester M, Kriegel H P, Sander J and Xu X W. 1996. A density-based algorithm for discovering clusters in large spatial databases with noise//Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining (KDD-96). Menlo Park, CA: AAAI: 226–231

Estivill-Castro V and Lee I. 2002. Argument free clustering for large spatial point-data sets via boundary extraction from Delaunay Diagram. Computers, Environment and Urban Systems, 26 (4): 315–334. [DOI: 10.1016/S0198-9715(01)00044-8]

Guo X C, Xi X T, Fan X L and Han X. 2015. Fuzzy C-Means clustering algorithm based on semi-supervised learning. Journal of Jilin University (Science Edition), 53 (4): 705–709. [DOI: 10.13413/j.cnki.jdxblxb.2015.04.21] ( 郭新辰, 郗仙田, 樊秀玲, 韩啸. 2015. 基于半监督的模糊C-均值聚类算法. 吉林大学学报(理学版), 53 (4): 705–709. [DOI: 10.13413/j.cnki.jdxblxb.2015.04.21] )

He H, Hu D and Yu X C. 2016. Land cover classification based on adaptive interval type-2 fuzzy clustering. Chinese Journal of Geophysics, 59 (6): 1983–1993. [DOI: 10.6038/cjg20160605] ( 贺辉, 胡丹, 余先川. 2016. 基于自适应区间二型模糊聚类的遥感土地覆盖自动分类. 地球物理学报, 59 (6): 1983–1993. [DOI: 10.6038/cjg20160605] )

Hong S Y and O’Sullivan D. 2012. Detecting ethnic residential clusters using an optimisation clustering method. International Journal of Geographical Information Science, 26 (8): 1457–1477. [DOI: 10.1080/13658816.2011.637045]

Jiao L M, Hong X F and Liu Y L. 2011. Self-organizing spatial clustering under spatial and attribute constraints. Geomatics and Information Science of Wuhan University, 36 (7): 862–866. [DOI: 10.13203/j.whugis2011.07.025] ( 焦利民, 洪晓峰, 刘耀林. 2011. 空间和属性双重约束下的自组织空间聚类研究. 武汉大学学报(信息科学版), 36 (7): 862–866. [DOI: 10.13203/j.whugis2011.07.025] )

Jiao L M, Zhang X and Mao L F. 2015. Self-organizing dual spatial clustering algorithm and its application in the analysis of urban sprawl structure. Journal of Geo-Information Science, 17 (6): 638–643. [DOI: 10.3724/SP.J.1047.2015.00638] ( 焦利民, 张欣, 毛立凡. 2015. 自组织双重空间聚类算法的城市扩张结构分析应用. 地球信息科学学报, 17 (6): 638–643. [DOI: 10.3724/SP.J.1047.2015.00638] )

Kang I S, Kim T W and Li K J. 1997. A spatial data miningmethod by Delaunay triangulation//Proceedingsof the 5th ACM International Workshop on ADVANCES in Geographic Information Systems. Las Vegas, Nevada, USA: ACM: 35–39 [DOI: 10.1145/267825.267836]

Li G Q, Deng M, Cheng T and Zhu J J. 2008. A dual distance based spatial clustering method. ActaGeodaetica et CartographicaSinica, 37 (4): 482–488. [DOI: 10.3321/j.issn:1001-1595.2008.04.014] ( 李光强, 邓敏, 程涛, 朱建军. 2008. 一种基于双重距离的空间聚类方法. 测绘学报, 37 (4): 482–488. [DOI: 10.3321/j.issn:1001-1595.2008.04.014] )

Li H F, Zhang K S and Jiang T. 2004. Minimum entropy clustering and applications to gene expression analysis//Proceedings of the 2004 IEEE Computational Systems Bioinformatics Conference. Stanford, CA, USA: IEEE: 142–151 [DOI:10.1109/CSB.2004.1332427]

Li K and Cao Z. 2016. A fuzzy clustering algorithm with generalized entropy based on neural network. Acta Electronica Sinica, 44 (8): 1881–1886. [DOI: 10.3969/j.issn.0372-2112.2016.08.016] ( 李凯, 曹喆. 2016. 一种基于神经网络的广义熵模糊聚类算法. 电子学报, 44 (8): 1881–1886. [DOI: 10.3969/j.issn.0372-2112.2016.08.016] )

Lin C R, Liu K H and Chen M S. 2005. Dual clustering: integrating data clustering over optimization and constraint domains. IEEE Transactions on Knowledge and Data Engineering, 17 (5): 628–637. [DOI: 10.1109/TKDE.2005.75]

Liu D and Sourina O. 2004. Free-parameters clustering of spatial data with non-uniform density//Proceedings of the2004 IEEE Conference on Cybernetics and Intelligent Systems. Singapore, Singapore:IEEE, 1 : 387–392. [DOI: 10.1109/ICCIS.2004.1460446]

Liu Q L, Deng M, Shi Y and Peng D L. 2011. A novel spatial clustering method based on multi-constraints. ActaGeodaetica et CartographicaSinica, 40 (4): 509–516. ( 刘启亮, 邓敏, 石岩, 彭东亮. 2011. 一种基于多约束的空间聚类方法. 测绘学报, 40 (4): 509–516. )

Liu Q L, Deng M, Shi Y and Wang J Q. 2012. A density-based spatial clustering algorithm considering both spatial proximity and attribute similarity. Computers and Geosciences, 46 : 296–309. [DOI: 10.1016/j.cageo.2011.12.017]

MacQueen J. 1967. Some methods for classification and analysis of multivariate observations//Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability. Berkeley, Calif: University of California Press, 1 : 281–297.

Mundur P, Rao Y and Yesha Y. 2006. Keyframe-based video summarization using Delaunay clustering. International Journal on Digital Libraries, 6 (2): 219–232. [DOI: 10.1007/s00799-005-0129-9]

Pakhira M K, Bandyopadlhyay S and Maulik U. 2004. Validity index for crisp and fuzzy clusters. Pattern Recognition, 37 (3): 487–501. [DOI: 10.1016/j.patcog.2003.06.005]

Sander J, Ester M, Kriegel H P and Xu X W. 1998. Density-based clustering in spatial databases: the algorithm gdbscan and its applications. Data Mining and Knowledge Discovery, 2 (2): 169–194. [DOI: 10.1023/A:1009745219419]

Shannon C E. 1948. A mathematical theory of communication. The Bell System Technical Journal, 27 (3): 379–423. [DOI: 10.1002/bltj.1948.27.issue-3]

Shi Y, Liu Q L, Deng M and Lin X M. 2012. A hybrid spatial clustering method based on graph theory and spatial density. Geomatics and Information Science of Wuhan University, 37 (11): 1276–1280. ( 石岩, 刘启亮, 邓敏, 林雪梅. 2012. 融合图论与密度思想的混合空间聚类方法. 武汉大学学报(信息科学版), 37 (11): 1276–1280. )

Shi Y, Deng M, Liu Q L and Tang J B. 2013. A multi-scale regionalization method for sea surface temperature based on a scale-space clustering. Geomatics and Information Science of Wuhan University, 38 (12): 1484–1489. [DOI: 10.13203/j.whugis2013.12.025] ( 石岩, 邓敏, 刘启亮, 唐建波. 2013. 融合尺度空间聚类思想的海温多尺度分区方法. 武汉大学学报(信息科学版), 38 (12): 1484–1489. [DOI: 10.13203/j.whugis2013.12.025] )

Slonim N, Atwal G S, Tkačik G and Bialek W. 2005. Information-based clustering. Proceedings of the National Academy of Sciences of the United States of America, 102 (51): 18297–18302. [DOI: 10.1073/pnas.0507432102]

Wu F, Qian H Z, Deng H Y and Wang H L. 2008.Intelligent Processing of Spatial Information for Map Generalization. Beijing: Science Press: 3–6 (武芳, 钱海忠, 邓红艳, 王辉连. 2008. 面向地图自动综合的空间信息智能处理. 北京: 科学出版社: 3–6)

Yan W M and Wu W M. 2007.Data Structure (C Language Edition). Beijing: Tsinghua University Press (严蔚敏, 吴伟民. 2007. 数据结构(C语言版). 北京: 清华大学出版社)

Zhang J G and Singh V P. 2012. Information Entropy: Theory and Application. Beijing: China Water Power Press (张继国, Singh V P. 2012. 信息熵-理论与应用. 北京: 中国水利水电出版社)

Zhang T, Ramakrishnan R and Livny M. 1996. BIRCH: an efficient data clustering method for very large databases. ACM SIGMOD Record, 25 (2): 103–114. [DOI: 10.1145/235968.233324]

Zhong C M, Miao D Q and Wang R Z. 2010. A graph-theoretical clustering method based on two rounds of minimum spanning trees. Pattern Recognition, 43 (3): 752–766. [DOI: 10.1016/j.patcog.2009.07.010]

Zhou Y L. 2011. Grid-Based and Information Entropy-Based Clustering Algorithm.Changsha: Hunan University (周悦来. 2011. 基于网格和信息熵的聚类算法. 长沙: 湖南大学)

摘要

关键词