The accurate calibration of space-based sensors is essential for interpreting the physical characteristics of observed objects. The accuracy demanded from data presents a challenge to the long-term stability of calibration. Onboard calibration systems for sensors are practically designed to achieve the highest stability; however, drifts of 1% to several percent over the lifetime of a sensor indicate limitations (Kieffer, et al., 1996).

The reflectance properties of the Moon are stable at the order of 10^–8 yr^–1 (Kieffer, et al., 2005). The intrinsic stability of the photometric properties of the lunar surface suggests that in-flight calibration can use the Moon as a long-term reference source (Kieffer, et al., 1998; 2003). Researchers at the U.S. Geological Survey have established the Moon as a viable calibration source in the visible and near-infrared spectral ranges (Buratti, et al., 2011; Stone, et al., 2006).

Lunar calibration and modeling are considerably less accurate when λ > 2.5 μm. Pugacheva, et al. (2001) derived an analytical expression that provided brightness temperature variations at any point on the Moon in the infrared (10—12 μm) spectral range as functions of albedo, phase angle, and the distance between the Sun and the Moon. Pugacheva, et al. (2001) used the model (Pugacheva, et al., 1999) to calibrate mid-infrared measurements from a geosynchronous satellite against the Moon. Extending this model to other infrared wavelengths is a challenging task because the brightness temperature of a specific location on the Moon depends on the wavelength. Thermal radiation is not only the function of surface emissivity but also of surface temperature. A sophisticated thermal model is required to predict the disk-resolved temperature of the Moon (Price, 2004).

This study aims to present a real-time model of lunar surface temperature, which may be of interest in the radiometric calibration of space-based sensors. Furthermore, lunar surface temperature is an essential parameter for exploring the Moon and a necessary boundary condition for studying lunar thermal evolution (Li, et al., 2010).

A physical model of lunar surface temperature is based on heat conduction theory. Racca (1995) developed a Moon surface temperature model by solving the heat conduction equation with the thermal-physical parameters of lunar regolith samples. His model aims to describe the lunar surface illuminated by the Sun at steady-state conditions, i.e., allowing sufficient time for the transient to vanish.

The following expression defines the Moon surface temperature model developed by Racca (1995)

$\small{\begin{array}{l}T\left({\phi, \psi } \right) = \\{\left[ {\displaystyle\frac{{\left({1 - \bar A} \right)}}{\varepsilon }\cos \phi \cos \psi \displaystyle\frac{{{E_{\rm{sun}}}}}{\sigma } + \displaystyle\frac{M}{\sigma }} \right]^{1/4}}\end{array}}$

(1)

where ϕ and ψ denote the latitude and longitude, respectively, of a given lunar location computed from a subsolar point; $\bar A$ is the single-scattering albedo (approximately set to 0.127); $\varepsilon $ is the infrared surface emissivity (approximately set to 0.97); $\sigma $ is the Stefan-Boltzmann constant 5.67×10^–8 W·m^–2·K^–4; M is a subsurface cooling flux 6 W·m^–2; and E_sun is the solar irradiance in W·m^–2.

The Sun is the sole energy source of the Moon. The lunar surface temperature is correlated with variations in the effective solar irradiance, which is a normal component of solar irradiance.

Most lunar surface temperature models, including Eq. (1), regard solar irradiance as invariable, and a variation in the effective solar irradiance is simply the cosine function of the solar incidence angle (Lawson, et al., 2000) or the selenographic coordinates of a location (Racca, 1995). The solar constant (integrated solar irradiance at 1 AU) varies with distance. When perihelion and aphelion distances are considered, the solar constant varies from 1418 W·m^–2 to 1326 W·m^–2, and a temperature variation of ±3 K is found at subsolar point ( Racca, 1995). Furthermore, when the trajectory of the Sun-Earth-Moon system is considered according to Kepler’s law and the rotation and revolution of the Moon, the relationship between the effective solar irradiance and solar irradiance is too simple and inaccurate to describe as a cosine function (Li, et al., 2008).

To improve the accuracy of the lunar surface temperature model, the effective solar irradiance should be described based on planetary theory VSOP82 and Chapront ELP-2000/82 lunar theory (Meeus, 1991).

The effective solar irradiance E_eff can be obtained from

$\small{{E_{\rm{eff}}} = {E_{\rm{sun}}} \cdot \cos i }$

(2)

where E_sun is the solar irradiance in W·m^–2, and i is the solar zenith angle in degree.

As shown in Eq. (2), the effective solar irradiance is related to solar irradiance and the solar zenith angle. To accurately calculate the effective solar irradiance, solar irradiance and the solar zenith angle should be analyzed comprehensively.

First, solar irradiance E_sun is calculated using the following formula

$\small{{E_{\rm{sun}}} = {S_0} \cdot R_{\rm{sm}}^{ - 2}} $

(3)

where S₀ is the solar constant, and R_sm is the distance from the Moon to the Sun in AU.

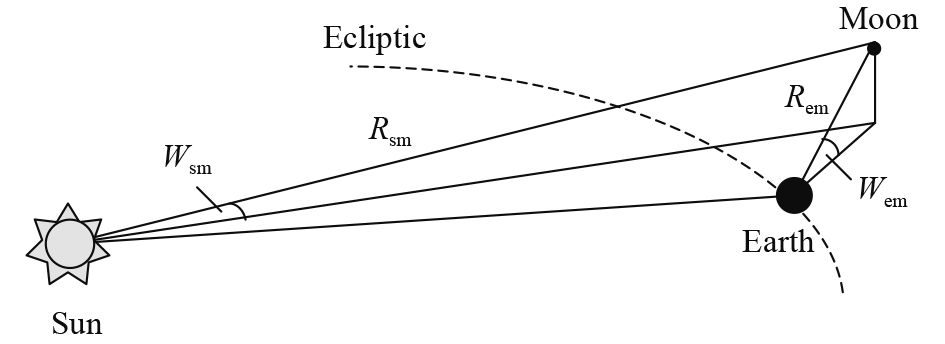
The geometric relationship among the Sun, the Earth, and the Moon is shown in Fig. 1. The distance R_sm is calculated by

$\small{{R_{\rm{sm}}} = {R_{\rm{em}}} \cdot \frac{{\sin {W_{\rm{em}}}}}{{\sin {W_{\rm{sm}}}}}}$

(4)

where R_em is the distance from the Earth to the Moon in AU, W_em is the geocentric latitude of the Moon, and W_sm is the ecliptic latitude of the Moon.

A relationship exists between W_em and W_sm, which can be expressed as

$\small{{W_{\rm{sm}}} = {W_{\rm{em}}} \cdot \frac{{{R_{\rm{em}}}}}{{{R_{\rm{se}}}}}}$

(5)

where R_se is the distance from the Sun to the Earth in AU. When Eq. (3) is substituted into Eq. (5), solar irradiance is obtained from

$\small{{E_{\rm{sun}}} = \frac{{{S_0}{{\sin }^2}\left( {{W_{\rm{em}}}{R_{\rm{em}}}/{R_{\rm{se}}}} \right)}}{{R_{\rm{em}}^2{{\sin }^2}{W_{\rm{em}}}}}}$

(6)

Second, the solar zenith angle i is determined from other known angles as below

$\small{i = {A_i} + {B_i}}$

(7)

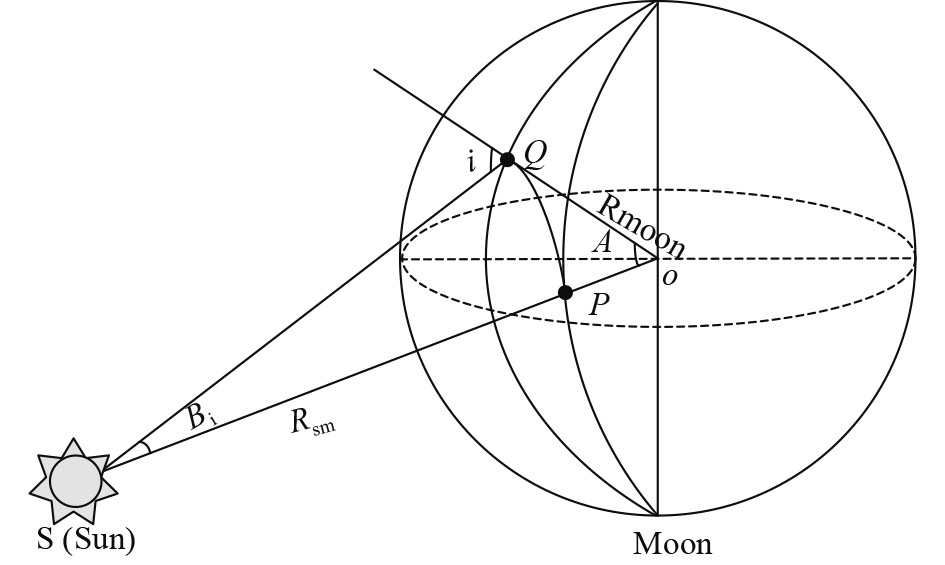
The relationship among angles i, A_i, and B_i (in degrees) is shown in Fig. 2. P and Q respectively denote the point directly under the Sun and the point of observation. J_p and W_p are the selenographic longitude and latitude of P, respectively. J_q and W_q are the selenographic longitude and latitude of Q, respectively.

On the basis of spherical trigonometry, the cosine of A_i is given by

$\small{\begin{aligned}\cos {A_i} = & \sin {W_q}\sin {W_p} +\\ &{ \cos {W_q}\cos {W_p}\cos \left( {{J_q} - {J_p}} \right)}\end{aligned}}$

(8)

Angle PQS between arc PQ and distance QS is obtained from

$\small{\angle PQS = {\tan ^{ - 1}}\left( {\frac{{\cos {A_i} - \displaystyle\frac{{{R_{moon}}}}{{{R_{moon}} + {W_{sm}}}}}}{{\sin {A_i}}}} \right)}$

(9)

where R_moon is the radius of the Moon in AU.

In triangle SQO, angle B_i is given by

$\small{\begin{aligned}{B_i} = &{180^ \circ } - {A_i} - \left( {{{90}^ \circ } + \angle PQS} \right)= \\&{ {{90}^ \circ } - ({A_i} + \angle PQS)}\end{aligned}}$

(10)

The solar zenith angle i can be calculated as

$\small{i = {A_i} + {B_i} = {90^ \circ } - \angle PQS}$

(11)

From Eq. (6) and Eq. (11), the effective solar irradiance is

$\small{\begin{aligned}{E_{\rm{eff}}} = & {E_{\rm{sun}}} \cdot \cos i =\\ &{ \displaystyle\frac{{{S_0}{{\sin }^2}\left( {{W_{\rm{em}}}{R_{\rm{em}}}/{R_{\rm{se}}}} \right)}}{{R_{\rm{em}}^2{{\sin }^2}{W_{\rm{em}}}}} \cdot \cos \left( {{{90}^ \circ } - \angle PQS} \right)}=\\ &{ \displaystyle\frac{{{S_0}{{\sin }^2}\left( {{W_{\rm{em}}}{R_{\rm{em}}}/{R_{\rm{se}}}} \right)}}{{R_{\rm{em}}^2{{\sin }^2}{W_{\rm{em}}}}} \cdot \cos }\angle PQS =\\ & \displaystyle \frac{{{S_0}{{\sin }^2}\left( {{W_{\rm{em}}}{R_{\rm{em}}}/{R_{\rm{se}}}} \right)}}{{R_{\rm{em}}^2{{\sin }^2}{W_{\rm{em}}}}} \cdot\\ & \cos \left[ {{{\tan }^{ - 1}}\left( { \displaystyle\frac{{\cos {A_i} - \displaystyle\frac{{{R_{\rm{moon}}}}}{{{R_{\rm{moon}}} + {W_{\rm{sm}}}}}}}{{\sin {A_i}}}} \right)} \right]\end{aligned}}$

(12)

The effective solar irradiance is obtained from Eq. (12). Parameters in Eq. (12), such as W_em, R_em, and R_se, can be calculated from astronomical algorithms for a given instant (dynamical time) (Meeus, 1991), which is beyond the scope of this study.

The surface temperature model of the Moon, which substitutes the effective solar irradiance in Eq. (12) into Eq. (1), is defined as below

$\small{\begin{aligned}T\left( {{J_q},{W_q}} \right) = & {\left[ {\displaystyle\frac{{\left( {1 - \bar A} \right)}}{\varepsilon }\displaystyle\frac{{{E_{\rm{eff}}}}}{\sigma } + \displaystyle\frac{M}{\sigma }} \right]^{1/4}} = \\ &{{{\left[ {\displaystyle\frac{{\left( {1 - \bar A} \right)}}{\varepsilon }\displaystyle\frac{{{E_{\rm{sun}}} \cdot \cos i}}{\sigma } + \displaystyle\frac{M}{\sigma }} \right]}^{1/4}}}\end{aligned}}$

(13)

where T is the temperature of the observation point for a given instant (dynamical time); and J_q and W_q are the selenographic longitude and latitude of the observation point, respectively.

Through Eq. (13), Eq. (12), and Eq. (8), the surface temperature of the Moon can be obtained for a given instant (dynamical time). This section will present several simulation results of the real-time model of lunar surface temperature.

Fig. 3 shows the diurnal variation of solar irradiance at point (0°E, 0°N) in 2015. The maximum and minimum solar irradiance are 1415.911 W m^–2 and 1321.065 W m^–2, respectively. The largest solar irradiance difference is approximately 100 W m^–2 between the perihelion and aphelion distances. Furthermore, the curve is not smooth in Fig. 3, where fluctuations are caused by the periodic revolution of the Moon around the Earth.

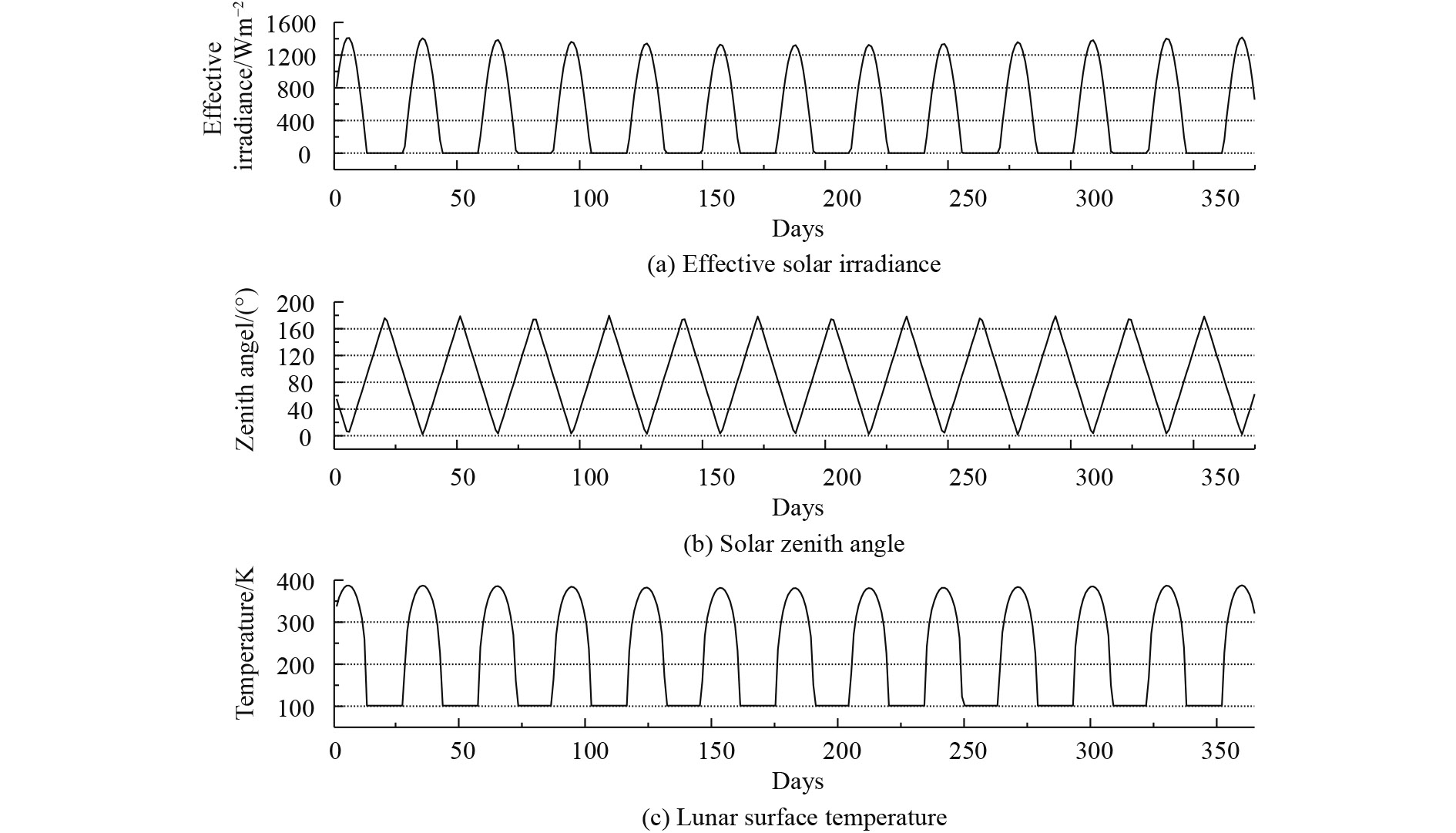
Fig. 4 and Fig. 5 show the diurnal variation in lunar surface temperature with the effective solar irradiance and the solar zenith angle at points (0°E, 0°N) and (0°E, 60°N), respectively. The maximum solar zenith angle at the determined point is nearly stable because the variation range of the subsolar selenographic latitude is only ±1.54242°, which is caused by the inclination of the mean lunar equator to the ecliptic latitude, that is, 1.54242°. The variation in the maximum lunar surface temperature at the determined point corresponds to the effective solar irradiance, which varies with the distance from the Earth to the Sun. Variation is more apparent at a higher latitude location; for example, it is approximately 6 K at 0°N and 12 K at 60°N.

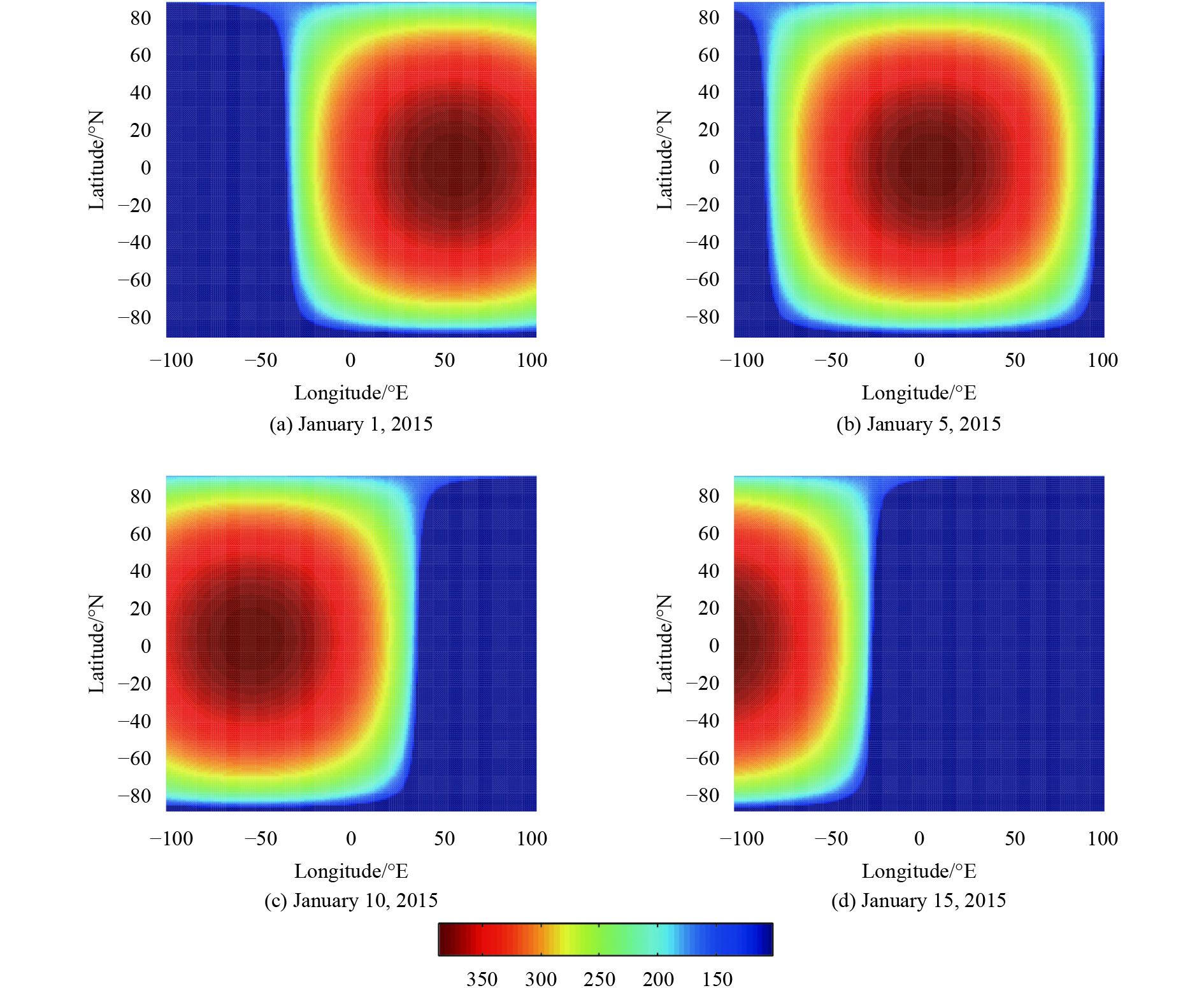
Fig. 6 presents the temperature distribution on the lunar surface at different times. In general, the same hemisphere of the Moon is always turned toward the Earth and only the illuminated fraction of the Moon’s disk is visible. The illuminated fraction changes due to the variation angle of the Sun as the Moon orbits the Earth. The navy blue part in Fig. 6 is not illuminated by the Sun. The subsolar selenographic latitude is nearly stable, whereas the longitude varies with time. Therefore, the temperature distribution along the longitude is asymmetrical, as shown in Fig. 6.

FY-2G is a Chinese geostationary meteorological satellite launched in 2014. It carries a visible and infrared spin scan radiometer. The FY-2G imager periodically captures images of the Moon in the corners and margins of a rectangular field of interest. Fig. 7 shows the infrared image of the Earth’s disk provided by FY-2G, with the Moon appearing at the top left corner of the image. Through the analysis of the stray light outside the Earth’s disk, lunar measurements will be compared with the lunar surface temperature model when the Moon appears at the bottom right corner outside of the Earth’s disk to reduce the stray light effect (Guo, et al., 2007).

Fig. 8 presents the results from the lunar surface temperature model and the lunar infrared images provided by FY-2G at different times. Various lines correspond to different times. The results from the temperature model are in the first column, whereas the measurements provided by FY-2G are in the second column.

When the relative motion of the Moon and FY-2G is considered, including the moon phase and libration shown in Fig. 9, the lunar images in the field of view of FY-2G should be accurately reprojected to the selenographic coordinate system to compare with the results from the lunar temperature model. The reprojected lunar images are presented in the third column of Fig. 8.

Fig. 9 shows the diurnal variation of the librations in longitude and latitude in 2015. The mean center of the Moon’s apparent disk is the origin of the system of selenographic coordinates on the surface of the Moon. The displacement at any time of the mean center of the disk from the apparent center represents the libration amount and is measured using the selenographic coordinates of the apparent center of the disk at that time (Meeus, 1991).

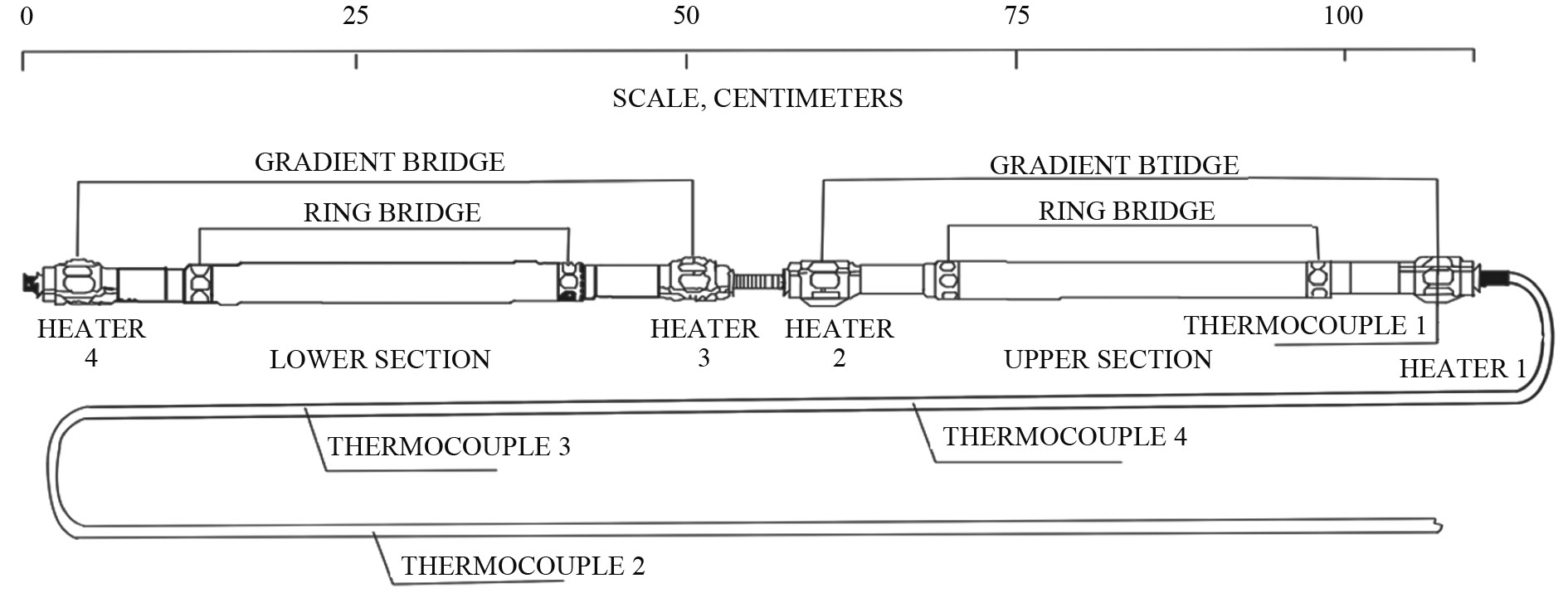
Apollo 15 was the first in a series of missions designed to explore the Moon over longer periods, greater ranges, and using more instruments for scientific data acquisition (Huang, 2008). The heat flow experiment at the Apollo 15 landing site is an important component of the Apollo Lunar Surface Experiments Package (ALSEP). The essential measurements for determining heat flow were made by two slender temperature-sensing probes placed into predrilled holes in the regolith and spaced approximately 10 m apart. Four thermocouple junctions in the cables connected each probe to the electronic unit (Langseth, et al., 1972).

Lunar surface temperatures were provided from five of the eight thermocouples in the probe cables, which were immediately above or nearly on the lunar surface (Apollo 15 mission report). Fig. 10 shows the actual emplacements of two probes and five thermocouples, which provide lunar surface temperatures. Fig. 11 shows the schematic of the heat flow probe. As shown in the figure, lunar surface temperatures were provided by Thermocouples 1 and 2 on Probe 1 and Thermocouples 1, 2, and 3 on Probe 2.

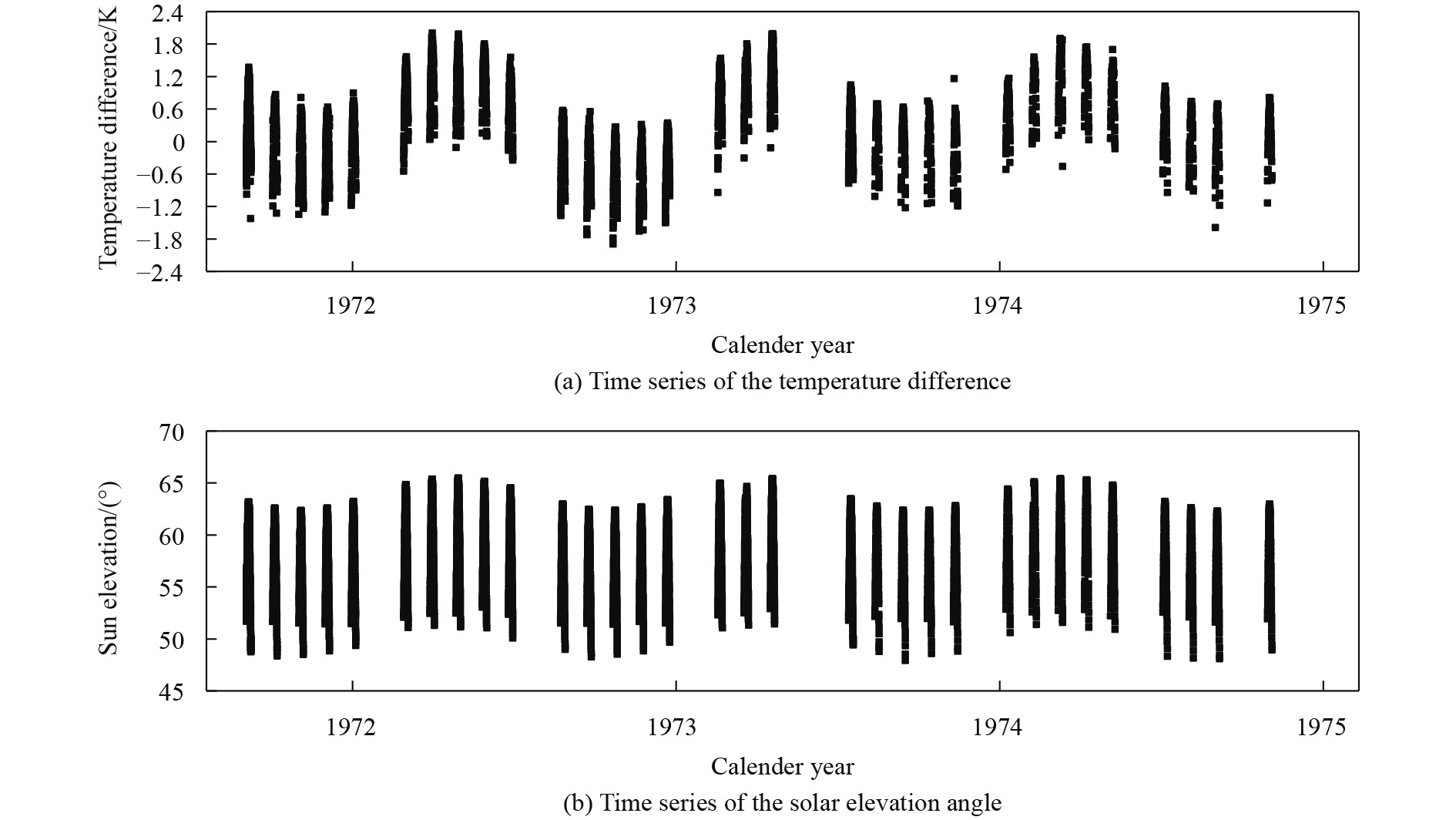
Five lunar surface temperature time series from the landing site of the Apollo 15 mission are shown in Fig. 12. The time series is part of the historical data archive PSPG-00093 of the U.S. National Space Science Data Center. The time series contains all the data from the time the Apollo 15 heat flow experiment started until its end in 1974 (description of Apollo heat flow experiment data tapes). The measured temperatures differ from one another probably due to specific settings, such as sensor orientation, detailed configuration of the regolith surface, and actual emplacements in the probe cables. All the aforementioned factors can affect the radiation imposed on a specific sensor, and consequently, the temperature of the sensor (Huang, 2008).

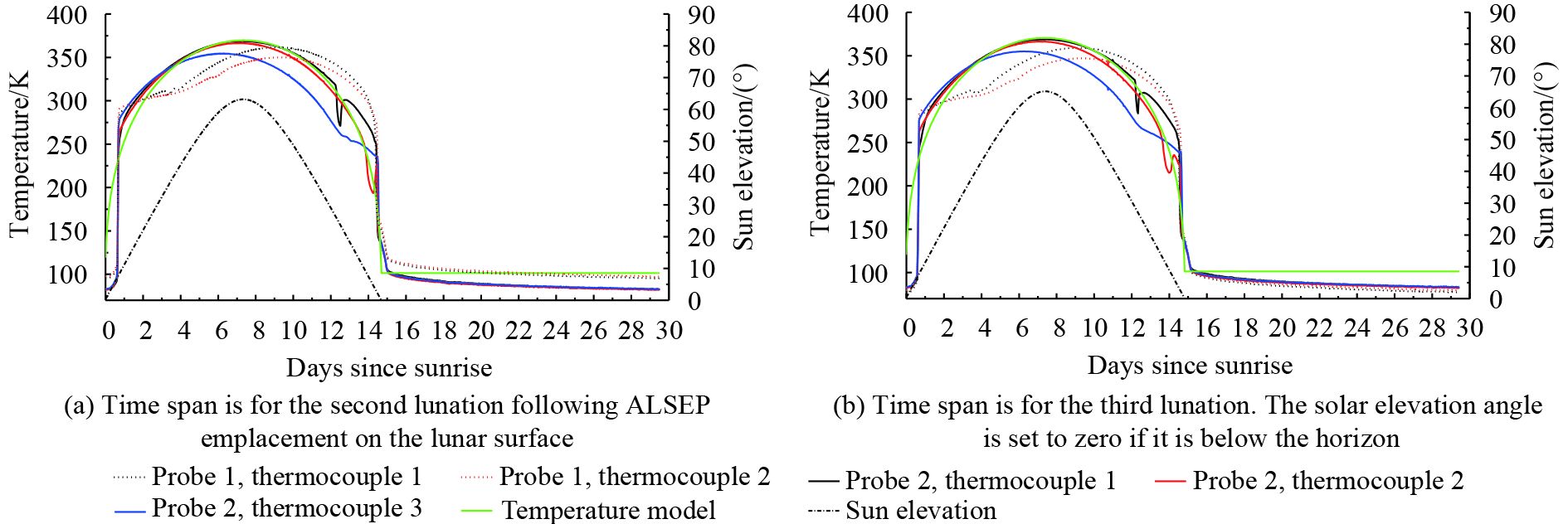
A sample temperature series obtained by the surface thermocouples with the elevation angle of the Sun above the surface is shown in Fig. 13. Several features are notable. First, the maximum temperature readings do not always correspond to the time of the solar zenith. This result can be attributed to the fact that the temperature of the thermocouples depends on the orientation of the cables where they are embedded. Second, irregularities are observed at specific time intervals that generally correspond to the shadowing of the sensor. Third, “bumps” in the temperature series after sunset correspond to solar radiation reflected off the surrounding terrain (Wieczorek, et al., 2006).

The response temperatures of Model (13) at the landing site of the Apollo 15 mission with an albedo of 0.148 and an infrared emissivity of 0.97, which correspond to the second and third lunations following ALSEP emplacement on the lunar surface, are plotted in the same graph with green lines. Despite irregularities and bumps, the calculated temperatures fit well with the measured data from Thermocouple 1 of Probe 2 when the solar elevation angle is greater than zero. From the analysis of the locations of the five thermocouples shown in Fig. 10, the first thermocouple on Probe 2 is closest to the lunar surface, and thus, its measured temperatures should approach lunar surface temperatures.

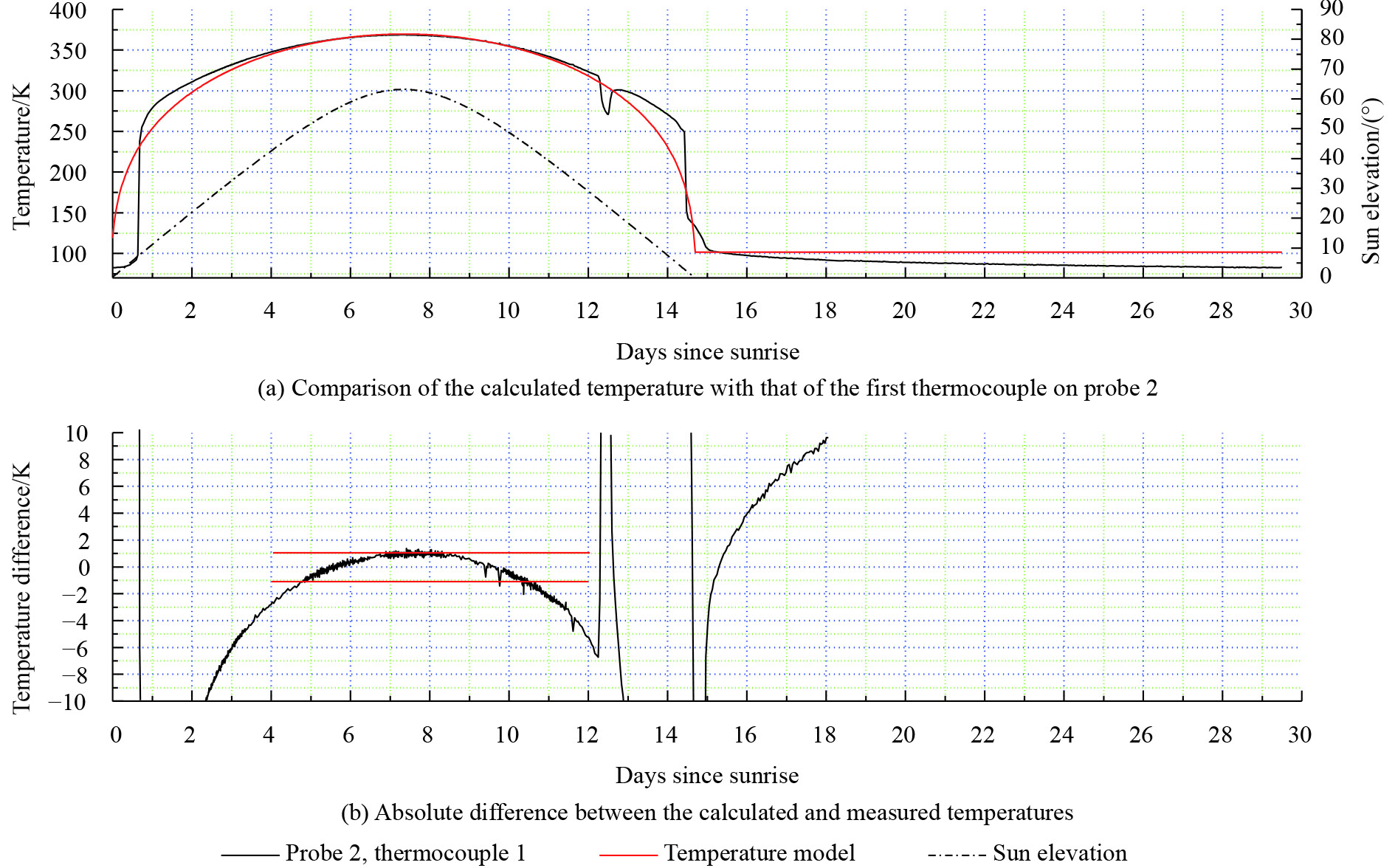
The comparison of the calculated temperature with that of the first thermocouple on Probe 2 for the second lunation following ALSEP emplacement on the lunar surface is shown in Fig. 14. From the fifth day to the tenth day since the elevation angle of the Sun was above the surface, the differences between the calculated and measured temperatures are relatively smaller and basically within ±1 K.

Fig. 15 shows the temperature differences in the four other lunations, and the same conclusion is obtained, that is, the differences between the calculated and measured temperatures are relatively smaller for the fifth day up to the tenth day since sunrise, and the differences are also within ±1 K.

Since the start of the Apollo 15 heat flow experiment until its end in 1974, 41 lunations occurred. The comparison of the calculated temperature with that of the first thermocouple on Probe 2 during this period is presented in Fig. 16, which only shows the fifth day up to the tenth day since the elevation angle of the Sun was above the surface. The elevation angle of the Sun is also shown in Fig. 16 for the aforementioned days. In the figure, the variation in temperature difference is approximately periodic and basically consistent with the variation in solar elevation angle.

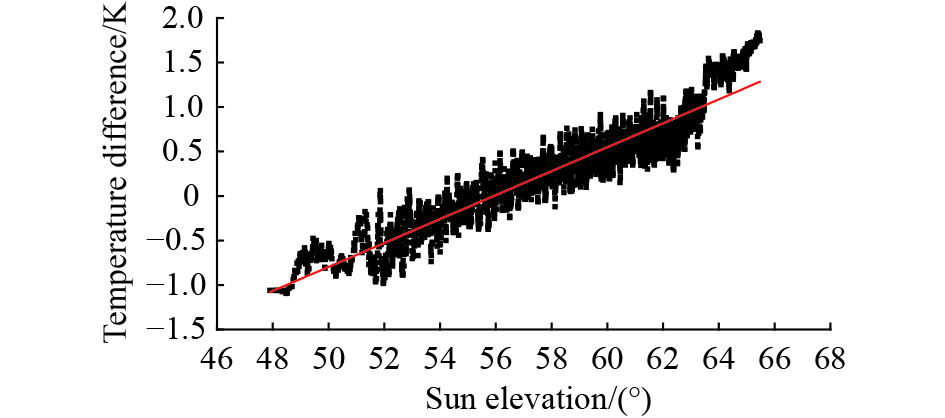
To further analyze the relationship between temperature difference and solar elevation angle, these factors are shown in Fig. 17 from the fifth day to the tenth day since the sunrise for the second lunation following ALSEP emplacement on the lunar surface. As shown in the figure, the variation in temperature difference is nearly consistent with that of the solar elevation angle, thereby implying that the temperature difference is linear with the solar elevation angle.

In all the 41 lunations that occurred during the entire period of the Apollo 15 heat flow experiment, a linear relationship existed between temperature difference and solar elevation angle during each period of the fifth day up to the tenth day since sunrise, as shown in Fig. 18. The differences between the calculated and measured temperatures are mostly within ±1 K.

Most of the lunar surface temperature models regard solar irradiance as invariable, and the variation in the effective solar irradiance is simply the cosine function of the solar incidence angle or the selenographic coordinates of the location. The relationship between the effective solar irradiance and solar irradiance as a cosine function is not sufficiently accurate.

This study considers the real-time variation in the effective solar irradiance of the lunar surface and establishes a real-time model of lunar surface temperature based on Racca’s lunar surface temperature steady-state model. In Racca’s model, the parameter of the effective solar irradiance can be calculated accurately and in real time.

The lunar surface temperature provided by the proposed real-time model can nearly accurately describe the variation in Moon phases based on qualitative comparisons with lunar infrared images provided by the FY-2G satellite.

The heat flow experiment provides the lunar surface temperature time series at the Apollo 15 landing site from the time the experiment started until its end in 1974. Despite the presence of irregularities and bumps, the result from the temperature model fits well with the measurement when the solar elevation angle is greater than zero. Furthermore, the differences between the calculated and measured temperature results are basically within ±1 K for the fifth day up to the tenth day since the elevation angle of the Sun was above the surface.