出版日期: 2017-11-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20176391
2017 | Volumn21 | Number 6
上一篇  |  下一篇
  
土壤蒸发和植被蒸腾遥感估算与验证
expand article info 宋立生1,2 , 刘绍民2 , 徐同仁2 , 徐自为2 , 马燕飞3
1. 西南大学 遥感大数据应用重庆市工程研究中心地理科学学院，重庆 400715
2. 北京师范大学 地理科学学部 地表过程与资源生态国家重点实验室，北京 100875
3. 邯郸学院 经济管理学院地理系，邯郸 056005
收稿日期: 2016-11-10; 优先数字出版日期: 2017-11-01
基金项目: 国家自然科学基金(编号：41531174)；国家重大科学研究计划课题(编号：2015CB953702)；西南大学博士基金(含人才引进计划)项目(编号：SWU11042)；中央高校基本科研业务费专项资金(编号：XDJK2017C004)
第一作者简介: 宋立生(1987—　)，男，副教授，研究方向为多尺度土壤蒸发和植被蒸腾遥感估算与验证等研究。E-mail：songls@swu.edu.cn
通讯作者简介: 刘绍民(1967—　)，男，教授，研究方向为水文气象与遥感等研究。E-mail：smliu@bnu.edu.cn
中图分类号: TP79
文献标识码: A

摘要

地表蒸散发是土壤—植被—大气系统中能量和水循环的重要环节，它包括土壤、水体和植被表面的蒸发，以及植被蒸腾。随着地表参数多源遥感产品的快速发展，利用不同地表参数遥感产品估算地表蒸散发以及其组分土壤蒸发和植被蒸腾成为日常监测越来越便利，监测尺度已从单站扩展到田块、区域乃至全球。目前地表蒸散发双层遥感估算模型按照建模机理的不同可分为：系列模型、平行模型、基于特征空间的模型、结合传统方法的模型以及数据同化方法。本文从模型构建物理机制、模型驱动数据以及模型输出结果验证等方面总结了上述模型的发展历史和现状，并指出在模型结构与参数化方案的优化、高分辨率模型驱动数据的发展、土壤蒸发和植被蒸腾像元尺度“地面真值”的获取等方面都仍需进一步完善。

关键词

土壤蒸发, 植被蒸腾, 遥感模型, 估算, 验证

Soil evaporation and vegetation transpiration: Remotely sensed estimation and validation
expand article info SONG Lisheng1,2 , LIU Shaomin2 , XU Tongren2 , XU Ziwei2 , MA Yanfei3
1.Chongqing Engineering Research Center for Remote Sensing Big Data Application, School of Geographical Sciences, Southwest University, Chongqing 400715, China
2.State Key Laboratory of Earth Surface Processes and Resource Ecology, Faculty of Geographical Science, Beijing Normal University, Beijing 100875, China
3.School of Economics and Management, Department of Geography, Handan University, Handan 056005, China

Abstract

Land surface evapotranspiration (ET) and its partitioning between evaporation (E) and transpiration (T) is a significant component of water and energy cycles at all scales, from field and watershed to regional and global, and is essential to many applications in climate, weather, hydrology, and ecology. The land surface ET and its components E and T can be produced conveniently at a range of spatial and temporal scales by combining the advanced remotely sensed data and its land surface products such as land surface temperature, leaf area index, and landcover, among others. This work aims to evaluate and summarize available remotely sensed models currently used to determine ET and components E and T. The remotely sensed-based model of land surface E and T has undergone several stages of development, including series and parallel energy balance models, spatial variability model, remote sensing and meteorological combination model, and data assimilation technology divided based on diverse model mechanisms. However, these models provide wide ranges of E and T, whose uncertainty may be limited by the unreasonable component temperatures partitioned from land surface temperature, parameterization of the stress factors of T from vegetation and E from soil surface, and uncertainty of the reproduced meteorological data as model input data. Future studies should improve model performance under heterogeneous surface and upscale the point or patch ground measurements of E and T to satellite pixel scale to validate remotely sensed model simulations.

Key words

soil evaporation, vegetation transpiration, remotely sensed model, estimation, validation

1 引　言

地表蒸散发是土壤—植被—大气系统中非常重要的物质、能量的转换和输送过程，它关联着地球上水、能量和碳的循环(Jung 等，2010)。地表蒸散发主要包括土壤、水体和植被表面截流的蒸发(Evaporation)以及植被的蒸腾(Transpiration)。从水量平衡的角度，蒸散发量可占全球年平均降水量的2/3 (Trenberth 等，2009)，其中植被蒸腾量在陆地蒸散发中所占的比例大于80%，这个比例在干旱区会更大(Jasechko 等，2013)；从能量平衡的角度，蒸散发约占地表可利用能量的59%(Trenberth 等，2009)。因此，准确地估算地表蒸散发及其组分土壤蒸发和植被蒸腾，不仅能满足对全球有限水资源的合理管理和农田最优灌溉决策工程等的需求，还能为各种气候变化情景下全球水循环的潜在变化提供重要的应对措施(Trenberth 等，2009)。

土壤蒸发和植被蒸腾可以通过小型蒸渗仪、便携式光合作用测量系统(Licor6400，静态箱—红外气体分析仪)、热扩散液流计等仪器进行分离观测或者利用稳定同位素技术等进行拆分。然而，地面观测的空间代表范围非常有限(Allen 等，2011)，加之地表覆盖类型和土壤水分等空间分布的非均匀性，导致土壤蒸发和植被蒸腾的空间异质性较强，因此地面观测的土壤蒸发和植被蒸腾往往很难满足区域和全球尺度的应用需求。相对于地表蒸散发单层模型只能估算地表蒸散发值，地表蒸散发双层模型可以同时估算地表蒸散及其组分土壤蒸发和植被蒸腾，有助于更好地理解流域尺度生态—水文过程，便于评估农田水分利用效率等，具有更多的应用价值。随着遥感技术的发展，地表蒸散发双层遥感估算模型能够较好地获取田块、区域乃至全球尺度时空连续的土壤蒸发和植被蒸腾。

自20世纪90年代以来，随着卫星遥感数据的获取越来越便捷，以及全球范围内通量站点的建立与观测数据共享，目前已发展了多种地表蒸散发双层遥感估算模型，特别是基于能量平衡机理的模型得到了显著发展，已应用于区域和全球(Kalma 等，2008；Li 等，2009；Wang和Dickinson，2012)。但是由于下垫面非均匀性和近地层气象条件的复杂性，模型估算地表蒸散发、土壤蒸发和植被蒸腾的精度还有待于进一步提高。同时，地面观测土壤蒸发和植被蒸腾的空间代表性非常有限，无法满足遥感模型估算土壤蒸发和植被蒸腾的验证需求。因此，有必要系统地综述土壤蒸发和植被蒸腾遥感估算模型的发展过程，总结目前地表蒸散发双层遥感估算模型以及模型估算结果验证等存在的主要问题，为进一步完善该类模型提供科学参考。

2 地表蒸散发双层遥感估算模型

地表蒸散发双层遥感估算模型在20世纪80年代首次被提出，随后不同类型模型也相继出现，并且在不同类型下垫面和气候条件下得到了较为广泛的推广和应用。根据模型机理和建模方式的不同可以分为以下5类：系列模型、平行模型、基于特征空间的模型、结合传统方法的模型以及数据同化方法。

2.1 系列模型

由于在真实下垫面，植被冠层并非单一、均匀和密封，是植被、土壤等组分的混合，而SEBAL (Surface Energy Balance Algorithm for Land)，METRIC (Mapping EvapoTranspiration with high Resolution and Internalized Calibration)，SEBS (Surface Energy Balance System)等单层模型认为：地面被一张大叶覆盖，地表蒸散发只来源于植被冠层，忽略了稀疏植被覆盖区中土壤蒸发的贡献(Zhang 等，2016)。而地表蒸散发双层遥感估算系列模型不仅考虑了地表蒸散发中植被和土壤的各自贡献，还考虑了土壤和植被之间的水热通量交换，模型机理更为合理。

2.1.1 S-W模型

为了考虑土壤对稀疏植被覆盖下地表通量的贡献，Shuttleworth & Wallace提出了经典的地表蒸散发双层估算系列模型(S-W)，该模型将底层土壤与植被冠层看作是上下叠加、彼此连续的湍流源。底层的水汽和热量汇合于植被冠层内部，并且只能通过顶层离开，整个冠层总热通量是各层热通量之和( Shuttleworth和Wallace，1985)。

$\lambda E{\rm{ = }}T + E$ (1)
$T = {C_{\rm{c}}}\frac{{\varDelta A + \left( {\rho {C_{\rm{p }}}D - \varDelta r_{\rm{a}}^{\rm{c}}{A_{\rm{s}}}} \right)/\left( {r_{\rm{a}}^{\rm{a}} + r_{\rm{a}}^{\rm{c}}} \right)}}{{\varDelta + \gamma \left( {1 + \left( {r_{\rm{s}}^{\rm{c}}/\left( {r_{\rm{a}}^{\rm{a}} + r_{\rm{a}}^{\rm{c}}} \right)} \right)} \right)}}$ (2)
$E = {C_{\rm{s}}}\frac{{\varDelta A + \left( {\rho {C_{\rm{p}}}D - \varDelta r_{\rm{a}}^{\rm{s}}\left( {A - {A_{\rm{s}}}} \right)} \right)/\left( {r_{\rm{a}}^{\rm{a}} + r_{\rm{a}}^{\rm{s}}} \right)}}{{\varDelta + \gamma \left( {1 + \left( {r_{\rm{s}}^{\rm{s}}/\left( {r_{\rm{a}}^{\rm{a}} + r_{\rm{a}}^{\rm{s}}} \right)} \right)} \right)}}$ (3)

式中，λE为地表总蒸散发；T为植被蒸腾；E为裸土蒸发；Cc和Cs分别为植被阻抗系数和土壤阻抗系数；ρ为空气密度；Cp为空气定压比热；A=Rn–G为可利用能量；D为参考高度处饱和水汽压差；As是裸土下垫面的可利用能量； $r_{\rm{a}}^{\rm{c}}$ 为冠层边界层阻抗； $r_{\rm{a}}^{\rm{a}}$ 为冠层表面到参考高度处空气动力学阻抗；Δ为饱和水汽压—气温曲线斜率；γ为干湿表常数； $r_{\rm{s}}^{\rm{c}}$ 为冠层阻抗； $r_{\rm{a}}^{\rm{s}}$ 为土壤表面与植被冠层之间热传输的空气动力学阻抗； $r_{\rm{s}}^{\rm{s}}$ 为土壤表面阻抗。

然而，在各层热通量累加时需要获取模型参数和小气候特征的空间分布状况，如冠层内各层的叶面积、叶倾角、辐射、温度、湿度、风速等，并且许多模型参数都无法直接测量，因此限制了该模型在区域尺度上的推广应用。随后，Shuttleworth和Gurney (1990) 针对该模型中的土壤、植被冠层和空气等众多阻抗参数作了详细的说明，给出具体的计算公式，并分析了植被温度、叶面积、空气温度等对模型中系列阻抗参数的影响，进一步提高了经典地表蒸散发双层估算模型的实用性。为了让经典系列模型能更好地应用于干旱半干旱的灌溉农田，Xin和Liu (2010)参考SEBS (Surface Energy Balance System)模型中确定干湿点的思路，利用地面观测的不同土壤水分条件下的红外温度数据集，以及辐射传输模型模拟的土壤和植被温度，建立了极端干燥和湿润能量控制条件下土壤和植被温度差异指数，并带入到S-W模型中计算土壤蒸发和植被蒸腾，以便简化S-W模型。Hu和Jia (2015)通过将微波和光学卫星遥感数据相结合，对S-W模型中阻抗等进行优化，增加Gash的树冠截流模型(Dijk等，2001)，构建了适用于区域尺度地表蒸散发计算的遥感S-W模型，并生产了全球尺度ETmonitor产品。

S-W模型虽然是最早提出的经典地表蒸散发双层估算模型，然而由于模型需要建立6个方程以求解6个未知数，每个参数的估算过程都比较复杂(高彦春和龙笛，2008)，诸多阻抗的参数化方案还是建立在单站尺度上，这在一定程度上阻碍了S-W系列模型的发展。虽然，有些学者针对典型植被覆盖下垫面提出了一些可行的模型参数化方案(Gardiol 等，2003；Ortega-Farias 等，2010)，但参数化方案的普适性较差，如何利用遥感数据和再分析气象数据对模型中多个阻抗建立参数化方案，更好地将S-W系列模型与遥感技术结合起来，应用到区域土壤蒸发和植被蒸腾估算上还需要进一步地研究。

2.1.2 TSEB系列模型

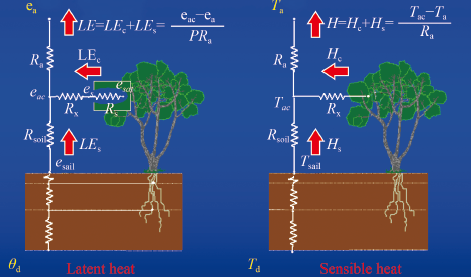
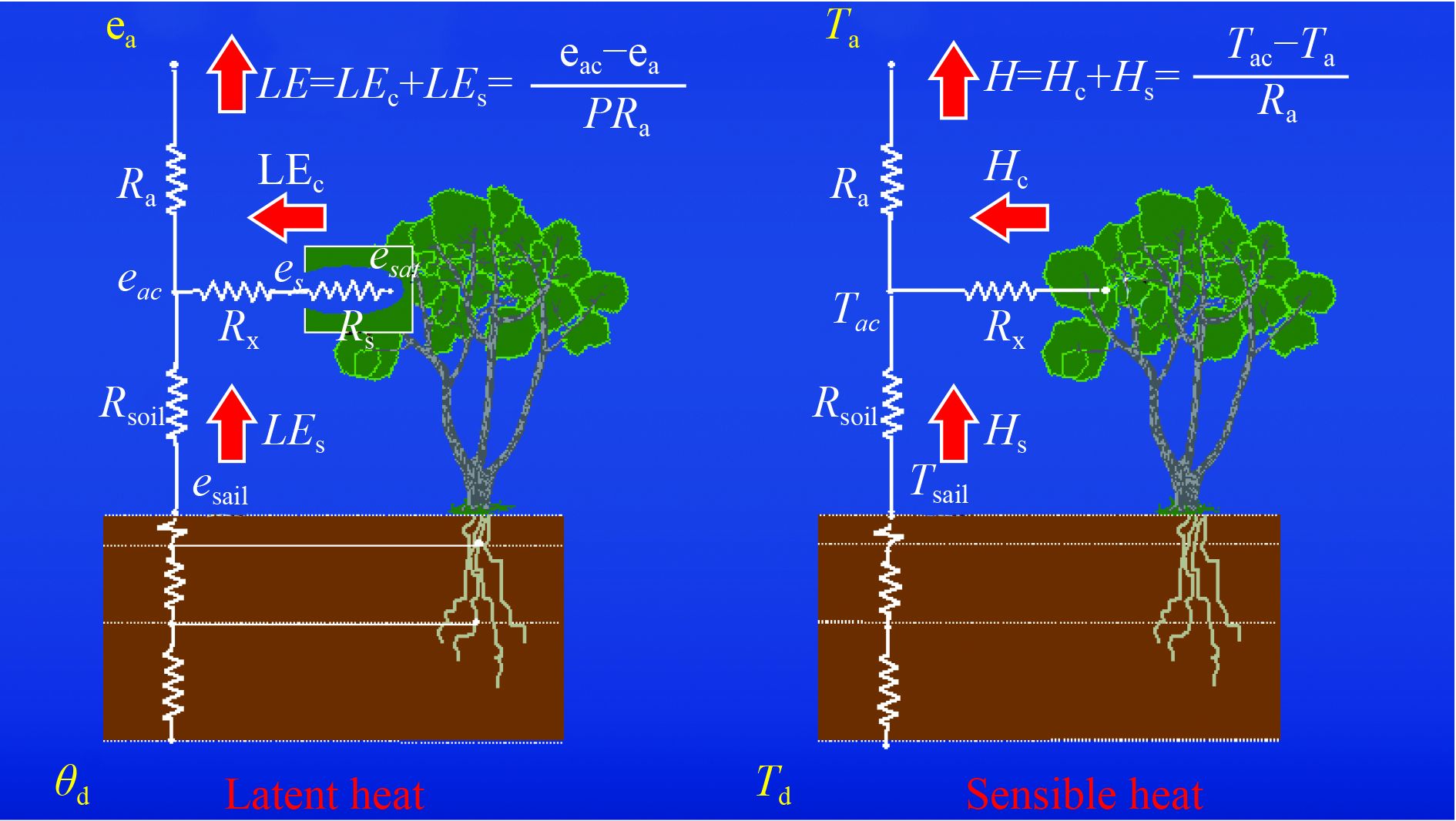
为了更好地应用地表蒸散发双层估算系列模型，使它能够与遥感技术相结合，并将尺度拓展到田块、流域甚至是全球。Norman等人(1995)将经典S-W模型的5个阻抗参数简化为植被冠层的总边界层阻抗和土壤表面阻抗，但是，模型仍然假设植被和土壤之间有水热交换，称为TSEB (Two Source Energy Blance)系列模型(图1)。


图 1 TSEB模型估算土壤蒸发和植被蒸腾概念图
Fig. 1 The schematic diagram of soil evaporation and vegetation transpiration estimated by TSEB model

TSEB系列模型主要优点是：(1) 模型可以应用混合地表温度(此时TSEB模型可称为TSEBPT)作为输入参数。(2) 通过引入植被和土壤的组分温度驱动TSEB模型(此时TSEB模型可称为TSEBCT)，提高土壤蒸发和植被蒸腾估算精度。(3) 空气温度的估算可结合当地气象站的观测。此模型的物理机制更明确，同时比S-W系列模型更容易操作(Norman 等，1995)。

模型中土壤和植被净辐射通量可以表达为

$Rn = R{n_{\rm{c}}} + R{n_{\rm{s}}}$ (4)
$\begin{aligned}R{n_{\rm{c}}} = & \left( {1 - {\tau _{{\rm{longwave}}}}} \right)\left( {{L_ \downarrow } + {\varepsilon _{\rm{s}}}\sigma T_{\rm{s}}^4 - 2{\varepsilon _{\rm{c}}}\sigma T_{\rm{c}}^4} \right) + \\ &\left( {1 - {\tau _{{\rm{solar}}}}} \right)\left( {1 - {\alpha _{\rm{c}}}} \right){S_ \downarrow }\end{aligned}$ (5)
$\begin{aligned}R{n_{\rm{s}}} = & {\tau _{{\rm{longwave}}}}{L_ \downarrow } + \left( {1 - {\tau _{{\rm{longwave}}}}} \right){\varepsilon _{\rm{c}}}\sigma T_{\rm{c}}^4) - \\ &{\varepsilon _{\rm{s}}}\sigma T_{\rm{s}}^4 + {\tau _{{\rm{solar}}}})\left( {1 - {\alpha _{\rm{s}}}} \right){S_ \downarrow }\end{aligned}$ (6)

式中，Rn、Rnc、Rns分别是地表、植被表层、土壤的净辐射；τlongwave是冠层长波透过率；L↓为向下长波辐射；εs和εc分别是土壤和植被的比辐射率；σ为Stefan-Boltzman常数5.67×10–8 W·m–2·K–4；Ts和Tc分别为土壤和植被的温度，单位为K；τsolar为太阳短波辐射直接透过率；αc和αs分别为植被和土壤的反照率；S↓为下行短波辐射，无观测数据时可用 ${S_ \downarrow } = {S_0}{C_{{\tau }}}\cos z'$ 来表达，S↓通常取1367 W·m–2，Cτ为太阳短波辐射的大气透过率，在晴空条件下取0.75，z′为太阳天顶角， $\cos z' = \cos \delta \cos \alpha \cos \omega t + $ $\sin \delta \sin \alpha $ (δ为太阳赤纬，α为当地纬度，ω为地球自转的角度)。

TSEB模型中植被和土壤感热通量可以表达为

${H_{\rm{c}}} = \rho {C_{\rm{p}}}\frac{{{T_{\rm{c}}} - {T_{{\rm{ac}}}}}}{{{r_{\rm{x}}}}}$ (7)
${H_{\rm{s}}} = \rho {C_{\rm{p}}}\frac{{{T_{\rm{s}}} - {T_{{\rm{ac}}}}}}{{{r_{\rm{s}}}}}$ (8)

式中，Tac为空气动力学温度；rx为冠层内植被阻抗；rs为土壤表面的空气动力学阻抗；其他与前文相同。

TSEB模型需要输入土壤和植被组分温度，然而，大部分时候只能获取地表混合温度，因此，需要通过引入其他信息，建立地表组分温度分解模型。在TSEB模型中，引入简化的Priestley-Taylor公式，从地表辐射温度中分解出植被温度(Norman 等，1995)，然后利用Stefan-Boltzman定律得到土壤温度。

$L{E_{\rm{c}}} = {\alpha _{\rm{c}}}{f_{\rm{g}}}\frac{\varDelta }{{\varDelta + \gamma }}R{n_{\rm{c}}}$ (9)
${H_{\rm{c}}} = \rho {C_{\rm{p}}}\frac{{{T_{\rm{c}}} - {T_{{\rm{ac}}}}}}{{{r_{\rm{x}}}}} = R{n_{\rm{c}}}\left[ {1 - {\alpha _{\rm{c}}}{f_{\rm{g}}}\frac{\varDelta }{{\varDelta + \gamma }}} \right]$ (10)

式中，αc为针对植被的P-T系数，一般认为植被不缺水，初始值为1.26；fg为植被中绿色部分的比例；Pv(θ)为植被覆盖度；其他参数含义与前文相同。

由于TSEB模型是利用Beer定律将混合地表净辐射分解为土壤净辐射和植被净辐射，在一些稀疏或者团簇状植被覆盖下垫面误差较大。Kustas和Norman (1999)从冠层辐射传输机理出发通过引入冠层长短波辐射透过率以及能够准确表达植被分布形状的植被聚集因子，建立了土壤和植被净辐射估算机理模型，提高了模型估算精度。另外，Anderson等人(1997)和Cammalleri等人(2012)分别提出了ALEXI (Atmosphere-Land EXchange Inverse)和TSEB-IC模型以期降低模型对空气温度数据的依赖性。ALEXI模型通过建立太阳升起后1.5—5.5小时地表温度上升速率和大气边界层增长模型，利用气象卫星如GOES (Geostationary Operational Environmental Satellites)观测的多时相地表温度输入到TSEB模型中，得到空气动力学温度和辐射温度之间的关系，最后估算出卫星过境时刻地表通量(Anderson 等，1997)。然而，静止气象卫星(GOES、FY-2、SEVIRI等)仅能获得低纬度地区高时间频率地表参数观测信息，很难获得全球尺度地表参数。TSEB-IC模型通过选取研究区潮湿或者全植被覆盖下的像元，结合P-T公式，估算研究区空气温度。但是该模型无法应用于非生长季，同时利用单个像元计算的空气温度代替整个研究区空气温度分布格局的合理性值得商榷(Cammalleri 等，2012)。Norman等人(2003)提出的DTD (Dual Temperature Difference)模型，通过输入两个时相地表温度数据，降低地表温度观测和反演等误差对模型的影响，提高了模型在区域尺度上估算地表蒸散发的精度。目前，TSEB模型与遥感技术相结合，已应用于流域、区域甚至全球尺度上。研究发现：该模型虽然能利用P-T公式分解植被和土壤温度，但是由于下垫面异质性和复杂近地层大气状况等因素的影响，模型估算地表通量的精度较低。若遥感反演的组分温度输入，可以提高TSEB模型在异质性下垫面估算地表蒸散发的精度(Song 等，2016b)。另外，在高植被覆盖和平流影响条件下，TSEB模型容易高估土壤蒸发，低估植被蒸腾(Colaizzi 等，2012；Song 等，2015)。通过引入优化的P-T公式，直接从混合辐射温度中分解出植被和土壤温度，提高组分温度分解精度(TSEB-A)，进而提高模型估算土壤蒸发和植被蒸腾的精度(Song 等，2016a)。

遥感数据的空间分辨率不同会影响到模型的输出结果(Long 等，2011)，研究结果表明：TSEB模型在30 m、120 m以及250 m分辨率下，模型估算结果与涡动相关仪观测结果更接近(Li 等，2008)，其原因是30 m或者120 m分辨率尺度与田块以及作物的空间异质性尺度相吻合，模型表现更好。目前遥感估算土壤蒸发、植被蒸腾以及地表蒸散发数据在农田水资源管理方面具有重要作用，但是获取田间尺度地表蒸散发遥感产品对于农田水资源管理更具有实际意义。因此，如何将遥感估算的地表蒸散发以及土壤蒸发、植被蒸腾产品进行时间尺度扩展和空间降尺度，获取时空连续的田块尺度地表蒸散发和土壤蒸发、植被蒸腾产品具有重要意义。目前，基于TSEB模型框架开发的DisALEXI模型利用GOES的多次观测，应用ALEXI方法中估算大气温度的算法，得到10 km尺度上离地表50 m高度处的大气温度，然后将该数据输入到MODIS、ASTER、Landsat等遥感数据源中估算10—1000 m尺度上地表蒸散发，并结合时空遥感数据融合算法，如STARFM(Spatial and Temporal Adaptive Reflectance Fusion Model)算法，对基于MODIS估算的公里级地表蒸散发产品进行空间降尺度，得到时空连续的田块尺度地表蒸散发产品(Cammalleri 等，2014；Semmens 等，2016)。算法的主要优点是利用较少的地面输入数据，进行地表蒸散发降尺度估算，但是，遥感影像数据之间空间分辨率的差异，以及空气温度的空间异质性都会影响该算法的应用和地表蒸散发和土壤蒸发、植被蒸腾的估算精度。

2.2 平行模型

在非均匀下垫面，植被呈斑块状镶嵌于裸土之间，植被和土壤的各源通量与空气只有垂直作用，彼此之间没有能量交换。这样源区内总通量为组分通量的面积加权，这类模型一般称为补丁模型(Blyth和Harding，1995)。Norman等人(1995)假设在地表土壤层和植被层最先单独与各自周围的空气发生能量交换与耦合，那么土壤表面温度与其周围空气的温度差以及植被表面温度与其周围的空气温度差将分别是影响土壤层和植被层感热通量的主要因子，且各通量之间没有相互作用。基于这些假设，提出了TSEB平行模型，其原理与S-W类蒸散发模型对地表土壤、植被与大气系统之间能量交换、耦合的表达存在一定的差异。实际上，在干旱半干旱区，植被的叶面积指数处于中低水平，风速也处于中等水平。另外，冠层上方的空气温度梯度比较小，这些都使得土壤层和植被层的阻抗之间联系较小。模型中的阻抗系统要比S-W模型中的简单，更容易估算，适合于干旱半干旱区的稀疏、团簇状植被覆盖区域。

在TSEB平行模型中，土壤表面和植被覆盖表面的能量只单独与周围的空气发生能量和水汽交换，彼此之间没有能量和水汽的交换。该类模型的土壤和植被净辐射以及潜热通量的求解与TSEB系列模型类似，但是由于该模型自身的缺陷，如在植被覆盖度较高的区域，土壤和植被之间存在能量和水汽的交换时，其假设不成立，因此当前TSEB系列模型的应用更为广泛。

2.3 基于特征空间的模型

基于特征空间的模型主要是充分利用遥感数据提供的地表多源空间信息，最大可能脱离模型对地面观测数据的依赖，提高模型在区域尺度上的易操作性。模型的主要思路是将地表温度和植被覆盖度投射到相同的坐标空间中，它们所构成的散点图包含了丰富的地表温度、植被覆盖、土壤含水量、地表蒸发比等信息，称为特征空间模型。在特征空间中，存在两个能够表达地表植被覆盖和土壤干湿状况的斜线，即干线和湿线，并且通过斜率线性内插的方法可以得到许多条类似干边和湿边的特征斜线，而落在斜线上的像元具有相同的土壤含水量，即土壤等湿度线(Carlson 2007；Wang和Dickinson 2012)。在土壤等湿度线上，像元的土壤温度相同，而且植被冠层的温度也相同。在地表温度—反照率特征空间中，假设下垫面是裸土和植被的混合体。然后，利用实际蒸散发和潜在蒸散发之间的互补关系，结合植被冠层导度来表征植被生理参数，估算植被蒸发比。并利用地表温度—植被覆盖度的特征空间推算出裸土蒸发比，对植被蒸发比和裸土蒸发比进行线性加权得到地表蒸发比，最后结合遥感数据估算地表蒸散发(Nishida 等，2003)。该类模型最大程度地脱离对地面观测数据的依赖，估算公式简单，可操作性较强。同时，假设忽略水平平流的影响，从土壤表面输送到界面的感热通量加上从植被冠层表面输送到界面的感热通量应该等于从界面输送到参考高度的感热通量，对于潜热通量也是如此。基于此可以把地表能量传输分割为两层，再结合像元组分排序对比法，将单一时相或者单一观测角度遥感影像混合像元的净辐射、辐射地表温度、地表反照率等分解为来自土壤和植被表面(张仁华，2009)，这类方法称为PCACA (Pixel Component Arranging and Comparing Algorithm)模型。该模型的求解过程降低了对地面观测气象数据的依赖，提高了区域尺度地表蒸散发双层遥感估算的可操作性。但是特征空间中裸土最大和最小温度以及植被最大和最小温度主要是通过像元温度统计或者回归的方法获取，这些温度端元获取的准确性将直接影响土壤蒸发和植被蒸腾估算的准确性。特征空间模型中的干边和湿边可以通过迭代方法确定，但是特征空间温度端元的分布受到研究区下垫面类型和云覆盖等的影响(Tang 等，2010)。Long和Singh (2012) 提出了地表蒸散发双层遥感估算梯形模型TTME(Two-source Trapezoid Model for Evapotranspiration)。该模型通过对两个极端情况下：极端干燥裸土和全植被覆盖条件下土壤阻抗和植被阻抗进行参数化，降低阻抗参数化精度对地表蒸散发双层遥感模型估算精度的影响等，能够避免高估植被蒸腾现象。同时，通过引入土壤和作物缺水指数，可以优化模型中组分温度分解模型，提高模型估算土壤蒸发和植被蒸腾的精度(Yang 等，2015)。

由于特征空间模型需要先确定干、湿边，再引入地表能量平衡模型，建立地表蒸散发双层遥感估算模型，但是干、湿边的确定仍存在一定的主观性和局地性，同时，“干边”或“湿边”温度高估/低估会导致潜热高估/低估(Long和Singh，2013)。另外，应用特征空间模型时需要研究区的植被覆盖度变化区间尽可能大，并包含干湿差异显著的土壤下垫面。这些都影响了基于特征空间的地表蒸散发双层遥感估算模型的估算精度和在不同下垫面类型和气候条件下的应用。

2.4 结合传统方法的模型

在遥感技术出现之前，已有学者基于地面观测站数据建立了一些传统的基于气象参数的地表蒸散发估算模型，如Penman-Monteith公式(Monteith，1965)、P-T公式(Priestley和Taylor，1972)等，此类模型适用于站点尺度，随着卫星遥感技术出现之后，该类模型与遥感技术相结合用于估算区域或者全球尺度上地表蒸散发，但是模型对气象数据需求较多。

Allen于1998年在传统的P-M模型的基础上对表面阻抗的计算公式进行了修正，用于计算参考作物潜在蒸散发(ET0)，并且引入了植被蒸腾系数和土壤蒸发系数将地表蒸散发分离为植被蒸腾和土壤蒸发(Allen 等，1998)。该模型被联合国粮农组织FAO(Food and Agriculture Organization)在全世界推广应用，一般称为FAO-56双作物系数模型，具体如下(Flumignan 等，2011)

$E{T_0} = \frac{{0.408\left( {Rn - G} \right) + \gamma \displaystyle\frac{{900}}{{T + 273}}{u_2}\left( {{e_{\rm{s}}} - {e_{\rm{a}}}} \right)}}{{\varDelta + \gamma \left( {1 + 0.34{u_2}} \right)}}$ (11)
$E = {K_{\rm{e}}}E{T_0}$ (12)
$E = {K_{{\rm{cb}}}}E{T_0}$ (13)

式中，ET0为潜在蒸散发；E和T分别为土壤蒸发和植被蒸腾；T为2 m高处的空气温度(℃)；u2是2 m高处的风速(m/s)；Ke和Kcb分别为土壤蒸发系数和植被蒸腾系数。

该模型由于输入参数较少，已被应用在小麦、玉米、果园、橄榄树等下垫面(Flumignan 等，2011；Paço 等，2009，2012；Rousseaux 等，2009)。但是，研究发现：该模型中的作物系数在不同的研究区差异较大，原模型中给出的参考数是通过经验关系得到的，无法应用于各类下垫面或者复杂下垫面。因此，在使用FAO-56双作物系数模型分离农田土壤蒸发和植被蒸腾时，先要对原模型的两个作物系数进行修正。同时，研究也发现：在潜在蒸发ET0较大时，容易出现植被蒸腾被高估的现象，其原因是：在充分灌溉的条件下，如果可利用能量限制了地表蒸散发，就会出现水分在植被内被蓄积的现象(Paço 等，2012)。

由于P-M模型的参数化方案和驱动数据都来源于地面观测数据，因此，只局限于在站点尺度上应用。随着遥感技术的发展，利用卫星遥感数据获取的地表参数信息计算模型中的参数，代替地面观测数据输入(Cleugh 等，2007)，将模型扩展到区域尺度甚至全球尺度。但是当植被水分和温度胁迫时，模型估算结果与地面观测数据之间差异较大。通过考虑温度和水分胁迫优化植被气孔导度参数化方案，并利用叶面积指数作为由气孔导度到冠层导度的尺度扩展因子，进而提出了结合遥感信息的P-M模型来估算全球地表蒸散发。该模型先单独计算土壤蒸发和植被蒸腾，然后再合并为地表蒸散发(Mu 等，2007)。然而，植被气孔导度不仅受到温度和水分的胁迫，而且在高温下，植被气孔导度会下降，甚至植被会关闭气孔进行自我保护。因此，在植被气孔导度参数化方案中同时需要考虑高温对植被气孔导度的影响(Yuan 等，2010)。然而，P-M遥感模型仍然利用比尔—朗伯定律，结合遥感植被信息将地表净辐射经验地分割为来自土壤和植被的部分。同时模型没有考虑到土壤水分的影响，造成模型在干旱区的估算精度较差。随后，Mu等人(2011)对该模型做了进一步完善：(1)改进了气孔导度、空气动力学阻抗和土壤表面阻抗的参数化方案；(2)模型计算过程中区分了干燥和湿润条件下的植被以及湿润和饱和的土壤表面；(3)简化了植被覆盖度的计算公式，增加了土壤热通量遥感估算模型，并通过时间尺度扩展得到白天和夜间地表蒸散发量，累加为日地表蒸散发。利用优化的P-M遥感模型生产了全球1 km 8天合成地表蒸散发产品MOD16。然而这类P-M遥感模型并没有考虑地表土壤水分胁迫对地表蒸散发的影响(Leuning 等，2008)，其主要原因是由于当前遥感土壤水分产品在空间分辨率和反演精度上都无法满足地表蒸散发遥感估算模型的需求。

为解决当前土壤水分产品空间分辨率粗的问题，可以应用再分析数据对P-M遥感模型中土壤水分胁迫因子进行参数化，如Morillas(2013)在Leuning(2008)等人的基础上引入3种土壤水分胁迫因子的参数化方案：(1)应用土壤水分再分析数据；(2)应用16天前期降雨和平衡态土壤蒸发之比作为土壤水分胁迫因子；(3)模拟降雨之后土壤干燥程度作为土壤胁迫因子。3种参数化方案分别在半干旱区和干旱区进行了验证，结果表明：在干旱半干旱下垫面应用第3种参数化方案估算的地表蒸散发的精度较高，主要是这类参数化方案能够很好地模拟在缺水条件下，土壤可利用水分对土壤蒸散发的限制作用。另外，区域尺度上土壤水分也可以通过可见光—热红外数据获取。总之，引入遥感反演的土壤水分因子可进一步优化土壤表面阻抗参数化方案，提高P-M遥感模型的估算精度和可操作性(Sun 等，2013)。

P-T公式的提出是基于无平流假设，以平衡蒸发为基础，通过引入P-T系数α得到无平流条件下潜在蒸散发的估算公式(Priestley和Taylor，1972)。然而，在不同地表类型和气候条件的影响下，P-T系数α的差异较大。因此许多学者提出了P-T系数α的参数化方案，并用于估算非饱和下垫面的实际蒸散发(Carlson，2007；Jiang和Islam，1999；Wang 等，2006)。由于植被蒸腾和土壤蒸发各自的约束因子差异较大，因此，α的参数化方案在区域尺度上应用的精度还有待提高。Fisher等人(2008)在原P-T公式的基础上，将地表蒸散发分为植被蒸腾、土壤蒸发和植被冠层截流蒸发3个部分计算，通过引入生态生理约束因子，如绿色植被覆盖度、植被叶片含水量等对P-T模型中植被蒸腾估算进行参数化，利用土壤水分对P-T遥感模型中估算土壤蒸发模块进行参数化，冠层截流蒸发可以利用近地层相对湿度和P-T模型进行估算(Fisher 等，2008)。基于遥感信息和再分析气象数据驱动该模型，生产了1986年—1993年全球1°分辨率的月蒸散量和2003年—2006年全球5 km分辨率的日蒸散发量产品(Fisher 等，2008；Vinukollu 等，2011)。但是，模型中关于土壤湿度、冠层湿度等约束因子的参数化方案中需要输入相对湿度、饱和水汽压差等气象要素，而这些气象要素很难应用遥感数据获取。再分析气象数据由于空间分辨率较粗会直接影响到P-T遥感模型的估算精度。基于热红外遥感数据，建立地表土壤热传导方程，估算表层土壤热惯量，反演区域表层土壤水分空间分布格局，取代P-T遥感模型中基于相对湿度、饱和水汽压差等气象要素的土壤水分参数化方案，可提高该模型的区域可操作性(Yao 等，2013)。但是基于遥感表观热惯量反演土壤水模型适用于裸土或者稀疏植被覆盖下垫面，随着植被覆盖度的增加，模型的适用性会逐渐降低。基于微波遥感不仅可以反演表层土壤水，而且获取的植被光学厚度可以作为植被含水量的监测指标。Miralles等人(2011)利用微波遥感反演的土壤水和植被光学厚度建立地表蒸散发胁迫指数，进而结合P-T遥感模型分别估算高植被覆盖、低矮植被覆盖和裸土下垫面的蒸散发，并加入冠层截留模型(Michel 等，2016)，实现陆表不同下垫面地表蒸散发遥感估算GLEM (Global Land Evaporation Amsterdam Model)，并生产了1980年—2014年全球尺度0.25°陆表蒸散发产品(Miralles 等，2016)。

由于这类模型都是基于传统的地表蒸散发估算模型结合遥感数据等而建立地表蒸散发双层遥感估算模型，对近地层空气温度、饱和水汽压差、相对湿度等参数的依赖性较强，目前这些参数在区域尺度上的精度仍需要进一步提高，因此会影响到模型估算土壤蒸发和植被蒸腾的精度。GLEM模型虽然通过引入微波遥感植被光学厚度和土壤水分数据建立植被蒸腾和土壤蒸发胁迫指数进而参数化植被蒸腾和土壤蒸发模块，但是微波遥感土壤水分产品在浓密植被覆盖下垫面的精度有待进一步提高，同时微波遥感产品的低空间分辨率限制了GLEM地表蒸散发产品空间分辨率的提升。

2.5 数据同化方法

由于遥感信息的瞬时性，且容易受到云、雨等不利天气的影响，很难得到时间连续的地表2维信息。因此，传统的地表蒸散发遥感估算模型通常受限于遥感数据的瞬时性，难以得到时间连续的区域值，而数据同化方法可以将遥感数据和过程模型结合起来，将多源遥感观测资料同化到过程模型中，解决遥感瞬间观测与地表过程连续变化之间的矛盾，获得时空连续的地表蒸散发数据(徐同仁 等，2009)。

目前，已有一些学者将陆面过程模型与数据同化技术相结合，尝试模拟长时间序列、时间上连续的土壤蒸发和植被蒸腾(Xia 等，2012a，b；Xu 等，2015；Yang 等，2007)。Caparrini等人(2004)基于变分数据同化方法CS-VDA (Combined-Source Variational Data Assimilation)(Caparrini 等，2003)和地表蒸散发双层遥感估算模型(TSEB)，构建双源变分数据同化系统DS-VDA(Dual-Source Variational Data Assimilation)，通过同化地表温度优化双层模型的热传导系数、土壤和植被蒸发比3个参数，可以模拟出植被覆盖条件下土壤蒸发和植被蒸腾的连续时间变化。Caparrini数据同化框架主要是利用Force-Restore方程作为物理约束条件，然而该方程相对简单，对地表温度的模拟容易引起较大误差，从而影响地表水热通量估算的精度。

Bateni和Liang (2012)将Force-Restore方程替换为土壤热传导方程(Heat Diffusion Equation)，取得了更准确的估算结果，进一步推动了该类方法的发展。Xu等人(2016)利用黑河中游大满超级站稳定同位素观测数据对DS-VDA模型估算的土壤蒸发和植被蒸腾进行了充分地验证，发现DS-VDA模型可以很好地估算土壤蒸发和植被蒸腾量。同时，DS-VDA模型在草地、农田和森林下垫面的表现都优于CS-VDA模型，能够更好地模拟地表水热通量的季节和年际变化特征(Bateni 等，2013a，b；Xu 等，2014)。CS-VDA模型将土壤和植被看作一个整体，并且参数化方案比较简单，但模型在稀疏植被下高估地表净辐射，在浓密植被覆盖下垫面低估地表净辐射(Bateni 等，2013b；Xu 等，2014)。

3 遥感估算土壤蒸发和植被蒸腾的验证

模型估算的土壤蒸发和植被蒸腾通常需要进行验证，主要是通过一定的误差评估方法，将模型的输出产品与独立获取的、能反映土壤蒸发和植被蒸腾的参考数据进行比较，而这些参考数据主要是通过地面观测试验来获取(Jia 等，2012)。对于模型估算土壤蒸发和植被蒸腾而言，应用地面观测数据进行验证不仅可以定量评估模型输出产品的精度，为产品的使用者提供参考，还可以优化估算模型，逐步提高模型估算土壤蒸发和植被蒸腾的精度。当前，国内外学者一直关注如何对遥感模型估算土壤蒸发和植被蒸腾值进行验证。通过地面观测可以获取土壤蒸发和植被蒸腾，进而对模型估算结果进行直接验证。但是目前很难直接观测到卫星像元尺度土壤蒸发和植被蒸腾，因而多数都利用涡动相关仪或者大孔径闪烁仪观测的地表蒸散发数据对模型估算结果进行间接检验。

3.1 直接验证

由于地面观测技术的滞后，至今难以从地面获取土壤蒸发和植被蒸腾像元尺度“地面真值”。因此，对于遥感估算的土壤蒸发和植被蒸腾验证只能局限于站点尺度。通常用小型蒸渗仪测量棵间土壤的蒸发量，它的时间尺度一般是几小时到日(Boast和Robertson，1982；Shawcroft和Gardner，1983)。直接观测植被蒸腾的方法主要有热扩散液流计(含探针式和包裹式等)等。该方法可以实现连续观测，精度较高，对作物、灌木和乔木等的正常生理活动不会产生较大影响，被认为是当前测量植被蒸腾速率最为有效的方法之一，并得到了广泛应用(Granier 等，1996)。近些年来，有许多学者应用小型蒸渗仪和热扩散液流计相结合的方式对地表蒸散发双层遥感模型估算土壤蒸发和植被蒸腾进行验证。利用热扩散液流计测定多棵植株的蒸腾速率，通过布设在棵间的小型蒸渗仪测量棵间土壤蒸发，然后验证模型估算的土壤蒸发和植被蒸腾(Colaizzi 等，2012；Lund和Soegaard，2003；Paço 等，2012)。但是热扩散液流法只能测定单株植被的蒸腾速率，同时小型蒸渗仪观测土壤蒸发的空间代表性非常有限，而遥感估算土壤蒸发和植被蒸腾是卫星像元平均值，如中分辨率卫星MODIS为1 km×1 km，两者存在空间尺度不匹配的问题。另外，将小型蒸渗仪观测土壤蒸发升尺度到卫星像元尺度时，还需要考虑遮阴和光照土壤表面蒸发的差异；而将热扩散液流计观测的单株植被蒸腾进行升尺度时不仅需要考虑植株的冠幅，而且叶面积指数往往和农作物蒸腾量具有显著相关性(Jiang 等，2016；Zhang 等，2011)。尺度扩展方法会带来不确定性，因此植被蒸腾从茎干、单株尺度扩展到像元尺度过程中产生的不确定性应该引起重视(Kool 等，2014)。

由于土壤蒸发和植被蒸腾的水汽信号存在差异，因此，可以利用稳定同位素技术跟踪和观测它们的水汽信号差异，确定生态系统蒸散δET、土壤蒸发δE和植被蒸腾δT。基于稳态假设ISS (Isotopic Steady State)，即植株的蒸腾通量是植株木质素水通量与植株叶片含水量在单位时间变化率的差值，并且质量通量和叶片内18O应满足质量平衡，则这一时刻的δT可取茎秆水18O值代替。δE可基于Craig-Gordon线性阻抗模型获得，进而根据质量守恒原理量化土壤蒸发和植被蒸腾对生态系统蒸散发贡献的比例(Wei 等，2015)，实现生态系统土壤蒸发和植被蒸腾拆分(Hu 等，2014；Wen 等，2012，2016；Williams 等，2004)。Song等人(2015，2016a，2016b)利用黑河中游张掖大满超级站稳定同位素拆分的土壤蒸发和植被蒸腾比例数据，分别从单站、田块尺度上验证地表蒸蒸散发双层遥感估算模型(涉及TSEBPT、TSEB-A、TSEBCT和DTD模型)估算的土壤蒸发和植被蒸腾的精度，并优化了TSEB模型，提高了模型估算土壤蒸发、植被蒸腾和地表蒸散发的精度。Yang等人(2015)利用该数据集比较了HTEM(Trapezoid framework-based ET model)模型和TSEB模型估算土壤蒸发和植被蒸腾的精度，探讨了模型估算误差的来源，有利于模型的进一步完善。然而，同位素稳态假设一般出现在中午时刻，且持续时间较短，因此只能获得中午时刻的土壤蒸发和植被蒸腾(Hu 等，2014；Welp 等，2008)；另外，稳定同位素技术拆分的土壤蒸发和植被蒸腾空间代表范围有限，需要结合其他地表参数进行尺度扩展到卫星像元尺度，以便对MODIS等、中低分辨率遥感估算结果进行验证。

当前最常用的地表通量观测仪器——涡动相关仪EC(Eddy-covariance)能够较准确地观测到地表蒸散发和二氧化碳通量，其中地表蒸散发一般是土壤蒸发和植被蒸腾的综合，二氧化碳通量是植被光合作用消耗和土壤呼吸作用产出的综合，而植被的蒸腾和光合作用在非常短的时间间隔(如涡动相关仪通常的观测频率：10 Hz)内为线性负相关，土壤呼吸和土壤蒸发为线性正相关。基于水汽通量和二氧化碳通量的变异相似理论可建立直接从涡动相关仪观测的高频水汽通量中分离出土壤蒸发和植被蒸腾的模型(Scanlon和Kustas，2010)，然后来验证双层遥感模型的估算结果。但是水汽通量分解模型中引入的等价函数—水分利用效率在日尺度上与土壤呼吸和土壤蒸发之间并没有相关性，同时该方法不适宜应用于多种植被混合的下垫面。通过引入地表蒸散发、植被初级生产力和大气饱和水汽压差可建立不同植被类型生态系统的水分利用率估算模型(Zhou 等，2014)，进而优化基于涡动相关仪观测的水汽和二氧化碳通量分离白天土壤蒸发和植被蒸腾的方法(Zhou 等，2016)，但是该方法并不适用于植被生长初期和末期，以及模型中3个参数的日变化为正余弦函数的假设往往很难满足，从而限制了该方法应用于双层遥感模型估算土壤蒸发和植被蒸腾的验证中。

3.2 间接验证

虽然涡动相关仪、波文比—能量平衡观测系统以及大型称重式蒸渗仪等只能测量地表蒸散发，其空间代表范围达几十到几百米，因此，这些仪器观测数据常常被应用于基于中高分辨率遥感数据(ASTER、Landsat TM/ETM+、航空遥感数据等)，结合地表蒸散发双层遥感模型估算蒸散发的验证中。目前普遍利用上述仪器观测的潜热通量验证地表蒸散发双层遥感模型结合中高分辨率遥感数据估算卫星、航空遥感过境时刻、日的地表蒸散发(Cammalleri 等，2014；Fisher 等，2008；Kustas和Anderson，2009；Long和Singh，2012；Mu 等，2011；Phillips 等，2009；Song 等，2016a, b；Xia 等，2016)，结果表明模型估算潜热通量和日地表蒸散发量的精度较高。闪烁仪可以测量1—10 km光径路线上的平均地表水热通量，其中常用的光学型与微波型闪烁仪的光径长度为500—5000 m，进一步提高了地面观测地表通量的空间代表性，与MODIS、NOAA/AVHRR、GEOS等中低分辨率遥感数据空间分辨率相匹配，因此用闪烁仪的观测数据来检验结合中低分辨率遥感数据和地表蒸散发双层遥感模型估算的蒸散发具有空间尺度上的优势。Tang等人(2011)利用修正后的MODIS地表温度和叶面积指数作为输入参数驱动TSEB模型，得到中国山东禹城地区的潜热通量空间分布，并利用大孔径闪烁仪和通量站观测数据检验模型输出结果，结果表明TSEB模型估算潜热通量的精度较高优于单层模型SEBS (Surface Energy Balance System)、TVT (surface Temperature-Vegetation index Triangle)的估算结果。另外，多模型/多产品之间的交叉验证也是地表蒸散发双层遥感模型估算的土壤蒸发、植被蒸腾和蒸散发真实性检验的一种方式，特别是在流域或者全球尺度检验中应用比较广泛。由于不同模型构建机理存在一定差异，并且都已在不同下垫面类型和气象条件下进行了验证和应用。通过不用模型之间的交叉验证不仅可以检验模型估算精度，还可以分析模型的区域适用性以及模型估算误差的来源(Gao和Long，2008)。而Kustas等人(2012)发现DTD模型不但精度优于TSEB平行和系列模型，而且地表温度输入数据的不确定性对DTD模型的估算结果影响最小。

由于地表蒸散发双层遥感模型估算的土壤蒸发、植被蒸腾和蒸散发值是像元平均值，而涡动相关仪和大孔径闪烁仪等观测通量源区的大小、位置和形状等并不固定，随架高、风速/风向、大气稳定度和地表粗糙度等而变化，两者在空间上难以匹配。虽然，通过引入通量足迹来选取验证像元的方法，即选取观测通量源区范围内的遥感像元，基于归一化的足迹权重值进行加权平均，即可得到与观测通量具有相同空间代表性的遥感估算值，再与观测值进行比较与验证，可以在一定程度上解决遥感估算值与地面观测值在空间尺度上不匹配的问题(Bai 等，2015)，但是由于观测通量源区往往无法一直完全覆盖整个或几个像元，这样对于中低分辨率遥感估算值而言，亚像元的非均一性也会对检验结果带来影响(Jia 等，2012)。因此，可以利用高分辨率遥感数据(航空遥感、高分辨率卫星遥感)逐级对中低分辨率遥感估算蒸散发开展验证(Zhang 等，2010)。Anderson等人(2008)利用高分辨率航空遥感数据估算的潜热通量并结合足迹模型对DisALEXI-LUE模型输出的低分辨率通量值进行了验证。随后，Anderson等人(2011)基于LandsatTM/ETM、MODIS和GOES数据，利用DisALEXI模型和STARFM数据融合方法，实现了遥感模型估算蒸散发的尺度上推，并检验了空间分辨率由高到低时模型估算结果的一致性。另外，可以通过多点观测的方式，如通量观测矩阵，捕捉非均匀下垫面地表水热通量的时空变化特征，结合尺度扩展方法和高分辨遥感数据获取卫星像元尺度地表蒸散发的“地面真值”，然后对遥感模型估算的地表蒸散发开展验证(Liu 等，2016)。

4 结　论

地表蒸散发双层遥感估算模型能够较好地模拟土壤—植被—大气之间的水热交换过程，已经成为目前估算区域和全球尺度上地表蒸散发及土壤蒸发和植被蒸腾的主要工具之一。土壤蒸发和植被蒸腾的准确分离相比于它们的叠加形式(地表蒸散发)，不仅更具应用价值，还具有更高的科学意义。对于农田灌溉，一般认为植被的蒸腾作用对于作物产量起着决定性的作用，而棵间土壤蒸发耗水往往造成水资源的浪费(Kool 等，2014)。特别是在干旱或者半干旱区域，一直在探求更好的农田灌溉措施，以便在保证作物产量的同时，减少土壤蒸发耗水量，提高农田水分利用效率(Agam 等，2012)。同时，准确分离估算土壤蒸发和植被蒸腾，不仅能更好地理解植被耗水需求，还有助于评估植被反馈作用在水循环中的重要意义(Newman 等，2006)。

随着多源遥感地表参数产品越来越容易获取，利用不同遥感地表参数产品估算土壤蒸发和植被蒸腾，以及地表蒸散发也越来越便利，其监测尺度已经从单站尺度扩展到田块、流域乃至是全球(Anderson 等，2004；Hong 等，2009；Kalma 等，2008；Li 等，2009)。目前，已经发展了S-W、TSEB、ALEXI、TTME、PCACA、P-M遥感模型、P-T遥感模型、GLEAM以及DS-VDA同化系统等一系列地表蒸散发双层遥感估算模型，它们已在不同下垫面类型和气象条件下进行了推广和应用，提高了模型估算地表蒸散发、土壤蒸发和植被蒸腾的精度。基于这些模型生产了区域和全球尺度的土壤蒸发和植被蒸腾产品，已应用于全球气候变化研究、农业干旱与生态监测、流域水资源管理等方面。

土壤蒸发和植被蒸腾遥感估算与验证等是一项极具挑战性的研究难题。地表异质性、复杂地形、平流等对模型估算的影响，单站上适用的模型和参数化方案扩展到区域尺度乃至全球尺度上是否仍然适用，目前小型蒸渗仪观测的土壤蒸发、热扩散液流计测定的植被蒸腾速率以及稳定同位素技术拆分的稳态时刻土壤蒸发和植被蒸腾比例等站点尺度观测值如何升尺度到卫星像元等，这些都是今后地表蒸散发双层遥感模型在区域乃至全球尺度上应用和验证等的关键所在，也是今后双层遥感模型的发展方向。具体如下：

(1) 双层遥感估算模型的优化。基于地表能量平衡方程估算土壤蒸发和植被蒸腾的模型，如S-W模型、TSEB系列和平行模型、结合传统方法的模型(P-T遥感模型等)、数据同化方法中的DS-VDA等，容易受到平流的影响。外部能量的输入使得原本的地表能量平衡方程失去了守恒，但是目前这类模型中都没有考虑外部输入能量的估算方法，因此影响了模型估算的精度。例如，TSEBPT模型中通过引入简化的P-T公式分解植被和土壤温度，通过调整系数αc使得模型能够在不同水热状况条件下应用。但是如果研究区受到平流和高植被覆盖的影响，近地层空气出现增温现象，甚至出现近地层空气温度高于地表温度现象(逆温)，地表蒸散发增加。此时，饱和水汽压差可以达到4 kPa，甚至更高，植被的P-T系数αc大于1.26(Agam 等，2010)。但是TSEBPT模型中只有降低αc的迭代机制，而无增加机制，导致TSEBPT模型低估植被蒸腾而高估土壤蒸发(Colaizzi 等，2012)。同时，在植被和非植被混合的下垫面，模型明显高估土壤蒸发，导致地表蒸散发高估。因此，需要发展能够适应复杂下垫面和不同气象条件的组分温度分解方法，进一步优化和完善地表蒸散发双层遥感估算模型。

(2) 高精度与时空分辨率驱动数据的发展。在区域尺度上，地表蒸散发双层遥感估算模型需要输入遥感反演地表参数产品以及卫星像元尺度的大气驱动数据(如气温、风速、辐射等)等。目前，可以利用地面气象台站观测的气象要素结合陆面过程数据同化模型或者中尺度气象数值预报模型等生产区域甚至全球尺度上再分析数据。但是目前主要的全球再分析数据空间分辨率非常低，如NASA生产的MERRA (Modern Era-Retrospective Analysis for Research and Applications)再分析数据的时间分辨率为6 h，空间分辨率在经线为2/3°，在纬线上为1/2°(http://gmao.gsfc.nasa.gov/research/merra/intro.php[2016-11-10])；欧洲中期天气预报中心(ECMWF)生产的ERA-Interim再分析数据的时间分辨率为6/12 h，空间分辨率为80 km，与当前主要的中低分辨率遥感数据(MODIS等，1 km×1 km)相比，难以满足地表蒸散发双层遥感估算模型对大气驱动数据时空分辨率的需求。随着遥感技术的发展，结合各类卫星传感器生产部分大气驱动数据成为重要的途径之一。如结合静止气象卫星和极轨卫星MODIS产品可以生产高时间和空间分辨率的太阳辐射产品(Huang 等，2012)。通过输入更高分辨率的太阳辐射数据可以提高地表蒸散发双层遥感模型估算土壤蒸发和植被蒸腾的精度。

另外，微波遥感反演的土壤水分产品的空间分辨率非常低，如欧空局SMOS(Soil Moisture and Ocean Salinity)卫星生产的土壤水分空间分辨率为40 km，NASA的SMAP卫星微波辐射计的土壤水分产品空间分辨率为36 km，风云3C的MWRI(Micro-Wave Radiation Imager)土壤水分产品等，与MODIS卫星数据相比，其空间分辨率仍然不能满足P-M遥感模型、P-T遥感模型、TSEB-A等模型的要求，限制了此类双层遥感估算模型的应用。

(3) 卫星像元尺度土壤蒸发和植被蒸腾“地面真值”的获取。地表蒸散发双层遥感估算模型的输出结果为土壤蒸发和植被蒸腾，虽然当前一些学者结合小型蒸渗仪、热扩散液流计的观测数据以及利用稳定同位素技术拆分的土壤蒸发和植被蒸腾对遥感估算值进行了验证，但是仪器观测值的空间代表性非常有限。由于地表的异质性，目前这些站点上观测的土壤蒸发或者植被蒸腾还很难升尺度到卫星像元尺度，无法对基于中低分辨率遥感数据得到的土壤蒸发和植被蒸腾进行验证。因此如何获取中低分辨卫星像元尺度(1 km×1 km)土壤蒸发和植被蒸腾的“地面真值”是今后地表蒸散发双层遥感估算模型验证的关键所在。

参考文献(References)

  • Agam N, Evett S R, Tolk J A, Kustas W P, Colaizzi P D, Alfieri J G, McKee L G, Copeland K S, Howell T A and Chávez JL. 2012. Evaporative loss from irrigated interrows in a highly advective semi-arid agricultural area. Advances in Water Resources, 50 : 20–30. [DOI: 10.1016/j.advwatres.2012.07.010]
  • Agam N, Kustas W P, Anderson M C, Norman J M, Colaizzi P D, Howell T A, Prueger J H, Meyers T P and Wilson T B. 2010. Application of the Priestley–Taylor approach in a two-source surface energy balance model. Journal of Hydrometeorology, 11 (1): 185–198. [DOI: 10.1175/2009JHM1124.1]
  • Allen R, Irmak A, Trezza R, Hendrickx J M H, Bastiaanssen W and Kjaersgaard J. 2011. Satellite-based ET estimation in agriculture using SEBAL and METRIC. Hydrological Processes, 25 (26): 4011–4027. [DOI: 10.1002/hyp.8408]
  • Allen R G, Pereira L S, Raes D and Smith M. 1998. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56. Rome: Food and Agriculture Organization of the United Nation
  • Anderson M C, Kustas W P, Norman J M, Hain C R, Mecikalski J R, Schultz L, González-Dugo M P, Cammalleri C, d’Urso G, Pimstein A and Gao F. 2011. Mapping daily evapotranspiration at field to continental scales using geostationary and polar orbiting satellite imagery. Hydrology and Earth System Sciences, 15 (1): 223–239. [DOI: 10.5194/hess-15-223-2011]
  • Anderson M C, Norman J M, Diak G R, Kustas W P and Mecikalski J R. 1997. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sensing of Environment, 60 (2): 195–216. [DOI: 10.1016/S0034-4257(96)00215-5]
  • Anderson M C, Norman J M, Kustas W P, Houborg R, Starks P J and Agam N. 2008. A thermal-based remote sensing technique for routine mapping of land-surface carbon, water and energy fluxes from field to regional scales. Remote Sensing of Environment, 112 (12): 4227–4241. [DOI: 10.1016/j.rse.2008.07.009]
  • Anderson M C, Norman J M, Mecikalski J R, Torn R D, Kustas W P and Basara J B. 2004. A multiscale remote sensing model for disaggregating regional fluxes to micrometeorological scales. Journal of Hydrometeorology, 5 (2): 343–363. [DOI: 10.1175/1525-7541]
  • Bai J, Jia L, Liu S M, Xu Z W, Hu G C, Zhu M J and Song L S. 2015. Characterizing the footprint of eddy covariance system and large aperture scintillometer measurements to validate satellite-based surface fluxes. IEEE Geoscience and Remote Sensing Letters, 12 (5): 943–947. [DOI: 10.1109/LGRS.2014.2368580]
  • Bateni S M and Liang S L. 2012. Estimating surface energy fluxes using a dual-source data assimilation approach adjoined to the heat diffusion equation. Journal of Geophysical Research, 117 (D17): D17118 [DOI: 10.1029/2012JD017618]
  • Bateni S M, Entekhabi D and Castelli F. 2013a. Mapping evaporation and estimation of surface control of evaporation using remotely sensed land surface temperature from a constellation of satellites. Water Resources Research, 49 (2): 950–968. [DOI: 10.1002/wrcr.20071]
  • Bateni S M, Entekhabi D and Jeng D S. 2013b. Variational assimilation of land surface temperature and the estimation of surface energy balance components. Journal of Hydrology, 481 : 143–156. [DOI: 10.1016/j.jhydrol.2012.12.039]
  • Blyth E M and Harding R J. 1995. Application of aggregation models to surface heat flux from the Sahelian tiger bush. Agricultural and Forest Meteorology, 72 (3/4): 213–235. [DOI: 10.1016/0168-1923(94)02164-F]
  • Boast C W and Robertson T M. 1982. A " Micro-Lysimeter” method for determining evaporation from bare soil: description and laboratory evaluation. Soil Science Society of America Journal, 46 (4): 689–696. [DOI: 10.2136/sssaj1982.03615995004600040005x]
  • Cammalleri C, Anderson M C, Ciraolo G, D’Urso G, Kustas W P, La Loggia G and Minacapilli M. 2012. Applications of a remote sensing-based two-source energy balance algorithm for mapping surface fluxes without in situ air temperature observations. Remote Sensing of Environment, 124 : 502–515. [DOI: 10.1016/j.rse.2012.06.009]
  • Cammalleri C, Anderson M C, Gao F, Hain C R and Kustas W P. 2014. Mapping daily evapotranspiration at field scales over rainfed and irrigated agricultural areas using remote sensing data fusion. Agricultural and Forest Meteorology, 186 : 1–11. [DOI: 10.1016/j.agrformet.2013.11.001]
  • Caparrini F, Castelli F and Entekhabi D. 2003. Mapping of land-atmosphere heat fluxes and surface parameters with remote sensing data. Boundary-Layer Meteorology, 107 (3): 605–633. [DOI: 10.1023/A:1022821718791]
  • Caparrini F, Castelli F and Entekhabi D. 2004. Variational estimation of soil and vegetation turbulent transfer and heat flux parameters from sequences of multisensor imagery. Water Resources Research, 40 (12): W12515 [DOI: 10.1029/2004WR003358]
  • Carlson T. 2007. An overview of the " Triangle Method” for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors, 7 (8): 1612–1629. [DOI: 10.3390/s7081612]
  • Cleugh H A, Leuning R, Mu Q Z and Running S W. 2007. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sensing of Environment, 106 (3): 285–304. [DOI: 10.1016/j.rse.2006.07.007]
  • Colaizzi P D, Kustas W P, Anderson M C, Agam N, Tolk J A, Evett S R, Howell T A, Gowda P H and O’Shaughnessy S A. 2012. Two-source energy balance model estimates of evapotranspiration using component and composite surface temperatures. Advances in Water Resources, 50 : 134–151. [DOI: 10.1016/j.advwatres.2012.06.004]
  • Dijk A I J M V and Bruijnzeel L A. 2001. Modelling rainfall interception by vegetation of variable density using an adapted analytical model. Journal of Hydrology, 247 : 230–238. [DOI: 10.1016/S0022-1694(01)00392-4]
  • Fisher J B, Tu K P and Baldocchi D D. 2008. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sensing of Environment, 112 (3): 901–919. [DOI: 10.1016/j.rse.2007.06.025]
  • Flumignan D L, de Faria R T and Prete C E C. 2011. Evapotranspiration components and dual crop coefficients of coffee trees during crop production. Agricultural Water Management, 98 (5): 791–800. [DOI: 10.1016/j.agwat.2010.12.002]
  • Gao Y C and Long D. 2008. Intercomparison of remote sensing-based models for estimation of evapotranspiration and accuracy assessment based on SWAT. Hydrological Processes, 22 (25): 4850–4869. [DOI: 10.1002/hyp.7104]
  • Gao Y C and Long D. 2008. Progress in models for evapotranspiration estimation using remotely sensed data. Journal of Remote Sensing, 12 (3): 515–528. [DOI: 10.11834/jrs.20080369] ( 高彦春, 龙笛. 2008. 遥感蒸散发模型研究进展. 遥感学报, 12 (3): 515–528. [DOI: 10.11834/jrs.20080369] )
  • Gardiol J M, Serio L A and Della Maggiora A I. 2003. Modelling evapotranspiration of corn (Zea mays) under different plant densities. Journal of Hydrology, 271 (1/4): 188–196. [DOI: 10.1016/S0022-1694(02)00347-5]
  • Granier A, Biron P, Köstner B, Gay L W and Najjar G. 1996. Comparisons of xylem sap flow and water vapour flux at the stand level and derivation of canopy conductance for Scots pine. Theoretical and Applied Climatology, 53 (1/3): 115–122. [DOI: 10.1007/BF00866416]
  • Hong S H, Hendrickx J M H and Borchers B. 2009. Up-scaling of SEBAL derived evapotranspiration maps from Landsat (30m) to MODIS (250m) scale. Journal of Hydrology, 370 (1/4): 122–138. [DOI: 10.1016/j.jhydrol.2009.03.002]
  • Hu G C and Jia L. 2015. Monitoring of evapotranspiration in a semi-arid inland river basin by combining microwave and optical remote sensing observations. Remote Sensing, 7 (3): 3056–3087. [DOI: 10.3390/rs70303056]
  • Hu Z M, Wen X F, Sun X M, Li L H, Yu G R, Lee X and Li S G. 2014. Partitioning of evapotranspiration through oxygen isotopic measurements of water pools and fluxes in a temperate grassland. Journal of Geophysical Research, 119 (3): 358–372. [DOI: 10.1002/2013JG002367]
  • Huang G H, Liu S M and Liang S L. 2012. Estimation of net surface shortwave radiation from MODIS data. International Journal of Remote Sensing, 33 (3): 804–825. [DOI: 10.1080/01431161.2011.577834]
  • Jasechko S, Sharp Z D, Gibson J J, Birks S J, Yi Y and Fawcett P J. 2013. Terrestrial water fluxes dominated by transpiration. Nature, 496 (7445): 347–350. [DOI: 10.1038/nature11983]
  • Jia Z Z, Liu S M, Xu Z W, Chen Y J and Zhu M J. 2012. Validation of remotely sensed evapotranspiration over the Hai River Basin, China. Journal of Geophysical Research, 117 (D13): D13113 [DOI: 10.1029/2011JD017037]
  • Jiang L and Islam S. 1999. A methodology for estimation of surface evapotranspiration over large areas using remote sensing observations. Geophysical Research Letters, 26 (17): 2773–2776. [DOI: 10.1029/1999GL006049]
  • Jiang X L, Kang S Z, Li F S, Du T S, Tong L and Comas L. 2016. Evapotranspiration partitioning and variation of sap flow in female and male parents of maize for hybrid seed production in arid region. Agricultural Water Management, 176 : 132–141. [DOI: 10.1016/j.agwat.2016.05.022]
  • Jung M, Reichstein M, Ciais P, Seneviratne S I, Sheffield J, Goulden M L, Bonan G, Cescatti A, Chen J Q, de Jeu R, Dolman A J, Eugster W, Gerten D, Gianelle D, Gobron N, Heinke J, Kimball J, Law B E, Montagnani L, Mu Q Z, Mueller B, Oleson K, Papale D, Richardson A D, Roupsard O, Running S, Tomelleri E, Viovy N, Weber U, Williams C, Wood E, Zaehle S and Zhang K. 2010. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature, 467 (7318): 951–954. [DOI: 10.1038/nature09396]
  • Kalma J D, McVicar T R and McCabe M F. 2008. Estimating land surface evaporation: a review of methods using remotely sensed surface temperature data. Surveys in Geophysics, 29 (4/5): 421–469. [DOI: 10.1007/s10712-008-9037-z]
  • Kool D, Agam N, Lazarovitch N, Heitman J L, Sauer T J and Ben-Gal A. 2014. A review of approaches for evapotranspiration partitioning. Agricultural and Forest Meteorology, 184 : 56–70. [DOI: 10.1016/j.agrformet.2013.09.003]
  • Kustas W and Anderson M. 2009. Advances in thermal infrared remote sensing for land surface modeling. Agricultural and Forest Meteorology, 149 (12): 2071–2081. [DOI: 10.1016/j.agrformet.2009.05.016]
  • Kustas W P and Norman J M. 1999. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agricultural and Forest Meteorology, 94 (1): 13–29. [DOI: 10.1016/S0168-1923(99)00005-2]
  • Kustas W P, Norman J M, Anderson M C and French A N. 2003. Estimating subpixel surface temperatures and energy fluxes from the vegetation index–radiometric temperature relationship. Remote Sensing of Environment, 85 : 429–440. [DOI: 10.1016/S0034-4257(03)00036-1]
  • Kustas W P, Alfieri J G, Anderson M C, Colaizzi P D, Prueger J H, Evett S R, Neale C M U, French A N, Hipps L E, Chávez J L, Copeland K S and Howell T A. 2012. Evaluating the two-source energy balance model using local thermal and surface flux observations in a strongly advective irrigated agricultural area. Advances in Water Resources, 50 : 120–133. [DOI: 10.1016/j.advwatres.2012.07.005]
  • Leuning R, Zhang Y Q, Rajaud A, Cleugh H and Tu K. 2008. A simple surface conductance model to estimate regional evaporation using MODIS leaf area index and the Penman-Monteith equation. Water Resources Research, 44 (10): W10419 [DOI: 10.1029/2007WR006562]
  • Li F Q, Kustas W P, Anderson M C, Prueger J H and Scott R L. 2008. Effect of remote sensing spatial resolution on interpreting tower-based flux observations. Remote Sensing of Environment, 112 (2): 337–349. [DOI: 10.1016/j.rse.2006.11.032]
  • Li Z L, Tang R L, Wan Z M, Bi Y Y, Zhou C H, Tang B H, Yan G J and Zhang X Y. 2009. A review of current methodologies for regional evapotranspiration estimation from remotely sensed data. Sensors, 9 (5): 3801–3853. [DOI: 10.3390/s90503801]
  • Liu S M, Xu Z W, Song L S, Zhao Q Y, Ge Y, Xu T R, Ma Y F, Zhu Z L, Jia Z Z and Zhang F. 2016. Upscaling evapotranspiration measurements from multi-site to the satellite pixel scale over heterogeneous land surfaces. Agricultural and Forest Meteorology, 230-231 : 97–113. [DOI: 10.1016/j.agrformet.2016.04.008]
  • Long D and Singh V P. 2012. A two-source trapezoid model for evapotranspiration (TTME) from satellite imagery. Remote Sensing of Environment, 121 : 370–388. [DOI: 10.1016/j.rse.2012.02.015]
  • Long D and Singh V P. 2013. Assessing the impact of end-member selection on the accuracy of satellite-based spatial variability models for actual evapotranspiration estimation. Water Resources Research, 49 (5): 2601–2618. [DOI: 10.1002/wrcr.20208]
  • Long D, Singh V P and Li Z L. 2011. How sensitive is SEBAL to changes in input variables, domain size and satellite sensor?. Journal of Geophysical Research, 116 (D21): D21107 [DOI: 10.1029/2011JD016542]
  • Lund M R and Soegaard H. 2003. Modelling of evaporation in a sparse millet crop using a two-source model including sensible heat advection within the canopy. Journal of Hydrology, 280 (1/4): 124–144. [DOI: 10.1016/S0022-1694(03)00222-1]
  • Michel D, Jiménez C, Miralles D G, Jung M, Hirschi M, Ershadi A, Martens B, McCabe M F, Fisher J B, Mu Q, Seneviratne S I, Wood E F and Fernández-Prieto D. 2016. The WACMOS-ET project–Part 1: tower-scale evaluation of four remote-sensing-based evapotranspiration algorithms. Hydrology and Earth System Sciences, 20 (2): 803–822. [DOI: 10.5194/hess-20-803-2016]
  • Miralles D G, Holmes T R H, De Jeu R A M, Gash J H, Meesters A G C A and Dolman A J. 2011. Global land-surface evaporation estimated from satellite-based observations. Hydrology and Earth System Sciences, 15 (2): 453–469. [DOI: 10.5194/hess-15-453-2011]
  • Miralles D G, Jiménez C, Jung M, Michel D, Ershadi A, McCabe M F, Hirschi M, Martens B, Dolman A J, Fisher J B, Mu Q Z, Seneviratne S I, Wood E F and Fernández-Prieto D. 2016. The WACMOS-ET project–Part 2: evaluation of global terrestrial evaporation data sets. Hydrology and Earth System Science, 20 (2): 823–842. [DOI: 10.5194/hess-20-823-2016]
  • Monteith J L. 1965. Evaporation and environment//Fogg G E, ed. The State and Movement of Water in Living Organisms. Cambridge: Cambridge University Press
  • Morillas L, Leuning R, Villagarcía L, García M, Serrano-Ortiz P and Domingo F. 2013. Improving evapotranspiration estimates in Mediterranean drylands: the role of soil evaporation. Water Resources Research, 49 (10): 6572–6586. [DOI: 10.1002/wrcr.20468]
  • Mu Q Z, Heinsch F A, Zhao M S and Running S W. 2007. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sensing of Environment, 111 (4): 519–536. [DOI: 10.1016/j.rse.2007.04.015]
  • Mu Q Z, Zhao M S and Running S W. 2011. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sensing of Environment, 115 (8): 1781–1800. [DOI: 10.1016/j.rse.2011.02.019]
  • Newman B D, Wilcox B P, Archer S R, Breshears D D, Dahm C N, Duffy C J, McDowell N G, Phillips F M, Scanlon B R and Vivoni E R. 2006. Ecohydrology of water-limited environments: a scientific vision. Water Resources Research, 42 (6): W06302 [DOI: 10.1029/2005WR004141]
  • Nishida K, Nemani R R, Running S W and Glassy J M. 2003. An operational remote sensing algorithm of land surface evaporation. Journal of Geophysical Research, 108 (D9): 4270 [DOI: 10.1029/2002JD002062]
  • Norman J M, Anderson M C, Kustas W P, French A N, Mecikalski J, Torn R, Diak G R, Schmugge T J and Tanner B C W. 2003. Remote sensing of surface energy fluxes at 101-m pixel resolutions . Water Resources Research, 39 (8): 1221 [DOI: 10.1029/2002WR001775]
  • Norman J M, Kustas W P and Humes K S. 1995. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agricultural and Forest Meteorology, 77 (3/4): 263–293. [DOI: 10.1016/0168-1923(95)02265-Y]
  • Ortega-Farias S, Poblete-Echeverría C and Brisson N. 2010. Parameterization of a two-layer model for estimating vineyard evapotranspiration using meteorological measurements. Agricultural and Forest Meteorology, 150 (2): 276–286. [DOI: 10.1016/j.agrformet.2009.11.012]
  • Paço T A, David T S, Henriques M O, Pereira J S, Valente F, Banza J, Pereira F L, Pinto C and David J S. 2009. Evapotranspiration from a Mediterranean evergreen oak savannah: the role of trees and pasture. Journal of Hydrology, 369 (1/2): 98–106. [DOI: 10.1016/j.jhydrol.2009.02.011]
  • Paço T A, Ferreira M I, Rosa R D, Paredes P, Rodrigues G C, Conceição N, Pacheco C A and Pereira L S. 2012. The dual crop coefficient approach using a density factor to simulate the evapotranspiration of a peach orchard: SIMDualKc model versus eddy covariance measurements. Irrigation Science, 30 (2): 115–126. [DOI: 10.1007/s00271-011-0267-3]
  • Phillips O L, Aragão L E O C, Lewis S L, Fisher J B, Lloyd J, López-González G, Malhi Y, Monteagudo A, Peacock J, Quesada C A, van der Heijden G, Almeida S, Amaral I, Arroyo L, Aymard G, Baker T R, Bánki O, Blanc L, Bonal D, Brando P, Chave J, de Oliveira Á C A, Cardozo N D, Czimczik C I, Feldpausch T R, Freitas M A, Gloor E, Higuchi N, Jiménez E, Lloyd G, Meir P, Mendoza C, Morel A, Neill D A, Nepstad D, Patiño S, Peñuela M C, Prieto A, Ramírez F, Schwarz M, Silva J, Silveira M, Thomas A S, ter Steege H, Stropp J, Vásquez R, Zelazowski P, Dávila E A, Andelman S, Andrade A, Chao K J, Erwin T, Di Fiore A, Honorio C E, Keeling H, Killeen T J, Laurance W F, Cruz A P, Pitman N C A, Vargas P N, Ramírez-Angulo H, Rudas A, Salamão R, Silva N, Terborgh J and Torres-Lezama A. 2009. Drought sensitivity of the amazon rainforest. Science, 323 (5919): 1344–1347. [DOI: 10.1126/science.1164033]
  • Priestley C H B and Taylor R J. 1972. On the assessment of surface heat flux and evaporation using large-scale parameters. Monthly Weather Review, 100 (2): 81–92. [DOI: 10.1175/1520-0493(1972)100<0081:OTAOSH>2.3.CO;2]
  • Rousseaux M C, Figuerola P I, Correa-Tedesco G and Searles P S. 2009. Seasonal variations in sap flow and soil evaporation in an olive (Olea europaea L . ) grove under two irrigation regimes in an arid region of Argentina. Agricultural Water Management, 96 (6): 1037–1044. [DOI: 10.1016/j.agwat.2009.02.003]
  • Scanlon T M and Kustas W P. 2010. Partitioning carbon dioxide and water vapor fluxes using correlation analysis. Agricultural and Forest Meteorology, 150 (1): 89–99. [DOI: 10.1016/j.agrformet.2009.09.005]
  • Semmens K A, Anderson M C, Kustas W P, Gao F, Alfieri J G, McKee L, Prueger J H, Hain C R, Cammalleri C, Yang Y, Xia T, Sanchez L, Alsina M M and Vélez M. 2016. Monitoring daily evapotranspiration over two California vineyards using Landsat 8 in a multi-sensor data fusion approach. Remote Sensing of Environment, 185 : 155–170. [DOI: 10.1016/j.rse.2015.10.025]
  • Shawcroft R W and Gardner H R. 1983. Direct evaporation from soil under a row crop canopy. Agricultural Meteorology, 28 (3): 229–238. [DOI: 10.1016/0002-1571(83)90028-6]
  • Shuttleworth W J and Gurney R J. 1990. The theoretical relationship between foliage temperature and canopy resistance in sparse crops. Quarterly Journal of the Royal Meteorological Society, 116 (492): 497–519. [DOI: 10.1002/qj.49711649213]
  • Shuttleworth W J and Wallace J S. 1985. Evaporation from sparse crops-an energy combination theory. Quarterly Journal of the Royal Meteorological Society, 111 (469): 839–855. [DOI: 10.1002/qj.49711146910]
  • Song L S, Kustas W P, Liu S M, Colaizzi P D, Nieto H, Xu Z W, Ma Y F, Li M S, Xu T R, Agam N, Tolk J A and Evett S R. 2016a. Applications of a thermal-based two-source energy balance model using Priestley-Taylor approach for surface temperature partitioning under advective conditions. Journal of Hydrology, 540 : 574–587. [DOI: 10.1016/j.jhydrol.2016.06.034]
  • Song L S, Liu S M, Kustas W P, Zhou J, Xu Z W, Xia T and Li M S. 2016b. Application of remote sensing-based two-source energy balance model for mapping field surface fluxes with composite and component surface temperatures. Agricultural and Forest Meteorology, 230-231 : 8–19. [DOI: 10.1016/j.agrformet.2016.01.005]
  • Song L S, Liu S M, Zhang X, Zhou J and Li M S. 2015. Estimating and validating soil evaporation and crop transpiration during the HiWATER-MUSOEXE. IEEE Geoscience and Remote Sensing Letters, 12 (2): 334–338. [DOI: 10.1109/LGRS.2014.2339360]
  • Sun L, Liang S L, Yuan W P and Chen Z X. 2013. Improving a Penman–Monteith evapotranspiration model by incorporating soil moisture control on soil evaporation in semiarid areas. International Journal of Digital Earth, 6 (S1): 134–156. [DOI: 10.1080/17538947.2013.783635]
  • Tang R L, Li Z L and Tang B H. 2010. An application of the Ts–VI triangle method with enhanced edges determination for evapotranspiration estimation from MODIS data in arid and semi-arid regions: implementation and validation . Remote Sensing of Environment, 114 (3): 540–551. [DOI: 10.1016/j.rse.2009.10.012]
  • Tang R L, Li Z L, Jia Y Y, Li C R, Sun X M, Kustas W P and Anderson M C. 2011. An intercomparison of three remote sensing-based energy balance models using Large Aperture Scintillometer measurements over a wheat–corn production region. Remote Sensing of Environment, 115 (12): 3187–3202. [DOI: 10.1016/j.rse.2011.07.004]
  • Trenberth K E, Fasullo J T and Kiehl J. 2009. Earth’s global energy budget. Bulletin of the American Meteorological Society, 90 (3): 311–323. [DOI: 10.1175/2008BAMS2634.1]
  • Vinukollu R K, Meynadier R, Sheffield J and Wood E F. 2011. Multi-model, multi-sensor estimates of global evapotranspiration: climatology, uncertainties and trends. Hydrological Processes, 25 (26): 3993–4010. [DOI: 10.1002/hyp.8393]
  • Wang K C and Dickinson R E. 2012. A review of global terrestrial evapotranspiration: observation, modeling, climatology, and climatic variability. Reviews of Geophysics, 50 (2): RG2005 [DOI: 10.1029/2011RG000373]
  • Wang K C, Li Z Q and Cribb M. 2006. Estimation of evaporative fraction from a combination of day and night land surface temperatures and NDVI: a new method to determine the Priestley–Taylor parameter. Remote Sensing of Environment, 102 (3/4): 293–305. [DOI: 10.1016/j.rse.2006.02.007]
  • Wei Z W, Yoshimura K, Okazaki A, Kim W, Liu Z F and Yokoi M. 2015. Partitioning of evapotranspiration using high-frequency water vapor isotopic measurement over a rice paddy field. Water Resources Research, 51 (5): 3716–3729. [DOI: 10.1002/2014WR016737]
  • Welp L R, Lee X, Kim K, Griffis T J, Billmark K A and Baker J M. 2008. δ18O of water vapour, evapotranspiration and the sites of leaf water evaporation in a soybean canopy . Plant, Cell and Environment, 31 (9): 1214–1228. [DOI: 10.1111/j.1365-3040.2008.01826.x]
  • Wen X F, Lee X, Sun X M, Wang J L, Hu Z M, Li S G and Yu G R. 2012. Dew water isotopic ratios and their relationships to ecosystem water pools and fluxes in a cropland and a grassland in China. Oecologia, 168 (2): 549–561. [DOI: 10.1007/s00442-011-2091-0]
  • Wen X F, Yang B, Sun X M and Lee X. 2016. Evapotranspiration partitioning through in-situ oxygen isotope measurements in an oasis cropland. Agricultural and Forest Meteorology, 230-231 : 89–96. [DOI: 10.1016/j.agrformet.2015.12.003]
  • Williams D G, Cable W, Hultine K, Hoedjes J C B, Yepez E A, Simonneaux V, Er-Raki S, Boulet G, de Bruin H A R, Chehbouni A, Hartogensis O K and Timouk F. 2004. Evapotranspiration components determined by stable isotope, sap flow and eddy covariance techniques. Agricultural and Forest Meteorology, 125 (3/4): 241–258. [DOI: 10.1016/j.agrformet.2004.04.008]
  • Xia T, Kustas W P, Anderson M C, Alfieri J G, Gao F, McKee L, Prueger J H, Geli H M E, Neale C M U, Sanchez L, Alsina M M and Wang Z J. 2016. Mapping evapotranspiration with high-resolution aircraft imagery over vineyards using one- and two-source modeling schemes. Hydrology and Earth System Science, 20 (4): 1523–1545. [DOI: 10.5194/hess-20-1523-2016]
  • Xia Y L, Mitchell K, Ek M, Cosgrove B, Sheffield J, Luo L F, Alonge C, Wei H L, Meng J, Livneh B, Duan Q Y and Lohmann D. 2012a. Continental-scale water and energy flux analysis and validation for North American Land Data Assimilation System project phase 2 (NLDAS-2): 2. Validation of model-simulated streamflow. Journal of Geophysical Research, 117 (D3): D03110 [DOI: 10.1029/2011JD016051]
  • Xia Y L, Mitchell K, Ek M, Sheffield J, Cosgrove B, Wood E, Luo L F, Alonge C, Wei H L, Meng J, Livneh B, Lettenmaier D, Koren V, Duan Q Y, Mo K, Fan Y and Mocko D. 2012b. Continental-scale water and energy flux analysis and validation for the North American Land Data Assimilation System project phase 2 (NLDAS-2): 1. Intercomparison and application of model products. Journal of Geophysical Research, 117 (D3): D3 [DOI: 10.1029/2011JD016048]
  • Xin X Z and Liu Q H. 2010. The two-layer surface energy balance parameterization scheme (TSEBPS) for estimation of land surface heat fluxes. Hydrology and Earth System Science, 14 (3): 491–504. [DOI: 10.5194/hess-14-491-2010]
  • Xu T R, Bateni S M, Liang S, Entekhabi D and Mao K B. 2014. Estimation of surface turbulent heat fluxes via variational assimilation of sequences of land surface temperatures from geostationary operational environmental satellites. Journal of Geophysical Research, 119 (18): 10780–10798. [DOI: 10.1002/2014JD021814]
  • Xu T R, Bateni S M, Margulis S A, Song L S, Liu S M and Xu Z W. 2016. Partitioning evapotranspiration into soil evaporation and canopy transpiration via a two-source variational data assimilation system. Journal of Hydrometeorology, 17 (9): 2353–2370. [DOI: 10.1175/JHM-D-15-0178.1]
  • Xu T R, Liu S M, Qin J and Liang S L. 2009. Estimation of sensible and latent heat flux by assimilating MODIS LST products. Journal of Remote Sensing, 13 (6): 989–1009. [DOI: 10.11834/jrs.20090602] ( 徐同仁, 刘绍民, 秦军, 梁顺林. 2009. 同化MODIS温度产品估算地表水热通量. 遥感学报, 13 (6): 989–1009. [DOI: 10.11834/jrs.20090602] )
  • Xu T R, Liu S M, Xu Z W, Liang S L and Xu L. 2015. A dual-pass data assimilation scheme for estimating surface fluxes with FY3A-VIRR land surface temperature. Science China Earth Sciences, 58 (2): 211–230. [DOI: 10.1007/s11430-014-4964-7]
  • Yang K, Watanabe T, Koike T, Li X, Fujii H, Tamagawa K, Ma Y M and Ishikawa H. 2007. Auto-calibration system developed to assimilate AMSR-E data into a land surface model for estimating soil moisture and the surface energy budget. Journal of the Meteorological Society of Japan Seris II, 85A : 229–242. [DOI: 10.2151/jmsj.85A.229]
  • Yang Y M, Su H B, Zhang R H, Tian J and Li L. 2015. An enhanced two-source evapotranspiration model for land (ETEML): Algorithm and evaluation. Remote Sensing of Environment, 168 : 54–65. [DOI: 10.1016/j.rse.2015.06.020]
  • Yang Y T, Long D, Guan H D, Liang W, Simmons C and Batelaan O. 2015. Comparison of three dual-source remote sensing evapotranspiration models during the MUSOEXE-12 campaign: revisit of model physics. Water Resources Research, 51 (5): 3145–3165. [DOI: 10.1002/2014WR015619]
  • Yao Y J, Liang S L, Cheng J, Liu S M, Fisher J B, Zhang X D, Jia K, Zhao X, Qin Q M, Zhao B, Han S J, Zhou G S, Zhou G Y, Li Y L and Zhao S H. 2013. MODIS-driven estimation of terrestrial latent heat flux in China based on a modified Priestley–Taylor algorithm. Agricultural and Forest Meteorology, 171-172 : 187–202. [DOI: 10.1016/j.agrformet.2012.11.016]
  • Yuan W P, Liu S G, Yu G R, Bonnefond J M, Chen J Q, Davis K, Desai A R, Goldstein A H, Gianelle D, Rossi F, Suyker A E and Verma S B. 2010. Global estimates of evapotranspiration and gross primary production based on MODIS and global meteorology data. Remote Sensing of Environment, 114 (7): 1416–1431. [DOI: 10.1016/j.rse.2010.01.022]
  • Zhang K, Kimball J S and Running S W. 2016. A review of remote sensing based actual evapotranspiration estimation. Wiley Interdisciplinary Reviews: Water, 3 (6): 834–853. [DOI: 10.1002/wat2.1168]
  • Zhang R H, Tian J, Li Z L, Su H B, Chen S H and Tang X Z. 2010. Principles and methods for the validation of quantitative remote sensing products. Science China Earth Sciences, 53 (5): 741–751. [DOI: 10.1007/s11430-010-0021-3]
  • Zhang R H. 2009. Quantitative Thermal Infrared Remote Sensing Model and Ground Experimental Foundation. Beijing: Science Publishing Press: 382–417 (张仁华. 2009. 定量热红外遥感模型及地面实验基础. 北京: 科学出版社: 382–417)
  • Zhang Y Q, Kang S Z, Ward E J, Ding R S, Zhang X and Zheng R. 2011. Evapotranspiration components determined by sap flow and microlysimetry techniques of a vineyard in northwest China: dynamics and influential factors. Agricultural Water Management, 98 (8): 1207–1214. [DOI: 10.1016/j.agwat.2011.03.006]
  • Zhou S, Yu B F, Huang Y F and Wang G Q. 2014. The effect of vapor pressure deficit on water use efficiency at the subdaily time scale. Geophysical Research Letters, 41 (14): 5005–5013. [DOI: 10.1002/2014GL060741]
  • Zhou S, Yu B F, Zhang Y, Huang Y F and Wang G Q. 2016. Partitioning evapotranspiration based on the concept of underlying water use efficiency. Water Resources Research, 52 (2): 1160–1175. [DOI: 10.1002/2015WR017766]
数据专区
  • 目录 目录
  • 文章信息 文章信息
  • 引用格式 引用格式
  • 地图 地图
  • 评论 评论
  • 图 图
  • 表 表
  • 二维码 二维码
  • 参考文献 参考文献
  • 多媒体 多媒体