|
收稿日期: 2016-11-23; 优先数字出版日期: 2017-09-01
基金项目: 国家自然科学基金(编号:41271435,41301479);辽宁省自然科学基金(编号:2015020190)
第一作者简介: 赵雪梅(1989— ),女,博士研究生,研究方向为模糊数学、信息几何在遥感影像处理中的应用。E-mail:374010101@qq.com
中图分类号: TP790
文献标识码: A
|
摘要
为了实现影像的自动化分割,提出一种利用非监督方式将观测数据采样化的遥感影像分割方法。该方法利用欧氏空间的概率分布建模采样数据和观测数据,并将其映射到黎曼空间,通过不断将观测数据转换为采样数据的方式实现影像的自动采样化。每次采样过程只需计算观测数据点到采样点的测地线距离,将距采样点测地线距离最小的观测数据转化为采样数据,以保证采样数据不断趋于该类数据的真实分割结果,同时使算法能够有效分割具有不同像素数的类别。将算法应用于模拟影像和真实遥感影像分割,对其分割结果以及传统基于统计、基于模糊的非监督算法和基于神经网络的监督算法相应分割结果定性定量的对比分析验证了该算法的有效性及可行性。
关键词
遥感影像分割, 非监督, 采样化, 映射, 黎曼空间
Abstract
Image segmentation is a very common application in remote sensing, in which the number of classes is always given by users. To segment remote sensing images automatically, a sampling method which can transmit observed data into sample data is proposed based on the characteristics in Riemannian space. Therefore, this paper presents an unsupervised image segmentation algorithm which can automatically segment remote sensing images by sampling the detected data into samples. First, model the initial samples obtained by block sampling or artificial sampling through Gaussian probability distribution function (pdf). Second, to take the neighborhood system of the detected image into consideration, Gaussian pdf is also employed to depict the features of the pixel and its correlation between neighbor pixels. Then both the samples and the detected image are mapped to the Riemannian space. In the Riemannian space, the similarity between the points expressing the detected image and the points standing for samples are measured by geodesic, which is the least distance on the curve surface of a manifold. The nearest points standing for the detected image to each sample are transmitted to samples and then the models of the samples are updated according to the new ones. By continually sampling, the models of the samples are tending to their real models, which represents the real segmentation through sampling the detected data. In each sample process, only the nearest detected data are transformed into sample data to make sure the presented algorithm can distinguish different classes with different number of pixels in it. Geodesic employed in this paper evaluates the differences between the detected model and the sample model to improve the accuracy of sampling. The proposed algorithm is carried out on synthetic and real remote sensing images. Experiments on synthetic image shows the changes of samples both in the image and in feature space. Display of the sampling process demonstrate that the models characterizing each class trends to the real ones and the samples tends to the real data of each class in the feature space. Analysis on segmentation results of HMRF-CSA, GRM-FCM, neural network and the proposed algorithms on real remote sensing images validate the effectiveness of the proposed algorithm. The overall accuracy of the proposed algorithm can even reach to 98.9%, which is much higher than those of the compared algorithms. Experiments on synthetic image show the models of samples can tends to real ones, which validate that the proposed sampling process is able to fit the real distributions of each class. Experimental results on real remote sensing images demonstrate that the effectiveness of sampling operation can distinguish classes with different number of pixels. Quantitative and qualitative analysis on the segmentation results show that the presented algorithm can segment remote sensing images accurately and quickly. Besides, the proposed algorithm can be used both as an unsupervised image segmentation algorithm to realize the segmentation of remote sensing images or as sampling process in supervised image segmentation algorithm to provide reliable sample results.
Key words
remote sensing image segmentation, unsupervised, sampling, mapping, Riemannian space
1 引 言
遥感影像分割,尤其是大尺度遥感影像分割,一直是遥感影像处理的重点难点问题(Michel 等,2015)。传统非监督方法主要分为基于统计的影像分割方法(Zhang 等,2014;Li和Feng,2016)和基于模糊的影像分割方法(于波 等,2013;Zhang 等,2016)。前者通过定义表征影像特征的统计模型,并求解相应模型参数获取影像最优分割结果。Blaiotta等人(2016)利用高斯混合模型描述影像统计分布,而后利用MAP方法求得使后验概率最大的分布参数,进而实现影像分割。Li等人(2016)利用Student’s T模型Dirichlet过程建模影像分布模型,并通过改进的EM方法求解该模型参数。然而,上述基于统计的分割方法在求解参数的过程中需要大量采样,导致算法运行速度较慢。而后者基于模糊的影像分割方法通过求解目标函数实现分割,无需采样,因此能够在一定程度上提高算法运行速度。Liu等人(2015)定义基于区域和基于像素的非相似性测度以增强同类像素间的相关性,并引入空间约束,以便提高分割精度。Zhao和Du(2016)利用Mahalanobis距离描述像素与聚类间的非相似性测度,并结合模糊聚类算法定义目标函数,而后通过最小化目标函数的方法实现影像分割。
传统非监督分割方法均在假设影像模型的基础上通过循环迭代的方式求得其最优解。但是循环迭代导致算法运行速度较慢,无法处理大尺度遥感影像。此外,非监督分割方法易陷入局部极值且其分割结果受相关参数影响较大(Gong 等,2013;Niu 等,2017)。基于监督的影像分割方法需预先在各类地物中采取30%的典型样本数据,通过样本数据训练分类器,而后根据分类器模型实现影像分割,分割过程无需循环迭代,且不依赖于相关参数。Sun等人(2015)利用稀疏多项式回归分类器训练采样数据,并通过MRF先验概率引入像素空间约束,进而提高分割精度。王春艳等人(2016)在一型模糊模型的基础上利用均值或标准差建立区间二型模糊模型,并赋予不同模糊模型以不同的权值,在此基础上构建基于一型和二型模糊模型的模糊隶属度,以表征像素隶属于不同类别的程度,进而实现分割决策。Zhao和Du(2016)提出一种基于降维和深度学习技术的光谱和空间特征提取方法。该方法利用平衡局部判别嵌入法从高维数据中提取特征信息,同时利用卷积神经网络自动识别空间相关特征,最后结合光谱和空间信息实现特征融合进而实现影像分割。
基于监督的分割方法能够有效解决非监督方法循环迭代易陷入局部极值且受相关参数影响较大的问题。但是分类器训练过程通常需要大量采样。当模型较为复杂时,分类器训练时间成倍增长。此外,当分割数据类型或传感器成像条件与训练样本不一致时,现有分类器无法满足新数据的分割需求,因此需要重新采样并训练新的分类器。综上所述,监督分割算法通常适用于大批量遥感影像数据处理,但当影像数据类型改变时,现有分类器也应重新训练。
为了避免非监督分割算法易陷入局部极值且受参数影响较大,以及监督算法人工训练分类器的问题,本文设计基于黎曼空间的观测数据“采样化”过程,通过将观测数据转换为采样数据的方式,在黎曼空间实现遥感影像自动采样化的同时获得相应分割结果。
2 算法描述
首先在欧氏空间分别建立采样数据和观测数据的分布模型,而后将其映射到黎曼空间,并通过黎曼空间测地线准则实现观测数据的采样化,其过程主要包含以下5个部分。
2.1 空间映射方法
已知欧氏空间的一个分布
|
$p\left( x \right) = \frac{1}{{\sqrt {2\pi } \sigma }}\exp \left\{ { - \frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\sigma ^{\rm{2}}}}}} \right\}$
|
(1) |
式中,x为随机变量,p(x)为其正态分布,μ,σ分别为该分布的均值和标准差。对式(1)作如下变形
|
$\begin{aligned} p\left( x \right) = & \exp \left\{ { - \displaystyle\frac{{{x^2}}}{{2{\sigma ^2}}} + \displaystyle\frac{{\mu x}}{{{\sigma ^2}}} - \displaystyle\frac{{{\mu ^2}}}{{2{\sigma ^2}}}} -\right.\\ & \left. {{\rm{ }} \ln \sigma - \displaystyle\frac{1}{2}\ln \left( {2\pi } \right)} \right\} \end{aligned}$
|
(2) |
令
|
$\left\{ \begin{array}{l}{r_1} = {x^2}\quad {r_2} = x\\[7pt]{\theta ^{\rm{1}}} = - \displaystyle\frac{1}{{2{\sigma ^2}}}\quad {\theta ^{\rm{2}}} = \displaystyle\frac{\mu }{{{\sigma ^2}}}\end{array} \right.$
|
(3) |
则
|
$\begin{aligned}\psi \left( {{\theta }} \right) = & \displaystyle\frac{{{\mu ^2}}}{{2{\sigma ^2}}}{\rm{ + }}\ln \sigma {\rm{ + }}\displaystyle\frac{1}{2}\ln \left( {2\pi } \right)=\\ & {\rm{ }} - \frac{{{{\left( {{\theta ^2}} \right)}^2}}}{{4{\theta ^1}}} - \displaystyle\frac{1}{2}\ln \left( { - 2{\theta ^1}} \right){\rm{ + }}\displaystyle\frac{1}{2}\ln \left( {2\pi } \right)\end{aligned}$
|
(4) |
式中,θ=(θ1,θ2),式(1)可表示为
|
$p\left( x \right) = \exp \left( {{r_k}{\theta ^k} - \psi \left( {{\theta}} \right)} \right)$
|
(5) |
式中,k为参数分量索引,{θk}为坐标系,(θ1,θ2)为随机变量x在该坐标系下的坐标(上下脚标均为参数索引,幂指数在括号外)。由爱因斯坦公约(Brody和Hook,2009),式(5)中
|
$\left\{ \begin{array}{l}{\eta _1} = \displaystyle\frac{{\partial \psi \left( {{\theta}} \right)}}{{\partial {\theta ^1}}} = \displaystyle\frac{{{{\left( {{\theta ^2}} \right)}^2}}}{{4{{\left( {{\theta ^1}} \right)}^2}}} - \displaystyle\frac{1}{{2{\theta ^1}}}\\[9pt]{\eta _2} = \displaystyle\frac{{\partial \psi \left( {{\theta}} \right)}}{{\partial {\theta ^2}}} = - \displaystyle\frac{{{\theta ^2}}}{{2{\theta ^1}}}\end{array} \right.$
|
(6) |
η的势能函数为
|
$\begin{aligned}\varphi \left( {{\eta}} \right) = & {\theta ^k}{\eta _k} - \psi \left( {{\theta}} \right) =\\& - \displaystyle\frac{1}{2}\ln \left\{ { - \left[ {{{\left( {{\eta _2}} \right)}^2} - {\eta _1}} \right]} \right\}\\& - \displaystyle\frac{1}{2}\ln \left( {2\pi } \right) - \displaystyle\frac{1}{2}\end{aligned}$
|
(7) |
2.2 观测数据建模
令X={xi|i=1,2,
|
${\mu _i} = \frac{{\sum\limits_{i' \in {{{N}}_i}} {{x_{i'}}} }}{{\# {N_i}}}$
|
(8) |
|
${\sigma _i} = \sqrt {\frac{{\sum\limits_{i' \in {{{N}}_i}} {{{\left( {{x_{i'}} - {\mu _i}} \right)}^2}} }}{{\# {N_i} - 1}}} $
|
(9) |
式中,#Ni表征该集合内像素个数。因此,第i个像素的分布可表示为
|
${p_i}\left( x \right) = \frac{1}{{\sqrt {2\pi } {\sigma _i}}}\exp \left\{ { - \frac{{{{\left( {x - {\mu _i}} \right)}^2}}}{{2\sigma _i^2}}} \right\}$
|
(10) |
根据2.1介绍的空间映射方法可将影像域由欧氏空间映射至黎曼空间。黎曼流形上一点不但能够描述欧氏空间像素的自身光谱测度,还包含影像域像素与邻域像素的统计关系,利用黎曼空间的坐标表征像素间的内在属性。而后在此基础上更加高效地利用影像特征分割。
2.3 采样数据建模
令S为采样数据集合,计算每个类别采样集合的均值和方差
|
${\mu _j} = \frac{{\sum\limits_{w \in {{{M}}_j}} {{x_w}} }}{{\# {M_j}}}$
|
(11) |
|
${\sigma _j} = \sqrt {\frac{{\sum\limits_{j \in {{{M}}_w}} {{{\left( {{x_w} - {\mu _j}} \right)}^2}} }}{{\# {M_w} - 1}}} $
|
(12) |
式中,j为类别索引,Mw为采样数据集合,w为集合索引,#Mw表征该集合内像素个数。因此,第j类的分布可表示为
|
${p_j}\left( x \right) = \frac{1}{{\sqrt {2\pi } {\sigma _j}}}\exp \left\{ { - \frac{{\left( {x - {\mu _j}} \right)}^2}{{2\sigma _j^2}}} \right\}$
|
(13) |
采用2.1介绍的映射方法可在黎曼空间构建采样数据模型,并以采样点的形式描述欧氏空间该类采样数据集的特性。该方法不但能够简化采样数据集的表达方式,准确建模采样数据,还能够更加准确地计算观测数据与采样数据的差异程度。
2.4 分割准则
黎曼空间两点间的距离(Amari 等,1992;Amari,1995)定义如下
|
$D\left[ {{p_i}||{p_j}} \right] = {\psi _{{p_i}}}\left( {{\theta}} \right) + {\varphi _{{p_j}}}\left( {{\eta}} \right) - {\theta ^k}{\eta _k}$
|
(14) |
式中,pi表示待分割影像在黎曼空间中的点(观测数据点),pj为采样数据映射在黎曼空间中的点(采样点)。根据式(14)能够计算黎曼空间中观测数据点到采样点的测地线距离,进而将观测数据点划分到距离最近的采样点代表的类别中。
2.5 分割策略
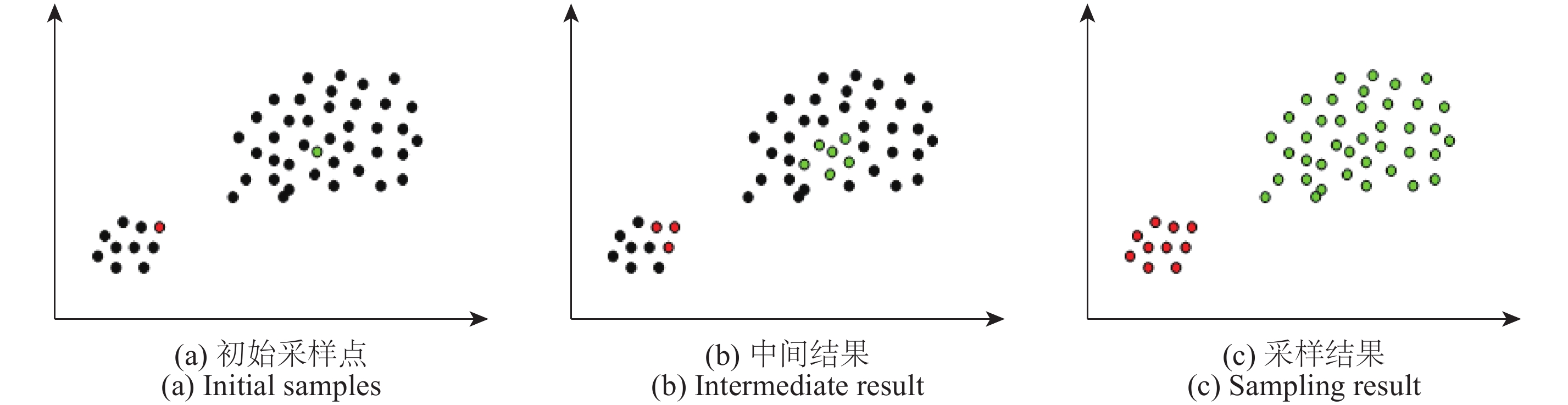
影像分割的主要挑战是表征各类别特征的模型的建立,模型选取的准确与否直接影响最终的分割结果。为了更加准确地建立采样数据模型,本文提出两种初始化采样策略:(1)人工选择:通过人工选择的方式,在各类中分别选取一个或多个采样点;(2)分段采样:假设影像包含c个类别,将影像像素灰度级平均分成c+1段,并取中间c个值作为初始采样点(图1(a),此时c=2,红色点为横纵坐标均为1/3位置的点;绿色点为横纵坐标均为2/3位置的点)。完成初始化采样后以初始采样点灰度值看作采样数据分布均值,并假设初始采样数据集方差为1,即可计算黎曼空间初始采样点的位置。然后计算每个观测数据点距采样点的距离,将距离采样点最近的、具有相同测地线距离的所有观测数据点转化为新的采样数据,并根据现有采样数据更新黎曼流形上的采样点。图1(b)表示图1(a)中距离原有采样点最近的观测数据被转换为采样数据的过程。通过不断采样化,观测数据逐渐被转换为采样数据,且采样数据逐渐收敛于各类真实数据。当完成所有影像数据的采样化时,即可得到影像分割结果(图1(c),观测数据全部转换为采样数据)。由于每次更新采样点对应欧氏空间的采样数据时,将距离采样点最近的且具有相同测地线距离的所有观测数据点视为新的采样数据,因此当影像域的灰度级一定时,影像越大,具有相同测地线距离的数据越多,分割效率越高。但当大部分数据点转化为采样点后,每次采样时距离采样模型最近的且具有相等测地线距离的数据点逐渐减少,分割效率降低。此时,可选取一定步长,将距离采样点最近的、步长内所有数据点视为采样点在欧氏空间的采样。
算法执行步骤为
(1)设置初始值:聚类数c,步长s;
(2)根据式(8)—(10)计算待分割影像中每个像素点在其邻域系统的高斯分布,并利用该高斯分布描述像素点特征;
(3)根据式(1)—(7)所示方法,将表征影像每个像素点特征的高斯分布映射到黎曼空间;
(4)通过人工选择或分段采样的方式初始化采样数据分布特征,并将其表示为黎曼流形上的采样数据点;
(5) 根据式(14)计算黎曼空间影像数据点与采样数据点的测地线距离;
(6)如果距离采样数据点最近的、具有相等测地线距离的点数大于给定步长s,则将满足条件的点视为黎曼空间采样数据点在欧氏空间中的采样;否则,取步长s内距离采样数据点最近的点,并将其视为黎曼空间采样数据点在欧氏空间中的采样;
(7)重复步骤(5)、(6)直到影像上的所有点均表示为采样点。
3 实验结果
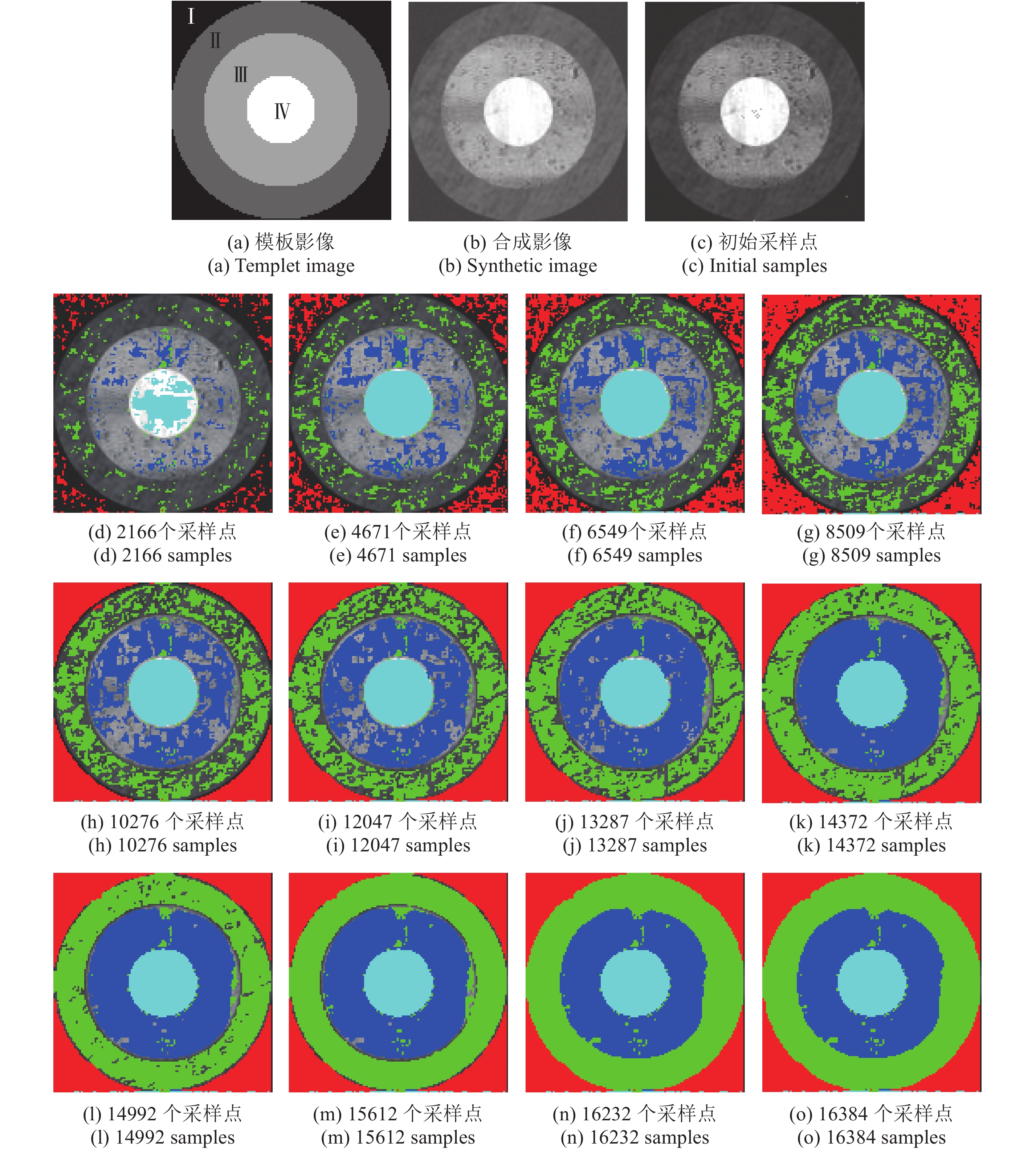
为了更加清楚的显示提出算法采样化过程,根据图2(a)模板影像生成一幅合成影像(图2(b)),其大小为128×128像素。以20次迭代为间隔,在原始影像上叠加采样化结果。图2(c)为通过分段采样的方式获取的初始采样数据,其中区域Ⅰ、Ⅱ、Ⅲ各初始化一个采样点(分别由红、绿、蓝色表示),区域Ⅳ内部光谱测度变化不甚明显,本次实验初始化结果中包含10个样本点(青色)。由于初始化采样点为分段点,无法保证影像中包含与其具有相同光谱测度的像素点,更无法保证其点数。故而初始化采样点不计入采样数据总数,因此表1初始化采样对应点数为0。提出算法每次采样化操作将距离采样点最近的且具有相同测地线距离的观测数据转换为采样数据。因此,图2采样数据随采样化进程逐渐增加(图中彩色显示的点即为采样数据)。结合表1不难看出,初始阶段采样化过程较为明显,每20次可采2000点左右。但随着采样化过程的发展,距离采样点测地线距离相等的点越来越少,每20次只能采1000点左右。而采样化后期,测地线距离相等的点越来越少,因此该阶段采样数据量受步长控制。本次实验采样步长为31个像素,因此后60次采样每20次只采620个像素点。图2(n)为16232个采样数据时的采样化结果。模板影像为128×128像素,因此此时结果中存在152个观测数据,剩余观测数据通过5次采样化过程得到如图2(o)所示分割结果。采样化过程即为影像分割过程,当所有观测数据点转换为采样数据点时实现影像分割。
表 1 采样点随采样过程的变化
Table 1 Sampling points change with sampling process
| 采样次数 | 0(初始化) | 20 | 40 | 60 | 80 | 100 |
| 点数 | 0 | 2166 | 4671 | 6549 | 8509 | 10276 |
| 点/20次 | 0 | 2166 | 2505 | 1878 | 1960 | 1767 |
| 采样次数 | 120 | 140 | 160 | 180 | 200 | 220 |
| 点数 | 12047 | 13287 | 14372 | 14992 | 15612 | 16232 |
| 点/20次 | 1771 | 1240 | 1095 | 620 | 620 | 620 |
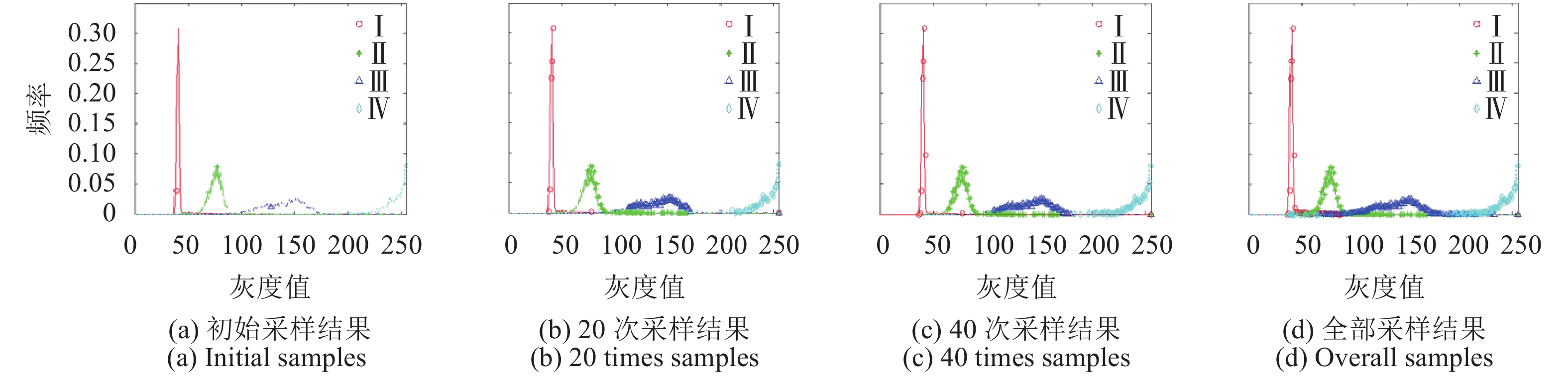
图3为图2(c)中采样数据点在其特征空间中真实分布的对应位置变化趋势。不难看出,图3(a)中除第二类初始采样数据位于其频率分布峰值外,其余采样数据均不同程度地偏离其频率分布峰值。本文利用高斯概率密度函数描述不同区域像素灰度分布特征,保证每个类别均可包含可取灰度级的任意值,因此初始采样点的准确与否对分割结果影响不大。虽然图3区域Ⅱ初始采样点的灰度值为该区域像素灰度级频率分布最高,但图2(d)前20次采样仍旧不能保证采样点均为区域Ⅱ内的点。相反,图3(a)中区域Ⅰ和区域Ⅲ初始采样数据相比区域Ⅱ不够准确,但由图2不难看出,后续采样化过程基本上能够保证采样点在区域Ⅰ和区域Ⅲ范围内。结合20次采样数据和40次采样数据分布(图3(b)—(c))可以看出,采样数据位置以初始值为中心逐渐包含整个数据分布。因此提出算法不但可以实现自动化影像分割,还能够作为自动化采样手段应用于监督分类,实现采样过程的自动化。
为了定量分析提出算法的分割精度,合成如图4(a)所示由不同纹理构成的模拟影像,其大小为256×256像素。图4(b)—(e)分别为HMRF-CSA算法(Zhang 等,2014)、GRM-FCM算法(赵雪梅 等,2014)、神经网络算法(ENVI)以及提出算法对其的分割结果。HMRF-CSA算法利用高斯混合模型建模影像区域分布特征,并结合HMRF建模影像标号场邻域关系,最终利用克隆选择算法和CSA采样算法估计模型参数,但区域Ⅰ和区域Ⅱ纹理特征较为明显,故高斯混合模型和标号场邻域系统无法有效区分不同纹理特征(图4(b))。GRM-FCM算法利用高斯回归模型建模不同区域分布特征,并通过HMRF模型增强标号场邻域像素相关性,但图4(a)中各区域纹理特征较为复杂,无法通过高斯回归模型准确建模,因此其分割结果不甚理想。此外,HMRF-CSA算法和GRM-FCM算法受相关参数影响较大,需多次实验选取最优参数。而神经网络算法需提前选择不同区域的典型样本,根据样本数据训练分类器,进而通过分类器分割原始影像。因此能够解决人工选取参数的问题,且其分割结果略优于HMRF-CSA算法和GRM-FCM算法。提出算法利用高斯分布描述影像邻域及类别内像素的相关性,并将其映射到黎曼空间求解,充分利用黎曼空间的几何性质,能够更加准确地描述像素与不同类别的差异程度,因此其分割结果较为理想。算法设计观测数据的采样化过程,无需采样即可实现遥感影像的自动化分割,且算法无需用户定义参数,有效避免传统非监督分割方法受参数影响较大以及监督分割方法需提前采样的问题。此外,基于MCMC采样方式求解的HMRF-CSA算法需2498.6 s完成分割;基于模糊的GRM-FCM算法需17.9 s,而提出算法需13.7 s完成分割。
表2为各算法对模拟影像的分割精度,其中用户精度为正确分割像素数与分割结果中该类别像素总数的比值;产品精度为正确分割像素数与该类别的真实像素数之比;总精度为正确分割像素数与总像素数之比。结合图4(b)分割结果,HMRF-CSA算法由于未能正确分割区域Ⅰ和区域Ⅱ,且把区域Ⅱ的部分像素分割到区域Ⅲ的类别中,其用户精度、产品精度及总精度均不理想。目视上GRM-FCM算法分割结果更加均匀,但实际上其分割精度低于HMRF-CSA算法。虽然神经网络算法分割结果区域Ⅲ包含少量噪声,但其总体精度高于HMRF-CSA算法和GRM-FCM算法。而提出算法利用黎曼流形上的点表征像素及其邻域的内在属性,结合测地线描述流形上两点间的最小距离,能够充分利用黎曼流形的几何性质,有效拟合影像特征并得到较高的分割精度(总精度98.9%,明显高于HMRF-CSA算法的83.9%,GRM-FCM算法的68.9%以及神经网络算法的88.5%)。
表 2 模拟影像各算法分割精度
Table 2 Accuracies of the segmentation of the simulated image from each algorithm
| /% | ||||
| 算法 | 精度 | 区域 | ||
| Ⅰ | Ⅱ | Ⅲ | ||
| HMRF-CSA | 用户精度 | 95.2 | 72.9 | 71.9 |
| 产品精度 | 85.7 | 73.2 | 99.1 | |
| 总精度 | 83.9 | |||
| GRM-FCM | 用户精度 | 94.9 | 47.7 | 48.1 |
| 产品精度 | 75.8 | 41.2 | 99.3 | |
| 总精度 | 68.9 | |||
| 神经网络 | 用户精度 | 91.6 | 79.1 | 97.2 |
| 产品精度 | 88.9 | 83.4 | 97.4 | |
| 总精度 | 88.5 | |||
| 提出算法 | 用户精度 | 99.3 | 97.6 | 100.0 |
| 产品精度 | 99.4 | 98.7 | 97.5 | |
| 总精度 | 98.9 | |||
为了进一步验证算法的有效性及可行性,分别由0.67 m分辨率EROS-B和0.5 m分辨率IKONOS等卫星截取4幅全色遥感影像(图5(a))。分别采用HMRF-CSA算法、GRM-FCM算法、神经网络算法和本文算法分割上述影像,分割结果为图5(b)—(e)。对于影像Ⅰ,HMRF-CSA算法未能有效区分建筑和地面;GRM-FCM算法分割结果中包含大量噪声;神经网络算法分割结果海面与地面交界处不够清晰;而提出算法分割结果较为理想。影像Ⅱ包含地物信息较为复杂,GRM-FCM算法无法有效区分不同类型植被;提出算法分割结果与HMRF-CSA算法和神经网络算法分割结果类似,但包含噪声明显少于上述两种算法。提出算法不但能够有效分割不同类型地物面积较为接近的影像(如影像Ⅰ、Ⅱ),还能够有效区分面积差异较大的不同地物(如影像Ⅲ、Ⅳ)。本文算法对影像Ⅲ的分割结果表明,该算法能够提取较为明显的线状地物同时忽略细小的线状地物,而其余3种算法分割结果中细小线状地物的表达得到了不同程度的加强,不利于反映地表真实状态。同样提出算法能够有效区分图5影像Ⅳ中的建筑和地面以及周围的植被,其余3种算法分割结果均存在不同程度的误分现象。提出算法采样化过程只将距离采样点最近的且具有相同测地线距离的观测数据点转换为采样数据,且满足条件的数据点少于一定步长时,转换步长内满足上述条件的观测数据。因此,提出算法不受目标尺度影响,能够准确区分不同尺度的目标。
表3为图5各算法分割结果精度。不难看出,基于非监督的HMRF-CSA算法和GRM-FCM算法对不同影像分割精度差异较大,说明这两种算法分别适用于不同类型影像。整体上看,非监督算法精度略低于基于监督的神经网络算法。而提出算法基于采样数据建模,不受分割参数影响,较之神经网络算法能够更加准确的描述影像分布特征,因此分割精度最高。
表 3 各算法分割精度
Table 3 Accuracy of each algorithm
| HMRF-CSA | HMRF-GRM | 神经网络 | 提出算法 | |
| 影像Ⅰ | 51.3 | 67.8 | 92.5 | 93.7 |
| 影像Ⅱ | 93.3 | 80.6 | 90.7 | 89.8 |
| 影像Ⅲ | 94.1 | 95.0 | 97.2 | 98.7 |
| 影像Ⅳ | 88.6 | 90.7 | 70.3 | 96.0 |
HMRF-CSA算法和GRM-FCM算法均依赖于参数选择,当算法初始参数不理想时,易陷入局部极值。实验中,不同影像需选取不同参数才能得到其最优结果。而神经网络算法通过采样数据构建分类器,虽然能够快速获取较好的分割结果,但算法对采样要求较高,且采样过程需人工操作,操作准确性直接影响采样数据建模的准确性,无法实现影像自动化分割。提出算法包括两种初始化策略:采用人工选择的方式初始化采样数据最少只需采取一个样本点即可保障采样模型收敛于真实分布模型,节省大量采样时间;分段采样的初始化方法取影像像素灰度级的c+1类分段值,能够在一定程度上表征各类像素光谱反射特征,且随着采样数据的增加,能够收敛于影像真实分布模型,进而实现算法的自动化分割。
算法耗时受计算机计算能力、数据表达方式、编程语言等诸多方面影响。不考虑这些外在影响,单纯从算法方面分析其复杂度。欧氏空间到黎曼空间映射只需计算一次,用o(N1)表示其复杂度,只与影像尺寸相关;采样化过程观测数据集逐渐减小,故其复杂度o(Ns)在迭代过程中递减;每次采样后,需更新采样数据点,其复杂度表示为o(Nup),与迭代次数相关。因此,算法总复杂度为o(N1+Ns+Nup)是一个随迭代递减的量,故提出算法具有较高的分割效率。由于采样化过程受每次采样个数影响,因此影像区域内纹理变化越规律,其分布函数越相似,每次采样个数越多,算法运行速度越快。
4 结 论
本文利用像素及其邻域像素信息构建观测数据高斯分布,并将采样数据和观测数据的高斯分布同时映射到黎曼空间,表达为黎曼流形上的点。而后将距离采样数据点最近的观测数据点转换为采样点,逐步实现观测数据的采样化,直到所有观测数据转换为采样数据。该算法具有以下几项优点:(1) 采用邻域信息构建像素点高斯分布,并结合黎曼空间测地线不但能够表征像素与邻域像素的内在统计相关性,还可以准确建模观测数据点与采样点的相似性,进而有效平滑噪声,提升算法的抗噪性。(2) 算法在每次更新采样数据后重新计算采样点分布,使采样数据模型逐渐逼近真实分割模型。(3) 在观测点转换为采样点的过程中,如果具有等测地线的观测点大于给定步长,则转化全部满足条件的观测点,否则转化步长内的所有观测点,因此提出算法能够准确趋向不同类别数据,且不受各类别像素数影响,进而得到较好的分割结果。(4) 算法利用概率分布建模采样数据和观测数据,在充分利用像素间相关性的同时,还能够避免将具有相同灰度值的像素分割到同一类别中。(5) 提出算法可作为监督分类算法的采样操作,实现监督分类算法的自动化。
参考文献(References)
-
Amari S, Kurata K and Nagaoka H. 1992. Information geometry of Boltzmann machines. IEEE Transactions on Neural Networks, 3 (2): 260–271. [DOI: 10.1109/72.125867]
-
Amari S I. 1995. Information geometry of the EM and em algorithms for neural networks. Neural Networks, 8 (9): 1379–1408. [DOI: 10.1016/0893-6080(95)00003-8]
-
Amari S and Nagaoka H. 2000. Methods of Information Geometry. Providence, RI: American Mathematical Society
-
Blaiotta C, Cardoso M J and Ashburner J. 2016. Variational inference for medical image segmentation. Computer Vision and Image Understanding, 151 : 14–28. [DOI: 10.1016/j.cviu.2016.04.004]
-
Brody D C and Hook D W. 2009. Information geometry in vapour-liquid equilibrium. Journal of Physics A: Mathematical and Theoretical, 42 (2): 023001 [DOI: 10.1088/1751-8113/42/2/023001]
-
Gong M G, Liang Y, Shi J, Ma W P and Ma J J. 2013. Fuzzy c-means clustering with local information and kernel metric for image segmentation. IEEE Transactions on Image Processing, 22 (2): 573–584. [DOI: 10.1109/TIP.2012.2219547]
-
Li L, Fan W T, Du J X and Wang J. 2016. A novel image segmentation approach based on truncated infinite Student’s t-mixture model//Huang D S, Han K and Hussain A, eds. Intelligent Computing Methodologies. Cham: Springer: 271–281 [DOI: 10.1007/978-3-319-42297-8_26]
-
Li Y F and Feng X C. 2016. A multiscale image segmentation method. Pattern Recognition, 52 : 332–345. [DOI: 10.1016/j.patcog.2015.10.004]
-
Liu G Y, Zhang Y and Wang A M. 2015. Incorporating adaptive local information into fuzzy clustering for image segmentation. IEEE Transactions on Image Processing, 24 (11): 3990–4000. [DOI: 10.1109/TIP.2015.2456505]
-
Michel J, Youssefi D and Grizonnet M. 2015. Stable mean-shift algorithm and its application to the segmentation of arbitrarily large remote sensing images. IEEE Transactions on Geoscience and Remote Sensing, 53 (2): 952–964. [DOI: 10.1109/TGRS.2014.2330857]
-
Niu S J, Chen Q, de Sisternes L, Ji Z X, Zhou Z M and Rubin D L. 2017. Robust noise region-based active contour model via local similarity factor for image segmentation. Pattern Recognition, 61 : 104–119. [DOI: 10.1016/j.patcog.2016.07.022]
-
Sun L, Wu Z B, Liu J J, Xiao L and Wei Z H. 2015. Supervised spectral-spatial hyperspectral image classification with weighted Markov random fields. IEEE Transactions on Geoscience and Remote Sensing, 53 (3): 1490–1503. [DOI: 10.1109/TGRS.2014.2344442]
-
Wang C Y, Xu A G, Li Y and Sui X. 2016. Segmentation of high-resolution remote sensing images with type-2 fuzzy model based on spatial relationship. Journal of Remote Sensing, 20 (1): 103–113. [DOI: 10.11834/jrs.20165139] ( 王春艳, 徐爱功, 李玉, 隋心. 2016. 融入空间关系的二型模糊模型高分辨率遥感影像分割. 遥感学报, 20 (1): 103–113. [DOI: 10.11834/jrs.20165139] )
-
Yu B, Meng J M, Zhang X and Ji Y G. 2013. Segmentation method for agglomerative hierarchical-based sea ice types using polarimetric SAR data. Journal of Remote Sensing, 17 (4): 887–904. [DOI: 10.11834/jrs.20132091] ( 于波, 孟俊敏, 张晰, 纪永刚. 2013. 结合凝聚层次聚类的极化SAR海冰分割. 遥感学报, 17 (4): 887–904. [DOI: 10.11834/jrs.20132091] )
-
Zhang M X, Jiao L C, Ma W P, Ma J J and Gong M G. 2016. Multi-objective evolutionary fuzzy clustering for image segmentation with MOEA/D. Applied Soft Computing, 48 : 621–637. [DOI: 10.1016/j.asoc.2016.07.051]
-
Zhang T, Xia Y and Feng D D. 2014. Hidden Markov random field model based brain MR image segmentation using clonal selection algorithm and Markov chain Monte Carlo method. Biomedical Signal Processing and Control, 12 : 10–18. [DOI: 10.1016/j.bspc.2013.07.010]
-
Zhao W Z and Du S H. 2016. Spectral-spatial feature extraction for hyperspectral image classification: a dimension reduction and deep learning approach. IEEE Transactions on Geoscience and Remote Sensing, 54 (8): 4544–4554. [DOI: 10.1109/TGRS.2016.2543748]
-
Zhao X M, Li Y and Zhao Q H. 2014. Image segmentation by fuzzy clustering algorithm combining hidden Markov random field and Gaussian regression model. Journal of Electronics and Information Technology, 36 (11): 2730–2736. [DOI: 10.3724/SP.J.1146.2013.01751] ( 赵雪梅, 李玉, 赵泉华. 2014. 结合高斯回归模型和隐马尔可夫随机场的模糊聚类图像分割. 电子与信息学报, 36 (11): 2730–2736. [DOI: 10.3724/SP.J.1146.2013.01751] )