出版日期: 2017-07-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20176217
2017 | Volumn21 | Number 4
上一篇 | 下一篇

卫星测高数据监测青海湖水位变化

赵云^1,2 , 廖静娟¹ , 沈国状¹ , 张学良³

1. 中国科学院遥感与数字地球研究所数字地球重点实验室，北京 100094

2. 中国科学院大学资源与环境学院，北京 100049

3. 中国地质大学(北京) 地球科学与资源学院，北京 100083

收稿日期: 2016-06-22

基金项目: 国家重点研发计划(编号：2016YFB0501501)；中国科学院一三五项目“全球典型科学要素产品及应用”(编号：Y6SG0300CX)

第一作者简介: 赵云(1991—　)，女，硕士研究生，研究方向为雷达对地观测数据处理与应用。E-mail：zhaoyun@radi.ac.cn

通讯作者简介: 廖静娟(1966—　)，女，研究员，研究方向为微波遥感。E-mail：liaojj@radi.ac.cn

中图分类号: P228

文献标识码: A

摘要

为了验证Cryosat-2/SIRAL数据监测湖泊水位的能力，提高其提取湖泊水位变化的精度，以青海湖为研究对象，利用主波峰重心偏移法、主波峰阈值法、主波峰5-β参数法、传统重心偏移法、传统阈值法和传统5-β参数法6种算法对Cryosat-2/SIRAL LRM 1级数据进行波形重跟踪，提取青海湖2010—2015年湖泊水位，对比不同算法获取水位的精度，并结合Envisat/RA-2 GDR数据，延长水位变化时间序列，获得青海湖2002年—2015年的水位变化信息。结果表明，主波峰5-β参数法提取湖泊水位的精度最好，均方根误差为0.093 m；对于GDR产品中LRM模式的3种数据，基于Refined OCOG算法的数据更适合湖泊水位的提取；青海湖2002年—2015年水位整体上涨，水位平均变化趋势为0.112 m/年，年内水位变化呈现明显的季节性。

关键词

卫星测高, Cryosat-2, Envisat/RA-2, 重跟踪, 水位, 青海湖

Monitoring the water level changes in Qinghai Lake with satellite altimetry data

ZHAO Yun^1,2 , LIAO Jingjuan¹ , SHEN Guozhuang¹ , ZHANG Xueliang³

1.Key Laboratory of Digital Earth Science, Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100094, China

2.College of Resources and Environment, University of Chinese Academy of Sciences, Beijing 100049, China

3.School of Earth Sciences and Resources, China University of Geosciences, Beijing 100083, China

Abstract

Lake is an important water resource and a sensitive indicator of climate and environment change. Satellite altimetry has been used as an alternative tool to measure lake levels since the 1990s. With the development of satellite altimetry technology, different altimetry thatcan be used for lake level monitoring has been launched. This paper aims to verify Cryosat-2/SIRAL data capabilities of monitoring lake level, improve the extraction accuracy of lake level changes, and monitor the water level change of Qinghai Lake. The boundary of the lake was first extracted using the image of MODIS13Q1 close to the date altimeter visited to ensure the observation points in the lake. This study used six kinds of algorithms to retrack Cryosat-2/SIRAL LRM level 1 data in order to extract the Qinghai Lake water levels from 2010 to 2015, including the primary peak Offset Center of Gravity (OCOG), primary peak threshold, primary peak 5-β parameter, traditional OCOG, traditional threshold, and traditional 5-β parameter methods. Furthermore, the Cryosat-2/SIRAL GDRs of LRM mode provides three different retrackers: UCL, refined CFI, and refined OCOG. The accuracy of all these different algorithms in extracting water level was then compared with the measured water level of the hydrological station using the indexes, such as the difference, correlation coefficient, and root mean square error (RMSE). The 2002 to 2015 water level time series of Qinghai Lake was obtained and combined with the Envisat/RA-2 GDR data by adding the differences between the lake levels extracted from Envisat/RA-2 and Cryosat-2/SIRAL. The seasonal and inter-annual variation features of Qinghai Lake water level were then analyzed. The results showed that the primary peak 5-β parameter retracker for Qinghai Lake performed the best with the least RMSE 0.093 m and a maximum correlation coefficient (0.956) among these retrackers. Generally, the water level extraction accuracy of the retrackers based on the primary peak is better than the retrackers based on the entire waveform. While for these waveforms which are influenced by land echo information, the primary peak OCOG algorithm and primary peak threshold algorithm presented were better than others. Comparing the three kinds of Cryosat-2/SIRAL GDR products for LRM patterns, the data based on the refined OCOG algorithm was more suitable for extraction of lake level. In addition, the water level of Qinghai Lake generally rose from 2002 to 2015 with the overall increasing trend of 0.112 m/a, with marked seasonal changes in a year. The water level began to rise in May and December each year, with respectively high peaks in September and January. Based on the preceding experiments and analysis, the Cryosat-2/SIRAL LRM data can be used to extract lake levels with high precision at approximately 1 dm. Retracking for altimetry level 1b data could improve the water level extraction accuracy. The best adaptive retracking algorithm for different types of lakes is often different because they show different echo waveforms. The analysis in the paper is rough; hence, the next step is selecting different types of lakes to obtain a detailed comparative analysis.

Key words

satellite altimetry, Cryosat-2, Envisat/RA-2, retracking, lake level, Qinghai Lake

1 引　言

湖泊作为重要的水资源，在维系流域生态平衡、满足生产生活用水、减轻洪涝灾害和提供丰富水产品等方面发挥着不可替代的作用(杨桂山等，2010)。湖泊水位是湖泊的重要特征，长时间的水位序列对区域气候变化十分敏感，水位的上升或下降反映着气候的变化及人类活动的影响，同时水位的稳定及可持续性变化又影响甚至制约着人类的生产生活。青海湖区属于全球气候变化的敏感地区和生态系统的典型脆弱地区，也是世界生物多样性保护的重要场所和世界著名的湿地和自然保护区，因此，研究青海湖水位的变化具有重要的意义和价值(姜卫平等，2008)。

卫星测高技术具有快速的全球覆盖能力，能够大尺度、周期性地探测陆表水的各种自然现象及其变化，具有其他观测技术无可比拟的优越性(高乐，2014)。利用星载高度计监测内陆水域变化，国内外已经做了许多研究(Frappart 等，2006；李建成等，2007；Zhang 等，2011；Michailovsky 等，2012；Gao 等，2013；Song 等，2015)。2010年4月8日，ESA发射了Cryosat-2卫星，其上搭载了先进的合成孔径干涉雷达高度计SIRAL，其轨道密集，可以监测更多湖泊。目前，该卫星应用于内陆水域水位监测的研究还较少。

对于内陆湖泊，由于水深较浅及陆地的影响，回波波形常被污染，导致卫星到被测水面的距离不准确，对波形数据进行重跟踪处理可以提高水位提取的精度(Hwang 等，2006；Bao 等，2009；Yang 等，2012；Kleinherenbrink 等，2014, 2015；Jain 等，2015)。本文在前人研究的基础上，以青海湖为研究对象，对Cryosat-2/SIRAL LRM模式的1级波形数据进行重跟踪，运用实测水位数据比较不同重跟踪算法所得水位的精度，选择最佳重跟踪算法，并结合Envisat/RA-2雷达高度计数据，延长水位时间序列，从而获得青海湖2002年—2015年的水位变化信息。

2 研究区概况与数据源

2.1 研究区概况

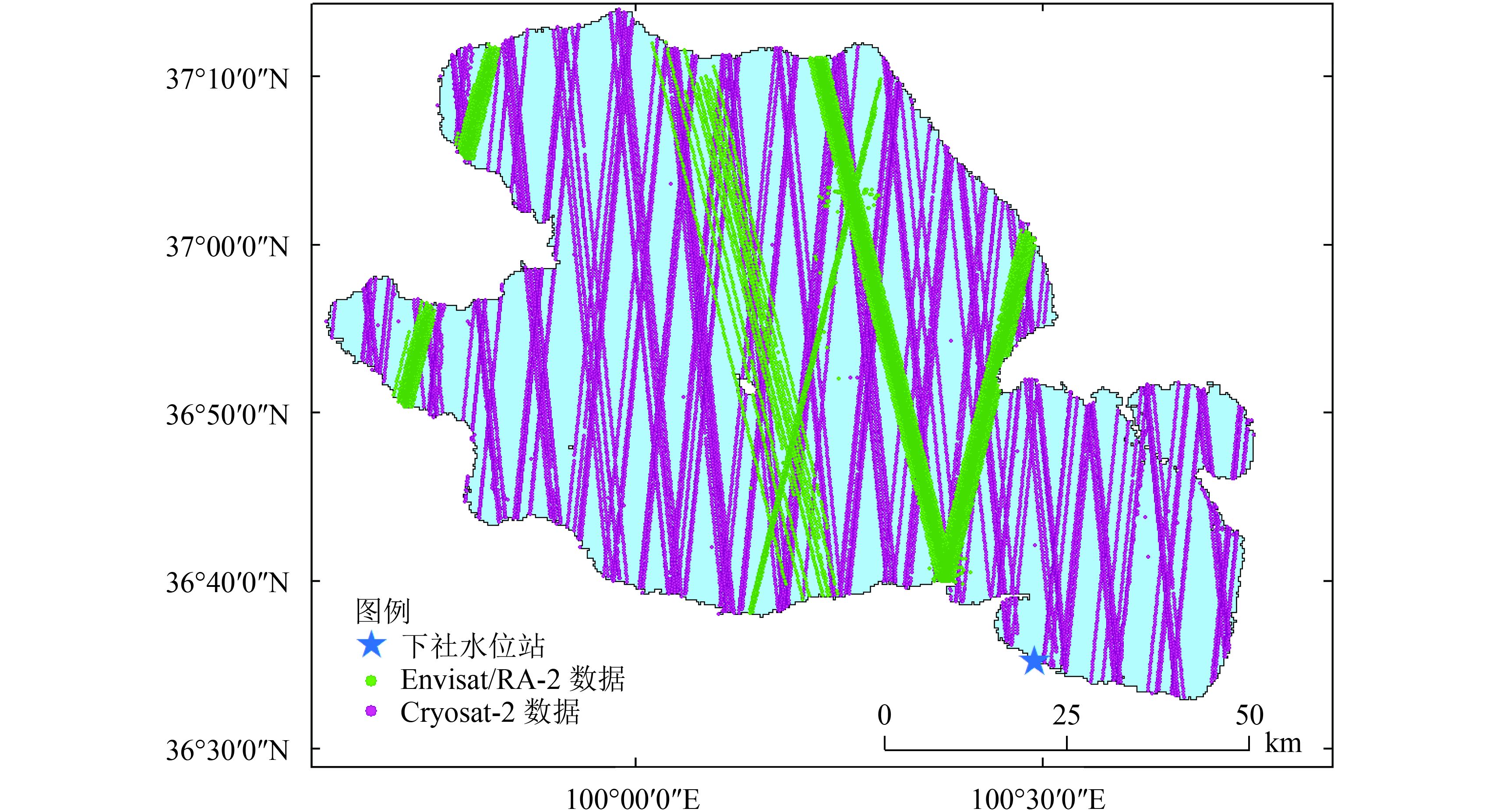
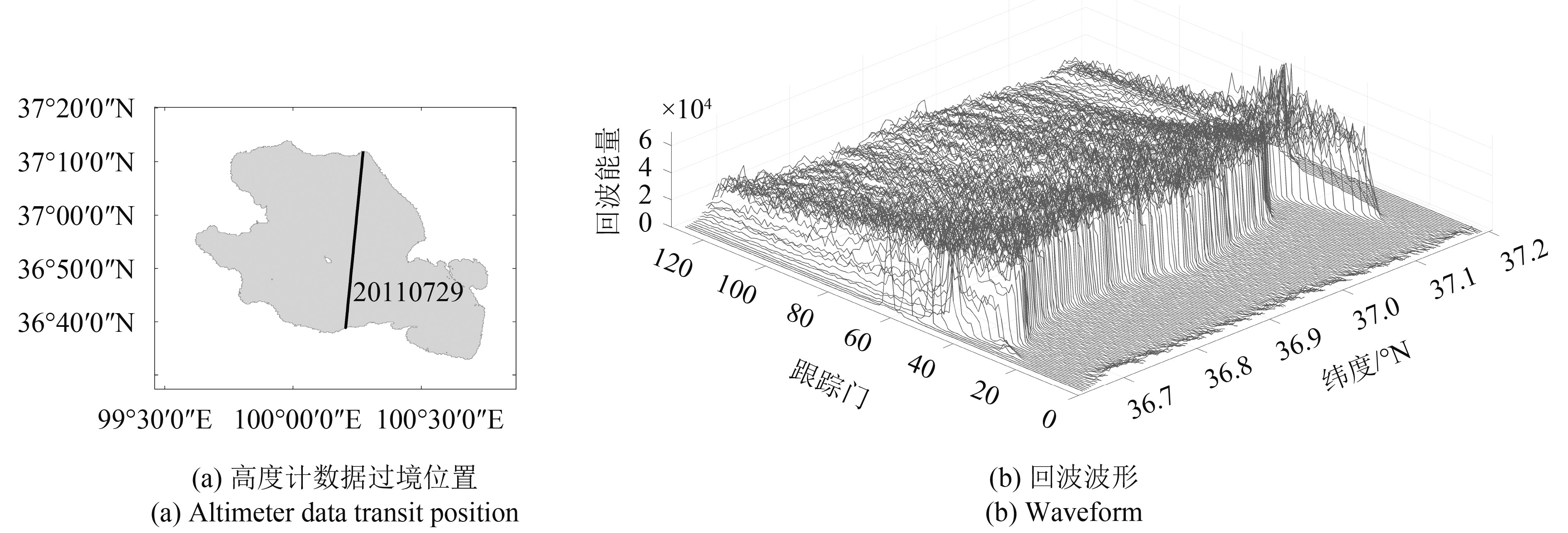
青海湖位于青藏高原的东北部，大通山、日月山、青海南山间，地理范围为36°15′—38°20′N，97°50′—101°20′E(图1)，是中国最大的内陆封闭湖。湖水面积近4300 km²，湖面东西长约106 km，南北宽约63 km，略呈椭圆形，地势西北高、东南低，平均水深约21 m。由于其处于中国东部季风区、西北干旱区和西南高寒区的交汇地带，具有明显的地区性气候特点，寒冷期长、干旱少雨、干燥多风、太阳辐射强、气温日差较大，对全球气候变化响应敏感(伊万娟等，2010；张金龙等，2013)。

从20世纪60年代至2004年，青海湖水位除个别年份略有上升外，总体呈现出明显的持续下降趋势，而到了2005年水位开始回升，连续7年呈现增长趋势，湖泊面积也相应扩大(伊万娟等，2010；李燕等，2014)。

图 1 青海湖位置及数据分布图

Fig. 1 Location of Qinghai Lake and data distribution map

2.2 数据源

本文所使用的数据资料主要包括：

(1) MODIS植被指数产品(MOD13Q1)。该产品是美国国家宇航局(NASA)提供的空间分辨率为250 m、时间间隔16 d的高时相大尺度数据，包括EVI、red_reflectance等12个波段，本文采用了归一化植被指数(NDVI)波段。

(2) Envisat/RA-2高度计数据。Envisat是欧空局(ESA)于2002年3月发射的极轨对地观测卫星，该卫星上携带的RA-2是在监测内陆水域水位方面应用较广泛的一种高度计数据，其GDR产品采用了Ocean、Ice-1、Ice-2和Sea-Ice共4种重跟踪算法，前人研究表明，基于Ice-1算法的数据最适用于陆地水文应用研究(Frappart 等，2006；Medina 等，2008)，故本文将采用此数据来提取青海湖水位，时间跨度为2002年—2011年。

(3) Cryosat-2/SIRAL高度计数据。Cryosat-2卫星工作在Ku波段，主要包括3种测量模式：低分辨率指向星下点的高度计测量模式(LRM)、SAR测量模式和SAR干涉测量模式(SARIn) (Wingham 等，2006；李建成和金涛勇，2013)。经过青海湖的数据为LRM测量模式，最新更新的GDR产品中，LRM模式数据采用了Refined CFI、UCL和Refined OCOG 3种重跟踪算法(Bouffard，2015)。本文采用2010年—2015年Cryosat-2/SIRAL LRM的1级数据和GDR数据。

(4) 青海湖下社水位站的2001年—2012年每年5月—10月的实测水位数据。

3 研究方法

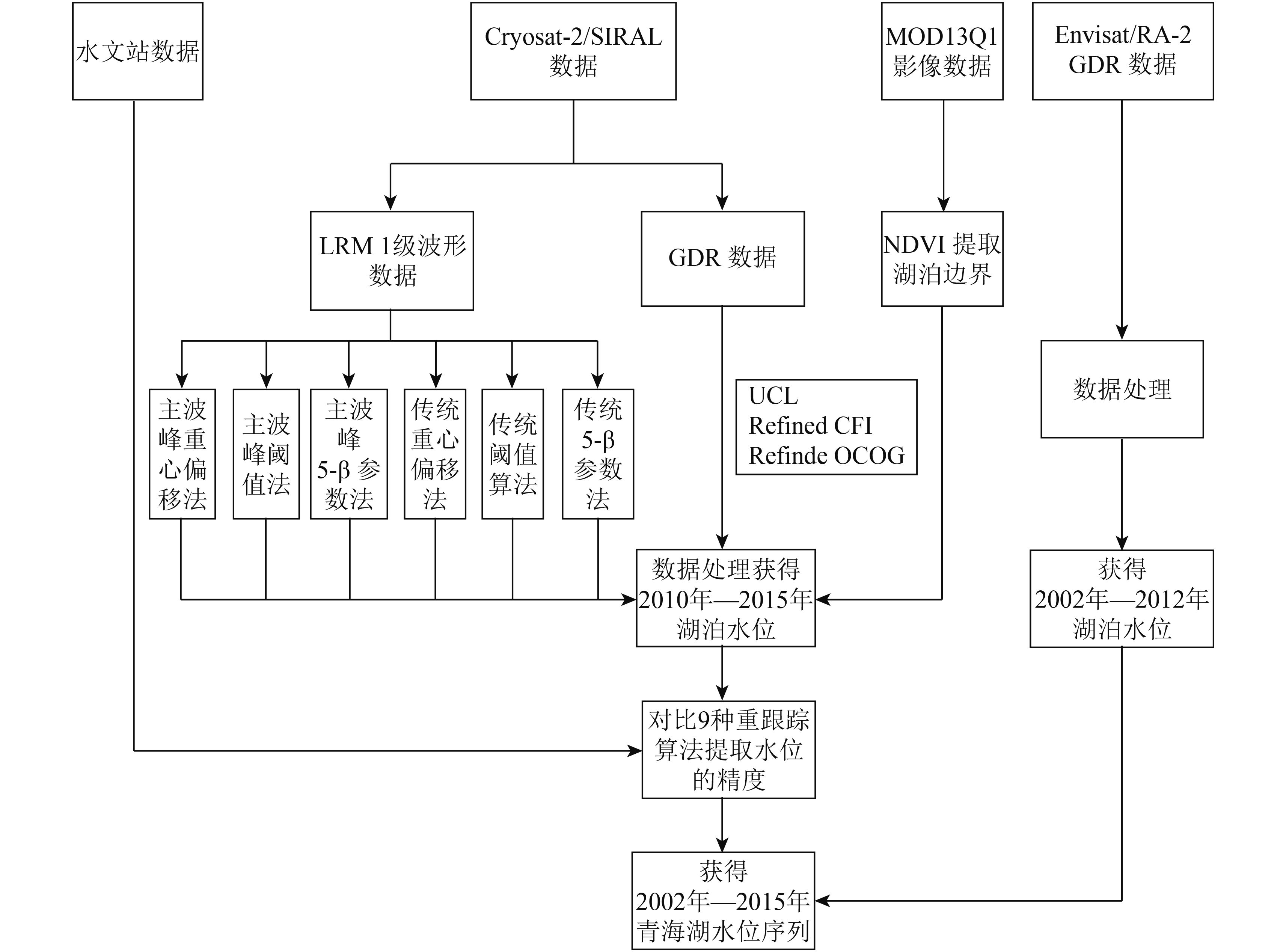
本文首先用MODIS图像提取湖泊边界，筛选湖泊范围内的高度计数据，然后对Cryosat-2/LRM 1级数据进行重跟踪获取青海湖2010年—2015年的湖泊水位，并根据实测水位进行精度验证，最后结合Envisat/RA-2的GDR数据，获取并分析2002年—2015年的水位变化信息。研究思路如图2所示。

图 2 研究思路流程

Fig. 2 The flow chart of the study

3.1 波形重跟踪算法

重跟踪就是用算法对原始波形进行模拟，重新计算波形前缘中点，根据其与原定中点的差值，获得距离改正值(d_r)，从而对高度计到被测水面的距离进行改正(褚永海等，2005)，具体如式(1)所示：

$\left\{ \begin{array}{l}{d_r} = ({C_{rt}} - {C_{nt}}) \times \displaystyle\frac{c}{2}{t_{_k}}\\{R_{cor}} = R + {d_r}\end{array} \right.$

(1)

式中，t_k为脉冲宽度，C_nt为原定中点，C_rt为重跟踪后确定的波形前缘中点，c为光速(299792458 m/s)，R为原距离，R_cor为改正后距离。对于Cryosat-2/SIRAL LRM数据，每个回波波形有128个采样点，故C_nt取值为63，t_k为3.125 ns。

如图2所示，本文对Cryosat-2/SIRAL LRM 1级数据采用了6种算法进行重跟踪处理，分别为主波峰重心偏移法、主波峰阈值法、主波峰5-β参数法、传统重心偏移法、传统阈值法和传统5-β参数法。这6种算法可以分为两类，一类是基于全波形的传统方法，一类是基于主峰子波形的改进算法。

传统重心偏移法(OCOG)是为了实现对波形的稳健跟踪，其基本思想是找到每个返回波形的重心，通过计算由波形值确定的矩形的重心和面积来确定波形的前缘中点(Wingham 等，1986；褚永海等，2005)，该方法计算简单方便。

传统阈值法(Threshold)是以OCOG算法为计算基础，根据振幅、最大波形采样等给出阈值，在该阈值的几个临近采样点之间进行线性内插，确定重定点(Davis，1996；高永刚，2006)。本文取OCOG算法所确定的矩形振幅的50%作为Threshold 算法的门槛值。

传统5-β参数法使用Brown模型，利用非线性最小二乘法拟合回波波形，通过迭代计算获得各β参数值，其中，β₃是与高度计所测距离有关的时间延迟，用于改正距离(Martin 等，1983；高永刚，2006)。

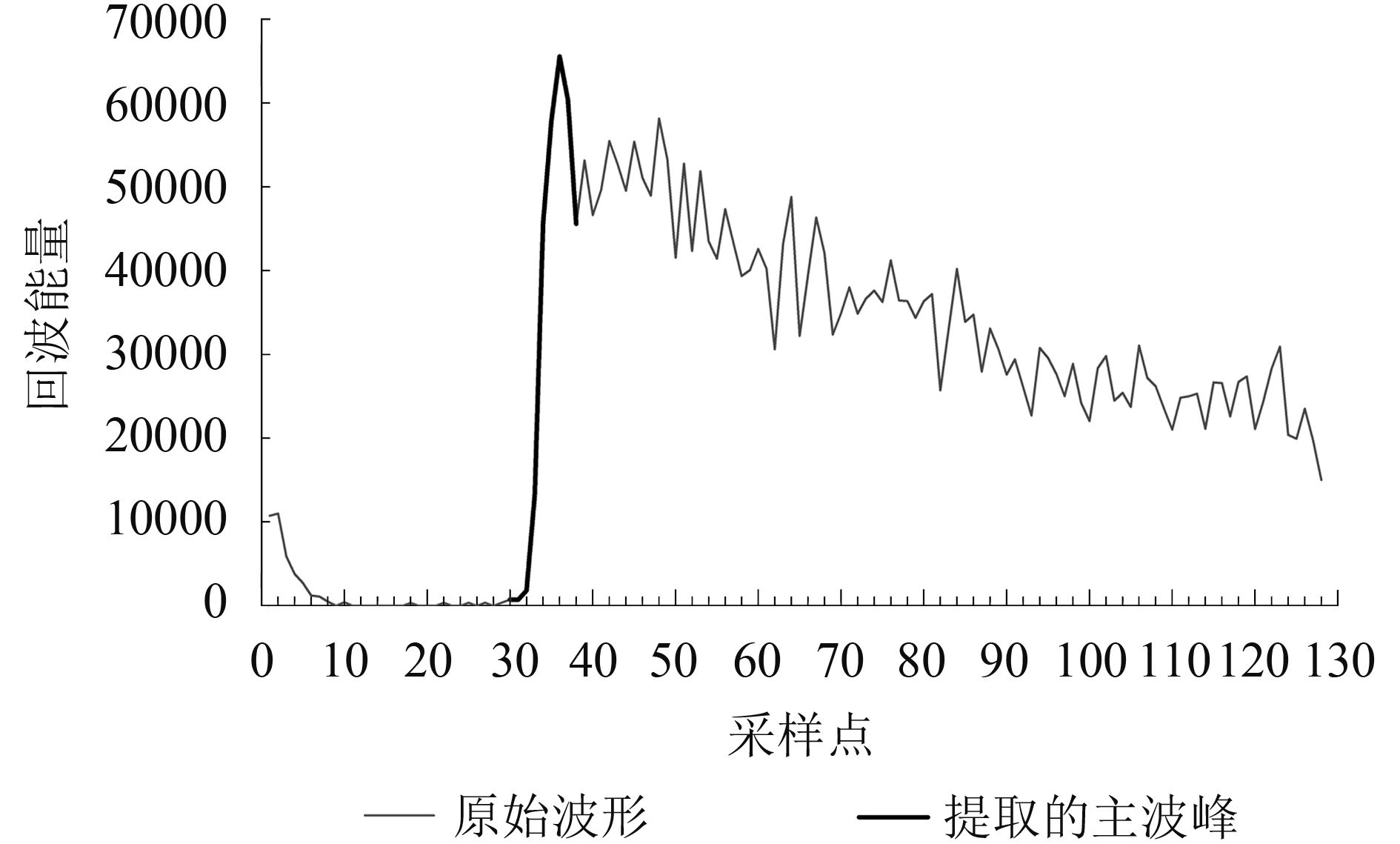
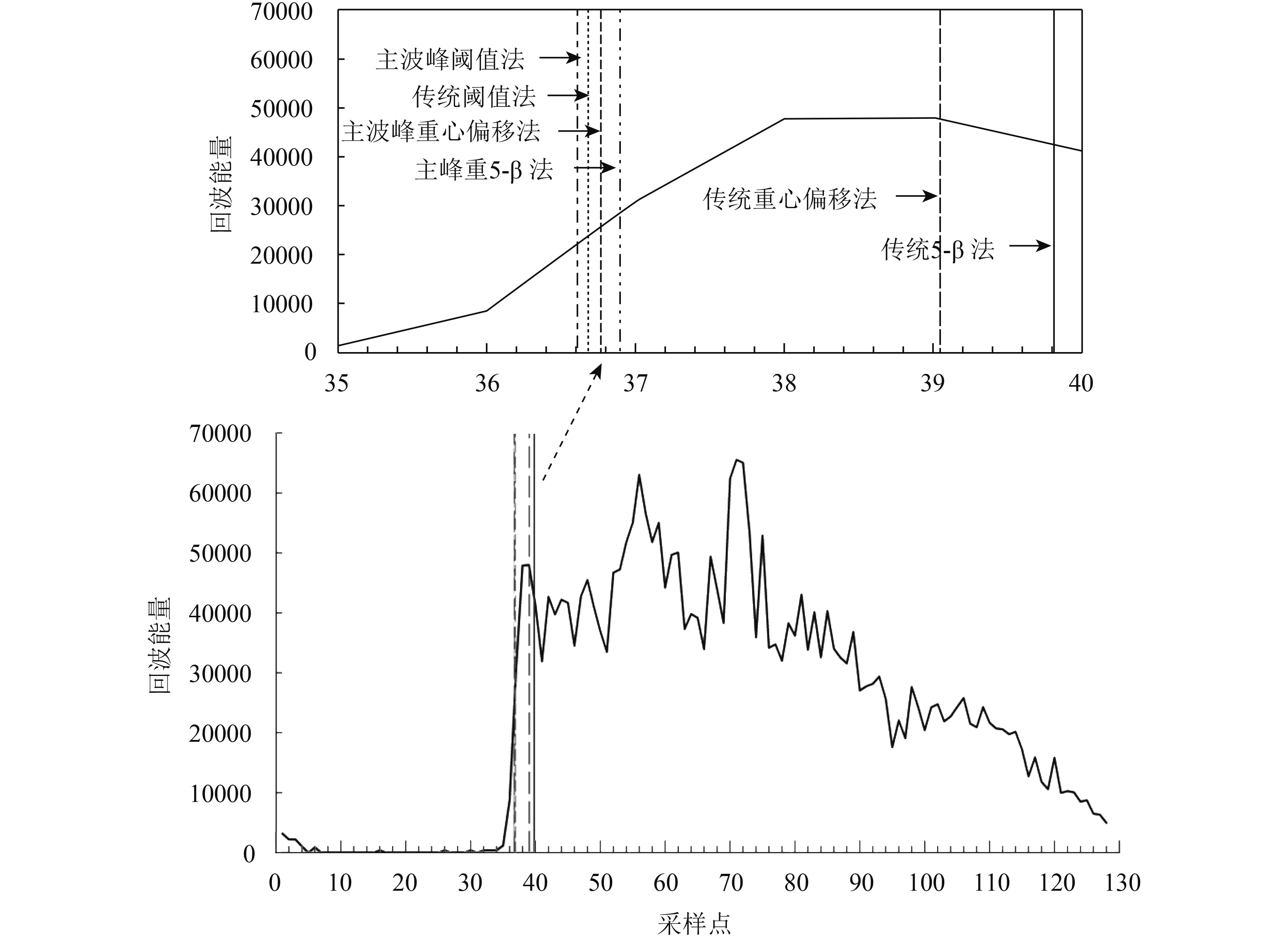
与上述3种传统算法相对应的基于主波峰的算法，计算过程类似，这里不再赘述，主要区别是只利用主峰子波形的数据。为提取主峰子波形，先用回波中的所有功率值来计算开始点与结束点阈值，然后根据两相邻跟踪门的回波功率差与这两个阈值的对比，确定最终主波峰的开始点与结束点。在实际操作时，由于提取的主波峰的跟踪门的数量较少，不足以用来重新拟合波形，经过试验，在前后各增加两个跟踪门效果较好(Jain 等，2015)，提取结果如图3所示。

图 3 主波峰提取示意图

Fig. 3 Extraction of primary peak

3.2 高度计数据获取湖泊水位

对Cryosat-2/SIRAL LRM的20 hz的1级波形数据用上述重跟踪算法获得改正后距离，根据式(2)，便获得湖面每个点的高程值h_ortho。

${h_{\rm{ortho}}} = {h_{\rm{alt}}} - R - \Delta R - {h_{\rm{geoid}}}$

(2)

式中，h_alt代表卫星的高度，h_geoid代表大地水准面高程，R代表雷达高度计到水面的距离，∆R代表各项改正值，这里主要运用了高度计数据中自带的干、湿对流层改正、电离层改正、海况偏差和潮汐改正。

然后进行数据的预处理：第1步，利用MOD13Q1数据的归一化植被指数NDVI，使用密度分割法提取青海湖边界，从而保证水位点在湖面上。第2步，对所有的20 hz的水位观测点，先目视解译剔除明显的异常水位，然后与总体平均值作差，再次目视解译剔除明显异常值。第3步，对于每一天的数据，用3σ准则剔除异常值，后将一天中的所有有效水位值取平均作为单天水位。第4步，对所有的单天水位用3σ原则，剔除异常单天水位。第5步，对整体单天水位数据用高斯滤波法去除噪声，得到较为干净的单天水位序列，选用的滤波窗口为半年(高永刚等，2008)。第6步，将上述单天水位按月取平均得到月平均水位，按年取平均得到年平均水位。

Cryosat-2/SIRAL GDR数据和Envisat/RA-2的GDR数据的处理过程与上述方法类似，不同的是Cryosat-2/SIRAL GDR数据集中直接提供了测量点的大地高，并且已进行了各种地球物理改正。

3.3 高度计提取湖泊水位高程基准转换与结果验证

Envisat/RA-2与Cryosat-2/SIRAL数据都运用了WGS84、EGM96参考系统，而水文站的实测水位数据采用1985年国家高程系统，因此在进行水位提取精度验证之前，要先完成高程系统的转换。研究中以实测水位的高程为基准，在青海湖地区，1985高程基准比WGS84基准高约40 cm(焦文海等，2002；郭海荣等，2004)，故要将高度计数据获得的水位减去该垂直偏差。对于各水位数据集与实测水位之间仍存在的系统偏差，则通过计算其间的平均差值，将高度计获得的水位变换到与实测水位相同的水平上来。然后，计算高度计提取的湖泊单天水位与对应实测水位的相关性与均方根误差(RMSE)，对比不同方法提取湖泊水位变化的精度。

由图1可知，两种高度计数据过境青海湖的轨迹差异明显，由于Cryosat-2的轨迹是随着时间不断移动的，且青海湖的东西方向水位差异并不明显，故本文并未考虑不同卫星轨道提取水位的差异，在接合这两种高度计提取的水位时，并不是针对同一观测点的数据进行处理，这也是上述两种水位数据集间系统差来源的一部分。

4 结果与讨论

4.1 Cryosat-2/SIRAL高度计数据提取水位的精度对比

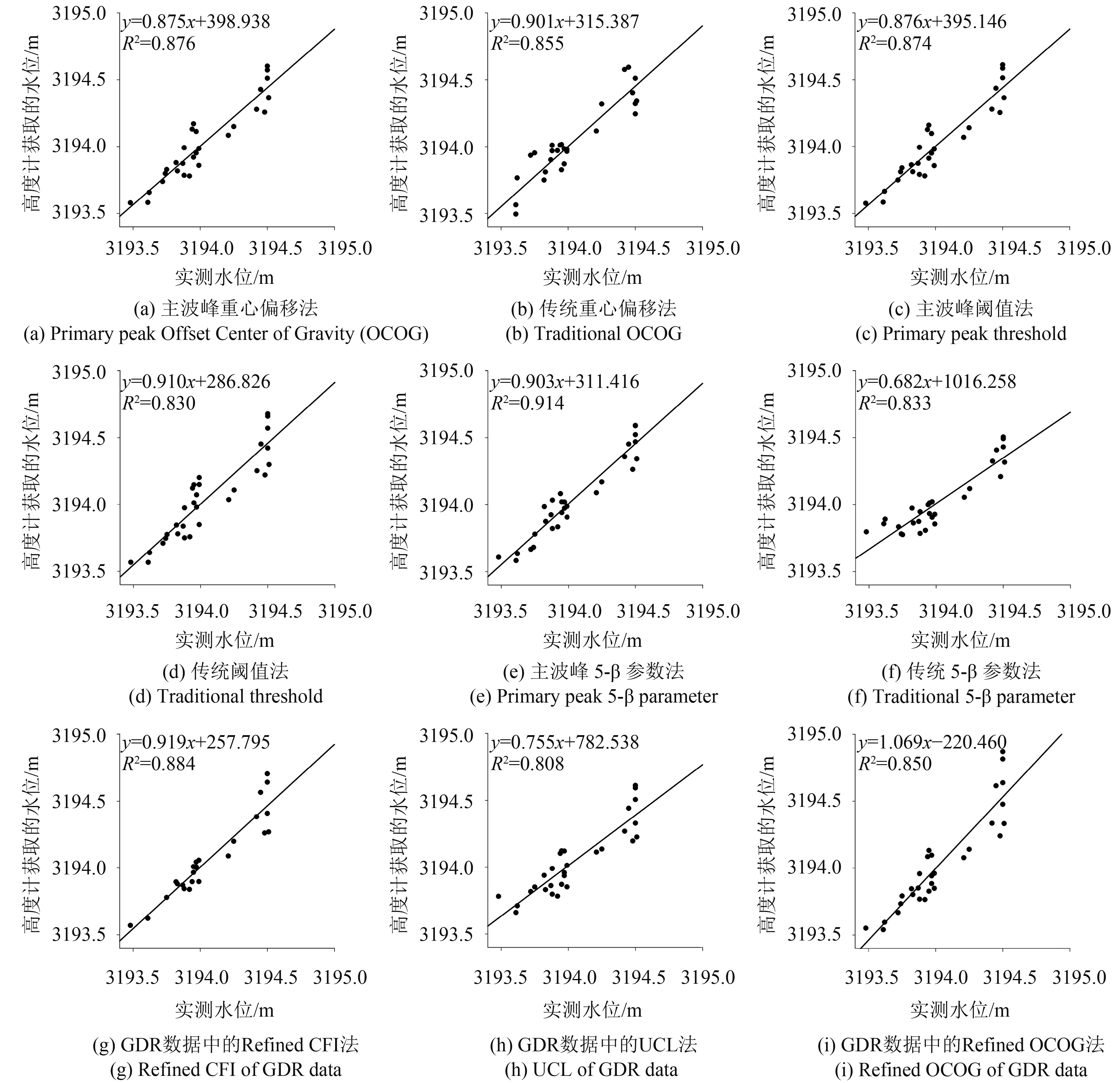
Cryosat-2/SIRAL LRM 1级数据经上述6种重跟踪算法处理后获得青海湖2010年—2015年的水位，而GDR产品本身有基于Refined CFI、UCL和Refined OCOG算法的3种数据，因此共获得9种水位提取结果。图4为2011年—2012年5月份到10月份间，这9种水位提取结果与实测水位的相关性示意图，表1为具体的对比统计数据，包括差值绝对值的最大值与最小值、均方根误差、相关系数及最终提取的有效单天水位的个数。实验结果表明，9种算法均可以提取湖泊水位，且精度均能达到1 dm左右。与其他几种重跟踪算法相比，主波峰5-β参数法提取的水位效果最好，具有最小均方根误差(0.093 m)和最大相关系数(0.956)，同时又能保证提取水位的数量，为最佳重跟踪算法。

图 4 Cryosat-2/SIRAL高度计数据获得水位与实测水位相关性

Fig. 4 Correlation of Cryosat-2/SIRAL data obtained and measured water levels

对于重心偏移法、阈值法与5-β参数法，与使用整个波形数据的传统算法相比，只用主波峰的改进算法提取的水位相关性更好、均方根误差更小，主波峰方法明显改善了传统重跟踪算法提取水位的精度。原因可能是，对于复杂波形，传统的利用整个波形数据获得的重定点，有可能偏离实际上的波形前缘中点，造成提取的距离错误，而只利用主波峰则有效地避免了这一点，如图5所示。

表 1 Cryosat-2/SIRAL高度计数据获得水位与实测水位比较统计表
Table 1 Comparative statistical of Cryosat-2/SIRAL data obtained and measured water levels

下载CSV

波形重跟踪算法	差值绝对值的最小值/m	差值绝对值的最大值/m	均方根误差/m	相关系数	总解算单天水位个数
主波峰重心偏移法	0.004	0.222	0.109	0.936	146
传统重心偏移法	0.010	0.255	0.121	0.925	149
主波峰阈值法	0.005	0.225	0.110	0.936	148
传统阈值法	0.003	0.260	0.132	0.911	152
主波峰5-β参数法	0.002	0.217	0.093	0.956	143
传统5-β参数法	0.004	0.317	0.137	0.913	146
GDR-Refined CFI	0.002	0.240	0.104	0.940	98
GDR-UCL	0.002	0.302	0.138	0.899	102
GDR-Refined OCOG	0.008	0.371	0.142	0.922	157
注：前6种算法用来对1级波形数据进行重跟踪处理，后3种算法为Cryosat-2/SIRAL GDR产品中自带的，已有处理好的数据。

图 5 不同重跟踪算法获得的重定点位置对比

Fig. 5 Retracked gates obtained by different retracking algorithms

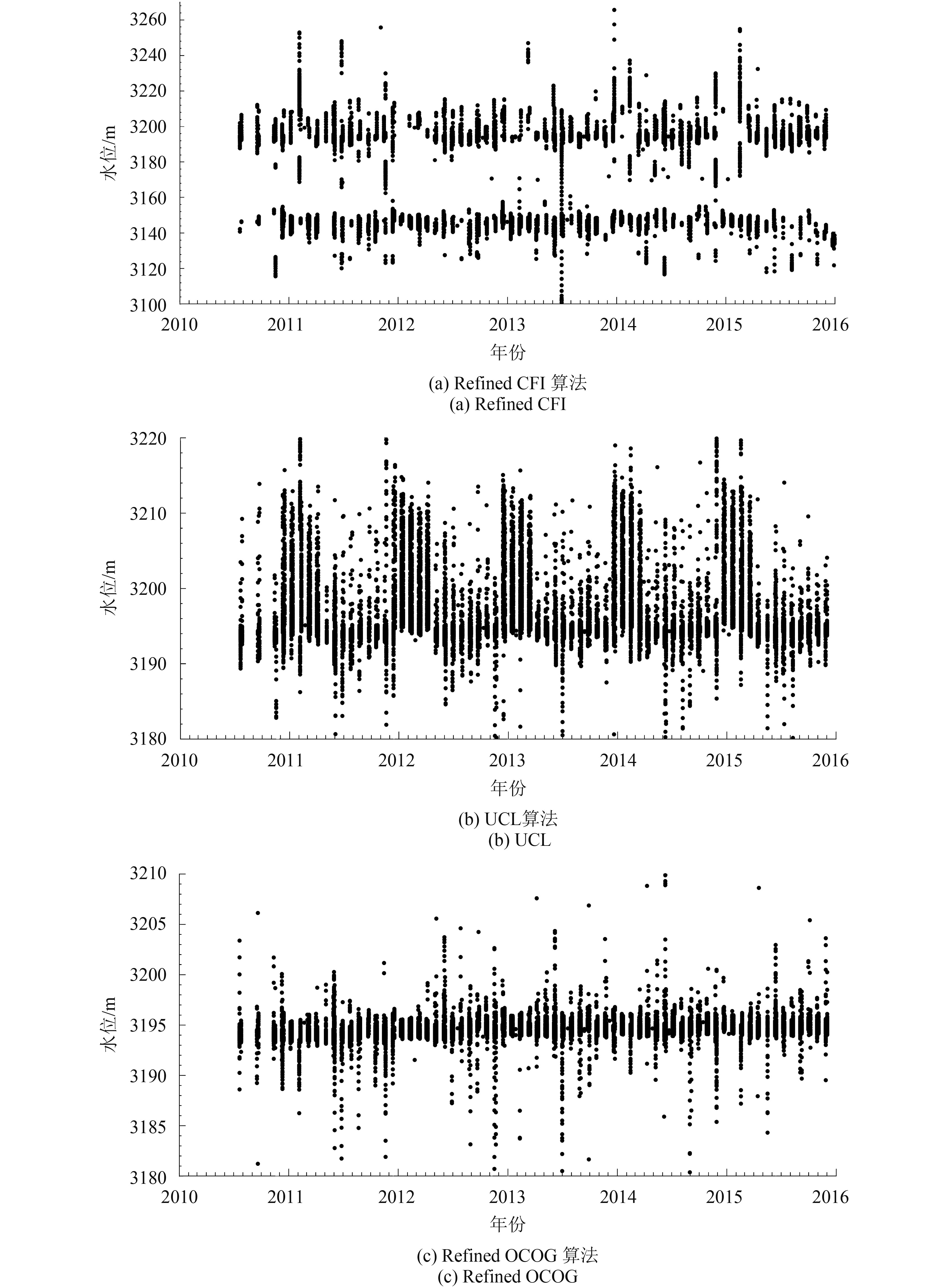
对于Cryosat-2/SIRAL GDR中LRM模式数据的3种重跟踪算法，Refined CFI算法具有较高的相关系数与较低的均方根误差，但是Refined CFI与UCL算法提取的单天水位的个数明显少于其他算法，原因是这两种数据在冬季结冰期(大约12月到次年3月)获取的水位出现异常。如图6所示，CFI算法获取的水位出现明显分层，而UCL算法在结冰期提取的水位呈现错乱，故两种数据提取的结冰期水位无效，而Refined OCOG算法提取的水位结果较好。因此，对于Cryosat-2/SIRAL GDR中的LRM数据，如果湖面无冰，则CFI算法提取水位的效果最佳，如果提取结冰期在内的长年水位，则基于Refined OCOG重跟踪算法的数据效果更佳。

图 6 Cryosat-2/SIRAL GDR数据中3种算法提取的所有水位值示意图

Fig. 6 All water levels extracted by the three algorithms of Cryosat-2/SIRAL GDR data

4.2 青海湖水位变化分析

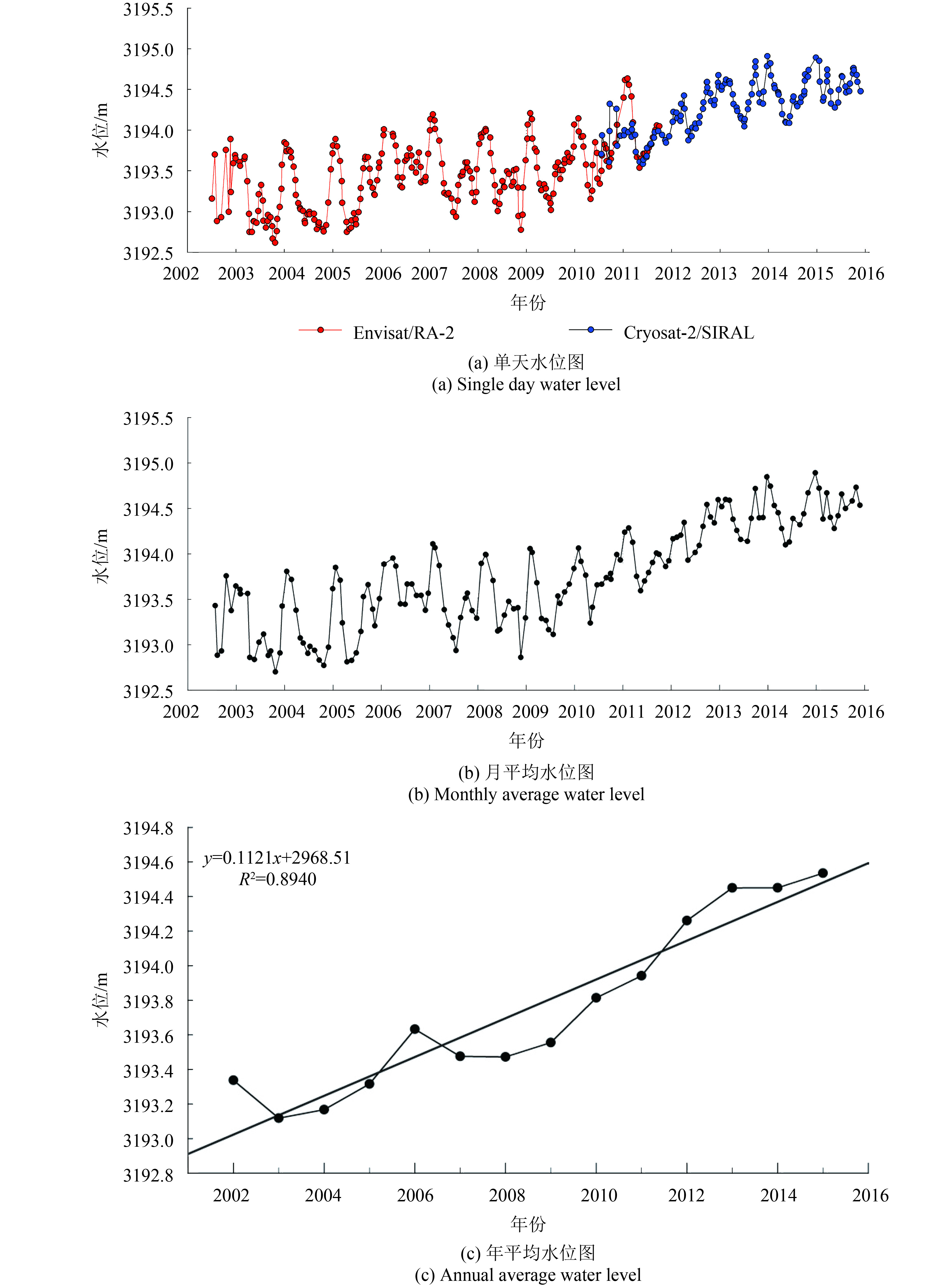
使用上述最佳重跟踪算法，即主波峰5-β参数法，对Cryosat-2/SIRAL LRM 1级波形数据进行重跟踪，提取青海湖2010年—2015年的水位。将该水位结果与用Envisat/RA-2 GDR产品中Ice-1数据提取的2002年—2011年的水位相结合，从而获得青海湖2002年—2015年的水位。图7为青海湖2002年—2015年的单天水位、月平均水位及年平均水位时间序列图。从图7(c)中可以看出，2002年到2003年青海湖水位下降，2003年到2004年基本持平，从2005年开始水位上升，2007年稍有下降，后持续上升。从2002年到2015年，青海湖水位整体变化趋势为0.112 m/a。由单天水位图(图7(a))和月平均水位图(图7(b))可以看出，每年5月份水位开始上涨，9月下旬水位达到峰值，后水位下降。高度计提取的水位显示，每年12月份水位开始上涨，次年1月份最高，后水位下降直到5月份，这与Lee等人(2011)和李林等人(2005)得到的结果相似，这可能是冬季湖水结冰后体积膨胀所致。

图 7 青海湖2002年—2015年水位变化时间序列图

Fig. 7 Water level changes of Qinghai Lake from 2002 to 2015

4.3 Cryosat-2/SIRAL高度计回波波形分析

为了进一步对比分析不同重跟踪算法提取水位的结果，以2011年7月29号过境青海湖的Cryosat-2 LRM模式的1级数据为例进行了波形分析。如图8所示，在高度计过境青海湖的过程中，回波波形呈现由尖峰波形—尖峰波形与(似)海洋波形的组合波形—(似)海洋波形—尖峰波形与(似)海洋波形的组合波形—尖峰波形的变化趋势(高乐，2014)，其中大部分为(似)海洋波形，这是由于青海湖面积较大，水深较深(平均水深为21 m)，受陆地影响的范围较小。也正因如此，上述的9种重跟踪算法提取青海湖水位的精度相差并不大(表1)。通过对多条波形数据的统计分析，我们得到，对于青海湖，高度计回波明显受陆地影响的范围约为5 km (15个点左右)。

图 8 青海湖2011年7月29日过境数据的波形图

Fig. 8 Data waveform through Qinghai Lake on 29 July, 2011

选取了14个靠近陆地边界的“复杂波形”进行了进一步分析(图9，其中图中的Rt1，Rt2， $ \cdots $ Rt9与表2相对应)，分别计算了不同重跟踪算法获得水位与实际水位的RMSE (表2)，我们发现，针对这种波形，主波峰重心偏移法和主波峰阈值法的重跟踪效果更好，均方根误差分别为0.224 m和0.231 m。

表 2 针对复杂波形的不同重跟踪算法提取水位结果对比表
Table 2 Comparison of different retrackers for combined waveform

下载CSV

编号	波形重跟踪算法	均方根误差/m
Rt1	主波峰重心偏移法	0.224
Rt2	传统重心偏移法	8.972
Rt3	主波峰阈值法	0.231
Rt4	传统阈值法	7.557
Rt5	主波峰5-β参数法	4.605
Rt6	传统5-β参数法	7.430
Rt7	GDR-Refined CFI	5.752
Rt8	GDR-UCL	4.611
Rt9	GDR-Refined OCOG	1.863

图 9 针对复杂波形的不同重跟踪算法提取水位结果图

Fig. 9 Water levels extracted by different retrackers for combined waveform

5 结　论

雷达高度计数据在监测内陆湖泊水位方面具有重要意义，波形重跟踪可以有效提高其提取水位的精度。本文对Cryosat-2/SIRAL LRM 1级数据进行了波形重跟踪，对比了多种算法所得水位的精度，并结合Envisat/RA-2的GDR数据，获取了青海湖2002年—2015年的水位变化信息。得出如下结论：

(1) 对比主波峰重心偏移法、主波峰阈值法、主波峰5-β参数法、传统重心偏移法、传统阈值法和传统5-β参数法，及Cryosat-2/SIRAL GDR产品中的Refined CFI、UCL、Refined OCOG重跟踪算法，针对整个青海湖非结冰期的水位的提取，主波峰5-β参数法为最佳算法，与实测水位相比具有最大相关系数(0.956)和最小均方根误差(0.093 m)；基于主波峰的改进算法提取水位的精度优于全波形的传统算法；而针对受陆地影响的“复杂波形”，主波峰重心偏移法和主波峰阈值法的重跟踪效果更好。

(2) 对于Cryosat-2/SIRAL GDR产品中的3种数据，若提取结冰期在内的湖泊水位，则基于Refined OCOG算法的数据效果更好，而基于Refined CFI算法和UCL算法的数据适合提取非结冰期的水位。

(3) 从2002到2004年青海湖水位下降，2005年到2015年水位上升，2002年—2015年水位平均变化速率为0.112 m/a；年内水位变化呈现季节性，每年5月份和12月份水位开始上升，峰值点分别出现在9月份和次年1月份左右。

Cryosat-2/SIRAL LRM卫星测高数据可以用于提取湖泊水位，且有较高的精度，为1 dm左右。对波形数据进行重跟踪可以有效提高高度计数据提取湖面水位的精度。而对于不同类型的湖泊，回波波形的表现不同，往往适应的重跟踪算法有所差别，本文的分析较为粗略，下一步，将选取不同类型的湖泊，进行详细对比分析。另外，本文并未考虑不同卫星轨道提取水位的差异，以及同一卫星重复轨道间的差距，该差异对提取水位精度的影响程度及如何将其有效消除，有待于进一步的研究。

志谢研究中用到的Envisat/RA-2和Cryosat-2/SIRAL高度计数据来源于欧洲航空局(ESA)，MODIS图像数据来源于美国国家航空航天局(NASA)，实测水位数据由青海省下社水文站提供，在此表示衷心的感谢！

参考文献(References)

Bao L F, Lu Y and Wang Y. 2009. Improved retracking algorithm for oceanic altimeter waveforms. Progress in Natural Science, 19 (2): 195–203. [DOI: 10.1016/j.pnsc.2008.06.017]

Bouffard J. 2015. CryoSat level-2 product evolutions and quality improvements in baseline C [J/OL]. [2016-03-1]. https://earth.esa.int/ web/guest/document-library/browse-document-library/-/article/ cryosat-level-2-product-evolutions-and-quality-improvements-in-baseline-c

Chu Y H, Li J C, Zhang Y, Xu X Y, Fan C B and Zou X C. 2005. Analysis and investigation of waveform retracking data of ENVISAT. Journal of Geodesy and Geodynamics, 25 (1): 76–80. [DOI: 10.3969/j.issn.1671-5942.2005.01.015] ( 褚永海, 李建成, 张燕, 徐新禹, 范春波, 邹贤才. 2005. ENVISAT测高数据波形重跟踪分析研究. 大地测量与地球动力学, 25 (1): 76–80. [DOI: 10.3969/j.issn.1671-5942.2005.01.015] )

Davis C H. 1996. A robust threshold retracking algorithm for extracting ice-sheet surface elevations from satellite radar altimeters // 1996 International Geoscience and Remote Sensing Symposium: Remote Sensing for a Sustainable Future. Lincoln, NE: IEEE: 1783–1787.

Frappart F, Calmant S, Cauhope M, Seyler F and Cazenave A. 2006. Preliminary results of ENVISAT RA-2-derived water levels validation over the Amazon basin. Remote Sensing of Environment, 100 (2): 252–264. [DOI: 10.1016/j.rse.2005.10.027]

Gao L. 2014. Monitoring the changes in lake level and glacier elevation in the Qinghai-Tibetan Plateau using satellite altimetry data. Beijing: University of Chinese Academy of Sciences: 30–90 (高乐. 2014. 基于卫星测高技术的青藏高原湖泊水位和冰川高程变化监测研究. 北京: 中国科学院大学: 30–90)

Gao L, Liao J J and Shen G Z. 2013. Monitoring lake-level changes in the Qinghai-Tibetan Plateau using radar altimeter data (2002-2012). Journal of Applied Remote Sensing, 7 (1): 073470 [DOI: 10.1117/1.JRS.7.073470]

Gao Y G. 2006. Lake level variations from satellite altimetry. Nanjing: Hohai University: 3–70 (高永刚. 2006. 利用卫星测高进行陆地湖泊水位变化监测. 南京: 河海大学: 3–70)

Gao Y G, Guo J Y and Yue J P. 2008. Lake level variations measurement with satellite altimetry. Science of Surveying and Mapping, 33 (6): 73–75. [DOI: 10.3771/j.issn.1009-2307.2008.06.024] ( 高永刚, 郭金运, 岳建平. 2008. 卫星测高在陆地湖泊水位变化监测中的应用. 测绘科学, 33 (6): 73–75. [DOI: 10.3771/j.issn.1009-2307.2008.06.024] )

Guo H R, Jiao W H and Yang Y X. 2004. The systematic difference and its distribution between the 1985 National Height Datum and the Global Quasigeoid. Acta Geodaetica et Cartographica Sinica, 33 (2): 100–104. [DOI: 10.3321/j.issn:1001-1595.2004.02.002] ( 郭海荣, 焦文海, 杨元喜. 2004. 1985国家高程基准与全球似大地水准面之间的系统差及其分布规律. 测绘学报, 33 (2): 100–104. [DOI: 10.3321/j.issn:1001-1595.2004.02.002] )

Hwang C, Guo J Y, Deng X L, Hsu H Y and Liu Y T. 2006. Coastal gravity anomalies from retracked geosat/GM altimetry: improvement, limitation and the role of airborne gravity data. Journal of Geodesy, 80 (4): 204–216. [DOI: 10.1007/s00190-006-0052-x]

Jain M, Andersen O B, Dall J and Stenseng L. 2015. Sea surface height determination in the Arctic using Cryosat-2 SAR data from primary peak empirical retrackers. Advances in Space Research, 55 (1): 40–50. [DOI: 10.1016/j.asr.2014.09.006]

Jiang W P, Chu Y H, Li J C and Yao Y S. 2008. Water level variation of Qinghai Lake from altimeteric data. Geomatics and Information Science of Wuhan University, 33 (1): 64–67. ( 姜卫平, 褚永海, 李建成, 姚永顺. 2008. 利用ENVISAT测高数据监测青海湖水位变化. 武汉大学学报(信息科学版), 33 (1): 64–67. )

Jiao W H, Wei Z Q, Ma X, Sun Z M and Li Y C. 2002. The origin vertical shift of National Height Datum 1985 with respect to the Geoidal Surface. Acta Geodaetica et Cartographica Sinica, 31 (3): 196–200. ( 焦文海, 魏子卿, 马欣, 孙中苗, 李迎春. 2002. 1985国家高程基准相对于大地水准面的垂直偏差. 测绘学报, 31 (3): 196–200. )

Kleinherenbrink M, Ditmar P G and Lindenbergh R C. 2014. Retracking Cryosat data in the SARIn mode and robust lake level extraction. Remote Sensing of Environment, 152 : 38–50. [DOI: 10.1016/j.rse.2014.05.014]

Kleinherenbrink M, Lindenbergh R C and Ditmar P G. 2015. Monitoring of lake level changes on the Tibetan Plateau and Tian Shan by retracking Cryosat SARIn waveforms. Journal of Hydrology, 521 : 119–131. [DOI: 10.1016/j.jhydrol.2014.11.063]

Lee H, Shum C K, Tseng K H, Guo J Y and Kuo C Y. 2011. Present-day lake level variation from Envisat altimetry over the northeastern Qinghai-Tibetan Plateau: Links with precipitation and temperature. Terrestrial, Atmospheric and Oceanic Sciences, 22 (2): 169–175. [DOI: 10.3319/TAO.2010.08.09.01(TibXS)]

Li J C, Chu Y H, Jiang W P and Xu X Y. 2007. Monitoring level fluctuation of lakes in Yangtze River basin by altimetry. Geomatics and Information Science of Wuhan University, 32 (2): 144–147. ( 李建成, 褚永海, 姜卫平, 徐新禹. 2007. 利用卫星测高资料监测长江中下游湖泊水位变化. 武汉大学学报(信息科学版), 32 (2): 144–147. )

Li J C and Jin T Y. 2013. On the main progress of satellite altimetry and its applications. Journal of Geomatics, 38 (4): 1–8. ( 李建成, 金涛勇. 2013. 卫星测高技术及应用若干进展. 测绘地理信息, 38 (4): 1–8. )

Li L, Zhu X D, Wang Z Y and Wang Q C. 2005. Impacting factors and changing tendency of water level in Qinghai Lake in recent 42 years. Journal of Desert Research, 25 (5): 689–696. ( 李林, 朱西德, 王振宇, 汪青春. 2005. 近42a来青海湖水位变化的影响因子及其趋势预测. 中国沙漠, 25 (5): 689–696. )

Li Y, Duan Y Q and Jin Y M. 2014. Analysis of features and causes of Qinghai Lake during the period of 1956-2011. Yellow River, 36 (6): 87–89, 112. ( 李燕, 段永强, 金永明. 2014. 1956-2011年青海湖变化特征及原因分析. 人民黄河, 36 (6): 87–89, 112. )

Martin T V, Zwally H J, Brenner A C and Bindschadler R A. 1983. Analysis and retracking of continental ice sheet radar altimeter waveforms. Journal of Geophysical Research, 88 (C3): 1608–1616. [DOI: 10.1029/JC088iC03p01608]

Medina C E, Gomez-Enri J, Alonso J J and Villares P. 2008. Water level fluctuations derived from ENVISAT Radar Altimeter (RA-2) and in-situ measurements in a subtropical waterbody: Lake Izabal (Guatemala) . Remote Sensing of Environment, 112 (9): 3604–3617. [DOI: 10.1016/j.rse.2008.05.001]

Michailovsky C I, McEnnis S, Berry P A M, Smith R and Bauer-Gottwein P. 2012. River monitoring from satellite radar altimetry in the Zambezi River basin. Hydrology and Earth System Sciences, 16 (7): 2181–2192. [DOI: 10.5194/hess-16-2181-2012]

Song C Q, Ye Q H, Sheng Y W and Gong T L. 2015. Combined ICESat and CryoSat-2 altimetry for accessing water level dynamics of Tibetan Lakes over 2003-2014. Water, 7 (9): 4685–4700. [DOI: 10.3390/w7094685]

Wingham D J, Francis C R, Baker S, Bouzinac C, Brockley D, Cullen R, de Chateau-Thierry P, Laxon S W, Mallow U, Mavrocordatos C, Phalippou L, Ratier G, Rey L, Rostan F, Viau P and Wallis D W. 2006. CryoSat: A mission to determine the fluctuations in Earth’s land and marine ice fields. Advances in Space Research, 37 (4): 841–871. [DOI: 10.1016/j.asr.2005.07.027]

Wingham D J, Rapley C G and Griffiths H D. 1986. New techniques in satellite altimeter tracking systems // Proceedings of IGARSS’86 Symposium. Zurich: ESA Publications Division, 3 : 1339–1344.

Yang G S, Ma R H, Zhang L, Jiang J H, Yao S C, Zhang M and Zeng H A. 2010. Lake status, major problems and protection strategy in China. Journal of Lake Sciences, 22 (6): 799–810. ( 杨桂山, 马荣华, 张路, 姜加虎, 姚书春, 张民, 曾海鳌. 2010. 中国湖泊现状及面临的重大问题与保护策略. 湖泊科学, 22 (6): 799–810. )

Yang L, Lin M S, Liu Q H and Pan D L. 2012. A coastal altimetry retracking strategy based on waveform classification and sub-waveform extraction. International Journal of Remote Sensing, 33 (24): 7806–7819. [DOI: 10.1080/01431161.2012.701350]

Yi W J, Li X Y, Cui B L and Ma Y J. 2010. Climate change and impact on water Level of the Qinghai Lake watershed. Journal of Arid Meteorology, 28 (4): 375–383. [DOI: 10.3969/j.issn.1006-7639.2010.04.001] ( 伊万娟, 李小雁, 崔步礼, 马育军. 2010. 青海湖流域气候变化及其对湖水位的影响. 干旱气象, 28 (4): 375–383. [DOI: 10.3969/j.issn.1006-7639.2010.04.001] )

Zhang G Q, Xie H J, Kang S C, Yi D H and Ackley S F. 2011. Monitoring lake level changes on the Tibetan Plateau using ICESat altimetry data (2003-2009). Remote Sensing of Environment, 115 (7): 1733–1742. [DOI: 10.1016/j.rse.2011.03.005]

Zhang J L, Chen Y, Ge J S and Nie X M. 2013. Land use/cover change and land resources management in the area around the Qinghai Lake of China in 1977-2010. Journal of Desert Research, 33 (4): 1256–1266. [DOI: 10.7522/j.issn.1000-694X.2013.00177] ( 张金龙, 陈英, 葛劲松, 聂学敏. 2013. 1997-2010年青海湖环湖区土地利用/覆盖变化与土地资源管理. 中国沙漠, 33 (4): 1256–1266. [DOI: 10.7522/j.issn.1000-694X.2013.00177] )

摘要

关键词