出版日期: 2017-07-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20175337
2017 | Volumn21 | Number 4
上一篇 | 下一篇

相位萃取技术在InSAR小数据集上的应用

张奎¹ , 汪慧¹ , 宋瑞庆² , 盛耀彬³

1. 重庆大学通信工程学院，重庆 400044

2. 中国地震局地震预测研究所地震预测重点实验室，北京 100036

3. 西南大学地理科学学院，重庆 400715

收稿日期: 2016-07-25

基金项目: 国家自然科学基金(编号：41404027，41461164004)；国家国际科技合作专项项目(编号：2105DFR21100)

第一作者简介: 张奎(1982—　)，男，讲师，研究方向为合成孔径雷达干涉测量理论和应用研究。E-mail：zk@cqu.edu.cn

中图分类号: TP701

文献标识码: A

摘要

相位萃取技术可最小化多基线InSAR处理中干涉像对的去相关噪声，已成为雷达干涉测量研究领域中热点技术之一。本文首先设计并实现了一套专门针对小数据集的基于相位萃取技术的多基线InSAR处理流程。整个流程分为两大模块。第一个模块为称为预处理模块，通过图像配准、地形相位移除等操作生成相位萃取技术所需的零基线SAR图像堆栈。第二个模块首先基于多视像元生成相干矩阵，并且在此基础上完成相位萃取操作。然后，利用小基线集技术的思想在萃取相位上分离出各相位稳定点上的形变情况。为了保证结果可靠性，在这一模块中还加入了大气相位预估与移除的步骤。最后，该流程被应用到了5景拍摄于太原地区的PALSAR图像上。实验结果表明，相位萃取技术在小数据集情况下仍然能够有效提升数据的相干性，这有利于多基线InSAR输出结果密度的提升。

关键词

相位萃取, 多基线InSAR, 小数据集, 相干性, 合成孔径雷达

The application of the phase reconstruction on small InSAR datasets

ZHANG Kui¹ , WANG Hui¹ , SONG Ruiqing² , SHENG Yaobin³

1.College of Communication Engineering, Chongqing University, Chongqing 400044, China

2.Institute of Earthquake Science, China Earthquake Administration, Beijing 100036, China

3.School of Geographical Science, Southwest University, Chongqing 400715, China

Abstract

Multi-baseline InSAR techniques have demonstrated their great potential in topographic mapping and ground surface deformation monitoring. In order to minimize the decorrelation noise between stacked SAR images in multi-baseline InSAR processes, the phase reconstruction technique has been developed recently and has become one of the hotspot techniques in radar interferometry. Due to budget limitations and unstable SAR image acquisition frequency, a lot of multi-baseline InSAR applications have to be carried out based on small image datasets. Researchers have made every endeavor to address this problem, some targeted multi-baseline InSAR processing strategies have been therefore developed. Unfortunately, there are few literatures discussing the application of phase reconstruction to small image datasets at this stage. This paper aims to evaluate the effectiveness of the phase reconstruction technique on a small SAR image datasets. A targeted multi-baseline InSAR processing scheme was designed and applied to real data. The main idea of phase reconstruction technique is to reform phase observations along a SAR stack by taking advantage of a maximum likelihood estimator which is defined on the coherence matrix estimated from each target. The proposed multi-baseline InSAR processing scheme is divided into two modules. The first one is named as " pre-processing module”, which generates the zero-baseline SAR image stack required by the phase reconstruction technique via a series of operations including image coregistration, topographic phase component removal, and so on. The second one firstly constructs coherence matrices based on multilooked pixels, thereby conducting phase reconstruction operations. Subsequently, it isolates ground surface deformation signals based on reconstructed phase observations by taking advantage of the small baseline subset technique. Noted that an atmospheric disturbances estimation and removal step was involved in this module in order to assure the reliability of the output measurements. The proposed scheme is subsequently applied to five PALSAR images acquired over Taiyuan, ShanXi Province, China. During the experimental process, the performance of the phase reconstruction technique in the case of small image subsets was analyzed in different aspects (e.g. the signal-to-noise ratio of the FFT based orbital fringe estimation process, the number of residues contained in phase unwrapping networks). The corresponding annual deformation rate field was presented, as well as the distribution of additional points obtained after the application of the phase reconstruction technique. The results has demonstrated that the phase reconstruction technique can effectively improve interferometric coherence even in the case of small image datasets, which is beneficial to the proliferation of the density of multi-baseline InSAR results. It must be noted that the size of the coherence matrix is relatively small in the case of small image datasets. Thus the precision of the phase reconstruction results is likely to be influenced by the low coherent elements of coherence matrix. In order to make the phase reconstruction technique work with small image datasets better, future works should try to eliminate the negative impacts of low-quality elements on the phase reconstruction procedure.

Key words

phase reconstruction, multi-baseline InSAR, small datasets, interferometric coherence, synthetic aperture radar

1 引　言

为了克服传统InSAR技术容易受时间、空间去相关及大气延迟干扰的缺点，Ferretti等人(2000)在21世纪初系统地提出了永久散射体干涉技术PSInSAR (Permanent Scatterer Interferometric SAR)。该技术可获取毫米级精度的地表形变时间序列，近年来已成功地应用到地壳运动(张景发等，2006；徐小波等，2012)、火山活动(许才军等，2011；季灵运等，2013)、城市地表沉降(葛大庆等，2007；李永生等，2013)、矿区开采沉陷(尹宏杰等，2011；刘振国等，2013)、滑坡(Lu 等，2012；廖明生等，2012)等领域中。PSInSAR的基本思想是通过使用多景SAR图像，生成具有不同时间基线和空间基线的多幅差分干涉图，利用各种相位成分的不同时间、空特性，在具有较高相位稳定性的点目标上精确地分离出地表形变所贡献的相位。由于该技术是基于单一主图像体系生成干涉图像堆栈(即从N景可用的SAR图像中选取一景作为主图像，生成N–1幅差分干涉图)，一般只有具备良好反射特性的永久散射体PS点(Permanent Scatterers)才能表现出较高的相位稳定性。然而，除城市区域外，PS点的密度一般不能得到有效保证。

为了提升监测结果密度，一系列基于自由干涉配对体系的多基线InSAR技术应运而生(Berardino 等，2002；吴涛等，2008；Liu 等，2009；Zhang 等，2012)。这类技术在所有可能的干涉组合中按照一定标准选取高相关性的像对，生成干涉图像堆栈，以此降低时间去相关和几何去相关的影响。在这类方法中，干涉像对的选取标准通常是基于时间、空间基线的。然而，干涉信号去相关实际上是取决于多种因素的，因此无法通过时间、空间基线建立一个统一并适用于所有应用的选取标准。Guarnieri和Tebaldini(2008)利用点目标的相干矩阵对SAR观测相位进行了萃取，从而在统计意义上最大化了干涉信号的相干性，避免了以上的问题(本文中将这一方法称之为相位萃取技术)。Ferretti等人(2011)提出了SqueeSAR技术。该技术在基于统计一致性点SHP (Statistically Homogeneous Pixels)生成的相干矩阵上进行相位萃取，避免了由于相干矩阵构建所造成的PS点丢失。SqueeSAR的提出使得相位萃取技术成为了多基线InSAR研究领域广泛关注的热点问题。

由于SAR数据采集频率的限制，很多实际应用不得不在小数据集的基础上进行多基线InSAR分析。针对这一问题，已有研究者提出了专门的算法并成功应用(Mora 等，2003)。但是，目前几乎没有文献讨论如何在小数据集情况下使用相位萃取技术的问题。本文提出了一种在小数据集上应用相位萃取技术的处理策略并将其成功应用到了拍摄于太原地区的五景SAR图像上。同时，从干涉条纹估计结果的信噪比、相位解缠残差点数量等方面对相位萃取技术的结果进行了评价。

2 相位萃取技术

假设输入图像已完成了配准操作并且其数量为N，则对于给定的像元点p，其观测向量可表示为

${{z}_p} = {\left[ {z_p^1,z_p^2, \ldots ,z_p^N} \right]^{\rm{T}}}$

(1)

式中，上标T表示矩阵转置， $z_p^N$ 为点p在第N幅输入SAR图像上的复数观测值。在以p点为中心的区域Ψ内，假设其相邻像元的观测值相互独立且同分布，则可得到该区域内观测值的协方差矩阵：

${V} = \frac{1}{{\varPsi} }\mathop \sum \limits_{q \in {\varPsi} } {{z}_q}z_q^{\rm{H}}$

(2)

式中，上标H代表共轭转置。根据中心极限定理，归一化后的SAR数据概率密度分布可认为是均值为0的正态分布(Cao 等，2015)。据此可给出该区域内任一点q的概率密度函数的简化形式(Guarnieri和Tebaldini，2008)：

$f\left( {y{\rm{|}}{\theta }} \right) = {\rm{exp}}\left( { - {{z}}_q^{\rm{H}}{{V}^{ - 1}}{{z}_q}} \right)$

(3)

式中，θ为未知的相位观测值向量。因此，可采用下述极大似然估计法来获取p点上的相位估计值：

$\hat{ {\theta} } = {\rm{arc}}\mathop {\max }\limits_{{\theta}} \left\{ {\mathop \prod \limits_{q \in {{\varPsi}} } {\rm{exp}}\left( { - {{z}}_q^{\rm{H}}{{V}^{ - 1}}{{z}_q}} \right)} \right\}$

(4)

实际应用中，在构造协方差矩阵V之前会对z_q进行归一化操作。这种情况下，可得到相干矩阵。使用相干矩阵可有效改善点目标样本后向散射强度的不平衡性，在实际操作中通常采用相干矩阵C来代替协方差矩阵V。相干矩阵可表示为

${C} = {\varPhi \varGamma }{{\varPhi }^{\rm{H}}}$

(5)

式中，Γ是一个N×N的实对称矩阵，其中的每个元素代表了相应干涉像对的“真实”相干系数。Φ是一个N×N的对角阵， ${\varPhi } = diag\left\{ {{\rm{exp}}\left( {j{{\theta}} } \right)} \right\}$ 。因此公式(4)可改写为

$\begin{array}{l}\hat {{\theta}} = {\rm{arc}}\mathop {\max }\limits_{\;\;\;\;\;\;\;\;\;\; {{\theta}}} \left\{ {\mathop \prod \limits_{q \in {{\varPsi}} } {\rm{exp}}\left( { - {z}_q^{\rm{H}}{\varPhi }{{\varGamma }^{ - 1}}{{\varPhi }^{\rm{H}}}{{z}_q}} \right)} \right\}\\\;\;\; = {\rm{arc}}\mathop {\max }\limits_{\;\;\;\;\;\;\;\;\;\; {{\theta}}} \left\{ {{\rm{exp}}\left[ { - trace\left( {{\varPhi }{{\varGamma }^{ - 1}}{{\varPhi }^{\rm{H}}}{C}} \right)} \right]} \right\}\\\;\;\; = {\rm{arc}}\mathop {\min }\limits_{\;\;\;\;\;\;\;\;\;\; {{\theta}}} \left\{ {{{\gamma }^{\rm{H}}}\left( {{{\varGamma }^{ - 1}} \circ {C}} \right){\gamma }} \right\}\end{array}$

(6)

式中， $ \circ $ 是点积运算符，γ是一个N维向量， ${\gamma } = {\rm{exp}}\left( {i{\theta }} \right)$ 。这是一个非线性的最优化问题，通常采用基于BFGS算法的相位三角测量法(PTA)来求得一个局部最优解(Ferretti 等，2011)，从而完成对相位的萃取。

3 处理策略

3.1 数据预处理

在实际应用中，式(6)中的Γ是无法获取的。由于相干矩阵元素的强度信息代表着对真实相干性的估计，因此通常使用|C|来代替Γ。如前所述，相干矩阵的构建过程是建立在样本实际相位值相同的假设之上的。因此，为了能够获取更加准确的相干性估值，有必要在相干矩阵建立之前对所有的输入SAR数据进行零基线处理，即消除所有干涉像对中的与地形和平地效应相关的相位成分。图1给出了进行相位萃取操作之前所需的预处理步骤流程。该流程的左半部分利用了两轨差分干涉测量的思想，将外部DEM投影到了雷达坐标系。在该流程的右半部分中，首先从输入的SAR图像中选取一景作为主图像，然后将其余的辅图像和它进行配准。接下来，利用投影后的高程数据将辅图像中相对于主图像的地形相位成分移除，并且利用轨道信息移除所有图像各自包含的平地相位成分，进而生成相位萃取技术所需的零基线SAR图像堆栈。

图 1 相位萃取技术所需的预处理流程

Fig. 1 The pre-processing work flow required by the phase reconstrucntion technique

3.2 基于相位萃取技术的小数据集多基线InSAR处理流程

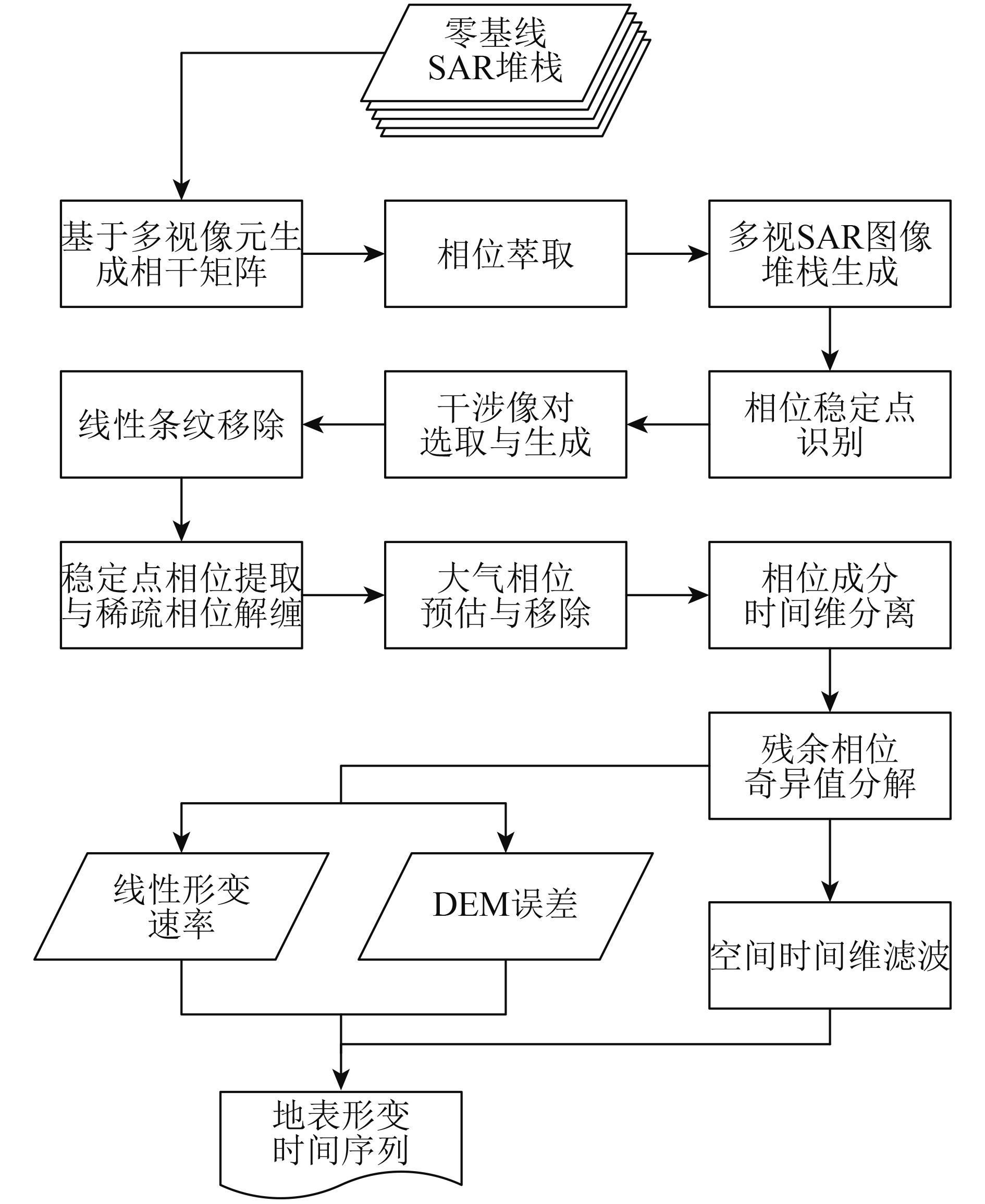
本文实验中使用的多基线InSAR处理流程如图2所示。下面按模块分别对各个步骤进行阐述。

图 2 基于相位萃取技术的小数据集多基线InSAR流程

Fig. 2 Amulti-baseline InSAR processing flow based on the phase reconstruction technique desinged for small subsets

(1) 基于多视像元生成相干矩阵在输入数据经过预处理后，设定一个多视窗口尺寸，将每个多视窗口视为一个像元。对于每一个多视像元p，使用其中包含的样本生成相应的相干矩阵。注意，为了保证相干矩阵的可靠性，应使用一个较大的窗口尺寸。

(2) 相位萃取使用目前应用最为广泛的Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法极小化公式(6)并得到萃取相位。

(3) 多视SAR图像堆栈生成基于在每一个多视像元上得到的萃取相位重建出相应的多视SAR图像堆栈。为了避免不必要的I/O操作，该步骤应该与相位萃取步骤同时进行。

(4) 相位稳定点识别对于一个多视像元p，按以下公式计算其萃取结果匹配度：

${\gamma _{{\rm{match}}}}\left( p \right) = \frac{1}{{{N^2} - N}}\mathop \sum \limits_r^N \mathop \sum \limits_s^N {{\rm{e}}^{j{\varphi _{rs}}}}{{\rm{e}}^{ - j{\theta _r}}}{{\rm{e}}^{j{\theta _s}}}$

(7)

式中，N为输入SAR图像的数量，φ_rs为C中r行s列元素的相位，θ_n表示第n个未知量。当γ_match(p)大于一个预设值时，认为p为一个相位稳定点。

(5) 干涉像对选取与生成为了避免DEM误差对后续相位解缠操作的影响，将空间基线相对较短的SAR图像对选取出来并生成相应的干涉图。由于在这里选取干涉像对的目的并不是减小散射体去相关的影响，因此在某些情况下(例如，研究区域地势平坦、使用了高精度与高分辨率的外部DEM)可以生成所有的干涉图，以提升后续相位分离操作中观测值的数量。

(6) 线性条纹移除利用FFT对各干涉图中的线性成分进行移除，以减小轨道误差对后续解算的影响。由于所有的干涉图都是在萃取相位的基础上生成的，它们都具有相当高的相关性。因此，条纹移除算法可达到相当高的信噪比，几乎不会出现错误的情况。

(7) 稳定点相位提取与稀疏相位解缠在每一景干涉图中提取出相位稳定点上的相位，并对其进行解缠。由于相位稳定点是离散分布的，因此需使用稀疏相位解缠技术完成该步骤。同样地，由于解缠操作是基于萃取相位的，其可靠性将大为提高。

(8) 大气相位预估与移除利用在预处理步骤中得到的雷达坐标系下的DEM，在各干涉像对中计算出解缠相位中与高程直接相关的大气成分并移除。由于之前的FFT算法只移除了线性轨道误差，在估计大气相位的同时可引入非线性的轨道误差模型，以达到进一步去除轨道误差的目的。

(9) 相位成分时间维分离对于一个给定的相位稳定点p，其观测值可表示为

$\begin{aligned}& \Delta {\phi ^k}\left( p \right) = \displaystyle\frac{{ - 4\pi }}{\lambda } \cdot {T^k} \cdot \Delta v\left( p \right)\\ & + \displaystyle\frac{{ - 4\pi \cdot B_ \bot ^k\left( p \right)}}{{\lambda \cdot R \cdot {\rm{sin}}\theta }} \cdot \Delta \varepsilon \left( p \right) + \Delta \phi _{\rm {sum}}^k\left( p \right)\\ &k = 1,2, \cdots ,N\end{aligned}$

(8)

式中，λ为信号波长，R为斜距，θ为本地入射角，T^k为第k幅干涉图的时间基线， ${B_ \bot ^k\left( p \right)}$ 为p点的垂直基线， $\Delta v\left( p \right)$ 和 $\Delta \varepsilon \left( p \right)$ 分别为未知的线性形变速率和DEM误差， $\Delta \phi _{{\rm{sum}}}^k\left( p \right)$ 为大气相位、轨道误差相位、非线性形变相位以及噪声相位的和。在传统在传统的多基线InSAR处理中，观测值 $\Delta {\phi ^k}\left( p \right)$ 通常是缠绕的。在这种情况下，广泛使用的解决该问题的方法主要有两种：(1)周期图法(Ferretti 等，2001)，(2)LAMBDA法(Kampes和Hanssen，2004)。本文所设计的数据处理策略是专门针对小数据集的，在该步骤之前在该步骤之前加入了“稀疏相位解缠”与“大气相位预估与移除”两个步骤。这使得我们可以直接使用非缠绕相位作为观测值。因此，这里直接使用最小二乘法求解出 $\Delta v\left( p \right)$ 和 $\Delta \varepsilon \left( p \right)$ 。计算完成后，按下面的公式评价相位分离操作的可靠性：

${\gamma _{{\rm{model}}}}\!\left( p \right)\! \!=\!\! \frac{1}{N}\left| {\mathop \sum \limits_{k = 1}^N {{\rm{e}}^{j\Delta {\varphi ^k}\left( p \right) - j\left[ {\frac{{ - 4{\rm{\pi }}}}{\lambda }{T^k}\Delta v\left( p \right) +\! \frac{{ - 4{\rm{\pi }} \cdot B_ \bot ^k\left( p \right)}}{{\lambda \cdot R \cdot sin\theta }}\Delta \varepsilon \left( p \right)} \right]}}}\! \right|$

(9)

当 ${\gamma _{{\rm{model}}}}\left( p \right)$ 大于某一预设值时，认为 $\Delta v\left( p \right)$ 和 $\Delta \varepsilon \left( p \right)$ 的估计结果是可靠的。否则，将p从相位稳定点集合中移除。

(10) 残余相位奇异值分解将获得的线性形变速率和DEM误差转换为相位并从观测值中移除得到残余相位。用基于奇异值分解的方法(Berardino 等，2002)恢复残余相位的时间顺序。

(11) 空间时间维滤波各相位稳定点的残余相位贡献包括以下几个部分：非线性形变、大气延迟、轨道误差相位以及噪声。大气延迟和轨道误差在空间维上高度相关，在时间维上不相关。非线性形变在空间维上相关性小于大气延迟和轨道误差，在时间维上高度相关。噪声在时间和空间维上都不相关。采用在空间维上进行高通滤波与在时间维上进行低通滤波的方式，提取出非线性形变，最终得到地表形变时间序列。

4 实验结果与分析

本文对上述全部流程进行了实现并将其应用到了真实的SAR数据上。为了验证相位萃取技术在小数据集情况下的应用效果，将该流程下得到的结果和在不使用相位萃取技术情况下的结果进行了比对。其中，我们调用了NLopt软件库中的L-BFGS算法完成相位萃取目标函数的最小化。

本文中使用的实验数据为2007年—2010年间ALOS卫星PALSAR传感器在太原地区采集的5景图像。表1给出了它们的详细信息。在预处理过程中，以2007年12月20日采集的图像为主图像，并截取出了以太原城区为中心的一块区域。辅图像配准完成后，使用了分辨率为3弧秒的SRTM DEM对输入图像做了零基线处理。接下来，按照上一节中描述的流程对零基线处理后的SAR图像堆栈进行处理。在这一过程中，用于生成相干矩阵的多视窗口大小设为20×10。 ${\gamma _{{\rm{model}}}}\left( p \right)$ 设置为0.25，总共获得了129013的相位稳定点。基于以下3 个原因，选择了所有的像对生成干涉图。第一，目标区域地势较为平坦；第二，使用的窗口尺寸较大，SRTM DEM相对于多视后SAR图像的分辨率足够高。第三，输入的SAR图像数量太少，可选择干涉像对的空间有限。

表 1 实验使用的5景PALSAR图像
Table 1 The five PALSAR images used in the experiment

下载CSV

序号	拍摄时间	极化方式	模式	轨道方向	入射角/(°)
1	2007-12-20	HH	FBS	升轨	34.3
2	2008-02-04	HH	FBS	升轨	34.3
3	2009-12-25	HH	FBS	升轨	34.3
4	2010-02-09	HH	FBS	升轨	34.3
5	2010-12-28	HH	FBS	升轨	34.3

处理流程中的一个步骤是基于FFT估计线性轨道误差。为了评价相位萃取技术的效果，我们记录了在每一景干涉图上FFT估计的信噪比，并且与直接在基于原始相位的干涉图上得到的信噪比进行了比对，如表2所示。这里的信噪比定义为频谱上最大频率强度和平均频率强度之间的比值，可反映条纹估计结果的可靠性以及干涉信号的相关性。在某种程度上，相位萃取操作可以被看作一个对干涉相位在时维上进行滤波的过程(Ferrett等，2011)。这意味着相位萃取操作之后，干涉相位中的高频成分会减少，FFT估计的信噪比会得到提升。表2的结果与该情况相符。这证明了相位萃取技术在小数据集的情况下仍然可有效发挥其作用。表2的后两栏表示在分别使用原始相位和萃取相位的情况下，定义在相位稳定点上的稀疏解缠网络在各个干涉像对中所包含的残差点数量。在第一个干涉像对上，两种情况下的残差点数量几乎没有区别。而在其他像对上，使用萃取相位时的残差点数量较使用原始相位时大幅减少。从表2中可以看出，第一个干涉像对的时间基线相比于其他像对要小许多，换句话说它的相干性比其他的像对要高，因此可以得出以下两个结论：第一，相位萃取有效地降低了干涉像对中的去相关噪声。第二，相位萃取过程尽量保持了高相干性像对上的干涉特性。图3展示的是经过大气相位预估与移除步骤后的非解缠相位。从图3中可以看出，此时得到的观测相位已能基本反映出研究区域内的地表形变趋势。

表 2 萃取相位和原始相位在FFT条纹估计信噪比方面和相位解缠残差点数量方面的比较
Table 2 Comparisions between the reconstructed phase and the originial phase in the aspects of the SNR of FFT fringe estimation and the number of phase unwrapping residues

下载CSV

序号	主图像	辅图像	原始相位方位向FFT信噪比	萃取相位方位FFT信噪比	原始相位距离FFT信噪比	萃取相位距离FFT信噪比	原始相位残差点数量	萃取相位残差点数量
1	2007-12-20	2008-02-04	8.9	69.3	4.8	36.5	706	708
2	2009-12-25	2010-02-09	8.9	72.4	4.7	37.9	438	326
3	2007-12-20	2010-02-09	5.5	24.8	2.9	11.3	4482	3650
4	2008-02-04	2010-12-28	4.8	22	2.7	10.6	6838	5400
5	2010-02-09	2010-12-28	5.5	27	3	14	6733	5581
6	2009-12-25	2010-12-28	4.6	23.2	2.5	11.9	13878	9358
7	2008-02-04	2009-12-25	4.3	18.9	2.2	8.9	10939	6835
8	2007-12-20	2009-12-25	4.9	21.4	2.6	10.3	6386	4266
9	2007-12-20	2010-12-28	4.2	19	2.4	9.3	10752	7185
10	2008-02-04	2010-02-09	4.9	21.2	2.6	10.2	6555	4653

图 3 经过大气相位预估与移除步骤后得到的非缠绕相位观测值

Fig. 3 The unwrapped phase observations resulting from the step of preliminary atmosphere estimation and removal

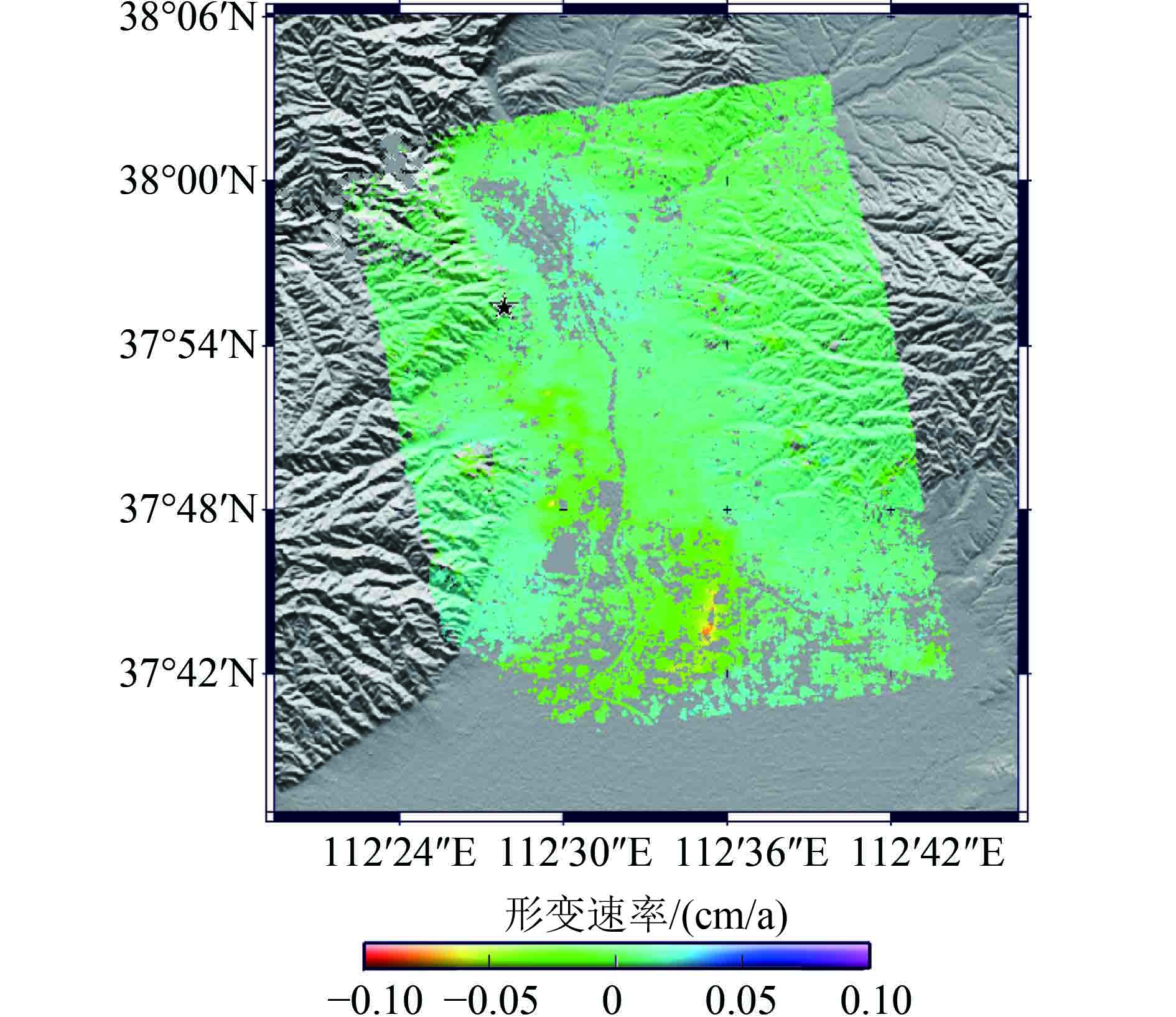
在相位成分时间维分离步骤中，使用 ${\gamma _{{\rm{model}}}}\left( p \right)$ 为0.8，在使用萃取相位时总共可获得102142个相位稳定点上的可靠沉降速率和DEM误差，而在使用原始相位时这一数值为91621。图4展示了使用萃取相位时得到的雷达视线向年形变速率图。可以看出，在太原的南部郊区出现了明显的地表形变，最大值约为8 cm/a。地表形变场的分布与文献(吴宏安等，2011)中的结果一致。图5表现的是仅能在使用萃取相位的情况下获得形变结果的点在研究区的分布情况。该图清楚地表明，即便是在小数据集的情况下，相位萃取技术仍能有效地提升多基线InSAR技术监测结果的密度。

图 4 基于相位萃取技术得到的年均形变速率结果

Fig. 4 The annual deformation rate map generated based on the phase reconstrcition technique

图 5 使用相位萃取技术后新增点的分布

Fig. 5 Additional points obtained after the application of the phase reconstruction technique

5 结　论

相位萃取技术能在统计意义上最大化干涉信号相干性，可有效提高多基线InSAR技术观测结果密度。目前，几乎还还没有文献对相位萃取技术在小数据集上的应用效果进行讨论。本文基于相位萃取技术设计并实现了一种小数据集多基线InSAR处理策略，并将其应用到了拍摄于太原地区的真实SAR数据上。实验结果表明，相位萃取技术在小数据集上仍能有效降低去相关噪声对多基线InSAR技术的影响。值得注意的是，在小数据集情况下相干矩阵的尺寸很小，相位萃取过程能使用的相位观测值数量是非常有限的。在这种情况下，相位萃取结果的精度极有可能受到相干矩阵中低质量元素的影响。为了提高相位萃取技术适应小数据集的能力，应通过一定方式尽量避免低质量元素对相位萃取过程的影响。

参考文献(References)

Berardino P, Fornaro G, Lanari R and Sansosti E. 2002. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Transactions on Geoscience and Remote Sensing, 40 (11): 2375–2383. [DOI: 10.1109/TGRS.2002.803792]

Cao N, Lee H and Jung H C. 2015. Mathematical framework for phase-triangulation algorithms in distributed-scatterer interferometry. IEEE Geoscience and Remote Sensing Letters, 12 (9): 1838–1842. [DOI: 10.1109/LGRS.2015.2430752]

Ferretti A, Fumagalli A, Novali F, Prati C, Rocca F and Rucci A. 2011. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Transactions on Geoscience and Remote Sensing, 49 (9): 3460–3470. [DOI: 10.1109/TGRS.2011.2124465]

Ferretti A, Prati C and Rocca F. 2000. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Transactions on Geoscience and Remote Sensing, 38 (5): 2202–2212. [DOI: 10.1109/36.868878]

Ferretti A, Prati C and Rocca F. 2001. Permanent scatterers in SAR interferometry. IEEE Transactions on Geoscience and Remote Sensing, 39 (1): 8–20. [DOI: 10.1109/36.898661]

Ge D Q, Guo X F, Wang Y, Wang Y and Liu S W. 2007. Surface deformation rate derivation based on differential interferograms stack. Remote Sensing for Land and Resources, 19 (1): 24–26. [DOI: 10.6046/gtzyyg.2007.01.04] ( 葛大庆, 郭小方, 王毅, 王艳, 刘圣伟. 2007. 基于序列差分干涉纹图的地表形变速率提取. 国土资源遥感, 19 (1): 24–26. [DOI: 10.6046/gtzyyg.2007.01.04] )

Guarnieri A M and Tebaldini S. 2008. On the exploitation of target statistics for SAR interferometry applications. IEEE Transactions on Geoscience and Remote Sensing, 46 (11): 3436–3443. [DOI: 10.1109/TGRS.2008.2001756]

Ji L Y, Xu J D, Zhao B, Wan Y and Shen H H. 2013. Present-day activity of Ashikule volcanic group from InSAR. Seismology and Geology, 35 (3): 532–541. [DOI: 10.3969/j.issn.0253-4967.2013.03.007] ( 季灵运, 许建东, 赵波, 万园, 申欢欢. 2013. 利用InSAR技术研究新疆阿什库勒火山群现今活动性. 地震地质, 35 (3): 532–541. [DOI: 10.3969/j.issn.0253-4967.2013.03.007] )

Kampes B M and Hanssen R F. 2004. Ambiguity resolution for permanent scatterer interferometry. IEEE Transactions on Geoscience and Remote Sensing, 42 (11): 2446–2453. [DOI: 10.1109/TGRS.2004.835222]

Li Y S, Zhang J F, Li Z H and Luo Y. 2013. Land subsidence in Beijing City from InSAR time series analysis with small baseline subset. Geomatics and Information Science of Wuhan University, 38 (11): 1374–1377. ( 李永生, 张景发, 李振洪, 罗毅. 2013. 利用短基线集干涉测量时序分析方法监测北京市地面沉降. 武汉大学学报(信息科学版), 38 (11): 1374–1377. )

Liao M S, Tang J, Wang T, Balz T and Zhang L. 2012. Landslide monitoring with high-resolution SAR data in the Three Gorges region. Science China Earth Sciences, 42 (2): 217–229. [DOI: 10.1007/s11430-011-4259-1] ( 廖明生, 唐婧, 王腾, BalzT, 张路. 2012. 高分辨率SAR数据在三峡库区滑坡监测中的应用. 中国科学:地球科学, 42 (2): 217–229. [DOI: 10.1007/s11430-011-4259-1] )

Liu G X, Buckley S M, Ding X L, Chen Q and Luo X J. 2009. Estimating spatiotemporal ground deformation with improved permanent-scatterer radar interferometry. IEEE Transactions on Geoscience and Remote Sensing, 47 (8): 2762–2772. [DOI: 10.1109/TGRS.2009.2016213]

Liu Z G, Bian Z F, Lv F X and Dong B Q. 2013. Subsidence monitoring caused by repeated excavation with time-series DInSAR. Journal of Mining and Safety Engineering, 30 (3): 390–395. ( 刘振国, 卞正富, 吕福祥, 董保权. 2013. 时序DInSAR在重复采动地表沉陷监测中的应用. 采矿与安全工程学报, 30 (3): 390–395. )

Lu P, Casagli N, Catani F and Tofani V. 2012. Persistent scatterers interferometry hotspot and cluster analysis (PSI-HCA) for detection of extremely slow-moving landslides. International Journal of Remote Sensing, 33 (2): 466–489. [DOI: 10.1080/01431161.2010.536185]

Mora O, Mallorqui J and Broquetas A. 2003. Linear and nonlinear terrain deformation maps from a reduced set of interferometric SAR Images. IEEE Transactions on Geoscience and Remote Sensing, 41 (10): 2243–2253. [DOI: 10.1109/TGRS.2003.814657]

Wu H A, Zhang Y H, Chen X Y, Zhong L, Du J, Sun Z H and Sun G T. 2011. Ground deformation monitoring using small baseline DInSAR technique: a case study in Taiyuan City from 2003 to 2009. Chinese Journal of Geophysics, 54 (3): 673–680. [DOI: 10.3969/j.issn.0001-5733.2011.03.006] ( 吴宏安, 张永红, 陈晓勇, ZhongL, 都洁, 孙中惠, 孙广通. 2011. 基于小基线DInSAR技术监测太原市2003～2009年地表形变场. 地球物理学报, 54 (3): 673–680. [DOI: 10.3969/j.issn.0001-5733.2011.03.006] )

Wu T, Zhang H, Wang C, Tang Y X and Wu H A. 2008. Retrieval of urban slow deformation using the multi-baseline DInSAR technique. Chinese Science Bulletin, 53 (15): 1849–1857. [DOI: 10.1007/s11434-008-0331-4] ( 吴涛, 张红, 王超, 汤益先, 吴宏安. 2008. 多基线距DInSAR技术反演城市地表缓慢形变. 科学通报, 53 (15): 1849–1857. [DOI: 10.1007/s11434-008-0331-4] )

Xu C J, He P and Wen Y M. 2011. Surface deformation of Mt. Etna, Italy from PSInSAR.Geomatics and Information Science of Wuhan University, 36 (9): 1012–1016. [DOI: 10.13203/j.whugis2011.09.015] ( 许才军, 何平, 温扬茂. 2011. 利用PSInSAR研究意大利Etna火山的地表形变. 武汉大学学报(信息科学版), 36 (9): 1012–1016. [DOI: 10.13203/j.whugis2011.09.015] )

Xu X B, Qu C Y, Shan X J, Ma C, Zhang G F and Meng X J. 2012. An experimental study of monitoring fault crustal deformation using PS-InSAR technology. Advances in Earth Science, 27 (4): 452–459. [DOI: 10.11867/j.issn.1001-8166.2012.04.0452] ( 徐小波, 屈春燕, 单新建, 马超, 张桂芳, 孟秀军. 2012. 基于PS-InSAR技术的断裂带地壳形变实验研究. 地球科学进展, 27 (4): 452–459. [DOI: 10.11867/j.issn.1001-8166.2012.04.0452] )

Yin H J, Zhu J J, Li Z W, Ding X L and Wang C C. 2011. Ground subsidence monitoring in mining area using DInSAR SBAS algorithm. ActaGeodaeticaet CartographicaSinica, 40 (1): 52–58. ( 尹宏杰, 朱建军, 李志伟, 丁晓利, 汪长城. 2011. 基于SBAS的矿区形变监测研究. 测绘学报, 40 (1): 52–58. )

Zhang J F, Gong L X and Jiang W L. 2006. Application of PS InSAR technique to measurement of long-term crustal deformation. Recent Developments in World Seismology (6): 1–6. [DOI: 10.3969/j.issn.0253-4975.2006.06.001] ( 张景发, 龚利霞, 姜文亮. 2006. PS InSAR技术在地壳长期缓慢形变监测中的应用. 国际地震动态 (6): 1–6. [DOI: 10.3969/j.issn.0253-4975.2006.06.001] )

Zhang K, Ge LL, Li X J and Ng A H M. 2012. Monitoring ground surface deformation over the North China Plain using coherent ALOS PALSAR differential interferograms. Journal of Geodesy, 87 (3): 253–265. [DOI: 10.1007/s00190-012-0595-y]

摘要

关键词