|
收稿日期: 2016-09-18
基金项目: 国家自然科学基金(编号:61571347,61201293);中央高校基本科研业务费专项资金(编号:JB150214)
第一作者简介: 张建龙(1976— ),男,副教授,研究方向为遥感图像处理、模式识别理论和应用。E-mail:jlzhang@mail.xidian.edu.cn
中图分类号: TN911.7
文献标识码: A
|
摘要
SRM(Statistical Region Merging)分割算法具有快速、稳定和抗噪强的优点,基于此,本文提出一种基于DSSRM(Dynamic Sorting Statistical Region Merging)级联分割的SAR图像变化检测方法。首先,针对SRM算法基于单特征静态排序导致的过分割问题,提出一种动态排序模式的DSSRM算法以减少差异图像分割错误,该算法建立基于合并区域的多特征马氏距离排序准则,在每次合并之后更新区域邻接矩阵并重新排序;然后,基于互信息最小化准则构造多通道差异数据集以提高算法对区域合并的约束能力;最后,提出一种级联分割变化检测框架,第1级利用SRM算法将差异图像映射到超像素空间,第2级采用DSSRM算法对超像素进行动态合并获得收敛的分割结果,第3级采用简化SRM方法进行三次合并获得最终的变化检测图。实验结果表明,该方法可以获得比SRM方法和目前流行方法更好的检测性能。
关键词
合成孔径雷达图像, 变化检测, 动态排序, 统计区域合并
Abstract
Synthetic Aperture Radar (SAR) images have region homogeneity with gray and texture. Considering that SRM (Statistical Region Merging) algorithms of image segmentation are efficient, stable and robust against noise, we propose a novel change detection method based on cascade segmentation with Dynamic Sorting Statistical Region Merging (DSSRM) algorithm. Firstly a DSSRM algorithm based on dynamic sorting is proposed to overcome conventional SRM's over-segmentation problem caused by single feature and static sorting. This algorithm takes the Manhattan distance of multi-feature of regions to be merged as the sorting criterion, and updates the adjacency matrix after each merging. Secondly based on the rule of minimizing mutual information we design a multi-channel complementary appearance model to improve the capability of constraint for region merging. Finally we present a cascade change detection framework with multiple levels. The first level projects difference image to super-pixel space via SRM, the second level utilizes DSSRM to dynamically merge regions; and the third level leverages a simplified SRM to realize region merging again to obtain final change detection map. Experimental results of the proposed method and proposed methods based on PCA and MRF are presented. By analysis and quantitative comparisons, the false alarm number and total of error number by DSSRMare decreased thereby the performance of KAPPA can get higher than methods based on PCA and MRF. DSSRM method is based on dynamic sorting algorithm with Manhattan distance of multi-feature of regions, it makes similar regions to be merged firstly. Experiments on construction of multi-channel illustrates that the more is the difference between channels the better is the performance of change detection. Our method improved the performance of SRM algorithm to avoid the over-segmentation phenomenon. Comparison experiments show that this method can obtain better performance of change detection than conventional SRM and state of art algorithms.
Key words
SAR image, change detection, MDSSRM, cascade segmentation
1 引 言
随着近几年遥感技术的迅猛发展,遥感数据数量日益增长并广泛应用于环境监测、大气分析和城市规划等领域。其中SAR图像变化检测被应用到军事和民用领域,主要涉及灾害(如洪水、火灾和地震)区域的定位、城市的扩张情况分析以及军事应用中打击效果的评估等方面,研究SAR图像变化检测具有重要意义。
在遥感图像变化检测中,SAR图像利用合成孔径雷达成像,不受包括云、雨等天气气候变化等因素影响,可以提供稳定的数据源,而且星载SAR有着固定的运行周期,能够对地面进行定期的重复观测,因此它比光学遥感更适合对地面进行动态监视。由于SAR成像易受相干斑噪声(Speckle Noise)影响,因此SAR图像去噪(Salmon,2010;Soni 等,2013)问题获得了广泛重视。遥感图像变化检测本质上是一个二分类问题,即将差异图像分为变化类和非变化类。基于像素的方法(Coppin 等,2004;Lu 等,2004)通常利用差异像素灰度特征进行分类,并使用聚类方法获取尽量好的分类结果,CVA(Change Vector Analysis)(Bovolo和Bruzzone,2007)方法则利用差异图像的变化特征向量提取变化部分,Celik(2009)利用PCA降维并使用Kmeans聚类完成变化检测过程,Gong等人(2014)将马尔可夫随机场和模糊聚类相结合根据新的能量函数改进变化检测结果。然而像素特征不具备语义特征,存在语义鸿沟问题,因此利用图像分割分离异质区域从而获得半语义信息成为图像理解和识别的关键技术。常用的图像分割方法包括谱聚类分割算法(贾建华和焦李成,2010;Gou 等,2013)、主动轮廓线分割(Feng 等,2013;Gao 等,2011;Wang 等,2014)、MRF分割(宋晓峰 等,2010;Xiong 等,2012)和SRM(Nock和Nielsen,2004;Lang 等,2014)统计区域合并算法等。近年来,已有部分学者将图像分割方法应用于遥感图像变化检测中,Hichri等人(2013)将基于马尔可夫随机场MRF(Markov Random Filed)和水平集分割方法引入变化检测,并使用SVM(Supporting Vector Machine)进行分类,这是一种监督学习方法需要一定数量的训练数据。万红林等人(2012)将交互式分割和决策融合引入SAR图像变化检测中,但该方法对种子点的选取非常敏感。佃袁勇等人(2016)结合Meanshift算法对高分辨遥感图像进行多尺度分割获得变化检测结果,取得了一定效果。Wang等人(2016)根据提取差异图像中SIFT (Scale-invariant Feature Transform)点并根据特征点利用大金法进行分割,该方法分割效果取决于对SIFT点的有效提取,可以看出基于分割方法的变换检测方法正在逐渐增多,但大部分方法需要训练数据获得稳定的监督分割。SRM算法是一种快速区域生成分割算法,通过建立图像的统计模型利用统计推理方法控制像素及区域的合并,设定同质区域判决规则获得准确的分割结果,SRM方法不依赖于数据的概率分布假设并拥有较好的抗噪能力。本文利用SRM统计分割模型设计了一种新的非监督变化检测方法。首先针对SRM算法单次静态排序易导致的过分割现象,提出了一种基于多特征马氏距离的排序准则和动态排序模式的DSSRM算法;其次建立最小互信息准则构造差异数据集提高合并过程中的约束力,进一步提高检测性能,最后,利用SRM、DSSRM和简化SRM构成级联分割结构完成对差异图像的变化检测。
2 基于DSSRM级联分割的变化检测方法
本节首先介绍SRM分割算法的基本原理和流程,分析算法的不足之处,在此基础之上提出DSSRM算法,其次介绍基于最小互信息准则的差异数据集构造过程,最后提出一种级联分割变化检测框架。
2.1 SRM分割方法
经典SRM算法是2004年由Nock和Nielsen提出的一种图像统计模型,算法主要根据图像区域的同质性质在概率空间中寻找最优合并区域,能够感知并快速捕获图像的主要结构,具有较强的抗噪性能,针对不同的内容复杂度可以实现多尺度分割,是一种高效的图像分割算法。
SRM算法主要针对RGB三通道彩色图像,假设图像I含有个像素,每个像素包含(R,G,B)3个颜色通道,每个通道取值范围为{1,2,
(1) 对于任意统计区域内部的任意颜色通道(R,G,B),统计像素在该通道内都应该具有同样的均值;
(2) 任意相邻统计区域中至少有一个颜色通道的均值与其他通道不相同。
根据上述统计区域的同质特性,推导出待合并区域对
| $P(R,R') = \left\{ {\begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}\!\!\!\!\!\! 1 \begin{array}{l}\forall a \in (R,G,B),\mathop {\max }\limits_{a \in \left\{ {R,G,B} \right\}} \\[8pt]\left| {\overline {{R'_{a}}} - \overline {{R_a}} } \right| \leqslant \sqrt {{b^2}(R) - {b^2}(R')} \end{array}\end{array}}\\[17pt]\!\!\!\!\!\! {\begin{array}{*{20}{c}}0 \quad\quad{{\text{其他}}}\end{array}}\end{array}} \right.$ | (1) |
| $b(R) = g\sqrt {\frac{1}{{2Q\left| R \right|}}\ln \frac{{\left\| {{R_{\left| R \right|}}} \right\|}}{\delta }} $ | (2) |
式中,
SRM算法的核心技术包括两部分:
(1) 排序算法。在判断是否合并之前首先要确定待合并的区域对
| $f(p,{p'}) = \mathop {\max }\limits_{a \in \left\{ {R,G,B} \right\}} \left| {p_{_a}' - {p_a}} \right|$ | (3) |
式中,(p,p’)为相邻像素对,
(2) 合并准则。判断满足什么样的条件图像区域对象
2.2 DSSRM方法
统计区域合并SRM算法存在不足之处:
(1)静态排序方式:SRM算法采用一次静态排序方式,排列顺序一次生成,在合并过程中并不更新,由于区域合并是一个动态过程,每次合并都可能生成新的区域,该区域的特征很可能发生改变,从而造成排列顺序的重新分布,显然一次排序无法适应合并区域特征的动态变化过程;
(2)单特征排序准则:SRM算法的排序准则主要基于像素对和区域对特征相关性,仅仅考虑灰度均值特征,初始合并的主要对象为像素,灰度均值能够准确代表像素特征,随着合并区域面积逐步增大,区域形状和纹理逐渐复杂,依赖单特征的灰度均值易造成图像局部过分割现象,如图2被圈中部分所示,Bern数据差异图像变化区域被腐蚀,造成检测漏警增大。
针对所述SRM算法的不足,提出一种多特征判决准则的动态排序算法DSSRM,考虑引入区域均值、区域面积和区域灰度直方图等特征,并采用无量纲的马氏距离构造排序函数,定义最优待合并区域对
| $(R,{R'}) = \arg \mathop {\max }\limits_{a \in \left\{ {{D_1},\cdots,{D_n}} \right\}} f({R_a},R_a^{'})$ | (4) |
式中,f
排序函数f
| $\left\{ \begin{array}{l}f(R,{R'}) = \sqrt {\left[ {{{H}_R} - {{H}_{{R'}}}} \right] \times {{S}^{ - 1}} \times {{\left[ {{{H}_R} - {{H}_{{R'}}}} \right]}^{\rm{T}}}} \\r(R,{R'}) = 1\\\max \left[ {\left| {\displaystyle\frac{{{A_R}}}{{{A_{{R'}}}}}} \right|,\left| {\displaystyle\frac{{{A_{{R'}}}}}{{{A_R}}}} \right|} \right] < \delta \end{array} \right.$ | (5) |
式中,
最后,为了适应区域合并过程中区域特征的动态变化特性,本文采用动态排序方式,每完成一次合并就重新计算新区域的特征向量,更新相邻矩阵,重新计算
综上所述,DSSRM算法流程如下:
(1) 遍历待分割图像I中相邻的区域,确定相邻区域对个数M,生成邻接矩阵B;
(2) 计算每个区域对的相似度
根据式(4)(5),确定候选合并区域对
(3) 根据式(1)(2)判断
结束。
2.3 基于最小互信息准则的的差异数据集构造
根据式(4)计算的排序函数中,
| $\left\{ \begin{array}{l}{D_1} = \left| {\log \displaystyle\frac{{{I_1}}}{{{I_2}}}} \right|\\{D_2} = 1 - {\rm{min}}\left( {\displaystyle\frac{{\mathop {{\mu _{{I_1}}}}\limits^ - }}{{\mathop {{\mu _{{I_2}}}}\limits^ - }},\displaystyle\frac{{\mathop {{\mu _{{I_2}}}}\limits^ - }}{{\mathop {{\mu _{{I_1}}}}\limits^ - }}} \right)\\[15pt]{D_3} = \log \left[ {\max \left( {\displaystyle\frac{{{g_{_1}}}}{{{g_{_2}}}},\displaystyle\frac{{{g_{_2}}}}{{{g_{_1}}}}} \right)} \right]\end{array} \right.$ | (6) |
Bern数据集两时相、对数比值差异图像、均值比值差异图像和高斯比值差异图像分别如图3(a)—(e)所示。
建立图像互信息最小准则构造差异数据集,对于输入图像A、B,互信息定义为式(7):
| $\left\{ \begin{array}{l}I(A,B) = H(A) + H(B) - H(A,B)\\H(A) = - \sum\limits_{i = 1}^n {{P_A}({a_i})\log } {P_A}({a_i})\\H(B) = - \sum\limits_{i = 1}^n {{P_B}({b_i})\log } {P_B}({b_i})\\H(A,B) = - \sum\limits_A {\sum\limits_B {{P_{AB}}({a_i},{b_i})} } \log {P_{AB}}({a_i},{b_i})\end{array} \right.$ | (7) |
式中,H(A)为图像A的熵,
统计常用的SAR图像变化检测Berne、Otawwa以及Yellow River数据的4种差异图像的互信息形成了列表,结果如表1所示,其中L表示对数比差异图,R表示均值比差异图,G表示高斯均值比差异图,符号‘&’连接计算互信息的对象。从表1中可以看出A&B的互信息最小,而B&C最大,即均值比值差异图和对数比值差异图之间的差异性最大,作为SRM最终的差异数据集。
表 1 3种差异图数据互信息统计结果
Table 1 Statistical result of mutual information for three difference images
| 数据集 | L&R | L&G | R&G |
| Bern | 1.2433 | 1.4344 | 1.5161 |
| Ottawa | 0.7279 | 0.7783 | 1.2522 |
| Yellow-river | 0.6154 | 0.8674 | 0.8338 |
| 平均 | 0.8622 | 1.0267 | 1.2007 |
2.4 基于DSSRM算法的级联分割检测框架
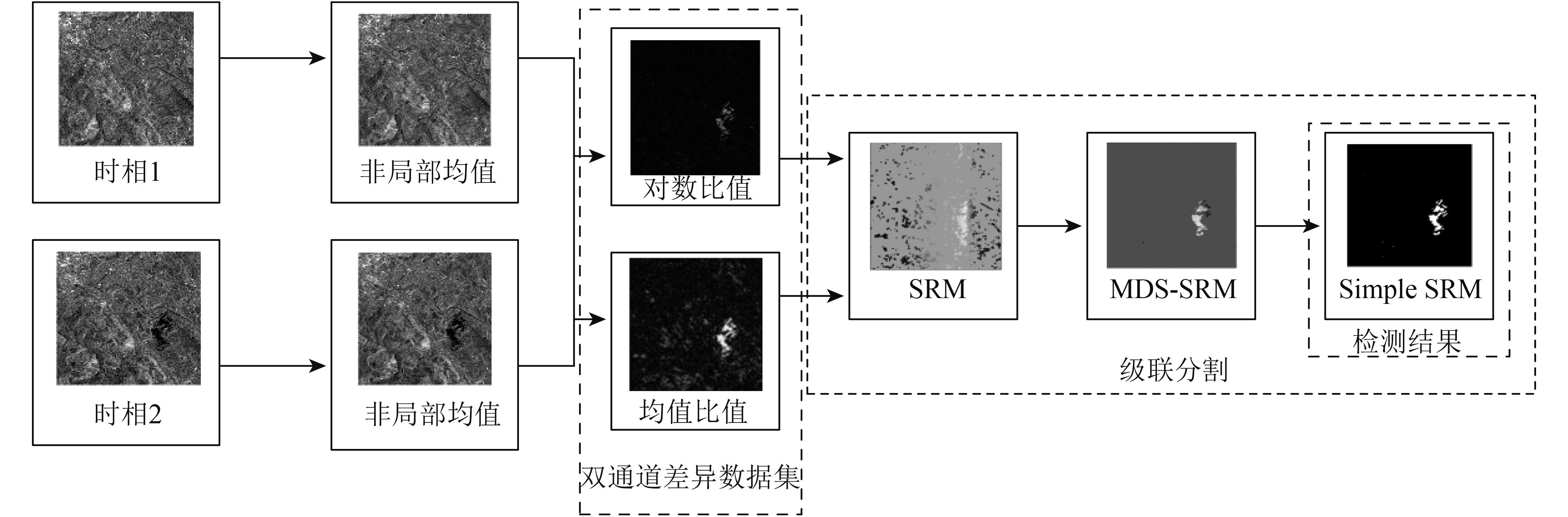
在DSSRM分割方法基础之上提出一种混合级联合结构的SAR图像变化检测框架,该框架结构如图4所示。首先利用非局部均值滤波去除SAR相干斑噪声,然后采用差异性较大的对数比和均值比方法构建双通道差异图像,最后利用混合级联结构对双通道差异图像提取变化区域,其中第一级采用原始SRM算法将差异图从像素空间转换为超像素空间,第二级利用DSSRM算法完成差异图像合并,最后使用简化的SRM算法获得最终的变化检测结果。
采用非局部均值滤波滤除SAR图像相干斑噪声,非局部均值通过使用图像中所有像素灰度值的加权平均值来得到待处理像素点的灰度估值,对于SAR图像的相干斑噪声有较好的效果。
已知一幅图像
| $NL\left( v \right)\left( i \right) = \sum\limits_{j \in {I}} {\omega \left( {i,j} \right)} v\left( i \right)$ | (8) |
式中,权值
3 实验结果与分析
为了验证基于DSSRM算法的混合级联框架在SAR图像遥感图像变化检测中的有效性,设计了3种仿真实验加以验证:(1)对比4种变化检测方法在SAR图像变换检测中的性能指标,包括SRM+Kmeans方法、PCA_Kmeans方法、Fuzzy+MRF以及基于双通道差异图及DSSRM算法的级联分割方法简称DSSRM;(2)对比在级联框架下单通道差异图方法、双通道差异图以及三通道差异图条件下的变化检测效果,验证差异图互信息准则的有效性;仿真数据集采用Bern数据集、Ottawa数据集和Yellow River数据集。数据集的分辨率分别为:301×301、290×350、291×306个像素大小。仿真实验的计算环境如下:CPU Intel(R) Core i5-34703.2 GHZ、内存4 G、WINDOWS 7操作系统,仿真软件版本MATLAB2013b。
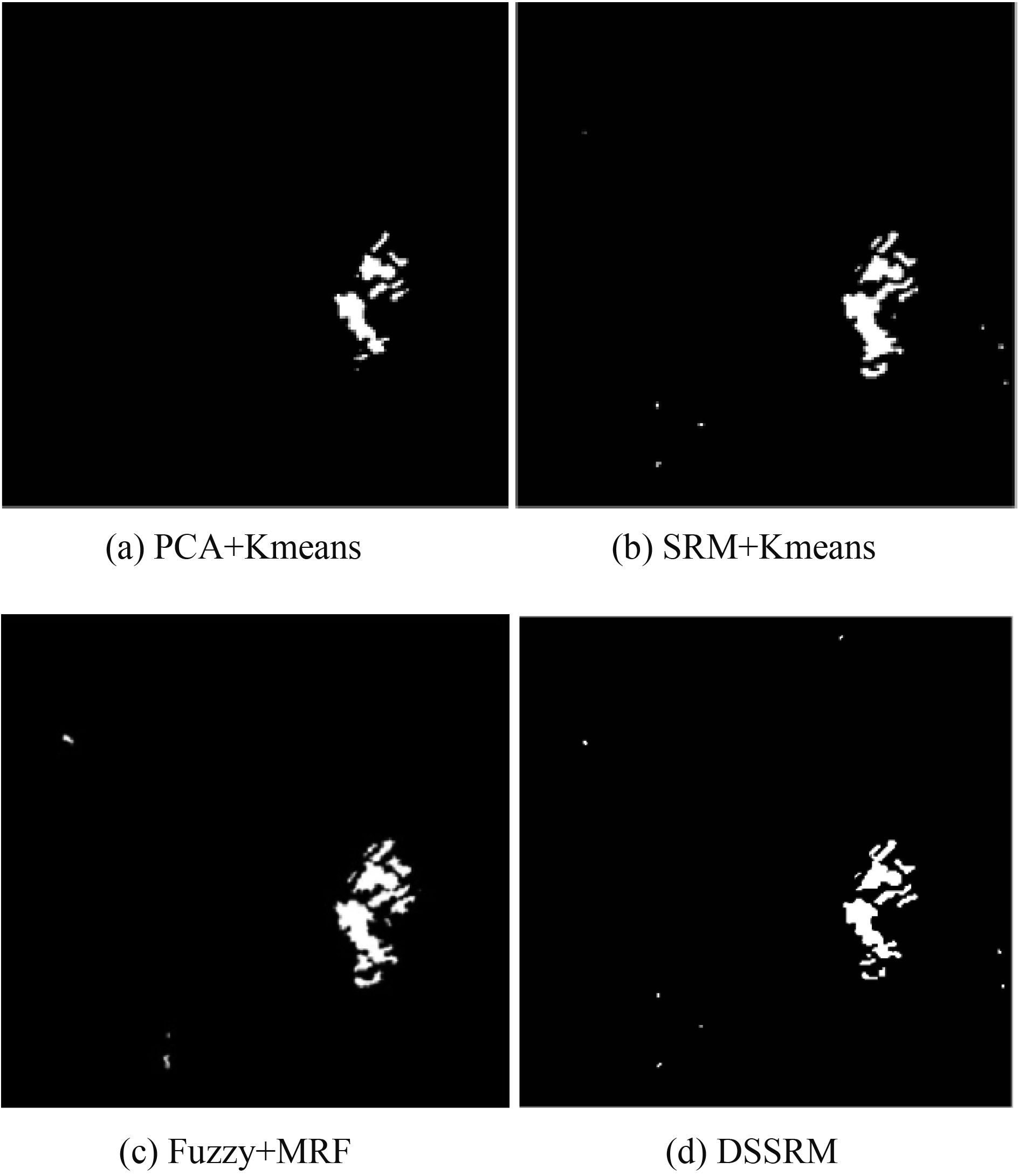
4种方法在Bern数据集上的检测结果如图6(a)—(d)所示,表2列出了4种方法在3种数据集上的检测性能指标对比,主要包括虚警像素个数Fp、漏警像素个数Fn,正确分类概率PCC以及一致性系数Kappa,并在表中用加粗方式标出了最佳检测指标。从表2可以看出,DSSRM方法相对于其他方法获得了更好的检测结果,尤其在虚警错误数上及总错误数上获得了较好的控制,使得虚警和漏警相对均衡,因此在Kappa系数上也获得了较好的性能指标。这主要得益于级联分割框架中SRM算法为初始分割将像素空间转换为超像素空间,使待合并区域具有部分语义信息,DSSRM利用区域特征使得最相似的区域首先合并,避免过分割现象,双通道数据也对进一步提高了合并的有效性。
表 2 4种检测算法的性能对比
Table 2 Performance comparison for four algorithms
| 数据集 | 方法 | Fp | Fn | Kappa | PCC |
| Bern | PCA+Kmeans | 258 | 146 | 0.8437 | 0.9955 |
| SRM | 287 | 114 | 0.8363 | 0.9956 | |
| FCM+MRF | 364 | 47 | 0.8413 | 0.9955 | |
| DSSRM | 208 | 117 | 0.8585 | 0.9963 |
为了验证互信息选择准则的正确性,对比在级联分割框架下单通道差异图(以对数比值差异图为例)、双通道差异图以及三通道差异图的变化检测结果分别如图7(a)(b)(c),各项性能指标如表3所示。双通道差异图获得了最好的检测结果,主要是因为对数比值和均值比值差异性最大,由于均值比值差异图和高斯比值差异图相似性较大,在合并过程降低了合并约束能力,导致了过分割现象,如图7(c)中的红圈部分,因此三通道差异图效果反而变差。仿真实验说明检测效果主要取决于通道差异性。
表 3 不同通道数条件下DSSRM变化检测性能对比
Table 3 Performance comparison of DSSRM algorithm on the condition of different channel number
| 数据集 | 方法 | Fp | Fn | Kappa | PCC |
| Bern | 单通道 | 238 | 114 | 0.8534 | 0.9961 |
| 两通道 | 208 | 117 | 0.8585 | 0.9963 | |
| 三通道 | 301 | 149 | 0.8147 | 0.9950 |
4 结 论
本文提出了一种基于DSSRM级联分割的SAR图像变化检测方法。DSSRM算法在半语义的图像超像素空间完成收敛合并,简化SRM则获得最终的变化检测结果。通过构造合并区域多特征的马氏距离空间作为排序准则,用动态更新方式替代一次静态排序过程,并利用最小互信息准则构造差异数据集提高合并的约束能力。实验表明,DSSRM的虚警错误比基于Kmeans和MRF的检测方法低,虚警概率和漏警概率更均衡,因此能够获得更高的检测性能。图像合并过程中尺度因子应与图像尺寸相关,如何根据SAR图像特征获得理想的尺度并探索自适应式尺度合并是本文下一步研究的方向。
参考文献(References)
-
Bovolo F and Bruzzone L. 2007. A theoretical framework for unsupervised change detection based on change vector analysis in the polar domain. IEEE Transactions on GeoscienceandRemote Sensing, 45 (1): 218–236. [DOI: 10.1109/TGRS.2006.885408]
-
Celik T. 2009. Unsupervised change detection in satellite images using principal component analysis and k-means clustering . IEEE Geoscience and Remote Sensing Letters, 6 (4): 772–776. [DOI: 10.1109/LGRS.2009.2025059]
-
Coppin P, Jonckheere I, Nackaerts K, Muys B and Lambin E. 2004. Digital change detection methods in ecosystem monitoring: a review. International Journal of Remote Sensing, 25 (9): 1565–1596. [DOI: 10.1080/0143116031000101675]
-
Dian Y Y, Fang S H and Yao C H. 2016. Change detection for high-resolution images using multilevel segment method. Journal of Remote Sensing, 20 (1): 129–137. [DOI: 10.11834/jrs.20165074] ( 佃袁勇, 方圣辉, 姚崇怀. 2016. 多尺度分割的高分辨率遥感影像变化检测. 遥感学报, 20 (1): 129–137. [DOI: 10.11834/jrs.20165074] )
-
Feng J, Cao Z and Pi Y. 2013. Multiphase SAR image segmentation with G0-statistical-model-based activecontours . IEEE Transactions on Geoscience and Remote Sensing, 51 (7): 4190–4199. [DOI: 10.1109/TGRS.2012.2227754]
-
Gao X B, Wang B, Tao D C and Li X L. 2011. A relay level set method for automatic image segmentation. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 41 (2): 518–525. [DOI: 10.1109/TSMCB.2010.2065800]
-
Gong M G, Su L Z, Jia M and Chen W S. 2014. Fuzzy clustering with a modified MRF energy function for change detection in synthetic aperture radar images. IEEE Transactions on Fuzzy Systems, 22 (1): 98–109. [DOI: 10.1109/TFUZZ.2013.2249072]
-
Gou S P, Zhuang X, Zhu H M and Yu T T. 2013. Parallel sparse spectral clustering for SAR image segmentation. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 6 (4): 1949–1963. [DOI: 10.1109/JSTARS.2012.2230435]
-
Hichri H, Bazi Y, Alajlan N and Malek S. 2013. Interactive segmentation for change detection in multispectral remote-sensing images. IEEE Geoscience and Remote Sensing Letters, 10 (2): 298–302. [DOI: 10.1109/LGRS.2012.2204953]
-
Jia J H and Jiao L C. 2010. Image segmentation by spectral clustering algorithm with spatial coherence constraints. Journal of Infrared and Millimeter Waves, 29 (1): 69–74. ( 贾建华, 焦李成. 2010. 空间一致性约束谱聚类算法用于图像分割. 红外与毫米波学报, 29 (1): 69–74. )
-
Lang F K, Yang J, Li D R, Zhao L L and Shi L. 2014. Polarimetric SAR image segmentation using statistical region merging. IEEE Geoscience and Remote Sensing Letters, 11 (2): 509–513. [DOI: 10.1109/LGRS.2013.2271040]
-
Lu D, Mausel P, Brondízio E and Moran E. 2004. Change detection techniques. International Journal of Remote Sensing, 25 (12): 2365–2407. [DOI: 10.1080/0143116031000139863]
-
Nock R and Nielsen F. 2004. Statistical region merging. IEEE Transactions on Pattern Analysis and Machine Intelligence, 26 (11): 1452–1458. [DOI: 10.1109/TPAMI.2004.110]
-
Salmon J. 2010. On two parameters for denoising with non-local means. IEEE Signal Processing Letters, 17 (3): 269–272. [DOI: 10.1109/LSP.2009.2038954]
-
Song X F, Wang S and Liu F. 2010. SAR image segmentation using Markov random field based on regions and Bayes belief Propagation. Acta Electronica Sinica, 38 (12): 2810–2815. ( 宋晓峰, 王爽, 刘芳. 2010. 基于区域MRF和贝叶斯置信传播的SAR图像分割. 电子学报, 38 (12): 2810–2815. )
-
Soni V, Bhandari A K, Kumar A and Singh G K. 2013. Improved sub-band adaptive thresholding function for denoising of satellite image based on evolutionary algorithms. IET Signal Processing, 7 (8): 720–730. [DOI: 10.1049/iet-spr.2013.0139]
-
Wan H L, Jiao L C and Xin F F. 2012. Interactive segmentation technique and decision-level fusion based change detection for SAR image. Acta Geodaeticaet Cartographica Sinica, 41 (1): 74–80. ( 万红林, 焦李成, 辛芳芳. 2012. 基于交互式分割技术和决策级融合的SAR图像变化检测. 测绘学报, 41 (1): 74–80. )
-
Wang B, Gao X B, Tao D C and Li X L. 2014. A nonlinear adaptive level set for image segmentation. IEEE Transactions on Cybernetics, 44 (3): 418–428. [DOI: 10.1109/TCYB.2013.2256891]
-
Wang Y, Du L and Dai H. 2016. Unsupervised SAR image change detection based on SIFT keypoints and region information. IEEE Geoscience and Remote Sensing Letters, 13 (7): 931–935. [DOI: 10.1109/LGRS.2016.2554606]
-
Xiong B L, Chen Q, Jiang Y M and Kuang G Y. 2012. A threshold selection method using two SAR change detection measures based on the Markov random field model. IEEE Geoscience and Remote Sensing Letters, 9 (2): 287–291. [DOI: 10.1109/LGRS.2011.2166149]