高光谱遥感是现代遥感技术迅猛发展的典型成果之一，是一种新兴且可靠的遥感观测技术(童庆禧 等，2006；Ablin和Sulochana，2013)。高光谱图像分类是遥感图像处理技术中的基本问题之一，也是遥感图像分析和解译的基础和关键(Sun 等，2015；杜培军 等，2016)。

高光谱图像分类是将高光谱图像中所有像素按某种属性分为若干类别的过程，结果受诸多因素影响，其中设计合适的分类算法尤为重要(Sun 等，2015)。通常情况下，监督算法在解决高光谱图像分类问题时表现优异，例如支持向量机(SVM)(Fauvel 等，2008；Melgani和Bruzzone，2004；杨国鹏 等，2008)、条件随机场(CRF) (Lafferty 等，2001)等。近几年来，CRF在遥感图像分类领域中备受关注。在数学描述上，CRF由关联势函数和交互势函数构成。关联势函数描述了样本观察量和其类别标签之间的关系。交互势函数则对空间相邻的标注样本点对应的观察量和类别标签的交互关系进行建模，它不仅能够描述相邻位置样本点对应的观察量之间的相似性，同时也能反映它们的类别兼容性。由于易于通过交互势函数引入空间信息(Zhong 等，2014)，CRF能够较好地解决遥感图像分类问题。Zhong和Wang(2008)将CRF应用到高光谱遥感图像分类领域中，并取得了良好的效果。随后，很多学者对CRF进行了改进(Zhong和Wang，2010；Zhong和Wang，2014；Zhong 等，2014)，使其在高光谱图像分类中得到充分的应用。但作为监督模型，CRF的性能受到标注样本数量的制约，主要表现为两个方面：(1)对关联势函数的影响。关联势函数通常由某监督类分类器获得的样本后验概率表示。当仅有少量标注样本存在时，该分类器的泛化能力不强，进而影响CRF的性能。(2)对交互势函数的影响。交互势函数在对空间信息进行建模时需要事先已知样本标签。当标注训练样本较少时，某标注样本的空间邻域样本中存在大量或全部为未标注样本，无法提供类别标签，此时交互势函数则无法充分挖掘空间信息，从而影响CRF的性能。

半监督学习是一种解决少量标注样本条件下分类问题的重要方法，它同时利用少量标注样本和大量未标注样本进行训练，以获得性能更强的分类器(Xia 等，2014；王立国 等，2016)。作为典型的半监督模型，拉普拉斯支持向量机(LapSVM)在高光谱分类中得到广泛应用(Gomez-Chova 等，2008；Gu和Feng，2013)。尽管LapSVM能够利用未标注样本，但它并不具备融合遥感图像中普遍存在的空间信息的能力(Yang 等，2014)。Yang等人(2014)在LapSVM基础上利用空间信息构造了一种新的模型，即空间-光谱拉普拉斯支持向量机(ssLapSVM)，该算法通过空间信息定义了空间权重矩阵，并同LapSVM自身的流型权重矩阵相结合，试图在标注样本和未标注样本之间建立更加紧密的联系，进而利用未标注样本隐含的信息获得样本观察量与标签之间的关系。但是ssLapSVM算法融合空间信息时仅考虑了空间相邻样本观察量之间的相似性，并未考虑它们之间的类别兼容性。

为了解决上述问题，本文在CRF框架下，通过重新设计关联势函数和改进交互势函数，提出了一种半监督CRF模型，即ssLapSVM-CRF*。在该模型中，针对CRF中关联势函数在标注样本不足时泛化能力不强的问题，通过定义半监督算法ssLapSVM为关联势函数，充分发挥ssLapSVM挖掘未标注样本信息的能力，提升少量标注样本情况下的高光谱遥感图像分类精度。同时，借助于CRF的交互势函数，克服了ssLapSVM在融合空间信息时不能考虑空间相邻样本之间类别兼容性的不足。另外，针对交互势函数在少量标注样本情况下挖掘空间信息能力下降的问题，本文将标注样本空间邻域的未标注样本也嵌入到交互势函数中，获得改进型交互势函数。在改进型交互势函数中，未标注样本的类别标签由关联势函数决定，并引入其类别概率(也由关联势函数ssLapSVM确定)作为权重因子。

为验证算法的有效性，本文在真实拍摄的高光谱数据集(Indian Pines和Pavia University)上进行实验，并与6种相关算法(4种监督算法，即SVM (Fauvel 等，2008)、SVM-CRF (李祖传 等，2011)、MLR (Zhong 等，2014)和MLR-CRF (简写为CRF) (Kae 等，2013)，和两种半监督算法，即LapSVM (Gu和Feng，2013)和ssLapSVM (Yang 等，2014))进行比较。另外，为了进一步评估算法性能，本文也将LapSVM定义为关联势函数，并同传统/改进型交互势函数结合，构造半监督CRF，并同上述以ssLapSVM为关联势函数的半监督CRF算法形成内部对比(相关算法命名见表1)。

CRF是Lafferty等人(2001)提出的一种判别式的概率无向图模型，具有强大的上下文信息融合能力。

假设 ${{G}} = ({{V}},{{E}})$ 为无向图， ${{{X}}_l} = \{ {{{x}}_i}|v \in {{V}}\} $ 是以G中结点i为索引的标注观察量x_i构成的集合。在给定观测序列 ${{{X}}_l}$ 的条件下，对应的标记序列 ${{{Y}}_l}$ 的联合后验概率分布为

$\begin{array}{l}{{{p}}_{{\pi }}}({{{Y}}_l}|{{{X}}_l}) = \displaystyle\frac{1}{{Z({{{X}}_l})}} \times \\\;\exp \left( {\sum\limits_{{{{x}}_i} \in {{{X}}_l}} {({\varphi _i}({y_i},{{{x}}_i};{{\alpha }}) + \lambda \sum\limits_{{{{x}}_j} \in {{E}}({{{x}}_i})} {{\theta _{ij}}({y_i},{y_j},{{{x}}_i},{{{x}}_j};\mu )} )} } \right)\end{array}$

(1)

式中， ${\varphi _i}( \cdot )$ 和 ${\theta _{ij}}( \cdot )$ 分别为关联势函数和交互势函数， ${{E}}({{{x}}_i})$ 为与 ${{{x}}_i}$ 相邻的点 ${{{x}}_j} \in {{{X}}_l}$ 构成的集合， $Z({{{X}}_l})$ 为拆分函数， $\lambda > 0$ 是折衷系数， ${{\pi }} = \{ {{\alpha }},\mu \} $ 为模型参数。

在CRF模型中，关联势函数在分类过程中起主导作用，通常用某监督分类器的后验概率表示，例如多项式逻辑回归(MLR)(Zhong 等，2014)、SVM(Zhong 等，2014)。作为监督分类器，MLR和SVM的性能受到标注样本数量的制约，进而导致CRF在少量标注样本条件下的分类能力受到限制。

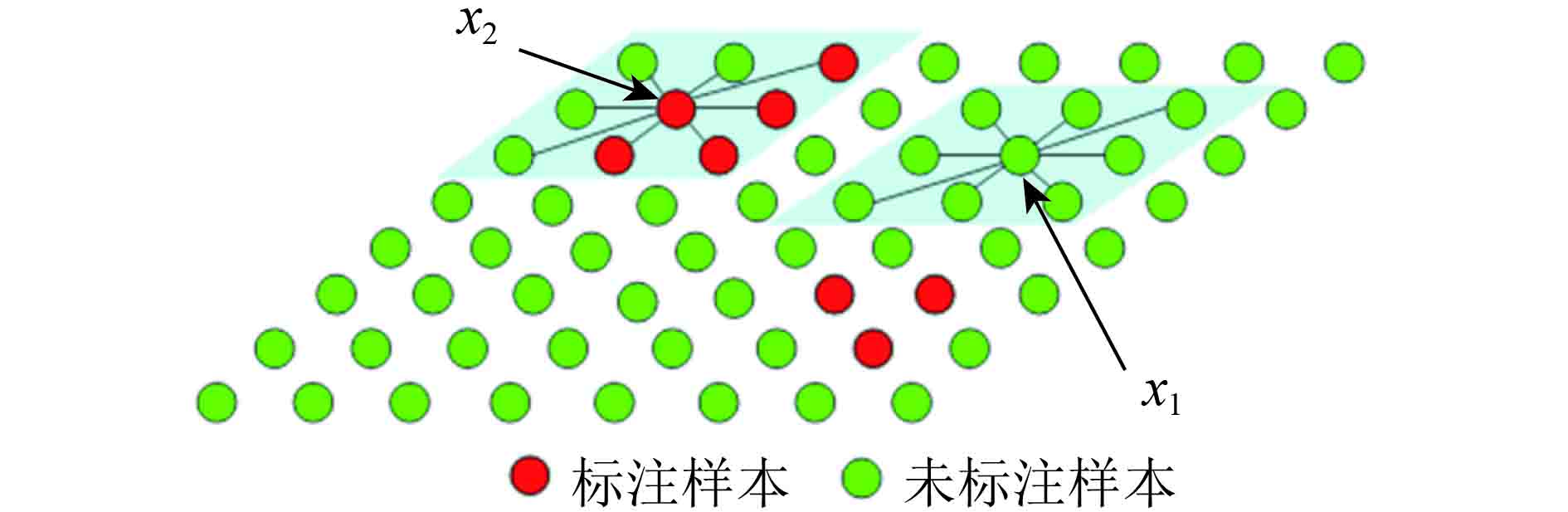
交互势函数是对空间相邻的标注样本点对应的观测量和类别标签的交互关系进行建模，通过对关联势函数获得的样本后验概率进行修正，以得到更加平滑、异类噪声点尽可能少的分类结果。在传统CRF中，交互势函数通常表示为

$\begin{array}{l}{\theta _{ij}}({y_i},{y_j},{{{x}}_i},{{{x}}_j}) = {t_{ij}}\exp ( - \mu ||{{{x}}_i} - {{{x}}_j}|{|^2})\\[7pt]{t_{ij}} = \left\{ \begin{array}{l} + 1\;\;\;\;\;{y_i} = {y_j}\\[5pt] - 1\;\;\;\;\;{y_i} \ne {y_j}\end{array} \right.\;\;\;\;\;\;{{{x}}_j} \in {{{{ N}}}^2}({{{x}}_i})\;\text{且}\;{{{x}}_j} \in {{{X}}_l}\end{array}$

(2)

从式(2)可看出，CRF中的交互势函数的修正和两样本的类别兼容性密切相关。但当标注样本较少时，某标注样本 ${{{x}}_i}$ 的空间邻域 ${{{{N}}}^2}({{{x}}_i})$ 中极有可能包含未标注样本，甚至全为未标注样本，如图1所示。由于 ${{{{N}}}^2}({{{x}}_i})$ 中未标注样本缺少标签信息，无法通过公式(2)建立 ${{{x}}_i}$ 和 ${{{{N}}}^2}({{{x}}_i})$ 中未标注样本之间的联系。但如果只考虑 ${{{{N}}}^2}({{{x}}_i})$ 中的标注样本，则不能充分描述样本 ${{{x}}_i}$ 和其周围邻域的空间关系，从而使得交互势函数的空间平滑作用下降，甚至失去作用。

LapSVM成功地将未标注样本隐含的信息加入到SVM的学习过程中，其性能比单纯使用标注样本训练得到的分类器有了显著提高。但在高光谱遥感图像分类的具体应用中，LapSVM忽略了遥感图像中普遍存在的空间信息。

Yang等人(2014)利用空间信息定义了空间权重矩阵 ${{{W}}^s}$ ，并将其同权重矩阵 ${{{W}}^m}$ 相结合，提出了ssLapSVM算法，其基本原理如下：

以二分问题为例，给定样本集合 ${{X}} = \left\{ {{{{X}}_l},{{{X}}_u}} \right\}$ ，其中 ${{{X}}_l} = \{ {{{x}}_i}\} _{i = 1}^{{n_l}}$ 为标注样本集，对应的标签 ${{{Y}}_l} = \{ {y_i} \in \{ + 1, - 1\} \} _{i = 1}^{{n_l}}$ ， ${{{X}}_u} = \{ {{{x}}_i}\} _{i = 1}^{{n_u}}$ 为未标注样本集。n_l和n_u分别为标注/未标注样本数量。ssLapSVM可以描述成如下所示的最小值优化问题：

$\begin{array}{l}\arg \min \displaystyle\frac{1}{{{n_l}}}\sum\limits_{i = 1}^{{n_l}} {V({{{x}}_i},{y_i},f)} + {\gamma _A}\left\| f \right\|_H^2 + {\gamma _M}\left\| f \right\|_M^2\\V({{{x}}_i},{y_i},f) = \max \{ 0,1 - {y_i}f({{{x}}_i})\} \\f({{x}}) = \displaystyle\sum\limits_{i = 1}^{{n_l} + {n_u}} {{\omega _i}K({{{x}}_i},{{x}}) + b} = {{{\omega }}^{\rm{T}}}{{{K}}_i}\left( {{{X}},{{{x}}_i}} \right) + b\\\left\| f \right\|_H^2 = {{{\omega }}^{\rm{T}}}{{K\omega }},\;\;\;\;{{\omega }} = {({\omega _1}, \cdots ,{\omega _{{n_l} + {n_u}}})^{\rm{T}}}\\\left\| f \right\|_M^2 = \displaystyle\sum\limits_{i,j = 1}^{{n_l} + {n_u}} {\left( {u{{W}}_{ij}^m + (1 - u){{W}}_{ij}^s} \right){{\left( {f({{{x}}_i}) - f({{{x}}_j})} \right)}^2}} \\{{W}}_{ij}^s = \left\{ \begin{array}{l}\exp \left( {\displaystyle\frac{{ - {{\left\| {{{{x}}_i} - {{{x}}_j}} \right\|}^2}}}{\sigma }} \right)\;{{{x}}_i} \in {{{N}}^1}({{{x}}_j})\;\text{或}\;{{{x}}_j} \in {{{N}}^1}({{{x}}_i})\\0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{其他}\end{array} \right.\end{array}$

(3)

式中， $V( \cdot ) = \max \{ 0,1 - {y_i}f({{{x}}_i})\} $ 为损失函数； $f( \cdot )$ 为决策函数； ${{{K}}_i}( \cdot ) = \left[ {K({{{x}}_1},{{{x}}_i}),K({{{x}}_2},{{{x}}_i}), \cdots ,} \right.$ ${ {K({{{x}}_{{n_l} + {n_u}}},{{{x}}_i})} ]^{\rm{T}}}$ 为样本x_i对应的核函数矩阵； $K( \cdot \;,\; \cdot )$ 为核函数； ${\gamma _{\rm{A}}}$ 和 ${\gamma _{\rm{M}}}$ 为折衷系数； ${{K}} = [ {{{{K}}_1}( {{{X}},{{{x}}_1}}), \cdots ,{{{K}}_{{n_l} + {n_u}}}} $ $ {( {{{X}},{{{x}}_{{n_l} + {n_u}}}})} ]$ ；ω和b为待估计的模型参数；权重矩阵 ${{{W}}^m}$ 常被定义为heat核函数(Geng 等，2012)；u为矩阵 ${{{W}}^s}$ 和 ${{{W}}^m}$ 的权重系数； ${{{N}}^1}({{x}})$ 表示样本点x的空间邻域 ${N_1} \times {N_1}$ 范围内的样本集合。

一旦获得模型的最优参数 ${{{\omega }}^*}$ 和 ${b^*}$ ，则当给定一个新的测试样本 ${{{x}}_*}$ ，LapSVM则可利用如下决策函数判断样本的类别标记(Gu和Feng，2013)：

$y_*' = {\mathop{\rm sgn}} (f({{{x}}_*})) = {\mathop{\rm sgn}} ({{{\omega }}^*}^{\rm{T}}{{{K}}_*}({{X}},{{{x}}_*}) + {b^*})$

(4)

空间信息的引入，使得ssLapSVM的性能相比于LapSVM有了较大的提升。但从式(3)中 ${{{W}}^s}$ 的定义不难看出，ssLapSVM中关于空间信息的融合仅仅考虑了样本观察量之间的相似性，缺少对类别兼容性信息的挖掘。

在CRF框架下，给定标注样本 ${{{X}}_l}$ ，对应的标签 ${{{Y}}_l}$ ，和未标注样本 ${{{X}}_u}$ ，本文算法的联合后验概率可表示为

$\begin{array}{l}{{{p}}_{{\pi }}}({{{Y}}_l}|{{{X}}_l}) = \displaystyle\frac{1}{{Z({{{X}}_l})}}\; \times \\\exp \left( {\sum\limits_{{{{x}}_i} \in {{{X}}_l}} {(\varphi _i'({y_i},{{{x}}_i},{{{X}}_u};{{\alpha }}) + \lambda \sum\limits_{{{{x}}_j} \in {{{{N}}}^{\;2}}\;({{{x}}_i})} {\theta _{ij}'({y_i},{y_j},{{{x}}_i},{{{x}}_j};\mu )} )} } \right)\end{array}$

(5)

式中， $\varphi _i'({y_i},{{{x}}_i},{{{X}}_u};{{\alpha }})$ 为改进的关联势函数，它将未标注样本 ${{{X}}_u}$ 引入CRF模型，衡量样本 ${{{x}}_i}$ 被标记为标签 ${y_i}$ 的可能性。 ${{{N}}^2}({{x}})$ 表示样本点x的空间邻域 ${N_2} \times {N_2}$ 范围内的样本集合。 $\theta _{ij}'( \cdot )$ 为改进的交互势函数，其利用空间信息，保证分类效果的空间平滑性。

为充分利用未标注样本隐含的信息，本文分别利用ssLapSVM定义关联势函数，实现半监督分类。此时，关联势函数定义为

$\varphi _i'({y_i},{{{x}}_i},{{{X}}_u};{{\alpha }}) = \log \left( {\sum\limits_{l = 1}^L {1({y_i} = l){P_*}(l|{{{x}}_i})} } \right)$

(6)

式中， $1( \cdot )$ 为指示函数，L为类别数， ${P_*}(l|{{{x}}_i})$ 为由 ${{\alpha }} = \{ {{\omega }},b\} $ 参数化的ssLapSVM获取的样本 ${{{x}}_i}$ 的类别概率。由于ssLapSVM为二值分类器，因此采用一对一策略实现多类别分类。类别概率 ${P_*}(l|{{{x}}_i})$ 由不同ssLapSVM分类器输出的二值概率共同获得(Zhong 等，2014)，如下式(7)所示

$\begin{array}{l}\mathop {\min }\limits_{{P_*}} \displaystyle\sum\limits_{l = 1}^L {\sum\limits_{j:j \ne l} {{{({p_{jl}}{P_*}(l|{{{x}}_i}) - {p_{lj}}{P_*}(j|{{{x}}_i}))}^2}} } \;\;\;\;\\{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\sum\limits_{l = 1}^L {{P_*}(l|{{{x}}_i}) = 1} \\{p_{jl}} = {p_*}(j|j - vs - l,{{{x}}_i}) = \displaystyle\frac{1}{{1 + \exp ( - f({{{x}}_i}))}}\\{p_{lj}} = {p_*}(l|j - vs - l,{{{x}}_i}) = \displaystyle\frac{1}{{1 + \exp ( - f({{{x}}_i}))}}\end{array}$

(7)

在标注训练样本数量较少的情况下，传统交互势函数的空间平滑作用会降低，甚至消失。在这种情况下，为保证交互势函数依然能够有效融合空间信息，本文对传统交互势函数进行改进，具体表达式为

$\begin{array}{l}\theta _{ij}'({y_i},{y_j},{{{x}}_i},{{{x}}_j}) = {t_{ij}}{\eta _j}\exp ( - \mu ||{{{x}}_i} - {{{x}}_j}|{|^2})\\{t_{ij}} = \left\{ \begin{array}{l} + 1\;\;\;\;\;{y_i} = {y_j}\\ - 1\;\;\;\;\;{y_i} \ne {y_j}\end{array} \right.\;\;\;\;\;\;{{{x}}_j} \in {{{{N}}}^2}({{{x}}_i})\\[10pt]{\eta _j} = \left\{ \begin{array}{l}1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{{x}}_j} \in {{{X}}_l}\\{P_*}(l|{{{x}}_j})\;\;\;\;\;\;{{{x}}_j} \notin {{{X}}_l}\end{array} \right.\end{array}$

(8)

式中， ${P_*}(l|{{{x}}_j})\; = \max \left( {{P_*}\left( {1|{{{x}}_j}} \right), \cdots ,{P_*}\left( {L|{{{x}}_j}} \right)} \right)$ 是无标签样本 ${{{x}}_j}$ 的最大条件概率，对应的类别标签为 ${y_j} = l$ 。在该式中，对于 ${{{{N}}}^2}({{{x}}_i})$ 中任意一个未标注样本 ${{{x}}_j}$ ，对应的标签 ${y_j} = l$ 由关联势函数获得，并引入其对应的概率 ${P_*}(l|{{{x}}_j})\;$ 作为权重，如式(8)，使其在少量标注样本条件下依然能够描述样本的空间信息。

在CRF框架下，本文算法整合了新的关联势函数和交互势函数来实现高光谱遥感图像的半监督分类。在训练过程中，采用分步学习的策略来估计模型的最优参数 ${{\varGamma }} = \{ {{\omega }},b,\mu \} $ ：(1)学习关联势函数(ssLapSVM)，获得模型最优参数 ${{{\omega }}^*}$ 和 ${b^*}$ ，并根据式(7)获得标注集 ${{{X}}_l}$ 中每个样本 ${{{x}}_i}$ 及其空间邻域 ${{{{N}}}^2}({{{x}}_i})$ 中未标注样本的多类别概率；(2)采用拟牛顿法(Kae 等，2013)最小化目标函数式(9)求解最优模型参数 ${\mu ^*}$ 。在推断过程中，给定测试集 ${{{X}}_t}$ ，采用Mean-field(Kae 等，2013)算法求解其对应的最优类别集 ${{{Y}}_t}$ 。

$\begin{array}{l}{\mu ^*} \approx \mathop {\arg \max }\limits_\mu \!\! \sum\limits_{{{{x}}_i} \in {{{X}}_l}} \!\! {\log \;p({y_i}|{{{x}}_i},{{{\omega}} ^*},{b^*};\mu )} = \mathop {\arg \max }\limits_\mu \!\! \sum\limits_{{{{x}}_i} \in {{{X}}_l}} \!\! {\log \displaystyle\frac{1}{{{z_i}}}\exp \left( {\varphi _i'({y_i},{{{x}}_i},{{{X}}_u},{{{\omega }}^*},{b^*}) + \lambda \!\!\! \sum\limits_{{{{x}}_j} \in {{{{N}}}^{\;2}}({{{x}}_i})} \!\!\! {\theta _{ij}'({y_i},{y_j},{{{x}}_i},{{{x}}_j};\mu )} } \right)} \\{z_i} = \sum\limits_{{y_i} \in \{ 1, \cdots ,L\} } {\exp \left( {\varphi _i'({y_i},{{{x}}_i},{{{X}}_u},{{{\omega }}^*},{b^*}) + \lambda \!\! \displaystyle\sum\limits_{{{{x}}_j} \in {{{{N}}}^{\;2}}({{{x}}_i})} \!\! {\theta _{ij}'({y_i},{y_j},{{{x}}_i},{{{x}}_j};\mu )} } \right)} \end{array}$

(9)

为验证算法性能，选择了通用的高光谱数据集进行实验，即Indian Pines和Pavia University数据集，并将本文算法和6种相关算法进行比较，包括SVM (Fauvel 等，2008)、SVM-CRF (李祖传 等，2011)、MLR (Zhong 等，2014)、CRF (Kae 等，2013)、LapSVM (Gu和Feng，2013)和ssLapSVM (Yang 等，2014)。为进一步评价算法能力，将本文算法同ssLapSVM-CRF、LapSVM-CRF和LapSVM-CRF*进行横向对比。客观评价指标采用类别精度(CA)和Kappa系数(Sun 等，2015)。Kappa系数计算方法同文献(Sun 等，2015)。需要强调的是，不同于文献(Yang 等，2014)，本文的评价指标结果均在测试集上进行统计，不包括参与训练的未标注训练样本集(由于未标注训练样本参与训练，会使训练所得模型在该样本上的分类精度明显偏高，进而使得最终的分类精度产生“虚高”现象)。同时，为消除随机性影响，所有统计实验结果均为10次结果的平均值。

实验所用高光谱数据集从[2014-04-07]http:// www.ehu.eus/ccwintco/index.php?title=Hyperspectral _Remote_Sensing_Scenes)获得，且每个数据集的光谱响应被归一到[0, 1]范围内。两个高光谱数据集的简介如下：

(1) Indian Pines数据集：大小为145×145，拥有200个波段。该数据集被划分为16个类别，其伪彩色图和地表覆盖真值图分别如图2(a)和(b)所示。

(2) Pavia University数据集：拥有103个波段，大小为610×340，全部地表覆盖被标注为9个类别，其伪彩色图和地表覆盖真值图分别如图5(a)和(b)所示。

影响本文算法性能的超参数主要包括：

(1) 关联势函数固有参数(表3)。鉴于径向基核函数(RBF)具有强大的数据表达能力，采用RBF作为核函数。在具体实验中，针对每个数据集，采用五折交叉验证分别训练 $L(L - 1)/2$ 个二值分类器，以获得最优的参数 ${\lambda _I},\;{\lambda _M} \in [1{{\rm{E}}{ - 7}},1{{\rm{E}}7}]$ ， $k \in [5,15]$ ， $u \in [0,1]$ ， $\sigma \in [1{{\rm{E}}{ - 7}},1{{\rm{E}}7}]$ 。ssLapSVM的空间邻域范围设定为 ${N_1} \times {N_1} = 3 \times 3$ ，其对相关算法的影响将在4.3.3中详细分析。

(2) 交互势函数固有参数：空间邻域范围 ${N_2} \times {N_2}$ 。在4.3.1节和4.3.2节中，交互势函数中的空间邻域范围设置同ssLapSVM算法，即 ${N_2} \times {N_2} = $ $ {N_1} \times {N_1} = 3 \times 3$ ，而其对本文算法的影响将在实验4.3.3中详细分析。

(3)在4.3.1节和4.3.2节中，折衷参数 $\lambda $ 统一设置为0.3。而折衷系数 $\lambda $ 对本文算法的影响将在实验4.3.3中详细分析。

在该数据集下，随机选择50%的真值样本点作为测试集。在其余真值中，从每个类别中随机选择5个真值样本点作为标注训练样本集，再随机选择2000个点构成未标注训练样本集，而剩余样本点作为验证集。测试集、标注和未标注训练样本集包含的真值样本点如图2(c)、(d)和(e)所示。

图2和表2分别列出了不同算法在Indian Pines(16类)数据集上的分类效果和客观评价结果(最优参数见表3)，从中可看出：

(1) 与其他半监督方法对比，当ssLapSVM-CRF*和LapSVM、ssLapSVM对比可知，同一地物内“噪声点”(异类地物)相对较少，例如图2(o)中Stone-Steel-Towers类别(C11)中包含的其他地物类别比图2(j)(k)明显减少，在Kappa系数客观评价指标上有明显提升(比ssLapSVM提升4.94%)。对比结果表明(尤其是同ssLapSVM相比较)：ssLapSVM-CRF*能够充分发挥CRF对空间信息的描述能力，通过不同的空间信息融合方式，综合考虑样本之间的相似性和类别标签的兼容性，有效地利用空间信息获得空间平滑性更好的分类结果。

(2) 与其他监督类算法对比，当ssLapSVM-CRF*和SVM、SVM-CRF、MLR、CRF4种监督类算法对比时可发现，所提算法的分类效果和Kappa系数都要优于监督类算法，有效地验证了本文通过半监督算法ssLapSVM定义CRF模型中关联势函数的可行性，发挥了ssLapSVM嵌入未标注样本信息的能力，弥补了CRF模型在此方面的不足，使得提出的半监督CRF模型在标注训练样本较少的情况下，依然能够获得较高的分类精度，提升分类能力。

(3) 所提方法之间对比，当进行横向对比时可知，采用改进型交互势函数的算法ssLapSVM-CRF*的分类精度要高于采用传统交互势函数的算法ssLapSVM-CRF，这说明本文提出的交互势函数在标注训练样本较少时具有更强的空间信息融合能力。这一结论也可从LapSVM-CRF*和LapSVM-CRF的对比中得到进一步验证。另外，以ssLapSVM为关联势函数的ssLapSVM-CRF*、ssLapSVM-CRF的性能明显强于以LapSVM为关联势函数的算法LapSVM-CRF*、LapSVM-CRF，这主要是由关联势函数在CRF框架下的主导作用所致。ssLapSVM的性能强于LapSVM，进而产生上述结果。

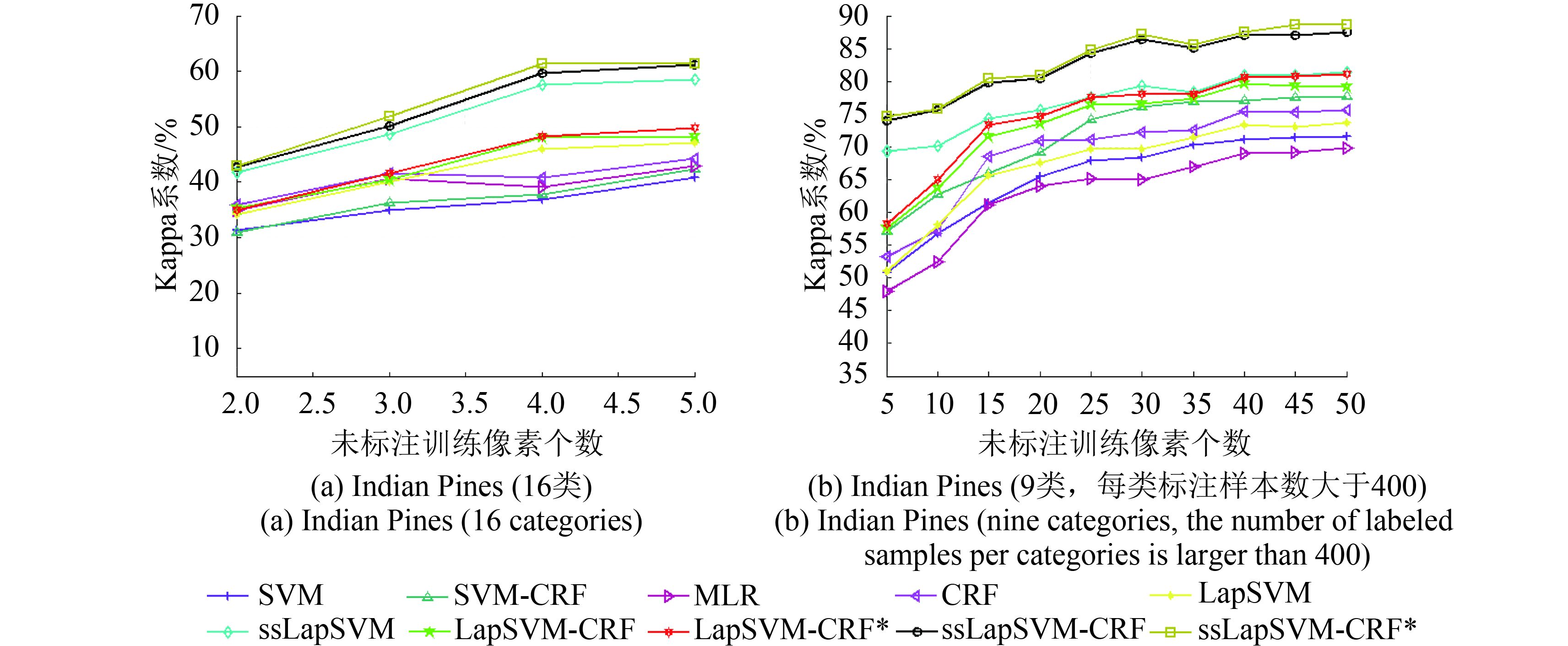
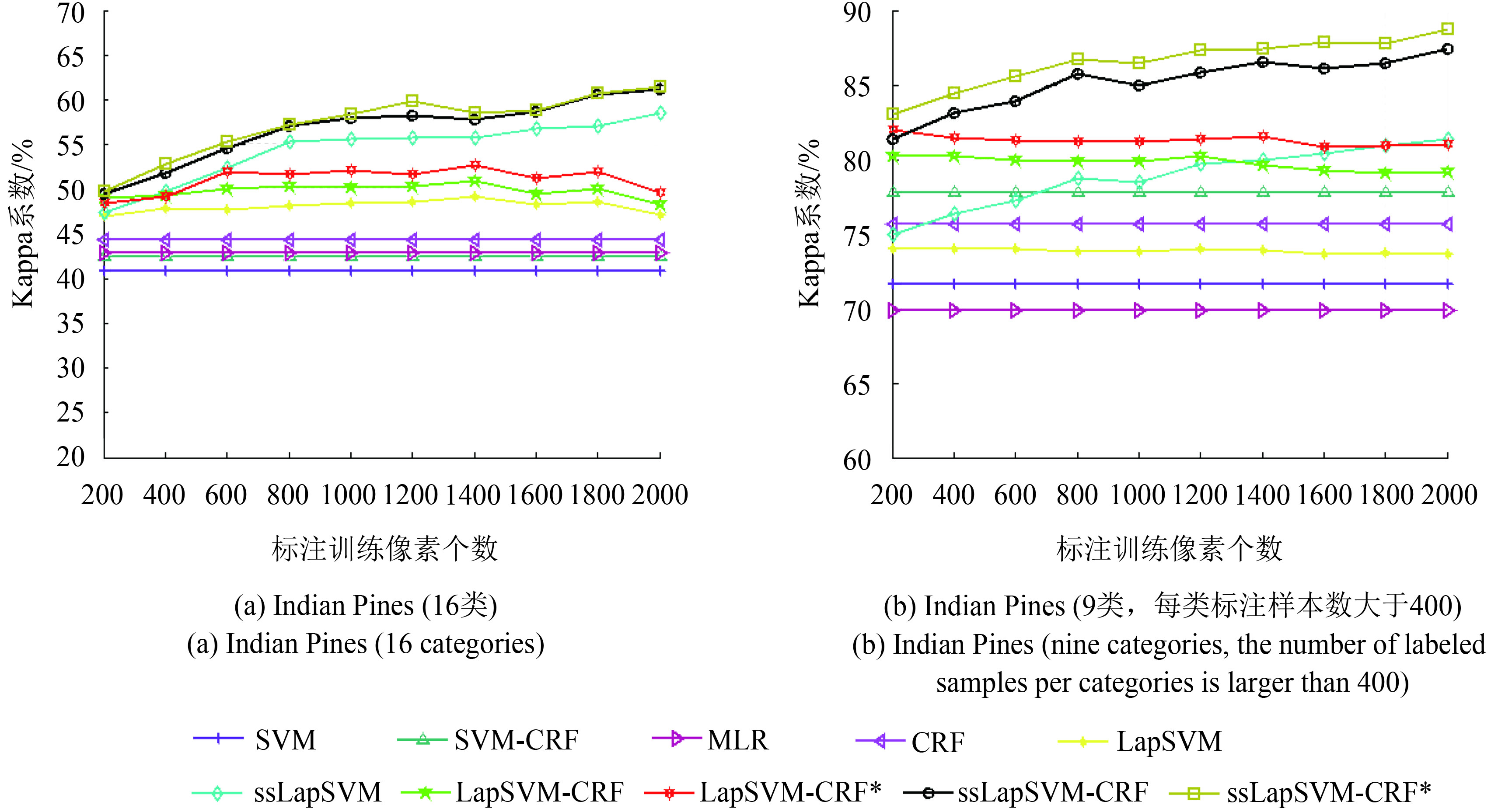
为充分验证本文算法的性能，对不同算法在标注/未标注训练样本数量变化条件下的分类结果进行比较，结果分别如图3(a)和图4(a)所示。

从图3(a)可知，在Indian Pines数据集下，ssLapSVM-CRF*在任意数量的标注样本下的表现都为最佳，分类精度远高于其他算法，这归功于两点：(1)关联势函数ssLapSVM提供了更具判别性的类别概率，这也体现了关联势函数的主导作用，(2)改进型交互势函数对空间信息的有力挖掘。

从图4(a)可知，在标注训练样本数量固定的情况下，ssLapSVM-CRF*受未标注样本数量的影响较大，分类精度随着未标注样本数量的增加而提升。这主要因为当未标注样本点较少时，整个训练集中存在空间相邻的样本点对则更少，此时ssLapSVM中构造的空间权重矩阵 ${{{W}}^s}$ 稀疏性过高(0值过多)，使得其融合空间信息的能力降低，影响自身算法性能，并进一步影响ssLapSVM-CRF*的分类能力。但对任意固定的未标注训练样本数量，本文提出的ssLapSVM-CRF*的分类精度都要优于其他算法。

为了进一步验证本文算法的性能，本文将Indian Pines数据集中标注样本数低于400的7个类别去掉，采用余下9个类别进行实验，将不同算法在标注、未标注训练样本变化条件下的分类精度进行了比较，如图3(b)和图4(b)所示，可以看出，本文算法依然展现出较好的分类性能。

在该数据集下，同样随机选择50%的真值样本点作为测试集。在其余真值点中，从每个类别随机选择50个真值样本点作为标注训练样本集，再随机选择2000个点构成未标注训练样本集，而剩余点作为验证集。测试集、标注和未标注训练样本集包含的真值样本点如图5(c)、(d)和(e)所示。

不同分类算法在Pavia University数据集的分类效果和客观评价结果分别如图5和表4所示(对应的最优参数见表5)。从图5和表4中可以看出：

(1) 与其他半监督方法对比，ssLapSVM-CRF*所得结果比LapSVM、ssLapSVM更加平滑，异类噪声点更少，每个子类别的分类精度都有提高，Kappa系数比对比算法中最优结果(ssLapSVM)提高4.16%。由此可知，所提算法继承了CRF模型的优点，通过引入空间信息，有效地提高高光谱遥感图像的分类精度。而且，在关联势函数ssLapSVM已考虑空间信息的情况下，本文算法通过交互势函数对空间信息的深入挖掘(兼顾样本相似性和标签差异性)，仍能进一步提高高光谱图像的分类精度。

(2) 与其他监督类算法对比：当同四种监督类算法对比时可知，本文算法均表现出较强大的分类能力，虽然某些类别精度下降(例如，类别C1、C9)，但在Kappa系数评价指标上有明显提高。特别地，当本文算法同两种CRF相关算法对比时，即CRF和SVM-CRF(提升3.28%)，可得出结论：本文通过半监督模型定义关联势函数的方法来构建半监督CRF模型的思路行之有效，提出的半监督CRF模型在标注训练样本较少的情况下，依然能够获得较高的分类精度。

(3) 所提方法之间对比，当将本文算法进行相互对比时可发现以ssLapSVM-CRF*的分类精度要明显高于ssLapSVM-CRF。这表明：提出的改进型交互势函数在考虑某标注样本周围全部的空间邻域样本的情况下更能够挖掘遥感图像普遍存在的空间信息，提高算法的性能。而且，上述结论可以进一步由LapSVM-CRF*和LapSVM-CRF之间的对比验证。

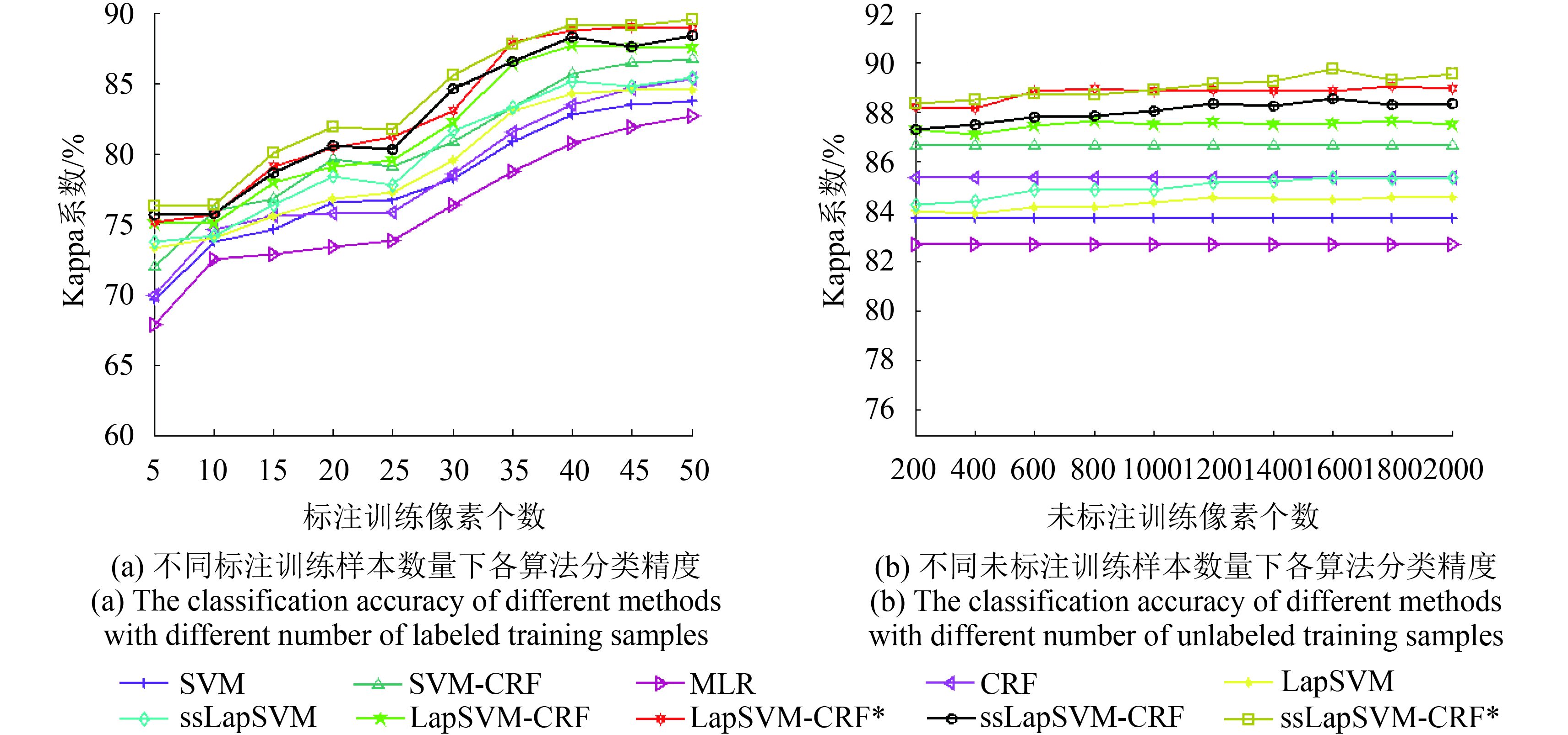
在该数据集中，不同算法在不同数量的标注/未标注样本变化情况下的分类结果如图6所示。

从图6(a)可知，当标注样本数量从5到50变化时，不同算法的分类精度都逐步提升，并且在任意固定数量的标注样本条件下，本文提出的算法均可获得较高的分类精度，获得较好的分类效果。

如图6(b)所示，当未标注样本从200到2000变化时，同Indian Pines数据集下分类结果相类似，ssLapSVM-CRF和ssLapSVM-CRF*对未标注样本数量的变化较为敏感，主要原因依然是未标注样本数量在一定程度影响了ssLapSVM中空间权重矩阵 ${{{W}}^s}$ 的空间信息融合能力，并进一步影响以ssLapSVM为关联势函数的ssLapSVM-CRF和ssLapSVM-CRF*的性能。但是，同Indian Pines数据集下结果类似，在任意固定的未标注训练样本数量下，本文提出的ssLapSVM-CRF*的分类精度都要高于其他算法。

在LapSVM-CRF、LapSVM-CRF*、ssLapSVM-CRF和ssLapSVM-CRF*中，空间邻域范围N₂可影响交互势函数，进而影响算法性能。而在ssLapSVM-CRF和ssLapSVM-CRF*中，N₁可影响关联势函数，从而影响算法最终分类能力。在高光谱图像分类中，常见的空间邻域定义方式有Von Neumann Neighborhood (V)、Moore Neighborhood (M)和Extended Moore Neighborhood (E)(Espínola 等, 2015)，如图7所示。

不同的空间邻域定义对本文算法的影响见图8。从中可以看出，在Indian Pines数据集上，随着空间邻域范围的增加(融合的空间信息随之增加)，同一算法的性能逐渐提升，但改进型交互势函数对算法性能的提升效果逐渐降低，甚至出现下降。例如，在Indian Pines(9类)数据集中，当空间邻域定义为V时，ssLapSVM-CRF*相比于ssLapSVM-CRF的提升幅度要大于空间邻域定义为M时的幅度，更大于E时的幅度。而在Indian Pines (16类)数据集中，当空间邻域定义为E时，ssLapSVM-CRF*的性能低于ssLapSVM-CRF。这主要是因为当空间邻域范围较大时，训练样本中包含了相对充足且具有空间相邻性的标注样本点对，传统交互势函数融合的空间信息量相对饱和，此时引入未标注样本所包含空间信息的作用则相对性的降低，并表现为改进型交互势函数对算法性能提升的幅度降低。而当空间邻域范围较大时，改进型交互势函数中会引入较大的噪声，因此导致了算法性能的降低。

在Pavia University数据集上，空间邻域范围的增加，使得算法能够融合的信息增加，因此同一算法的性能逐渐提升。但相比V和M，空间邻域定义为E时，改进型交互势函数对空间信息的挖掘效果更为明显，其原因是Pavia University的空间分辨率较高(1.3 m)，具有更加丰富的空间细节信息，小范围的空间邻域(V和M)不足以充分挖掘复杂的空间细节信息。

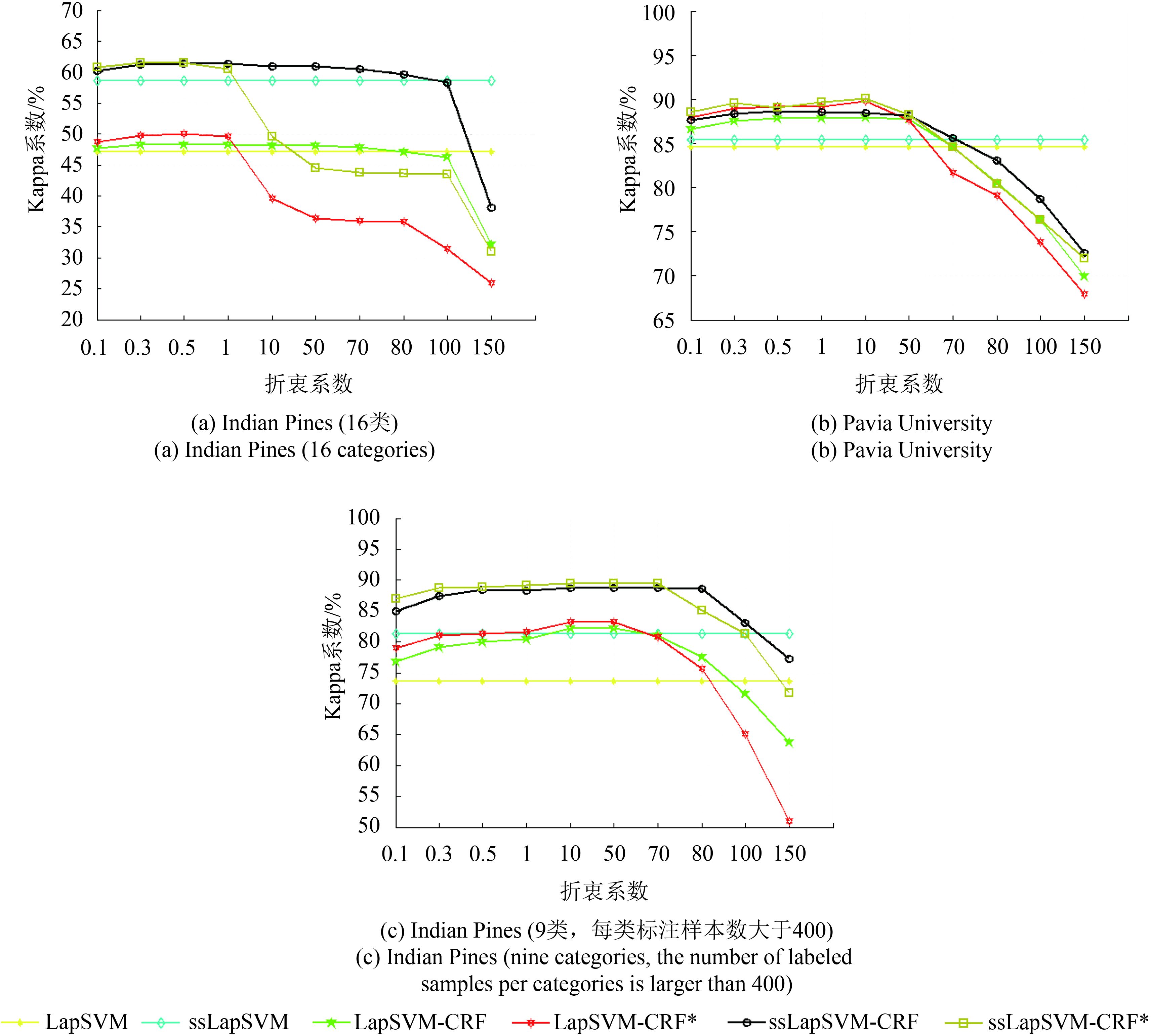
折衷系数λ衡量了关联势函数和交互势函数之间的重要性。从图9可以看出，当λ逐渐增加时，本文算法通过交互势函数融合的空间信息逐渐增加，性能逐步提升。但是当折衷系数继续增加时，交互势函数的作用超越了关联势函数的主导作用，从而使得算法的性能出现下降。

本文算法通过引入未标注训练样本信息和进一步挖掘空间信息来提升高光谱遥感图像的分类精度，然而在一定程度上增加了算法的空间与时间复杂度。

在本文算法中，影响其空间复杂度的因素主要为训练和测试过程中核矩阵的计算，包括标注训练样本及其空间邻域样本、测试样本及其空间邻域样本共4类样本对应的核矩阵。例如，在Indian Pines(16类)数据集上，标注训练样本数为5个/每类，未标注训练样本数为2000个，测试样本数为5128，空间邻域定义为M(8邻域)，需要计算的4类核函数?矩阵的维数分别为2010×80，2010×640，2010×5128和2010×41024。从中可以看出，在考虑空间8邻域样本信息时，需要消耗的内存空间直接增加了8倍，具有较高的空间复杂度。

以Indian Pines(16类)数据集中实验为例，不同算法的运行时间(50次结果的平均值)如表6所示。从中可以看出，本文算法需要消耗较多的时间进行训练和测试，其时间主要消耗在二值分类器的训练以及样本多类别概率的计算。

从表2和表4可知，改进型交互势函数对算法精度的提升均在1%左右，为了充分验证改进型交互势函数的有效性，利用Z-检验进行显著性分析。Z-检验是利用标准正态分布理论来推断差异发生的概率(P值)，从而比较两组样本平均数的差异是否显著，P值越大，则差异越显著。在Z-检验算法中，Z值的表达式为

$Z = {\bar X_1} - {\bar X_2}/\sqrt {\frac{{{S_1}}}{{{n_1}}} + \frac{{{S_2}}}{{{n_2}}}} $

(10)

式中， ${\bar X_1}$ 和 ${\bar X_2}$ 分别为不同算法的Kappa系数统计平均值，S₁和S₂分别为不同算法的Kappa系数统计标准差，n₁和n₂分别为不同算法的独立重复实验次数。在获得Z值后，通过查正态分布表获取差异发生的概率(P值)。

表7和表8记录了不同次数独立重复实验下采用改进型交互势函数的相关算法的显著性分析结果。从中可以看出，在不同数据集下，虽然改进型交互势函数对算法分类精度的提升幅值均在1%左右，但差异发生的概率(P值)较大，这表明改进型交互势函数对算法性能的提升效果是十分显著的。而且，随着独立重复实验次数的增加(独立重复实验次数越多，获得的平均精度统计结果以及标准差越能反映总体精度的真实情况)，P值呈现出了逐渐增大的趋势(在3个数据集中，P值均>95%@50次)，有效地验证了改进型交互势函数的有效性。

为解决少量标注样本条件下的高光谱遥感图像分类问题，基于CRF框架，通过重新设计关联势函数和改进交互势函数，提出了半监督CRF分类算法，即ssLapSVM-CRF*。实验选择了两个通用数据集对模型进行测试，结果表明：

(1) 相比于6种已有算法和3种内部算法，本文算法ssLapSVM-CRF*具有较强的分类能力。

(2) 标注/未标注训练样本数量是影响分类精度的重要因素，而在不同数量的标注/未标注训练样本条件下，本文算法均表现出良好的分类性能。

(3) 空间信息是遥感图像分类中十分重要的信息，可有效提高算法的分类能力。并且，考虑空间信息越充足，算法能力越强。

总的来说，本文针对少量标注样本条件下的高光谱遥感图像的分类问题，提出了行之有效的半监督分类算法。

但是，本文算法在训练过程中采用了分布式的学习策略，效率较低，而且分布式的学习策略忽略了关联/交互势函数在整体训练过程中的相互影响。因此在后续工作中，需要针对性地提出一种更加高效且合理的训练方法，提高模型的学习效率，将其进一步推向工程应用。此外，论文采用的半监督分类模型均为二值模型，在解决多分类问题时需要训练多达 $L(L - 1)/2$ 个二值分类器，该过程十分繁琐，因此在后续工作中，针对二值半监督分类器寻找快速有效的参数寻优策略或将其扩展多类半监督分类器也是需要研究的重点。另外，本文算法具有较高的空间复杂度和时间复杂度，模型的训练和测试需要消耗较大的内存空间和计算时间，因此如何优化模型，降低空间和时间复杂度也将是下一步工作的重点。