|
收稿日期: 2016-04-07; 优先数字出版日期: 2016-10-04
基金项目: 国家重点基础研究发展计划(973计划)(编号:2013CB733406);国家自然科学基金(编号:41371341);遥感科学国家重点实验室开放基金项目(编号:OFSLRSS201313)
第一作者简介: 朱琳清(1988— ),男,硕士研究生,研究方向为定量遥感。E-mail:
aqiankunjian@126.com
通讯作者简介: 周纪(1983— ),男,副教授,研究方向为定量遥感。E-mail:
jzhou233@uestc.edu.cn
中图分类号: TP79
文献标识码: A
|
摘要
航空热红外遥感影像的航带宽度一般较为有限,通常需要进行连续飞行获得多个航带才能覆盖一个较大的研究区;由于地表温度随时间变化迅速,不同航带间地表温度存在差异。因此,进行不同航带影像拼接之前,需要对不同航带的地表温度进行时间归一化。本文基于温度日变化模型,构建了航空遥感地表温度时间归一化方法;结合HiWATER试验区高密度的气象观测数据,分析了天气晴朗条件下,风速的大小和波动剧烈程度对地表温度日变化模型的影响,在此基础上发展了一种考虑风速影响的改进温度日变化模型。验证结果表明:两种模型均能够减小观测时间不同导致的地表温度瞬时波动差异;考虑风速影响的改进模型比未改进模型的精度提高0.3—0.6 K,且其提供的地表温度在时间尺度变化上更加符合实际情况。本研究建立的相关模型对于卫星遥感地表温度的时间归一化也具有借鉴意义。
关键词
地表温度, 时间归一化, 温度日变化模型, 航空遥感
Abstract
Airborne thermal infrared remote sensing can obtain Land Surface Temperature (LST) data at a high spatial resolution. However, the swath width of airborne stripes is commonly limited, and researchers must generally acquire multiple stripes of continuous flights to cover a larger study area. LST changes rapidly over time, and the temperature clearly varies among different stripes. Thus, the temporal normalization of LST is necessary to obtain a large scene mosaicking image of different airborne stripes. However, studies on the temporal normalization of airborne LST are still rare to date. The present study first developed a practical method based on the Diurnal Temperature Cycle (DTC) model to temporally normalize the airborne LSTs in cloud-free skies. We assumed that two factors (i.e., the typical diurnal pattern and instantaneous fluctuation from the mean atmospheric conditions) were involved in detecting LST. We then established an Improved DTC (IDTC) model that analyzes the influences of wind speed and fluctuations that cannot be measured by the DTC model. The temporal normalization of the LST requires two parts. The first aspect is the DTC variables, includingTa,tm,ts, andδT. Each land cover type has its unique DTC pattern because of its physical characteristics. Therefore,in-situ LSTs in a diurnal cycle at each ground site were employed to calculate the DTC variables through the Levenberg-Marquardt method. A look-up table (LUT) for the DTC variables of different land cover types was then constructed. The linear regression technique was subsequently utilized to evaluate the LST instantaneous fluctuation of the second part. The TASI stripes were checked pixel by pixel. The variables for each pixel were then searched from the LUT to normalize each TASI stripe.First, the DTC and IDTC models were evaluated in the temporal normalization of the TASI LST on July 10, 2012 by selecting the Heihe Watershed Allied Telemetry Experimental Research (HiWATER) experiment region as the study area. Results show that the TASI LST normalized by the IDTC model was generally more consistent with the ground measured LST than the DTC model. The accuracy of the IDTC model was approximately 0.3 K to 0.6 K higher than the DTC model. Second, to better demonstrate the performance of the IDTC model in the entire study area, the TASI LST images that had been normalized to the ASTER overpass time (12:12 local time) were up-scaled to 90 m and then compared with the ASTER LST. The data indicate that both the temporal normalization methods (DTC and IDTC models) could decrease the LST differences among different TASI stripes. The TASI LST normalized by the IDTC model was more consistent with the ASTER LST, especially in the Gobi Desert and desert steppe. Third, the temporal normalization of the ground measured LST was also implemented to test the IDTC model. It further demonstrates that the IDTC model was better than the DTC model in the temporal normalization of airborne LST.This study proposes a practical method that temporally normalizes the airborne LST based on the DTC and IDTC models to lower the temperature difference among different stripes. Results indicate that the temporal normalization based on the DTC and IDTC models can effectively obtain a large scene composed of multiple flight lines before mosaicking different stripes. The IDTC model, which involves the influences of wind speed and LST fluctuation, also performs better than the DTC model. Our present research has presented a new perspective on the temporal normalization of satellite LST.
Key words
land surface temperature, temporal normalization, diurnal temperature cycle model, airborne remote sensing
1 引 言
地表温度是大气与地表之间相互作用的一个关键参数。在水文、生态、气候和气象等许多相关应用模型中,地表温度也是必要输入参数之一。目前热红外遥感和被动微波遥感是观测获取不同空间尺度地表温度的有效方法(Li 等,2013a;Zhou 等,2015a)。但是,遥感获取的地表温度是一个瞬时数值,通常不能直接满足研究者对于非成像时刻地表温度需求。地表温度时间维快速变化的特征,也使得对比和融合不同观测时间的遥感地表温度变得非常困难(Duan 等,2014)。航空热红外遥感提供的地表温度,是研究地表温度尺度效应、发展尺度转换模型、检验卫星遥感地表温度产品以及估算高空间分辨率蒸散发、土壤湿度等参数的重要数据。但是由于航空热红外遥感影像的航带宽度一般较为有限,往往需要通过连续飞行获得的多个航带才能覆盖一个较大的研究区。因此,使用航空遥感地表温度之前常常需要对不同航带的地表温度进行时间归一化(Rahaman 等,2015)。
温度日变化DTC(Diurnal Temperature Cycle)模型已被用于描述昼夜周期内地表温度在时间维上的连续变化(Jin和Dickinson,1999;Göttsche和Olesen,2001;Jin和Treadon,2003;Zhou 等,2013;Duan 等,2014)。若研究区DTC模型的特征参数已知,则能通过DTC模型预测任何时刻的地表温度,并用于对遥感地表温度进行时间归一化(Zhou 等,2013)。目前针对极轨卫星和静止卫星获取的地表温度数据,有很多DTC模型时间归一化的应用(Jiang 等,2006)。但是,由于航空反演的地表温度数据较少,针对航空遥感反演的地表温度时间归一化的相关研究也很少。此外,目前大多数经验统计型的DTC模型大都基于在所考虑时间范围内天气晴朗、风速较小且恒定的假设。实际上地表温度对于大气状况非常敏感。在真实的自然状况下,云量、风速的大小和波动的剧烈程度可能会对DTC模型应用的结果产生重要的影响。然而,迄今为止考虑天气因素对DTC模型应用结果影响的研究还很少。
2012年起,“黑河流域生态-水文过程综合遥感观测联合试验” HiWATER(Heihe Watershed Allied Telemetry Experimental Research)在中国西北黑河流域开展(李新 等,2012;Li 等,2013b;Xu 等,2013;Liu 等,2016)。基于HiWATER试验在黑河中游核心区域的高密度观测的地表温度数据和气象数据,本文建立了一种将DTC模型应用于航空遥感地表温度时间归一化的实用方法,并发展了一种考虑瞬时天气因素波动的改进温度日变化模型IDTC(Improved DTC)。基于本文建立的模型,能够利用航空遥感地表温度构建时间尺度上高密度的地表温度数据,进而满足地表蒸散发等实际应用对于高时空分辨率地表温度数据的需求。
2 研究区与数据
2.1 研究区与地面站点
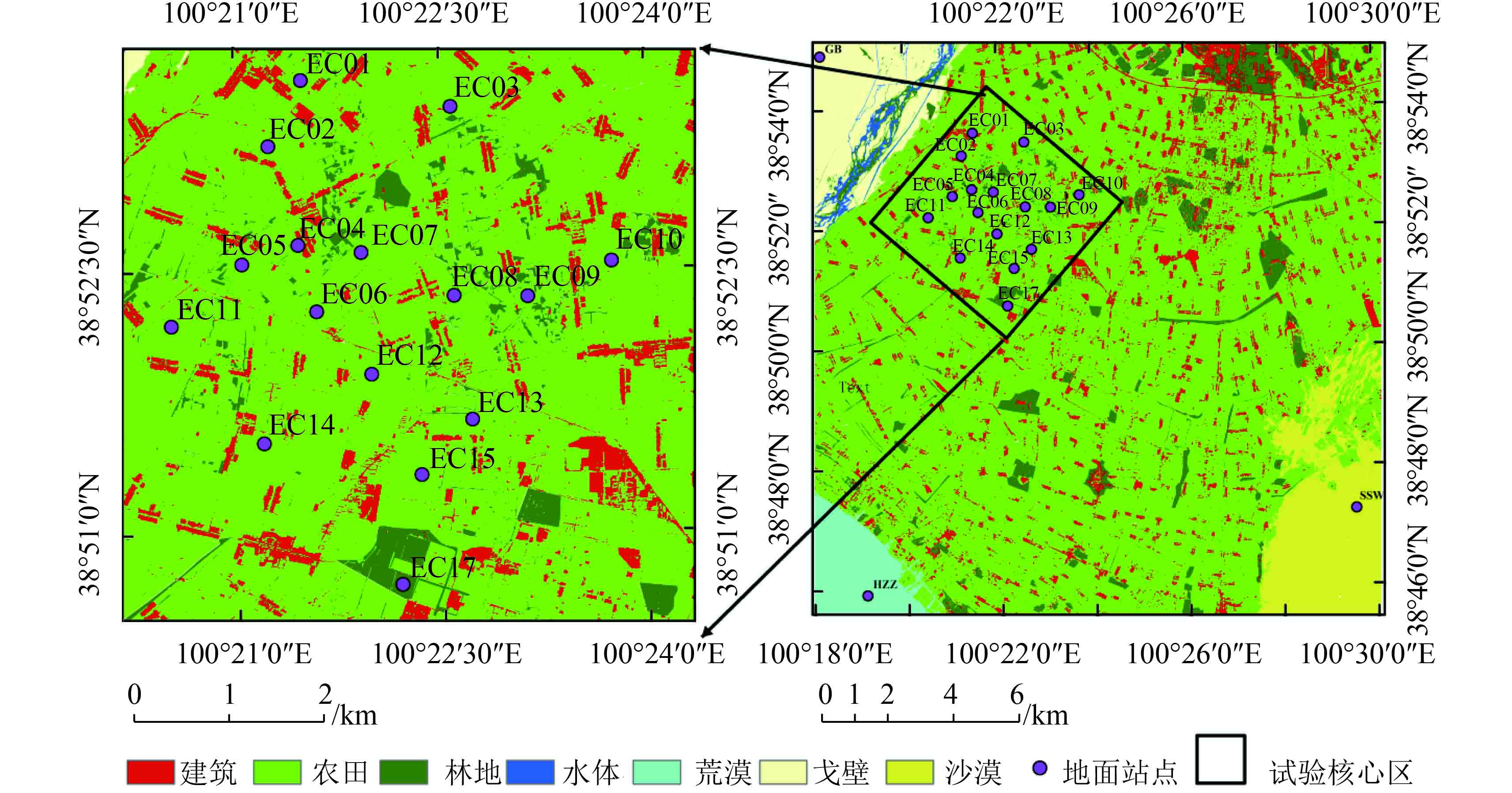
研究区为HiWATER试验于2012年在黑河中游(甘肃省张掖市)布置的加密观测试验区及周边地区。研究区的地势平坦,其海拔高度约为1480 m。研究区的地物覆盖类型为:农田(夏季以玉米地和蔬菜地为主)、裸土、建筑区域、戈壁、荒漠、沙漠、果园和防护林等(图1)。试验人员在绿洲农田中设置了5.5×5.5 km核心试验区,在核心区内设有17个自动气象站(EC01-EC17,如图1所示)(Liu 等,2011,2016;Li 等,2013b;Xu 等,2013)。因为EC16站点没有地表温度观测数据,因此本文没有选用该站点。绿洲外围主要为大面积的沙漠、戈壁、荒漠和湿地,试验人员在这4种土地覆盖类型的区域中分别设置了1个自动气象站,分别为神沙窝沙漠站(SSW)、巴吉滩戈壁站(GB)、花寨子荒漠站(HZZ)和湿地站。因湿地站点实测的地表温度有较大的不确定性,本文所选研究区未包含湿地站。所选站点包括村庄站点(EC04)、果园站点(EC17)、沙漠站点(SSW)、戈壁站点(GB)和荒漠站点(HZZ)各一个以及14个农田站点(如图1所示)。各站点的仪器型号、安装高度和视场范围大小等均可参考Zhou等人(2015b)。
2.2 数据及处理
选用2012年7月10日覆盖研究区的航空热红外遥感数据,传感器为机载热红外成像光谱仪TASI(Thermal Airborne Spectrographic Imager)。传感器型号为TASI-600,具备性能较好的技术参数,在8—11.5 μm范围内共有32个波段,成像方式为推扫式(Wang 等,2011)。飞机飞行高度为2500 m,TASI影像的空间分辨率为3 m。研究区共有13条航带,它们获取的时间为11:11—13:44(北京时间,下同)。地表温度通过地表温度—发射率分离算法反演得到,其精度优于1.5 K(Wang 等,2011)。利用决策树和目视解译的方法,将研究区的TASI地表温度影像分成7种不同的地物覆盖类型,分别为水体、农作物、防护林和果园、建筑用地、戈壁、沙漠和荒漠。分类的整体精度为86.5%,Kappa系数为82.2%。
上述站点中,除EC16外其余19个站点均安装有辐射四分量传感器,能够提供长波辐射观测数据,进而可转换得到地表温度:
| ${T_{\rm{s}}} = \sqrt[\displaystyle 4]{{\frac{{{L^ \uparrow } - (1 - \varepsilon ){L^ \downarrow }}}{{\varepsilon \sigma }}}}$ | (1) |
式中,Ts为四分量辐射视场内的地表真实温度,单位为K;L↑大气上行长波辐射,L↓为大气下行长波辐射,单位为W/m2;ε为四分量辐射视场内的混合地表发射率,该数据是由组分发射率根据组分覆盖度加权求和得到;σ为斯蒂芬—玻尔兹曼常数,取值为5.67×10–8W/m2K4(Zhou 等,2015b)。
选用2.1节中的19个自动气象站于2012年7月5日和7月10日每10 min获得一次的地面观测数据,包括常规气象要素、长波和短波辐射数据。使用短波辐射数据作为一种辅助数据,来判断天气的晴朗状况。另外,由于研究区内无水体温度观测站点,故选用研究区之外临近的二坝水库站点(38.9159°N, 100.6159°E)观测数据。该站点距离研究区的中心约为20 km,水体表面温度通过SI-111红外辐射计(光谱响应范围为8—14 μm)测量的亮温计算得到。
3 研究方法
3.1 地表温度时间归一化方法
地表温度在一个昼夜周期内的变化可以使用如下模型表示(Jin和Dickinson,1999):
| ${T_{\rm{s}}}\left( t \right) = {\bar T_{\rm{s}}}\left( t \right) + {T_{\rm{s}}}^\prime \left( t \right)$ | (2) |
式中,Ts(t)表示t时刻的地表温度,
据式(2),可得到地表温度从从t1到t2时刻的变化ΔTs(t1→t2):
| $\begin{aligned}\Delta {T_{\rm{s}}}\left( {{t_1} \! \to \! {t_2}} \right) \!= & {T_{\rm{s}}} \! \left( {{t_2}} \right) - {T_{\rm{s}}}\left( {{t_1}} \right) \!= \\ & \left[ {{{\bar T}_{\rm{s}}} \! \left( {{t_2}} \right) \! - \! {{\bar T}_{\rm{s}}} \! \left( {{t_1}} \right)} \right] + \left[ {{{T'}_{\rm{s}}} \! \left( {{t_2}} \right) - {{T'}_{\rm{s}}}\left( {{t_1}} \right)} \right]\end{aligned}$ | (3) |
因此,可根据下式将t1时刻的地表温度归一化到t2时刻:
| ${T_{\rm{s}}}\left( {{t_2}} \right) = {T_{\rm{s}}}\left( {{t_1}} \right) + \left[ {{{\bar T}_{\rm{s}}}\left( {{t_2}} \right) - {{\bar T}_{\rm{s}}}\left( {{t_1}} \right)} \right] + \left[ {{{T'}_{\rm{s}}}\left( {{t_2}} \right) - {{T'}_{\rm{s}}}\left( {{t_1}} \right)} \right]$ | (4) |
| ${\bar T_{\rm{s}}}(t) \!=\! \left\{ \begin{array}{l}\!\!\!\! {T_0} + {T_{\rm{a}}}\cos \left( {\displaystyle\frac{\pi }{\omega }\left( {t - {t_{\rm{m}}}} \right)} \right)t < {t_{\rm{s}}}\\\!\!\!\! \left( {{T_0} \!+\! \delta T} \right) \!+\! \left[ \! {{T_{\rm{a}}}{\rm{cos}}\left( \displaystyle{\frac{\pi }{\omega }\left( {{t_{\rm{s}}} \!-\! {t_{\rm{m}}}} \right)} \right) \!-\! \delta T} \! \right] \! \exp \! \left[ \! {\displaystyle\frac{{ \!-\! (t \!-\! {t_{\rm{s}}})}}{k}} \! \right] \! t \!\! \geqslant \!\! {t_{\rm{s}}}\end{array} \right.$ | (5) |
式中,T0表示日出时刻地表温度;Ta表示地表温度在一个昼夜周期中的变化幅度;ω为日照时长,表示日出到日落的这段时间;tm为昼夜周期中最高地表温度的时刻;ts为地表温度呈指数函数衰减的起始时刻;δT为T0与T(t→∞)的差值;k为衰减系数,可以通过下式计算(Göttsche和Olesen,2001):
| $k = \frac{\omega }{{\rm{\pi }}}\left[ {{{\tan }^{ - 1}}\left( {\frac{\pi}{\omega }\left( {{t_{\rm{s}}} - {t_{\rm{m}}}} \right)} \right)} \right] - \frac{{\delta T}}{{{T_{\rm{a}}}}}{\sin ^{ - 1}}\left( {\frac{\pi}{\omega }\left( {{t_{\rm{s}}} - {t_{\rm{m}}}} \right)} \right)$ | (6) |
根据式(4)、式(5)可得到:
| ${T_{\rm{s}}}({t_2})\left\{ \begin{aligned}& {T_{\rm{s}}}({t_1}) + {T_{\rm{a}}}\left[ {{\rm{cos}}\left( {\frac{\pi }{\omega }\left( {{t_2} - {t_{\rm{m}}}} \right)} \right) - {\rm{cos}}\left( {\frac{\pi }{\omega }\left( {{t_1} - {t_{\rm{m}}}} \right)} \right)} \right] + \left[ {T_{\rm{s}}^\prime \left( {{t_2}} \right) - T_{\rm{s}}^\prime \left( {{t_1}} \right)} \right] {t_1} < {t_2} \leqslant {t_{\rm{s}}}\\& {T_{\rm{s}}}({t_1}) + \delta T + \left[ {{T_{\rm{a}}}{\rm{cos}}\left( {\frac{\pi }{\omega }\left( {{t_{\rm{s}}} - {t_{\rm{m}}}} \right)} \right) - \delta T} \right]\exp \left[ {\frac{{ - \left( {{t_2} - {t_{\rm{s}}}} \right)}}{k}} \right] - {T_{\rm{a}}}\cos \left( {\frac{\pi }{\omega }\left( {{t_1} - {t_{\rm{m}}}} \right)} \right) + \left[ {T_{\rm{s}}^\prime \left( {{t_2}} \right) - T_{\rm{s}}^\prime \left( {{t_1}} \right)} \right] {t_1} \leqslant {t_{\rm{s}}};{t_2} > {t_{\rm{s}}}\\& {T_{\rm{s}}}({t_1}) - \delta T - \left[ {{T_{\rm{a}}}{\rm{cos}}\left( {\frac{\pi }{\omega }\left( {{t_{\rm{s}}} - {t_{\rm{m}}}} \right)} \right) - \delta T} \right]\exp \left[ {\frac{{ - \left( {{t_1} - {t_{\rm{s}}}} \right)}}{k}} \right] - {T_{\rm{a}}}\cos \left( {\frac{\pi }{\omega }\left( {{t_2} - {t_{\rm{m}}}} \right)} \right) + \left[ {T_{\rm{s}}^\prime \left( {{t_2}} \right) - T_{\rm{s}}^\prime \left( {{t_1}} \right)} \right] {t_{\rm{2}}} \leqslant {t_{\rm{s}}};{t_1} > {t_{\rm{s}}}\\& {T_{\rm{s}}}({t_1}) + \left[ {{T_{\rm{a}}}{\rm{cos}}\left( {\frac{\pi }{\omega }\left( {{t_{\rm{s}}} - {t_{\rm{m}}}} \right)} \right) - \delta T} \right]\left[ {\exp \left( {\frac{{ - \left( {{t_2} - {t_{\rm{s}}}} \right)}}{k}} \right) - \exp \left( {\frac{{ - \left( {{t_1} - {t_{\rm{s}}}} \right)}}{k}} \right)} \right] + \left[ {T_{\rm{s}}^\prime \left( {{t_2}} \right) - T_{\rm{s}}^\prime \left( {{t_1}} \right)} \right] {t_{\rm{s}}} \leqslant {t_1} < {t_2}\end{aligned} \right.$ | (7) |
式(7)表明,实现地表温度时间归一化还需要t1和t2时刻地表温度瞬时波动的差异。本文假设
| ${T_{\rm{s}}}^\prime \left( t \right) = f\left( {\rho} \right)$ | (8) |
式中, ρ 表示气象变量的影响因子向量集;f为影响因子与地表温度瞬时波动的映射函数。
因经典的DTC模型并未考虑地表温度的瞬时波动
3.2 查找表构建与地表温度瞬时波动的量化
地表温度的时间归一化需要输入两部分的未知参数。首先第一部分的未知参数是DTC模型的变量,包括Ta,tm,ts及δT。由于不同地物覆盖类型都有其独特的物理性质,故每一种地物覆盖类型各有其地表温度日变化特征(Jin和Dickinson,1999;Jin和Treadon,2003;Zhou 等,2013;Duan 等,2014)。因此,利用DTC模型进行时间归一化时,需要建立一个针对不同地物覆盖类型DTC模型变量的查找表,如表1。查找表的构建过程如下:
(1) 根据不同的地物覆盖类型,挑选相应站点的实测地表温度数据。
(2) 通过分析对比,选出EC02-03、05-15等站点的实测温度数据作为农田地物类型的研究数据,EC17站点的实测温度数据作为林地地物类型的研究数据,二坝水库的实测温度数据作为水体类型的研究数据,农村屋顶的实测温度数据作为建筑类型的研究数据,GB站点的实测温度数据作为戈壁类型的研究数据,SSW站点的实测温度数据作为沙漠地物类型的研究数据,HZZ站点的实测温度数据作为荒漠地物类型的研究数据。
(3) 将每个站点在一个昼夜周期内的实测地表温度,作为模型的输入数据,通过Levenberg-Marquardt方法计算拟合得到DTC模型的变量(Moré 等,1978)。
(4) 不同地物类型的DTC模型变量获取方法与(3)相同,进而构建得到查找表1。
然后,通过程序对TASI影像航带逐个像元进行检查,判断其地物覆盖类型,最后根据查找表搜索每个像元的DTC模型的变量参数。为了训练得到函数表达式f,对每个站点的地表温度瞬时波动和气象变量进行了相关性分析,本文采用线性回归的方法研究地表温度瞬时波动和气象变量的关系,具体如式(9)。由于不同的时间窗口风速的大小和变化的剧烈程度不同,因此本文选择的时间窗口为考虑归一化的整个时间段,即北京时间9:00—18:00和11:00—15:00(风速变化较大且比较剧烈)两个不同的时间窗口。
| ${T_{\rm{s}}}^\prime \left( t \right) = {K_{{\rm{LC}}}}*W + {b_{\rm {LC}}}$ | (9) |
式中,KLC表示线性回归的系数,该系数依赖于地表覆盖类型;W表示不同气象变量(例如风速、气温、气压和空气湿度等);bLC表示线性回归方程的常数项,与KLC类似,bLC也取决于地物覆盖类型。
3.3 方法应用与评价
本文将TASI影像各个条带的地表温度归一化到北京时间9:00—18:00的整点时刻,以及部分TASI条带的获取时刻。然后利用地面站点实测的地表温度来验证时间归一化后的地表温度。此外,将不同条带的TASI地表温度归一化到12:12,并且进行不同条带影像的拼接。由于研究区内部绿洲的地表异质性较大,直接对TASI归一化结果进行升尺度到与2012年7月10日ASTER相同的90 m空间分辨率时,尺度效应可能会对升尺度结果带来误差。因此,本文采取以下方法对TASI时间归一化的结果进行了评估分析。首先,直接将TASI归一化的结果与ASTER进行对比,从视觉上直观判断归一化结果地表温度的空间分布变化情况以及与ASTER地表温度的差异。其次,为了能够对对归一化的结果进行定量的分析,分别从TASI归一化结果中裁剪出农田、林地、水体、建筑、戈壁、沙漠和荒漠等均一地物覆盖类型的影像,然后对裁剪的不同地物类型的TASI影像进行升尺度,升尺度到与ASTER相同的90 m的空间分辨率,最后分别与裁剪出的每种地物覆盖类型区域相同的ASTER影像进行对比。TASI温度升尺度的采用像素聚集(pixel aggregation)方法,Liu等人(2006)和Chen等人(2012)研究了尺度效应对地表温度的影响,发现对于平坦均一性地表而言,采用像素聚集进行地表温度升尺度的误差很小。ASTER的地表温度通过辐射传输方程方法反演得到,波段选用第13波段,辐射传输模型采用MODTRAN5,大气廓线由张掖市气象局观测站(39°05′N,100°17′E)采用GTS1型数字式探空仪获得,探空数据日期与ASTER日期相同,地表发射率基于实测发射率波谱根据第13波段的光谱响应函数积分得到(Zhou 等,2015b)。在下垫面均一化的绿洲站点,反演得到的ASTER地表温度的均方根误差约为1.5 K(Zhou 等,2015b)。
在基于实测地表温度对TASI地表温度时间归一化结果的验证中,采用平均偏差MBE(Mean Bias Error)和均方根误差RMSE(Root-Mean Squared Error)进行定量化的比较。由于ASTER地表温度本身具有不确定性,故在将TASI地表温度时间归一化结果与其对比时,采用MBD(Mean Bias Difference)和RMSD(Root-Mean Squared Difference)。
为了进一步研究天气相对晴朗条件下,风速的大小和波动的剧烈程度对DTC模型时间归一化结果的影响,还选用了2012年7月5日的实测地表温度数据进行模拟实验。首先使用DTC模型对站点实测的温度数据进行拟合,得到一天中平均天气状况下的地表温度。为更好的测试效果,然后将所要归一化时刻和前后十分钟的实测温度数据去掉,进行地表温度的波动和风速的线性回归,得到地表温度的波动和风速的关系模型。最后,将所要归一化的时刻的风速代入关系模型中计算得到该时刻地表温度的波动,然后对DTC模型时间归一化的结果进行改进,进而实现IDTC模型对站点实测温度数据的时间归一化。
针对实测地表温度数据时间归一化的时间窗口选择与TASI航空遥感地表温度时间归一化类似,选择9:00—18:00和11:00—16:00(即风速变化较大且波动剧烈)两个不同的时间窗口进行研究。本部分为模拟实验,用以在TASI地表温度时间归一化之外,补充说明考虑风速影响的IDTC模型时间归一化的改进效果。
4 结果与分析
4.1 DTC拟合与地表温度瞬时波动的影响因子分析
2012年7月10日不同地表覆盖类型的DTC模型的参数,如表1所示。正如预期的由于不同物体的热学性质不同,DTC模型的参数依赖于地表覆盖类型。DTC拟合值与真实值的相关系数和RMSE表明,DTC模型能够较好地拟合绝大部分站点的地表温度观测数据。对比不同地表覆盖类型的RMSE,可以看出热惯量较小的地物覆盖类型的RMSE较大(如戈壁、荒漠等),反之亦然。DTC模型的误差部分来自于天气变化导致的地表温度瞬时波动。但是,较小的RMSE并不表明可以获得较小的时间归一化误差,因为也可能是在该地区和目标时刻天气变化影响因素正反相抵消造成的。
表 1 2012年7月10日不同地表覆盖类型的DTC模型参数
Table 1 The calculated DTC parameters of different land cover types on July 10, 2012
| 地表覆盖类型 | T0/K | Ta/K | tm/h | ts/h | δT/K | RMSE/K |
| 农田 | 291.15 | 11.32 | 14.64 | 20.73 | 0.57 | 0.48 |
| 林地 | 290.77 | 14.24 | 14.58 | 20.37 | 1.66 | 0.41 |
| 水体 | 295.58 | 4.32 | 16.50 | 17.69 | 6.89 | 0.36 |
| 建筑 | 297.87 | 48.73 | 14.36 | 18.89 | 13.06 | 1.22 |
| 戈壁 | 285.99 | 37.87 | 14.37 | 18.31 | 9.75 | 2.30 |
| 沙漠 | 285.36 | 42.34 | 14.22 | 18.19 | 10.12 | 1.14 |
| 荒漠 | 280.67 | 49.88 | 13.93 | 18.07 | 13.87 | 1.35 |
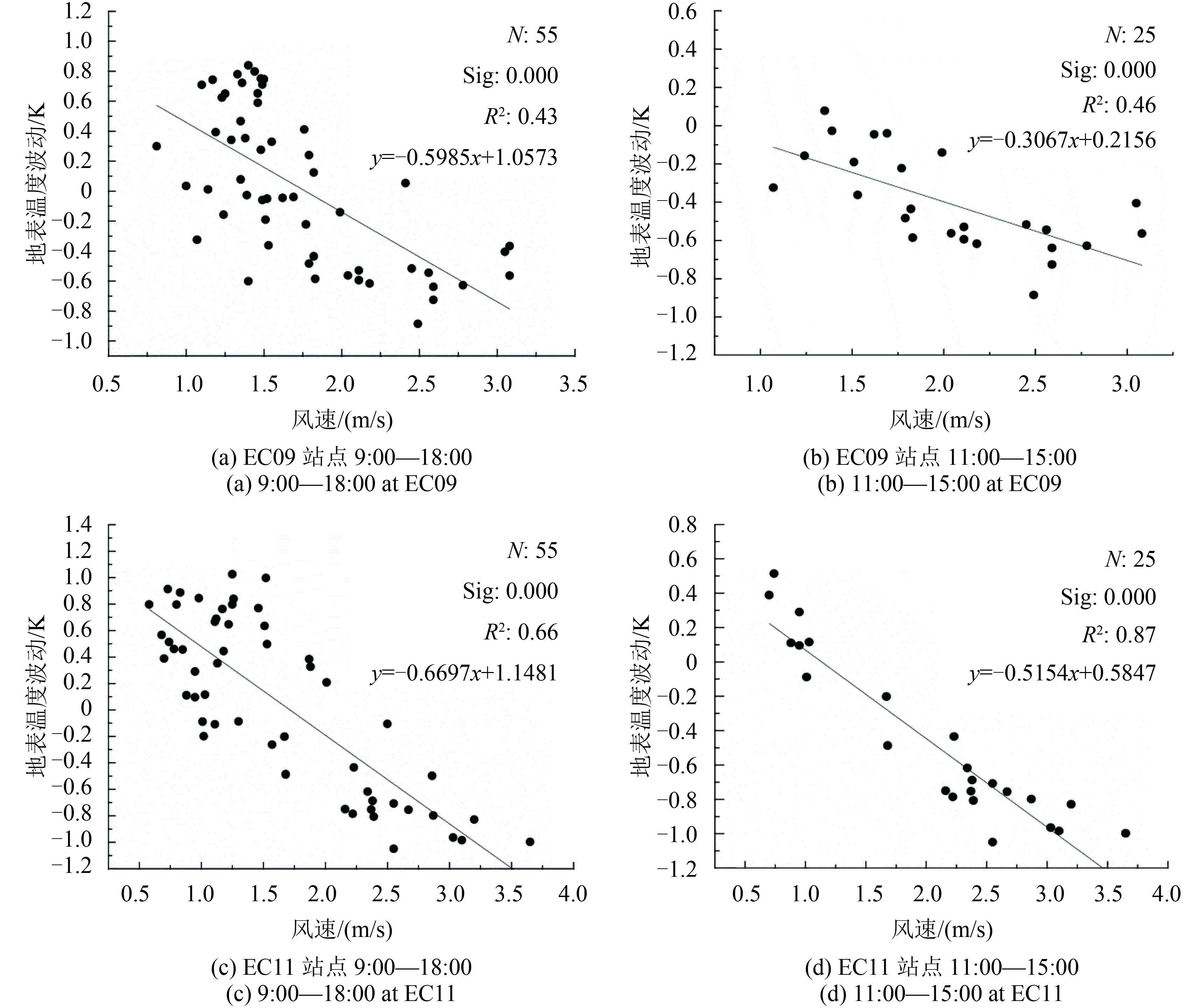
针对地面各实测站点计算得到地表温度瞬时波动
4.2 基于实测地表温度的TASI地表温度时间归一化结果验证
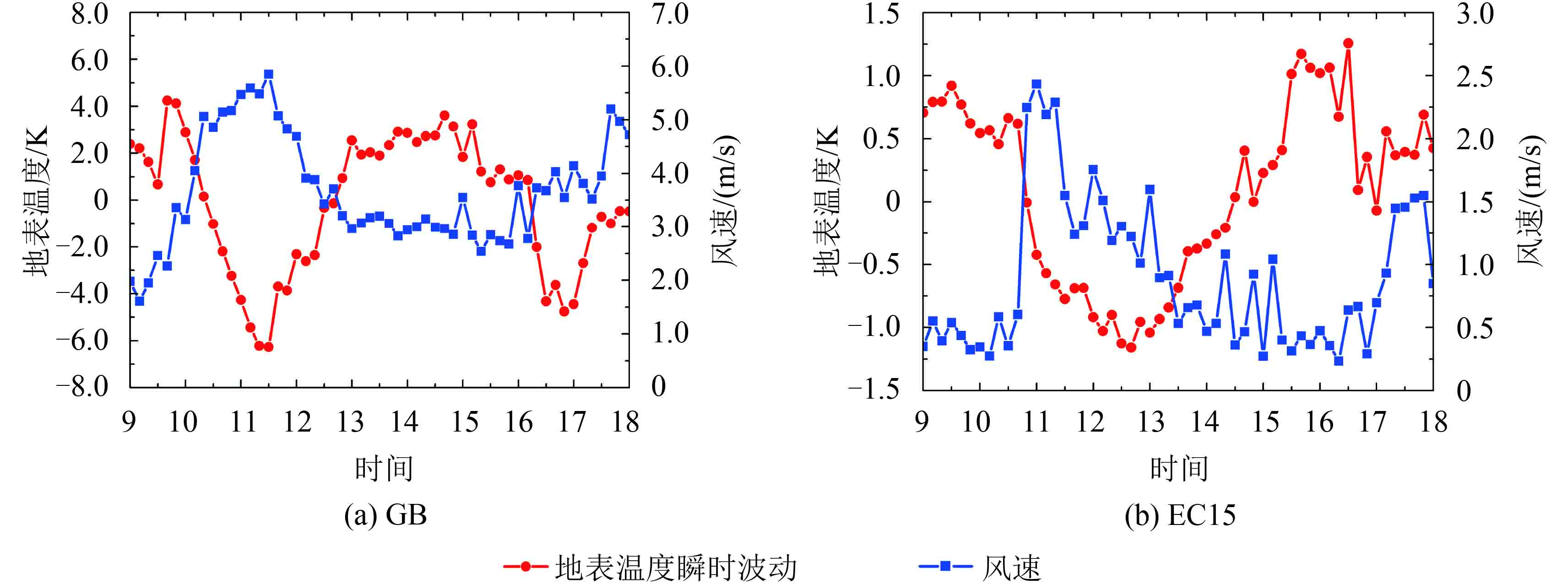
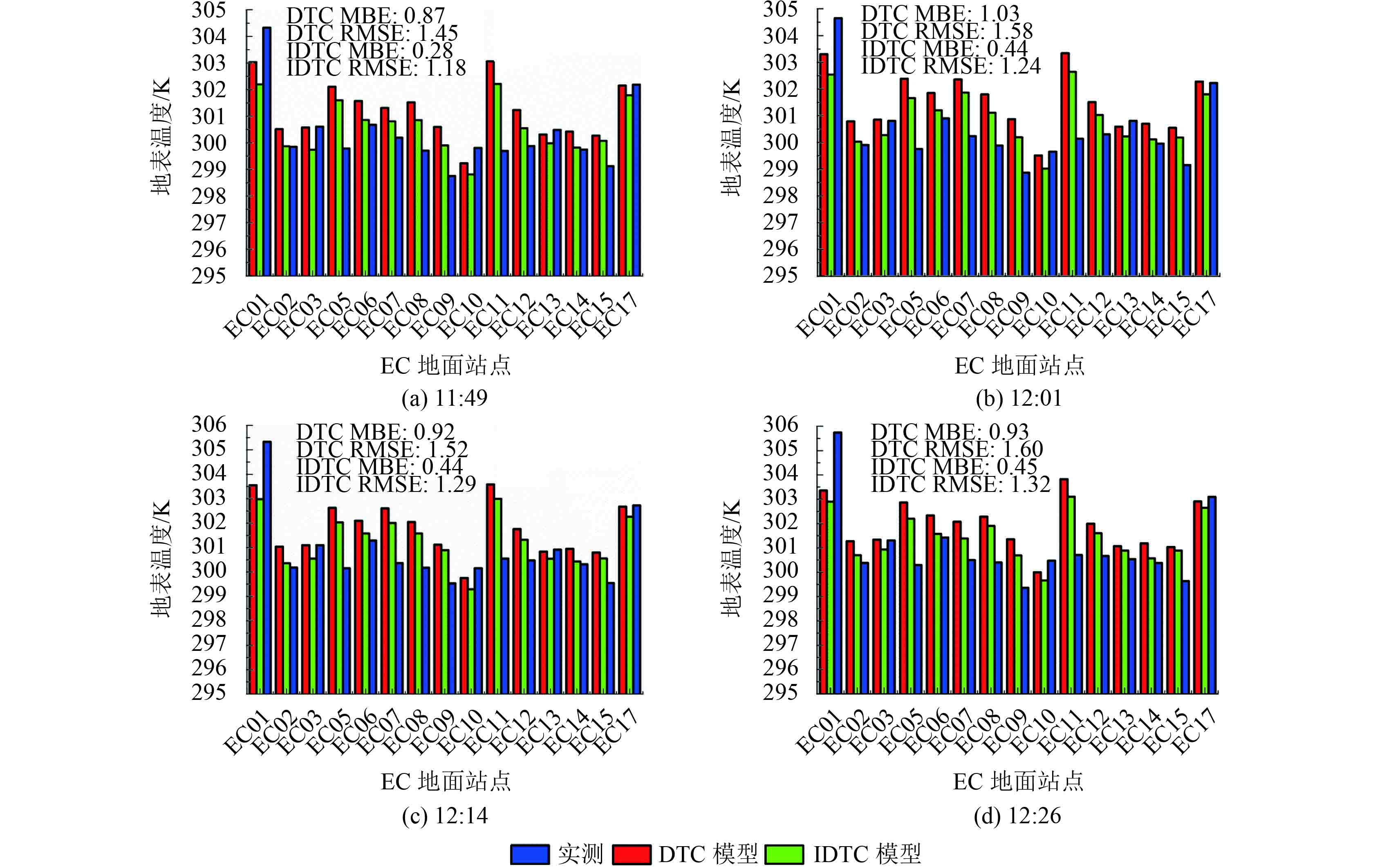
表2为TASI未归一化、采用DTC模型和IDTC模型对TASI地表温度进行时间归一化结果的RMSE和MBE。其中IDTC模型时间归一化的结果,整体的MBE和RMSE较DTC模型小。从结果来看,IDTC模型能够较好地进行TASI航空遥感地表温度的时间归一化。表2表明,两个不同的时间窗口TASI时间归一化结果表现出一定的差异。第1个时间窗口时间归一化的结果中,部分时刻的结果中IDTC模型并没有使时间归一化结果的误差减小,例如9:00、10:00、16:00、17:00和18:00等时刻,其余时刻IDTC模型减小了时间归一化结果的误差。第2个时间窗口归一化的结果中,整体上IDTC模型在各个时刻时间归一化结果的RMSE和MBE都要小于DTC模型。通过分析各个站点9:00—18:00这段时间的风速变化,发现风速在11:00—15:00这段时间内较大且波动较剧烈(图2)。因此这段时间风速的影响较大,考虑风速影响的IDTC模型能够较好的减小时间归一化结果的误差。由于其余的时间风速较小,风速对地表温度的变化影响相对也较小,所以其余时刻IDTC模型没有提高时间归一化结果的精度。从图4中可以看出,不同站点在不同时刻时间归一化的结果也表现出一定的差异,其中EC01站点时间归一化结果误差较大,分析发现EC01站地物类型是菜地,归一化时输入的模型参数是玉米地的参数,因此导致DTC模型和IDTC模型时间归一化的结果与实测地表温度差异较大。因此,研究区地物覆盖类型的分类精度,也是影响DTC和IDTC模型时间归一化精度的原因。
表 2 对TASI地表温度时间归一化结果的验证
Table 2 Validation results of TASI LST normalized by the DTC model and IDTC model
| 归一化目标时刻 | 未归一化/K | DTC模型/K | IDTC模型(9:00—18:00) | IDTC模型(11:00—15:00) | |||||||
| MBE | RMSE | MBE | RMSE | MBE | RMSE | MBE | RMSE | ||||
| 9:00 | 6.08 | 6.14 | 0.40 | 0.94 | 0.79 | 1.22 | — | — | |||
| 10:00 | 3.37 | 3.41 | –0.23 | 0.94 | 0.08 | 0.86 | — | — | |||
| 11:00 | 2.39 | 2.68 | 0.74 | 1.37 | 0.05 | 1.25 | –0.09 | 1.16 | |||
| 11:49 | 1.27 | 1.81 | 0.87 | 1.45 | 0.50 | 1.22 | 0.28 | 1.18 | |||
| 12:01 | 1.15 | 1.67 | 1.03 | 1.58 | 0.64 | 1.37 | 0.44 | 1.24 | |||
| 12:14 | –0.07 | 2.86 | 0.92 | 1.52 | 0.63 | 1.29 | 0.44 | 1.29 | |||
| 12:26 | –0.22 | 2.90 | 0.93 | 1.60 | 0.71 | 1.49 | 0.45 | 1.32 | |||
| 13:00 | –1.00 | 3.16 | 0.72 | 1.56 | 0.70 | 1.53 | 0.45 | 1.43 | |||
| 14:00 | –2.01 | 3.56 | 0.29 | 1.47 | 0.48 | 1.59 | 0.21 | 1.56 | |||
| 15:00 | –2.50 | 3.85 | –0.13 | 1.47 | 0.09 | 1.41 | –0.18 | 1.40 | |||
| 16:00 | –1.97 | 3.51 | –0.04 | 1.54 | 0.23 | 1.58 | — | — | |||
| 17:00 | –0.26 | 2.93 | 0.74 | 1.28 | 0.93 | 1.49 | — | — | |||
| 18:00 | 0.50 | 2.95 | 0.11 | 1.14 | 0.03 | 1.16 | — | — | |||
4.3 TASI地表温度时间归一化结果与ASTER地表温度的对比
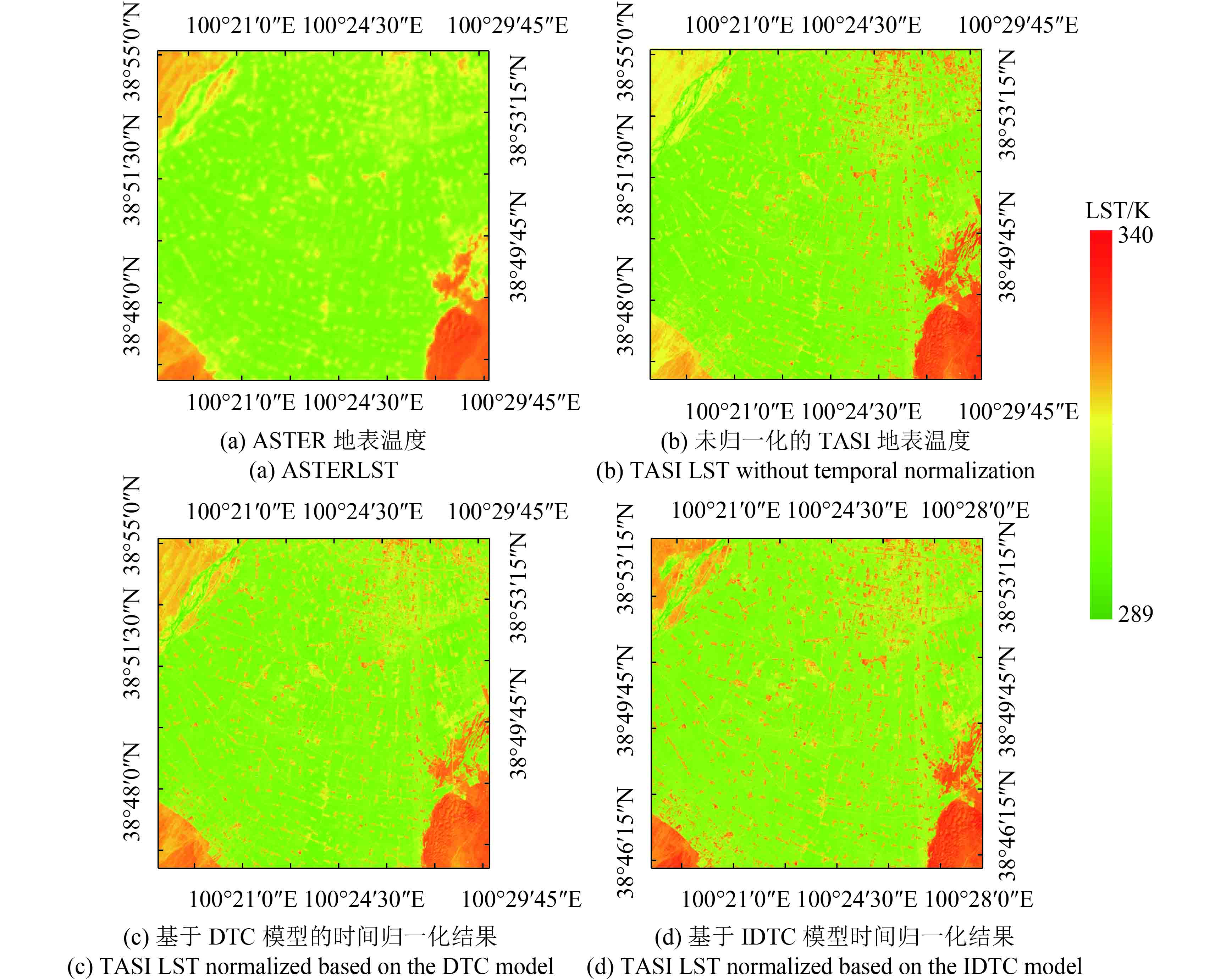
为了更好地测试DTC模型和IDTC模型在整个研究区域的应用效果,将TASI各航带的地表温度时间归一化到当天ASTER的过境时间,然后直接与ASTER地表温度进行对比,结果如图5所示。图5表明利用IDTC模型进行TASI的时间归一化,能够很好的消除由于观测时间不同导致的地表温度的差异,并且相比于DTC模型,IDTC模型时间归一化后的地表温度误差较小,并且能够较好的与ASTER地表温度相吻合。
图5表明:(1)不进行TASI的时间归一化时,戈壁和花寨子荒漠的地表温度与ASTER的地表温度差异较大。(2)TASI归一化前后,绿洲内的地表温度差异较小,且与ASTER地表温度较为接近,其原因在于浓密植被温度变化较小。(3)TASI时间归一化以后,戈壁和花寨子荒漠的地表温度与ASTER地表温度的吻合效果较好。根据不同模型进行时间归一化得到的TASI地表温度与ASTER地表温度的偏差,与地表覆盖类型具有显著关系,如表3所示。表3表明:(1)DTC和IDTC模型时间归一化以后,各种地物覆盖类型的TASI地表温度相对于ASTER地表温度的MBD和RMSD均减小了,再次说明进行航空遥感地表温度的时间归一化可以有效减小由于观测时间不同导致的地表温度的差异。(2)IDTC模型的MBD和RMSD总体上小于DTC模型,表明即便是在天气晴朗条件下,考虑风速影响能够在一定程度上提高时间归一化结果的精度。(3)基于IDTC模型的时间归一化结果中戈壁和花寨子荒漠的精度提高比较显著,其余地物类型的精度提高较小。
表 3 不同地物覆盖类型的TASI LST相对于ASTER LST的差异
Table 3 Differences of the TASI LST and ASTER LST of different land cover types
| /K | ||||||||
| 地物覆盖类型 | 未归一化 | 基于DTC模型 | 基于IDTC模型 | |||||
| MBD | RMSD | MBD | RMSD | MBD | RMSD | |||
| 农田 | –0.07 | 1.13 | 0.43 | 1.11 | 0.02 | 0.70 | ||
| 林地 | –0.01 | 1.06 | 0.30 | 1.11 | 0.04 | 0.91 | ||
| 水体 | –1.21 | 4.10 | –0.22 | 4.01 | –0.16 | 3.42 | ||
| 建筑 | –1.23 | 4.25 | –0.22 | 2.16 | 0.08 | 1.47 | ||
| 戈壁 | –4.87 | 5.01 | –1.52 | 1.94 | –1.04 | 1.50 | ||
| 沙漠 | 2.38 | 2.98 | –1.15 | 2.17 | –1.19 | 2.12 | ||
| 荒漠 | –5.07 | 5.50 | –1.25 | 2.34 | –0.26 | 2.00 | ||
4.4 针对地面实测站点地表温度时间归一化
2012年7月5日天气相对比较晴朗,并且在9:00—18:00这段时间内,大部分时间风速较大且波动剧烈,可以进一步分析验证风速对DTC模型时间归一化的影响。各时刻的地表温度时间归一化的MBE与RMSE如表4、表5所示。
表 4 2012年7月5日第1个时间窗口(9:00—18:00)各个时刻时间归一化误差
Table 4 Errors of the temporally normalized LST in the first temporal window (9:00—18:00)on July 5, 2012
| /K | |||||
| 归一化目标 时刻 |
DTC模型 | IDTC模型 | |||
| MBE | RMSE | MBE | RMSE | ||
| 9:00 | 1.43 | 1.46 | 1.60 | 2.00 | |
| 10:00 | –0.47 | 0.48 | –0.14 | 0.18 | |
| 11:00 | –0.85 | 0.89 | –0.51 | 0.75 | |
| 11:30 | –0.01 | 0.18 | –0.11 | 0.24 | |
| 12:00 | 0.17 | 0.26 | –0.07 | 0.24 | |
| 12:30 | 0.67 | 0.68 | 0.27 | 0.34 | |
| 13:00 | 0.77 | 0.78 | 0.32 | 0.48 | |
| 13:30 | 0.42 | 0.44 | 0.07 | 0.17 | |
| 14:00 | 0.30 | 0.33 | 0.03 | 0.16 | |
| 14:30 | 0.04 | 0.17 | –0.12 | 0.22 | |
| 15:00 | –0.34 | 0.38 | –0.31 | 0.41 | |
| 15:30 | –0.42 | 0.45 | –0.33 | 0.45 | |
| 16:00 | –0.33 | 0.36 | –0.25 | 0.34 | |
| 17:00 | 0.04 | 0.13 | 0.14 | 0.20 | |
| 18:00 | –0.57 | 0.58 | 0.49 | 0.48 | |
表 5 2012年7月5日第2个时间窗口(11:00—16:00)各个时刻时间归一化误差
Table 5 Errors of the temporally normalized LST in the second temporal window (11:00—16:00) on July 5, 2012
| /K | |||||
| 归一化目标时刻 | DTC模型 | IDTC模型 | |||
| MBE | RMSE | MBE | RMSE | ||
| 11:00 | –0.85 | 0.89 | –0.06 | 0.31 | |
| 11:30 | –0.01 | 0.18 | 0.01 | 0.22 | |
| 12:00 | 0.17 | 0.26 | –0.13 | 0.34 | |
| 12:30 | 0.67 | 0.68 | 0.00 | 0.17 | |
| 13:00 | 0.77 | 0.78 | 0.25 | 0.28 | |
| 13:30 | 0.42 | 0.44 | –0.01 | 0.11 | |
| 14:00 | 0.30 | 0.33 | 0.03 | 0.22 | |
| 14:30 | 0.04 | 0.17 | –0.01 | 0.19 | |
| 15:00 | –0.34 | 0.38 | –0.07 | 0.15 | |
| 15:30 | –0.42 | 0.45 | –0.09 | 0.16 | |
| 16:00 | –0.33 | 0.36 | 0.07 | 0.13 | |
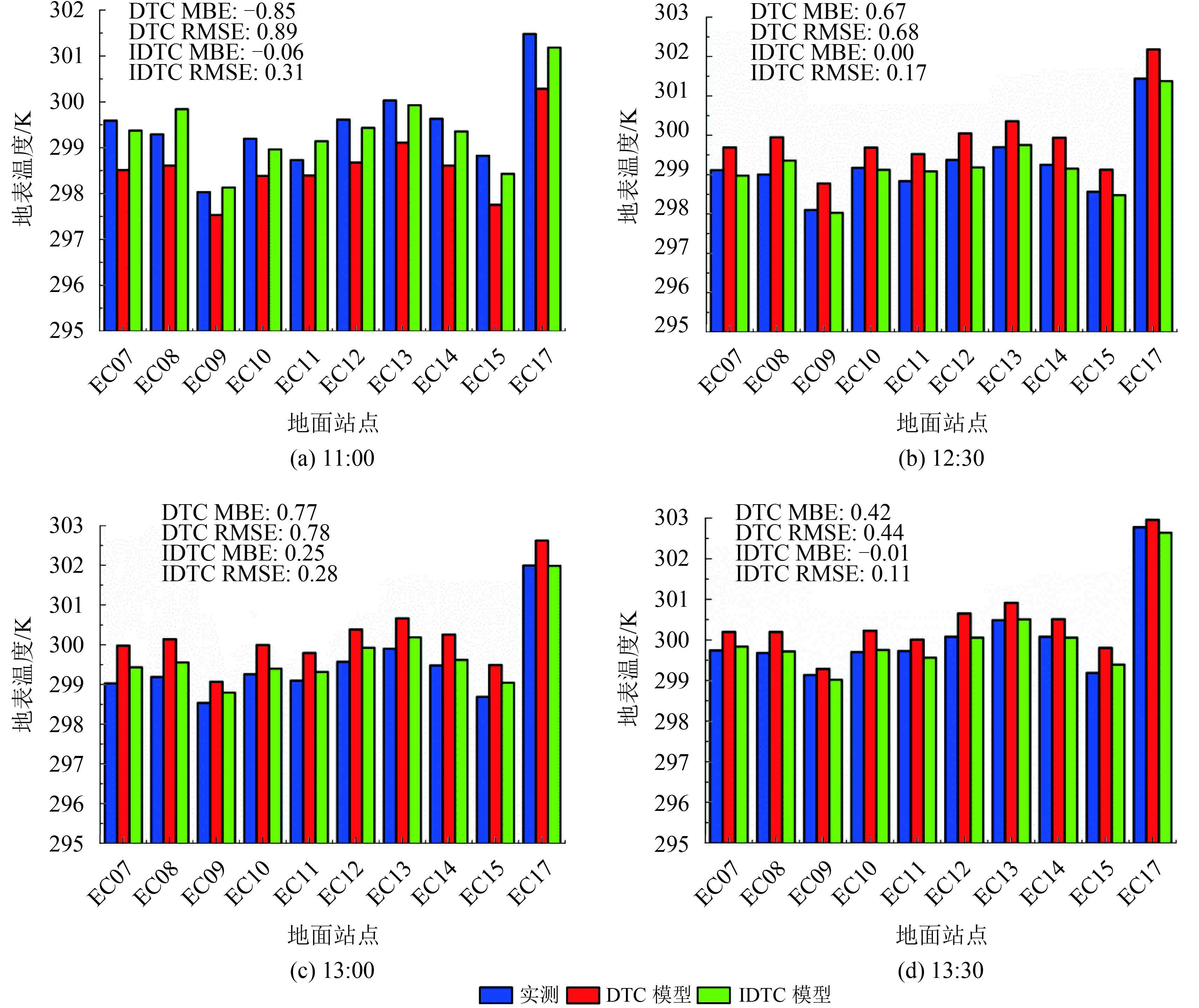
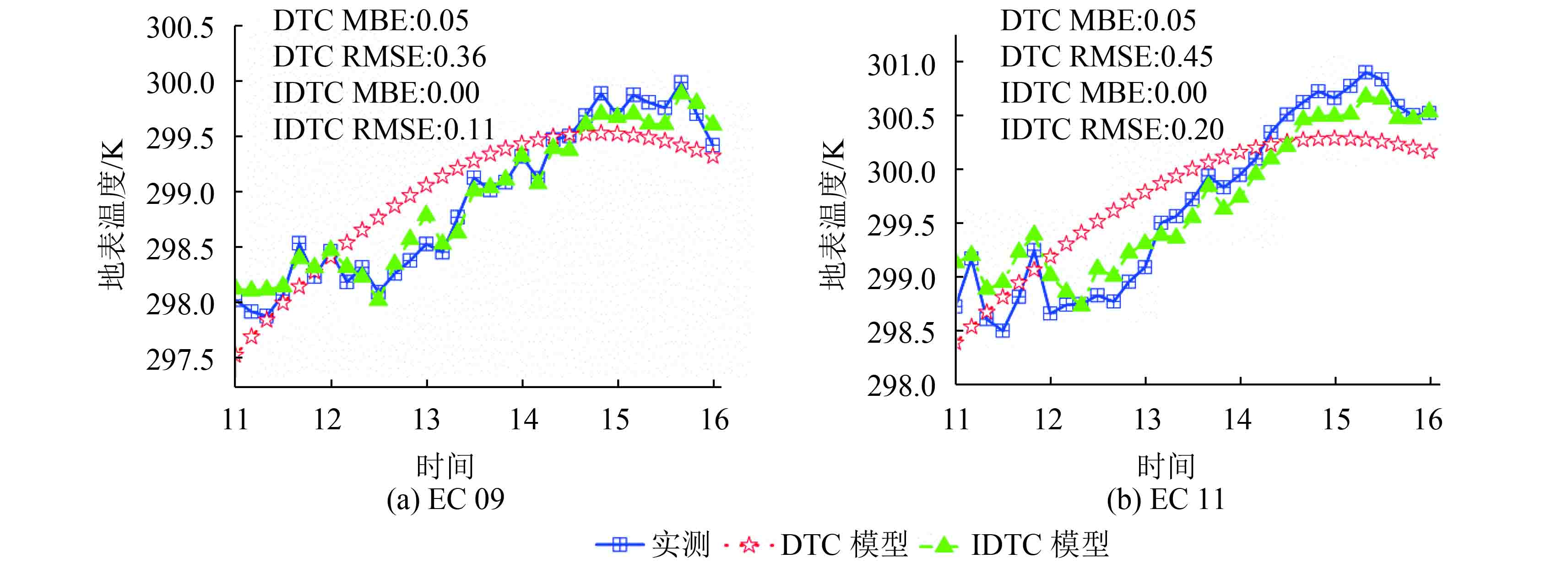
在天气晴朗的条件下,针对实测站点的时间归一化结果,两个不同研究时间窗口,DTC模型和IDTC模型归一化的结果呈现一定的差异。从表4中可以看出,在第1个时间窗口的时间归一化结果中,除了部分时刻之外(如9:00和17:00),绝大部分时刻IDTC模型时间归一化结果的RMSE和MBE均小于DTC模型的结果。第2个时间窗口研究的结果,从表5中可以看出IDTC模型时间归一化的结果的RMSE和MBE均小于DTC模型的结果。从图6和图7中可以看出,各个站点IDTC模型的时间归一化结果更接近于站点实测的地表温度,两者吻合的情况较好。通过分析该天9:00—18:00时段的风速变化,发现11:00—16:00这段时间风速较大,并且该段时间风速波动比较剧烈。因此在风速较大且波动剧烈的时间段,地表温度受风速波动的影响也较大。其余时间风速较小且稳定,此时对地表温度的波动影响也较小,这也是不同的时间窗口归一化结果出现差异的原因。
5 结 论
地表温度在时间尺度上快速变化,使得卫星遥感提供的地表温度在满足使用者对非成像时刻地表温度的需求时,需要开展其时间归一化。航空热红外遥感因其影像幅宽有限,不同航带的地表温度一般需要时间归一化之后才具有实际使用价值。以2012年HiWATER试验区为研究区,借助地面高密度的气象观测数据,本文引入温度日变化(DTC)模型,建立了面向TASI航空遥感地表温度的时间归一化方法。针对DTC模型面向天气状况稳定的假设,从地表温度瞬时波动与气象要素的关系入手,进一步发展了改进的温度日变化(IDTC)模型,并将其用于TASI地表温度的时间归一化。利用实测地表温度、ASTER地表温度对TASI地表温度时间归一化结果进行了验证和评价,并借助实测地表温度开展了模拟分析。
研究表明,基于DTC模型和IDTC模型的TASI航空遥感地表温度时间归一化,可以减小由于观测时间不同导致的地表温度的差异,且有利于不同TASI影像条带之间的拼接,进而得到较大空间范围内的地表温度影像。与ASTER地表温度的对比表明进行航空遥感地表温度的时间归一化有助于减小地表温度的瞬时波动差异,便于不同条带影像的拼接。
在天气相对比较晴朗条件下,风速较大且波动剧烈时对地表温度的影响客观存在,应用模型时应该考虑风速对于模型应用结果的影响。基于实测站点地表温度的验证中,大部分时刻IDTC模型时间归一化结果误差比较小。在不同研究时间段内,IDTC模型时间归一化结果具有一定的差异,在风速较大且变化剧烈的时间段,IDTC模型精度较高。IDTC模型对于不同的地表覆盖类型表现出一定的差异性。其中,植被稀少的地区(如戈壁和荒漠),IDTC模型精度提高比较显著;其余的地表覆盖类型(如农田、防护林等),DTC模型和IDTC模型归一化的结果差异较小。经过分析,出现上述现象的原因可能是:(1)该研究区经常出现西北风,其中戈壁和荒漠分别处于研究区的西北和西南面,因此受风速的影响比较显著;(2)戈壁和荒漠地区相比于绿洲比较空旷,没有建筑和植被等对风速的减缓作用,这也导致这些地区地表温度受风速的影响比较强烈;(3)由于戈壁和沙漠的热惯量一般较绿色植被小,其温度变化速度相对绿色植被快。总体上,基于IDTC模型的时间归一化比DTC模型具有较高的精度,前者较后者精度提高0.3—0.6 K。此外,IDTC模型提供的时间归一化结果在时间尺度变化趋势上与实际情况更加吻合。
志 谢 此次野外实验数据的获取得到了黑河数据中心支持,同时也离不开HiWATER试验期间参与野外试验的科学家、工程师和学生所付出的辛勤劳动,在此表示衷心的感谢!
参考文献(References)
-
Chen X H, Yamaguchi Y, Chen J and Shi Y S. 2012. Scale effect of vegetation-index-based spatial sharpening for thermal imagery: a simulation study by ASTER data. IEEE Geoscience and Remote Sensing Letters, 9 (4): 549–553. [DOI: 10.1109/LGRS.2011.2174453]
-
Duan S B, Li Z L, Tang B H, Wu H and Tang R L. 2014. Generation of a time-consistent land surface temperature product from MODIS data. Remote Sensing of Environment, 140 : 339–349. [DOI: 10.1016/j.rse.2013.09.003]
-
Duan S B, Li Z L, Wang N, Wu H and Tang B H. 2012. Evaluation of six land-surface diurnal temperature cycle models using clear-skyin situ and satellite data . Remote Sensing of Environment, 124 : 15–25. [DOI: 10.1016/j.rse.2012.04.016]
-
Göttsche F M and Olesen F S. 2001. Modelling of diurnal cycles of brightness temperature extracted from METEOSAT data. Remote Sensing of Environment, 76 (3): 337–348. [DOI: 10.1016/S0034-4257(00)00214-5]
-
Göttsche F M and Olesen F S. 2009. Modelling the effect of optical thickness on diurnal cycles ofland surface temperature. Remote Sensing of Environment, 113 (11): 2306–2316. [DOI: 10.1016/j.rse.2009.06.006]
-
Inamdar A K, French A, Hook S, Vaughan G and Luckett W. 2008. Land surface temperature retrieval at high spatial and temporal resolutions over the southwestern UnitedStates. Journal of Geophysical Research: Atmospheres, 113 (D07): D07107 [DOI: 10.1029/2007JD009048]
-
Jiang G M, Li Z L and Nerry F. 2006. Land surface emissivity retrieval from combined mid-infrared and thermal infrared data of MSG-SEVIRI. Remote Sensing of Environment, 105 (4): 326–340. [DOI: 10.1016/j.rse.2006.07.015]
-
Jin M L. 2000. Interpolation of surface radiative temperature measured from polar orbiting satellites to a diurnal cycle: 2. Cloudy-pixel treatment. Journal of Geophysical Research: Atmospheres, 105 (D3): 4061–4076. [DOI: 10.1029/1999JD901088]
-
Jin M L and Dickinson R E. 1999. Interpolation of surface radiative temperature measured from polar orbiting satellites to a diurnal cycle: 1. Without clouds. Journal of Geophysical Research: Atmospheres, 104 (D2): 2105–2116. [DOI: 10.1029/1998JD200005]
-
Jin M L and Treadon R E. 2003. Correcting the orbit drift effect on AVHRR land surface skin temperature measurements. International Journal of Remote Sensing, 24 (22): 4543–4558. [DOI: 10.1080/0143116031000095943]
-
Li X, Cheng G D, Liu S M, Xiao Q, Ma M G, Jin R, Che T, Liu Q H, Wang W Z, Qi Y, Wen J G, Li H Y, Zhu G F, Guo J W, Ran Y H, Wang S G, Zhu Z L, Zhou J, Hu X L and Xu Z W. 2013a. Heihe watershed allied telemetry experimental research (HiWATER): scientific objectives and experimental design. Bulletin of the American Meteorological Society, 94 (8): 1145–1160. [DOI: 10.1175/BAMS-D-12-00154.1]
-
Li X, Liu S M, Ma M G, Xiao Q, Liu Q H, Jin R, Che T, Wang W Z, Qi Y, Li H Y, Zhu G F, Guo J W, Ran Y H, Wen J G and Wang S G. 2012. HiWATER: an integrated remote sensing experiment on hydrological and ecological processes in the Heihe River Basin. Advancesin Earth Science, 27 (5): 481–498. ( 李新, 刘绍民, 马明国, 肖青, 柳钦火, 晋锐, 车涛, 王维真, 祁元, 李弘毅, 朱高峰, 郭建文, 冉有华, 闻建光, 王树果. 2012. 黑河流域生态-水文过程综合遥感观测联合试验总体设计. 地球科学进展, 27 (5): 481–498. )
-
Li Z L, Tang B H, Wu H, Ren H Z, Yan G J, Wan Z M and Trigoe I Fand Sobrinog J A. 2013b. Satellite-derived land surface temperature: current status and perspectives. Remote Sensing of Environment, 131 : 14–37. [DOI: 10.1016/j.rse.2012.12.008]
-
Liu SM, Xu ZW, Song LS, Zhao QY, Ge Y, Xu TR, Ma YF, Zhu ZL, Jia ZZ and Zhang F. 2016. Upscaling evapotranspiration measurements from multi-site to the satellite pixel scale over heterogeneous land surfaces. Agricultural and Forest Meteorology : [DOI: 10.1016/j.agrformet.2016.04.008]
-
Liu SM, Xu ZW, Wang WZ, Jia Z Z, Zhu M J, Bai J and Wang JM. 2011. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrology and Earth System Sciences, 15 (4): 1291–1306. [DOI: 10.5194/hess-15-1291-2011]
-
Liu Y B, Hiyama T and Yamaguchi Y. 2006. Scaling of land surface temperature using satellite data: acase examination on ASTER and MODIS products over a heterogeneous terrain area. Remote Sensing of Environment, 105 (2): 115–128. [DOI: 10.1016/j.rse.2006.06.012]
-
Moré J J.1978. The Levenberg-Marquardt algorithm: implementation and theory //Proceedings of the Biennial Conference, Lecture Notes in Mathematics. Berlin Heidelberg: Springer: 105–116
-
Quan J L, Chen Y H, Zhan W F, Wang J F, Voogt J and Li J. 2014. A hybrid method combining neighborhood information from satellitedata with modeled diurnal temperature cycles over consecutive days. Remote Sensing of Environment, 155 : 257–274. [DOI: 10.1016/j.rse.2014.08.034]
-
Rahman M M, Hay G J, Couloigner I, Hemachandran B and Bailin J. 2015. A comparison of four relative radiometric normalization (RRN) techniques for mosaicing H-res multi-temporal thermal infrared (TIR) flight-lines of a complex urban scene. ISPRS Journal of Photogrammetry and Remote Sensing, 106 : 82–94. [DOI: 10.1016/j.isprsjprs.2015.05.002]
-
Schädlich S, Göttsche F M and Olesen F S. 2001. Influence of land surface parameters and atmosphere on METEOSAT brightness temperatures and generation of land surface temperature maps by temporally and spatially interpolating atmospheric correction. Remote Sensing of Environment, 75 (1): 39–46. [DOI: 10.1016/S0034-4257(00)00154-1]
-
Van den BerghF, van WykM A and van WykB J. 2006. Comparison of data-driven andmodel-driven approaches to brightness temperature diurnal cycle interpolation // 17th Annual Symposium of the Pattern Recognition Association of South Africa, Parys, South Africa
-
Wang H S, Xiao Q, Li H and Zhong B. 2011. Temperature and emissivity separation algorithm for TASI airborne thermal hyperspectral data//Proceedingsof the 2011International Conference on Electronics, Communications and Control.Ningbo, China: IEEE: 1075–1078
-
Xu Z W, Liu S M, Li X, Shi S J, Wang J M, Zhu Z L, Xu T R, Wang W Z and Ma M G. 2013. Intercomparison of surface energy flux measurement systems used during the HiWATER-MUSOEXE. Journal of Geophysical Research: Atmospheres, 118 (23): 13140–13157. [DOI: 10.1002/2013JD020260]
-
Zhou J, Chen Y H, Wang J F and Zhan W F. 2011. Maximum nighttime urban heat island (UHI) intensity simulation by integrating remotely sensed data and meteorological observations. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 4 (1): 138–146. [DOI: 10.1109/JSTARS.2010.2070871]
-
Zhou J, Chen Y H, Zhang X and Zhan W F. 2013. Modelling the diurnal variations of urban heat islands with multi-source satellite data. International Journal of Remote Sensing, 34 (21): 7568–7588. [DOI: 10.1080/01431161.2013.821576]
-
Zhou J, Dai F N, Zhang X D, Zhao S J and Li M S. 2015a. Developing a temporally land cover-based look-up table (TL-LUT) method for estimating land surface temperature based on AMSR-E data over the Chinese landmass. International Journal of Applied Earth Observation and Geoinformation, 34 : 35–50. [DOI: 10.1016/j.jag.2014.07.001]
-
Zhou J, Li M S, Liu S M, Jia Z Z and Ma Y F. 2015b. Validation and Performance Evaluations of Methods for Estimating Land Surface Temperatures from ASTER Data in the Middle Reach of the Heihe River Basin, Northwest China. Remote Sensing, 7 (6): 7126–7156. [DOI: 10.3390/rs70607126]