|
收稿日期: 2016-06-27; 修改日期: 2016-07-04;
优先数字出版日期: 2016-09-25
基金项目: 国家重点基础研究发展计划(973计划)(编号: 2013CB733402);国家自然科学重点基金(编号: 41331171)
第一作者简介:
阎广建(1972-), 男, 教授, 遥感科学国家重点实验室副主任, 研究方向为多角度遥感研究。E-mail:gjyan@bnu.edu.cn
中图分类号: TP79
文献标识码: A
文章编号: 1007-4619(2016)05-0958-21
|
摘要
叶面积指数是对地遥感的关键参数。间接测量法快速高效,已广泛应用于叶面积指数的地面测量和遥感验证中,服务于众多行业和领域,表现为论文被引数远远大于发文数。从理论基础、代表算法、测量仪器、影响因素几个方面全面总结了叶面积指数间接测量方法的发展和现状,指出聚集/尺度效应、叶倾角分布、木质组分、地形效应是影响测量精度的关键因素,针对这些影响因素对未来发展方向进行了展望。
关键词
叶面积指数 , 间接测量 , 聚集效应 , 尺度效应 , 叶倾角分布 , 木质组分 , 地形效应
Abstract
Leaf Area Index(LAI) is a key parameter for terrestrial remote sensing. Indirect methods are fast and efficient, and they arewidely used in ground measurement and the remote sensing validation of the LAI. These methods servea large number of industries and fields, as theircitation count is far greater than theirliterature count. This paper comprehensively reviews the development and current status of indirect LAI measurement with regard to theories, algorithms, instruments, and influence factors. The latest progress and future prospects are summarized and discussed onthe basis off our challenges, including clumping/scale effect, leaf angle distribution, woody component, and slope effect. First, the basic concepts and theoretical background are summarized to provide an overview of indirect LAI measurement. The basic concepts include LAI definition, gap probability, leaf angle distribution, leaf projection function, clumping index, needle-to-shoot area ratio, and woody-to-total area ratio. Theoretical derivations begin with the introduction of Beer's law on indirect LAI measurement, followed by three essential adaptations concerning leaf angle distribution, clumping effect, and woody component. Second, representative methods for quantifying the clumping effect are reviewed, with the clumping effect beingthe most important factor. These methods consist of the finite-length averaging method, the gap-size distribution method, the combination of finite-length averaging and gap-size distribution method, and the path length distribution method. Third, representative instruments for indirect measurement are reviewed. These instruments include LAI-2000, TRAC, line quantum sensors (AccuPAR, SunScan, and LAInet), DEMON, imaging instruments (HemiView, MVI, and MCI), and LiDAR. Airborne and spaceborne LiDAR are also reviewed because they also use Beer's law as the indirect LAI measurement. Finally, four key factors that limit indirect LAI measurement accuracy are discussed. These factors are the clumping/scale effect, leaf angle distribution, woody component, and slope effect. The mixed effects of these factors are also explained.The clumping effect has attracted the most attention in the community, with several related methods having beendeveloped and being widely used in field measurement. The non-randomness inside canopies and the scale effect of measurement is also worth studying further. The theory of leaf angle distribution is well-developed, whereas the spherical distribution assumption (G≡0.5) is often used because of the inconvenience of measurement. The spherical distribution assumption should be used with caution because it is only valid near a zenith angle of 57.3°. The efforts to develop fast and automatic methods for measuring leaf angle distribution show greatpromise. The importance of woody components is widely recognized, but they are always ignored in measurement because commercial instruments are incapable of distinguishing woody components. Near-infrared technology and instruments should be applied to ground measurement to distinguish the LAI from the plant area index. The slope effect has attracted more attention than before. Research shows that it canbe ignored when the slope is less than 30°; otherwise, it could be a moderate source of error. Generally, making a break through in theories is difficult, although the main constraints have been identified and much progress hasbeen made. With a focuson these aspects, developing new instruments and calculation and validation methods, further exploring existing data, and finally improving the accuracy and stability of indirect LAI measurement are endeavors worth pursuing.
Key words
leaf area index , indirect measurement , clumping effect , scale effect , leaf angle distribution , woody components , slope effect
1 引言
叶面积指数(LAI)表示单位地表面积上叶片面积的多少, 是植被结构的核心参数, 也是全球变化研究的关键参数之一(Gcos, 2011)。一方面, LAI主导植被光合和呼吸作用, 进而影响全球物质循环尤其是碳循环(Chapin等, 2006;Clark等, 2008;Fan等, 2014;Tian等, 2015)。另一方面, 植被冠层对光线的拦截直接影响地气系统辐射乃至全球能量平衡(Bonan等, 1993;Jin和Zhang, 2002)。
LAI地面测量对农林调查、生态监测与评估至关重要, 也是遥感真实性检验的基础(Gower等, 1999;Bréda, 2003;张仁华等, 2010;刘洋等, 2013)。测量方法可分为直接与间接两大类。直接测量法主要通过测量仪器(如LI-3000、LI-3100、AM-3000、CI-202等)手工量测部分叶片的表面积, 根据定义计算叶面积指数。完全的手工直接测量仅适用于小样方低矮植被, 在森林冠层中, 通常只直接测量较小数量的叶片样本, 建立叶面积与叶片重量(称重法)或枝干结构参数(异速生长法)的经验关系, 通过尺度上推来计算植株乃至样方的LAI(Daughtry, 1990;Gower等, 1999)。在样本具有足够代表性的情况下, 直接测量法的结果较为准确, 因此常被用来验证间接测量法。但直接测量法费时费力, 劳动强度较大, 且通常对植被具有破坏性, 仅适用于小范围测量, 难以满足大尺度、高时间分辨率的测量需求(Jonckheere等, 2004;Weiss等, 2004)。间接测量法主要通过其他参数来反推叶面积指数, 代表性的有光学测量法和斜点样方法。Jonckheere等人(2004)认为异速生长法为接触式的间接测量方法, 但由于需要直接测量部分叶片表面积和枝干结构参数建立统计关系, 本文将其归为直接测量方法。光学测量法利用光学仪器获取的冠层间隙率/透过率来反演LAI, 快速高效, 目前被广泛应用于LAI地面测量和遥感验证中(Chen, 1996;邹杰和阎广建, 2010;Qu等, 2014)。相比之下, 斜点样方法需要利用探针进行大量采样, 具有较大的工作量(Jonckheere等, 2004)。因此目前光学测量法已成为间接测量方法的代表。
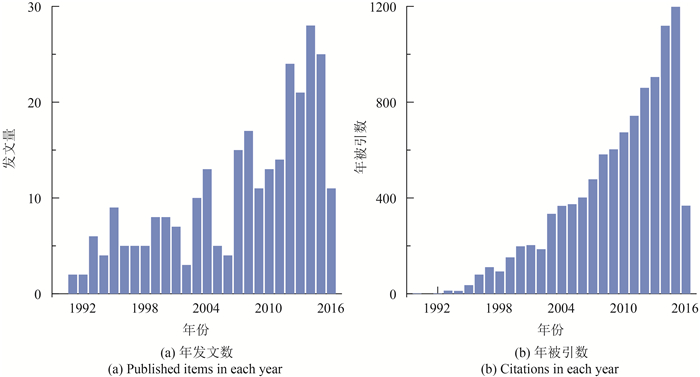
LAI间接测量方法自20世纪90年代起发展十分迅速, 应用极其广泛。在WoS(Web of Science)数据库中, 以叶面积指数、测量、间接或光学仪器为关键词进行组合检索, 结果显示其发文数总体呈上升趋势, 近年来约在25篇/年(图 1(a)), 主要分布在农林、遥感、地学等相关期刊中(表 1)。相比发文数, 被引数则高出一到两个数量级, 2015年被引接近1200次, 约是当年发文数的48倍(图 1(b))。引用数与发文数的巨大差异表明, LAI间接测量方法已经在科学界获得了广泛认可, 并在更大领域和更多行业得到了大量应用和关注。同时也说明有关LAI间接测量理论及方法的研究相对难度大, 成果产出少。
表 1 发表 4篇或以上叶面积指数间接测量相关文章的国际期刊(数据来源为WoS,检索时间为2016年6月20日)
Table 1 International journals that have published more than four papers related to indirect leaf area index measurement(The search was conducted on June 20, 2016 using WoS)
| 期刊 | 发文数/篇 |
| Agricultural and Forest Meteorology | 38 |
| Journal of Applied Remote Sensing | 28 |
| Forest Ecology snd Management | 11 |
| Remote Sensing of Environment | 8 |
| Canadian Journal of Forest Research | 7 |
| Remote Sensing | 7 |
| Tree Physiology | 6 |
| Field Crops Research | 6 |
| International Journal of Remote Sensing | 5 |
| Agronomy Journal | 4 |
| Global Change Biology | 4 |
LAI间接测量方法自20世纪90年代起开始, 通过国际合作被引入中国(Lang和项月琴, 1989;王锦地等, 1995), 2000年后有一定发展。在中国科学引文数据库CSCD(Chinese Science Citation Database)中, 以叶面积指数、测量、间接或光学仪器为关键词进行组合检索, 近10年来发文数约在5篇每年(图 2(a)), 主要分布在生态、农业、遥感、地学、林学等相关期刊中(表 2)。被引数同样高于发文数, 2014年最多, 被引57次(图 2(b)), 但是相对比例远低于国外。
表 2 发表 2篇或以上叶面积指数间接测量相关文章的国内期刊(数据来源为CSCD,检索时间为2016年6月20日)
Table 2 Domestic journals that have published more than two papers related to indirect leaf area index measurement(The search was conducted on June 20, 2016 using CSCD)
| 期刊 | 发文数/篇 |
| 《农业工程学报》 | 7 |
| 《生态学报》 | 6 |
| 《遥感学报》 | 5 |
| 《生态学杂志》 | 4 |
| 《地球信息科学学报》 | 4 |
| 《应用生态学报》 | 3 |
| 《东北林业大学学报》 | 2 |
| 《中国科学(D辑)地球科学》 | 2 |
| 《遥感技术与应用》 | 2 |
LAI间接测量方法的理论基础为Beer定律, 最初用来描述光线在均匀介质中的衰减规律, 应用到实际植被冠层时面临着聚集效应、木质组分和叶倾角分布等多种因素的影响, 可能给LAI估算带来30%-70%的误差(Chen和Cihlar, 1995b;Cutini等, 1998;Weiss等, 2004;胡容海和阎广建, 2012)。在过去几十年里, 国内外学者针对这些问题, 对模型进行了不断的验证、分析和改进, 从多个方面提高了LAI地面间接测量的精度(Gower等, 1999;Bréda, 2003;Weiss等, 2004)。近年来, 一些新的方法、仪器、平台被开发并应用于LAI间接测量。本文从理论、方法、仪器、影响因素几方面系统总结其发展、现状及最新进展, 并对未来的发展趋势进行展望。
2 基本概念和理论背景
2.1 LAI定义
LAI是一个无量纲的量, 最初被定义为单位地表面积上光合组织的单面面积(Watson, 1947)。该定义适用于叶片平坦且两面面积相等的阔叶, 但对于弯曲、卷起的叶片或者针叶不明确。针对这一问题, 学术界基于各自的应用需求, 提出了多种新的定义, 代表性的有单位地表最大投影叶面积(Myneni等, 1997)、总拦截面积的一半(Gower等, 1999;Bréda, 2003;张仁华等, 2010)、总面积的一半(Chen等, 1991;Fassnacht等, 1994)。其中拦截或投影面积相关的定义主要考虑物理意义, 如辐射拦截;总面积相关的定义则主要考虑生物意义, 如气体交换。这些定义在叶片平坦的阔叶林中没有区别, 但在其他情况下存在一定差异。目前, 被广泛采用的定义是单位地表面积上, 叶片总面积的一半(Chen等, 1991;Fassnacht等, 1994;Jonckheere等, 2004)。
由于仪器信号及算法原理的制约, 实际地面间接测量受到木质组分及聚集效应影响, 其结果往往与LAI的定义不完全一致, 但却往往被混用。为了明确区分这些不同的结果, 学术界提出了更多的相关定义。一是大部分间接测量仪器通过单一可见光波段测量间隙率, 无法区分叶片与枝干等非光合作用组分, 对于树林冠层, 其结果实际上是包含了叶面积指数和木质面积指数(WAI)的总面积指数(PAI)(Neumann等, 1989)。二是其理论基础Beer定律假设叶片随机分布, 在3维结构高度复杂、叶片聚集分布的现实森林场景中, 直接应用Beer定律会低估LAI, 其结果被定义为有效叶面积指数(LAIe)或有效总面积指数(PAIe)。此外, 一些定义更加明确划分了绿色叶片与光合作用器官。绿叶面积指数(GLAI)明确了只包括绿色的叶片。绿面积指数(GAI)则包含绿色的叶片和其他植物器官, 以考虑一些植株的绿色茎干同样参与光合作用的情况。由于大多数用户最为关心植被的光合作用, LAI(GLAI、GAI)的定义被广泛接受并应用于MODIS、GEOLAND和GLOBCARBON等全球遥感产品的生产中(Myneni等, 2002;Plummer等, 2006;Baret等, 2013)。
在大多数研究中, LAI、GLAI和GAI基本等价。但PAIe、LAIe通常都与LAI差异较大, 树林冠层中PAI与LAI也差异较大。然而, 受限于商业化LAI测量仪器的局限性, 这几个定义常被混合使用, PAIe、LAIe和PAI常被用作LAI, 可能带来较大误差, 需要引起注意。
2.2 Beer定律及间隙率模型
LAI地面间接测量的理论基础为Beer定律。Beer定律最初用于描述均匀介质中光辐射随传播路径长度的衰减规律(Ross, 1981), 后被用于描述均匀植被冠层对光线的截获, 建立了LAI与间隙率之间的关系(De wit, 1965;Monteith, 1965;Monsi和Saeki, 2005), 即
| $ P\left(\theta \right)= {{\rm{e}}^{ - G\left(\theta \right)\cdot {\rm{LAI}}/\cos \left(\theta \right)}} $ | (1) |
式中, P(θ)为θ天顶角方向的透过率或间隙率, LAI表示叶面积指数, G(θ)为叶片在θ天顶角方向的投影比例。
式(1)阐述的是某一天顶角下冠层间隙率公式, 在实际测量中, 往往测量多天顶角下的冠层间隙率数据, LAI可表达为天顶角方向的积分(Miller, 1967;Chen和Black, 1991), 即
| $ {\rm{LAI}} = 2\int_0^{{\rm{\pi }}/2} { - \ln \left[ {P\left(\theta \right)} \right] \cdot \cos \left(\theta \right)\cdot \sin \left(\theta \right){\rm{d}}\theta } $ | (2) |
式中, P(θ)为θ天顶角下所有方位角方向间隙率的平均值。G函数被假设为0.5, 不随角度变化。
离散天顶角下总的LAI可以表示为各天顶角计算结果的加权和, 即
| $ {\rm{LAI}} = \sum\limits_{i = 1}^n {{\rm{LAI}}\left({{\theta _i}} \right){W_i}} $ | (3) |
式中, n代表离散天顶角的数量, LAI(θi)为θi天顶角下的LAI值, Wi为各天顶角权重, 为sin(θi)dθi的归一化。
科研人员基于上述理论研制了多种基于间隙率的LAI间接测量仪器, 并在小麦、玉米等低矮作物的测量中取得了较好的效果(Ross, 1981;Welles和cohen, 1996;刘刚等, 2008)。但很快发现, 将这些间接测量仪器应用到3维结构高度复杂的森林冠层测量时, 将带来30%-70%的低估(Chen和Cihlar, 1995b;Weiss等, 2004;邹杰和阎广建, 2010;刘志理等, 2014;尹高飞等, 2014)。造成误差的根源是植被冠层并非均匀介质, 叶片偏离随机分布假设。式(1)的经典形式考虑了叶倾角分布的影响, 但未考虑聚集效应、非光合作用组分等因素的影响。
2.3 叶倾角分布与G函数
叶片投影G函数定义为单位叶面积在垂直于观测方向的平面上的投影系数(Ross, 1981), 表示为
| $ G(\theta,\;\phi)= \frac{1}{{2{\rm{\pi }}}}\int_0^{2{\rm{\pi }}} {{\rm{d}}{\phi _l}} \int_0^{{\rm{\pi }}/2} {g({\theta _l},\;{\phi _l})} \left| {{r_l} \cdot r} \right|{\rm{d}}{\theta _l} $ | (4) |
式中, g(θl, φl)表示叶片角度分布函数, 定义为叶片角度的概率密度函数, 满足
| $ {r_l} \cdot r = \cos(\theta)\cos({\theta _l})+ \sin(\theta)\sin({\theta _l})\cos({\phi _l} - \phi) $ | (5) |
由于大多数冠层叶片在方位角方向近似均匀分布, 通常仅需要测量叶片倾角(天顶角)来描述叶片角度分布(Ross, 1981)。叶倾角分布函数g(θl)定义为叶片倾角的概率密度函数, 满足
| $ G(\theta)= \int_0^{{\rm{\pi }}/2} {A(\theta,{\theta _l})} g({\theta _l}){\rm{d}}{\theta _l} $ | (6) |
| $ A(\theta,{\theta _l})= \left\{ \begin{array}{l} \cos \theta \cos {\theta _l}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\quad |\cot \theta \cot {\theta _l}| > 1\\ \cos \theta \cos {\theta _l}[1 +(2/{\rm{\pi }})(\tan \Psi - \Psi)]|\cot \theta \cot {\theta _l}| \le 1 \end{array} \right. $ | (7) |
式中,
针对叶倾角分布, 目前学者们已经提出了许多方法来对其进行刻画, 主要包括De Wit的三角分布函数(De Wit, 1965;Pisek等, 2011), 双参数的Beta分布函数, 单参数的椭圆分布函数(Campbell, 1990)和双参数的椭圆分布函数(Kuusk, 1995)。
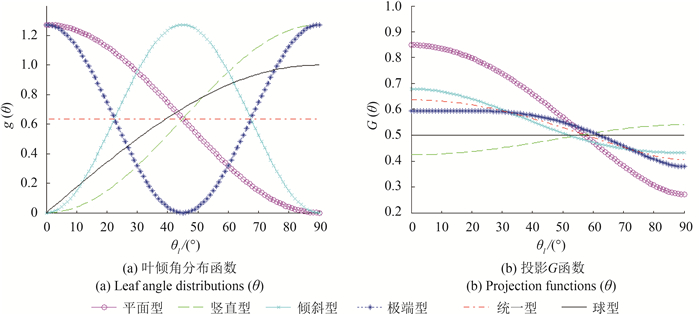
De Wit(1965)针对叶片倾角分布不同的倾向, 提出了6种典型的叶倾角分布, 即平面型(planophile)、竖直型(erectophile)、倾斜型(plagiophile)、极端型(extremophile)、统一型(uniform)和球型(spherical), 如图 3所示, 函数形式及平均叶倾角见表 3。
表 3 典型叶倾角分布g函数
Table 3 Typical leaf angle distribution g(θl)
| 分布类型 | g(θl) | θ/(°) |
| 平面型 |
|
26.76 |
| 竖直型 | 63.24 | |
| 倾斜型 |
|
45.00 |
| 极端型 |
|
45.00 |
| 统一型 |
|
45.00 |
| 球型 |
|
57.30 |
2.4 聚集指数及束簇面积比
在实际测量中, 很多学者认识到了LAI地面间接测量存在低估问题, 并定义了聚集指数的概念来定量衡量冠层非随机分布的程度, 以修正LAI的估算结果。Nilson(1971)系统地总结了太阳直射光在植被冠层内的传播规律, 得到了间隙率与LAI之间关系的统一表达式, 并基于马尔可夫模型引入了一个修正参数λ0来描述冠层的聚集情况, 被沿用至今, 即
| $ P\left(\theta \right)= {{\rm{e}}^{ - {\lambda _0} \cdot G\left(\theta \right)\cdot {\rm{LAI}}/\cos \theta }} $ | (8) |
式中, λ0=1代表随机分布, λ0 > 1代表规则分布, λ0 < 1代表聚集分布。该参数也被Chen等人(1991)称为聚集指数Ω, 即
| $ \Omega = {\rm{LA}}{{\rm{I}}_{\rm{e}}}/{\rm{LAI}} $ | (9) |
式中, LAIe称为有效叶面积指数, 定义为聚集指数Ω和LAI的乘积(Black等, 1991;Chen和Black, 1991)。聚集指数计算公式如下
| $ \mathit{\Omega} = {\mathit{\Omega} _{\rm{E}}}/{\gamma _{\rm{E}}} $ | (10) |
式中, ΩE为光学仪器可以探测到的聚集指数, 表征叶片或针叶簇尺度的聚集;γE用于将针叶簇面积转换成针叶面积, 称为束簇面积比, 通过手工测量得到(Chen和Cihlar, 1995a)。对于阔叶林γE=1, Ω=ΩE。
为了定量地计算聚集指数ΩE以消除LAI的低估现象, 科学家提出了多种方法, 其中代表性的包括有限长度平均法(Lang和Xiang, 1986)、间隙大小分布法(Chen和Cihlar, 1995a;Leblanc, 2002)、间隙大小分布与有限长度平均联合算法(Leblanc等, 2005b)、以及路径长度分布法(Hu等, 2014), 详见第3节。
2.5 木质面积比
在森林中测量时, 由于传统光学仪器无法区分叶片和枝干, 研究人员逐渐认识到光学间接测量方法测得的实际是包含了木质组分影响的PAI(Neumann等, 1989;Whitford等, 1995;Chen, 1996)。而森林冠层的光合作用及物质能量交换仅与叶片有关, 故需要剔除木质组分的影响。
Chen(1996)引入了参数α, 表示植物木质面积指数占总面积指数的比例, 则LAI和PAI之间的关系可以表述为
| $ {\rm{LAI}} =(1 - \alpha)\cdot {\rm{PAI}} $ | (11) |
式中, PAI可以通过植被冠层的总间隙率计算得到, 均匀分布情况下, 由式(12)就可方便计算, 即
| $ {\rm{PAI}} = \frac{{ - \ln \left[ {P\left(\theta \right)} \right] \cdot \cos \theta }}{{G\left(\theta \right)\cdot {\rm{ }}\mathit{\Omega} }} $ | (12) |
木质组分测量主要可分为3类:(1)手工直接测量, 根据测量的枝干维度, 通过经验关系来计算木质面积(Lang等, 1991;Deblonde等, 1994;Liu等, 2015), 较为费时费力, 不便操作。(2)落叶期测量, 由于传统仪器无法区分木质组分, 早期木质面积比的测量通过落叶期和生长期两个时期的测量实现(Cutini等, 1998;Barclay等, 2000;苏宏新等, 2012)。但该方法不适用于常绿林, 并且没有考虑两个时期枝干的变化以及枝叶的相互遮挡(Zou等, 2009)。(3)近红外光学测量, 利用近红外波段木质组分低反射的特征, 将枝干与树叶分开(Kucharik等, 1998a;阎广建等, 2008;Zou等, 2009;Liu等, 2011;Hu等, 2016)。该方法在测量效率和准确性上都有较大优势。但由于目前商业化间接测量仪器都不具备近红外波段, 在实际测量中应用较少。
3 间接测量方法
3.1 有限长度平均法
Lang和Xiang(1986)基于统计学的原理提出了有限长度平均法。该方法认为在有限长度的子样线上对冠层间隙率求对数平均可以获取较准确的叶面积指数, 消除样线之间的聚集。
有限长度平均法认为子样线内部叶片随机分布, 满足Beer定律假设, 其叶面积指数为
| $ {\rm{LA}}{{\rm{I}}_{LX}}(\theta)= - \frac{{\overline {\ln(P(\theta))} .\cos(\theta)}}{{G\left(\theta \right)}} $ | (13) |
式中, P(θ)为θ天顶角下各有限长度子样线上的间隙率,
根据聚集指数的定义, 有限长度平均法的聚集指数可表示为
| $ {\mathit{\Omega} _{LX}}\left(\theta \right)= \frac{{\ln \left[ {\overline {P\left(\theta \right)} } \right]}}{{\overline {\ln \left[ {P\left(\theta \right)} \right]} }} $ | (14) |
式中,
有限长度平均法存在两个前提假设:(1)在有限长度的子样线内, 叶片随机分布;(2)有限长度子样线内存在不同大小的间隙, 即间隙率不为0。对0求对数是无意义的, 所以当子样线不包含任何间隙时需要进行修正。目前主要有两种修正方法(Walter等, 2003), 一种忽略无间隙的子样线, 而实际上, 无间隙的子样线区域中叶片很密集、LAI很高, 直接删除必然会带来LAI的低估。另一种应用广泛的方法是为无间隙的样线分配一个间隙(Leblanc等, 2005b), 即
| $ {\rm{LA}}{{\rm{I}}_{\max }}(\theta)= - \ln(\frac{{0.5}}{{{N_{{\rm{pixel}}}}}})\cdot \cos(\theta)/G\left(\theta \right) $ | (15) |
式中, Npixel是子样线上像素的数目, LAI上限为10(Pisek等, 2011)。
由于有限长度平均法操作简单, 并能在一定程度上消除聚集效应, 目前已被广泛应用于农作物的叶面积指数测量中(Lang等, 1991;Ryu等, 2012;Liu等, 2013)。
3.2 间隙大小分布法
间隙大小分布法最初由Chen和Cihlar(1995a)提出, 用来量化森林冠层聚集效应, 随后Leblanc(2002)用一个归一化因子将计算得到的LAI扩展到最初的样线上。该方法根据模拟的随机分布状态下的间隙累计分布函数和实测值进行对比, 定量衡量了冠层内部的聚集效应, 在很大程度上消除了树冠间的大间隙。
利用光学仪器设备, 可以获取间隙累计分布函数Fm(λ, θ), 该函数定义为间隙大小大于λ的所有间隙占样线的比例。同时, 对于叶片均匀随机分布的冠层, 可以从数学上推导出其间隙大小累计分布函数为
| $ \begin{array}{l} {F_r}\left({\lambda,\theta } \right)= \\ \left({1 + {L_p}\left(\theta \right)\frac{\lambda }{{{W_p}\left(\theta \right)}}} \right)\exp \left[ { - {L_p}\left(\theta \right)\left({1 + {L_p}\left(\theta \right)\frac{\lambda }{{{W_p}\left(\theta \right)}}} \right)} \right] \end{array} $ | (16) |
式中, Fr(λ, θ)表示随机冠层中的间隙累计分布函数, Lp表示投影叶面积指数, 初值为-ln[Fm(0, θ)], Wp是叶片的平均投影宽度。
考虑到大间隙是LAI低估的主要原因, 实测数据中出现概率超过Fr(λ, θ)的间隙被认为是非随机的大间隙, 将被移除。在每轮的间隙移除操作后, 将生成一个新的间隙累计分布函数Fmr(λ, θ), 并通过新的-ln[Fmr(0, θ)]重新计算Lp。通过多轮迭代后, 最后的实测间隙累计分布函数Fmr(λ, θ)将接近随机状态下的间隙累计分布函数。迭代停止的条件是, Lp的增长小于0.01, 或者Fmr(λ, θ)的一部分落到Fr(λ, θ)下面(Chen和Cihlar, 1995a)。
由于Fmr(λ, θ)代表的是移除大间隙后的样线, 样线的长度发生了变化。Leblanc(2002)用一个归一化因子将计算得到的LAI扩展到最初的样线上, 即
| $ LA{I_{cc}}\left(\theta \right)= - \frac{{\ln [{F_{{\rm{mr}}}}(0,\theta)] \cdot \cos(\theta)}}{{G\left(\theta \right)}} \cdot \frac{{1 - {F_{\rm{m}}}(0,\theta)}}{{1 - {F_{{\rm{mr}}}}(0,\theta)}} $ | (17) |
聚集指数相应表示为
| $ {\Omega _{CC}} = \frac{{\ln \left[ {{F_{\rm{m}}}\left({0,\theta } \right)} \right]}}{{\ln \left[ {{F_{{\rm{mr}}}}\left({0,\theta } \right)} \right]}} \cdot \frac{{1 - {F_{{\rm{mr}}}}\left({0,\theta } \right)}}{{1 - {F_{\rm{m}}}\left({0,\theta } \right)}} $ | (18) |
由于间隙大小分布法可以有效地消除树冠间大间隙引起的低估, 目前已被广泛的用于森林LAI的测量中(Chen等, 1997;Chen, 2001 Leblanc和周宇宇等, 2003)。
3.3 间隙大小分布及有限长度平均联合法
为了解决有限长度平均法中子样线内部的聚集问题, 以及弥补间隙大小分布法对树冠内光线穿越路径不均一考虑不足的问题, LeblancLeblanc等人(2005a)提出了一种间隙大小分布及有限长度平均联合法。在有限长度子样线内部采用间隙大小分布法去除大间隙, 使得每条子样线的累计间隙率趋于随机分布。最终的LAI可以表示为
| $ {\rm{LA}}{{\rm{I}}_{{\rm{CLX}}}}\left(\theta \right)= \frac{{\sum\limits_{k = 1}^n {\ln \left[ {{P_k}\left(\theta \right)} \right]/{\Omega _{CCk}}\left(\theta \right)\cdot \cos(\theta)} }}{{n \cdot G\left(\theta \right)}} $ | (19) |
式中, n代表子样线数量, ΩCCk(θ)是间隙大小分布法计算的第k条子样线的聚集指数, Pk(θ)是第k条子样线的间隙率。
实验结果表明, 该方法在某些场景中可以较好地补偿LAI低估误差, 但其精度对子样线长度的选择很敏感, 并且目前还没有科学合理的办法可以提供子样线长度的先验知识(Macfarlane等, 2007;Pisek等, 2011)。
3.4 路径长度分布法
为了修正树冠形状导致的冠层尺度聚集, HuHu等人(2014)在Beer定律原型基础上引入了路径长度分布, 提出了路径长度分布法。该方法不仅可以计算冠层间的聚集效应, 而且可以刻画和修正由于冠层形状导致的冠层内部间隙率的不均匀分布。
LAI可以表示为路径长度的积分形式, 即
| $ LA{I_{{\rm{PATH}}}}\left(\theta \right)= \int_0^1 {(FAVD \cdot {l_{\max }})\cdot \cos \theta } \cdot lr \cdot {p_{lr}}\left({lr} \right){\rm{d}}\left({lr} \right) $ | (20) |
式中, FAVD表示叶面积体密度, lmax表示观测方向路径长度的最大值, lr为各路径长度除以lmax归一化后的相对路径长度, plr(lr)为路径长度分布函数。相对路径长度分布可根据光学仪器实测的间隙剖面求得, 对于LAI-2000((LI-COR Inc., Nebraska, USA))等仅提供总间隙的仪器, 也可以使用椭圆树冠截面的假设(Hu等, 2014)。中间变量FAVD·lmax则通过式(21)利用优化算法反演求得, 即
| $ \overline {P\left(\theta \right)} = \int_0^1 {{{\rm{e}}^{ - G\left(\theta \right)\cdot(FAVD \cdot {l_{\max }})\cdot lr}} \cdot {p_{lr}}\left({lr} \right){\rm{d}}\left({lr} \right)} $ | (21) |
式中,
实地测量及计算机模拟验证表明, 路径长度分布法可以较好地刻画和消除树冠内部路径长度不一致导致的聚集, 在各种场景中误差都在10%以内, 有效提高了目前地面LAI间接测量的精度(Hu等, 2014, 2016;Zeng等, 2015;Yan等, 2016)。叶面积指数间接测量代表性方法如表 4所示。
表 4 叶面积指数间接测量代表性方法
Table 4 Representative methods for indirect LAI measurement
| LAI间接测量算法 | 主要公式 |
| Beer定律 |
|
| 有限长度平均法(Lang和Xiang, 1986) |
|
| 间隙大小分布法(Chen和Cihlar, 1995a;Leblanc, 2002) |
|
| 间隙大小分布法及有限长度平均联合法(Leblanc等, 2005b) |
|
| 路径长度分布法(Hu等, 2014) |
|
| 注: Fm(0,θ)和F mr(0,θ)分别为去除大间隙前和去除大间隙后的总间隙率,Pk(θ)和ΩCCk(θ)分别为第k个子样线的间隙率和间隙大小分布法聚集指数,plr(lr)为路径长度分布函数。 | |
4 间接测量仪器
为了满足LAI间接测量的需求, 大量形式各异的仪器被研制出来。这些仪器均基于LAI间接测量相关理论, 测量物理量为冠层透过率或间隙率。但在数据获取、测量方式、处理方法、适用范围上都有一些差异(表 5)。
表 5 叶面积指数间接测量代表性仪器
Table 5 Representative instruments for indirect LAI measurement
| 仪器 | 测量光谱范围/nm | 测量值 | 传感器 | 间隙分布信息 | 参考值 | 实时结果 | 天顶角/(°) | 方位角 |
| LAI-2000 | 320-490 | 散射光 | 鱼眼光学传感器 | 无 | 需要 | 是 | 0-75 | 全方位 |
| TRAC | PAR(400-700) | 直射光 | 3个光量子传感器 | 有 | 需要 | 否 | 太阳入射方向 | 太阳入射方向 |
| AccuPAR | PAR(400-700) | 直射光和散射光 | 80个光量子传感器 | 有 | 需要 | 是 | - | - |
| SunScan | PAR(400-700) | 直射光和散射光 | 64个光量子传感器 | 有 | 需要 | 是 | - | - |
| LAInet | - | 直射光和散射光 | 9个光量子传感器 | 有 | 需要 | 否 | - | - |
| DEMON | 430 | 直射光 | 1个光量子传感器 | 无 | 需要 | 是 | 太阳入射方向 | 太阳入射方向 |
| 鱼眼相机 | 全波段(视相机而定) | 半球相片 | CCD相机 | 有 | 不需要 | 否 | 0-90 | 全方位 |
| MVI | 可见光(400-620)和 近红外(720-950) |
半球相片 | CCD相机 | 有 | 不需要 | 否 | 0-90 | 全方位 |
| MCI | 可见光(390-690)和 近红外(760-900、850-900) |
半球相片 | CCD相机 | 有 | 不需要 | 否 | 0-90 | 全方位 |
| 地基LiDAR | 视仪器而定 | 距离/回波强度 | 激光器 | 有 | 不需要 | 否 | 视仪器而定 | 全方位 |
| 机载LiDAR | 视仪器而定 | 距离/回波强度 | 激光器 | 有 | 不需要 | 否 | 视仪器而定 | 垂直航向 |
| 星载LiDAR | 视仪器而定 | 距离/回波强度 | 激光器 | 无 | 不需要 | 否 | 视仪器而定 | 垂直轨道 |
4.1 LAI-2000
LAI-2000是一款通过测量天空漫射光下冠层的透射估算LAI的便携式仪器。它配备有148°视场角的鱼眼镜头并在5个中心环(7°、23°、38°、53°、68°)感应测量, 波谱响应范围为320-490 nm, 可以尽量减少冠层散射光的影响, 有效地区分冠层和天空组分(LI-COR, 1992)。
外业测量时, 操作人员通过将LAI-2000置于冠层上下分别测量, 得到的各同心环感应器在冠层上下测量值之比即为冠层对5个方向的散射光透过率, 然后基于间隙率模型可以通过仪器内部软件反演得到冠层叶面积指数, 其计算公式简化为
| $ LAI = - 2\sum\limits_{i = 1}^5 {\ln(P({\theta _i}))\cos({\theta _i})w({\theta _i})} $ | (22) |
式中,
LAI-2000计算的理论模型基于4个基本的假设(Jonckheere等, 2004):(1)叶片是光学黑体, 可以吸收所有接收到的光;(2)叶片空间随机分布;(3)叶片方位角随机分布;(4)冠层组分实际大小远小于同心环投影面积。
LAI-2000携带方便, 测量时实时计算和显示测量结果, 是目前应用较为广泛的LAI间接测量仪器, 但其结果仅为LAIe。实际应用中发现, LAI-2000在连续、均质的冠层测量时具有较好的结果(Levy和Jarvis, 1999;吴彤等, 2006), 而在不连续和异质的冠层中测量时, 往往会出现不同程度的偏差(Dufrêne和Bréda, 1995)。LAI-2000测量天空漫射光下冠层的透射, 受太阳直射光影响明显, 最佳观测时间为阴天及黎明前、黄昏后天气条件(Chen等, 1997)。同时由于LAI-2000需要冠层顶部或附近空旷区域辐射参考值来提高LAI测量的精度, 在一些林分密度大的林区及复杂地形区往往难以实现(邹杰和阎广建, 2010)。
4.2 TRAC
TRAC(Tracing Radiation and Architecture of Canopies)通过测量透过冠层的太阳直射光来获取间隙率, 可以计算LAI和聚集指数。主要由3个量子传感器(400-700 nm)、信号放大器、模数转换器、微处理器、存储器等组成。3个量子传感器均测量光合有效辐射(PAR), 其中朝上的两个传感器分别测量直射透射PAR和散射PAR, 朝下的量子传感器测量地面反射PAR(Leblanc等, 2005a)。
外业测量时, 操作人员手持仪器沿样线横切方向以约0.3 m/s匀速前进, 从测量的高密度PAR数据可以得到冠层间隙率和冠层间隙大小分布。样线选择时需要综合考虑树的高度和太阳高度角, 森林中推荐的样线长度为100-300 m(Leblanc等, 2005a)。
TRAC测量的是太阳入射方向的数据, 通常需要多个角度、数次测量来保证足够的样方代表性, 建议在0-60°天顶角等间隔观测(Leblanc等, 2005a)。如需测量不同角度的聚集指数信息, 则需要在不同太阳角度的多个时间段多次观测(Pisek等, 2011;Ryu等, 2012)。由于TRAC样线需垂直于太阳, 样线位置在一天之间会随着太阳方位的变化而移动。同时TRAC的间隙率计算依赖太阳直射光, 需要在稳定的晴朗无云条件下进行测量。
4.3 线阵光量子探测器
AccuPAR和SunScan探测器和LAInet无线传感器网络(屈永华等, 2012)均由线性规则排列的传感器组成, 其中AccuPAR探测器由80个独立的光电二极管组成, SunScan探测器由64个独立的光电二极管组成, 光电二极管波谱感应范围在400-700 nm, 可用于接收直/散射PAR。LAInet则由一套包含3个光量子传感器的冠层上部节点和多套包含9个光量子传感器的无线网络组成, 通过全天候自动观测来得到较为可靠的结果(Qu等, 2014)。
AccuPAR、SunScan和LAInet探测器测量原理均基于Beer定律, 结果均为LAIe。AccuPAR和SunScan使用Campbell(1986)的叶倾角椭圆分布函数, 其计算公式为
| $ {\rm{LAI}} = - \ln(P(\theta))/K(x,\theta) $ | (23) |
式中, θ表示太阳天顶角, K(x, θ)表示消光系数, 即
| $ K(x,\theta)= \frac{{\sqrt {{x^2} + {{\tan }^2}(\theta)} }}{{x + 1.702{{(x + 1.12)}^{ - 0.708}}}} $ | (24) |
式中, x为椭圆纵轴与横轴的比值, 取值范围为0.1-10, 当x取1时, 表示球型分布(Campbell, 1986;刘镕源等, 2011)。
辐射测量最主要的问题是测量值之间存在较大的差异, 因此需要使用仪器进行多次测量来得到可靠的结果。AccuPAR和SunScan可以同时测量太阳直射和散射, 在晴天和阴天条件下均可以进行测量, 但由于太阳半影效应的影响, 两者均不适用于针叶林地测量(Jonckheere等, 2004)。
4.4 DEMON
DEMON是一款通过直接测量太阳直射辐射在冠层顶部和底部的强度从而计算LAI的仪器(Welles, 1990;Jonckheere等, 2004)。DEMON传感器配备了过滤器来仅接受430 nm波段附近的太阳直射光, 以减少冠层散射光的影响(Welles, 1990)。同时DEMON配备处理器, 用来计算和存储大量横断面的间隙率对数平均数据(Jonckheere等, 2004)。
外业测量时, 操作人员通过手持仪器平行于太阳光线入射方向以恒定速度行进。DEMON仅测量太阳入射天顶角方向的间隙率, 通常为了提高LAI的测量精度, 需要在不同的太阳高度角下多次测量, 并且根据冠层的空间异质性程度, 测量样线长度一般设为300 m或更长。
DEMON测量太阳的直射辐射, 因此需要在天空晴朗无云时进行测量。同时DEMON在测量时需要覆盖不同的太阳高度角, 所以在一天内往往要进行多次测量, 非常耗时。由于LAI-2000单次测量可得5个天顶角方向间隙率, 因此LAI测量时DEMON往往被LAI-2000取代(Jonckheere等, 2004)。
4.5 成像设备
通过摄影的方式获取冠层图像, 进一步分类获取间隙率的设备和方法也得到了广泛应用, 包括半球光学摄影和多光谱摄影两类。HemiView是数字半球摄影(DHP)类设备的代表, 由180°鱼眼镜头、高分辨率数码相机以及自稳定平台组成, 可以水平向上或向下拍摄。通过HemiView配套软件分析半球相片, 可提取间隙率、间隙分布和LAI。常见的鱼眼镜头投影方式有极化投影和立体等角投影(Frazer等, 1997)。传统半球摄影法在可见光波段成像, 其冠层影像可以分为天空和冠层组分两大类, 和前面提到的设备一样, 不能进一步区分叶子和木质组分。
多光谱摄影方法是一种利用多光谱相机对冠层成像, 利用植被冠层在可见光波段强吸收和在近红外波段高反射、高透射的特点, 对冠层各组分进行详细分类, 从中分析计算LAI的方法。相对于传统的半球摄影方法, 多光谱摄影方法可以将所拍摄的影像细分类为天空、树枝、树干等组分, 可以用于木质面积比与总面积指数、冠层基本组分及木质组分聚集指数的测量, 从而提高地面LAI测量精度(Zou等, 2009)。
多光谱摄影方法应用于LAI测量最早见于Kucharik等人(1997)研制的多波段植被成像仪(MVI)。该仪器配备有16位CCD多光谱相机, 可以快速拍摄冠层可见光波段(400-620 nm)及近红外波段(720-950 nm)影像。Kucharik等人(1998a)对比了该仪器测量LAI和直接测量LAI的结果, 发现两者差异在5%以内, 验证了该设备的有效性。阎广建等人(2008)研制了一套低成本、便携、多用途的多光谱冠层成像仪(MCI)。MCI集成了两个可见光相机及一个近红外相机, 设计了可在任意天顶角及方位角方向旋转的云台, 可以获取冠层任意天顶角和方位角的立体影像, 能够方便计算多角度聚集指数和木质面积比(Zou等, 2009)。MCI在中国黑河和承德等大型遥感实验中被用于植被结构参数测量, 提高了植被结构参数的测量精度(Fu等, 2011;Tian等, 2011)。
MVI和MCI在晴朗和阴天条件下均可测量, 在实际拍摄时, 应避免在强光和阴暗条件下进行, 以免影响影像分类的精度, 进而影响LAI测量的精度。
采用摄影类的设备和方法时, 相机的曝光设置、相机类型、影像分辨率等观测条件均会不同程度地影响LAI测量的精度。
4.6 激光雷达
激光雷达(LiDAR)是一种使用激光作为光源, 对目标进行探测、测距, 得到高精度3维点云的主动遥感仪器(Peduzzi等, 2012), 目前已经广泛地应用于树高、胸径、叶面积指数和叶倾角分布等植被结构参数的获取(Lim等, 2003;骆社周等, 2013;Culvenor等, 2014;Zhao等, 2015;苏伟等, 2016)。LiDAR一般由激光测距系统、激光扫描系统、位置与姿态测量系统组成, 依据回波对于LAI的计算, 其理论基础依然是Beer定律, 只不过利用激光脉冲的穿透率进行计算(Zheng和moskal, 2009)。根据搭载平台的不同LiDAR可以分为地基、机载和星载激光雷达。
较传统LAI光学测量仪器, 地基LiDAR可以获取树木冠层精确的3维结构信息, 且可以避免云的影响(Zheng和Moskal, 2009), 受天气等外界因素影响小, 外业测量结果容易控制。在传统的离散回波数据外, 波形数据也开始被用于LAI的估算中, 并逐渐成为一个新的研究热点(Zhao等, 2011;Yao等, 2011)。尽管地基LiDAR在森林叶面积指数测量中已广泛应用, 但由于其获取冠层上部点云能力较弱, 仍需要通过与其他仪器或者人工测量结合来提高叶面积指数测量的精度(Hilker等, 2010)。此外, LAI测量结果也受到天顶角分层和高度分层的影响(Zhu等, 2011), 而单木LAI的测量更为复杂(Zhu和Zhang, 2011)。在实际测量中, 考虑到树木的遮挡, 为了获取完整的样方点云, 获得更全面的采样代表性, 往往需要一个样区内布设多个站点(Zhang等, 2016)。
相比之下, 机载LiDAR没有太多的遮挡问题, 通过GPS和惯导实时获取飞行过程中的姿态参数, 结合激光测距信息计算目标点的3维坐标。机载LiDAR光斑较大, 通常部分打在植被上, 部分打在地面上, 难以得到准确的间隙率信息, 多用激光穿透指数(LPI)来代替(Morsdorf等, 2006)。通过LAI与LPI、点云比例或其他中间参数构建的半经验回归方程来实现LAI反演(Lim等, 2003;Solberg等, 2009;Zhao和Popescu, 2009;Alonzo等, 2015)。研究表明, 基于LPI和Beer定律的半经验半物理模型效果最佳, 既具有一定的物理意义, 同时减轻了光学影像反演中的饱和问题(Lefsky等, 2002;Richardson等, 2009;崔要奎等, 2011)。机载LiDAR可以快速获取一定范围内森林植被结构信息, 但受限于较大的光斑及较稀疏的激光点云密度, 在计算间隙率及LAI中存在不确定性, 往往还需依赖地面参考值。
星载LiDAR可以对地球表面进行连续的观测(Zwally等, 2002;Abshire等, 2005;Sirota等, 2005)。以搭载于ICESat卫星上的地球科学激光测高系统(GLAS)为代表, 发射大光斑激光脉冲, 接收来自地面和植被冠层的混合信息, 通过分析回波波形数据得到植被冠层的3维结构, 近年来已被用于LAI反演(Luo等, 2013;Tang等, 2014;Zhang等, 2014;骆社周等, 2015)。与地基LiDAR和机载LiDAR相比, 星载LiDAR可面向全球快速测量, 但是由于光斑大, 在反演LAI时仍然面临不小的挑战(Popescu等, 2011;Rosette等, 2013), 需要大型地面实验来验证其结果的有效性。
5 影响测量精度的主要因素
LAI间接测量的精度受到聚集/尺度效应、叶倾角分布、木质组分、地形效应等多种因素的影响, 这些因素在影响方式、影响大小以及受重视程度上都存在较大差异。从影响方式上, 聚集导致LAI低估, 木质组分导致LAI高估, 叶倾角分布球型分布假设则可能给LAI带来较大不确定性, 地形效应的影响相对较小, 但是坡度较大时, 也将带来不小误差。聚集效应在理论研究和实际测量中受到广泛重视, 其修正理论及方法不断发展并在实际测量中得到应用。木质组分虽然在学术界得到了关注, 也有相应的修正方法和设备样机, 但尚没有商业化的设备, 在实际测量中考虑较少。叶倾角分布对LAI间接测量的影响在理论上很直观, 但由于测量不便, 在实际测量中往往使用球型分布假设。
5.1 聚集/尺度效应
聚集效应是影响LAI间接测量精度的最主要因素之一, 也是在研究和实际应用中受到最多关注的因素。大量研究表明, 直接应用Beer定律可能给LAI间接测量带来30%-70%的低估(Chen和Cihlar, 1995b;Weiss等, 2004;胡容海和阎广建, 2012)。
叶片的聚集效应导致叶片分布偏离随机, 产生大间隙, 主要体现为树冠间的大间隙, 在树冠内或更小尺度上, 叶片分布又趋于随机。因此很多聚集指数算法的原理是在更小的尺度上应用Beer定律, 如将树冠内与树冠间分离计算的间隙大小分布法(Chen和Cihlar, 1995a;Leblanc, 2002), 对间隙率数据分段计算再求平均的有限长度平均法(Lang和Xiang, 1986), 以及在间隙率数据微元尺度上应用Beer定律再积分的路径长度分布法(Hu等, 2014)。
聚集效应引起的LAI低估程度, 与叶片偏离非随机分布的程度直接相关。基于间隙率的LAI间接测量方法, 早期应用于叶片接近均匀分布的小麦、玉米等低矮冠层, LAI误差总体在15%以内(Welles和Norman, 1991)。而当应用于3维结构复杂、叶片聚集严重的森林冠层时, 很快发现间接测量结果与直接测量相比低估约30%-70%(Chen等, 1991;Gower和Norman, 1991;Lang等, 1991)。后续一些聚集指数算法被开发出来(Lang和Xiang, 1986;Chen和Cihlar, 1995b;Leblanc, 2002), 更多的聚集指数计算结果及地面验证也再次印证了这种低估(Fassnacht等, 1994;Stenberg, 1996;Cutini等, 1998;Gonsamo和Pellikka, 2009;Zou等, 2015)。此外, 在针叶林中, 由于光学仪器只能探测到针叶簇尺度的信息, 还需借助直接采样测得的束簇面积比来修正实际叶面积指数(Stenberg, 1996;Chen等, 1997)。聚集效应引起的低估不仅存在于树林中, 在垄行结构明显的小麦等连续低矮植被中, 也可能存在11%的低估(Baret等, 2010)。而在植株较小、未封垄时, 这种低估更为严重, 可能产生约20%-60%的低估(Demarez等, 2008)。
聚集效应对LAI间接测量的影响较大, 从理论研究和实际测量上都得到了较多的重视。有限长度平均法, 作为修正聚集效应的早期尝试, 很大程度上修正了叶片非随机分布引起的低估(Lang和Xiang, 1986;Lang等, 1991;Smith, 1993)。尽管该方法无法处理子样线内聚集, 且子样线无间隙时可能给结果带来不确定性, 但由于其简单易用的特点, 目前仍被广泛应用(Macfarlane等, 2007;Baret等, 2010;Ryu等, 2012)。间隙大小分布法可以有效消除树冠间大间隙的影响, 主要用在对TRAC测量数据的处理中, 目前广泛用于森林LAI测量(Leblanc, 2002;Gonsamo和Pellikka, 2009;Pisek等, 2011)。由于间隙大小分布法未能完全修正树冠内聚集, 科学家尝试联合有限长度平均法与间隙大小分布法, 取得了一定的效果(Leblanc等, 2005b;Gonsamo和Pellikka, 2009;Leblanc和Fournier, 2014), 然而该方法对子样线长度选择较为敏感(Pisek等, 2011)。针对上述方法或无法处理样线内聚集, 或无法完全消除树冠内聚集的问题, Hu等人(2014)开发了路径长度分布法, 抓住了聚集效应引起的主要矛盾, 有效消除了树冠内路径长度不一致引起的最高25%的聚集(Zeng等, 2015;Hu等, 2016;Yan等, 2016)。
叶片聚集导致光线穿越植被的路径长度发生变化, 引起间隙率的空间不均一性, 当把指数形式的间隙率方程应用到一定的区域时就产生了尺度效应, 对于同样的间隙分布, 不同的分割计算尺度将导致不同的结果, 因此利用Beer定律计算LAI所面临的聚集问题, 实质上是一个尺度问题(Yan等, 2016)。不同的聚集效应消除方法在应用到不同的计算尺度时差异明显。有限长度平均法、有限长度平均与间隙大小分布联合法、路径长度分布法, 这3种方法本身包含子样线分割操作, 因此在不同尺度下适应性较好, 在各种场景中20 m以上尺度上即趋于稳定。间隙大小分布法和直接利用Beer定律计算有效LAI, 则对尺度较为敏感, 计算尺度越大, 统计样本越多, 间隙大小分布越稳定。一般垄行植被, 计算结果在大于一个周期后趋于稳定, 而森林场景则需要100 m以上的尺度才趋于稳定(Yan等, 2016)。对总样线应用聚集指数算法优于对分样线应用算法后求平均。在实际测量中, 受限于样方边界, 一个样地通常通过多次测量来覆盖, 尤其是当样方较小时, 建议将多次测量数据组合后, 再选择应用相应算法。
总体上说, 聚集/尺度问题对叶面积指数测量影响较大, 应注意区分有效叶面积指数和真实叶面积指数。针对聚集/尺度问题的理论和方法研究有较大发展, 然而假设依然存在, 有必要进一步验证现有方法, 关注树冠内部的聚集和测量的尺度问题。
5.2 叶倾角分布
叶倾角分布在LAI间接测量理论发展的初期就受到关注, 理论较成熟, 然而实际测量难度大, 计算中往往采用球型分布假设, 将G函数取值0.5, 这个取值在57.3°左右是合适的, 但在接近0°和90°时误差较大。
早在20世纪五六十年代, 学术界就认识到叶倾角对透过率及叶面积指数测量的影响, 并在建模时引入了G函数表征叶片投影对光线的影响, 被沿用至今(Monsi和Saeki, 1953;Watson, 1958;Monteith, 1965;Monsi和Saeki, 2005;Wang等, 2007;Pisek等, 2011)。依据De wit(1965)所提出的典型的叶倾角分布计算, G函数取值在0.27-0.84之间高度可变(图 3), 而实际的间接测量中通常采用球型分布(G≡0.5)来简化计算(Lang, 1991;Chen和Black, 1992;Baret等, 2010;Leblanc和Fournier, 2014)。这种简化主要是由于叶倾角分布的直接测量十分困难, 而观测天顶角在57.3°附近时, 各种叶倾角分布的G函数都接近0.5(Wilson, 1960;Baret等, 2010)。从表 3可以发现, 球型分布的平均叶倾角刚好是57.3°。但是这种近似需要小心使用, 尤其观测角度接近0°或90°时, 0.5的取值可能给LAI估算带来高达68%的误差。
叶倾角测量方法主要可以分为3大类:(1)直接接触式测量, 利用带铅锤的量角器、电子量角器、或者数字化仪测量一定数量叶片的倾角, 并进行统计(Lang, 1973;Hutchison等, 1986;Thanisawanyangkura等, 1997)。直接测量的结果较为准确, 但测量高大树木时较为困难, 有研究通过液压升降机来进行测量(Hutchison等, 1986)。(2)在假设叶片随机分布的情况下, 利用Beer定律中光线透过率与路径长度、叶倾角分布的关系来求解(Welles和Norman, 1991;Kucharik等, 1998b)。然而叶片随机假设实际上很难满足, 叶倾角分布和聚集指数本身都是需要反演的内容, 是一个欠定问题, 反演精度难以保证。(3)通过水平相机在多方位角摄影, 人工选取与相机方向完全垂直的叶片(在相片中体现为一条线), 并量取角度(Ryu等, 2010;Pisek等, 2011;Zou等, 2014)。该方法尽管很大程度上依赖人工操作, 效率上并没有太大提升, 但很大程度上提高了高大树木测量的可行性, 并被应用到无人机平台上(Mcneil等, 2016)。
总体来说, 目前尚没有完全自动化的叶倾角分布测量方法, 在叶面积指数测量中应重视叶倾角分布的影响。在57.3°天顶角附近进行测量是无奈的选择, 如要利用其他角度测量数据, 尤其是0°天顶角的数据时, 必须考虑叶倾角分布对G函数的影响。
5.3 木质组分
在树林冠层中, 木质组分是影响叶面积指数测量的一大因素, 可以带来约7%-40%的高估(Bréda, 2003)。尽管学术界认识到了其重要性, 但受限于现有商业化测量仪器只有一个可见光波段的限制, 难以有效消除木质组分的影响, 在实际测量中考虑较少。
传统间接测量仪器无法区分非光合作用组分(主要为木质组分)与光合作用组分(主要为叶片)。木质组分导致的LAI高估是显而易见的, 已被公认为森林叶面积指数测量的一个重要误差来源(Whitford等, 1995;Chen等, 1997)。不同树种木质组分影响也有较大差异, 直接测量显示木质组分在红松树林中占8%-12%, 而在北美短叶松林中占10%-33%(Deblonde等, 1994)。GowerGower等人(1999)给出了一些树种木质面积比的经验数值, 但是木质面积比随着天顶角和方位角的变化而变化(Zou等, 2009), 不同时期也有不同的木质面积比, 因此光学间接测量方法利用经验数值会带来误差。
总体而言, 木质组分对LAI间接测量高估的机理较为清晰, 基于近红外摄影的方法较为便捷高效, 但尚未进行商业化推广应用。木质面积比随树种、时间、角度变化而变化, 间接测量中有必要考虑这种变化对结果的影响。
5.4 地形效应
由于大部分地面间接测量开展于平坦地区, 地形效应相对研究较少。近10余年来, 随着遥感在复杂地形区的深入开展, 叶面积指数间接测量的地形效应也逐渐凸显出来。在坡度大于30°的情况下, 地形效应是叶面积指数间接测量的一个中等误差源。
地形效应的直观体现是, 间隙率在上坡方向增大, 在下坡方向减小, 其原因主要为路径长度的差异(Walter和Torquebiau, 2000)。然而地形效应修正是否有必要, 依然存在不同的看法(Duursma等, 2003;Schleppi等, 2007)。现有研究的共识是, 在坡度小于30°的情况下, 地形效应对叶面积指数间接测量影响较小, 可以忽略;而当坡度大于30°时, 地形效应, 将成为一个中等误差源(Duursma等, 2003;España等, 2008;Gonsamo和Pellikka, 2008)。
在坡地上的测量主要分为两大类, 水平测量(平行于水平面)或倾斜测量(平行于坡面)。研究表明, 在小于30°的坡面上, 水平测量与倾斜测量差异较小, 上坡方向的高估与下坡方向的低估基本抵消(España等, 2008;Gonsamo和Pellikka, 2008)。当坡度大于30°时, 水平测量结果将低于倾斜测量结果(Schleppi等, 2007;Gonsamo和Pellikka, 2008)。当倾斜测量时, 各种方法对结果的处理也有所区别, 一种方法是仪器平行于坡面测量, 结果除以坡度余弦(Montes等, 2007;Schleppi等, 2007;Gonsamo和Pellikka, 2008), 另一种是通过修正不同天顶角的路径长度, 将坡度间隙率转换到平地间隙率(España等, 2008)。多方法比较验证表明, España等人(2008)和Gonsamo和Pellikka(2008)的方法在叶倾角球型分布的假设下, 效果最好。而当叶倾角分布不满足球型分布假设时, España等人(2008)的方法更好一些。
总体而言, 地形效应研究较少, 但随着未来复杂地形研究的深入, 对地形效应的关注将成为不可避免的趋势。
5.5 多因素相互作用
目前, 对上述因素的研究和验证通常是在简化其他影响因素的情况下独立进行的, 而在高度复杂的自然界中, 上述因素客观上耦合在一起, 这给建模和验证都带来几何倍数的难度提升。
一是如何对单个因素进行准确的实地验证。比如, 在森林场景中, 聚集效应、木质组分通常耦合在一起, 如果不考虑木质组分, 用直接测量的叶面积指数来验证间接测量的总面积指数, 显然将低估聚集效应;如果不考虑聚集效应, 用直接测量的叶面积指数来验证有效叶面积指数, 显然将造成木质组分的低估。最后的结果是多因素综合影响的结果, 很难分离出它们各自的影响(Hu等, 2016)。
二是多因素并存时, 如何对各个因素进行修正。如木质组分也存在聚集效应, 且与叶片相互遮挡, 木质组分和聚集效应存在相互影响。多因素的相互作用, 广泛存在于地面验证和实际计算中, 但研究相对较少。在多因素并存的场景中, 其验证有必要系统考虑。计算机模拟技术可以模拟结构可控、叶面积精确已知的3维真实场景, 为LAI间接测量方法的验证提供了新的可能(Hu等, 2014)。
6 结论与展望
LAI间接测量方法高效便捷, 被广泛应用于地面叶面积测量与遥感验证中。本文从理论、方法、仪器、影响因素等方面, 系统总结了LAI间接测量方法的发展、现状及最新进展。
LAI间接测量方法起源于Beer定律, 应用到地面LAI测量中主要受到聚集/尺度效应、叶倾角分布、木质组分、地形效应的影响。经过数十年的发展, LAI间接测量在数据获取方式、理论和方法改进、真实性检验方面都有了较大进展。但其测量精度仍然受到数个关键因素的制约, 有待进一步提高。
从数据获取方式看, 早期主要通过光量子传感器(DEMON)或鱼眼光学传感器(LAI-2000)测量总的透过率, 随后发展了相机(DHP、MVI、MCI等)或移动的光量子传感器(TRAC)获取间隙分布信息并修正聚集效应带来的LAI低估, 并采用红外摄影技术(MVI, MCI)区分木质组分并修正木质组分带来的LAI高估。近年来, 可获得3维信息的LiDAR被更多地用于间隙分布及叶面积体密度的获取研究中, 然而目前LiDAR所提供的3维信息尚未得到充分的利用, 3维点云信息通常被投影为2维间隙率使用, 进一步挖掘利用其3维信息是未来的重要研究方向。
从理论和计算方法看, 近年来研究主要集中在聚集效应、叶倾角分布、非光合作用组分、地形效应4个方面:(1)聚集效应研究较为深入, 目前有多种聚集指数算法, 已经广泛应用于实际地面测量中。树冠内部的不均匀性、测量尺度的影响仍然值得进一步研究。(2)叶倾角分布理论研究较为完善, 但实际测量不便, 常使用球型分布假设(G=0.5), 该假设在57.3°天顶角左右是适用的, 在其他情况需要慎重使用, 未来有必要研究叶倾角分布快速自动测量方法。(3)木质面积比的问题已经被学术界认识到, 利用近红外摄影装置可以有效消除木质组分影响, 但由于现有商业化设备无法区分叶片与木质组分, 在实际测量中往往被忽视或使用经验值代替, 未来有必要在实际测量中应用最新的测量方法与仪器, 并重视LAI与PAI的差异。(4)地形效应逐渐被重视, 研究表明, 坡度小于30°时地形效应可以忽略, 坡度大于30°时则不可忽略, 目前已有相关修正方法, 未来仍需考虑其他多因素共存的影响。
从真实性检验看, 间接测量方法的验证很大程度上依赖于直接测量, 费时费力, 不确定性大, 总体上较为困难。LAI定义差异、多影响因素的耦合以及地面测量的困难与代表性, 都给验证带来了较多不确定性。近年来发展的计算机真实场景模拟技术, 可以直接从几何上提供准确的LAI真值与间隙率数据, 为解决验证问题提供了可能。未来仍需致力于提高模拟场景的真实性, 进一步逼近现实植被冠层。
总体来看, LAI间接测量在理论和方法上的突破较难, 但是影响测量精度提高的因素比较明确, 围绕这些因素, 研制更多新型测量仪器, 发展新的计算和验证方法, 进一步挖掘已有测量数据的信息, 提高野外测量精度及稳定性, 是未来的研究方向。
参考文献(References)
-
Abshire J B, Sun X L, Riris H, Sirota J M, McGarry J F, Palm S, Yi D H, Liiva P.2005.Geoscience Laser Altimeter System (GLAS) on the ICESat Mission:on-orbit measurement performance. Geophysical Research Letters, 32 : L21S02 DOI: 10.1029/2005gl024028.
-
Alonzo M, Bookhagen B, McFadden J P, Sun A, Roberts D A.2015.Mapping urban forest leaf area index with airborne lidar using penetration metrics and allometry. Remote Sensing of Environment, 162 : 141–153. DOI: 10.1016/j.rse.2015.02.025.
-
Barclay H J, Trofymow J A , Leach R I.2000.Assessing bias from boles in calculating leaf area index in immature Douglas-fir with the Li-Cor canopy analyzer. Agricultural and Forest Meteorology, 100 (2/3): 255–260. DOI: 10.1016/s0168-1923(99)00091-x.
-
Baret F, de Solan B, Lopez-Lozano R, Ma K , Weiss M.2010.GAIestimates of row crops from downward looking digital photos taken perpendicular to rows at 57. 5°zenith angle:theoretical considerations based on 3D architecture models and application to wheat crops.Agricultural and Forest Meteorology, 150 (1): 1393–1401. DOI: 10.1016/j.agrformet.2010.04.011.
-
Baret F, Weiss M, Lacaze R, Camacho F, Makhmara H, Pacholcyzk P , Smets B.2013.Geov1:LAI and FAPAR essential climate variables and FCOVER global time series capitalizing over existing products. Part1:principles of development and production.Remote Sensing of Environment, 137 : 299–309. DOI: 10.1016/j.rse.2012.12.027.
-
Black T A, Chen J M, Lee X H , Sagar R M.1991.Characteristics of shortwave and longwave irradiances under a Douglas-fir forest stand. Canadian Journal of Forest Research, 21 (7): 1020–1028. DOI: 10.1139/x91-140.
-
Bonan G B, Pollard D , Thompson S L.1993.Influence of subgrid-scale heterogeneity in leaf area index, stomatal resistance, and soil moisture on grid-scale land-atmosphere interactions. Journal of Climate, 6 (10): 1882–1897. DOI: 10.1175/1520-0442(1993)006.
-
Bréda N J J.2003.Ground-based measurements of leaf area index:a review of methods, instruments and current controversies. Journal of Experimental Botany, 54 (392): 2403–2417. DOI: 10.1093/jxb/erg263.
-
Campbell G S.1986.Extinction coefficients for radiation in plant canopies calculated using an ellipsoidal inclination angle distribution. Agricultural and Forest Meteorology, 36 (4): 317–321. DOI: 10.1016/0168-1923(86)90010-9.
-
Campbell G S.1990.Derivation of an angle density function for canopies with ellipsoidal leaf angle distributions. Agricultural and Forest Meteorology, 49 (3): 173–176. DOI: 10.1016/0168-1923(90)90030-A.
-
Chapin F S Ⅲ, Woodwell G M, Randerson J T, Rastetter E B, Lovett G M, Baldocchi D D, Clark D A, Harmon M E, Schimel D S, Valentini R, Wirth C, Aber J D, Cole J J, Goulden M L, Harden J W, Heimann M, Howarth R W, Matson P A, McGuire A D, Melillo J M, Mooney H A, Neff J C, Houghton R A, Pace M L, Ryan M G, Running S W, Sala O E, Schlesinger W H , Schulze E D.2006.Reconciling carbon-cycle concepts, terminology, and methods. Ecosystems, 9 (7): 1041–1050. DOI: 10.1007/s10021-005-0105-7.
-
Chen J M.1996.Optically-based methods for measuring seasonal variation of leaf area index in boreal conifer stands. Agricultural and Forest Meteorology, 80 (2/4): 135–163. DOI: 10.1016/0168-1923(95)02291-0.
-
Chen J M , Black T A.1991.Measuring leaf-area index of plant canopies with branch architecture. Agricultural and Forest Meteorology, 57 (1/3): 1–12. DOI: 10.1016/0168-1923(91)90074-Z.
-
Chen J M , Black T A.1992.Defining leaf area index for non-flat leaves. Plant, Cell & Environment, 15 (4): 421–429. DOI: 10.1111/j.1365-3040.1992.tb00992.x.
-
Chen J M, Black T A , Adams R S.1991.Evaluation of hemispherical photography for determining plant area index and geometry of a forest stand. Agricultural and Forest Meteorology, 56 (1/2): 129–143. DOI: 10.1016/0168-1923(91)90108-3.
-
Chen J M, Cihlar J.1995a.Plant canopy gap-size analysis theory for improving optical measurements of leaf-area index. Applied Optics, 34 (27): 6211–6222. DOI: 10.1364/AO.34.006211.
-
Chen J M, Cihlar J.1995b.Quantifying the effect of canopy architecture on optical measurements of leaf area index using two gap size analysis methods. IEEE Transactions on Geoscience and Remote Sensing, 33 (3): 777–787. DOI: 10.1109/36.387593.
-
Chen J M, Rich P M, Gower S T, Norman J M, Plummer S.1997.Leaf area index of boreal forests:theory, techniques, and measurements. Journal of Geophysical Research, 102 (D24): 29429–29443. DOI: 10.1029/97jd01107.
-
Clark D B, Olivas P C, Oberbauer S F, Clark D A, Ryan M G.2008.First direct landscape-scale measurement of tropical rain forest leaf area index, a key driver of global primary productivity. Ecology Letters, 11 (2): 163–172. DOI: 10.1111/j.1461-0248.2007.01134.x.
-
Cui Y K, Zhao K G, Fan W J, Xu X R.2011.Retrieving crop fractional cover and lai based on airborne lidar data. Journal of Remote Sensing, 15 (6): 1282–1294. DOI: 10.11834/jrs.20110395. ( 崔要奎, 赵开广, 范闻捷, 徐希孺. 2011. 机载lidar数据的农作物覆盖度及LAI反演. 遥感学报, 15 (6): 1282–1294. DOI: 10.11834/jrs.20110395. )
-
Culvenor D S, Newnham G J, Mellor A, Sims N C , Haywood A.2014.Automated in-situ laser scanner for monitoring forest leaf area index. Sensors, 14 (8): 14994–15008. DOI: 10.3390/s140814994.
-
Cutini A, Matteucci G , Mugnozza G S.1998.Estimation of leaf area index with the Li-Cor LAI 2000 in deciduous forests. Forest Ecology and Management, 105 (1/3): 55–65. DOI: 10.1016/s0378-1127(97)00269-7.
-
Daughtry C S T.1990.Direct measurements of canopy structure. Remote Sensing Reviews, 5 (1): 45–60. DOI: 10.1080/02757259009532121.
-
De Wit C T.1965.Photosynthesis of Leaf Canopies.Wageningen:Centre for Agricultural Publications and Documentation http://edepot.wur.nl/187115
-
Deblonde G, Penner M, Royer A.1994.Measuring leaf-area index with the Li-Cor LAI-2000 in pine stands. Ecology, 75 (5): 1507–1511. DOI: 10.2307/1937474.
-
Demarez V, Duthoit S, Baret F, Weiss M , Dedieu G.2008.Estimation of leaf area and clumping indexes of crops with hemispherical photographs. Agricultural and Forest Meteorology, 148 (4): 644–655. DOI: 10.1016/j.agrformet.2007.11.015.
-
Dufrêne E , Bréda N.1995.Estimation of deciduous forest leafarea index using direct and indirect methods. Oecologia, 104 (2): 156–162. DOI: 10.1007/Bf00328580.
-
Duursma R A, Marshall J D, Robinson A P.2003.Leaf area index inferred from solar beam transmission in mixed conifer forests on complex terrain. Agricultural and Forest Meteorology, 118 (3/4): 221–236. DOI: 10.1016/S0168-1923(03)00109-6.
-
Fan W J, Liu Y, Xu X R, Chen G X , Zhang B T.2014.A new fapar analytical model based on the law of energy conservation:a case study in China. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7 (9): 3945–3955. DOI: 10.1109/Jstars.2014.2325673.
-
Fassnacht K S, Gower S T, Norman J M , McMurtric R E.1994.A comparison of optical and direct methods for estimating foliage surface area index in forests. Agricultural and Forest Meteorology, 71 (1/2): 183–207. DOI: 10.1016/0168-1923(94)90107-4.
-
Frazer G W, Lertzman K P and Trofymow J A.1997.A Method for Estimating Canopy Openness, Effective Leaf Area Index, and Photosynthetically Active Photon Flux Density Using Hemispherical Photography and Computerized Image Analysis Techniques.Pacific Forestry Centre Victoria, BC http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.477.483&rep=rep1&type=pdf
-
Fu Z, Wang J D, Song J L, Zhou H M, Pang Y , Chen B S.2011.Estimation of forest canopy leaf area index using modis, misr, and lidar observations. Journal of Applied Remote Sensing, 5 : 053530 DOI: 10.1117/1.3594171.
-
GCOS.2011.Systematic Observation Requirements for Satellite-Based Products for Climate.Supplemental Details to the Satellite-Based Component of the Implementation Plan for the Global Observing System for Climate in Support of the UNFCCC-2011 Update.World Meteorological Organization.[2016-06-20].http://www.wmo.int/pages/prog/gcos/Publications/gcos-154.pdf http://www.wmo.int/pages/prog/gcos/Publications/gcos-154.pdf
-
Gonsamo A , Pellikka P.2008.Methodology comparison for slope correction in canopy leaf area index estimation using hemispherical photography. Forest Ecology and Management, 256 (4): 749–759. DOI: 10.1016/j.foreco.2008.05.032.
-
Gonsamo A , Pellikka P.2009.The computation of foliage clumping index using hemispherical photography. Agricultural and Forest Meteorology, 149 (10): 1781–1787. DOI: 10.1016/j.agrformet.2009.06.001.
-
Gower S T, Kucharik C J , Norman J M.1999.Direct and indirect estimation of leaf area index, fAPAR, and net primary production of terrestrial ecosystems. Remote Sensing of Environment, 70 (1): 29–51. DOI: 10.1016/s0034-4257(99)00056-5.
-
Gower S T , Norman J M.1991.Rapid estimation of leafarea index in conifer and broad-leaf plantations. Ecology, 72 (5): 1896–1900. DOI: 10.2307/1940988.
-
Hilker T, van Leeuwen M, Coops N C, Wulder M A, Newnham G J, Jupp D L B , Culvenor D S.2010.Comparing canopy metrics derived from terrestrial and airborne laser scanning in a Douglas-fir dominated forest stand. Trees-Structure and Function, 24 (5): 819–832. DOI: 10.1007/s00468-010-0452-7.
-
Hu R H, Luo J H, Yan G J, Zou J and Mu X H.2016.Indirect measurement of forest leaf area index using path length distribution model and multispectral canopy imager.IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, in press[DOI:10.1109/JSTARS.2016.2569469]
-
Hu R H , Yan G J.2012.Indirect measurement of forest LAI to deal with the underestimation problem based on beer-lambert law. Journal of Geo-Information Science, 14 (3): 366–375. DOI: 10.3724/sp.j.1047.2012.00366. ( 胡容海, 阎广建. 2012. 对Beer-Lambert定律间接测量森林LAI的误差低估分析. 地球信息科学学报, 14 (3): 366–375. DOI: 10.3724/sp.j.1047.2012.00366. )
-
Hu R H, Yan G J, Mu X H , Luo J H.2014.Indirect measurement of leaf area index on the basis of path length distribution. Remote Sensing of Environment, 155 : 239–247. DOI: 10.1016/j.rse.2014.08.032.
-
Hutchison B A, Matt D R, Mcmillen R T, Gross L J, Tajchman S J , Norman J M.1986.The architecture of a deciduous forest canopy in eastern Tennessee, U. S.A..Journal of Ecology, 74 (3): 635–646. DOI: 10.2307/2260387.
-
Jin M , Zhang D L.2002.Observed variations of leaf area index and its relationship with surface temperatures during warm seasons. Meteorology and Atmospheric Physics, 80 (1/4): 117–129. DOI: 10.1007/s007030200019.
-
Jonckheere I, Fleck S, Nackaerts K, Muys B, Coppin P, Weiss M , Baret F.2004.Review of methods for in situ leaf area index determination:Part I. Theories, sensors and hemispherical photography.Agricultural and Forest Meteorology, 121 (1/2): 19–35. DOI: 10.1016/j.agrformet.2003.08.027.
-
Kucharik C J, Norman J M , Gower S T.1998a.Measurements of branch area and adjusting leaf area index indirect measurements. Agricultural and Forest Meteorology, 91 (1/2): 69–88. DOI: 10.1016/s0168-1923(98)00064-1.
-
Kucharik C J, Norman J M , Gower S T.1998b.Measurements of leaf orientation, light distribution and sunlit leaf area in a boreal aspen forest. Agricultural and Forest Meteorology, 91 (1/2): 127–148. DOI: 10.1016/S0168-1923(98)00058-6.
-
Kucharik C J, Norman J M, Murdock L M , Gower S T.1997.Characterizing canopy nonrandomness with a multiband vegetation imager (MVI). Journal of Geophysical Research, 102 (D24): 29455–29473. DOI: 10.1029/97jd01175.
-
Kuusk A.1995.A fast, invertible canopy reflectance model. Remote Sensing of Environment, 51 (3): 342–350. DOI: 10.1016/0034-4257(94)00059-V.
-
Lang A R G.1973.Leaf orientation of a cotton plant. Agricultural Meteorology, 11 : 37–51. DOI: 10.1016/0002-1571(73)90049-6.
-
Lang A R G.1991.Application of some of Cauchy's theorems to estimation of surfaceareas of leaves, needles and branches of plants, and light transmittance. Agricultural and Forest Meteorology, 55 (3/4): 191–212. DOI: 10.1016/0168-1923(91)90062-U.
-
Lang A R G, McMurtrie R E , Benson M L.1991.Validity of surface area indices of Pinus radiata estimated from transmittance of the sun's beam. Agricultural and Forest Meteorology, 57 (1/3): 157–170. DOI: 10.1016/0168-1923(91)90084-4.
-
Lang A R G , Xiang Y Q.1986.Estimation of leaf area index from transmission of direct sunlight in discontinuous canopies. Agricultural and Forest Meteorology, 37 (3): 229–243. DOI: 10.1016/0168-1923(86)90033-x.
-
Lang A R G, 项月琴.1989.从太阳直接辐射透过率推算非连续冠层的叶面积指数//农业生态环境研究.北京:气象出版社:266-279
-
Leblanc S G.2002.Correction to the plant canopy gap-size analysis theory used by the tracing radiation and architecture of canopies instrument. Applied Optics, 41 (36): 7667–7670. DOI: 10.1364/AO.41.007667.
-
Leblanc S G , Chen J M.2001.A practical scheme for correcting multiple scattering effects on optical LAImeasurements. Agricultural and Forest Meteorology, 110 (2): 125–139. DOI: 10.1016/s0168-1923(01)00284-2.
-
Leblanc S G, Chen J M, Fernandes R, Deering D W , Conley A.2005b.Methodology comparison for canopy structure parameters extraction from digital hemispherical photography in boreal forests. Agricultural and Forest Meteorology, 129 (3/4): 187–207. DOI: 10.1016/j.agrformet.2004.09.006.
-
Leblanc S G , Fournier R A.2014.Hemispherical photography simulations with an architectural model to assess retrieval of leaf area index. Agricultural and Forest Meteorology, 194 : 64–76. DOI: 10.1016/j.agrformet.2014.03.016.
-
Leblanc S G, Chen J M and Kwong M.2005a.Tracing Radiation and Architecture of Canopies Manual 2.1.4.1-27
-
Lefsky M A, Cohen W B, Parker G G , Harding D J.2002.LiDAR remote sensing for ecosystem studies. BioScience, 52 (1): 19–30. DOI: 10.1641/0006-3568(2002)052[0019:Lrsfes]2.0.Co;2.
-
Levy P E, Jarvis P G.1999.Direct and indirect measurements of LAI in millet and fallow vegetation in HAPEX-sahel. Agricultural and Forest Meteorology, 97 (3): 199–212. DOI: 10.1016/s0168-1923(98)00092-6.
-
Li-COR.1992.LAI-2000 Plant Canopy Analyzer.Instruction Manual
-
Lim K, Treitz P, Wulder M, St-Onge B , Flood M.2003.LiDARremote sensing of forest structure. Progress in Physical Geography, 27 (1): 88–106. DOI: 10.1191/0309133303pp360ra.
-
Liu G, Xie Y, Gao X F , Duan X W.2008.Application of sunscan canopy analysis system in measuring leaf area index of soybean. Chinese Journal of Ecology, 27 (5): 862–866. ( 刘刚, 谢云, 高晓飞, 段兴武. 2008. Sunscan冠层分析仪在测量大豆叶面积指数中的应用. 生态学杂志, 27 (5): 862–866. )
-
Liu J G, Pattey E , Admiral S.2013.Assessment of in situ crop LAImeasurement using unidirectional view digital photography. Agricultural and Forest Meteorology, 169 : 25–34. DOI: 10.1016/j.agrformet.2012.10.009.
-
Liu R Y, Wang J H, Yang G J, Huang W J, Li W G, Chang H , Li X W.2011.Comparison of ground-based LAImeasuring methods on winter wheat. Transactions of the CSAE, 27 (3): 220–224. DOI: 10.3969/j.issn.1002-6819.2011.03.042. ( 刘镕源, 王纪华, 杨贵军, 黄文江, 李伟国, 常红, 李小文. 2011. 冬小麦叶面积指数地面测量方法的比较. 农业工程学报, 27 (3): 220–224. DOI: 10.3969/j.issn.1002-6819.2011.03.042. )
-
Liu Y K, Hu R H, Mu X H and Yan G J.2011.A method for leaf gap fraction estimation based on multispectral digital images from Multispectral Canopy Imager//Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium.Vancouver, BC:IEEE:3042-3045[DOI:10.1109/IGARSS.2011.6049858]
-
Liu Y, Liu R G, Chen J M, Cheng X , Zheng G.2013.Current status and perspectives of leaf area index retrieval from optical remote sensing data. Journal of Geo-Information Science, 15 (5): 734–743. DOI: 10.3724/SP.J.1047.2013.00734. ( 刘洋, 刘荣高, 陈镜明, 程晓, 郑光. 2013. 叶面积指数遥感反演研究进展与展望. 地球信息科学学报, 15 (5): 734–743. DOI: 10.3724/SP.J.1047.2013.00734. )
-
Liu Z L, Jin G Z, Zhou M.2014.Measuring seasonal dynamics of leaf area index in a mixed conifer-broadleaved forest with direct and indirect methods. Chinese Journal of Plant Ecology, 38 (8): 843–856. DOI: 10.3724/sp.j.1258.2014.00079. ( 刘志理, 金光泽, 周明. 2014. 利用直接法和间接法测定针阔混交林叶面积指数的季节动态. 植物生态学报, 38 (8): 843–856. DOI: 10.3724/sp.j.1258.2014.00079. )
-
Liu Z L, Jin G Z, Zhou M.2015.Evaluation and correction of optically derived leaf area index in different temperate forests. iForest-Biogeosciences and Forestry, 9 : 55–62. DOI: 10.3832/ifor1350-008.
-
Luo S Z, Wang C, Li G C, Xi X H.2013.Retrieving leaf area index using ICESat/GLAs full-waveform data. Remote Sensing Letters, 4 (8): 745–753. DOI: 10.1080/2150704x.2013.790573.
-
Luo S Z, Wang C, Xi X H, Nie S, Xia X B , Wang Y P.2015.Forest leaf area index estimation using combined ICESat/GLAS and optical remote sensing image. Journal of Infrared and Millimeter Waves, 34 (2): 243–249. DOI: 10.11972/j.issn.1001-9014.2015.02.020. ( 骆社周, 王成, 习晓环, 聂胜, 夏少波, 万怡平. 2015. 星载激光雷达GLAS与TM光学遥感联合反演森林叶面积指数. 红外与毫米波学报, 34 (2): 243–249. DOI: 10.11972/j.issn.1001-9014.2015.02.020. )
-
Luo S Z, Wang C, Zhang G B, Xi X H , Li G C.2013.Forest leaf area index (LAI) inversion using airborne LiDAR data. Chinese Journal of Geophysics, 56 (5): 1467–1475. DOI: 10.6038/cjg20130505. ( 骆社周, 王成, 张贵宾, 习晓环, 李贵才. 2013. 机载激光雷达森林叶面积指数反演研究. 地球物理学报, 56 (5): 1467–1475. DOI: 10.6038/cjg20130505. )
-
Macfarlane C, Hoffman M, Eamus D, Kerp N, Higginson S, McMurtrie R , Adams M.2007.Estimation of leaf area index in eucalypt forest using digital photography. Agricultural and Forest Meteorology, 143 (3/4): 176–188. DOI: 10.1016/j.agrformet.2006.10.013.
-
España M L, Baret F , Weiss M.2008.Slope correction for LAI estimation from gap fraction measurements. Agricultural and Forest Meteorology, 148 (10): 1553–1562. DOI: 10.1016/j.agrformet.2008.05.005.
-
McNeil B E, Pisek J, Lepisk H , Flamenco E A.2016.Measuring leaf angle distribution in broadleaf canopies using UAVs. Agricultural and Forest Meteorology, 218-219 : 204–208. DOI: 10.1016/j.agrformet.2015.12.058.
-
Miller J B.1967.A formula for average foliage density. Australian Journal of Botany, 15 (1): 141–144. DOI: 10.1071/BT9670141.
-
Monsi M, Saeki T.1953.Über den Lichtfaktor in den Pflanzengesellschaften und seine Bedeutung für die Stoffproduktion. Japanese Journal of Botany, 14 (1): 22–52.
-
Monsi M , Saeki T.2005.On the factor light in plant communities and its importance for matter production. Annals of Botany, 95 (3): 549–567. DOI: 10.1093/Aob/Mci052.
-
Monteith J L.1965.Light distribution and photosynthesis in field crops. Annals of Botany, 29 (1): 17–37.
-
Montes F, Pita P, Rubio A , Canellas I.2007.Leaf area index estimation in mountain even-aged Pinus silvestris L. stands from hemispherical photographs.Agricultural and Forest Meteorology, 145 (3/4): 215–228. DOI: 10.1016/j.agrformet.2007.04.017.
-
Morsdorf F, Kötz B, Meier E, Itten K I , Allgöwer B.2006.Estimation of LAI and fractional cover from small footprint airborne laser scanning data based on gap fraction. Remote Sensing of Environment, 104 (1): 50–61. DOI: 10.1016/j.rse.2006.04.019.
-
Myneni R B, Hoffman S, Knyazikhin Y, Privette J L, Glassy J, Tian Y, Wang Y, Song X, Zhang Y, Smith G R, Lotsch A, Friedl M, Morisette J T, Votava P, Nemani R R , Running S W.2002.Global products of vegetation leaf area and fraction absorbed par from year one of modis data. Remote Sensing of Environment, 83 (1/2): 214–231. DOI: 10.1016/S0034-4257(02)00074-3.
-
Myneni R B, Ramakrishna R, Nemani R , Running S W.1997.Estimation of global leaf area index and absorbed par using radiative transfer models. IEEE Transactions on Geoscience and Remote Sensing, 35 (6): 1380–1393. DOI: 10.1109/36.649788.
-
Neumann H H, Den Hartog G, Shaw R H.1989.Leaf area measurements based on hemispheric photographs and leaf-litter collection in a deciduous forest during autumn leaf-fall. Agricultural and Forest Meteorology, 45 (3/4): 325–345. DOI: 10.1016/0168-1923(89)90052-x.
-
Nilson T.1971.A theoretical analysis of the frequency of gaps in plant stands. Agricultural Meteorology, 8 : 25–38. DOI: 10.1016/0002-1571(71)90092-6.
-
Peduzzi A, Wynne R H, Fox T R, Nelson R F , Thomas V A.2012.Estimating leaf area index in intensively managed pine plantations using airborne laser scanner data. Forest Ecology and Management, 270 : 54–65. DOI: 10.1016/j.foreco.2011.12.048.
-
Pisek J, Lang M, Nilson T, Korhonen L , Karu H.2011.Comparison of methods for measuring gap size distribution and canopy nonrandomness at Järvselja Rami (Radiation transfer Model Intercomparison) test sites. Agricultural and Forest Meteorology, 151 (3): 365–377. DOI: 10.1016/j.agrformet.2010.11.009.
-
Plummer S, Arino O, Simon M , Steffen W.2006.Establishing a earth observation product service for the terrestrial carbon community:the globcarbon initiative. Mitigation and Adaptation Strategies for Global Change, 11 (1): 97–111. DOI: 10.1007/s11027-006-1012-8.
-
Popescu S C, Zhao K G, Neuenschwander A , Lin C S.2011.Satellite lidar Vs. small footprint airborne lidar:comparing the accuracy of aboveground biomass estimates and forest structure metrics at footprint level.Remote Sensing of Environment, 115 (11): 2786–2797. DOI: 10.1016/j.rse.2011.01.026.
-
Qu Y H, Han W C, Fu L Z, Li C R, Song J L, Zhou H M, Bo Y C, Wang J D.2014.Lainet-a wireless sensor network for coniferous forest leaf area index measurement:design, algorithm and validation. Computers and Electronics in Agriculture, 108 : 200–208. DOI: 10.1016/j.compag.2014.08.003.
-
Qu Y H, Wang J D, Dong J , Jiang F B.2012.Design and experiment of crop structural parameters automatic measurement system. Transactions of the CSAE, 28 (2): 160–165. DOI: 10.3969/j.issn.1002-6819.2012.02.028. ( 屈永华, 王锦地, 董健, 姜富斌. 2012. 农作物冠层结构参数自动测量系统设计与试验. 农业工程学报, 28 (2): 160–165. DOI: 10.3969/j.issn.1002-6819.2012.02.028. )
-
Richardson J J, Moskal L M , Kim S-H.2009.Modeling approaches to estimate effective leaf area index from aerial discrete-return LIDAR. Agricultural and Forest Meteorology, 149 (6/7): 1152–1160. DOI: 10.1016/j.agrformet.2009.02.007.
-
Rosette J, North P R J, Rubio-Gil J, Cook B, Los S, Suarez J, Sun G Q, Ranson J , Blair J B.2013.Evaluating prospects for improved forest parameter retrieval from satellite lidar using a physically-based radiative transfer model. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 6 (1): 45–53. DOI: 10.1109/Jstars.2013.2244199.
-
Ross J K.1981.The Radiation Regime and Architecture of Plant Stands.The Hague:Dr.W.Junk Publishers http://www.springer.com/us/book/9789061936077
-
Ryu Y, Sonnentag O, Nilson T, Vargas R, Kobayashi H, Wenk R, Baldocchi D D.2010.How to quantify tree leaf area index in an open savanna ecosystem:a multi-instrument and multi-model approach. Agricultural and Forest Meteorology, 150 (1): 63–76. DOI: 10.1016/j.agrformet.2009.08.007.
-
Ryu Y, Verfaillie J, Macfarlane C, Kobayashi H, Sonnentag O, Vargas R, Ma S Y , Baldocchi D D.2012.Continuous observation of tree leaf area index at ecosystem scale using upward-pointing digital cameras. Remote Sensing of Environment, 126 (1): 116–125. DOI: 10.1016/j.rse.2012.08.027.
-
Schleppi P, Conedera M, Sedivy I , Thimonier A.2007.Correcting non-linearity and slope effects in the estimation of the leaf area index of forests from hemispherical photographs. Agricultural and Forest Meteorology, 144 (3/4): 236–242. DOI: 10.1016/j.agrformet.2007.02.004.
-
Sirota J M, Bae S, Millar P, Mostofi D, Webb C, Schutz B , Luthcke S.2005.The transmitter pointing determination in the geoscience laser altimeter system. Geophysical Research Letters, 32 : L22S11 DOI: 10.1029/2005gl024005.
-
Smith N J.1993.Estimating leaf area index and light extinction coefficients in stands of Douglas-fir (Pseudotsuga menziesii). Canadian Journal of Forest Research, 23 (2): 317–321. DOI: 10.1139/x93-043.
-
Solberg S, Brunner A, Hanssen K H, Lange H, Næsset E, Rautiainen M , Stenberg P.2009.Mapping LAI in a Norway spruce forest using airborne laser scanning. Remote Sensing of Environment, 113 (11): 2317–2327. DOI: 10.1016/j.rse.2009.06.010.
-
Stenberg P.1996.Correcting LAI-2000 estimates for the clumping of needles in shoots of conifers. Agricultural and Forest Meteorology, 79 (1/2): 1–8. DOI: 10.1016/0168-1923(95)02274-0.
-
Su H X, Bai F , Li GQ.2012.Seasonal dynamics in leaf area index in three typical temperate montane forests of China:a comparison of multi-observation methods. Chinese Journal of Plant Ecology, 36 (3): 231–242. DOI: 10.3724/SP.J.1258.2012.00231. ( 苏宏新, 白帆, 李广起. 2012. 3类典型温带山地森林的叶面积指数的季节动态:多种监测方法比较. 植物生态学报, 36 (3): 231–242. DOI: 10.3724/SP.J.1258.2012.00231. )
-
Su W, Zhan J G, Zhang M Z, Wu D Y , Zhang R.2016.Estimation method of crop leaf area index based on airborne LiDAR data. Transactions of the Chinese Society for Agricultural Machinery, 47 (3): 272–277. DOI: 10.6041/j.issn.1000-1298.2016.03.038. ( 苏伟, 展郡鸽, 张明政, 吴代英, 张蕊. 2016. 基于机载Lidar数据的农作物叶面积指数估算方法研究. 农业机械学报, 47 (3): 272–277. DOI: 10.6041/j.issn.1000-1298.2016.03.038. )
-
Tang H, Dubayah R, Brolly M, Ganguly S , Zhang G.2014.Large-scale retrieval of leaf area index and vertical foliage profile from the spaceborne waveform lidar (Glas/Icesat). Remote Sensing of Environment, 154 : 8–18. DOI: 10.1016/j.rse.2014.08.007.
-
Thanisawanyangkura S, Sinoquet H, Rivet P, Cretenet M , Jallas E.1997.Leaf orientation and sunlit leaf area distribution in cotton. Agricultural and Forest Meteorology, 86 (1/2): 1–15. DOI: 10.1016/S0168-1923(96)02417-3.
-
Tian X, Li Z Y, van der Tol C, Su Z, Li X, He Q S, Bao Y F, Chen E X , Li L H.2011.Estimating zero-plane displacement height and aerodynamic roughness length using synthesis of LiDAR and SPOT-5 data. Remote Sensing of Environment, 115 (9): 2330–2341. DOI: 10.1016/j.rse.2011.04.033.
-
Tian Y, Zheng Y, Zheng C M, Xiao H L, Fan W J, Zou S B, Wu B, Yao Y Y, Zhang A J , Liu J.2015.Exploring scale-dependent ecohydrological responses in a large endorheic river basin through integrated surface water-groundwater modeling. Water Resources Research, 51 (6): 4065–4085. DOI: 10.1002/2015WR016881.
-
Walter J-M N, Fournier R A, Soudani K , Meyer E.2003.Integrating clumping effects in forest canopy structure:an assessment through hemispherical photographs. Canadian Journal of Remote Sensing, 29 (3): 388–410. DOI: 10.5589/m03-011.
-
Walter J M N , Torquebiau E F.2000.The computation of forest leaf area index on slope using fish-eye sensors. Comptes Rendus De l'Académie des Sciences-Serie Ⅲ-Sciences de la Vie, 323 (9): 801–813. DOI: 10.1016/S0764-4469(00)01229-4.
-
Wang J D, Li X W , Strahler A H.1995.An indirect estimating method of foliage area volume density and leaf-area index of tree crown. Remote Sensing of Environment China, 10 (4): 288–297. ( 王锦地, 李小文, StrahlerA H. 1995. 树冠叶面积体密度和叶面积指数的间接估值方法研究. 环境遥感, 10 (4): 288–297. )
-
Wang W M, Li Z L , Su H B.2007.Comparison of leaf angle distribution functions:effects on extinction coefficient and fraction of sunlit foliage. Agricultural and Forest Meteorology, 143 (1/2): 106–122. DOI: 10.1016/j.agrformet.2006.12.003.
-
Watson D J.1947.Comparative physiological studies on the growth of field crops:I. Variation in net assimilation rate and leaf area between species and varieties, and within and between years.Annals of Botany, 11 (1): 41–76.
-
Watson D J.1958.The dependence of net assimilation rate on leaf-area index. Annals of Botany, 22 (1): 37–54.
-
Weiss M, Baret F, Smith G J, Jonckheere I , Coppin P.2004.Review of methods for in situ leaf area index (LAI) Determination:Part Ⅱ. Estimation of LAI, errors and sampling.Agricultural and Forest Meteorology, 121 (1/2): 37–53. DOI: 10.1016/j.agrformet.2003.08.001.
-
Welles J M.1990.Some indirect methods of estimating canopy structure. Remote Sensing Reviews, 5 (1): 31–43. DOI: 10.1080/02757259009532120.
-
Welles J M , Cohen S.1996.Canopy structure measurement by gap fraction analysis using commercial instrumentation. Journal of Experimental Botany, 47 (9): 1335–1342. DOI: 10.1093/jxb/47.9.1335.
-
Welles J M , Norman J M.1991.Instrument for indirect measurement of canopy architecture. Agronomy Journal, 83 (5): 818–825. DOI: 10.2134/agronj1991.00021962008300050009x.
-
Whitford K R, Colquhoun I J, Lang A R G, Harper B M.1995.Measuring leafarea index in a sparse eucalypt forest-a comparison of estimates from direct measurement, hemispherical photography, sunlight transmittance and allometric regression. Agricultural and Forest Meteorology, 74 (3/4): 237–249. DOI: 10.1016/0168-1923(94)02189-Q.
-
Wilson J W.1960.Inclined point quadrats. New Phytologist, 59 (1): 1–7. DOI: 10.1111/j.1469-8137.1960.tb06195.x.
-
Wu T, Ni S X, Li Y M , Chen J.2006.A comparison on the algorithms for retrieval of LAI based on gap fraction of vegetation canopy. Journal of Nanjing Normal University (Natural Science), 29 (1): 111–115. DOI: 10.3969/j.issn.1001-4616.2006.01.026. ( 吴彤, 倪绍祥, 李云梅, 陈健. 2006. 由冠层孔隙度反演植被叶面积指数的算法比较. 南京师大学报(自然科学版), 29 (1): 111–115. DOI: 10.3969/j.issn.1001-4616.2006.01.026. )
-
Yan G J, Hu R H, Wang Y T, Ren H Z, Song W J, Qi J B , Chen L.2016.Scale effect in indirect measurement of leaf area index. IEEE Transactions on Geoscience and Remote Sensing, 54 (6): 3475–3484. DOI: 10.1109/TGRS.2016.2519098.
-
Yan G J, Zhang W M, Zhu L, Liu Y Q and Zou J.2008.Multispectral canopy imager (MCI).C.N., 200810227995.X (阎广建, 张吴明, 朱凌, 刘亚琪, 邹杰.2008.多光谱冠层成像方法及仪器.中国, 200810227995.X) http://industry.wanfangdata.com.cn/jx/Detail/Patent?id=Patent_CN200810227995.X
-
Yao T, Yang X Y, Zhao F, Wang Z S, Zhang Q L, Jupp D, Lovell J, Culvenor D, Newnham G, Ni-Meister W, Schaaf C, Woodcock C, Wang J D, Li X W , Strahler A.2011.Measuring forest structure and biomass in New England forest stands using Echidna ground-based LiDAR. Remote Sensing of Environment, 115 (11): 2965–2974. DOI: 10.1016/j.rse.2010.03.019.
-
Yin G F, Liu Q H, Li J, Zeng Y L , Xu B D.2014.Effect of crown shape on the estimation of gap probability and leaf area index. Journal of Remote Sensing, 18 (4): 752–759. DOI: 10.11834/jrs.20143205. ( 尹高飞, 柳钦火, 李静, 曾也鲁, 徐保东. 2014. 树冠形状对孔隙率及叶面积指数估算的影响分析. 遥感学报, 18 (4): 752–759. DOI: 10.11834/jrs.20143205. )
-
Zeng Y L, Li J, Liu Q H, Hu R H, Mu X H, Fan W L, Xu B D, Yin G F , Wu S B.2015.Extracting leaf area index by sunlit foliage component from downward-looking digital photography under clear-sky conditions. Remote Sensing, 7 (10): 13410–13435. DOI: 10.3390/rs71013410.
-
Zhang G, Ganguly S, Nemani R R, White M A, Milesi C, Hashimoto H, Wang W L, Saatchi S, Yu Y F , Myneni R B.2014.Estimation of forest aboveground biomass in California using canopy height and leaf area index estimated from satellite data. Remote Sensing of Environment, 151 : 44–56. DOI: 10.1016/j.rse.2014.01.025.
-
Zhang R H, Tian J, Li Z L, Su H B, Chen S H , Tang X Z.2010.Principles and methods for the validation of quantitative remote sensing products. Science China Earth Sciences, 40 (2): 211–222. DOI: 10.1007/s11430-010-0021-3. ( 张仁华, 田静, 李召良, 苏红波, 陈少辉. 2010. 定量遥感产品真实性检验的基础与方法. 中国科学地球科学, 40 (2): 211–222. DOI: 10.1007/s11430-010-0021-3. )
-
Zhang W M, Chen Y M, Wang H T, Chen M, Wang X Y , Yan G J.2016.Efficient registration of terrestrial LiDARscans using a coarse-to-fine strategy for forestry applications. Agricultural and Forest Meteorology, 225 : 8–23. DOI: 10.1016/j.agrformet.2016.05.005.
-
Zhao F, Yang X Y, Schull M A, Román-Colón M O, Yao T, Wang Z S, Zhang Q L, Jupp D L B, Lovell J L, Culvenor D S, Newnham G J, Richardson A D, Ni-Meister W, Schaaf C L, Woodcock C E , Strahler A H.2011.Measuring effective leaf area index, foliage profile, and stand height in New England forest stands using a full-waveform ground-based lidar. Remote Sensing of Environment, 115 (11): 2954–2964. DOI: 10.1016/j.rse.2010.08.030.
-
Zhao K G, García M, Liu S, Guo Q H, Chen G, Zhang X S, Zhou Y Y , Meng X L.2015.Terrestrial LiDARremote sensing of forests:maximum likelihood estimates of canopy profile, leaf area index, and leaf angle distribution. Agricultural and Forest Meteorology, 209-210 : 100–113. DOI: 10.1016/j.agrformet.2015.03.008.
-
Zhao K G , Popescu S.2009.Lidar-based mapping of leaf area index and its use for validating GLOBCARBONsatellite LAIproduct in a temperate forest of the southern USA. Remote Sensing of Environment, 113 (8): 1628–1645. DOI: 10.1016/j.rse.2009.03.006.
-
Zheng G , Moskal L M.2009.Retrieving leaf area index (LAI) using remote sensing:theories, methods and sensors. Sensors, 9 (4): 2719–2745. DOI: 10.3390/S90402719.
-
Zhou Y Y, Tang S H, Zhu Q J, Li J T, Sun R , Liu S H.2003.Measurement of Lai in Changbai Mountains nature reserve and its result. Resources Science, 25 (6): 38–42. DOI: 10.3321/j.issn:1007-7588.2003.06.007. ( 周宇宇, 唐世浩, 朱启疆, 李江涛, 孙睿, 刘素红. 2003. 长白山自然保护区叶面积指数测量及结果. 资源科学, 25 (6): 38–42. DOI: 10.3321/j.issn:1007-7588.2003.06.007. )
-
Zhu Z and Zhang W M.2011.Estimating the LAI of a single tree from terrestrial laser scanner data//Proceedings of the 2011 International Conference on Remote Sensing, Environment and Transportation Engineering (RSETE).Nanjing, China:IEEE:4947-4951[DOI:10.1109/RSETE.2011.5965422]
-
Zhu Z, Zhang W M, Zhu L and Zhao J.2011.Research on different slicing methods of acquiring LAI from terrestrial laser scanner data//Proceedings of the 2011 IEEE International Conference on Spatial Data Mining and Geographical Knowledge Services (ICSDM).Fuzhou, China:IEEE:295-299[DOI:10.1109/ICSDM.2011.5969050]
-
Zou J, Yan G J, Zhu L , Zhang W M.2009.Woody-to-total area ratio determination with a multispectral canopy imager. Tree Physiology, 29 (8): 1069–1080. DOI: 10.1093/treephys/tpp042.
-
Zou J , Yan G J.2010.Optical methods for in situ measuring leaf area index of forest canopy:areview. ChineseJournal of Applied Ecology, 21 (11): 2971–2979. ( 邹杰, 阎广建. 2010. 森林冠层地面叶面积指数光学测量方法研究进展. 应用生态学报, 21 (11): 2971–2979. )
-
Zou J, Yan G J , Chen L.2015.Estimation of canopy and woody components clumping indices at three mature picea crassifolia forest stands. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 8 (4): 1413–1422. DOI: 10.1109/Jstars.2015.2418433.
-
Zou X C, Mõttus M, Tammeorg P, Torres C L, Takala T, Pisek J, Mäkelä P, Stoddard F L , Pellikka P.2014.Photographic measurement of leaf angles in field crops. Agricultural and Forest Meteorology, 184 : 137–146. DOI: 10.1016/j.agrformet.2013.09.010.
-
Zwally H J, Schutz B, Abdalati W, Abshire J, Bentley C, Brenner A, Bufton J, Dezio J, Hancock D, Harding D, Herring T, Minster B, Quinn K, Palm S, Spinhirne J , Thomas R.2002.ICESat's laser measurements of polar ice, atmosphere, ocean, and land. Journal of Geodynamics, 34 (3/4): 405–445. DOI: 10.1016/S0264-3707(02)00042-X.