Print

出版日期: 2016-07-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20165259
2016 | Volumn20 | Number 4





                              上一篇|





下一篇
技术方法
结合投影变换和相位相关的海冰运动监测
expand article info 胡迎迎 , 郎文辉 , 张盼 , 杨学志
合肥工业大学计算机与信息学院, 安徽 合肥 230009
收稿日期: 2015-11-28; 修改日期: 2016-03-03; 优先数字出版日期: 2016-07-25
基金项目: 国家自然科学基金（编号:61271381，61371154，61102154）；航空科学基金（编号:201301P4007）；中央高校基本科研业务费专项资金资助（编号:2012HGCX0001）
第一作者简介: 胡迎迎(1988-),女,硕士研究生。研究方向为数字图像分析与处理。E-mail:huyy1117@163.com
通讯作者简介: 郎文辉(1965-),男,副教授。研究方向为遥感图像处理,智能信息处理。E-mail:langwh@hfut.edu.cn
中图分类号: TP751.2
文献标识码: A
文章编号: 1007-4619(2016)04-0579-11

摘要

为提高对渤海海冰旋转和平移运动的监测精度，提出一种基于投影变换的相位相关跟踪方法。选取连续8景静止水色成像仪（GOCI）图像序列，根据特征图像窗口的投影变换构造辅助函数，通过寻求函数最优解得到旋转角度集合，选择修正相关系数确定最佳旋转角度，同时根据相位信息实现海冰样本间亚像素级别的平移跟踪，消除传统相位相关法中因忽略图像相频特性所造成的匹配误差。实验结果表明，以手动测量的旋转角度为基准，该方法和传统相位相关法的旋转监测均方根误差的最大值/平均值分别为0.59/0.50与1.41/0.94，跟踪速度提高了50.6%；海冰平移运动的速度矢量与辽东湾的现场实测数据及历史资料记录数据基本一致。该方法对渤海海冰旋转和平移运动具有较好的跟踪效果。

关键词

GOCI , 投影变换 , 相位相关 , 渤海海冰 , 旋转 , 平移

Monitoring sea ice motion by combining projection transformation and phase correlation
expand article info HU Yingying , LANG Wenhui , ZHANG Pan , YANG Xuezhi
School of Computer and Information, Hefei University of Technology, Hefei 230009, China

Abstract

The Bohai Sea is located in the sea area of China with the highest latitude. This region is an important economic development zone in China. However, sea ice and its drift often block shipping vessels, destroy offshore structures, and limit development of the marine industry. Thus, sea ice monitoring techniques must be developed. Phase correlation based on polar transformation is extensively applied to image registration and sea ice tracking because of its robustness; however, this method results in various forms of noise and is insensitive to illumination changes. In addition, this approach can capture the translational and rotational motions of sea ice. Nevertheless, polar coordinate transformation and its subsequent operation extract amplitude information alone and ignore phase characteristics, which determine the position of each frequency. Consequently, errors in the matching results significantly increased. Moreover, traditional phase correlation involves several Fourier transformation and inverse transformation, which may increase computational burden and reduce tracking efficiency. By considering the limitations of sea ice tracking through phase correlation, this paper presents another approach for phase correlation based on projection transformation by combining the unique characteristics of sea ice in the Bohai Sea based on GOCI to track and monitor sea ice motion. First, sea ice samples with identified; stable characteristics were quantitatively selected and projected into the one-dimensional space to minimize the function of rotational components. The characteristics of individual images and the relationship among them were fully considered. This step is crucial for setting appropriate correlation values to discriminate good angles from mixed ones. Next, the measured errors generated from the two methods were compared and analyzed based on the manual tracking results. The translation components can be determined from differences among the phase representatives of the cross power spectral function and extended to the sub-pixel level. Outliers should be excluded during the entire process by using correlation coefficients, visual inspection, and two-way matching. Finally, the derived sea ice motion in the Bohai Sea was analyzed with insitu data and historical records. Results show that the maximum/average of root-mean-square error between the rotation angles via the proposed method and manual measurements is 0.59/0.50, whereas that between the traditional technique and manual values is 1.41/0.94. The running speed increased by 50.6%. In terms of translation, the sea ice motion field agrees well with insitu data and historical records of the Bohai Sea. Recent developments in local research on sea ice motion usually ignore the rotational condition. This paper presents a method that combines phase correlation and projection transformation based on GOCI to simultaneously track and monitor sea ice rotation and translation in the Bohai Sea. Projection transformation replaces the polar coordinates, thereby improving the matching errors generated from the traditional method. Sea ice translation is derived from phase information in terms of image feature windows. This method can efficiently track sea ice motion.

Key words

GOCI , projection transform , phase correlation , sea ice of Bohai Sea , rotation , translation

1 引 言

渤海是中国纬度最高的海域，也是重要的经济开发区。然而，渤海海冰及其漂移运动对航运交通、海上建筑物和海洋产业常产生不同程度的影响，甚至造成巨大的经济损失(张晰，2011)。因此，亟需开展海冰运动跟踪算法的研究。

目前，针对极地海冰研究，已开展的海冰运动(平移和旋转)跟踪方法包括最大互相关(Lavergne等，2010)、模式识别(Yu等，2009；Hollands和Dierking，2011)和相位相关法等。此外，Kwok等(1990)基于浮冰-水道边界的形状描述子，提出两种跟踪特征海冰旋转和平移的方法；Das Peddada和McDevitt(1996)提出了LARA算法，该方法充分考虑北极海冰的几何特性，以统计的方式在有限范围内搜索匹配浮冰。然而，上述方法的适用对象主要是极地海冰，该区域海冰以季节性多年冰为主，并存在大量的块状浮冰。显然，渤海海冰与极地海冰的特性差异较大(杨国金，2000；张方俭，1979)，需要研究适用于该区域海冰的跟踪方法。

单一的相位相关法能够跟踪监测大幅度平移运动，对各类噪声具有较强的鲁棒性，而且对光照变化不敏感。但是，对于既有平移又有旋转的图像，相关平面的峰值不能对其进行准确地定位及跟踪，当旋转角度超过一定阈值时，该方法甚至完全失效。因此，相位相关法多与极坐标变换相结合，广泛应用于图像配准(Reddy和Chatterji，1996；Keller等，2005；Sarvaiya等，2012)与海冰漂移跟踪(Liu等，2012)等领域。然而，基于极坐标变换的相位相关法，在跟踪海冰的平移和旋转运动时，仅提取幅频信息进行极坐标变换和相关运算，而忽略了决定图像中各频率位置分布的相位信息。因此，仅考虑图像的幅频特性将大幅度削弱图像的匹配效果，增大后续的跟踪误差。此外，该方法涉及多次傅里叶变换及其反变换，计算量较大，跟踪效率不高。

针对基于极坐标变换的相位相关法在匹配精度和运行效率方面存在的问题，国内图像匹配领域的众多学者开展了多方面的研究。韦春桃等人(2011)根据对数极坐标中半径和角度的独立性，提出一种改进的相位相关法，但是该算法易受限制，整体效率不高。罗镇宝等人(2008)结合投影变换，利用傅里叶变换的共轭对称性，探索出一种图像快速匹配算法。

为消除传统方法在海冰监测中存在的缺陷，本文基于GOCI数据，结合渤海海冰独有的性质，提出一种基于投影变换的相位相关法。首先，分别从参考图像和目标图像选取一定数量的特征海冰，作为拟匹配样本组合，经投影变换将计算过程转化到一维空间求最优解。其次，确定旋转角度后，充分考虑单个图像特性及图像间的联系，设置修正相关系数来筛选得到最佳角度。再以手动测量的旋转角度为基准，对传统的旋转跟踪方法及本文方法进行误差比较分析。同时，通过跟踪相位相关函数的相位变化来确定海冰的平移运动，并将其精度提高到亚像素水平。再分别利用互相关系数及目视检测、双向匹配法先后两次对异常值进行过滤处理。最后，将得到的渤海海冰运动矢量场与现场数据及历史资料进行比较和分析。

2 算 法

2.1 传统算法

常用于海冰运动监测的方法为基于极坐标变换的相位相关法，其原理如下：

设图像${f_2}(x，y)$是图像${f_1}(x，y)$经平移$({x_0}，{y_0})$、旋转${\psi _0}$得到的图像，则自变量间的矩阵关系可表示为

$ \left[ {\begin{array}{*{20}{c}} x\\ y \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos {\psi _0}}& { - \sin {\psi _0}}\\ {\sin {\psi _0}}& {\cos {\psi _0}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x^{'}} + {x_0}}\\ {{y^{'}} + {y_0}} \end{array}} \right] $ (1)

式中，x、y、x'、y'表示图像像素点的自变量，(x，y)、(x'，y')为图像上任意点的像素坐标，f1(x，y)、f2(x，y)则分别为图像的灰度值。图像之间的关系可表示为

$ \begin{aligned} {f_2}(x，y)= & {f_1}(x\cos {\psi _0} + y\sin {\psi _0} - {x_0}，\\ & {\kern 1pt}- x\sin {\psi _0} + y\cos {\psi _0} - {y_0}) \end{aligned} $ (2)

由傅里叶旋转平移特性，得到

$ \begin{split} \\[-12pt] {F_2}(\xi，\eta)= {{\rm{e}}^{ - i2{\rm{\pi }}(\xi {x_0} + \eta {y_0})}}{F_1}(\xi \cos {\psi _0} + \\ \eta \sin {\psi _0}，- \xi \sin {\psi _0} + \eta \cos {\psi _0}) \end{split} $ (3)

由上式可得到

$ \begin{aligned} & {F_1}(\xi，\eta)= \mathcal{F}({f_2}(x，y)) = \\ & \quad\quad\quad\quad \mathcal{F}({f_2}((x{'} + {x_0})\cos {\theta _0} -(y{'} + {y_0})\sin {\theta _0}，\\ &(x{'} + {x_0})\sin {\theta _0} +(y{'} + {y_0})\cos {\theta _0})) = \\ & \quad\quad\quad\quad {F_2}(\xi \cos {\theta _0} - \eta \sin {\theta _0}，- \xi \sin {\theta _0} + \eta \cos {\theta _0})\\ & \exp(i2\pi((\xi \cos {\theta _0} - \eta \sin {\theta _0}){x_0} +(- \xi \sin {\theta _0} + \eta \cos {\theta _0}){y_0})) \end{aligned} $ (4)

式中，$(\xi，\eta)$为图像经过傅里叶变换之后任意点的频域坐标，${F_1}(\xi，\eta)$、${F_2}(\xi，\eta)$分别为图像f1(x，y)、f2(x，y)的傅里叶变换，符号$\mathcal{F}$表示傅里叶变换。

从上述推导过程可知，图像傅里叶变换的幅度谱与图像具有相同的旋转角度，图像的平移转换为频谱的相移(Sarvaiya等，2012)。由于相位谱同时具有平移与旋转两种特性，故首先通过极坐标变换，利用幅度谱求出图像间的旋转角度，这对于监测平移运动是十分必要的。

对上式两边同时求模，得

$ \left| {{F_1}(\xi，\eta)} \right| = \left| {{F_2}(\xi \cos {\psi _0} - \eta \sin {\psi _0}，} \right.\left. { - \xi \sin {\psi _0} + \eta \cos {\psi _0})} \right| $ (5)

由笛卡尔坐标系向极坐标平面投影，其中

$ \left\{ \begin{array}{l} \rho= \sqrt {{\xi ^2} + {\eta ^2}} \\ \psi= \arctan(\eta /\xi) \end{array} \right. $ (6)

式中，ρ表示极坐标平面的半径，$\psi $表示极坐标平面的角度。于是，式(3)可化简为

$ {P_1}(\rho，\psi)= {P_2}(\rho，\psi+ {\psi _0}) $ (7)

根据傅里叶平移特性

$ {P_2}(u，v)= {{\rm e}^{ - j2\pi v{\psi _0}}}{P_1}(u，v) $ (8)

归一化互功率谱，

$ M(x，y)= {\mathcal{F}^{ - 1}}\left({\frac{{{P_2}(u，v){P_1}{{(u，v)}^ * }}}{{\left| {{P_2}(u，v){P_1}{{(u，v)}^ * }} \right|}}} \right) $ (9)

式(7)—(9)中，P1、P2为图像在极坐标平面的表示，u、v为极坐标平面的自变量，M表示互功率谱，${\mathcal{F}^{ - 1}}$为傅里叶逆变换。

显然，在原坐标系中，图像之间的旋转可转化为极坐标系(沿角度轴)的平移运动，相位相关函数峰值所在的坐标即为平移量。式(4)右边的f1(x，y)频谱由相位谱和幅度谱组成，其中图像的相位信息决定了各个频率的位置分布。然而，由式(4)变换到式(5)的过程中，仅提取了图像的幅频特性，丢弃了原图像本身的相位信息及图像之间因发生平移变换而产生的相移。因此，该算法不能准确地跟踪海冰的位置变化。此外，实施多次傅里叶变换及其反变换的计算量较大，故需对基于极坐标变换的相位相关法进行改进。

2.2 本文算法

2.2.1 算法原理

在2维空间内，Radon变换可理解为函数f(x，y)沿直线x在$\theta $角方向上做投影变换(即线积分)得到的像。从数学角度上看，Radon变换是从(x，y)空间映射到$(\hat x，\theta)$空间的变换(Bracewell等，1993 )。其中，

$ \hat x = x\cos \theta+ y\sin \theta $ (10)

式中，$\theta $为两坐标轴逆时针方向的夹角，x、y分别为原坐标系中的横、纵坐标，$\hat x$为原坐标系逆时针旋转角度$\theta $得到的新坐标系的横坐标值。

Radon变换的基本定义为

$ \begin{array}{l} \Re f(\hat x，\theta)= \int\limits_{ - \infty }^{ + \infty } {f(x，y)} {\rm{d}}\hat y = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \int\limits_{ - \infty }^{ + \infty } {f(\hat x\cos \theta- \hat y\sin \theta，\hat x\sin \theta+ \hat y\cos \theta)} {\rm{d}}\hat y \end{array} $ (11)

式中，$\Re $为Radon变换的符号。其中新旧坐标之间的关系为

$ \left[ {\begin{array}{*{20}{c}} x\\ y \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta }& { - \sin \theta }\\ {\sin \theta }& {\cos \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\hat x}\\ {\hat y} \end{array}} \right] $ (12)

设直角坐标系中f(x，y)的傅里叶变换为f(u，v)，则其投影变换在极坐标空间为1维傅里叶变换$P(\hat u，\theta)\Leftrightarrow p(\hat x，\theta)$，原频域函数f(u，v)可写成$F = \left({\widehat u\cos \theta，\widehat u\sin \theta } \right)$。

根据第2.1节的分析，对原始参考图像及目标图像中提取的特征子图像窗口沿着直线$\hat u$分别在$\psi= 0$和$\psi= {\psi _0}$两个方向上进行投影变换，得${S_1}(\hat u，0)$、${S_2}(\hat u，{\psi _0})$。

此处，定义1维函数

$\chi (\psi )=\left| \left| {{S}_{2}}(\hat{u}\text{,}\psi ) \right|\text{ }/\left| {{S}_{2}}(\hat{u}\text{,}\psi ) \right|\left| {{S}_{1}}(\hat{u}\text{,}0)+\varepsilon \right|-1 \right|$ (13)

式中，$\varepsilon $为任意小的正整数。${S_2}(\hat u，\psi)$、${S_1}(\hat u，0)$为投影变换的结果，$\chi(\psi)$为定义的函数值。以式(11)取代式(6)—(9)，对海冰样本之间的旋转和平移运动单独计算。当自变量$\psi $不断变化时，函数值随之变化，在$\psi= {\psi _0}$处，函数有最小值，即$\chi({\psi _0})= 0$。此时的${\psi _0}$即为海冰样本的旋转角度。由于实序列的傅里叶变换具有共轭对称性，在确定旋转角度时，会存在180°模糊。解决方法如下：假设${\psi _0}$是文中计算得到的旋转角度，首先，将其中一幅图像进行旋转，如目标图像旋转${\psi _0}$，计算两幅图像之间的平移。其次，目标图像旋转(180°+${\psi _0}$)，再次计算两幅图像之间的平移。如果旋转${\psi _0}$时，相位相关函数的峰值较大，则正确的旋转角度为${\psi _0}$，否则为180°+${\psi _0}$。确定旋转角度之后，将其中一幅子图像反向旋转，则式(2)简化为

$ {f_2}(x，y)= {f_1}(x - {x_0}，y - {y_0}) $ (14)

对上式两边进行傅里叶变换

$ {F_2}(\xi，\eta)= {e^{ - j2\pi(\xi {x_0} + \eta {y_0})}}{F_1}(\xi，\eta) $ (15)

于是，冲激函数的最值即为平移分量(x0，y0)

$ \begin{split} & \arg({\mathcal{F}^{ - 1}}({F_2}(\xi，\eta){F_1}^ *(\xi，\eta)/\\ &(\left| {{F_2}(\xi，\eta)} \right|\left| {{F_1}^ *(\xi，\eta })\right|)) = \\ &\delta(x - {x_0}，y - {y_0}) \end{split} $ (16)

式中，${F_1}^ *(\xi，\eta)$为${F_1}(\xi，\eta)$的共轭，符号arg表示取最值，$\delta $表示冲激函数。

经过以上过程，得到海冰样本之间的旋转角度和整数级别的平移分量。为了进一步得到亚像素级别的平移分量，利用拉格朗日二元三点插值法(颜何生，2005)，计算指定插值点(x0，y0)处的函数近似值。该过程包括两步：

(1)选取插值点(x，y)附近9个点，其坐标值为${u_n} <{u_{n + 1}} <{u_{n + 2}}$，${v_m} <{v_{m + 1}} <{v_{m + 2}}$；

(2)利用二元三点插值公式

$ {w^*} = \sum\limits_{i = n}^{n + 2} {\sum\limits_{j = m}^{m + 2} {\left({\prod\limits_{ p = n\atop p \ne i}^{n + 2} {\frac{{u - {u_p}}}{{{u_{i - }}{u_p}}}} } \right)\left({\prod\limits_{ q = m\atop q \ne j}^{m + 2} {\frac{{v - {v_q}}}{{{v_j} - {v_q}}}} } \right){w_{ij}}} } $ (17)

计算得到插值点(x0，y0)的函数近似值${w^ * } = w({x_0}，{y_0})$。

2.2.2 算法流程

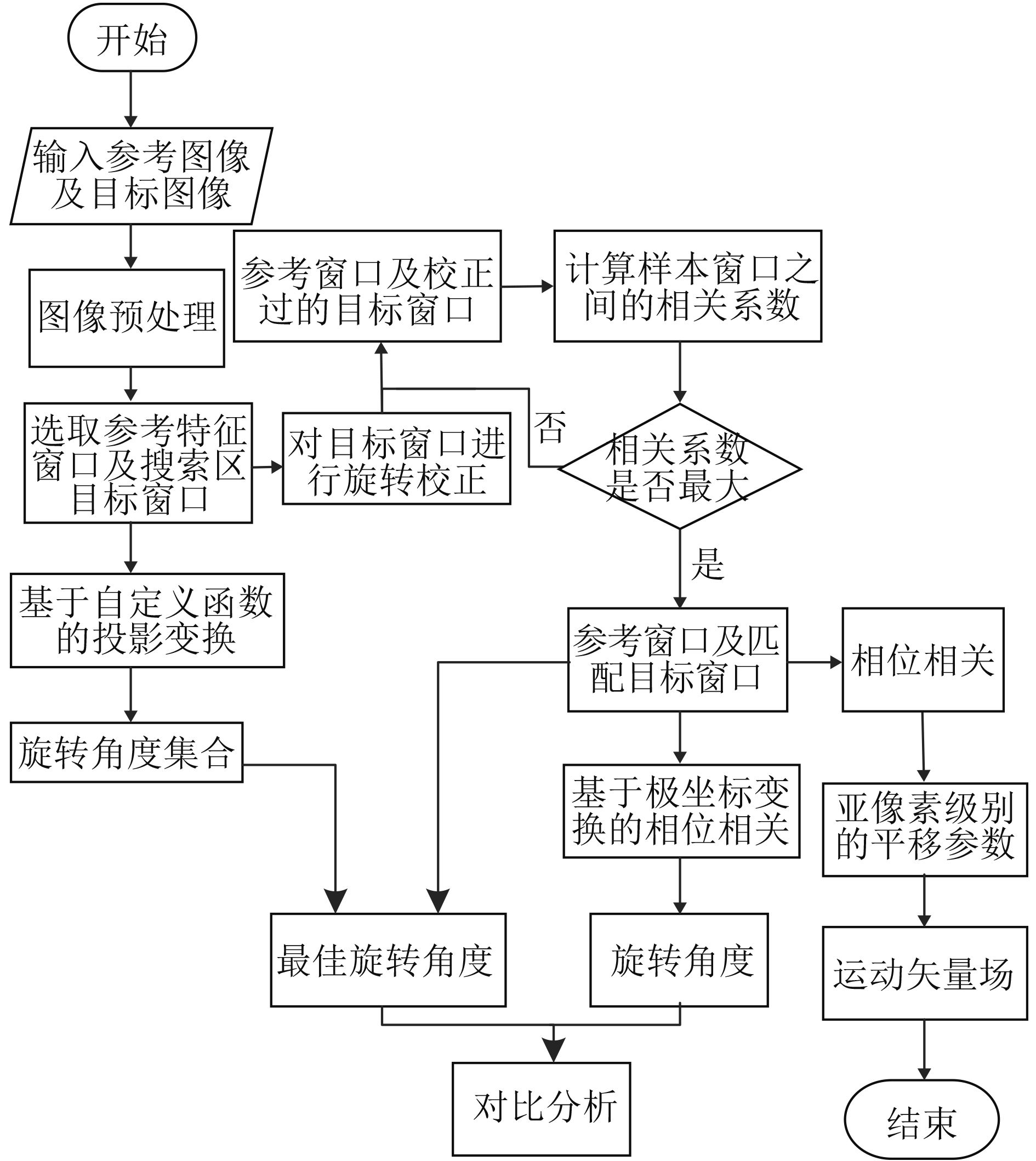
本文所用的算法流程图如图 1所示。具体步骤如下：


图 1 本文算法流程图
Fig. 1 Flow chart of algorithm

(1) 对于间隔为1 h的两幅GOCI影像，根据采集时间依次作为参考图像和目标图像，原始图像的尺寸为5568×5685像素。

(2) 分别对参考图像和目标图像进行预处理，包括提取渤海辽东湾区域，RGB伪彩色波段合成，直方图匹配及中值滤波，从而得到相同区域不同成像时间的图像组合。

(3) 输入经过预处理的图像组合，以固定的图像窗口(25×25像素)选择参考图像中特征较为明显的区域作为特征海冰样本，并在目标图像搜索范围内定位相同窗口大小的待匹配特征区域集合。

(4) 对每组拟匹配的参考图像窗口与目标图像窗口分别在不同方向上进行投影变换，从而将计算过程转换到1维平面求解函数最小值，此时对应的函数自变量即为旋转角度。

(5) 对参与步骤(4)的目标特征窗口进行旋转校正，消除旋转分量后，计算仅剩下平移分量的拟匹配样本组的修正互相关系数，通过最大相关系数定位目标图像中的匹配样本区域，从而确定最佳匹配组合。计算公式为

$ f(I，J)= \frac{{(2{\mu _I}{\mu _J} + {C_1})(2\left| {{\sigma _{IJ}}} \right| + {C_2})}}{{({\mu _I}^2 + {\mu _J}^2 + {C_1})(\sigma _I^2 + \sigma _J^2 + {C_2})}} $ (18)

式中，$0 \leqslant f(I，J)\leqslant 1$，I、J分别是参考图像和待匹配图像，${\mu _I}\text{、}{\mu _J}\text{、}{\sigma _I}\text{、}{\sigma _J}\text{、}{\sigma _{IJ}}$分别表示图像I、J的灰度均值、标准差及协方差。该方法不仅考虑了单个图像的基本性质，也将图像之间的联系作为考虑的范畴，比最大互相关法更加全面和可靠。

(6) 利用基于极坐标变换的相位相关法(即式(1)—(9))确定相似特征窗口的旋转参数；以手动测量的旋转角度为基准，将确定的旋转角度与本文算法进行对比分析，计算均方根误差。

(7) 确定旋转分量之后，利用相位相关函数确定匹配样本之间的平移坐标。

(8) 所有匹配样本之间的平移和旋转参数确定之后，为了提高跟踪精度，对相位相关峰值进行简单而高效的二元三点插值，计算得渤海海冰的亚像素运动跟踪结果，最终得到整个辽东湾的海冰运动矢量图。

3 实验与分析

3.1 实验数据

极地海冰监测常用的数据包括微波辐射计数据、微波散射计数据和合成孔径雷达(SAR)数据，而渤海海水运动比较剧烈，海冰易变形。因此，低分辨率的辐射计和散射计数据以及卫星重访时间较长的SAR数据，并不适合监测渤海海冰的运动状况。

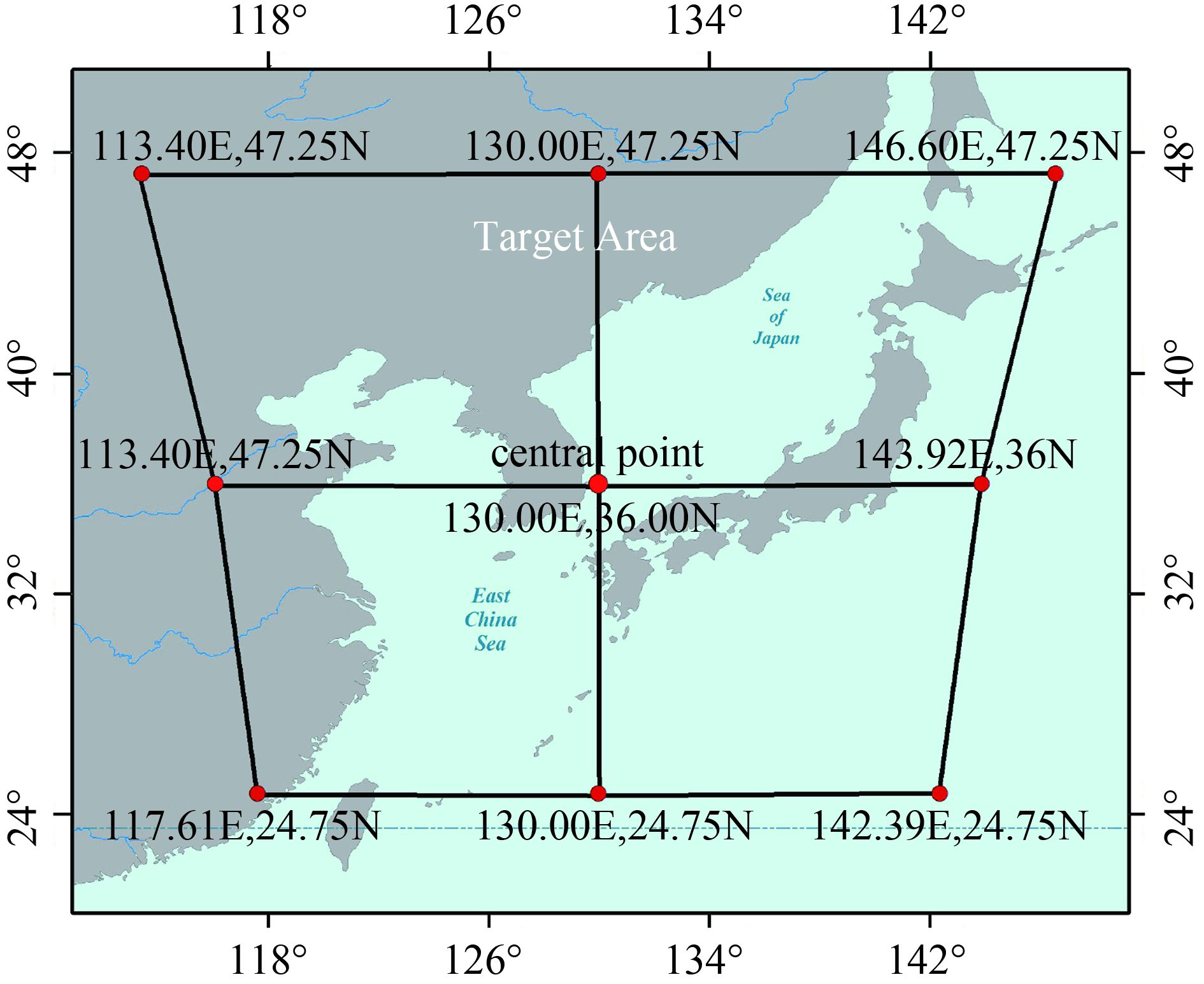
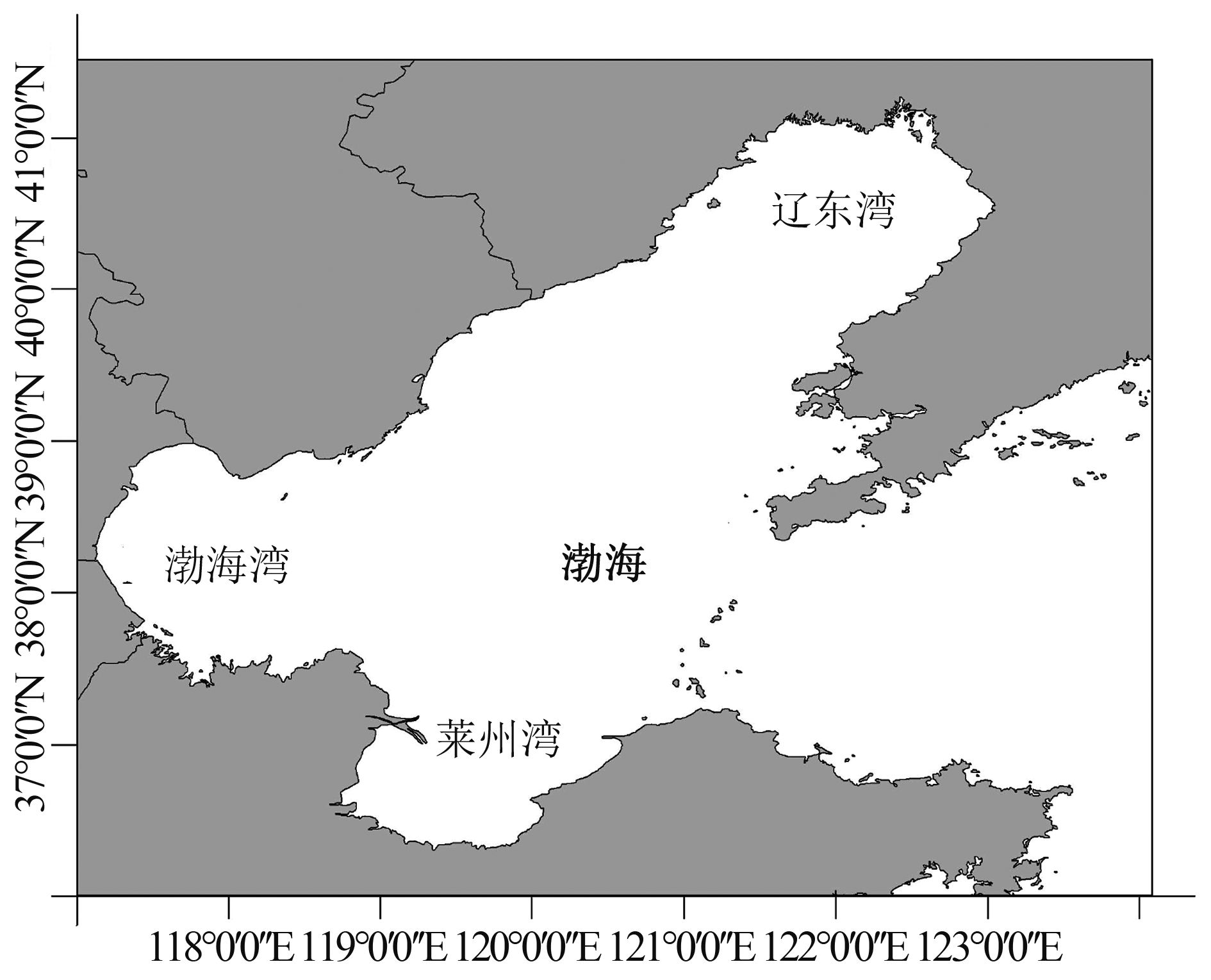
GOCI为相对地球静止的传感器，成像区域的中心位置为(130°E，36°N)，覆盖韩国、日本和中国海域(如图 2所示)，大小为2500×2500 km。本文的研究区域仅为渤海海域(如图 3所示)，使用相关软件从GOCI原始影像(如图 4所示)中截取部分图像(如图 5所示)，起点坐标为(630，1544)，大小为874×844像素。GOCI传感器有8个波段(6个可见光和2个近红外)，使用波段6(680 nm)、波段5(660 nm)、波段4(555 nm)分别填充R、G、B通道合成RGB伪彩色图像。其他预处理过程还包括：利用直方图匹配方法补偿影像亮度不均所带来的误差；对影像进行中值滤波，去除影像中孤立的噪声点，并保持影像的边缘信息。从而，提高影像的跟踪精度(Lang等，2014)。


图 2 GOCI成像区域
Fig. 2 GOCI target area


图 3 渤海海域
Fig. 3 The location of Bohai sea


图 4 2012-01-29 8:16—15:16 GOCI原始假彩色图像
Fig. 4 GOCI original false colour images from 8:16 to 15:16 on February 19，2012


图 5 图 4预处理图像
Fig. 5 Preprocessed images of figure 4

实验数据为2012年1月29日08:16—15:16(北京时间)渤海辽东湾白天无云或少云区域的8景数据，该时间段内海冰处于盛冰期；图像空间分辨率为500 m，时间分辨率为1 h；白天成像8次。8景数据均经上述一系列预处理，可实现对渤海海冰运动的实时监测。原始假彩色图像如图 4(a)—(h)所示，经过预处理之后的图像如图 5(a)—(h)所示。

3.2 旋转跟踪结果及分析

窗口边长的选择，又叫孔径问题。如果窗口设置得过小，往往会丢失可跟踪的海冰特征，甚至不能覆盖最大可能位移，从而得到错误的跟踪结果。相反，窗口过大，该研究区域的运动将变得复杂化。因此，需要折中考虑上述问题(Fily和Rothrock，1987)。

由于研究区域仅限于渤海北部的辽东湾，采用目视解译法即可快速准确的挑选出具有明显特征的图像窗口，特征区域分布于海冰密度较高的冰区，便于进行跟踪(Komarov和Barber，2012)。据历史资料记载，位于辽东湾的海冰最大运动速度约为1 m/s，相邻图像滞后时间为1 h，则最大可能位移为7.2像素；选择最大位移的3倍以上作为搜索区域，设置搜索区域为30×30像素；以单个像素为间隔，步长设为500 m；特征窗口取为25×25像素(Lang等，2014)。

从目标图像搜索区左上角逐行逐列进行跟踪，得到不同相关程度的旋转角度集合。互相关方法不能解决图像旋转问题，需要消除拟匹配样本的旋转运动。计算参考窗口和一系列目标窗口的互相关系数，将最大系数对应的目标窗口(一般为0.9)作为最佳匹配窗口，该窗口计算出的旋转角度即为实际的角度。

由于缺乏现场实测数据，需手动测量子图像之间的旋转，并以其为基准，分别将本文算法和传统方法求出的旋转角度进行比较分析。手动测量执行过程如下：提取参考图像和目标图像的匹配特征点，然后取出相邻点的坐标值进行计算(Liu等，2012；Gong等，2015；Hollands等，2015)。如果两点之间的海冰没有破碎，两幅图像上两点连线的夹角即为旋转角度。图像中共标出20个点，计算出10个位置的旋转角度。估计的旋转分量使用均方根误差进行评估。取部分实验结果进行分析，2012-01-29 8:16—9:16以及10:16— 11:16的旋转跟踪结果分别见表 1、表 2。

表 1 2012-01-29 8:16—9:16旋转跟踪结果
Table 1 The results of tracking rotation motion at 8:16—9:16 am on February 19，2012

下载CSV 
/(°)
样本区域 传统方法 旋转角度
本文方法		 手动测量
窗口1 8.6 7.8 8.1
窗口2 10.6 12.0 11.5
窗口3 8.5 7.4 7.6
窗口4 10.6 11.2 11.0
窗口5 12.6 14.0 13.0
窗口6 9.5 8.6 9.1
窗口7 18.9 17.3 18.0
窗口8 7.8 5.9 6.8
窗口9 10 8.8 9.0
窗口10 14.9 12.9 13.6

表 2 2012-01-29 10:16—11:16旋转跟踪结果
Table 2 The results of tracking rotation motion at 10:16—11:16 am on February 19，2012

下载CSV 
/(°)
样本区域 传统方法 旋转角度
本文方法		 手动测量
窗口1 8.5 8.1 8.2
窗口2 11.0 9.2 10.0
窗口3 9.0 7.4 8.1
窗口4 6.5 4.5 5.0
窗口5 6.7 5.5 5.9
窗口6 5.5 2.6 3.5
窗口7 8.6 6.9 7.6
窗口8 2.8 1.5 1.6
窗口9 4.1 2.8 3.0
窗口10 5.3 4.9 4.8

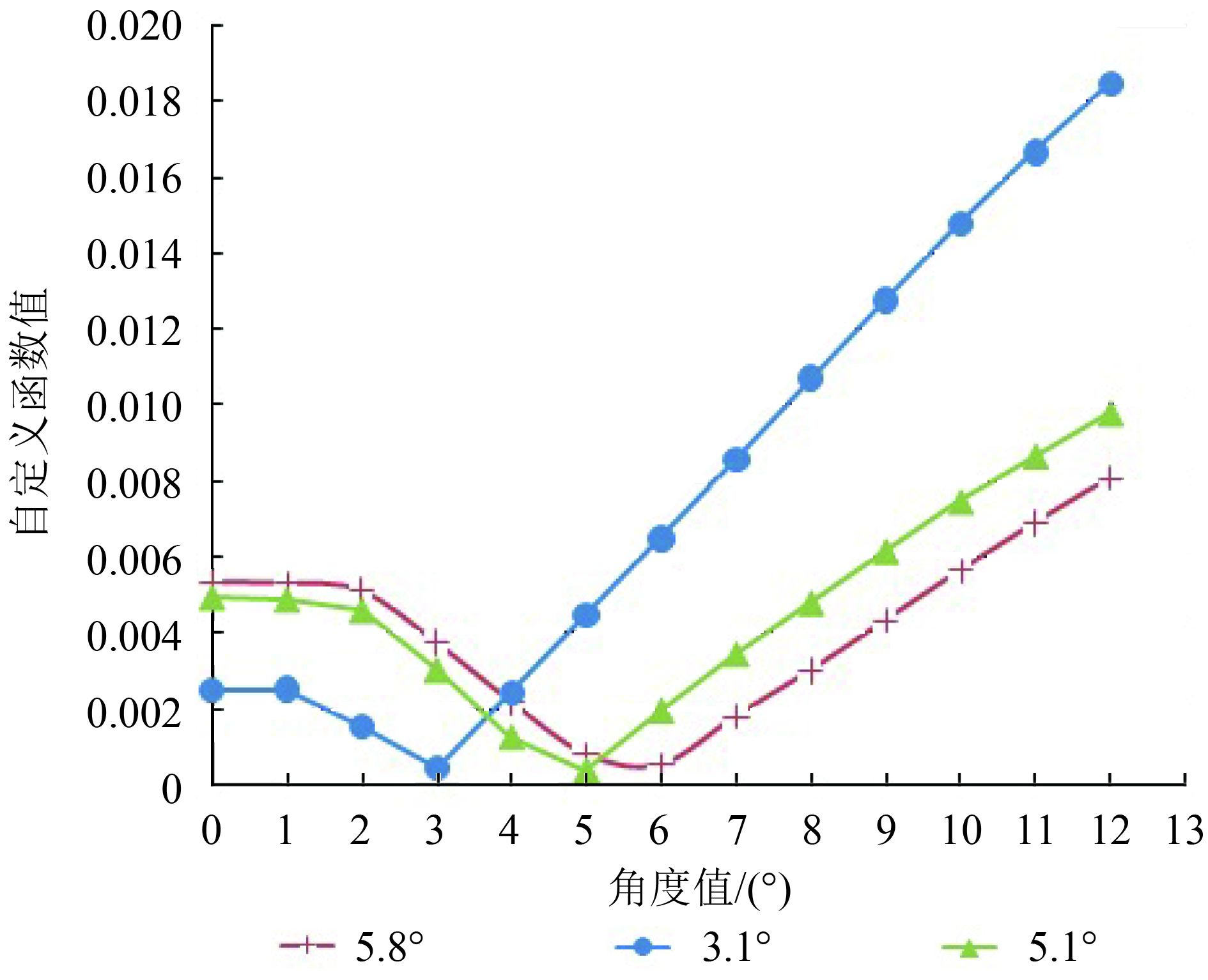
按照式(13)确定函数的最小值及旋转角度值${\psi _0}$。实验结果的角度模糊性消除之后，最终得到的角度值即为海冰的旋转量，函数值随旋转角度的变化曲线如图 6所示。可见，当旋转角度分别为5.8°、3.1°和5.1°时，函数值随着角度的增加缓慢减小，达到最低点时，对应的角度即为旋转角度，之后近似呈线性趋势增加。


图 6 自定义函数随不同旋转角度的变化
Fig. 6 The variation with different rotation angles of self-difining funtion

由表 1、表 2可知，两种方法测得的角度基本一致，间隔1 h的海冰图像的旋转角度范围约为7°—20°；基于极坐标变换的相位相关法测量角度的均方根误差(RMSE)为0.86、1.12，而本文方法测得的均方根误差分别为0.59、0.54，明显改善了传统方法的匹配精度。旋转跟踪的8幅图像，每组图像之间的RMSE为0.4—0.59，如表 3所示。若只是衡量结果的准确度，不是算法的精确度，该误差范围内的结果是可以接受的。实验发现，跟踪结果误差较大的区域往往是冰边缘区，该区域海水运动剧烈，海冰发生了形变，基于区域的方法不能正确跟踪该区运动结果；特征不明显或者不易跟踪保持的区域往往在目标图像上找不到正确的匹配位置，难以确定正确的旋转角度；由于运动的异质性，设置一个特征窗口不能正确反映该区域的真实运动状况。

表 3 旋转跟踪结果的均方根误差
Table 3 RMSE of tracking rotation

下载CSV 
实验图像 RMSE(传统方法) RMSE(本文方法)
图 4(a)(b) 0.86 0.59
图 4(b)(c) 0.75 0.45
图 4(c)(d) 1.12 0.54
图 4(d)(e) 1.41 0.46
图 4(e)(f) 0.91 0.55
图 4(f)(g) 0.88 0.52
图 4(g)(h) 0.64 0.40

表 4为基于极坐标变换的相位相关法(传统方法)和基于自定义函数的投影变换法(本文算法)之间的算法复杂度的比较结果。实验平台为Matlab 7.10.0，PC配置为Corei3 3.4 GHZ，内存4 GB。传统方法计算图像之间的运动参数需要6次2维FFT、3次2维IFFT运算、频谱幅度运算、对数极坐标映射、互功率谱归一化运算及相关平面求峰值运算。其中运算量主要来自傅里叶变换及其逆变换，若N=300，则至少需要3×106次复数乘加运算。然而，利用本文方法只需计算2次FFT、1次FFT、1次投影变换以及求函数最小值运算，从运行时间来看，本文方法比传统方法快50.6%。

表 4 算法复杂度对比
Table 4 The comparison of complexity

下载CSV 
跟踪算法 算法复杂度 运行时间/s
传统方法 6次FFT(O(nlogn))，3次IFFT(O(nlogn))，
2次排序(O(logn2))，映射(O(logn2)，
角度变换(O(1))，双三次插值(O(1))		 1.066443
本文算法 2次FFT(O(nlogn))，1次IFFT(O(nlogn))，
若干乘加(O(1))		 0.708017

3.3 平移跟踪结果的分析及验证

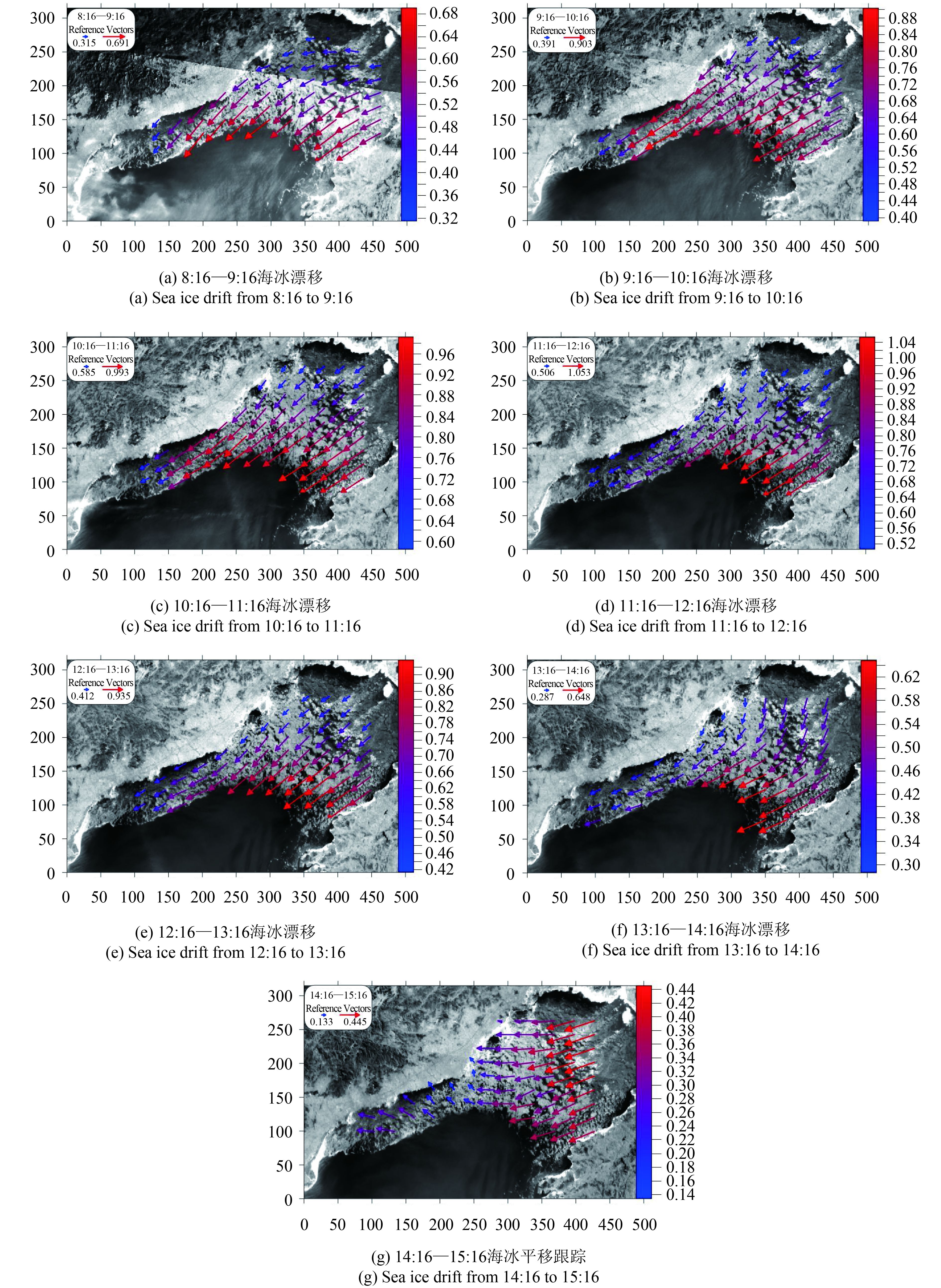
位于渤海北部的辽东湾冰期最长，通常出现在每年11月底到翌年3月初，属于季节性海冰(白珊等，1999)。图 7(a)—(g)为渤海辽东湾漂移跟踪结果(过滤掉错误跟踪结果后)。由于实验数据有限，实验期间的渤海区域仅辽东湾的海冰特征最易跟踪获取。因此，仅以该区域海冰的运动状况为代表。据统计资料显示，渤海辽东湾的平均漂移速度0.4—0.5 m/s，最大平均速度为0.7—0.9 m/s。由图 7可以看到，2012年01月29号渤海海冰从北京时间8:16到15:16，实验获取的辽东湾海冰漂移速度从0.315 m/s到1.053 m/s变化，在冰水分界区域以及靠近沿岸的区域，海冰平移速度达到1.0 m/s以上，辽东湾沿岸流冰偏南方向频率均超过偏北方向频率，尤其东岸海域最为明显，运动方向以西南方向为主。辽东湾东岸比西岸海冰运动速度大，辽东湾个别区域出现了明显的无冰区，这是因为在云层覆盖或者无明显特征海冰的区域没有选择海冰样本。


图 7 2012-02-19渤海辽东湾海冰平移结果
Fig. 7 Sea ice drift of Liaodongwan in Bohai Sea on February 19，2012

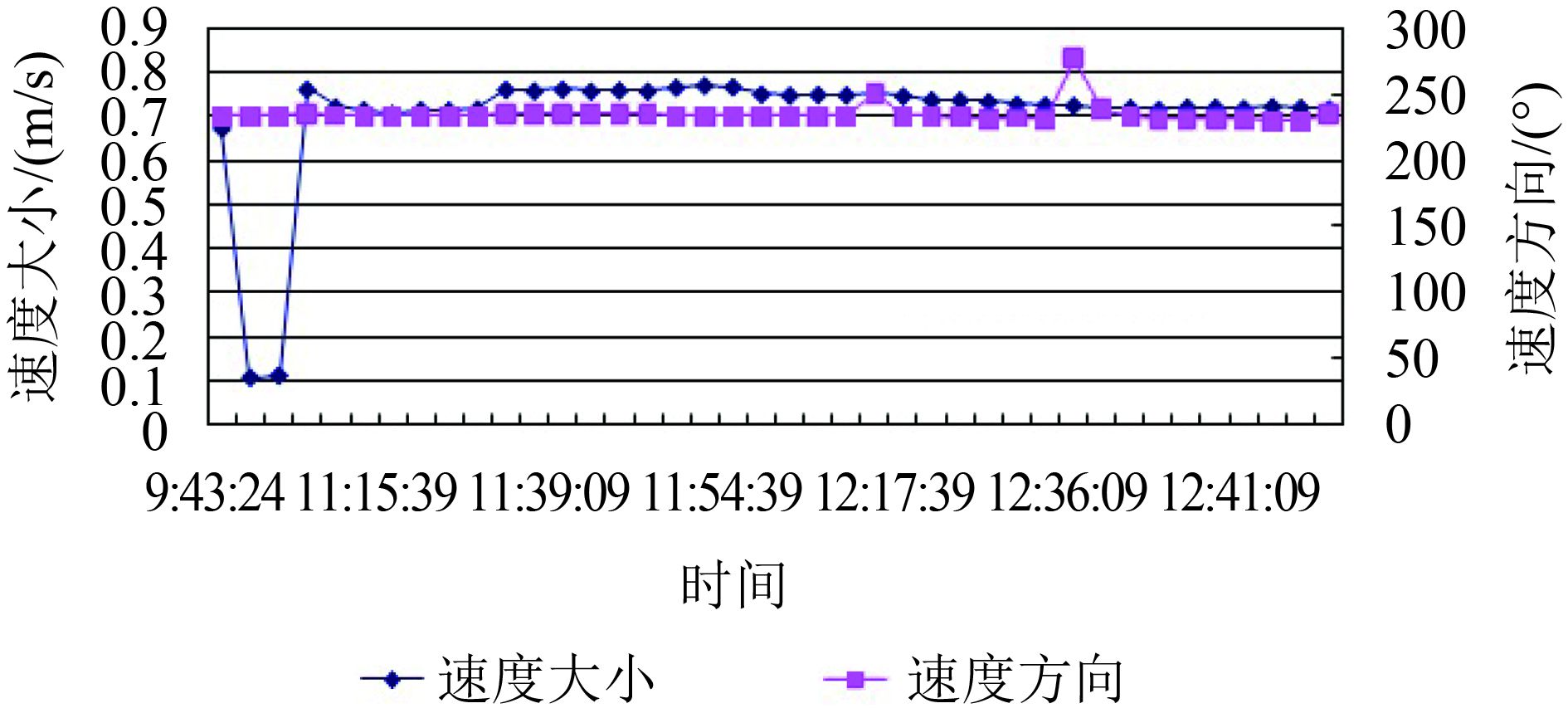
为了评估算法的质量，将漂移矢量场与人工搜集的参考数据进行比较。人工参考数据来自浮标站或海洋观测站的现场实测结果，目前，渤海的浮标站仍在建设中，实际获取的浮标数据只有2012年01月29号一天的数据，从实测数据轨迹曲线可知(如图 8所示)，当日的海冰漂移速度为0.1—0.8 m/s，以西南方向为主，跟踪结果与实测数据基本吻合。由于现场数据面积较小，无法对实验结果获取的漂移速度和方向进行定量分析，本文对此仅作定性的研究。


图 8 2012-01-29鲅鱼圈现场实测数据轨迹
Fig. 8 The trajectory of in-suit data derived from Bayuquan January on 29，2012

3.4 错误矢量的过滤

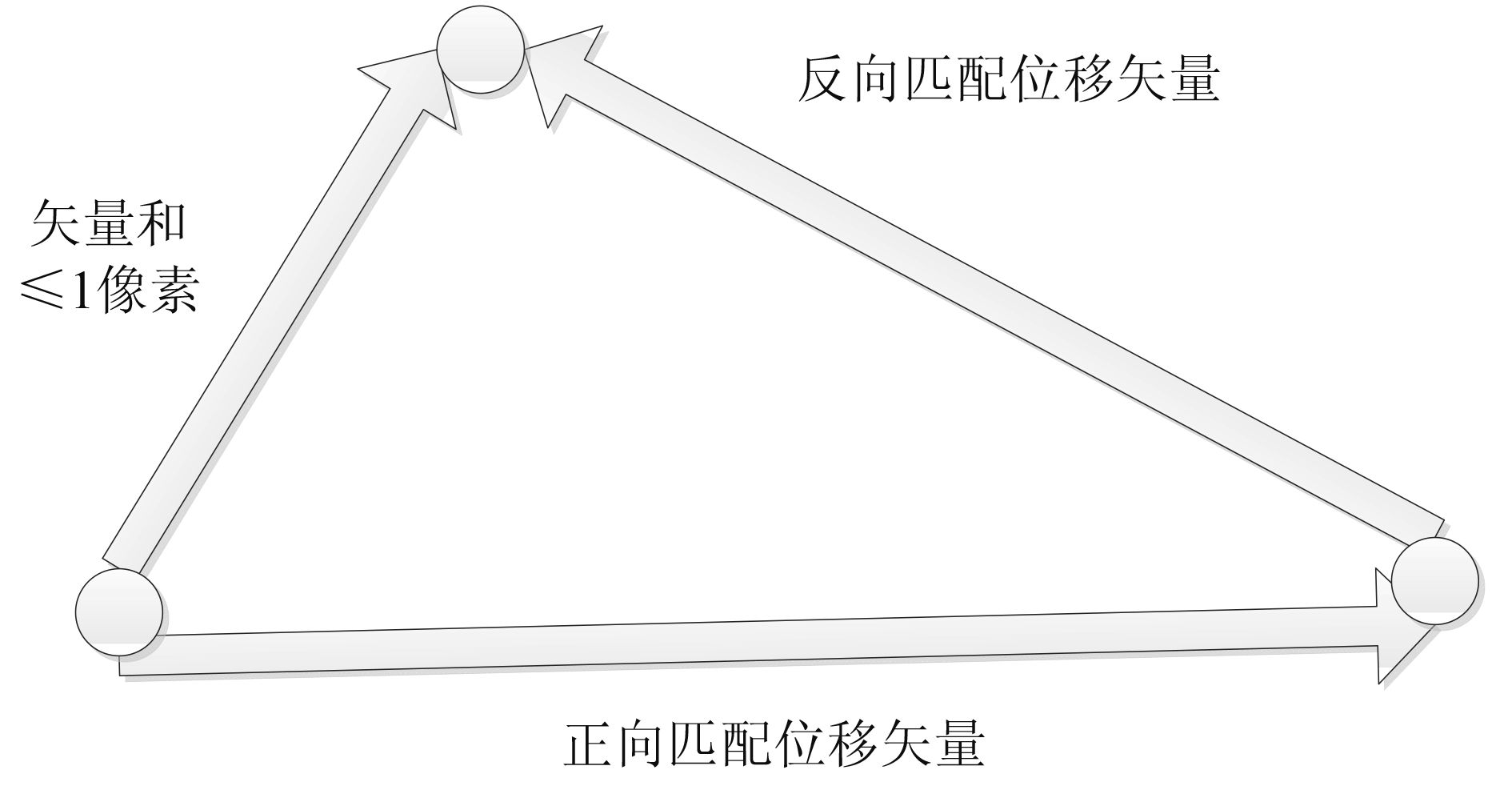
为了过滤匹配错误的样本，许多研究建议设置互相关系数的阈值，排除一些相关系数比较小、方向差异较大或与周围矢量场明显不同的速度矢量。但是，上述方法仍不能完全过滤错误矢量。文中利用双向匹配法进行二次过滤。正向匹配按照参考图像区域到匹配图像区域的顺序得到特征样本，并进行后续一系列运算，最终得到参考图像海冰样本及其相应匹配样本的中心坐标。其次按照相反的顺序进行反向搜索，又得到一组互相匹配的海冰特征样本集。理想情况下，正、反向匹配位移之和为零，即匹配程度最高。据此特性，设计一种错误矢量的过滤方法：如果同一特征区域海冰样本的正、反向位移矢量之和的绝对值大于1个像素，则丢弃该区域的特征样本，否则保留。计算过程如图 9所示。


图 9 正向—反向匹配图
Fig. 9 Forward and reverse matching

4 结 论

以往开展的海冰漂移监测中，常忽略海冰的旋转，本文对渤海海冰同时开展了旋转和平移的监测。利用投影变换代替极坐标变换，消除了传统相位相关方法中忽略相位信息所带来的跟踪误差，并结合相位相关法，以样本窗口为单位跟踪渤海辽东湾的海冰运动。以手动测量的旋转角度为基准，与传统方法相比，本文方法测得的角度均方根误差明显降低，该方法与传统相位相关法的旋转监测均方根误差的最大值/平均值分别为0.59/0.50与1.41/0.94，跟踪速度提高了50.6%。根据现场测试数据，渤海辽东湾2012年01月29号鲅鱼圈的海冰平移速度大小为0.11—0.78 m/s，漂移方向以西南为主，本文实验结果与之基本吻合。此外，在实验所选取的时间段内，计算得到的辽东湾海冰平移速度变化范围与历史资料记载基本一致。

基于区域的匹配方法能够快速地获取匹配区域，但是该算法对于边缘冰区效果不佳。未来应结合特征跟踪的方法，并融入特征提取算法，如sift、harris等算子实现精度更高的匹配；中国的海洋观测站尚在建设中，未来更多的浮标数据将对算法的定量验证提供充分的条件；使用多源遥感数据或者分辨率更高的遥感数据用于渤海海冰运动分析，将得到更加全面、准确的结果。

参考文献(References)

  • Bai S, Liu Q Z, Li H, Wu H D.1999.Sea ice in the Bohai sea of China. Marine Forecasts, 16 (3) : 1–9 .
  • ( 白珊, 刘钦政, 李海, 吴辉锭. 1999. 渤海的海冰. 海洋预报, 16 (3) : 1–9. )
  • Bracewell R N, Chang K Y, Jha A K, Wang Y H.1993.Affine theorem for two-dimensional Fourier transform. Electronics Letters, 29 (3) : 304 [DOI:10.1049/el:19930207]
  • Das Peddada S, McDevitt R.1996.Least average residual algorithm(LARA) for tracking the motion of Arctic sea ice. IEEE Transactions on Geoscience and Remote Sensing, 34 (4) : 915–926 . [DOI:10.1109/36.508408]
  • Fily M, Rothrock D A.1987.Sea ice tracking by nested correlations. IEEE Transactions on Geoscience and Remote Sensing, GE-25 (25) : 570-–580 . [DOI:10.1109/TGRS.1987.289836]
  • Gong S W, Chen Z and Zhang X. 2015. Extraction of drift direction and speed of sea ice of the Huanghai and Bohai Sea based on GOCI satellite//International Industrial Informatics and Computer Engineering Conference.[s.l.]:Atlantis Press:895-898
  • Hollands T, Dierking W.2011.Performance of a multiscale correlation algorithm for the estimation of sea-ice drift from SAR images:initial results. Annals of Glaciology, 52 (57) : 311–317 . [DOI:10.3189/172756411795931462]
  • Hollands T, Linow S, Dierking W.2015.Reliability measures for sea ice motion retrieval from synthetic aperture radar images. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 8 (1) : 67–75 . [DOI:10.1109/JSTARS.2014.2340572]
  • Keller Y, Averbuch A, Israeli M.2005.Pseudopolar-based estimation of large translations, rotations, and scalings in images. IEEE Transactions on Image Processing, 14 (1) : 12–22 . [DOI:10.1109/TIP.2004.838692]
  • Kwok R, Curlander J C, McConnell R, Pang S S.1990.An ice-motion tracking system at the Alaska SAR facility. IEEE Journal of Oceanic Engineering, 15 (1) : 44–54 . [DOI:10.1109/48.46835]
  • Komarov A and Barber D. 2012. Detection of sea ice motion from coand cross-polarization Radarsat-2 images//2012 IEEE International Geosciences and Remote Sensing Symposium (IGARSS). Munich:IEEE:3277-2280[DOI:10.1109/IGARSS.2012.6350604]
  • Lang W H, Wu Q, Zhang X, Meng J M, Wang N, Cao Y J.2014.Sea ice drift tracking in the Bohai Sea using geostationary ocean color imagery. Journal of Applied Remote Sensing, 8 (1) : 083650 [DOI:10.1117/1.JRS.8.083650]
  • Lavergne T, Eastwood S, Teffah Z, Schyberg H, Breivik L A.2010.Sea ice motion from low-resolution satellite sensors:an alternative method and its validation in the Arctic. Journal of Geophysical Research, 115 : C10032 [DOI:10.1029/2009JC005958]
  • Liu H X, Wang L, Tang S J, Jezek K C.2012.Robust multi-scale image matching for deriving ice surface velocity field from sequential satellite images. International Journal of Remote Sensing, 33 (6) : 1799–1822 . [DOI:10.1080/01431161.2011.602128]
  • Luo Z B, Zhang Y K and Wu Z J. 2008. Image fast matching algorithm based on extended phase correlation//Graphics Technology and Application Progress-the Third Image Technology and Application of Academic Conference Proceedings. Beijing:China Society of Image and Graphics, 182-187
  • Reddy B S, Chatterji B N.1996.An FFT-based technique for translation, rotation, and scale-invariant image registration. IEEE Transactions on Image Processing, 5 (8) : 1266–1271 . [DOI:10.1109/83.506761]
  • Sarvaiya J N, Patnaik S, Kothari K.2012.Image registration using log polar transform and phase correlation to recover higher scale. Journal of Pattern Recognition Research, 7 (1) : 90–105 . [DOI:10.13176/11.355]
  • Wei C T, Wu P, Zhang Z X, Zhang J Q.2011.An image matching algorithm based on improved log-polar image transform. Bulletin of Surveying and Mapping, (4) : 19–22 .
  • ( 韦春桃, 吴平, 张祖勋, 张剑清. 2011. 一种改进的相位相关的影像配准方法. 测绘通报, (4) : 19–22. )
  • Yan H S.2005.The Application of Binary three Lagrange polynomial in water calculation. China Science and Technology Information, (13) : –92, 86 .
  • ( 颜何生. 2005. 二元三点拉格朗日插值法在水能计算中的应用. 中国科技信息, (13) : –92, 86. )
  • Yang G J. Sea Ice Engineering. Beijing: Petroleum industry press 2000 : 1 -50.
  • ( 杨国金. 2000. 海冰工程学. 北京: 石油工业出版社 : 1 -50. )
  • Yu J, Yang Y, Liu A K, Zhao Y H.2009.Analysis of sea ice motion and deformation in the marginal ice zone of the Bering Sea using SAR data. International Journal of Remote Sensing, 30 (14) : 3603–3611 . [DOI:10.1080/01431160802585355]
  • Zhang F J.1979.Basic feature of sea ice in China. Marine Science and Technology Information, (6) : 99–125 .
  • ( 张方俭. 1979. 我国海冰的基本特征. 海洋科技资料, (6) : 99–125. )
  • Zhang X. 2011. Research on Sea Ice Thickness Detectionby Polarimetric SAR in Bohai Sea. Qingdao:Ocean University of China, 1-14