A kernel contextual bandit recommendation algorithm
-
摘要: 个性化推荐服务在当今互联网时代越来越重要，但是传统推荐算法不适应一些高度变化场景。将线性上下文多臂赌博机算法(linear upper confidence bound, LinUCB)应用于个性化推荐可以有效改善传统推荐算法存在的问题，但遗憾的是准确率并不是很高。本文针对LinUCB算法推荐准确率不高这一问题，提出了一种改进算法K-UCB(kernel upper confidence bound)。该算法突破了LinUCB算法中不合理的线性假设前提，利用核方法拟合预测收益与上下文间的非线性关系，得到了一种新的在非线性数据下计算预测收益置信区间上界的方法，以解决推荐过程中的探索–利用困境。实验表明，本文提出的K-UCB算法相比其他基于多臂赌博机推荐算法有更高的点击率(click-through rate, CTR)，能更好地适应变化场景下个性化推荐的需求。Abstract: Personalized recommendations are becoming increasingly significant in the Internet era; however, conventional recommendation algorithms cannot adapt to the highly changing scenarios. Applying the linear contextual bandit algorithm (linear upper confidence bound, LinUCB) to personalized recommendations can effectively overcome the limitations of conventional recommendation algorithms; however, the accuracy is not sufficiently high. Herein, an improved kernel upper confidence bound (K-UCB) algorithm is proposed to handle the insufficient recommended accuracy of the LinUCB algorithm. The proposed algorithm breaks through the unreasonable linear hypothesis of the LinUCB algorithm and uses the kernel method to fit the nonlinear relation between the expected reward and context. A new method for calculating the upper confidence bound of estimate rewards under nonlinear data is established to the exploration–exploitation balance in the recommendation process. Experiments show that the proposed K-UCB algorithm exhibits higher recommended accuracy than other recommendation algorithms based on multiarmed bandits and can better adapt to the need for personalized recommendations in changing scenarios.
-
个性化推荐在各种系统中被广泛应用，通过为用户提供定制化的网络服务，可以很好地满足用户的个性化需求，从而提升用户满意度。尽管传统推荐算法在一些领域已经非常成功，但是仅适用于用户和内容变化小的相对静态的场景[1]。例如，传统协同过滤[2-3]需要在用户和内容有大量重叠的消费记录等信息的场景下才能应用，而基于内容的推荐算法[4-5]推荐倾向于过于相似的内容，对新用户的推荐存在困难。
现实生活中存在着快速变化的推荐环境，其内容领域每时每刻都在发生着变化，内容的流行程度随着时间而变化，大量没有任何历史记录的新用户也不断进入推荐系统。在这种场景下推荐系统必须能够快速获得用户的兴趣偏好，才能更好地为用户提供个性化服务。快速获得用户兴趣信息和短期内用户体验是竞争关系，一方面需要关注能够提高用户兴趣的内容，另一方面也需要探索新内容以全面改善用户体验，这就产生了探索–利用困境(exploration-exploitation dilemma，EE)[6]。为了实现用户的长期体验，必须平衡探索和利用的矛盾。
多臂赌博机[7-9]是平衡这一矛盾的有效模型，多臂赌博机又可以按照是否考虑状态分为上下文无关多臂赌博机和上下文多臂赌博机[10-11]。上下文无关多臂赌博机算法主要有ε-greedy[12]、UCB1[13]、Thompson sampling[14]等。这类上下文无关的多臂赌博机算法应用于推荐系统中，没有利用用户和内容的上下文信息，因此导致推荐准确性不高。
上下文多臂赌博机算法将内容和用户等上下文信息融入推荐决策过程，可以提高推荐准确率。LinUCB (linear upper confidence bound)是一种成功应用于雅虎新闻推荐系统的上下文多臂赌博机算法，可以有效提高在快速变化环境下的推荐准确率[15]。但是LinUCB算法为了简化模型和降低计算成本，假设期望收益和上下文是线性关系的。这种线性假设在现实中往往是不成立的，所以导致LinUCB算法的推荐准确率并不高。Agrawal等[16]提出的汤普森采样算法LinTS，同样是基于线性收益上下文赌博机模型。
在LinUCB算法基础上，结合传统推荐算法提出了很多改进算法。文献[17]结合协同过滤的思想将用户之间的影响融合到LinUCB算法，提出了GOB.Lin算法。文献[18]提出了利用用户信息在线聚类算法CLUB，对用户聚类。文献[19]提出了对用户和内容双聚类的COFIBA算法。文献[20]提出结合潜在因子的fatorUCB算法。这些传统推荐算法与多臂赌博机的结合可以提升推荐效果，但都属于结合创新，没有改进线性收益的上下文多臂赌博机模型。
本文突破了LinUCB算法线性假设的前提，提出了一种基于核方法[21]在非线性前提下计算预测收益置信区间上界的方法，从模型上改进基于线性收益的上下文多臂赌博机，提高了算法的推荐准确率。
1. 背景模型
1.1 上下文多臂赌博机
推荐系统中EE问题方面一个得到广泛研究的模型就是上下文多臂赌博机模型，将该模型形式化来进行更好的理解。上下文多臂赌博机是指面对K个臂,每轮选择其中一个臂并获得收益，一共进行T轮选择，目标是使T轮之后总的收益更高。上下文多臂赌博机在每一轮中：
1）观察当前上下文信息
$\boldsymbol{x}$ 。上下文总结了当前的环境，如日期、天气、用户等影响做出选择的信息。2）根据历史记录，算法选择一个臂
$a$ 并获得真实收益$r$ 。预测收益由上下文信息$\boldsymbol{x}$ 所决定。3）算法根据最新得到的观测历史
$(\boldsymbol{x},a,r)$ ，更新下一轮选择策略。多臂赌博机最大化总收益的优化目标可以等价替换为更常用的累积遗憾，表示为
$$ {R_T}: = E\left[ {\sum\limits_{t = 1}^T {(r_t^ * - {r_t})} } \right] $$ 式中：
${r_t}$ 为在每一轮中实际获得的收益；$r_t^ * $ 为每一轮中最佳选择的收益。可以很自然地将上下文多臂赌博机建模为推荐算法。以新闻推荐为例，将新闻文章库中的文章定义为臂，通过上下文信息为用户推荐这些臂(文章)。观察所推荐文章的反馈，当推荐文章被点击则收益为1，否则为0。最后根据历史收益信息，调整选择策略。这样一段时间后最大化上下文多臂赌博机的收益相当于最大化点击数，也就是推荐系统的目标点击率(click-through rate, CTR)更高。
1.2 LinUCB算法
LinUCB是一种上下文多臂赌博机算法，该算法基于期望收益
$r$ 和上下文$\boldsymbol{x}$ 是线性关系的假设，得到了线性条件下的预测收益及其置信区间的闭式解，然后利用预测收益的置信区间上界来平衡探索与利用的矛盾。LinUCB算法的主要过程如下:1) 计算预测收益。
${\boldsymbol{x}_{t,a}} \in {{\bf{R}}^d}$ 表示关于用户$t$ 和内容$a$ 的上下文特征向量，${\boldsymbol{\theta }_a}$ 为内容$a$ 的预测线性参数，则预测收益表示为$$ {y_{t,a}} = \boldsymbol{\theta }_a^{\text{T}}{\boldsymbol{x}_{t,a}} $$ (1) ${\boldsymbol{X}_a}$ 是关于内容$a$ 的上下文特征的构造矩阵，每一行表示一个上下文${\boldsymbol{x}_{t,a}}$ ,一共m行，定义如下:$$ {\boldsymbol{X}_a}: = {\left[ {{\boldsymbol{x}_{1,a}}\;{\boldsymbol{x}_{2,a}}\; \cdots \;{\boldsymbol{x}_{m,a}}} \right]^{\text{T}}} \in {{\bf{R}}^{m \times d}} $$ ${\boldsymbol{X}_a}$ 中的m个上下文对应的实际收益表示为${\boldsymbol{y}_a}$ 。在训练数据$({\boldsymbol{X}_a},{\boldsymbol{y}_a})$ 上应用岭回归可得到内容$a$ 的预测线性参数为$$ {\boldsymbol{\theta }_a} = {(\boldsymbol{X}_a^{\text{T}}{\boldsymbol{X}_a}\boldsymbol{ + }{\boldsymbol{I}_d})^{ - 1}}\boldsymbol{X}_a^{\text{T}}{\boldsymbol{y}_a} $$ (2) 然后通过式(1)和式(2)计算得到预测收益。
2) 计算预测收益的置信区间。根据文献[22]可知，在线性条件下有
$$ \left| {\boldsymbol{\theta }_a^{\text{T}}{\boldsymbol{x}_{t,a}} - {{\boldsymbol{y}}_{t,a}}} \right| \leqslant \alpha \sqrt {\boldsymbol{x}_{t,a}^{\text{T}}{{(\boldsymbol{X}_a^{\text{T}}{\boldsymbol{X}_a}\boldsymbol{ + }{\boldsymbol{I}_d})}^{ - 1}}{\boldsymbol{x}_{t,a}}} $$ (3) 式(3)成立的概率至少为
$1 - \delta $ ,$\delta $ 为任意大于0的实数，$\alpha = 1 + \sqrt {\ln (2/\delta )/2} $ 是一个常数。实际上式(3)给出的预测收益的置信区间半径c为$$ c = \alpha \sqrt {\boldsymbol{x}_{t,a}^{\text{T}}{{(\boldsymbol{X}_a^{\text{T}}{\boldsymbol{X}_a}\boldsymbol{ + }{\boldsymbol{I}_d})}^{ - 1}}{\boldsymbol{x}_{t,a}}} $$ (4) 3) 由式(1)和式(4)可以得到每轮的选择策略，即对每一轮选择置信区间上界最大的内容
${a_t}$ 进行推荐$$ {a_t} = {{\rm{argmax}}_{a \in A}}(\boldsymbol{\theta }_a^{\text{T}}{\boldsymbol{x}_{t,a}} + c) $$ 最大置信区间上界是一种利用估计中的不确定性来平衡探索和利用的方法。算法对不确定性采取乐观的态度，将对收益估计的置信区间上界作为选择内容的依据。这样选择的好处在于:如果选择的内容是最佳的，则成功得到了收益;如果选择的内容并非最佳，则进一步消除了置信区间上界最大内容的不确定性。最后根据所选择内容
${a_t}$ 的真实收益更新内容${a_t}$ 的线性参数${\boldsymbol{\theta }_a}$ 。LinUCB本质上是一种基于线性收益的上下文多臂赌博机，但是在现实的网络服务中获取到的数据往往并不是线性关系，所以导致LinUCB算法应用于个性化推荐预测准确率不高。
2. K-UCB算法
为了解决LinUCB算法线性假设造成的推荐准确率不高，本文提出了K-UCB(kernel upper confidence bound)算法，基于核方法实现了在高维线性空间计算预测收益及其置信区间，从而提高了推荐准确率。
2.1 算法设计
核方法是一种解决非线性问题的有效方法，其主要思想是将非线性数据向高维空间映射，使其在高维空间中转换为线性数据，然后就可以利用成熟的线性空间知识在高维空间中解决原先的非线性问题。
在核方法思想下，将上下文特征向量
$\boldsymbol{x}$ 映射到合适的高维空间，在这个高维空间中预测收益和上下文特征向量是线性关系，此时可以用基于线性收益的上下文赌博机知识来解决非线性收益的问题。在高维空间中计算预测收益及其置信区间:1) 计算预测收益。假设原空间向量
$\boldsymbol{x}$ 映射到高维空间后表示为${\boldsymbol{\varphi}} (\boldsymbol{x})$ 。高维空间中两个向量的内积可以表示为核函数$k(\boldsymbol{x},\boldsymbol{x'}) = {\boldsymbol{\varphi}} (\boldsymbol{x}) \cdot {\boldsymbol{\varphi}} (\boldsymbol{x'})$ 。对应原空间中构造矩阵$ \boldsymbol{X} $ ，则映射后上下文特征的构造矩阵$ {\boldsymbol{X}_\varphi } $ 表示为$$ {\boldsymbol{X}_\varphi }: = {\left[ {{\boldsymbol{\varphi}} ({\boldsymbol{x}_1}){\text{ }}{\boldsymbol{\varphi}} ({\boldsymbol{x}_2}){\text{ }} \cdots {\text{ }}{\boldsymbol{\varphi}} ({\boldsymbol{x}_m})} \right]^{\text{T}}} $$ 对训练数据
$({\boldsymbol{X}_\varphi },\boldsymbol{y})$ 使用核岭回归方法,则需要预测的上下文${\boldsymbol{x}^* }$ 的预测收益为$$ \begin{gathered} {{\boldsymbol{y}}^*} = {\boldsymbol{y}^{\text{T}}}{({({\boldsymbol{X}_{\boldsymbol{\varphi}} }\boldsymbol{X}_{\boldsymbol{\varphi}} ^{\text{T}}\boldsymbol{ + }{\boldsymbol{I}_m})^{ - 1}})^{\text{T}}}{\boldsymbol{X}_{\boldsymbol{\varphi}} }\varphi ({\boldsymbol{x}^ * }) =\\ {\boldsymbol{y}^{\text{T}}}{({(\boldsymbol{K + }{\boldsymbol{I}_m})^{ - 1}})^{\text{T}}}{\boldsymbol{k}_{X{x^*} }}\\ \end{gathered} $$ (5) 式中
${\boldsymbol{k}_{X{x^*} }}$ 为$ \boldsymbol{X} $ 中m个上下文特征与需要预测的上下文${\boldsymbol{x}^ * }$ 构成的核向量:$$ {\boldsymbol{k}_{X{x^*} }}: = {[k({\boldsymbol{x}_1}\;{\boldsymbol{x}^ * })\;k({\boldsymbol{x}_2}\;{\boldsymbol{x}^ * })\; \cdots \;k({\boldsymbol{x}_m}\;{\boldsymbol{x}^ * })]^{\text{T}}} $$ 而K则为m个上下文特征构成的核矩阵:
$$ \boldsymbol{K}: = \left( {\begin{array}{*{20}{c}} {k({\boldsymbol{x}_1}\boldsymbol{,}{\boldsymbol{x}_1})}&{k({\boldsymbol{x}_1}\boldsymbol{,}{\boldsymbol{x}_2})}& \cdots &{k({\boldsymbol{x}_1}\boldsymbol{,}{\boldsymbol{x}_m})} \\ {k({\boldsymbol{x}_2}\boldsymbol{,}{\boldsymbol{x}_1})}&{k({\boldsymbol{x}_2}\boldsymbol{,}{\boldsymbol{x}_2})}& \cdots &{k({\boldsymbol{x}_2}\boldsymbol{,}{\boldsymbol{x}_m})} \\ \vdots & \vdots &{}& \vdots \\ {k({\boldsymbol{x}_m}\boldsymbol{,}{\boldsymbol{x}_1})}&{k({\boldsymbol{x}_m}\boldsymbol{,}{\boldsymbol{x}_2})}& \cdots &{k({\boldsymbol{x}_m}\boldsymbol{,}{\boldsymbol{x}_m})} \end{array}} \right) $$ K为半正定的核矩阵，所以
${(\boldsymbol{K + }{\boldsymbol{I}_m})^{ - 1}}$ 一定存在。2) 计算预测收益的置信区间。由于映射后高维空间满足线性关系，则映射后高维空间与原空间是类似的，满足:
$$ \left| {{\boldsymbol{\theta }^{\text{T}}}{\boldsymbol{\varphi}} ({\boldsymbol{x}^ * }) - {{\boldsymbol{y}}^ * }} \right| \leqslant \alpha \sqrt {{{\boldsymbol{\varphi}} ^{\text{T}}}({\boldsymbol{x}^ * }){{(\boldsymbol{X}_\varphi ^{\text{T}}{\boldsymbol{X}_\varphi }\boldsymbol{ + }{\boldsymbol{I}_d})}^{ - 1}}{\boldsymbol{\varphi}} ({\boldsymbol{x}^ * })} $$ (6) 式(6)成立的概率至少为
$1 - \delta $ ,$\delta $ 为任意大于0的实数,$\alpha = 1 + \sqrt {\ln (2/\delta )/2} $ 是一个常数，此时同样也有与原空间形式类似的置信区间半径c:$$ c = \alpha \sqrt {{{\boldsymbol{\varphi}} ^{\text{T}}}({\boldsymbol{x}^ * }){{(\boldsymbol{X}_\varphi ^{\text{T}}{\boldsymbol{X}_\varphi }\boldsymbol{ + }{\boldsymbol{I}_d})}^{ - 1}}{\boldsymbol{\varphi}} ({\boldsymbol{x}^ * })} $$ (7) 需要将式(7)变为核函数的形式，利用Sherman-Morrison-Woodbury公式, Sherman-Morrison-Woodbury公式描述如下:
$\boldsymbol{A} \in {{\bf{R}}^{n \times n}}$ 为${\bf{R}}$ 域上非奇异矩阵，$\boldsymbol{U},\boldsymbol{V} \in {{\bf{R}}^{n \times k}}$ ，若$\boldsymbol{A} + \boldsymbol{U}{\boldsymbol{V}^T}$ 非奇异，则有$$ {(\boldsymbol{A} + \boldsymbol{U}{\boldsymbol{V}^{\text{T}}})^{ - 1}} = {\boldsymbol{A}^{ - 1}} - {\boldsymbol{A}^{ - 1}}\boldsymbol{U}{({\boldsymbol{I}_k}\boldsymbol{ + }{\boldsymbol{V}^{\text{T}}}{\boldsymbol{A}^{ - 1}}\boldsymbol{U})^{ - 1}}{\boldsymbol{V}^{\text{T}}}{\boldsymbol{A}^{ - 1}} $$ (8) 式(8)提供了将式(7)变为核函数形式的一种途径，使式(8)中
$\boldsymbol{A} = {\boldsymbol{I}_d},\boldsymbol{U }= {\boldsymbol{X}}_\varphi ^{\text{T}},\boldsymbol{V }={\boldsymbol{X}_\varphi }$ ，那么有$$ \begin{gathered} {\text{ }}{{\boldsymbol{\varphi}} ^{\text{T}}}({\boldsymbol{x}^ * }){(\boldsymbol{X}_{\boldsymbol{\varphi}} ^{\text{T}}{\boldsymbol{X}_{\boldsymbol{\varphi}} } + {\boldsymbol{I}_d})^{ - 1}}{\boldsymbol{\varphi}} ({\boldsymbol{x}^ * }) =\\ {{\boldsymbol{\varphi}} ^{\text{T}}}({\boldsymbol{x}^ * })({\boldsymbol{I}_m} - \boldsymbol{X}_\varphi ^{\text{T}}{({\boldsymbol{X}_\varphi }\boldsymbol{X}_\varphi ^{\text{T}}\boldsymbol{ + }{\boldsymbol{I}_m})^{ - 1}}{\boldsymbol{X}_\varphi }){\boldsymbol{\varphi}} ({\boldsymbol{x}^ * }) =\\ {{\boldsymbol{\varphi}} ^{\text{T}}}({\boldsymbol{x}^ * }){\boldsymbol{\varphi}} ({\boldsymbol{x}^ * }) - {{\boldsymbol{\varphi}} ^{\text{T}}}({\boldsymbol{x}^ * })\boldsymbol{X}_\varphi ^{\text{T}}{({\boldsymbol{X}_\varphi }\boldsymbol{X}_\varphi ^{\text{T}}\boldsymbol{ + }{\boldsymbol{I}_m})^{ - 1}}{\boldsymbol{X}_\varphi }{\boldsymbol{\varphi}} ({\boldsymbol{x}^ * }) =\\ k({\boldsymbol{x}^ * },{\boldsymbol{x}^ * }) - \boldsymbol{k}_{X{x^*} }^{\text{T}}{(\boldsymbol{K} + {\boldsymbol{I}_m})^{ - 1}}{\boldsymbol{k}_{X{x^* }}} \\ \end{gathered} $$ (9) 将式(9)代入式(7)可以得到核函数形式的置信区间半径为
$$ c = \alpha \sqrt {k({\boldsymbol{x}^ * },{\boldsymbol{x}^ * }) - \boldsymbol{k}_{Xx^* }^{\text{T}}{{(\boldsymbol{K} + {\boldsymbol{I}_m})}^{ - 1}}{\boldsymbol{k}_{Xx^* }}} $$ (10) 3) 计算逆矩阵。核函数形式的预测收益式(5)及其置信区间式(10)中都有
${(\boldsymbol{K} + {\boldsymbol{I}_m})^{ - 1}}$ 这一项，将该逆矩阵记为${\boldsymbol{V}_m}$ 。${\boldsymbol{V}_m}$ 大小为m$ \times $ m，直接求逆矩阵复杂度为O(m3)，当m很大时代价很大，算法失去实际意义。为解决这个问题，本文将矩阵求逆修改为迭代计算方式。根据文献[23]可知，实对称矩阵有求逆迭代算法。实对称矩阵${\boldsymbol{W}}_n $ 如式(11)所示：$$ {\boldsymbol{W}_n} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{W}_{n - 1}}}&\boldsymbol{e} \\ {{\boldsymbol{e}^{\text{T}}}}&p \end{array}} \right] $$ (11) 式中：
${\boldsymbol{W}_n} \in {{\bf{R}}^{n \times n}}$ ，${\boldsymbol{W}_{n - 1}} \in {{\bf{R}}^{(n - 1) \times (n - 1)}}$ 均为实对称矩阵；$\boldsymbol{e}$ 为$n - 1$ 维向量，${\boldsymbol{e}^{\text{T}}}$ 是其转置；$p$ 是常数。$ {\boldsymbol{W}_n} $ 的逆矩阵可以通过迭代计算，即$$ \begin{gathered} \boldsymbol{W}_n^{ - 1} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{W}_{n - 1}^{ - 1}}&\boldsymbol{0} \\ {{\boldsymbol{0}^{\text{T}}}}&0 \end{array}} \right] + \frac{1}{{p + {\boldsymbol{e}^{\text{T}}}\boldsymbol{b}}}\left[ {\begin{array}{*{20}{c}} {\boldsymbol{bb}}^{\rm{T}}&\boldsymbol{b} \\ {{\boldsymbol{b}^{\text{T}}}}&1 \end{array}} \right] \\ \boldsymbol{b } = - \boldsymbol{W}_{n - 1}^{ - 1}\boldsymbol{e} \\ \end{gathered} $$ (12) 式(12)可由块矩阵求逆定理证明。
$\boldsymbol{K} + \boldsymbol{I}$ 也是实对称矩阵，形式为$$ {\boldsymbol{K}_m} + {\boldsymbol{I}_m} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{K}_{m - 1}} + {\boldsymbol{I}_{m - 1}}}&{{\boldsymbol{k}_{X * }}} \\ {\boldsymbol{k}_{X * }^{\text{T}}}&{k({\boldsymbol{x}^ * },{\boldsymbol{x}^ * })} \end{array}} \right] $$ 满足式(11)的定义,可以得到其逆矩阵
$\boldsymbol{V}$ 的迭代计算方法:$$ \begin{gathered} {\boldsymbol{V}_m} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{V}_{m - 1}}}&\boldsymbol{0} \\ {{\boldsymbol{0}^{\text{T}}}}&0 \end{array}} \right]{\text{ + }}\frac{1}{{k({\boldsymbol{x}^ * },{\boldsymbol{x}^ * }) + \boldsymbol{k}_{Xx^* }^{\text{T}}\boldsymbol{b}}}\left[ {\begin{array}{*{20}{c}} {\boldsymbol{bb}}^{\rm{T}}&\boldsymbol{b} \\ {{\boldsymbol{b}^{\text{T}}}}&1 \end{array}} \right] \\ \boldsymbol{b } = - {\boldsymbol{V}_{m - 1}}{\boldsymbol{k}_{Xx^* }} \\ \end{gathered} $$ (13) 这样就可以通过式(13)不断迭代来计算逆矩阵，减少了该算法的计算成本。
2.2 算法流程
K-UCB算法需要输入超参数
$ \alpha 、\beta $ 的值，其中$\alpha $ 控制探索与利用的平衡，$\beta $ 是核函数的参数。为需要推荐的每个用户计算内容池${\boldsymbol{A}_t}$ 中每个内容预测收益的置信区间上界，选择置信区间上界最大的内容进行推荐，并获得点击反馈，根据历史收益情况，更新选择策略。算法 K-UCB算法
输入 探索参数
$\alpha $ ，核函数参数$\beta $ ；输出 推荐记录。
1）获取当前用户
${u_t}$ 的内容池${\boldsymbol{A}_t}$ ，获取内容池中所有内容$a \in {\boldsymbol{A}_t}$ 的上下文${\boldsymbol{x}_a}$ 。2）根据式(5)计算所有内容的预测收益
$ {y_a} $ 。3）根据式(10)计算所有内容的预测收益的置信区间上界
${c_a}$ 。4）计算所有内容预测收益的置信区间上界，选择置信区间上界最大的内容
${a_t} = {\rm{argmax}}_{a \in {\boldsymbol{A}_t}}({y_a} + {c_a})$ 。5）将内容
${a_t}$ 推荐给用户，观察获得的实际收益${r_t}$ ，输出推荐记录$\left( {{u_t},{a_t},{r_t}} \right)$ 。6）更新内容
${a_t}$ 的参数：${\boldsymbol{X}_{{a_t}}} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{X}_{{a_t}}}} \\ {{\boldsymbol{x}_{t,{a_t}}}} \end{array}} \right], {\boldsymbol{y}_{{a_t}}} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{y}_{{a_t}}}} \\ {{r_t}} \end{array}} \right]$ ，$\begin{aligned}\boldsymbol{b } = - {\boldsymbol{V}_{{a_t}}}{\boldsymbol{k}_X}_{{a_t}} , {\boldsymbol{V}_{{a_t}}} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{V}_{{a_t}}}}& \boldsymbol{0} \\ {{\boldsymbol{0}^{\text{T}}}}&0 \end{array}} \right] + \frac{1}{{k({\boldsymbol{x}_{{a_t}}},{\boldsymbol{x}_{{a_t}}};\beta ) +\boldsymbol{k}_{X{a_t}}^{\text{T}}\boldsymbol{b}}}\left[ {\begin{array}{*{20}{c}} {\boldsymbol{bb}}&\boldsymbol{b} \\ {{\boldsymbol{b}^{\text{T}}}}&1 \end{array}} \right] \end{aligned}$ 。7）执行1）为下一位用户推荐，直至没有新的用户需要推荐则退出算法。
3. 实验与结果
在本节中首先介绍了各个对比算法的设置，并使用这些算法在合成数据和真实场景数据集(雅虎新闻数据集)上进行实验。
3.1 算法对比
1）Random ：随机策略总是以相等的概率选择一个内容。这个算法不需要参数，也不会随着时间学习。在本文中随机策略用来衡量其他算法的提升。
2）ε-greedy[12]：该算法统计每个内容的收益，以
$\varepsilon $ 概率随机选择候选内容，以$1 - \varepsilon $ 概率选择收益最高的内容。参数$\varepsilon $ 控制探索程度。3）UCB1[13]：该算法统计每个内容的收益，并估计收益的置信区间，置信区间为
$c = \alpha /\sqrt {\ln t} $ ，式中t为内容的历史总推荐次数，t越大内容的收益信息越明确，置信区间会越小，参数$\alpha $ 控制探索程度。4）Thompson sampling[14]：该算法假设每个内容都服从一个收益分布估计,每轮从估计的分布采样，选取采样值最大的内容推荐，最后根据收益情况更新内容的收益分布。这里采用Beta分布作为先验分布。
5）LinUCB[15]：算法在UCB1基础上加入上下文，基于线性收益假设预测收益及其置信区间。参数
$\alpha $ 控制探索程度。3.2 合成数据集
为了测试K-UCB的性能，合成了3组不同的上下文多臂赌博机数据。每组设置K=4个臂，进行T=15000轮实验，每一轮中臂的上下文
${\boldsymbol{x}_{t,k}}$ 是随机采样产生的20维单位向量。设置3组不同收益，由以下函数产生:$$ {r_1}(\boldsymbol{x}) = {\boldsymbol{\theta }^{\text{T}}}\boldsymbol{x} + \eta $$ $$ {r_2}(\boldsymbol{x}) = 3{({\boldsymbol{\theta }^{\text{T}}}\boldsymbol{x})^3} + 5{({\boldsymbol{\theta }^{\text{T}}}\boldsymbol{x})^2} + \eta $$ $$ {r_3}(\boldsymbol{x}) = \cos (3{\boldsymbol{\theta }^{\text{T}}}\boldsymbol{x}) + \eta $$ 式中：
$\boldsymbol{\theta }$ 是20维单位向量；$\eta \~ N(0,1)$ 为噪声项。图1为LinUCB和K-UCB算法在3组不同收益函数${r_1}(x)$ 、${r_2}(x)$ 和${r_3}(x)$ 下累积遗憾随学习轮次的变化曲线,且LinUCB和K-UCB算法参数都经过调优。如图1(a)所示，在${r_1}(x)$ 线性收益条件下，K-UCB和LinUCB算法累积遗憾随着学习轮次增多逐渐增长缓慢，但是LinUCB收敛速度优于K-UCB算法。在${r_2}(x) $ 和${r_3}(x) $ 非线性收益下，LinUCB算法效果不佳，累积遗憾不会随着学习轮次增多而降低增长速度。而K-UCB算法表现良好，随着学习轮次增多，累积遗憾增长放缓，该实验表明在非线性收益数据下K-UCB较LinUCB累积遗憾更低，性能更好。
图 1 LinUCB和K-UCB算法在不同收益假设上的比较Fig. 1 Comparison of LinUCB and K-UCB on different reward hypothesis
下载:
全尺寸图片
3.3 Yahoo News数据集
真实场景数据采用雅虎新闻数据集R6A – Yahoo! Front Page Today Module User Click Log Dataset[24]。该数据集收集了从2009年5月1日到10日的访问流量数据约3600万条。
如表1所示，每一条数据记录一个由4个部分组成的完整的事件，分别是推荐的文章id，用户的点击反馈以及用户和文章的6维特征。用户和文章的6维特征向量都是原始特征（如用户对应的性别、年龄、地理和行为等特征，文章对应的分类、主题等特征）通过降维和双线性模型联合分析构建的。
表 1 雅虎新闻数据集Table 1 Yahoo! News dataset字段 解释 1 推荐的文章id 2 点击反馈值(0或者1) 3 当前用户的6维特征 4 当前文章池中文章的6维特征 当算法选择的文章与记录数据不同时，无法观测到所选择文章的收益。本文采用文献[25]提出的离线评估方法，这种方法被证明是无偏的估计。在这种评估方法下，给定当前日志记录，如果算法选择了与日志记录相同的内容,则该事件被保留，即添加到历史记录中,同时更新总推荐次数N和总收益R。如果算法选择了一个不同于日志记录的内容，那么该事件将完全被忽略，算法将继续处理下一个事件而不改变其状态。基于这种拒绝采样的评估方法，将实际点击次数与推荐总次数的比值(R/N)定义为文章点击率。点击率是推荐算法的最常用指标，点击率越高意味着累积遗憾越小。
推荐系统通常在小部分流量中学习，然后将学习到的知识应用到其余的大部分流量中，所以本实验将数据分为学习桶和部署桶进行，学习桶分配20%的随机流量数据，部署桶分配80%的随机流量数据。数据更多的部署桶模拟真实的部署环境，其点击率数据更为重要，但学习桶中点击率高意味着学习效率更快，所以实验给出了两个桶中的点击率数据。
实验分为3步：①确定3种对比算法(ε-greedy、UCB1和LinUCB)的最佳参数；②确定K-UCB的核函数选择和参数选择；③将所有对比算法均在最优条件下进行比较。
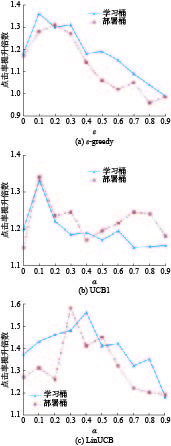
1) 寻找ε-greedy、UCB1和LinUCB的最佳参数设置，图2为3个算法在不同参数下的性能折线图。
如图2所示，3个算法在学习桶和部署桶都是大致中间高两边低。这是因为当参数ε或者
$\alpha $ 过小时，没有足够的探索，算法无法识别出好的文章，导致点击量较少。另一方面，当参数太大时，算法会过度探索，从而浪费了一些增加点击次数的机会。从图2中可以看到，ε-greedy、UCB1和LinUCB的最佳参数分别为0.2、0.1和0.3。
图 2 算法在不同参数下的点击率提升倍数Fig. 2 CTR lift of the algorithms under different parameters下载:
全尺寸图片
2) 表2为不同的核函数在最佳参数组合下所得到的相对点击率结果。其中
$\alpha $ 为平衡探索利用程度的参数，线性核具体表示为$$ k(\boldsymbol{x},\boldsymbol{x'}) = {\boldsymbol{x}^{\text{T}}}\boldsymbol{x'} $$ 多项式核具体表示为
$$ k({\boldsymbol{x}},{\boldsymbol{x}}′)={({\boldsymbol{g}}\cdot{\boldsymbol{x}}^{\text{T}}{\boldsymbol{x}}′ +c)}^{d} $$ 高斯核具体表示为
$$ k(\boldsymbol{x},\boldsymbol{x'}) = \exp ( - \beta \cdot ||\boldsymbol{x} - \boldsymbol{x'}|{|^2}) $$ 从表2可以看出，雅虎新闻数据集在线性核函数时表现不佳，表明数据在原始空间是线性不可分的。在多项式核函数时点击率较线性核有提升，较高斯核效果略差。所以K-UCB算法选择高斯核函数进行雅虎新闻数据集的实验。
表 2 核函数选择Table 2 Kernel function selection核函数 最佳参数 学习桶 部署桶 线性核 α=0.2 1.35 1.31 多项式核 α=0.2,g=0.1,c=1,d=2 1.48 1.45 高斯核 α=0.2，β=0.1 1.72 1.68 以高斯核函数为例说明具体参数选择方法，设置30组
$(\alpha ,\beta )$ 参数组合进行网格搜索，表3和表4分别为在学习桶和部署桶中30组不同参数组合下K-UCB算法的点击率提升倍数。表 3 学习桶中网格搜索K-UCB参数结果Table 3 Grid search results of K-UCB in Learning Bucketα β 0.01 0.05 0.1 1 10 0.1 1.20 1.62 1.50 1.28 1.28 0.2 1.40 1.67 1.72 1.32 1.12 0.3 1.22 1.62 1.6 1.39 0.96 0.4 1.44 1.61 1.58 1.08 1.04 0.5 1.42 1.40 1.26 1.08 0.96 0.6 1.32 1.35 1.24 1.16 1.04 表 4 部署桶中网格搜索K-UCB参数结果Table 4 Grid search results of K-UCB in Deploying Bucketα β 0.01 0.05 0.1 1 10 0.1 1.12 1.62 1.49 1.36 1.32 0.2 1.32 1.65 1.68 1.36 1.04 0.3 1.12 1.61 1.63 1.39 1.09 0.4 1.36 1.61 1.59 1.06 1.04 0.5 1.41 1.34 1.46 1.20 1.12 0.6 1.36 1.14 1.26 1.16 1.04 从表3和表4中可以看到，当
$\alpha $ 过大过小时点击率都不高，这与1）的原理和结果相似。$\beta $ 是高斯核函数控制分类能力的参数，调整$\beta $ 也是寻找合适高维空间的过程。当$\beta $ 过小和过大时，点击率提升都不高，说明没有找到合适的特征高维空间。在$\beta = 0.1$ 这一列点击率大致较其他$\beta $ 取值高，说明找到了一个合适的特征高维空间。通过网格化搜索，在表中找到了最佳的参数组合，即$\alpha = $ $ 0.2$ ，$\beta = 0.1$ ，这个参数下学习桶和部署桶中点击率提升都最大。通过2）找到了K-UCB算法在雅虎新闻数据集上的最佳核函数和最佳参数，使用这组参数与其他算法进行比较。
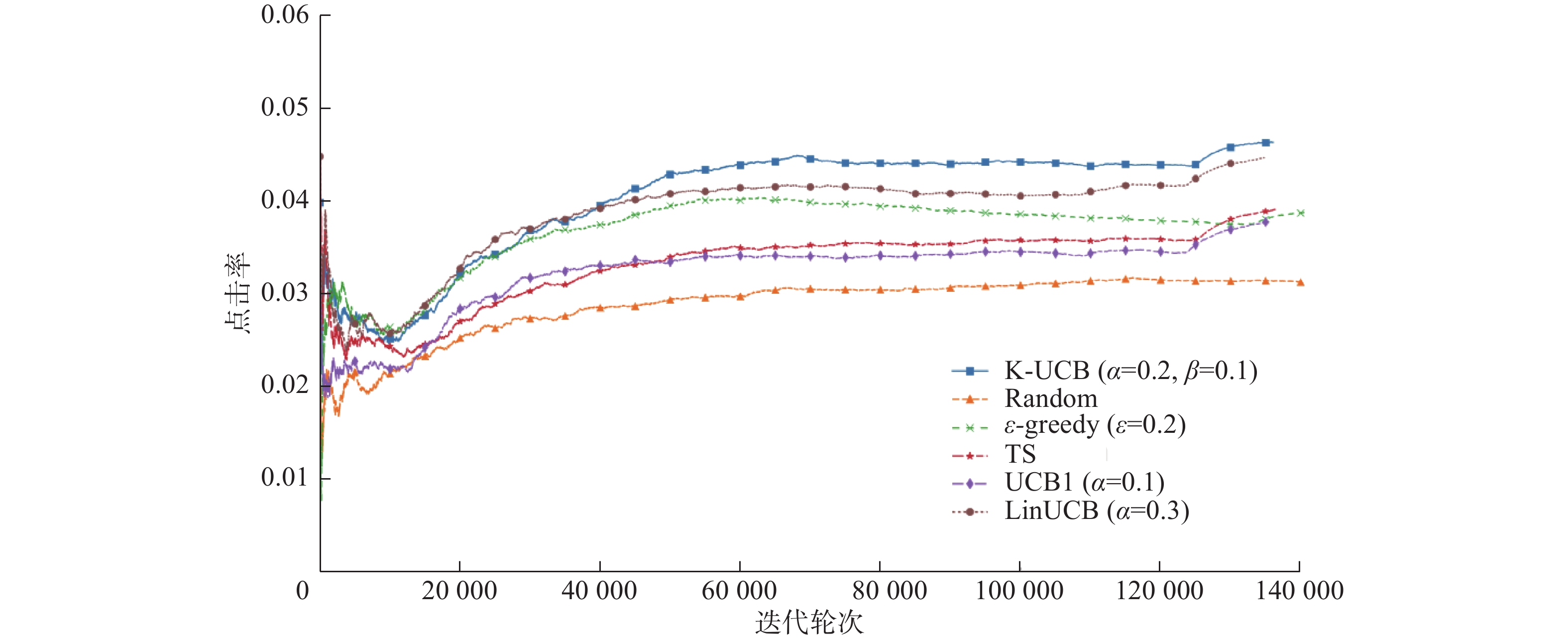
3)对比不同算法在最佳参数下的点击率。如图3和图4分别为学习桶和部署桶中各个对比算法的点击率随迭代轮次的变化曲线。
图 3 算法在学习桶中的点击率Fig. 3 CTRs of various algorithms in Learning Bucket下载:
全尺寸图片
图 4 算法在部署桶中的点击率Fig. 4 CTRs of various algorithms in Deploying Bucket下载:
全尺寸图片
从图3和图4中可以看到，Random策略下点击率最低，这个策略达到稳定后点击率基本不会变化。去除轮次较小时的随机波动干扰，上下文无关的多臂赌博机算法(ε-greedy、Thompson sampling 和UCB1)点击率曲线明显低于上下文多臂赌博机算法(LinUCB和K-UCB),这说明利用上下文信息可以明显提高点击率，因此在推荐系统中应该尽可能利用上下文信息提高推荐准确率，从而更好地满足用户的个性化需求。学习桶和部署桶中K-UCB算法的点击率曲线都高于LinUCB算法，尤其在部署桶中K-UCB算法较LinUCB算法点击率提升了约8%，证明了本文所提出算法的有效性。
该实验表明K-UCB算法比其他基于多臂赌博机的推荐算法更适应真实的非线性数据场景下的个性化推荐。
4. 结束语
本文提出了一种LinUCB改进算法K-UCB，通过核方法将非线性问题转化为线性问题。在合成数据集上验证了K-UCB可以有效降低非线性环境下的累积遗憾，在雅虎新闻数据集上相比于基于线性收益的LinUCB算法，点击率最高提升了8%。将线性收益假设转变为更一般的收益假设，可以提高上下文多臂赌博机的推荐准确率。多臂赌博机适应动态推荐环境的特性，可以改善传统推荐算法，这也是未来可以进一步研究的方向。
-
图 1 LinUCB和K-UCB算法在不同收益假设上的比较
Fig. 1 Comparison of LinUCB and K-UCB on different reward hypothesis
下载:
全尺寸图片
图 2 算法在不同参数下的点击率提升倍数
Fig. 2 CTR lift of the algorithms under different parameters
下载:
全尺寸图片
图 3 算法在学习桶中的点击率
Fig. 3 CTRs of various algorithms in Learning Bucket
下载:
全尺寸图片
图 4 算法在部署桶中的点击率
Fig. 4 CTRs of various algorithms in Deploying Bucket
下载:
全尺寸图片
表 1 雅虎新闻数据集
Table 1 Yahoo! News dataset
字段 解释 1 推荐的文章id 2 点击反馈值(0或者1) 3 当前用户的6维特征 4 当前文章池中文章的6维特征 表 2 核函数选择
Table 2 Kernel function selection
核函数 最佳参数 学习桶 部署桶 线性核 α=0.2 1.35 1.31 多项式核 α=0.2,g=0.1,c=1,d=2 1.48 1.45 高斯核 α=0.2，β=0.1 1.72 1.68 表 3 学习桶中网格搜索K-UCB参数结果
Table 3 Grid search results of K-UCB in Learning Bucket
α β 0.01 0.05 0.1 1 10 0.1 1.20 1.62 1.50 1.28 1.28 0.2 1.40 1.67 1.72 1.32 1.12 0.3 1.22 1.62 1.6 1.39 0.96 0.4 1.44 1.61 1.58 1.08 1.04 0.5 1.42 1.40 1.26 1.08 0.96 0.6 1.32 1.35 1.24 1.16 1.04 表 4 部署桶中网格搜索K-UCB参数结果
Table 4 Grid search results of K-UCB in Deploying Bucket
α β 0.01 0.05 0.1 1 10 0.1 1.12 1.62 1.49 1.36 1.32 0.2 1.32 1.65 1.68 1.36 1.04 0.3 1.12 1.61 1.63 1.39 1.09 0.4 1.36 1.61 1.59 1.06 1.04 0.5 1.41 1.34 1.46 1.20 1.12 0.6 1.36 1.14 1.26 1.16 1.04 -
[1] ADOMAVICIUS G, TUZHILIN A. Toward the next generation of recommender systems: a survey of the state-of-the-art and possible extensions[J]. IEEE transactions on knowledge and data engineering, 2005, 17(6): 734–749. doi: 10.1109/TKDE.2005.99 [2] SCHAFER J B, FRANKOWSKI D, HERLOCKER J, et al. Collaborative filtering recommender systems[M]//BRUSILOVSKY P, KOBSA A, NEJDL W. The Adaptive Web. Berlin, Germany: Springer, 2007: 291−324. [3] SARWAR B, KARYPIS G, KONSTAN J, et al. Item-based collaborative filtering recommendation algorithms[C]//Proceedings of the 10th International Conference on World Wide Web. New York: ACM, 2001: 285−295. [4] BASU C, HIRSH H, COHEN W. Recommendation as classification: using social and content-based information in recommendation[C]//Proceedings of the Fifteenth National/Tenth Conference on Artificial Intelligence/Innovative Applications of Artificial Intelligence. Madison: WI, 1998: 714−720. [5] PAZZANI M J, BILLSUS D. Content-based recommendation systems[M]//BRUSILOVSKY P, KOBSA A, NEJDL W. The Adaptive Web. Berlin, Germany: Springer, 2007: 325−341. [6] AGARWAL D, CHEN B C, ELANGO P. Explore/exploit schemes for web content optimization[C]//Proceedings of the Ninth IEEE International Conference on Data Mining. Miami Beach: TEEE, 2009: 1−10. [7] SLIVKINS A. Introduction to multi-armed bandits[J]. Foundations and trends® in machine learning, 2019, 12(1/2): 1–286. [8] ABBASI-YADKORI Y, PÁL D, SZEPESVÁRI C. Improved algorithms for linear stochastic bandits[C]//Proceedings of the 24th International Conference on Neural Information Processing Systems. Granada, Spain, 2011: 2312−2320. [9] BUBECK S, CESA-BIANCHI N. Regret analysis of stochastic and nonstochastic multi-armed bandit problems[J]. Foundations and trends® in machine learning, 2012, 5(1): 1–122. [10] CHU Wei, LI Lihong, REYZIN L, et al. Contextual bandits with linear payoff functions[C]//Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics. Fort Lauderdale, USA, 2011: 208−214. [11] BOUNEFFOUF D, BOUZEGHOUB A, GANÇARSKI A L. A contextual-bandit algorithm for mobile context-aware recommender system[C]//Proceedings of the 19th International Conference on Neural Information Processing. Berlin: Springer, 2012: 324−331. [12] LANGFORD J, ZHANG Tong. The Epoch-Greedy algorithm for contextual multi-armed bandits[C]//Proceedings of the 20th International Conference on Neural Information Processing Systems. Vancouver British, Columbia, Canada, 2007: 817−824. [13] AUER P, CESA-BIANCHI N, FISCHER P. Finite-time analysis of the multiarmed bandit problem[J]. Machine learning, 2002, 47(2): 235–256. [14] THOMPSON W R. On the likelihood that one unknown probability exceeds another in view of the evidence of two samples[J]. Biometrika, 1933, 25(3/4): 285–294. doi: 10.2307/2332286 [15] LI Lihong, CHU Wei, LANGFORD J, et al. A contextual-bandit approach to personalized news article recommendation[C]//Proceedings of the 19th International Conference on World Wide Web. New York: ACM, 2010: 661−670. [16] AGRAWAL S, GOYAL N. Thompson sampling for contextual bandits with linear payoffs[C]//Proceedings of the 30th International Conference on International Conference on Machine Learning. New York: ACM, 2013: III-1220-III-1228. [17] CESA-BIANCHI N, GENTILE C, ZAPPELLA G. A gang of bandits[C]//Proceedings of the 26th Intermational Conference on Neural Information Processing Systems. New York: ACM, 2013: 737−745. [18] GENTILE C, LI Shuai, ZAPPELLA G. Online clustering of bandits[C]//Proceedings of the 31th International Conference on Machine Learning. Beijing, China, 2014: 757−765. [19] LI Shuai, KARATZOGLOU A, GENTILE C. Collaborative filtering bandits[C]//Proceedings of the 39th International ACM SIGIR conference on Research and Development in Information Retrieval. Pisa, Italy, 2016: 539−548. [20] WANG Huazheng, WU Qingyun, WANG Hongning. Factorization bandits for interactive recommendation[C]//Proceedings of the 31st AAAI Conference on Artificial Intelligence. San Francisco, United States, 2017: 2695−2702. [21] SCHÖLKOPF B, SMOLA A J. Learning with kernels: support vector machines, regularization, optimization, and beyond[M]. Cambridge, Mass: MIT Press, 2002. [22] WALSH T J, SZITA I, DIUK C, et al. Exploring compact reinforcement-learning representations with linear regression[C]//Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence. Montreal, Quebec, Canada, 2009: 591−598. [23] 张国亮, 沈慧, 石峰, 等. 大型实对称矩阵分块迭代求逆算法[J]. 无线互联科技, 2015(6): 127–129. ZHANG Guoliang, SHEN Hui, SHI Feng, et al. Block iterative inverse algorithm for a iarge-scale real matrix[J]. Wireless internet technology, 2015(6): 127–129. [24] Yahoo! Webscope Program. Yahoo! front page today module user click log dataset, version 1.0[EB/OL]. (2020–12–22)[2021–05–26] http://webscope.sandbox.yahoo.com. [25] LI Lihong, CHU Wei, LANGFORD J, et al. Unbiased offline evaluation of contextual-bandit-based news article recommendation algorithms[C]//Proceedings of the fourth ACM International Conference on Web Search and Data Mining. Hong Kong, China, 2011: 297−306.
