Fault detection method and its application using GAN with an encoded input
-
摘要: 针对传统基于生成对抗网络的故障检测方法中，生成器输入使用随机噪声，不包含训练集中有效信息造成模型检测效果不够理想的问题，提出一种采用编码输入的生成对抗网络故障检测策略。通过引入自编码器，基于最小化重构误差构建隐变量空间，将降维后的隐变量信息作为生成器输入以提升生成对抗网络的训练效果；进一步考虑故障检测方法中基于生成器的统计量计算成本高和对离群点敏感的问题，计算待测样本经编码后的隐变量到训练集隐变量空间中心点的曼哈顿距离，并作为新统计量进行故障检测。将所提故障检测方法用于田纳西伊斯曼过程及实际的磨煤机过程，本文方法较传统生成对抗网络故障检测在田纳西伊斯曼过程上报警率提升了13%，在磨煤机过程上各统计量报警率均得到了显著提升且本文所提统计量将传统方法中针对生成器的统计量大大降低了检测用时，从而验证了方法的有效性和性能。Abstract: In a traditional fault detection method based on a generative adversarial network, random noise is used as the generator input, which does not contain the effective information of training sets and causes unsatisfactory fault detection by the model. This paper proposes a generative adversarial network fault detection strategy using an encoded input. By introducing an autoencoder based on minimizing the reconstruction error, a latent variable space is constructed. The latent variable information after dimensionality reduction is used as the generator input to improve the training effect of the generated confrontation network. Furthermore, a generator-based statistic has drawbacks such as high computational cost and sensitivity to outliers. The Manhattan distance is calculated beginning from the encoded hidden variable of the sample to be tested to the center of the hidden variable space of the training set. This distance is then used as a new statistic for fault detection. The proposed fault detection method is used in the TE and actual coal pulverization processes. Compared with the traditional GAN fault detection, the alarming rate of the TE process increases by 13%. The alarming rate of all statistics in the coal pulverization process also improves considerably. The proposed statistics greatly reduce the detection time for generators in traditional methods, which validates their effectiveness and performance.
-
迅速准确地检出故障工况并进行故障隔离对现代工业生产过程的安全性及产品质量具有重要意义[1]。随着生产工艺复杂程度及自动化水平的提升，在故障检测中建立过程机理模型变得更加困难且不易求取，基于简化后模型的检测效果也并不理想。近年来，基于数据驱动的故障检测方法得到了广泛关注和应用[2]，其中常用的有主元分析法(principal component analysis, PCA)[3]、偏最小二乘回归(partial least squares, PLS)[4]、基于k近邻算法的故障检测(fault detection using k-nearest neighborhood, FD-KNN)[5]等。
基于数据的故障检测方法中，建模数据对于故障检测的效果起着决定性作用。传统机器学习方法中的浅层模型往往无法满足过程大数据的解析需求，因此学者们提出了不同的深层模型以解决实际复杂问题[6-9]。其中，生成对抗网络[10](generative adversarial network, GAN)由于其特殊的训练思想及生成能力受到了研究人员的广泛关注，已被应用于图像、视频、文本处理等领域。文献[11]提出一种新的对抗训练方法并证明了其在指定数据集上的准确性，提升了卷积语义分割网络的训练效果。文献[12]提出一种感知生成对抗网络，减少了小对象与大对象之间的表示差异，从而有效改善了低分辨率与高噪声带来的小对象检测困难问题。通过训练深度卷积生成对抗网络，文献[13]有效地提取出文本信息特征从而生成逼真的图像。利用一种基于多尺度密集注意力的生成对抗网络框架，文献[14]解决了现有方法无法处理复杂运动及远距离依赖的问题。近几年GAN研究和应用的不断扩展，逐渐应用到了复杂工业过程监控领域。
文献[15]利用GAN生成虚假故障样本，实现训练集中正常与异常样本的平衡，再由深度神经网络进行分类从而实现故障检测。文献[16]采用深层卷积GAN生成旋转轴承的二维图像信息以提升训练集样本平衡性，采用卷积神经网络区分样本类别。上述方法可以看作GAN在工业过程中的一种运用，但其实际是通过有监督分类算法实现样本的分类，对于故障类型多且未知的过程如TE过程，效果并不理想，本文后续所提故障检测训练集均仅包含正常工况样本。
经典的故障检测方法，比如PCA通过选取方差贡献率大的主元检测故障，易忽略方差贡献率小的变量[17]。基于KNN的故障检测方法假设异常样本较正常工况样本在变量上会存在较大偏差，计算样本的KNN距离作为统计量进行故障检测。上述两种传统算法在故障检测前都存在着先验假设，对故障检测的效果具有一定影响。对此，Wang等[18]提出了基于生成对抗网络的异常检测方法，并在手写数据集(national institute of standards and technology, NIST)及田纳西伊斯曼(Tennessee Eastman, TE)过程仿真中验证了方法的有效性。基于GAN的故障检测方法采用正常工况数据训练生成对抗网络，根据网络中的生成器及判别器构建统计量进行故障检测，因此不存在对故障产生的先验假设，而是通过判别器从真实样本及虚假样本中提取出的潜隐特征并计算概率判断故障是否发生，更贴合检测过程中故障类型及发生原因未知的背景。文献[19]利用风电机组数据训练GAN，通过判别器输出概率判断机组运行状态是否健康。但基于GAN的故障检测方法采用经典的生成对抗网络模型，不可避免地存在着训练困难及模式崩溃的问题。为此许多学者从生成对抗网络结构及寻找最佳GAN模型的角度进行了改进。文献[20]引入BiGAN模型，在保证检测精度的同时大大减少了程序耗时。文献[21]构建了一个基于自编码器的性能指标来衡量生成模型的生成能力，选取最优的生成模型作为最终的分类器。但上述方法中生成器均采用随机噪声作为输入，生成器得到的有效信息少，生成样本不逼真，以致判别器性能在对抗过程中提升有限，故障检出率不高。
综上所述，为进一步提升基于GAN的故障检测的性能与效果，结合自编码器提出一种基于改进GAN的故障检测方法(fault detection using GAN with encoded input, EIGAN)。首先，在训练数据集上通过最小化重构误差，得到自编码器模型，并将训练集经自编码器降维后的隐变量作为生成器输入，进行生成对抗网络的训练；然后，分别根据判别器及自编码器提取出的隐变量空间对正常工况样本计算统计量，并得出控制限；最后，计算待测样本的统计量，结合控制图进行故障检测。将本文所提方法用于TE过程及火力发电厂磨煤机的故障检测，获得了较好的检测结果，从而验证了方法的有效性。
1. 基于生成模型的故障检测原理
1.1 生成对抗网络
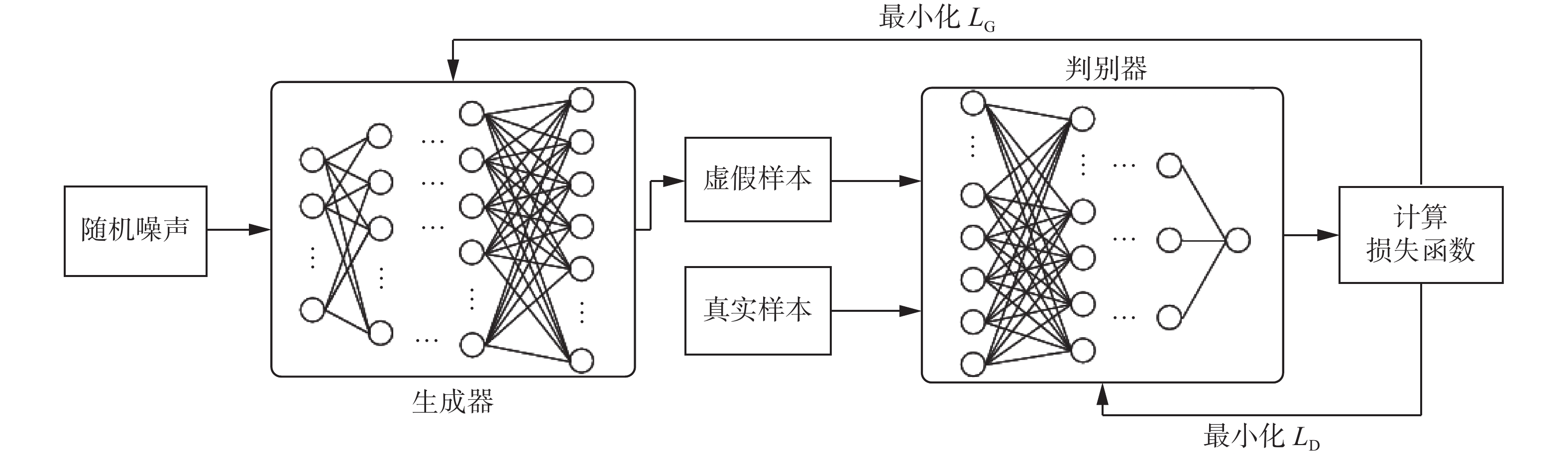
生成对抗网络是一种基于对抗思想进行训练的网络结构，通过寻找零和博弈中的纳什平衡确定模型中的参数[22]，其结构如图1所示。生成对抗网络包含1个生成器和1个判别器，两者均为深层神经网络。生成器的目标是生成与真实样本近似的以致判别器区分不出的“虚假样本”；相反，判别器的目标则是区分真实样本和虚假样本，将这2种样本实现正确的分类。
生成对抗网络的训练过程为：样本数为
$ b $ 、特征数为$ n $ 的小批量真实样本${\boldsymbol{X}_{b \times n}}$ 与生成器生成的虚假样本${\boldsymbol{G}_{b \times n}}$ 一并送给判别器；判别器通过计算样本$ x $ 的得分$ D(x) $ 判别真伪，在每一次的训练中，通过梯度下降方法对生成器和判别器的模型参数进行更新，以最小化两者各自的代价函数$ {L_D} $ 和$ {L_G} $ ，其计算过程分别如式(1)和(2)所示：$$ \begin{gathered} {L_D} = {{\rm E}_{x \sim {P_{{\text{data}}}}}}[ - {\text{log}}(D(x)] + {{\rm E}_{z \sim P(z)}}[ - {\text{log}}(1 - D(G(z)))] \end{gathered} $$ (1) $$ {L_G} = {{\rm E}_{z \sim {P_{\rm{latent}}}}}[ - {\text{log}}(D(G(z)))] $$ (2) 式中：
$ {\rm E} $ 表示求期望；$ x \sim {P_{{\text{data}}}} $ 表示样本$ x $ 服从真实样本的数据分布；$ z \sim {P_{{\text{latent}}}} $ 表示变量$ z $ 服从隐变量空间的数据分布；$ G(z) $ 表示将隐变量$ z $ 映射到与真实样本维度一致的生成样本空间；$ D( \cdot ) $ 表示判别器输出，其值位于0~1；假设样本$ u $ 为某一未知样本，$ D(u) $ 越趋向于1，则判别器认为样本$ u $ 为真实样本的概率越大，反之，为虚假样本的概率越大；$ {{\rm{E}}_{x \sim {P_{{\text{data}}}}}}[ - {\text{log}}(D(x))] $ 表示输入为真实数据时，判别器输出概率的熵。
图 1 生成对抗网络的结构Fig. 1 Architecture of GAN
下载:
全尺寸图片
1.2 故障检测原理
Wang等[18]首先提出了基于GAN的异常点检测，将训练数据集进行最值归一化后进行网络训练，得到模型后，按照式(3)、(4)分别计算出统计量和控制限（本文采用核密度估计方法计算控制限，置信度取95%）；最后如式(5)所示，通过比较待测样本
$ x' $ 的统计量与控制限大小，判断待测样本是否为故障样本。$$ \begin{gathered} {G_{{\text{score}}}}{\text{ = }}{f_G}{\text{(}}x{\text{) = }}\mathop {\min }\limits_{z \sim {P_{{\text{latent}}}}} {\left\| {x - G(z)} \right\|^2} \hfill \\ {D_{{\text{score}}}}{\text{ = }}{f_D}{\text{(}}x{\text{)}} = {\text{1}} - D{\text{(}}x{\text{)}} \hfill \\ \end{gathered} $$ (3) $$\left\{\begin{gathered} {T_G}=f_{\rm{KDE}}\left(\{{G_{{\rm{score}}}}|x \in {X_{{\rm{train}}}}\} ,0.95\right)\\ {T_D}=f_{\rm{KDE}}\left(\{{D_{{\rm{score}}}}|x \in {X_{{\rm{train}}}}\},0.95\right)\\ \end{gathered}\right. $$ (4) $$ \left\{\begin{gathered} {l_G}(x') = {\rm{sgn}} ({f_G}{\text{(}}x'{\text{)}} - {T_G}) \hfill \\ {l_D}(x') = {\rm{sgn}} ({f_D}{\text{(}}x'{\text{)}} - {T_D}) \hfill \\ \end{gathered} \right.$$ (5) 式中：
$ x $ 为待计算统计量的待测样本；$\mathop {\min }\limits_{z \sim {P_{{\rm{latent}}}}} {\left\| {x - G(z)} \right\|^2}$ 表示待测样本$ x $ 到其在生成样本集中最近邻样本的平方欧氏距离；$ D{\text{(}}x{\text{)}} $ 表示输入为$ x $ 时判别器的输出；$f_{\rm{KDE}}( \{ {G_{{\rm{score}}}}|x \in {X_{{\rm{train}}}}\},0.95 )$ 表示对训练集统计量利用核密度估计(kernel density estimation, KDE)函数计算控制限，置信度选取0.95；$ {l_G}(x') $ 表示利用$ {G_{{\text{score}}}} $ 统计量对样本$ x' $ 的故障检测函数；${\rm{sgn}} ()$ 为符号函数；${\rm{sgn}} ({f_G}{\text{(}}x'{\text{)}} - {T_G})$ 对样本$ x' $ 的$ {G_{{\text{score}}}} $ 统计量与$ {G_{{\text{score}}}} $ 控制限的差求取符号函数，若为1则表示样本故障，否则样本正常；$ {D_{{\text{score}}}} $ 控制限及其故障检测函数同$ {G_{{\text{score}}}} $ 类似，故不做赘述。2. 基于改进GAN的故障检测策略
2.1 改进生成器输入
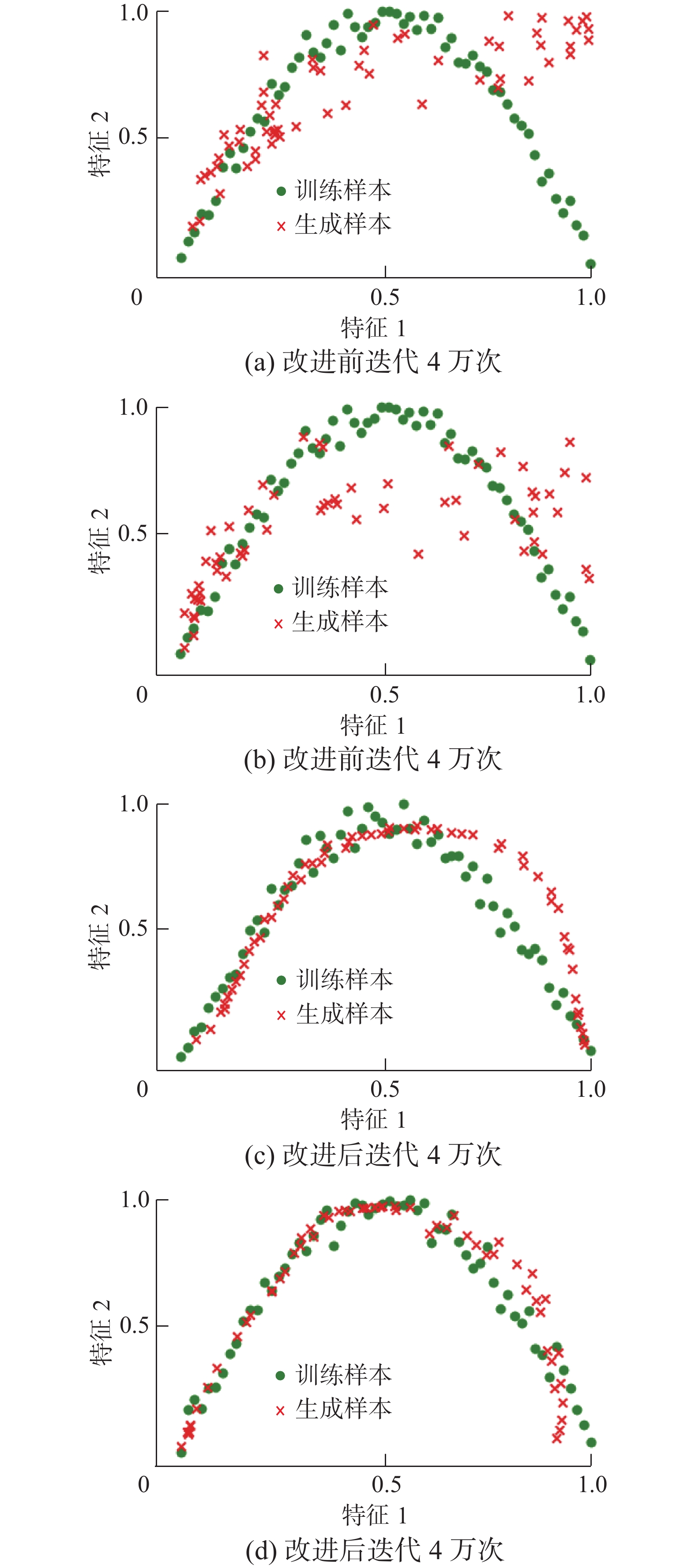
生成器的本质为多层感知机，由于网络结构及每一层中神经元的作用，可以提取出有利于提升拟合精度的潜隐特征。与此同时，每一层网络中适当的激活函数也使得模型可以更好地拟合出训练集数据分布中的非线性和多模态特征。如图2所示的生成器生成样本：图(a)、(b)、(c)分别表示某非线性真实样本数据分布情况及不同训练次数后生成器生成样本的分布情况；图(d)、(e)、(f)分别表示某多模态真实样本数据分布情况及不同训练次数后生成器生成样本的分布情况。其中绿色点表示真实样本数据分布，红色点表示生成样本数据分布，横轴、纵轴表示生成样本的两个维度。从图2中可以看出，经过一定次数的训练后，生成器可以生成与真实样本数据分布近似的样本。但传统生成对抗网络中生成器采用均值为0标准差为1的正态分布作为输入，生成器要从这样一个隐变量空间映射到与真实样本相似的空间分布，需要较长的时间成本；同时生成样本与真实样本的相似性也较差，对于最终的判别器效果具有一定影响。
图 2 生成器生成样本Fig. 2 Generated sample from generator下载:
全尺寸图片
如何给生成器一个包含训练数据集更多信息的低维特征是本文改进GAN用于故障检测的一个动机，PCA作为一种降维方法，虽然能保证提取出的主成分含有较多的信息，但受制于变量服从线性相关及高斯分布的假设，具有一定的局限性。本文采用自编码器[23]提取低维特征，其网络结构如图3所示。不同于PCA方法：1）自编码器特殊的网络结构及引入的激活函数使得自编码器可以同时获取原始信息中线性与非线性特征；2）由于自编码器解码后的重构输出要与输入尽可能地接近，这也保证了编码器提取出的特征能够包含更多输入数据的信息。
图 3 自编码器结构Fig. 3 Architecture of autoencoder下载:
全尺寸图片
最小化式(6)所示的代价函数得到自编码器网络参数，从而提取出训练集中较大程度表示原有数据信息的隐变量，将这组隐变量作为生成器的输入，生成样本过程如图4所示，其中绿色样本点表示真实数据分布，红色样本点表示生成器生成虚假数据分布。对比图4(a)、(c)、(b)和(d)可以看出，改进生成器输入后，有效提升了生成器的生成能力，在相同迭代次数下，改进后的生成器生成的样本分布更接近真实数据分布，从而有效地避免了以随机正态分布作为生成器输入的不足。
$$ L(\theta ) = \left\| {{\boldsymbol{X'}} - {\boldsymbol{X}}} \right\|_2^2 $$ (6) 式中：
$ \theta $ 表示自编码器网络参数；${\boldsymbol{X}}$ 表示自编码器输入；${\boldsymbol{X'}}$ 表示自编码器对输入${\boldsymbol{X}}$ 的重构输出；$\left\| {{\boldsymbol{X'}} - {\boldsymbol{X}}} \right\|_2^2$ 表示自编码器与其重构输出的平方欧氏距离。
图 4 改进前后生成样本分布对比Fig. 4 Comparison of generated sample distribution before and after improvement下载:
全尺寸图片
2.2 基于自编码器的统计量改进
GAN故障检测中将待测样本与其在生成器生成数据分布中最近邻样本间的欧氏距离作为统计量，这种统计量计算方法只寻找待测样本与生成数据中的最近邻样本，生成数据中的离群点对于检测结果具有很大的干扰；此外由于涉及欧氏距离的计算，无论是求统计量过程中计算生成数据间两两样本的距离，还是待测样本到生成数据的欧氏距离，都存在着样本数量多，数据维度高导致计算量大的问题。针对上述问题，本文提出一种新的统计量如式(7)所示：
$$ {E_{{\text{score}}}}{\text{ = }}{\left\| {E(x) - \bar E({X_{{\rm{train}}}})} \right\|_1} $$ (7) 式中：
$ E(x) $ 表示待测样本经自编码器编码后的降维输出；$\bar E({X_{\rm{train}}})$ 表示训练集经自编码器编码后降维输出的均值；${\left\| {E(x) - \bar E({X_{{\rm{train}}}})} \right\|_1}$ 为二者的曼哈顿距离。通过比较待测样本映射到隐变量空间中的向量与训练集对应隐变量分布间的距离，即曼哈顿距离。在减少计算量的同时也降低了离群点对统计量的影响。针对新统计量的控制限计算如式(8)所示，本文采用核密度估计方法确定控制限，置信度选0.95。
$$ {T_E}=f_{\rm{KDE}}(\{{E_{{\rm{score}}}}|x \in {X_{{\rm{train}}}}\},0.95 ) $$ (8) 由于编码器输出小于1，故式(8)中采用曼哈顿街区距离避免误差被缩小；
$f_{\rm{KDE}}( \{{E_{{\rm{score}}}}|x \in {X_{{\rm{train}}}}\} , $ $ 0.95)$ 表示对训练集$ {E_{{\text{score}}}} $ 统计量以0.95作为置信度采用KDE计算控制限。综上所述，本文提出的基于编码器输入的改进GAN故障检测方法，检测流程如图5所示，算法分为离线建模和在线检测两部分。其中，离线建模部分对正常工况下的训练数据集进行相关计算，得到训练集各样本的统计量，再根据置信度及核密度估计方法确定控制限；在线检测部分对未知的待测样本计算其统计量并与控制限比较，判断是否发生故障。
图 5 改进GAN故障检测流程Fig. 5 Fault detection process using improved GAN下载:
全尺寸图片
3. 算法的应用仿真
3.1 TE过程
美国Eastman化学公司依据实际化工反应过程开发了TE仿真平台，其产生的过程数据作为基准数据被广泛应用于不同故障检测方法中[24]。TE工艺过程如图6所示，共包含5个操作单元和8个组成部分，含22个过程测量变量、19个成分测量变量及12个操纵变量，本文选取22个过程变量及除搅拌速度外的11个操作变量用于建模与检测，详细的变量描述可参见文献[25]。数据分为训练集和测试集两部分，除正常工况数据外，还包含21种异常工况。训练集对应正常工况下采集到的数据，测试集则为21种异常工况下的数据，同时测试集中故障均在第161个样本处被引入。
图 6 TE工艺过程示意图Fig. 6 TE process diagram下载:
全尺寸图片
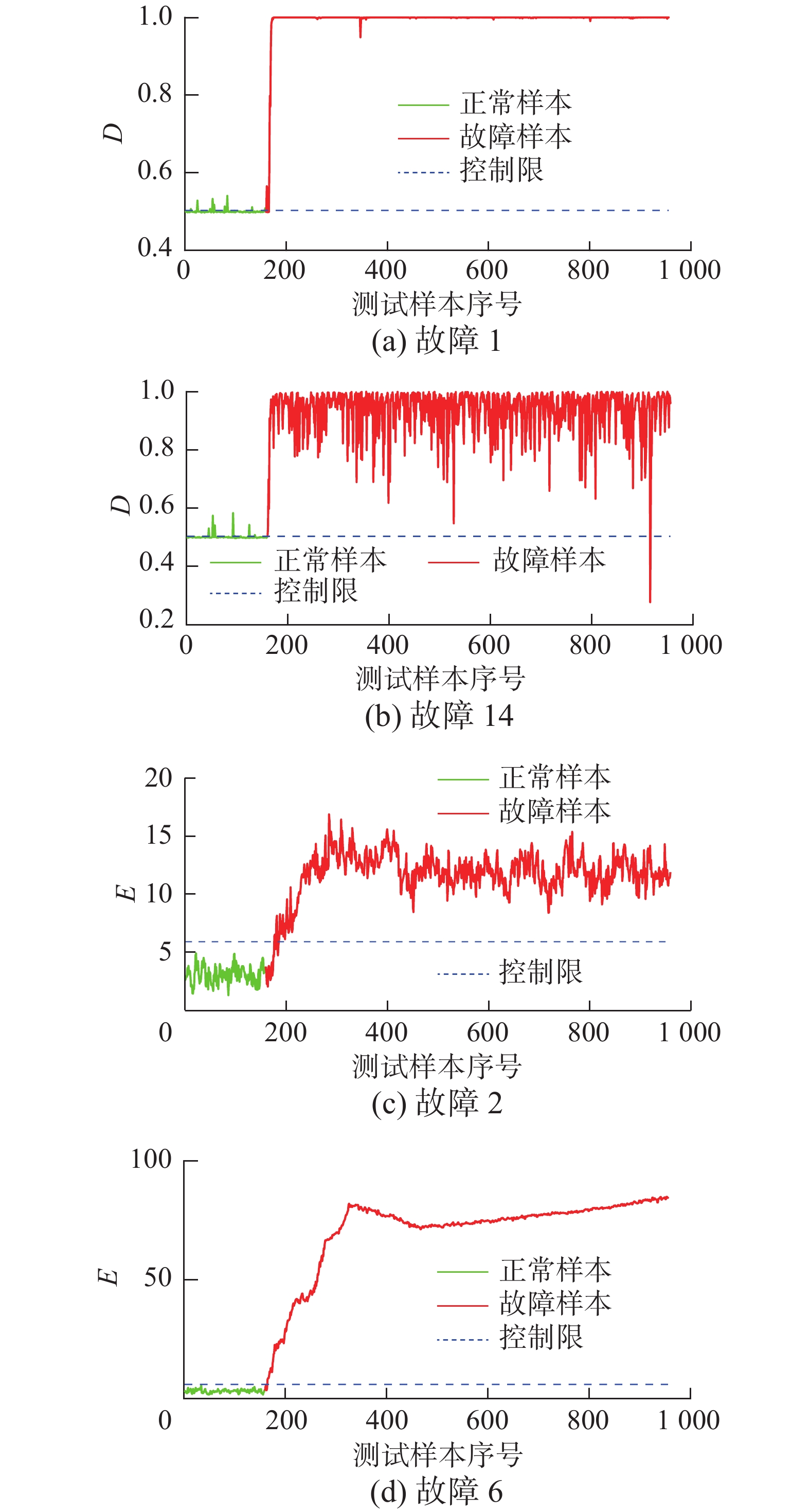
首先将训练数据集通过自编码器得到维度为4的隐变量作为生成器输入；然后对生成对抗网络进行训练，网络中生成器及判别器均采用多层感知机，生成器各层神经元个数分别为4、15、30、60、33，判别器各层神经元个数分别为33、60、30、10、1；除判别器及生成器的输出层采用sigmoid激活函数外，其余层均采用lekay-relu激活函数；进一步再计算出统计量及控制限。对测试集计算统计量，结合控制限绘制控制图如图7所示。可以看出，本文所提算法可以很好地通过统计量将正常工况样本与异常工况的样本区分开来，从而验证了其作为故障检测算法的有效性。
图 7 TE过程制图Fig. 7 Control plot of TE process下载:
全尺寸图片
同时将本文所提算法与传统的故障检测算法进行对比，结果如表1所示。对比GAN故障检测[18]结果可以看出，本文方法通过改进生成器输入，有效地改善了生成对抗网络的训练效果，提升了判别器区分真假样本的能力，从而提高了异常样本的故障检出率。与此同时，对比2种传统的故障检测方法（PCA[3]及FD-KNN[5]），本文所提算法具有更高的报警率。
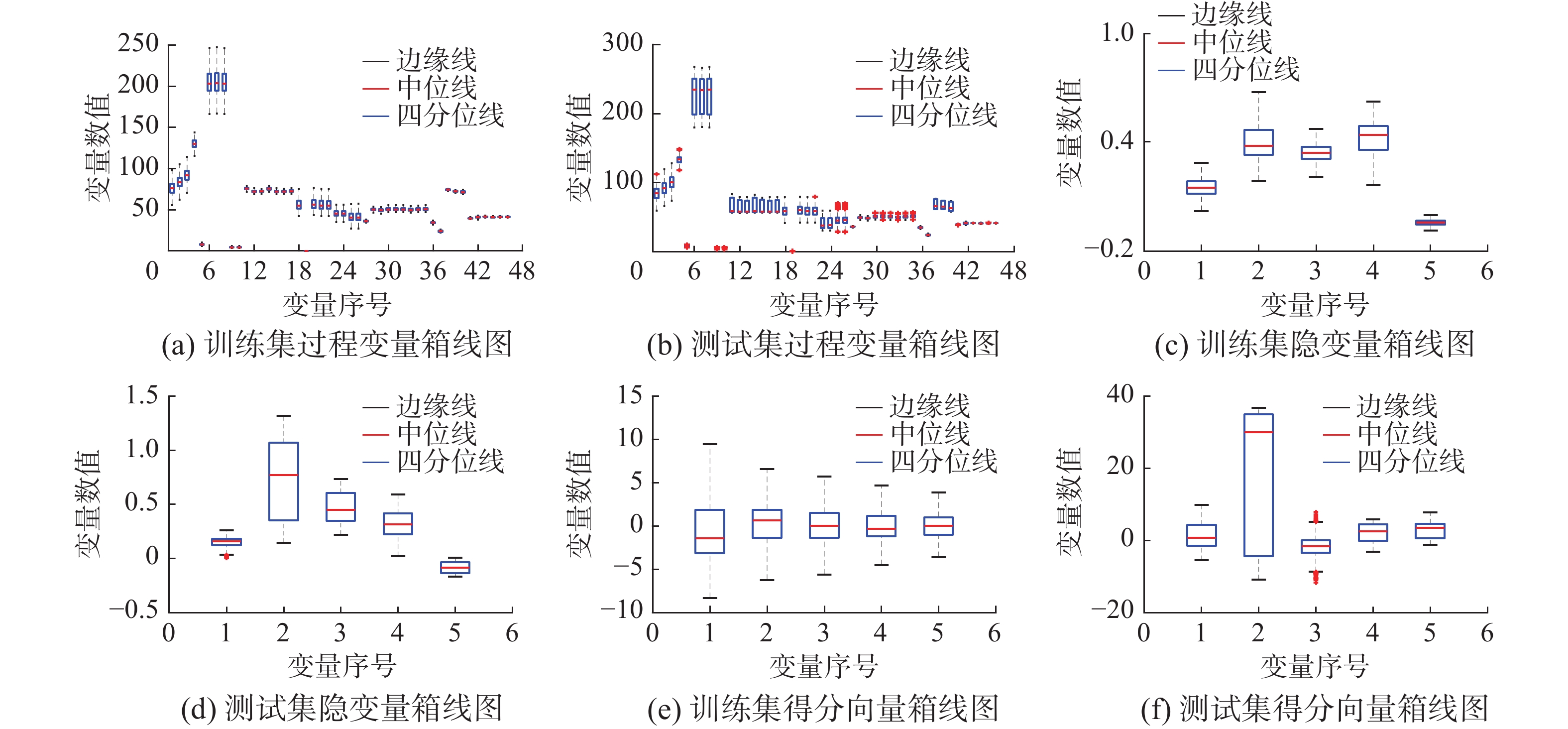
表 1 TE过程报警率对比Table 1 TE process alarm rate comparison故障编号 kNN PCA GAN EIGAN 1 0.995 0.998 0.989 0.996 2 0.983 0.984 0.972 0.981 3 0.013 0.009 0.019 0.150 4 0.970 1 0.227 0.599 5 0.260 0.241 0.264 0.907 6 1 1 1 1 7 1 1 0.912 0.892 8 0.976 0.969 0.941 0.910 9 0.023 0.018 0.015 0.133 10 0.428 0.296 0.508 0.647 11 0.670 0.708 0.442 0.723 12 0.989 0.984 0.905 0.946 13 0.946 0.951 0.946 0.907 14 1 1 0.935 0.999 15 0.030 0.014 0.023 0.194 16 0.275 0.181 0.551 0.657 17 0.911 0.940 0.847 0.937 18 0.896 0.899 0.895 0.904 19 0.086 0.110 0.190 0.429 20 0.481 0.453 0.502 0.681 21 0.426 0.426 0.347 0.543 平均报警率 0.636 0.628 0.592 0.721 为进一步对结果进行分析，对TE过程训练集及故障2、6、14对应的测试集通过自编码器提取隐变量并绘制箱线图，如图8所示，将图(a)分别与图(b)、(c) 、(d)对比可以发现：使用自编码器提取TE过程特征信息在还原原始数据集信息的同时，编码器提取出的故障样本的隐变量与正常样本隐变量具有明显的差异性，这也很好地解释了图7(c)、(d)中
$ E_{\rm{score}} $ 统计量能很好地检出故障2、6、14的原因。
图 8 TE过程正常工况与部分故障的隐变量箱线图对比Fig. 8 Comparison of hidden variable box plots between normal operating conditions and partial failures of TE process下载:
全尺寸图片
3.2 磨煤机数据仿真
磨煤机作为火力发电厂中的核心设施，准确快速地检出故障对安全高效地发电具有重要意义。用于对比仿真的磨煤机数据被划分为训练集和测试集两部分，训练集包含3500个正常工况数据，测试集包括1000个数据，其中前500个是正常工况下记录得到的，后500个为异常工况（输出煤粉温度降低）下记录的数据。训练集和测试集中过程变量个数均为46，关于磨煤机过程变量的详细描述见表2。
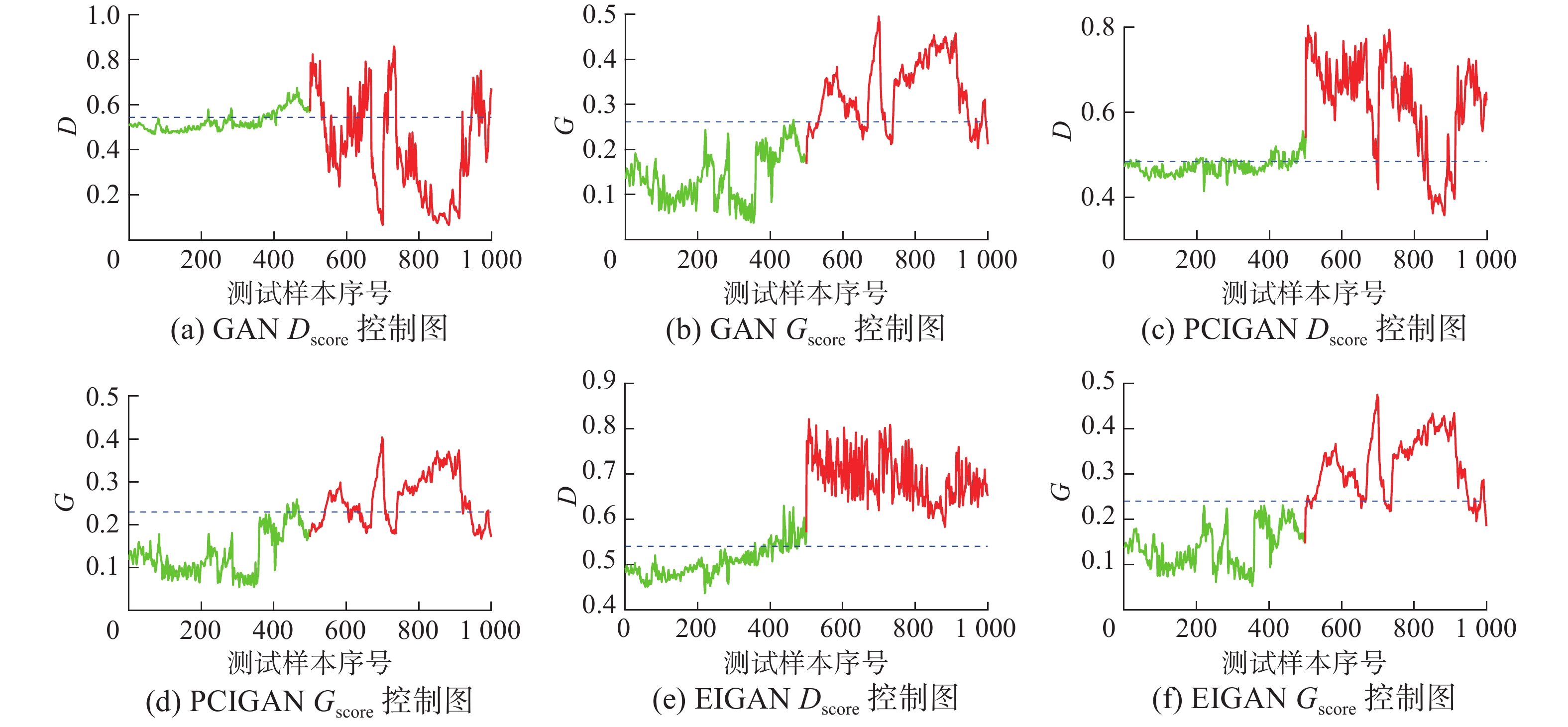
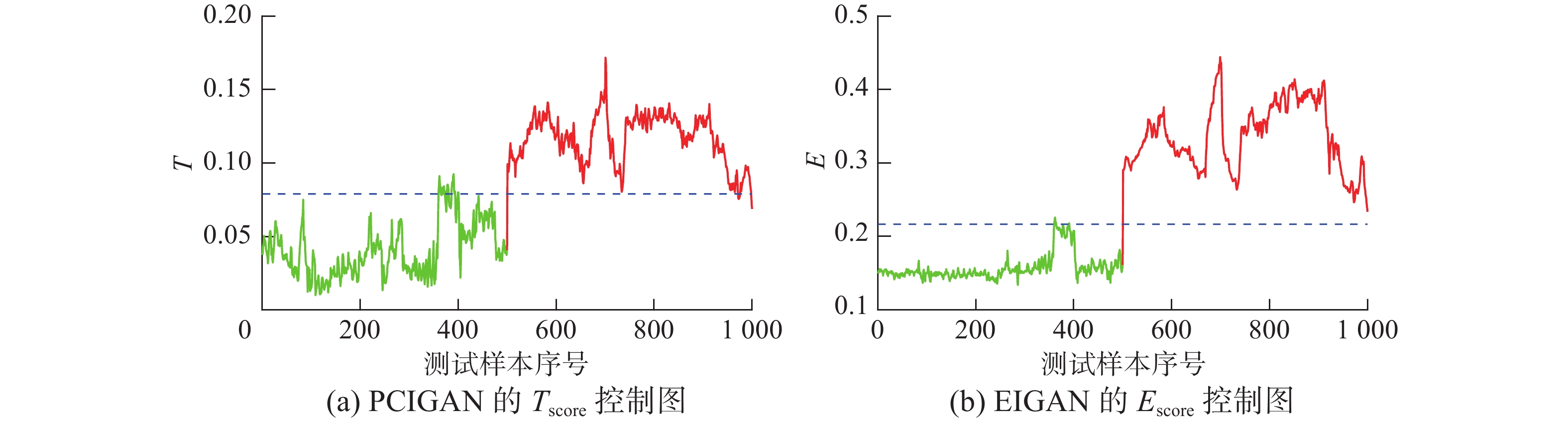
对传统GAN、采用PCA降维数据作为生成器输入的GAN（principal component based GAN，PCGAN）及本文所提的改进GAN三者进行相同的参数初始化及网络结构设置，即生成器与判别器层数、每一层神经元个数、每一层激活函数、梯度更新规则、学习率设置（采用指数衰减法，基学习率为0.01，衰减系数为0.95，衰减速率为2000次迭代）均相同，训练相同次数后，采用
$ {D_{{\text{score}}}} $ 、$ {G_{{\text{score}}}} $ 、$ {E_{{\text{score}}}} $ 和$ {T_{{\text{score}}}} $ 统计量对磨煤机数据进行故障检测，其中$ {T_{{\text{score}}}} $ 为类比$ {E_{{\text{score}}}} $ 统计量对采用主成分输入的GAN故障检测方法计算得到的统计量，如式(9)所示：$$ \begin{gathered} {\boldsymbol{X}} = {\boldsymbol{XP}}{{\boldsymbol{P}}^{\rm{T}}} + {\boldsymbol{X\tilde P}}{{{\boldsymbol{\tilde P}}}^{\rm{T}}} \hfill \\ {T_{{\text{score}}}} = {\left\| {{\boldsymbol{xP}} - \overline {{\boldsymbol{XP}}} } \right\|_1} \hfill \\ \end{gathered} $$ (9) 式中：
${\boldsymbol{X}} \in {{\bf{R}}^{m\times n}}$ ，${\boldsymbol{x}} \in {{\bf{R}}^{1\times n}}$ 分别为训练集和待测样本；${\boldsymbol{P}} \in {{\bf{R}}^{n\times k}}$ ，${\boldsymbol{\tilde P}} \in {{\bf{R}}^{n\times(n - k)}}$ 分别为为主元载荷矩阵和残差载荷矩阵；${\boldsymbol{xP}}$ 、$\overline {{\boldsymbol{XP}}}$ 分别为待测样本得分向量和训练集得分向量均值；$ {T_{{\text{score}}}} $ 为统计量仿照本文所提$ {E_{{\text{score}}}} $ 统计量。计算了${\boldsymbol{xP}}$ 、$\overline {{\boldsymbol{XP}}}$ 间的曼哈顿街区距离，从而衡量以PCA提取信息作为GAN输入时故障检测效果的好坏。表 2 磨煤机过程变量描述Table 2 Variable description of coal pulverizer process变量序号 变量描述 变量序号 变量描述 1~4 进气流量（1~4） 26 主热气挡板阀开度 5 进气压力 27 分离器电流 6~8 进气温度（1~3） 28 分离器频率 9~13 煤原料（1~5） 29 分离器速度 14~15 输出煤粉压力（1~2） 30~35 电机定子温度（1~6） 16~22 输出煤粉温度（1~7） 36~37 电机轴承温度（1~2） 23 主冷气挡板控制 38~40 转子轴承油温 24 主冷气挡板阀开度 41~42 推力轴承温度 25 主热气挡板控制 43~46 变速箱油池温度 磨煤机过程检测结果对比图如图9、10所示，检测效果见表3。可以看出采用包含信息量更多的编码器输出作为生成器输入，在帮助生成器生成更接近真实数据分布的虚假样本的同时也提升了判别器的效果，从而使得基于判别器的
$ {D_{{\text{score}}}} $ 统计量能更好地检出故障。通过表3及对比图10(a)、(b)，可以发现相较于PCA得到的主成分，采用自编码器降维后隐变量作为生成器输入，使得生成对抗网络在低误报的同时具有更高的报警率，从而体现出自编码器降维后得到的数据较PCA降维后的数据包含更多原始数据中的信息，对生成对抗网络具有更好的训练效果。另外，本文所提统计量对比传统GAN故障检测算法中的两种统计量对于磨煤机数据进行故障检测用时如表4所示。结合表3、表4可以看出本文基于自编码器隐变量空间提出的统计量较传统GAN故障检测中的$ G_{\rm{score}} $ 统计量，计算速度得到了很大提升。而检测用时与GAN故障检测中$ D_{\rm{score}}$ 及PCGAN故障检测中$ T_{\rm{score}}$ 统计量为同一数量级的同时，检测效果均优于二者。
图 9 磨煤机过程控制图对比Fig. 9 Comparison of control plot of coal pulzerizer process下载:
全尺寸图片
图 10 关于生成器输入的统计量检测结果对比Fig. 10 Comparison of the statistics using different generator input下载:
全尺寸图片
表 3 磨煤机过程检测结果对比Table 3 Comparison of detection results of coal pulverizer process方法 GAN PCGAN EIGAN 统计量 $D_{\rm{score} }$ $G_{\rm{score}}$ $D_{\rm{score} }$ $G_{\rm{score}}$ $T_{\rm{score}}$ $D_{\rm{score} }$ $G_{\rm{score}}$ $E_{\rm{score}}$ 报警率 0.152 0.768 0.834 0.605 0.988 1.000 0.886 1.000 误报率 0.295 0.004 0.230 0.004 0.046 0.212 0 0.006 表 4 磨煤机过程检测时间对比Table 4 Comparison of detection time of coal pulverizer process方法 GAN PCIGAN EIGAN 统计量 $D_{\rm{score}}$ $G_{\rm{score}}$ $D_{\rm{score}}$ $T_{\rm{score}}$ $D_{\rm{score}}$ $E_{\rm{score}}$ 检测用时/s 0.032 20.730 0.032 0.018 0.040 0.048 对磨煤机数据训练集、测试集及其经自编码器编码后的隐变量空间绘制箱线图，如图11所示。通过对比图11(a)、(c)、(e)可以看出：经自编码器提取出的隐变量空间及PCA方法提取出的得分向量空间去除了线性相关及冗余的变量，以少量的变量最大程度地还原了原有数据集中的信息。但对比图11(d)、(f)发现测试集经自编码器提取出的隐变量空间在变量2、3、5上均表现出了与训练集隐变量空间的差异性，而测试集经PCA方法提取出的隐变量空间仅在变量2上表现出了与训练集隐变量空间的差异性。此外，训练集经PCA方法提取出的隐变量分布的离散程度高于测试集隐变量分布，不利于故障检测。这也解释了本文所提的
$ E_{\rm{score}} $ 统计量较$ T_{\rm{score}} $ 统计量有利于故障检测的原因。
图 11 磨煤机数据及其隐变量箱线图Fig. 11 Pulverizer data and its hidden variable box plot下载:
全尺寸图片
4. 结束语
本文提出了一种采用编码输入的生成对抗网络故障检测方法，通过引入自编码器，将自编码器降维后的数据作为生成对抗网络中生成器的输入，改善了传统生成对抗网络中生成器使用随机噪声作为输入带来的缺乏有效信息训练过程缓慢的问题，提升了生成对抗网络的训练效果和检测性能。所提方法与其他传统故障检测方法相比，在TE及磨煤机过程仿真中具有更高的报警率，表明了方法的有效性和可靠性。但在仿真过程中发现生成对抗网络最终得到的生成器模型对于故障检测贡献率不高，与此同时判别器在对样本进行故障检测时仅考虑了待测样本维度上的信息。如何更好地利用生成器设计统计量及改进判别器模型得到关于待测样本更多更丰富的信息是未来需要进一步考虑和研究的问题。
-
图 1 生成对抗网络的结构
Fig. 1 Architecture of GAN
下载:
全尺寸图片
图 2 生成器生成样本
Fig. 2 Generated sample from generator
下载:
全尺寸图片
图 3 自编码器结构
Fig. 3 Architecture of autoencoder
下载:
全尺寸图片
图 4 改进前后生成样本分布对比
Fig. 4 Comparison of generated sample distribution before and after improvement
下载:
全尺寸图片
图 5 改进GAN故障检测流程
Fig. 5 Fault detection process using improved GAN
下载:
全尺寸图片
图 6 TE工艺过程示意图
Fig. 6 TE process diagram
下载:
全尺寸图片
图 7 TE过程制图
Fig. 7 Control plot of TE process
下载:
全尺寸图片
图 8 TE过程正常工况与部分故障的隐变量箱线图对比
Fig. 8 Comparison of hidden variable box plots between normal operating conditions and partial failures of TE process
下载:
全尺寸图片
图 9 磨煤机过程控制图对比
Fig. 9 Comparison of control plot of coal pulzerizer process
下载:
全尺寸图片
图 10 关于生成器输入的统计量检测结果对比
Fig. 10 Comparison of the statistics using different generator input
下载:
全尺寸图片
图 11 磨煤机数据及其隐变量箱线图
Fig. 11 Pulverizer data and its hidden variable box plot
下载:
全尺寸图片
表 1 TE过程报警率对比
Table 1 TE process alarm rate comparison
故障编号 kNN PCA GAN EIGAN 1 0.995 0.998 0.989 0.996 2 0.983 0.984 0.972 0.981 3 0.013 0.009 0.019 0.150 4 0.970 1 0.227 0.599 5 0.260 0.241 0.264 0.907 6 1 1 1 1 7 1 1 0.912 0.892 8 0.976 0.969 0.941 0.910 9 0.023 0.018 0.015 0.133 10 0.428 0.296 0.508 0.647 11 0.670 0.708 0.442 0.723 12 0.989 0.984 0.905 0.946 13 0.946 0.951 0.946 0.907 14 1 1 0.935 0.999 15 0.030 0.014 0.023 0.194 16 0.275 0.181 0.551 0.657 17 0.911 0.940 0.847 0.937 18 0.896 0.899 0.895 0.904 19 0.086 0.110 0.190 0.429 20 0.481 0.453 0.502 0.681 21 0.426 0.426 0.347 0.543 平均报警率 0.636 0.628 0.592 0.721 表 2 磨煤机过程变量描述
Table 2 Variable description of coal pulverizer process
变量序号 变量描述 变量序号 变量描述 1~4 进气流量（1~4） 26 主热气挡板阀开度 5 进气压力 27 分离器电流 6~8 进气温度（1~3） 28 分离器频率 9~13 煤原料（1~5） 29 分离器速度 14~15 输出煤粉压力（1~2） 30~35 电机定子温度（1~6） 16~22 输出煤粉温度（1~7） 36~37 电机轴承温度（1~2） 23 主冷气挡板控制 38~40 转子轴承油温 24 主冷气挡板阀开度 41~42 推力轴承温度 25 主热气挡板控制 43~46 变速箱油池温度 表 3 磨煤机过程检测结果对比
Table 3 Comparison of detection results of coal pulverizer process
方法 GAN PCGAN EIGAN 统计量 $D_{\rm{score} }$ $G_{\rm{score}}$ $D_{\rm{score} }$ $G_{\rm{score}}$ $T_{\rm{score}}$ $D_{\rm{score} }$ $G_{\rm{score}}$ $E_{\rm{score}}$ 报警率 0.152 0.768 0.834 0.605 0.988 1.000 0.886 1.000 误报率 0.295 0.004 0.230 0.004 0.046 0.212 0 0.006 表 4 磨煤机过程检测时间对比
Table 4 Comparison of detection time of coal pulverizer process
方法 GAN PCIGAN EIGAN 统计量 $D_{\rm{score}}$ $G_{\rm{score}}$ $D_{\rm{score}}$ $T_{\rm{score}}$ $D_{\rm{score}}$ $E_{\rm{score}}$ 检测用时/s 0.032 20.730 0.032 0.018 0.040 0.048 -
[1] 彭开香, 马亮, 张凯. 复杂工业过程质量相关的故障检测与诊断技术综述[J]. 自动化学报, 2017, 43(3): 349–365. PENG Kaixiang, MA Liang, ZHANG Kai. Review of quality-related fault detection and diagnosis techniques for complex industrial processes[J]. Acta automatica sinica, 2017, 43(3): 349–365. [2] 刘强, 卓洁, 郎自强, 等. 数据驱动的工业过程运行监控与自优化研究展望[J]. 自动化学报, 2018, 44(11): 1944–1956. LIU Qiang, ZHUO Jie, LANG Ziqiang, et al. Perspectives on data-driven operation monitoring and self-optimization of industrial processes[J]. Acta automatica sinica, 2018, 44(11): 1944–1956. [3] 曹跃, 陈志文, 袁小锋, 等. 部分子块通讯的分布式PCA厂级工业过程监测方法[J]. 控制与决策, 2020, 35(6): 1281–1290. CAO Yue, CHEN Zhiwen, YUAN Xiaofeng, et al. Distributed PCA for plant-wide processes monitoring with partial block communication[J]. Control and decision, 2020, 35(6): 1281–1290. [4] 童楚东, 史旭华, 蓝艇. 正交信号校正的自回归模型及其在动态过程监测中的应用[J]. 控制与决策, 2016, 31(8): 1505–1508. TONG Chudong, SHI Xuhua, LAN Ting. Orthogonal signal correction based auto-regression model with application to dynamic process monitoring[J]. Control and decision, 2016, 31(8): 1505–1508. [5] 冯立伟, 张成, 李元, 等. 基于标准距离k近邻的多模态过程故障检测策略[J]. 控制理论与应用, 2019, 36(4): 553–560. doi: 10.7641/CTA.2018.70806 FENG Liwei, ZHANG Cheng, LI Yuan, et al. Fault detection strategy of standard-distance-based k nearest neighbor rule in multimode processes[J]. Control theory and applications, 2019, 36(4): 553–560. doi: 10.7641/CTA.2018.70806 [6] HUANG Yi, SUN Shiyu, DUAN Xiusheng, et al. A study on deep neural networks framework[C]//2016 IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC). Xi’an: IEEE, 2016: 1519−1522. [7] CHEN Xuemei, ZHENG Xuelong, WANG Zijia, et al. Multi-frequency data fusion for attitude estimation based on multi-layer perception and Cubature Kalman Filter[J]. IEEE access, 2020, 8: 144373–144381. doi: 10.1109/ACCESS.2020.3012984 [8] LIU Shuo, LIU Yulong, GU Yuhai, et al. Method of extracting gear fault feature based on stacked autoencoder[J]. The journal of engineering, 2019, 2019(23): 8765–8769. doi: 10.1049/joe.2018.9101 [9] MIAO Jun, SUN Keqiang, LIAO Xuan, et al. Human segmentation based on compressed deep convolutional neural network[J]. IEEE access, 2020, 8: 167585–167595. doi: 10.1109/ACCESS.2020.3023746 [10] GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial networks[J]. Advances in neural information processing systems, 2014, 3(11): 2672–2680. [11] LUC P, COUPRIE C, CHINTALA S, et al. Semantic segmentation using adversarial networks[EB/OL].(2016−11−25)[2021−02−03]https://arxiv.org/abs/1611.08408. [12] LI Jianan, LIANG Xiaodan, WEI Yunchao, et al. Perceptual generative adversarial networks for small object detection[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu: IEEE, 2017: 1951−1959. [13] REED S E, AKATA Z, YAN Xinchen, et al. Generative adversarial text to image synthesis[C]//Proceedings of the 33nd International Conference on Machine Learning (ICML). New York: ACM, 2016: 1060−1069. [14] JIANG Tao, LI Yunsong, XIE Weiying, et al. Discriminative reconstruction constrained generative adversarial network for hyperspectral anomaly detection[J]. IEEE transactions on geoscience and remote sensing, 2020, 58(7): 4666–4679. doi: 10.1109/TGRS.2020.2965961 [15] LEE Y O, JO J, HWANG J. Application of deep neural network and generative adversarial network to industrial maintenance: a case study of induction motor fault detection[C]//2017 IEEE International Conference on Big Data (Big Data). Boston: IEEE, 2017: 3248−3253. [16] VIOLA J, CHEN Yangquan, WANG Jing. FaultFace: deep convolutional generative adversarial network (DCGAN) based ball-bearing failure detection method[J]. Information sciences, 2021, 542: 195–211. doi: 10.1016/j.ins.2020.06.060 [17] 顾炳斌, 熊伟丽, 史旭东. 基于故障敏感主元的多块PCA故障监测方法[J]. 高校化学工程学报, 2019, 33(6): 1499–1508. GU Bingbin, XIONG Weili, SHI Xudong. Multi-block PCA process monitoring based on fault sensitive principal components[J]. Journal of chemical engineering of Chinese universities, 2019, 33(6): 1499–1508. [18] WANG Huangang, LI Xin, ZHANG Tao. Generative adversarial network based novelty detection usingminimized reconstruction error[J]. Frontiers of information technology and electronic engineering, 2018, 19(1): 116–125. [19] 金晓航, 许壮伟, 孙毅, 等. 基于生成对抗网络的风电机组在线状态监测[J]. 仪器仪表学报, 2020, 41(4): 68–76. JIN Xiaohang, XU Zhuangwei, SUN Yi, et al. Online condition monitoring of wind turbine based on generative adversarial network[J]. Chinese journal of scientific instrument, 2020, 41(4): 68–76. [20] YANG Xin, FENG Dajun. Generative adversarial network based anomaly detection on the benchmark Tennessee Eastman process[C]//2019 5th International Conference on Control, Automation and Robotics (ICCAR). Beijing: IEEE, 2019: 644−648. [21] SPYRIDON P, BOUTALIS Y S. Generative adversarial networks for unsupervised fault detection[C]//2018 European Control Conference (ECC). Limassol: IEEE, 2018: 691−696. [22] 陈伟宏, 安吉尧, 李仁发, 等. 深度学习认知计算综述[J]. 自动化学报, 2017, 43(11): 1886–1897. CHEN Weihong, AN Jiyao, LI Renfa, et al. Review on deep-learning-based cognitive computing[J]. Acta automatica sinica, 2017, 43(11): 1886–1897. [23] 袁非牛, 章琳, 史劲亭, 等. 自编码神经网络理论及应用综述[J]. 计算机学报, 2019, 42(1): 203–230. YUAN Feiniu, ZHANG Lin, SHI Jinting, et al. Theories and applications of auto-encoder neural networks: a literature survey[J]. Chinese journal of computers, 2019, 42(1): 203–230. [24] 顾炳斌, 熊伟丽. 基于多块信息提取的PCA故障诊断方法[J]. 化工学报, 2019, 70(2): 736–749. GU Bingbin, XIONG Weili. Fault diagnosis based on PCA method with multi-block information extraction[J]. CIESC journal, 2019, 70(2): 736–749. [25] GE Zhiqiang, SONG Zhihuan. Distributed PCA model for plant-wide process monitoring[J]. Industrial & engineering chemistry research, 2013, 52(5): 1947–1957.
