装备维修保障的物力资源是装备维修保障活动顺利开展的物质保证，其中备件的经费消耗占到装备保障总经费的1/3左右^[1-2]，因此，维修备件的库存优化技术成为车辆装备保障系统最为关注的保障领域之一，它是促进装备保障效能和经济效能相统一发展的有效技术手段^[3]。目前较多的车辆装备维修备件存在消耗规律难以掌握、库存控制周期较长、维修备件被大量闲置、在库车辆备件周转率低等问题。传统上为了达到很高的保障效能会存储过多的维修备件，导致经费消耗很快。因此，如何合理地设置维修备件的库存控制方案，发挥最大的经济效益，保证规定的保障效能就显得十分重要。

备件消耗预测常见的方法是历史映射法^[4-7]，该类方法被广泛应用于具有规律性的预测问题中，并对数据有较高的要求。对于车辆装备而言，维修计划往往和车辆装备的摩托小时消耗量有着密切的关系。由于车辆摩托小时的收支平衡具有较长的周期性，且每个年度的动用计划存在较大差异，这将直接影响到车辆的自然随机故障率以及定时定程维修频次。因此，单靠历史数据映射法对车辆装备备件进行预测准确度并不高，容易形成库存积压或缺货严重等一系列不良的状况^[8]。最新的研究方向是借鉴企业供应链管理系统中的库存控制方法，通过多品种项目联合补货^[9-10]手段研究车辆装备维修备件的库存决策方案。多品种项目联合补货库存控制模型的基本数学原理是EOQ (economic order quantity)系列模型。EOQ系列模型从库存管理角度出发，适用于定期库存检查或连续库存检查方式的库存系统，用于研究如何调整补货间隔期和补货批量可以使得维修备件满足军事需求，且库存费用最小^[11-12]，如今，EOQ改进形式被广泛应用于维修器材的供应系统。张建荣等^[13]考虑了物资的保障度构建了多品种联合补货模型，所构建的模型可以在每个补货时将物资订购至最大库存，与单品种库存策略相比，经费节省效果显著。Wang等^[14]提出了一种带有环境检测算子和两种不同环境变化响应策略的改进粒子群算法，有效求解多品种联合补货数学模型。根据实际问题特点，Li等^[15]建立了一种带有资源约束的军用机消耗品联合补货数学模型，并提出了一种改进的自适应遗传算法求解了该模型，所建模型具有较高的应用价值。Zeng等^[16]针对联合补货问题的数学特性，设计了一种有效的基于模拟退火的混合差分进化算法，实验表明，该算法能够鲁棒、精确地解决这一不确定性多项式难题。

本文根据车辆的动用计划，分析了车辆动用计划期内预防性定时定程维修和修复性自然随机故障维修下的备件消耗特点，以此建立了基于动用强度的车辆装备备件消耗量模型和备件库存控制模型，并设计了改进的果蝇优化算法对模型进行了求解。

1 车辆装备备件消耗量模型 1.1 车辆装备备件消耗过程分析

备件消耗主要是由车辆动用计划下装备的维修维护产生的。动用计划是通过运用现有的智能算法合理地分配用车任务，构造以重点用车、一般用车、控制用车为主的动用车使用计划，以保持合适的摩托小时梯次储备。在该梯次储备下，年度进行维修的装备数量稳定变化，尽量早地产生大、中修装备，进入滚动式循环动用^[17]。因此车辆装备维修保障任务主要分为定时定程维修和自然随机故障维修。

定时定程维修包括大修、中修、小修，由车辆动用强度决定。而动用强度与车辆的摩托小时有关，所以一般以车辆支出的摩托小时为依据判断大、中、小修。大修、中修和小修需要按照一定的标准和要求，分别进行全面性的恢复修理、基本或部分恢复修理和一般性维护活动。每种维修都有一定的维修技术标准和工艺要求，以某型装甲车为例，该装甲车的大、中、小修的维修间隔期分别为900、450、150摩托小时，每个大修间隔期内进行大、中、小修的次数比例为1∶1∶4，如图1所示。维修类别主要包括底盘、武器、火控系统、电气设备及检测仪表、三防装置、指控通信设备等类别。一般大修之后，车辆装备如新，达到收支平衡，摩托小时归零。

修复性修理是指未使用到规定的修理间隔期限出现的损坏故障。这类故障往往与车辆的摩托小时消耗紧密相关，可通过车辆历史故障数据信息和现有的一些预测模型，如神经网络、ARMA模型、灰色预测模型等即可预测出基于车辆摩托小时故障率。一般而言，当前摩托小时支出量越多，发生随机故障的概率越大。图2给出了规定维修间隔期的车辆装备备件更换策略。

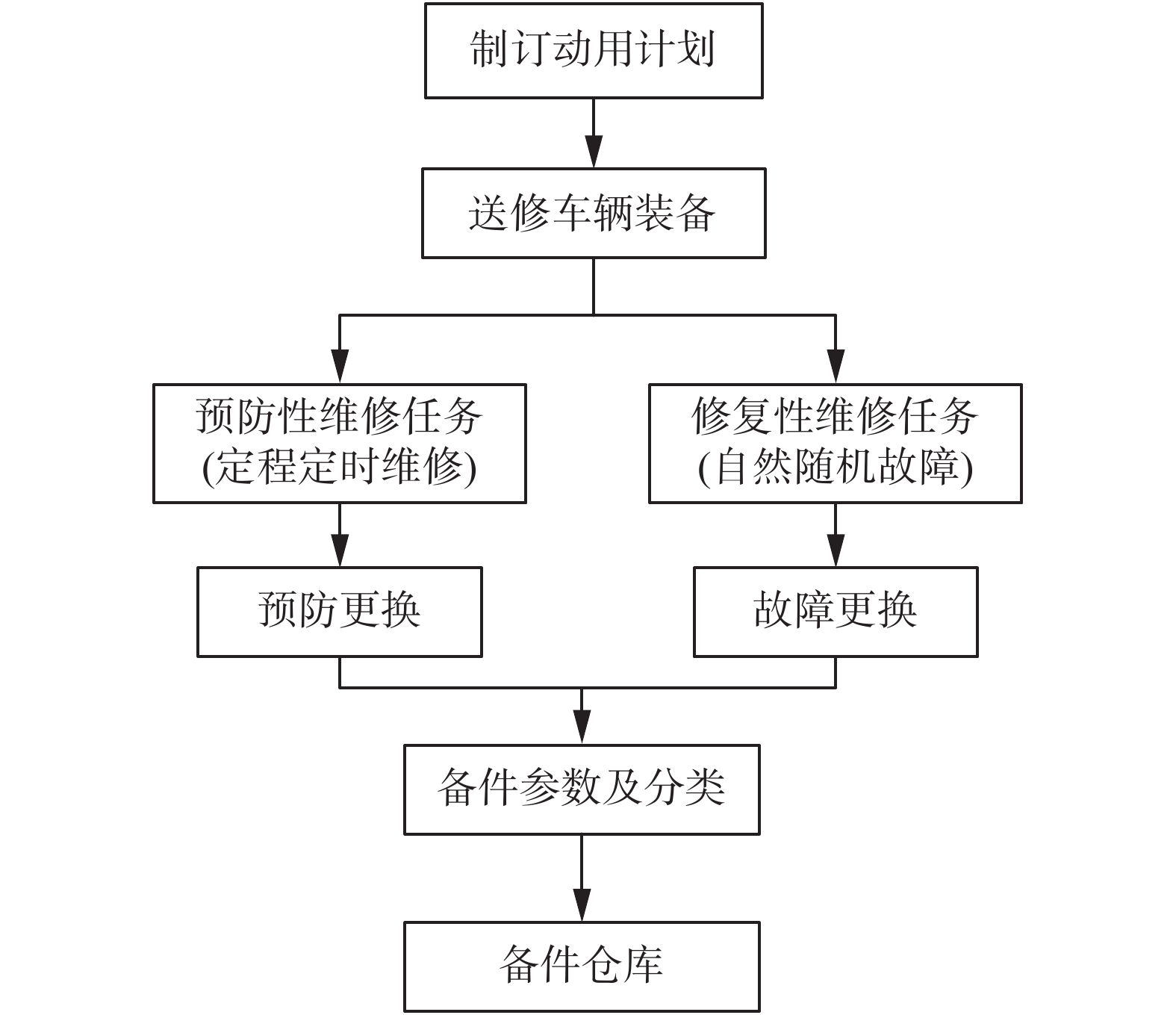
综上，维修任务下备件的消耗过程如图3所示。首先，制订保障期内车辆装备的动用计划，动用计划下的车辆装备将产生对应的送修计划，主要包括预防性维修和修复性维修。其中，预防性维修任务主要考虑车辆装备的定时定程维修，修复性维修主要考虑自然随机故障维修。然后，维修任务产生备件更换，包括备件预防性更换和故障性更换两种情况，最后根据备件的相关数据，进行仓库的库存控制优化。

1.2 车辆装备备件消耗量模型

上面分析了基于定时定程维修和自然随机故障维修产生备件消耗的两种情况。对历史数据做回归分析容易得出各类故障维修与备件消耗量的对应关系。这里假设已知车辆装备的备件需求率，建立动用计划期内的备件消耗量预测模型。这里所需的基本符号如表1所示。

1)定时定程维修备件消耗量

动用计划下的定时定程维修类型完全按照摩托小时间隔划分为小、中、大修，并假设大修之后车辆如新，摩托小时归零。建立定时定程维修备件消耗模型，假设 $ N $ 台同类型车辆在保障时间内产生的 $ j $ 类维修的次数为 $ {Z_j} $ ^[18]：

$ {Z_j} = \sum\limits_{k = 1}^N {\left\lfloor {\frac{{{M_k} - {M_{jk}} + {{\rm{EM}}_k}}}{{{{\rm{IM}}_j}}}} \right\rfloor } $

(1)

那么动用计划下定时定程维修备件 $ i $ 预计消耗量为 $ D' $ ：

$ {D'_i} = \sum\limits_{\forall f} {\sum\limits_{j = 1}^3 {{Z_j} \cdot } {\gamma _{jf}} \cdot {c_{fi}}} $

(2)

2)随机故障维修备件消耗量

车辆的随机备件消耗与车辆的故障规律、装备技术状况和使用条件等因素有着直接的关系，主要取决于车辆使用强度。本文根据当前摩托小时的消耗量来度量使用强度。车辆的自然随机故障多为小修范围，且产生小修的故障率较稳定。根据现有的一些方法^[19-20]对历史数据进行分析处理，可得到摩托小时分段故障率。大修之后车辆装备如新，摩托小时归零，所以只在一个大修周期内进行分段。

规定 $ l $ 为摩托小时分段的标识，按照每100摩托小时划分一个大修周期，共分为 $ L $ 段，即 $L = $ $ \left\lfloor {\rm{IM_3}/100} \right\rfloor + 1 = \max l$ 。 $ {\lambda _l} $ 表示摩托小时段 $ l $ 的故障率。所以随机自然故障维修台次 $ {H_f} $ 可通过式(3)确定：

$ {H_f} = \sum\limits_{\forall l} {\sum\limits_{\forall k} {\Delta {M_{kl}}{\lambda _l}{\beta _f}} } $

(3)

式中： $ {\beta _f} $ 为 $ f $ 类故障的占比； $ \Delta {M_{kl}} $ 为第 $ k $ 台车在每个摩托小时段 $ l $ 的预计摩托小时消耗量。所以自然随机故障维修备件 $ i $ 消耗量计算如式(4)：

$ {D''_i} = \sum\limits_{\forall f} {({H_f} \cdot {c_{fi}})} $

(4)

3)动用计划下备件消耗量模型

动用计划下备件消耗量主要来自定时定程维修备件消耗量和随机故障维修备件消耗量，所以备件 $ i $ 消耗量计算如式(5)：

$ \begin{array}{l} {D_i} = {D'_i} + {D''_i} = \displaystyle\sum\limits_{\forall f} {\displaystyle\sum\limits_{j = 1}^3 {{Z_j} \cdot } {\gamma _{jf}} \cdot {c_{fi}}} + \displaystyle\sum\limits_{\forall f} {({H_f} \cdot {c_{fi}})} \end{array} $

(5)

2 车辆装备备件库存控制模型

科学的备件库存管理，可以在保证仓库一定服务水平的同时，有效降低库存成本。一般来说，库存成本主要包括补货成本和存储成本。建立基于定期检查策略库存策略的联合补货策略库存模型。备件中补货周期最短的为基本补货周期 $ T $ ，其他备件 $ i $ 的补货周期均是该周期的 $ {k_i} $ 倍， $ {k_i} $ 为大于零的整数。其他基本假设：1)订购的提前期可忽略不计；2)缺货成本无限大，即不允许缺货；3)不考虑仓库的容量限制。库存控制模型如下：

在 $ N $ 种装备备件中，第 $ i $ 种备件的订购量 $ {Q_i} $ 为

$ {Q_i} = {D_i}{k_i}T, \;\;i = 1,2, \cdots, N $

(6)

那么所有装备备件的年平均存储成本 $ {C_h} $ 为

$ {C_h} = \frac{1}{2}\sum\limits_{i = 1}^N {{Q_i}{h_i}} = {{\left( {\sum\limits_{i = 1}^N {{k_i}T{D_i}} } \right)} / 2} $

(7)

式中 $ {h_i} $ 表示备件 $ i $ 的单位存储成本。同样容易得出所有装备备件的年平均补货成本 $ {C_r} $ 为

$ {C_r} = \left( {{R / T}} \right) + \sum\limits_{i = 1}^N {\left( {{{{r_i}} / {{k_i}T}}} \right)} $

(8)

式中： $ R $ 表示主要补货成本； $ {r_i} $ 表示备件 $ i $ 的额外补货成本单位存储成本。所以车辆装备备件库存控制年平均成本 $ C $ 为

$ \begin{array}{l} C(T,K) = {C_h} + {C_r} = \displaystyle\sum\limits_{i = 1}^N {\dfrac{{{k_i}T{D_i}}}{2}} + \dfrac{R}{T} + \displaystyle\sum\limits_{i = 1}^N {\dfrac{{{r_i}}}{{{k_i}T}}} \end{array} $

(9)

式中 $ K = \{ {k_1},{k_2}, \cdots,{k_N}\} $ 。

3 算法设计

果蝇优化算法(fruit fly optimization algorithm, FOA) 是模拟果蝇觅食行为而提出的一种基于群体性搜索的随机优化算法，现在已被广泛应用在各领域的优化设计中。果蝇算法操作方便，简单明了。但本文模型涉及的决策变量较多，果蝇在全局中飞行以寻找更优的个体进行迭代，在迭代后期会由于个体集聚度变大导致群体多样性减少，因此果蝇到后期容易出现陷入局部最优解的问题^[21-22]。研究发现多种群位置更新^[23-24]和自适应进化策略^[25-26]是提高智能算法搜索效率的有效方法。为了解决果蝇算法的这一问题，对果蝇优化算法进行了改进。引入麻雀搜索算法(sparrow search algorithm, SSA)中多类种群位置更新方式^[27]，提出改进的果蝇优化算法(improve the fruit fly optimization algorithm, IFOA)。

3.1 界限确定

对于给定的 $ K $ ， $ C $ 是关于基本周期 $ T $ 的凸函数，通过 $\left( {{{\partial C} / {\partial T}}} \right) = 0$ 求得关于 $ K $ 的最优基本周期 $ {T^*} $ ：

$ {T^*}(K) = \sqrt {{{2\left( {R + \sum\limits_{i = 1}^N {\frac{{{r_i}}}{{{k_i}}}} } \right)} / {\sum\limits_{i = 1}^N {{k_i}{D_i}{h_i}} }}} $

(10)

将式(10)代入式(9)可得关于 $ K $ 的最优成本函数：

$ C(K) = \sqrt {2(R + \sum\limits_{i = 1}^N {\frac{{{r_i}}}{{{k_i}}}} )\sum\limits_{i = 1}^N {{D_i}{k_i}{h_i}} } {\text{ }} $

(11)

可以看出，最优解关键是由 $\left\{ {{k_1},{k_2}, \cdots,{k_i}, \cdots,{k_N}} \right\}$ 值决定。这里采用改进的果蝇优化算法求解模型。为了减少搜索空间，对 $ {k_i} $ 界限作以下设置。

$ {k_i} $ 为大于零的整数，所以显然可以设置下限 ${k_{{\rm{LB}}i}}$ =1。另一方面，通过 $\left( {{{\partial C} / {\partial {k_i}}}} \right) = 0$ 和基本不等式(12)，易得出不等式(13)：

$ {k_i}({k_i} - 1) \leqslant k_i^2 \leqslant {k_i}({k_i} + 1) $

(12)

$ {k_i}({k_i} - 1) \leqslant \frac{{2{r_i}}}{{{D_i}{h_i}{T^2}}} \leqslant {k_i}({k_i} + 1) $

(13)

所以 $ {k_i} $ 上界 ${k_{{\rm{UB}}i}}$ 满足式(14)：

$ {k_{{\rm{UB}}i}}({k_{{\rm{UB}}i}} - 1) \leqslant \frac{{2{r_i}}}{{{D_i}{h_i}T_{\min }^2}} \leqslant {k_{{\rm{UB}}i}}({k_{{\rm{UB}}i}} + 1) $

(14)

式中 ${T_{\min }} = \mathop {\min }\limits_{1 \leqslant i \leqslant N} \sqrt {\dfrac{2{r_i}}{{D_i}{h_i}}}$ 。

3.2 种群更新方式

实际问题备件种类数量较多，果蝇个体位置向量较长，传统的气味浓度判断值 $ {S_y} $ 计算方法也将变得复杂，且存在求解空间分布不均匀的缺陷^[28]。为了避免果蝇距离 $ {\text{Dis}}{{\text{t}}_y} $ 的计算，使计算简单有效，设置每个果蝇个体 $ y $ 的位置为 $ {X_y} = \left( {x_y^1,x_y^2, \cdots,x_y^N} \right) $ 对应着 $ N $ 个备件的周期乘子 $ K $ 。直接将果蝇的气味浓度判定值设定为 $ {S_y} = {X_y} $ 。引入SSA多类种群位置更新方式如下：

1)果蝇“发现者”位置更新方式

设置果蝇“发现者”，进行大方向范围搜索，是一种多样性保存策略。

$ X_y^{t + 1} = X_y^t + {\text{rand}}({\text{F}}{{\text{R}}_1}) $

(15)

式中飞行方向 $ {\text{F}}{{\text{R}}_1} $ 由初始搜索飞行范围决定。

2)果蝇“跟随者”位置更新方式

设置果蝇“跟随者”，跟随发现者进行二次搜索，是一种加速收敛的策略。

$ X_y^{t + 1} = X_d^{t + 1} + {\text{rand}}\left( {{\text{F}}{{\text{R}}_2}} \right) $

(16)

式中： $ X_d^{t + 1} $ 为“发现者”目前所占据的最优位置； $ {\text{F}}{{\text{R}}_2} $ 为个体飞行范围，由 $ X_d^{t + 1} $ 决定，果蝇个体随机飞向发现者最优位置附近，可通过设置 $ {\text{F}}{{\text{R}}_2} $ 值为零的分量的个数约束飞向最优位置的距离，零分量的个数越多，意味着距离全局最优位置越近。

3)果蝇“反捕食行为”方式

通过设置“反捕食行为”来防止果蝇总是停留在某一位置，陷入局部最优，是一种最优保存策略。

$ X_y^{t + 1} = X\_{\text{axis}} + {\text{rand}}\left( {{\text{F}}{{\text{R}}_3}} \right) $

(17)

式中： $ X\_{\text{axis}} $ 为当前迭代下的全局最优位置； $ {\text{F}}{{\text{R}}_3} $ 为个体飞行范围，由 $ X\_{\text{axis}} $ 决定，果蝇个体随机飞向全局最优位置附近，可通过设置 $ {\text{F}}{{\text{R}}_3} $ 值为零的分量的个数约束飞向最优位置的距离，零分量的个数越多，意味着距离全局最优位置越近。

果蝇优化算法步骤：

1)初始化参数。设置种群规模、最大迭代次数、飞行方向，果蝇各类群体比例。随机初始化果蝇个体位置。

2)计算果蝇的气味浓度值。气味浓度判断值 $ {S_y} = {X_y} $ ，将 $ {S_y} $ 代入味道浓度判定函数 $ F(X) $ 中，本文的判定函数 $ F(X) $ 为总成本函数 $ C(K) $ 。计算每个个体当前位置的味道浓度值 $ {\text{Smel}}{{\text{l}}_y} $ ， $ {\text{Smel}}{{\text{l}}_y} = F({S_y}) $ 。

3)对气味浓度值进行排序 $ {\text{sort}}({X_i}) $ 。记录种群的全局历史最佳位置 $ X\_{\text{axis}} $ 和最佳气味浓度值 $ {\text{Smellbest}} $ ；根据气味浓度值大小和群体比例参数 $ M $ 设置果蝇“发现者”“跟随者”和“反捕食行为”群体。

4)多类种群位置更新。根据式(15)~(17)更新果蝇群体位置。

5)重复步骤2)~4)，直到迭代次数最大，停止迭代并输出结果。

4 仿真与分析 4.1 实例仿真

以某后勤保障区域的车辆装备维修保障活动为例，对某类型车辆装备的维修备件进行优化配置。要求根据车辆的故障规律与动用计划，分析维修备件的需求规律，并对备件进行库存控制决策优化。考虑4类故障和5类备件，车辆装备的小修、中修、大修的间隔期分别为250、500和1000 h，其他基础数据如表2所示，部分数据来源于文献[15]。

为了验证模型的适用性，设计以下两个仿真实例。实例1用于验证不同初始摩托小时下，各预计摩托小时支出量与备件消耗量的关系；实例2用于优化备件库存控制方案。

实例1仿真：以某后勤保障区的车辆装备为例，设置1~4号车辆装备的初始摩托小时分别为1、251、501、751 h。根据车辆的故障信息与备件需求信息，研究这4辆车在摩托小时预计支出量在0~1000 h时各备件消耗量的变化情况。在给定的参数范围下，随机生成实例数据，通过1.2小节中的方法计算1、3、5号备件消耗量随摩托小时支出量的变化规律。

实例2仿真：给定10辆一般用车和30辆重点用车的动用计划参数信息，如表3所示。第2年动用的车辆装备接着第1年之后继续使用，分别制定这两年的库存控制方案，使得年度库存成本最优。根据给定参数范围，随机生成实例。设定IFOA迭代次数为200次，果蝇群体大小为30。果蝇“发现者”“跟随者”以及“反捕食行为”比例分别为50%、20%、30%。仿真运行30次，并对最佳运行结果方案进行详细分析。为了验证算法的优越性，这里选择遗传算法进行对比实验，设置交叉概率为0.9，变异概率为0.1。

4.2 仿真分析

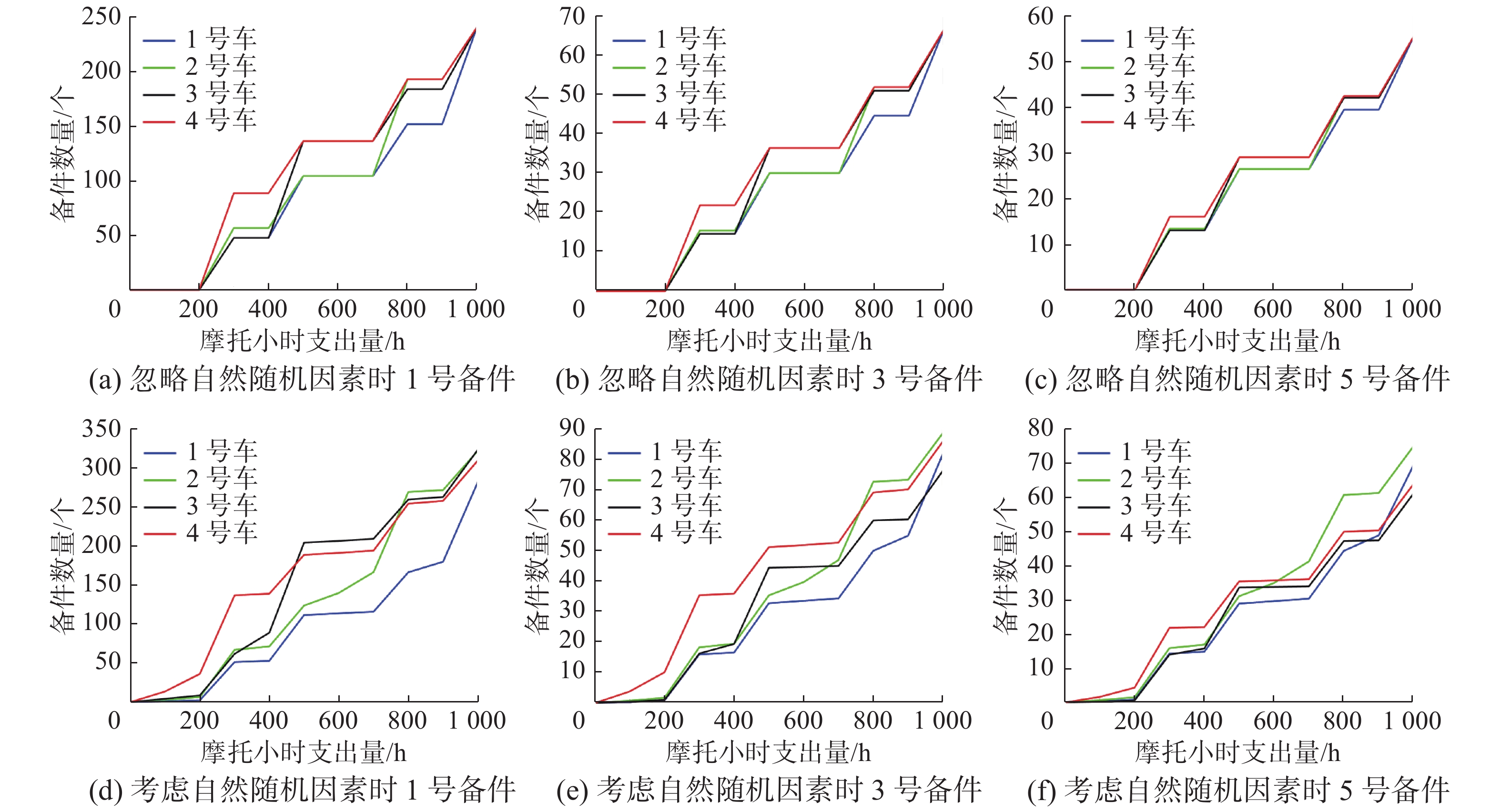
实例1仿真分析：1至4号车辆装备的初始摩托小时分别为1、251、501、751 h。通过1.2小节中方法计算1、3、5号备件消耗量随摩托小时支出量的变化规律，仿真结果如图4所示，主要包括忽略自然随机因素和考虑自然随机故障时两部分的备件消耗规律。

图4中的(a)、(b)、(c)分别对应忽略自然随机因素时，各车辆装备1、3、5号备件的消耗量规律，即仅考虑定程维修下车辆在摩托小时各备件消耗量随摩托小时支出量的变化规律。可以看出，备件的消耗具有一定的周期性，且不同初始摩托小时的车辆备件消耗量图像可以通过平移重合。这是因为，在不考虑自然随机故障时，由于车辆的维修间隔期不变，故车辆维修产生周期性。另一方面，由于各车初始摩托小时支出量不同，导致各车辆装备的备件消耗量具有超前或滞后的现象。可以看出，各车辆装备在摩托小时预计支出量为1000 h时，各车辆装备的备件消耗量相同，这是因为初始摩托小时分别为1、251、501、75 1 h的4辆车在预计支出量为1000 h时显然均经历了1次大修、1次中修和2次小修，与实际情况一致。仿真结果说明，车辆装备的定时定程维修和备件消耗具有显著的规律性，这是由车辆装备按照发动机摩托小时的支出量和各级维修维护的规定决定的。

图4中的(d)、(e)、(f)分别对应考虑自然随机因素时，各车辆装备1、3、5号备件的消耗量规律，即考虑定时定程维修和自然随机故障维修下车辆在摩托小时各备件消耗量随摩托小时支出量的变化规律。可以看出，备件的消耗不再具有周期性，且车辆装备的图像与图(a)、(b)、(c)相比发生了明显变化。这是因为，在考虑自然随机故障时，自然随机故障率随摩托小时支出量的变化而变化。摩托小时支出量越高其随机故障率越大，为了对比加入随机故障因素后，备件消耗量的变化规律，以3、4号车为例说明。3、4号车的备件消耗量最先加速上升，这是因为其初始摩托小时较大，所以自然随机故障率也大的原因。在支出量达到300 h和500 h时，备件消耗量开始缓慢上升，与实际情况相适应，这是因为大修后摩托小时归零，随机故障率减小导致的。一般情况下车辆装备的备件消耗规律性弱于仅考虑定时定程维修的备件消耗规律，大修之前车辆装备的备件消耗增量相比大修之后更大。掌握车辆装备备件的消耗规律，可以避免库存积压或严重缺货等不良现象发生。

方案2仿真分析：首先，根据第1年的初始摩托小时与预计摩托小时支出量，容易计算出年末摩托小时支出量，即为第2年的初始摩托小时。通过1.2小节中方法计算各备件的消耗量，结果如表4所示，然后根据计算结果进行基于定期检查策略的库存决策优化，对运行结果方案进行详细分析。

表4给出了40辆车辆装备连续两年的备件消耗量。从表4中容易看出，第2年的备件消耗量明显高于第1年的消耗量，这是因为第2年的所有车辆装备摩托小时预计支出量是第1年的两倍，导致第2年的需求量与第1年的需求量有明显的差异，这表明动用计划严重影响着备件消耗量。另外，由于第2年的车辆类型和数量没有发生变化，一般来说第2年的备件消耗量大约等于第1年的2倍，这与仿真结果中第2年备件的增长率不一致，主要是因为第1年的车辆经过一年的使用，存在车辆经过大修之之后，车辆如新，即摩托小时归零的情况，第2年初始摩托小时降低。而第1年未经过大修的车辆装备，摩托小时不归零，第2年的初始摩托小时增加，这当然也就导致了故障发生规律的改变。仿真结果说明，车辆装备的备件消耗率受自然随机故障率和定时定程大修影响较大，车辆装备的备件科学预算应符合实际情况。

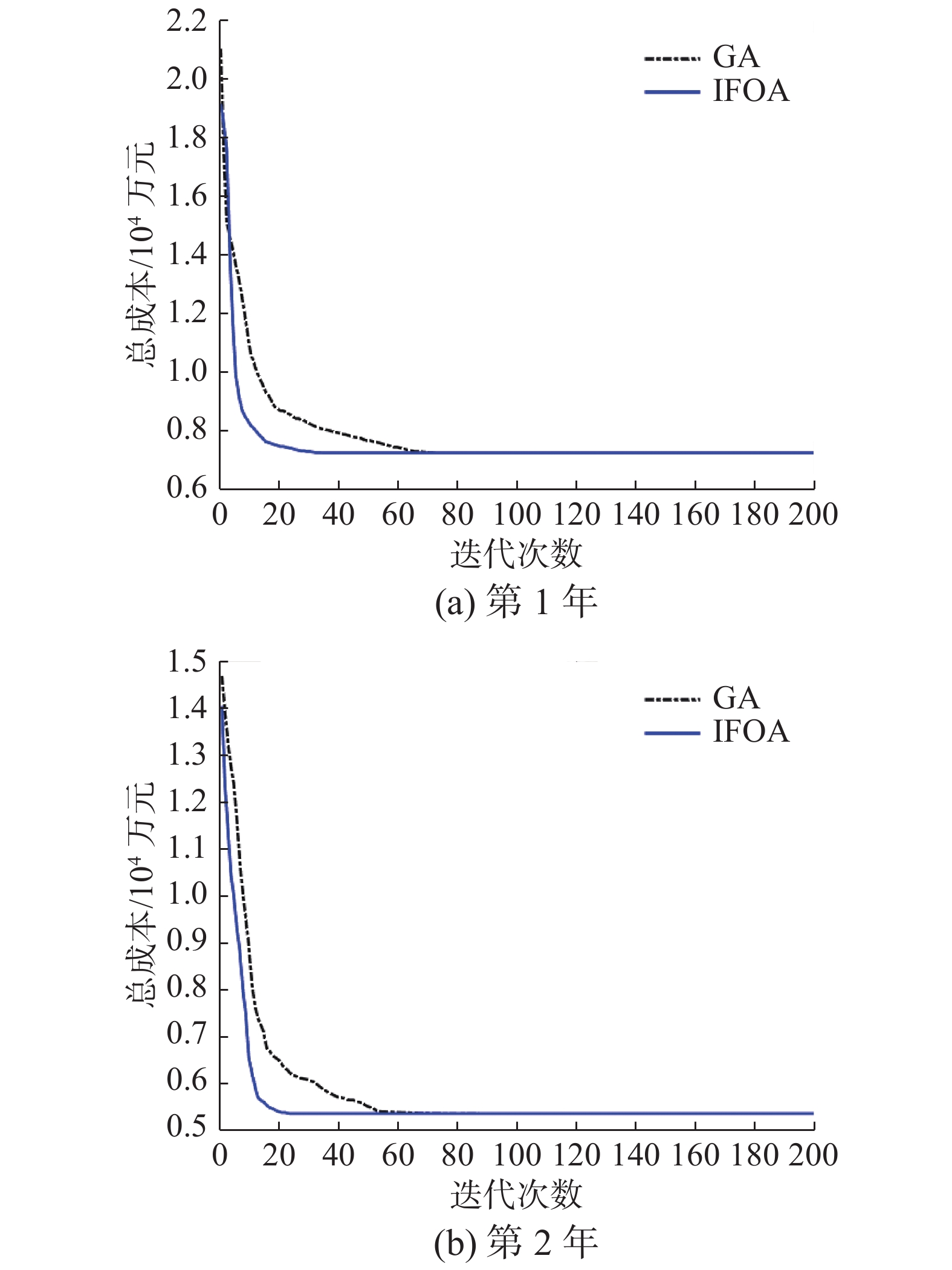
图5展示了第一年和第二年IFOA的收敛过程对比图，容易看出平均优化过程与最佳优化过程在40次迭代以后开始重合且收敛，这意味着每一次的运行结果均可达到最优的库存成本。使用IFOA和GA两类算法再次同时独立求解算例30次，算法的收敛过程如图6所示。从图6中可以看出，无论是第一年还是第二年，IFOA算法收敛速度都更快。这是因为通过对模型结构特点的分析，确定了决策变量的界限，显著减小了算法的搜索空间。另外，IFOA算法利用多类种群位置更新方式，设置果蝇“发现者”进行大方向范围搜索，是一种多样性保存策略，提高了果蝇全局搜索能力。设置果蝇“加入者”跟随“发现者”进行二次搜索，提高了算法的收敛速度。设置“反捕食行为”来防止果蝇总是停留在某一位置，解决了算法容易陷入局部极值的问题。该算法即使是较小的种群规模，收敛速度依然很快，适用于大规模的备件联合补货问题。

表5、6展示了两个年度的库存控制计划方案，第一年度的基本循环周期 $T = 0.094\;1$ 年，即34天左右，各备件的基本周期乘子分别为1、1、1、2和3，即1至3号备件每隔34天补货一次，4号备件每隔68天补货一次，5号备件每隔102天补货一次。5种备件的每次补货量分别为295、254、58、280和191个。在该决策方案设置下，维修备件库存总成本可达到最小。同理，第二年度 $ T = 0.068\;2 $ 年，即25天左右，备件 $ i $ 每隔 $ {T_i} $ 天补货一次。

5 结束语

在动用维修保障计划期内，车辆装备的日常维修主要包括预防性维修维护和修复性维修。考虑车辆的定时定程维修维护和自然随机故障维修两类维修方式，分析动用使用计划下车辆装备的备件消耗规律，计算了一般用车和重点用车在保障期的备件消耗量。另外，通过引入麻雀搜索算法中的多类种群位置更新方式改进了果蝇优化算法，并以此计算车辆装备的备件库存控制模型。本文根据实际某型车辆装备的实践特点建立的备件预测模型，不仅适用于动用使用计划的车辆装备，同样也适用于备件消耗历史数据有限、信息内容不完善等其他动用计划下的备件资源预测问题。