年龄因素导致人脸识别准确率降低，如何抑制年龄因素是人脸识别技术中的关键。在2015年，Chen等^[1]将一般的人脸识别模型应用在跨年龄人脸识别任务中，研究结果显示准确率降低13%以上，直接说明了年龄的变化会降低人脸识别率。目前跨年龄人脸识别研究主要分为三类：生成方法、判别方法和基于深度学习的方法^[2-6]。生成方法先构建一个模拟人脸老化或者年轻化的生成模型，在人脸匹配阶段，生成目标年龄的人脸，以此来降低年龄因素对人脸识别的影响。该方法需要准确的数据标签和先验参数假设，对非受限环境敏感，生成的图像会增加噪声，影响匹配结果^[7-9]。判别方法先提取出随年龄变化稳定的人脸特征，再进行人脸识别。2013年，Gong等^[10]提出了一种隐藏因子分析(HFA)的方法，该方法分别提取年龄相关的人脸特征以及不随年龄变化的稳定特征，对这两个特征建模，然后用期望最大化(EM)算法估计参数，以此实现跨年龄的人脸识别。2016年，Gong等^[11]又提出了一种最大熵特征描述符(MEFD)的方法，该方法根据最大熵将面部图像的微观特征编码为一组离散代码，通过密集采样编码的面部图像，提取大量具有区分性和表达性的信息，进一步对跨年龄人脸特征进行分析。2017年，Xu等^[12]依据年龄变化是一种非线性变换，提出了一种耦合自动编码器网络(CAN)的方法，由两个浅层神经网络组成，适用于复杂的非线性老化过程。由于卷积神经网络具有从原始特征中端到端学习非线性特征的优势^[13-14]，基于深度学习的跨年龄人脸识别方法相继提出。Wang等^[15]提出正交嵌入卷积神经网络模型(OE-CNN)，该方法将面部特征分解成两个正交分量，分别表示年龄特征和身份特征，以实现跨年龄人脸识别。Wen等^[16]提出了一种并行的卷积神经网络模型(LF-CNN)学习年龄不变的人脸特征，并且提出了LIA分析法进行参数更新，代替了传统梯度下降法。

本文基于判别方法提出一种跨年龄人脸验证网络模型，首先改进LBP算法，提出双编码平均局部二值模式算法(DCALBP)。该算法使用邻域像素的平均值与中心像素的差值以及差值的绝对值作为差值阈值和幅度阈值，可减少光照和高频噪声对像素值的影响，同时丰富纹理特征信息，降低特征维度。以3×3像素块为例，将8点采样降为4点采样，编码数量从2⁸=256降为2⁴=16。之后采取多任务方式，应用CCA算法融合DCALBP和HOG提取的人脸纹理形状特征，得到一维的年龄特征信息。另外，本文引入孪生网络(siamese network)进行特征匹配，从网络提取的特征中分离出年龄特征信息，得到具有年龄不变性的人脸特征，从而完成跨年龄人脸验证任务。

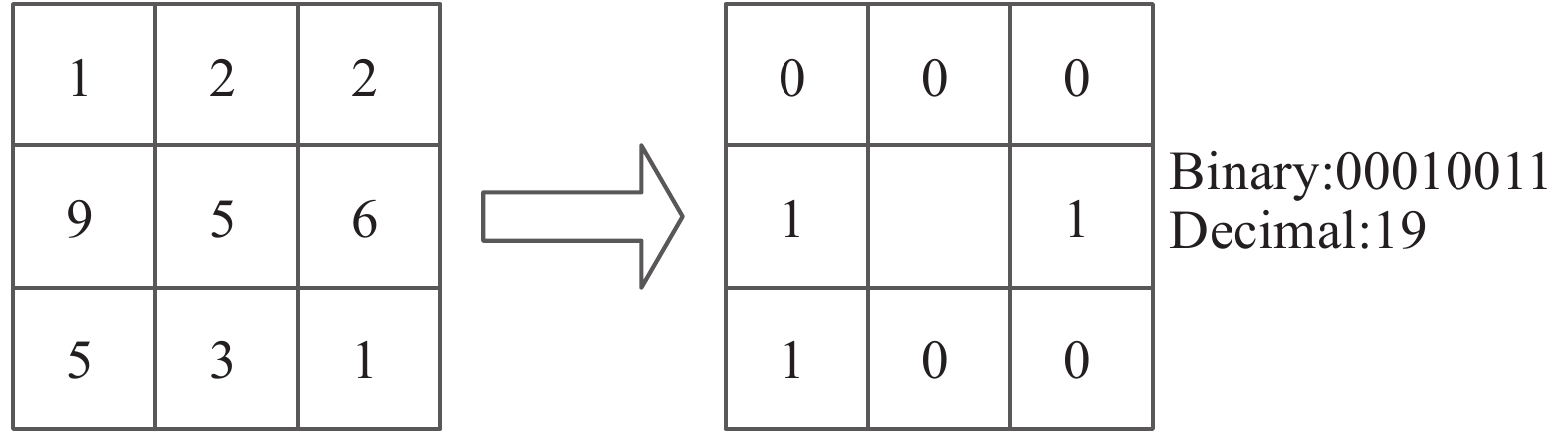
1 DCALBP算法 1.1 LBP算法

局部二值模式(LBP)是一种描述图像局部纹理特征的算子^[17]，以中心像素灰度值为阈值，相邻像素的灰度值与其比较，若邻域像素灰度值大于等于阈值，记为1，反之记为0。对其结果进行编码，得到相应的二进制数，转为十进制，作为该点的LBP编码值，用来表示这个区域的纹理信息。LBP编码公式如下：

${\rm{LBP}}({x_c},{y_c}) = \sum\limits_{p = 0}^{N - 1} {S({i_p} - {i_c}){2^p}} $

(1)

$S(x) = \left\{ \begin{array}{l} 1,\quad x \geqslant 0 \\ 0,\quad x < 0 \end{array} \right.$

(2)

式中： $({x_c},{y_c})$ 是中心像素点； $i_c$ 表示中心像素点的灰度值； $N$ 表示邻域像素点的个数； ${i_p}(p = 0,1 \cdot \cdot \cdot \; p - 1)$ 表示邻域像素点的灰度值。以 $3\times3$ 像素窗口为例，LBP计算过程如图1所示。

传统LBP只考虑了邻域像素灰度值与中心像素灰度值之间的关系，没有考虑邻域像素灰度值之间的影响。针对这一问题，后来有研究者提出一种中心对称局部二值模式(CS-LBP)，即设置一个阈值 $T$ ，将中心对称的两个邻域像素灰度值相减，与阈值 $T$ 相比较，大于等于 $T$ 取1，反之取0。编码公式为

${\rm{CS - LB}}{P_{R,N}}(c) = \sum\limits_{p = 0}^{\frac{N}{2} - 1} {S({i_p} - {i_{p + \frac{N}{2}}}){2^p}} $

(3)

$S(x) = \left\{ \begin{array}{l} 1,\quad x \geqslant T \\ 0,\quad x < T \end{array} \right.$

(4)

式中： $R$ 表示区域半径 $(R = 1)$ ； $N$ 表示邻域像素点个数 $(N = 8)$ ； ${i_p}$ 表示邻域像素点 $p(p = 0,1 ,\cdots, 7)$ 灰度值； $T$ 为阈值。

1.2 DCALBP算法

传统LBP方法和改进后的CS-LBP算法，都是8点采样，且CS-LBP算法中阈值为预设值，需要根据先验知识进行设置,很难定义一个合适的阈值。本文提出的DCALBP方法将采样点降低到4个，减少特征向量的维度，同时考虑了光照变化不均匀时对像素的影响，采样点的灰度值用相邻像素点和自身灰度值的平均值代替，引入两个阈值变量，分别为差值阈值 $d$ 和幅度阈值 $t$ ，两个变量的计算公式为

$d = \frac{1}{N}\sum\limits_{p = 0}^{N - 1} {({i_{2p + 1}} - {i_c})} $

(5)

$t = \frac{1}{N}\sum\limits_{p = 0}^{N - 1} {|{i_{2p + 1}} - {i_c}|} $

(6)

其中， $N$ 表示采样点的个数； $i_c$ 表示中心像素点的灰度值； ${i_{2p + 1}}(p = 0,1,2 \cdot \cdot \cdot )$ 表示采样点的灰度值。

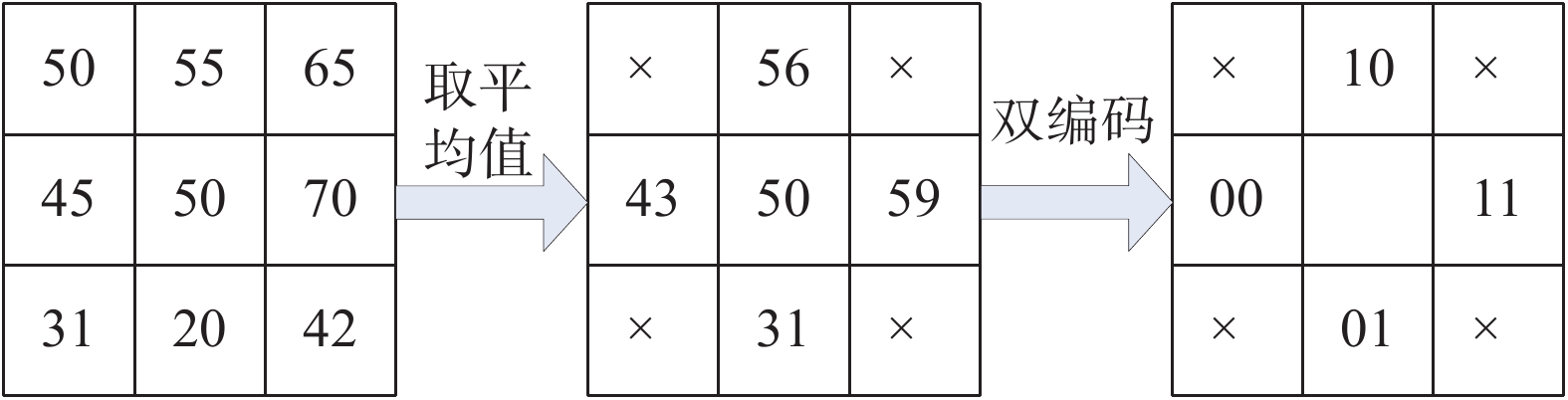
为了提取出丰富的面部纹理信息，DCALBP采用双编码的方法。取采样点与中心像素点灰度值的差值，差值大于等于阈值 $d$ ，编码为1，反之为0，得到第一位编码值。第二位编码值与采样点与中心像素灰度值的绝对值有关，绝对值大于等于 $t$ ，编码为1，反之为0。编码公式如下：

${\rm{DCALB}}{{\rm P}_N} = \sum\limits_{p = 0}^{N - 1} {({S_{(1)}}({i_p},{i_c}){2^{2p}} + } {\kern 1pt} {S_{(2)}}({i_p},{i_c}){2^{2p + 1}})$

(7)

$S({i_p},{i_c}) = \left\{ \begin{array}{l} 00,\quad{i_p} - {i_c} < d\;{\rm{and}}\;|{i_p} - {i_c}| < t \\ 01,\quad{i_p} - {i_c} < d\;{\rm{and}}\;|{i_p} - {i_c}| \geqslant t \\ 10,\quad{i_p} - {i_c} \geqslant d\;{\rm{and}}\;|{i_p} - {i_c}| < t \\ 11,\quad{i_p} - {i_c} \geqslant d\;{\rm{and}}\;|{i_p} - {i_c}| \geqslant t \end{array} \right.$

(8)

其中 ${S_{(1)}}$ 和 ${S_{(2)}}$ 分别表示 $S({i_p},{i_c})$ 编码中的第一位和第二位编码值。以3×3的窗口，采样点为4 $(N = 4)$ 为例，DCALBP编码过程如图2所示。

首先求取4个采样点的灰度值，灰度值取整，根据式(5)，差值阈值为 $d = \dfrac{1}{4}[(56 - 50) + (59 - 50) + $ $(31 - 50) + (43 - 50)] = - 2.75 $ ，根据式(6)，幅度阈值 $t \!=\! \dfrac{1}{4}[|56 - 50| + |59 - 50| + |31 - 50| + |43 - 50|] \!=\! 7.75$ 。由式(7)、(8)，得到DCALBP编码值。由于二值编码模式经循环位移后会产生不同的编码结果，为了保证算法的旋转不变性，取最小值为DCALBP的值。图2中，循环移位后二值编码分别为： ${(10110100)_2} \!\!=\!\! {(180)_{10}}$ ， ${(00101101)_2} \!\!=\! \!{(45)_{10}}$ ， ${(01001011)_2} \!\!= $ $ {(75)_{10}}$ ， ${(11010010)_2} = {(210)_{10}}$ ，取最小值，故该像素点的DCALBP值为45。

1.3 CCA特征融合

典型相关性分析(canonical correlation analysis，CCA)用来挖掘两个来自于同一个体的多维数据之间的联系^[18]。CCA将多维向量X和Y通过线性变换为U和V，计算U和V之间的相关系数，从而得到二者的相关性。该算法将两组特征向量的典型特征作为有效特征，既达到特征融合的目的，又消除了特征向量之间的信息冗余，同时起到降维的作用。在本研究中，首先应用DCALBP和HOG算法分别提取人脸纹理特征和形状特征向量，用X、Y表示，然后引入CCA算法将两组向量通过线性变换投影到一维空间，求出投影向量a和b，使得 ${ U} = {{ a}^{\bf{T}}}{ X}$ 和 ${ V} = {{ b}^{\bf{T}}}{ Y}$ 之间的相关系数 ${\rm{Coor}}({ U},{ V})$ 最大。向量X和Y的协方差矩阵为 ${ \varSigma} = \left[ \begin{array}{l} {{ \varSigma} _{XX}}\;{{ \varSigma} _{XY}} \\ {{ \varSigma} _{YX}}\;{{ \varSigma} _{YY}} \end{array} \right]$ ，其中 ${{ \varSigma} _{XX}} = {\rm{cov}} ({ X},{ X})$ ，表示X的协方差矩阵； ${{ \varSigma} _{XY}} = {\rm{cov}} ({ X},{ Y})$ ， ${{ \varSigma} _{YX}} = {\rm{cov}} ({ Y},{ X})$ ，表示X和Y的互协方差矩阵； ${{ \varSigma} _{YY}} = {\rm{cov}} ({ Y},{ Y})$ ，表示Y的协方差矩阵。先求出 ${ U} = {{ a}^{\bf{T}}}{ X}$ 和 ${ V} = {{ b}^{\bf{T}}}{ Y}$ 的方差和协方差，有:

${\rm{var}} ({ U}) = {\rm{var}} ({{ a}^{\bf{T}}}{ X}) = {{ a}^{\bf{T}}}{{ \varSigma} _{XX}}{ a}$

(9)

${\rm{var}} ({ V}) = {\rm{var}} ({{ b}^{\bf{T}}}{ Y}) = {{ b}^{\bf{T}}}{{ \varSigma} _{YY}}{ b}$

(10)

${\rm{cov}} ({ U},{ V}) = {\rm{cov}} ({{ a}^{\bf{T}}}{ X},{{ b}^{\bf{T}}}{ Y}) = {{ a}^{\bf{T}}}{{ \varSigma} _{XY}}{ b}$

(11)

然后求U和V的相关系数:

$\; \rho = {\rm{Corr}}({ U},{ V}) \!=\! \frac{{{\rm{cov}} ({ U},{ V})}}{{\sqrt {{\rm{var}} ({ U})} \sqrt {{\rm{var}} ({ V})} }} \!=\! \frac{{{{ a}^{\bf{T}}}{{ \varSigma} _{XY}}{ b}}}{{\sqrt {{{ a}^{\bf{T}}}{{ \varSigma} _{XX}}{ a}} \sqrt {{{ b}^{\bf{T}}}{{ \varSigma} _{YY}}{ b}} }}$

(12)

此时，问题转化为，求解出投影向量a、b，使得相关系数 $\rho $ 最大。分母固定，求解分子最大值，即：令 $ {{ a}}^{{\bf{T}}}{{ \varSigma} }_{XX}{ a}=1$ ， ${{ b}}^{{\bf{T}}}{{ \varSigma }}_{YY}{ b}=1 $ ， ${{ a}^{\bf{T}}}{{ \varSigma} _{XY}}{ b}$ 最大，构造拉格朗日等式，有：

$L({ a},{ b}) = {{ a}^{\bf{T}}}{{ \varSigma} _{XY}}{ b} - \frac{\lambda }{2}({{ a}^{\bf{T}}}{{ \varSigma} _{XX}}{ a} - 1) - \frac{\theta }{2}({{ b}^{\bf{T}}}{{ \varSigma} _{YY}}{ b} - 1)$

(13)

求导得出：

$\left\{ \begin{array}{l} \dfrac{{\partial { L}}}{{\partial { a}}} = {{ \varSigma} _{XY}}{ b} - \lambda {{ \varSigma} _{XX}}{ a} \\ \dfrac{{\partial { L}}}{{\partial { b}}} = {{ \varSigma} _{YX}}{ a} - \theta {{ \varSigma} _{YY}}{ b} \end{array} \right.$

(14)

令导数为0，则有：

$\left\{ \begin{array}{l} {{ \varSigma} _{XY}}{ b} - \lambda {{ \varSigma} _{XX}}{ a} = 0 \\ {{ \varSigma} _{YX}}{ a} - \theta {{ \varSigma} _{YY}}{ b} = 0 \end{array} \right.$

(15)

由此求出 $\lambda = \theta = {{ a}^{\bf{T}}}{{ \varSigma} _{XY}}{ b}$ ，对式(15)进一步简化，有：

$\left\{ \begin{array}{l} { \varSigma} _{XX}^{ - 1}{{ \varSigma} _{XY}}{ b} = \lambda { a} \\ { \varSigma} _{YY}^{ - 1}{{ \varSigma} _{YX}}{ a} = \lambda { b} \end{array} \right.$

(16)

转化成矩阵的形式，即：

$\left[ \begin{array}{l} { \varSigma} _{XX}^{ - 1}\quad0 \\ 0\quad{ \varSigma} _{YY}^{ - 1} \end{array} \right]\left[ \begin{array}{l} 0\quad{{ \varSigma} _{XY}} \\ {{ \varSigma} _{YX}}\quad0 \end{array} \right]\left[ \begin{array}{l} { a} \\ { b} \end{array} \right] = \lambda \left[ \begin{array}{l} { a} \\ { b} \end{array} \right]$

对 $\left[ \begin{array}{l}{ \varSigma} _{XX}^{ - 1}\quad0 \\ 0\quad{ \varSigma} _{YY}^{ - 1} \end{array} \right]\left[ \begin{array}{l} 0\quad{{ \varSigma} _{XY}} \\ {{ \varSigma} _{YX}}\quad0 \end{array} \right]$ 求出最大特征值 $\lambda $ ，即可以求出向量a、b和 $\ \rho $ 。得到的a、b称为典型向量，融合后的特征向量为 $f({ x}) = { U} + { V} = {{ a}^{\bf{T}}}{ X} + {{ b}^{\bf{T}}}{ Y}$ ，作为年龄特征向量。

1.4 Siamese Network网络模型

人脸验证任务的目的就是比较两幅输入人脸图片的匹配程度，因此需要构建一个卷积神经网络，实现图像对输入、输出两幅图片的相似度量值。在2005年，Chopra^[19]提出了一种用于图片匹配的卷积神经网络结构，称之为孪生网络(Siamese Network)，该网络通过两个共享权值的卷积神经网络(CNN)提取特征，再进行特征匹配。在本文的网络结构中，对Siamese Network进行了改进，把CNN结构替换为ResNet，该结构在2015年被何凯明团队提出^[20]，由多个残差块组成,结构中使用了“shortcut connection”的连接方式，很好地解决了深层网络中梯度弥散和训练困难的问题。整体的模型流程图如图3所示。

首先构建一个映射函数 ${G_W}({ X})$ ，把输入图片 ${{ T}_1}$ 、 ${{ T}_2}$ 作为参数自变量，输出得到特征向量 ${{ G}_W}({{ T}_1})$ 、 ${{ G}_W}({{ T}_2})$ ，分离出年龄特征向量，得到两组年龄无关的特征向量进行相似度量，通过反向传播，不断优化网络参数，使得两张同一人脸图片的距离相似度量值最小化，两张不同人脸图片的距离相似度量值最大化，以此来实现人脸验证。其计算过程为

$f({ x}) = {{ a}^{\bf{T}}}{ X} + {{ b}^{\bf{T}}}{ Y}$

(17)

$h({ x}) = {{ G}_W}({ x}),{ x} = { T}$

(18)

$g({ x}) = h({ x}) - \mu f({ x})$

(19)

${E_W}(g({ x})) = ||{g_1}({ x}) - {g_2}({ x})||$

(20)

式中：X表示纹理特征；Y表示轮廓特征；a和b是CCA算法中的投影向量； $f({ x})$ 即是X和Y特征融合后的年龄特征向量。 $h({ x})$ 表示输入图像的整个人脸特征， $\ \mu $ 表示年龄特征向量的权值，经过实验验证，当 $\ \mu {\rm{ = }}0.{\rm{72}}$ 时，实验结果最优。 $g({ x})$ 表示特征分离得到的与年龄无关的人脸特征向量， ${E_W}(g({ x}))$ 为相似性度量函数，表示图片对的匹配程度。引入损失函数Contrastive Loss，通过反向传播不断更新网络的权值，降低损失值，优化网络性能。损失函数表达式如下：

${\rm{Loss}} = \frac{1}{{2N}}\sum\limits_{n = 1}^N {y{d^2} + (1 - y)\max {{(m - d,0)}^2}} $

(21)

$d = \sqrt {\sum\limits_{i = 1}^P {(x_1^i - x_2^i} {)^2}} $

(22)

式中： $d$ 代表两个样本特征之间的欧氏距离； $P$ 表示样本的特征维数。 $y$ 表示图像对中两个样本是否匹配， $y = 0$ 表示不匹配，此时 ${\rm{Loss}}\! =\! \dfrac{1}{{2N}}\sum\limits_{n = 1}^N {\max {{(m - d,0)}^2}} $ ,即两个样本不同时，特征空间的欧氏距离越小，损失越大； $y = 1$ 表示匹配，此时 ${\rm{Loss}} = \dfrac{1}{{2N}}\sum\limits_{n = 1}^N {{d^2}}$ ，即两个样本相似时，如果在特征空间的欧氏距离较大，损失就会越大，说明网络模型不好，则会训练优化模型。 $m$ 为设定好的阈值，取值为1.25，表示只考虑欧氏距离在 $0\sim m$ 的特征，超过阈值时， ${\rm{Loss}} = 0$ ； $N$ 为样本数。

2 实验过程及结果 2.1 数据集及实验参数

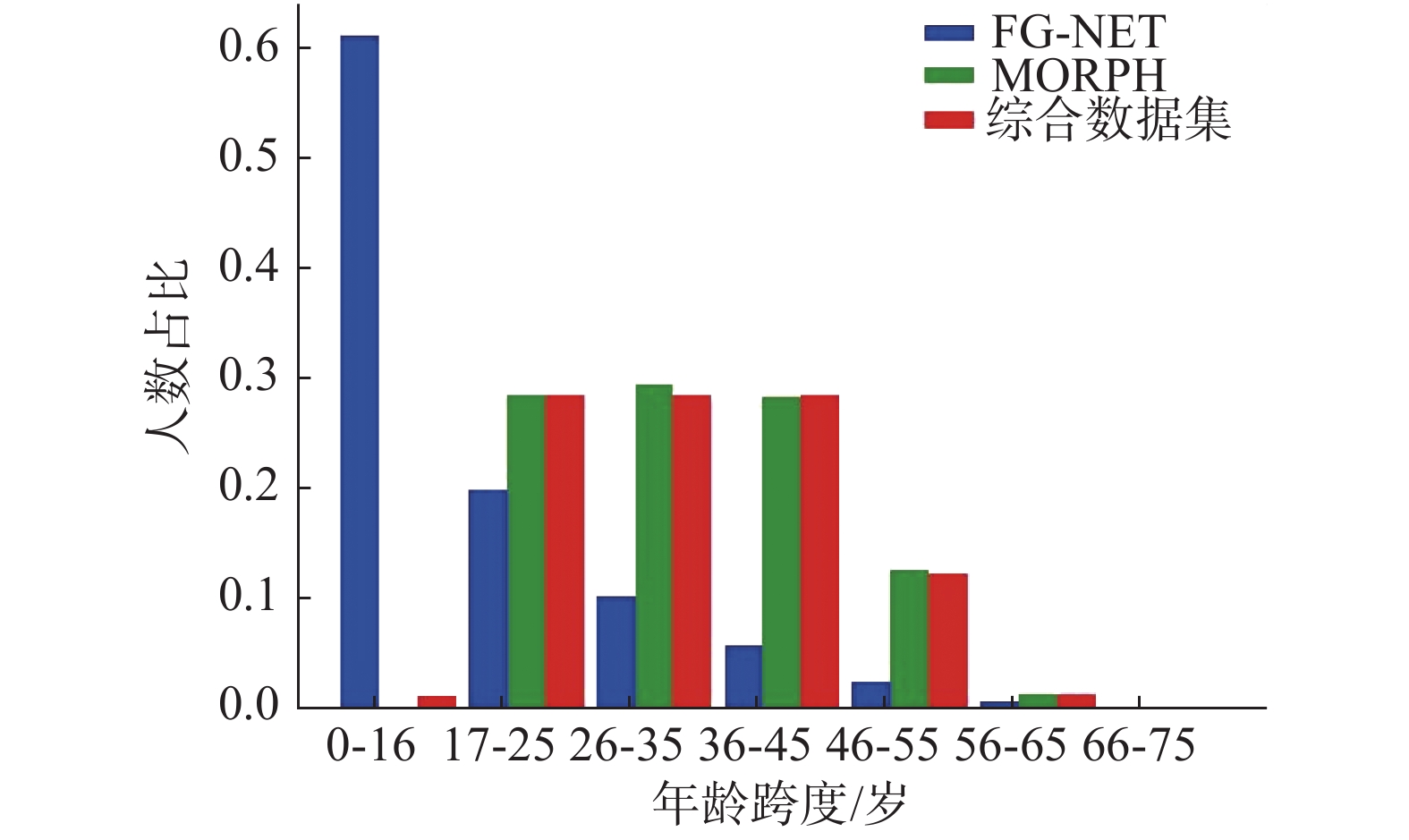
本次实验所使用的数据集有3种，分别是FG-NET数据集、MORPH2数据集以及从FG-NET数据集、MORPH2数据集中按照实验所需选择图片构成一个综合数据集。综合数据集年龄跨度为0~62岁，包括13040人52840张照片，正样本为同一人不同年龄段的图像对，负样本为两类，一类是不同人同一年龄段的图像对，一类是不同人不同年龄段的图像对。其中训练集包括30000个图像对，验证集包括4000个图像对，测试集包括4000个图像对。每个图像对有对应的标签，1表示正样本，0表示负样本。3个数据集的年龄段占比分布如图4所示。

2.1.1 数据预处理

采用MTCNN检测人脸关键点，通过相似性变换实现人脸对齐，检测出人脸区域，统一将输入图片像素大小裁剪为224×224。为了防止过拟合，在训练的过程中为保证样本的多样性，采用在线数据增强的方式，对训练集数据进行随机翻转、水平镜像、亮度变换的操作，最后对图片数据归一化，归一化区间为[−1,1]。

2.1.2 实验参数设置

本实验模型使用的框架为Pytorch框架，batch_size设为64，学习率预设为0.01，实验过程中防止学习率过大带来模型振荡的问题，采用Warmup Learning的方法对学习率进行处理，训练开始使用较小的学习率，设为0.0001，迭代训练3次后，学习率恢复为预设值，之后每迭代50次，学习率下降1/10，迭代次数设为200，动量因子设为0.9。

2.2 实验结果 2.2.1 在FG-NET数据集上的实验结果

FG-NET数据集包含82个人1002张不同年龄段的面部图像，年龄范围在0~69周岁，其年龄段分布如表1所示。

18岁以下的人脸图像占据该数据集的61%以上，而人脸轮廓纹理变化最大的便是婴幼儿到青少年时期，此数据集给人脸验证算法带来了很大的难度，因此要对数据进行更加科学的处理。训练集选取了60个人不同年龄段的照片，从每个年龄段中选取图片组成正样本图像对和负样本图像对，如表2所示。不同方法在FG-NET数据集上的实验结果如表3所示。

2.2.2 在MORPH2数据集上的实验结果

MORPH2收录了同一个人在不同年龄段的图片。该数据集包括13000个人的55134张图片，人物年龄跨度为16~77岁。训练集选取6000人不同年龄段的照片，正样本为每个人年龄跨度最大的两张图片，即6000个样本对，负样本为6000人中不同人不同年龄的两张图片，也组成6000个样本对。验证集为不包括训练集的3000人的数据集，测试集为不包括训练集和验证集的4000人样本对，正负样本对的选取方式和训练集相同。不同方法在MORPH2上的实验结果如表4所示。

2.2.3 在综合数据集上的实验结果

FG-NET数据集数量少，且18岁以下的数据量占据整个数据集的60%以上，MORPH数据集数据量足够，但是不包含幼儿时期的数据，且两个数据集中60岁以上的数据呈现个位数的情况，为了提高算法的鲁棒性和泛化性，对两个数据集进行整理，整合成一个包含13040人52840张照片的数据集，年龄跨度为0~77，表5是本文提出的方法在综合数据集上的实验结果。

3 结束语

本文提出了一种基于深度学习算法与传统图像算法相融合的跨年龄人脸验证方法，该方法分别提取人脸特征信息和年龄特征信息，并通过特征分离得到具有年龄不变性的人脸特征。为了更好地匹配人脸特征，本文利用孪生网络的结构特性，对人脸特征进行相似性度量，判定匹配程度，得到跨年龄人脸验证结果。为了验证算法的鲁棒性，在FG-NET、MORPH以及两个数据集的综合数据集上进行实验，得到理想的效果，验证了此方法的有效性。