大量的图像样本数据和强大的计算资源,使得深度学习在图像处理领域有着广阔的应用前景。深度学习从大量的样本中学习样本的特征分布,然后经过多次迭代优化各层权重,最后通过分类器实现图像分类[1-3]。但是在一些特殊或者难以复现的场景中,难以获得足够的样本[4]。由于样本数量很少,使用深层神经网络往往会导致过拟合的现象出现,减少网络层数则会影响特征提取,导致分类正确率下降[5]。小样本图像分类现在仍是深度学习中一个重要的研究问题[6]。
小样本学习问题由李飞飞等[7]于2006年提出,使用贝叶斯的方法在一个或少数几个图像学习问题中成功提取出了信息模型。文献[8]于2015年提出分层贝叶斯模型,该模型能从少量样本中完成计算任务,并且达到了相当于人类水平的识别率。随后迁移学习的提出给小样本学习带来了新的处理方法[9]。文献[10]提出一种基于堆栈降噪自编码与支持向量回归机的混合模型,在相似源域大数据上预训练混合模型借助对该知识的迁移,在目标域微调该混合模型,从而提升支持向量回归机在小样本噪声数据上的学习预测精度。
目前对于小样本图像分类问题,主要有增加样本数量和根据问题选择特定算法两种方式[11-12]。最初的样本数量增强技术,例如原始样本的旋转、翻转和增加对比度等方法,在一定程度上解决了样本的数量问题,但是往往因为相似度过大,产生过拟合现象。如今,统计学上的各种采样方法、生成对抗网络的提出,为样本的数量增强提供了新的解决思路[13]。文献[14]采用Bootstrap法来解决电力负荷数据少的问题,利用放回重复抽样的方法得到新的样本,利用一种类比关系来进行统计推断,将小样本转换为大样本问题,但是该方法会造成被估参数的均值过分依赖样本子集的情况,不利于参数估计的稳健性。根据研究问题的不同,选择特定的算法也可以显著地提高实验效果[15-16]。文献[17]提出了利用蒙特卡洛随机试验可以对特征参量进行统计估计的特性,计算高光谱图像的最优降维特征数,对小样本的高光谱图像进行降维,实验证明使用该方法后图像的分类精度有了较大提高。但是,蒙特卡罗的结果和准确性很大程度依赖于母体所建立的数学模型。
2005年Chopra等[18]第一次提出了孪生网络的结构,该方法在人脸识别数据集上进行训练和测试,取得了很好的识别效果。孪生网络创新地采用了两个样本组成一对作为神经网络的输入的结构。在不改变样本数量的条件下,增加了整体样本循环一个批次的训练次数,更有效地完成特征的提取,减少因样本少带来的过拟合问题。在处理类别较多、每个类别样本少的分类任务有着极强的优势。
为了解决小样本图像分类问题,采用以变分自编码器为核心的孪生网络结构来实现对小样本图像数据的分类。特征提取通过变分自编码器来实现,无需人工提取,而孪生网络的相似度匹配结构,可以有效地提高分类的正确率。
1 相关理论 1.1 孪生网络孪生网络是一种特殊类型的神经网络结构,与传统一个学习过程对应一个输入然后进行分类的模型不同,该神经网络每个学习过程具有两个输入,使用相同权重的神经网络对两个输入数据进行处理,计算提取到的特征的相似度来分辨两个数据的是否为同一类别。孪生网络结构如图1所示。

|
Download:
|
| 图 1 孪生网络结构 Fig. 1 Siamese network | |
最初的孪生网络基于全连接网络。网络有
| ${{{h}}_{1,m}} = \max (0,{{W}}_{l - 1}^{\rm{T}}{{{h}}_{1,(l - 1)}} + {b_l})$ | (1) |
| ${{{h}}_{{\rm{2}},m}} = \max (0,{{W}}_{l - 1}^{\rm{T}}{{{h}}_{{\rm{2}},(l - 1)}} + {b_l})$ | (2) |
式中:
经过输入层和隐藏层的前馈操作后,在距离层按式(3)比较孪生网络生成的特征的距离E(W),用来评估特征的相似程度。
| $E\left( W \right) = ||{{{h}}_{1,m}} - {{{h}}_{2,m}}||$ | (3) |
孪生网络结构具有两个权重相同、结构相同的姐妹网络。输入图像两两组成一对,图像对中的两个图像将分别送到两个姐妹网络中,然后使用对比损失函数来优化网络。原始的姐妹网络使用的是全连接结构,全连接网络参数众多,训练效率低。文献[19]对网络的特征提取过程进行改进,使用卷积神经网络作为姐妹网络来提取图像特征,取得了很好的效果。但是,卷积神经网络在样本数据量小时,易于产生过拟合现象。
使用孪生网络训练时,由于其逐对训练的原理,将有平方级别对的数据可以来训练模型,这让模型很难过拟合。假设数据集样本有
| ${N_{{\rm{pairs}}}} = \frac{{(C \cdot E)}}{{2!(C \cdot E - 2)}}$ | (4) |
以Omniglot数据集为例,对于数据集中的964类(每类20个样本),剔除其中相同类别的配对,仍有183160对组合。孪生网络在不增加样本的前提下,通过输入对匹配的方式,增加了样本的训练次数,从而提高了网络的学习能力,避免出现过拟合问题。
1.2 变分自编码器变分自编码器是2014年提出的一种基于变分贝叶斯推断的生成式结构模型[20]。变分自编码器总体上分为两个神经网络:Encoder和Decoder。Encoder通过变分参数的不断迭代、更新来最大化观测数据的边缘似然函数的下界,近似不可观测变量的后验概率,输出隐变量的概率分布。Decoder则是根据Encoder输出的隐变量概率分布还原生产原始数据的近似概率分布。
变分自编码器具有和Dropout类似正则化作用的隐层采样过程,这使得模型的整个训练过程不容易发生过拟合问题[21],与传统特征提取模型相比,更加适合解决样本数量较少的问题。变分自编码器现在已经广泛应用于高维数据降维、特征提取等方面[17-24]。
2 基于孪生变分自编码器的小样本图像分类 2.1 孪生变分自编码结构综合变分自编码器减少过拟合问题和孪生网络扩大样本训练次数的优点,对孪生网络进行改进,使用变分自编码器的Encoder结构代替全连接网络提取样本特征,减少了网络参数,提高训练效率。孪生变分自编码器首先建立变分自编码器网络进行特征提取的无监督学习,然后使用两个权重完全相同的变分自编码器Encoder结构搭建孪生网络用于提取样本特征,在距离层计算特征向量的相似度,得到输入样本的分类结果。最后,对神经网络权重进行训练、调整。孪生变分自编码器结构如图2所示。
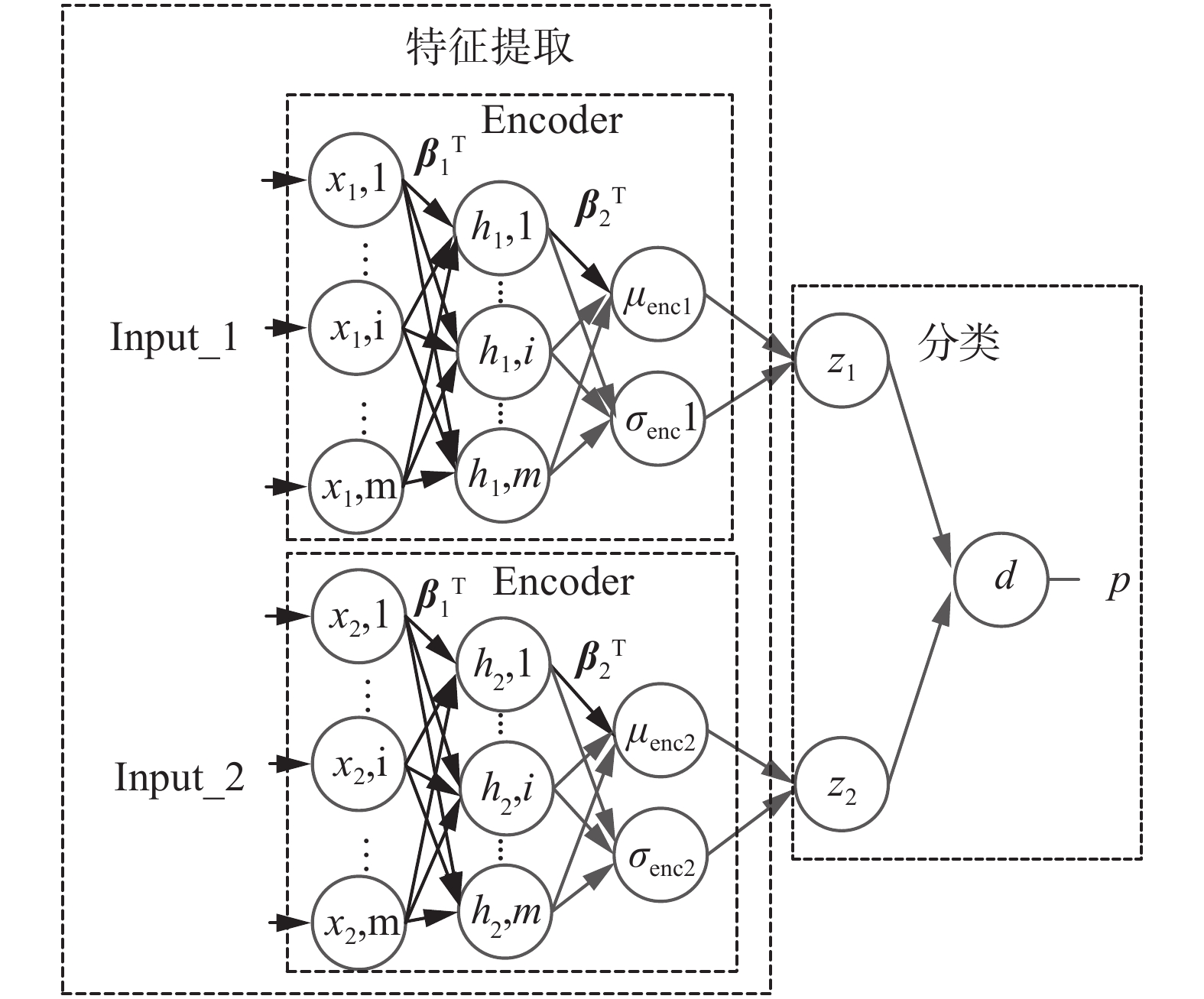
|
Download:
|
| 图 2 孪生变分自编码器结构 Fig. 2 Siamese variational auto-encoder | |
Input_1、Input_2是样本数据的一组组合输入,特征提取功能由变分自编码器的Encoder实现,
根据图2的孪生变分自编码器结构,给出相应孪生变分自编码器的计算流程,如图3所示。
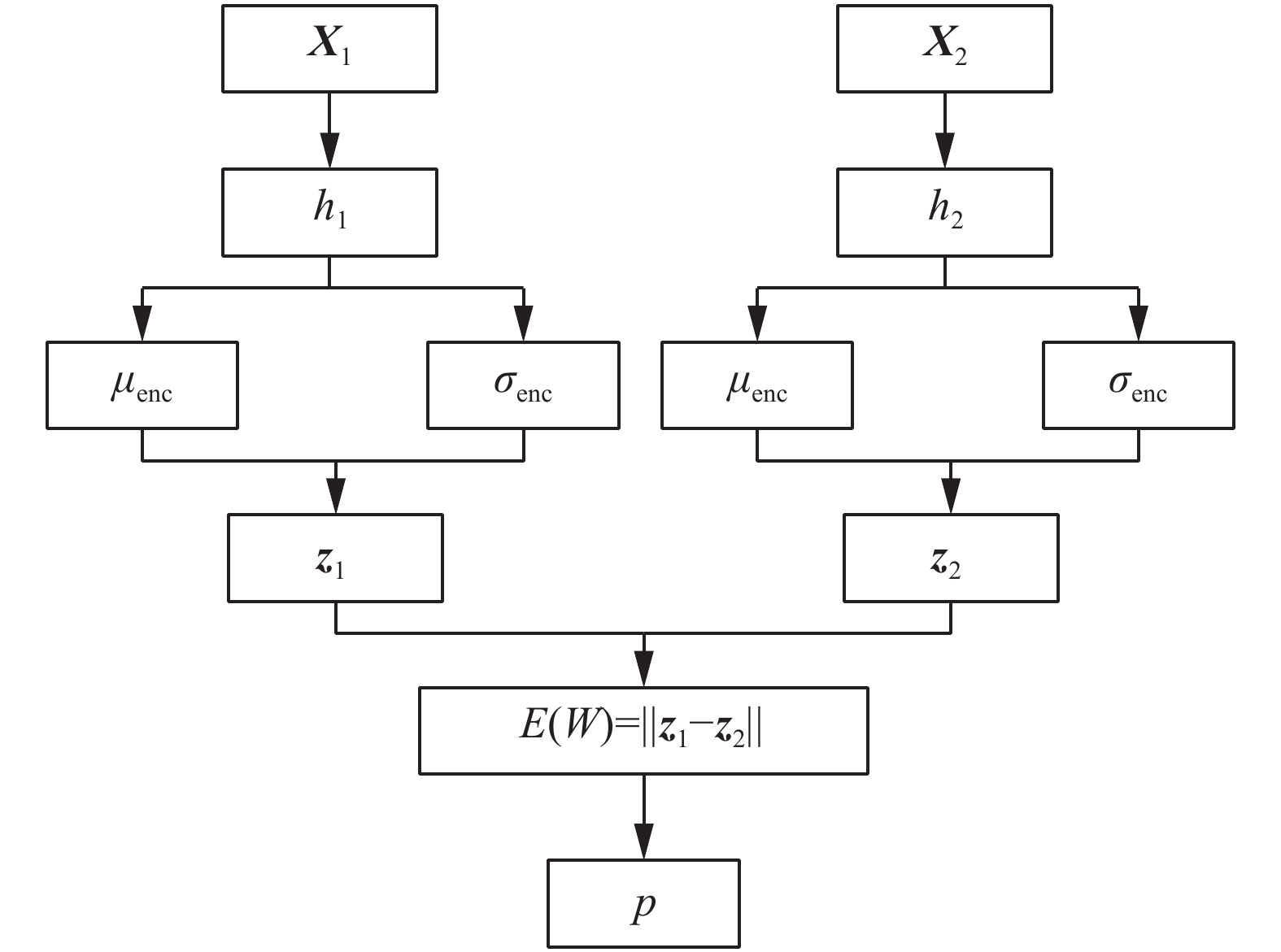
|
Download:
|
| 图 3 孪生变分自编码器的计算流程 Fig. 3 Computation process of S-VAE | |
图3中
利用上述孪生变分自编码器的结构和计算流程对小样本图片进行分类的具体过程如下:
1)将数据集以适当的比例分为训练数据集和测试数据集,对训练数据集使用变分自编码器进行无监督的学习,训练特征提取模型。
2)初始化孪生变分自编码器结构,载入训练好的特征提取模型,将训练数据集作为输入对网络进行训练,调整网络各层权值。
3)将测试数据集作为输入,利用训练好的网络来进行分类任务。
2.2 孪生变分自编码器特征提取孪生变分自编码器特征提取采用的是变分自编码器的Encoder结构。变分自编码器是一个无监督学习的神经网络,本质上是构建了一个从隐变量
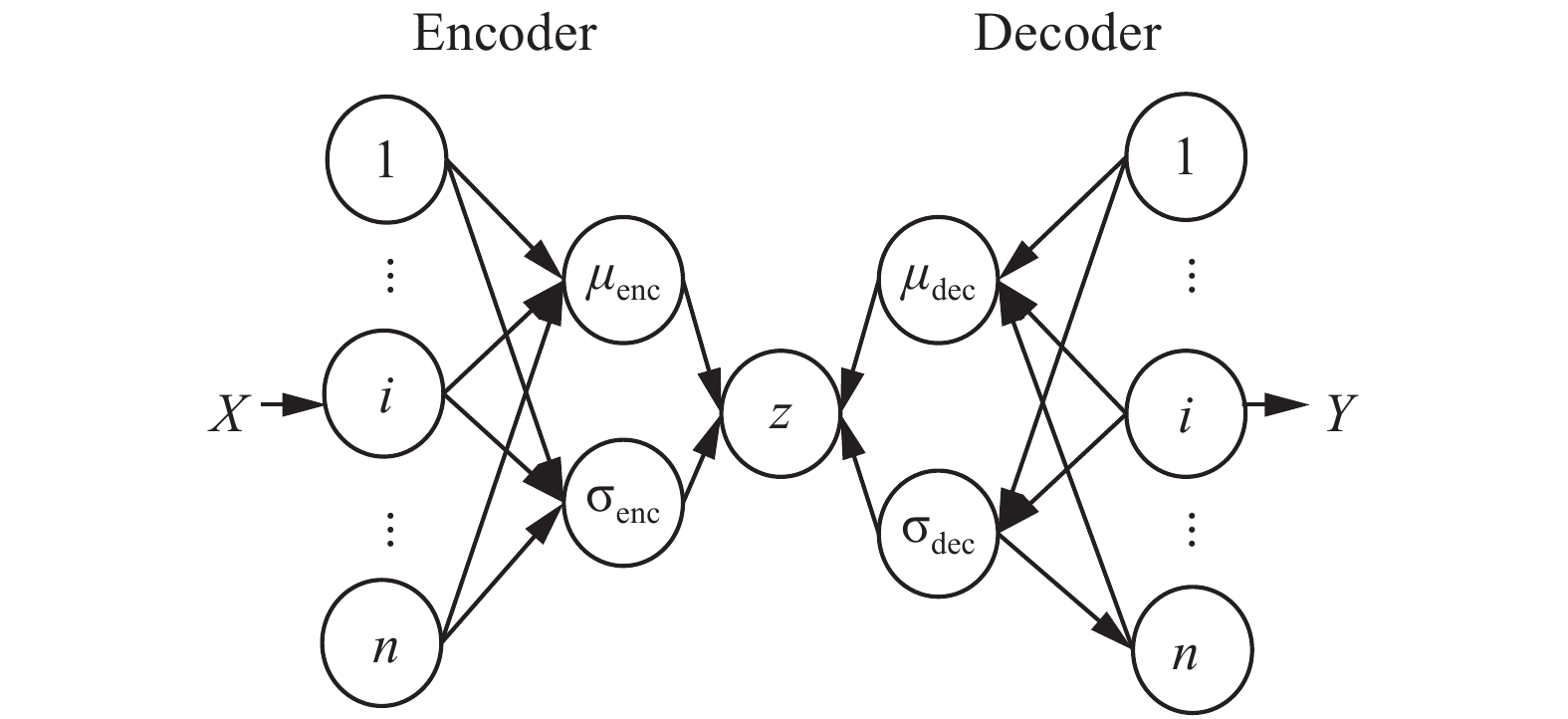
|
Download:
|
| 图 4 变分自编码器 Fig. 4 Variational auto-encoder | |
对于原始样本集X,定义其特征值为隐变量
| $p(z|x) = \frac{{p(x|z)p(z)}}{{p(x)}}$ | (5) |
但是,边缘似然概率密度函数
| ${D_{KL}}(p(z|x){\rm{||}}q(z|x)) = \sum {p(z|x)\log \frac{{p(z|x)}}{{q(z|x)}}} $ | (6) |
根据变分贝叶斯方法,样本数据x的边缘似然函数可以简化为
| $ \log {p_\theta }({x^{(i)}}) = {D_{KL}}({q_\varphi }(z|{x^{(i)}})||{p_\theta }(z|{x^{(i)}})) + L(\theta ,\varphi ;{x^{(i)}}) $ | (7) |
式中:
| $\begin{gathered} \log {p_\theta }({x^i}) \geqslant L(\theta ,\varphi ;{x^{(i)}}) = {\rm{ - }}{D_{KL}}({q_\varphi }(z|{x^{(i)}})||{p_\theta }(z))+ \\ {E_{q\varphi (z|{x^{(i)}})}}[\log {p_\theta }({x^{(i)}}|z)] \end{gathered} $ | (8) |
通过最大化变分下界,即可以得到样本集的最优估计。同时,可以将式(8)重写为
| $\begin{gathered} L\left( {\theta ,\phi ;{x^{\left( i \right)}}} \right) = \\ \frac{1}{2}\sum\limits_{j = 1}^J {\left( {1 + \log \left( {{{\left( {\sigma _{{\rm{enc}}j}^{\left( i \right)}} \right)}^2}} \right) - {{\left( {\mu _{{\rm{enc}}j}^{\left( i \right)}} \right)}^2} - {{\left( {\sigma _{{\rm{enc}}j}^{\left( i \right)}} \right)}^2}} \right)} + \\ \frac{1}{L}\sum\limits_{l = 1}^L {\left( { - \log \left( {\sigma _{{\rm{dec}}}^{\left( {i,j} \right)}\sqrt {2\pi } } \right) - \frac{{{{\left( {{x^i} - \mu _{{\rm{dec}}}^{\left( {i,j} \right)}} \right)}^2}}}{{2\sigma _{{\rm{dec}}}^{{{\left( {i,j} \right)}^2}}}}} \right)} \\ \end{gathered} $ | (9) |
式中:
针对图3孪生变分自编码器的计算流程,孪生变分自编码器特征提取过程可以表示为
| $\left\{ \begin{gathered} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{h_1} = f({W_{{h_1}}}x + {b_{{h_1}}}) \\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{\mu _{{\rm{enc}}}} = f({W_{{\mu _{enc}}}}x + {b_{{\mu _{enc}}}}) \\ \!\!\!\!\!\!\!\!\!\!\!\!\log {\sigma _{{\rm{enc}}}} = f({W_{{\sigma _{enc}}}}x + {b_{{\sigma _{enc}}}}) \\ z = {\mu _{{\rm{enc}}}} + {\sigma _{enc}} \odot \varepsilon ,{\rm{ }}\varepsilon \sim N(0,1) \end{gathered} \right.$ | (10) |
式中:
两个原始数据成对输入Encoder,通过训练好的编码器网络进行分布参数提取,可以得到两个输入数据的特征向量
| ${E_W} = ||{z_1} - {z_2}||$ | (11) |
使用sigmoid函数将匹配度映射到[0,1]之间成为一个分类结果的概率,同时方便使用交叉熵作为训练网络的代价函数。相似度为
| $p = \sigma \left( {\sum\limits_j {||{z_1} - {z_2}||} } \right)$ | (12) |
孪生网络的对比损失函数为
| $L\left( W \right) = \sum\limits_{i = 1}^p {L\left( {W,{{\left( {Y,{X_1},{X_2}} \right)}^i}} \right)} $ | (13) |
式(13)可以展开为
| $\begin{gathered} L\left( {W,{{\left( {Y,{X_1},{X_2}} \right)}^i}} \right) = \left( {1 - Y} \right)\left( {{E_w}{{\left( {{X_1},{X_2}} \right)}^i}} \right)+ \\ Y\left( {{\rm{ - }}{E_w}{{\left( {{X_1},{X_2}} \right)}^i}} \right) \\ \end{gathered} $ | (14) |
式中:
| $\begin{gathered} L\left( {W,{{\left( {Y,{z_1},{z_2}} \right)}^i}} \right) = \left( {1 - Y} \right)\log \left( {p{{\left( {{z_1},{z_2}} \right)}^i}} \right) + \\ Y\log \left( {1 - p{{\left( {{z_1},{z_2}} \right)}^i}} \right) \end{gathered} $ | (15) |
式中:Y为输入对是否是同类的标签;
实验使用Tensorflow框架设计神经网络并进行训练和测试,实验的硬件环境为i5-8300H处理器,8 GB内存,软件环境为Windows 10操作系统。
Omniglot数据集拥有50种文字,1623类手写字符。对于每类字符仅有20个样本,每个样本分别由不同的人绘制而成,分辨率为

|
Download:
|
| 图 5 Omniglot数据集 Fig. 5 Omniglot dataset | |
针对Omniglot数据集的测试实验主要围绕N-way K-shot展开:每种方法利用未经训练的N类中的K个已标记的样本进行训练,然后对一组属于N类中不相交的未标记样本进行分类。本文进行的实验是5-way 1-shot、5-way 5-shot、20-way 1-shot和20-way 5-shot。
3.2 Omniglot分类实验分析整个模型分为5层,特征提取部分网络层数为3层。第1层输入层为22050个节点,第2层为2048个节点,第3层为4个节点,第4层为4个节点,第5层输出层为1个节点。训练该模型提取样本图像的高层语义特征,然后再针对样本图像提取的高层语义特征利用孪生变分自编码器模型进一步进行训练,最后使用分类器进行分类。
通过Omniglot数据集对孪生变分自编码器进行测试,与原始孪生网络以及其他针对小样本图像分类方法实验结果进行对比。实验中用于对比的小样本分类方法主要有文献[25]中引用的原始孪生网络实验结果、文献[19]中提出的卷积孪生网络、文献[26]提出的分层贝叶斯学习方法(HBPL)以及文献[27]提出的预采样匹配网络(SSMN)。实验结果如表1所示。
| 表 1 Omniglot数据集N-way K-shot平均正确率 Tab.1 Average accuracy of N-way K-shot of Omniglot dataset |
从表1中可以看出,S-VAE实验结果中,4种条件下孪生变分自编码器分类结果均高于卷积孪生神经网络。20-way 1-shot情况下略微低于HBPL模型,较其他方法,孪生变分自编码器具有更高的分类正确率。20-way 5-shot 情况下本文提出的模型正确率最高,为98.9%。从表中可以看出,S-VAE相较于原始的孪生网络分类正确率在4个对比实验下均有所提高,平均提高3.1%。
由于HBPL模型是一种针对Omniglot进行特定处理的方法,在Omniglot笔画层次上进行图像的分割,继而进行学习,缺乏在其他问题上的拓展能力。因此,对余下3种算法和本文提出的模型,进行训练时间的比较,结果如表2所示。
从表2的训练时间来看,孪生变分自编码器在训练接近2个小时后,可以完成训练,并且训练用时最短,这说明孪生变分自编码器可以实现对小样本数据的快速分类,相较于另外3种算法,效率更高。
| 表 2 Omniglot数据集N-way K-shot训练时间 Tab.2 Training time of N-way K-shot of Omniglot dataset |
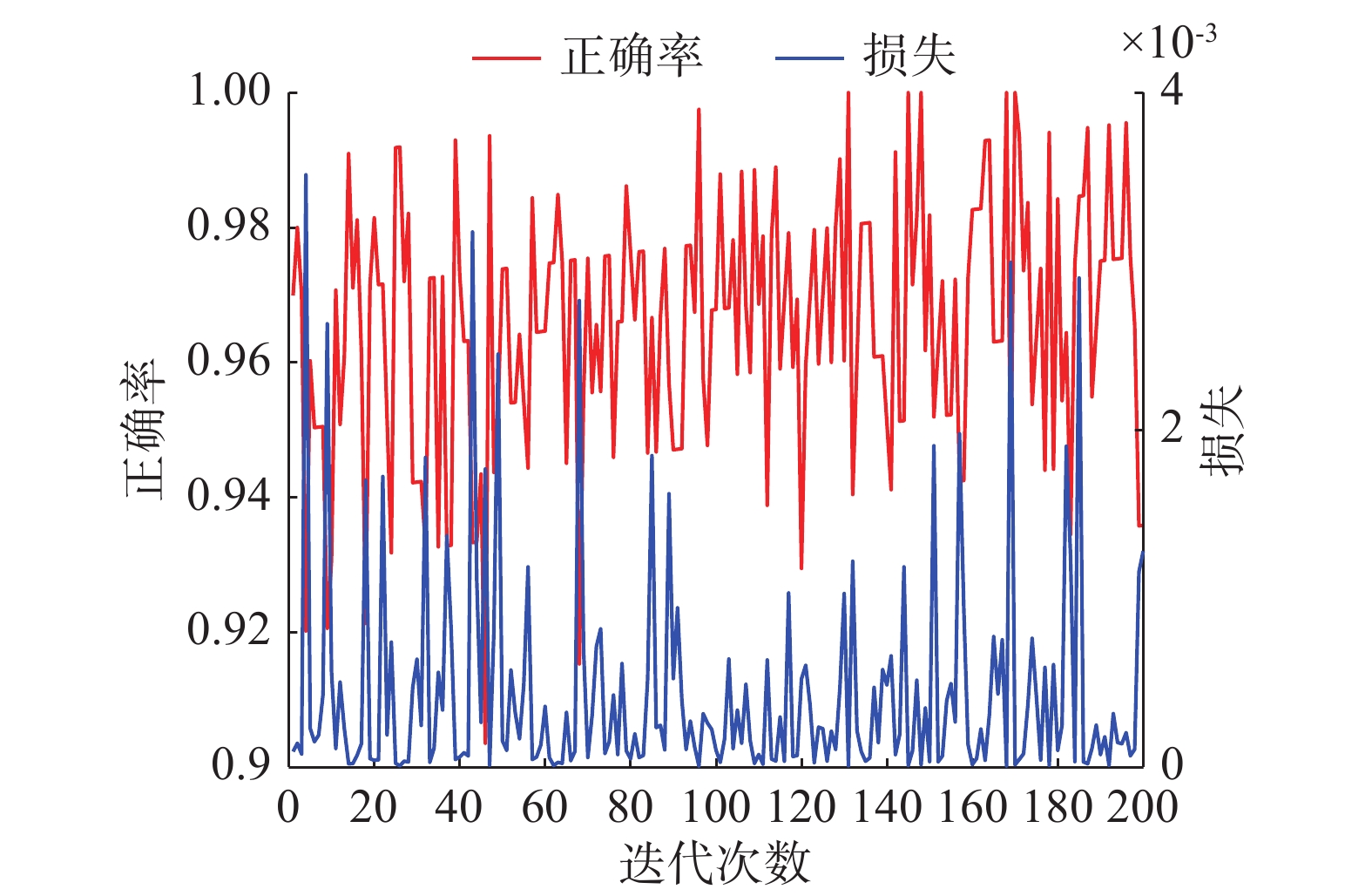
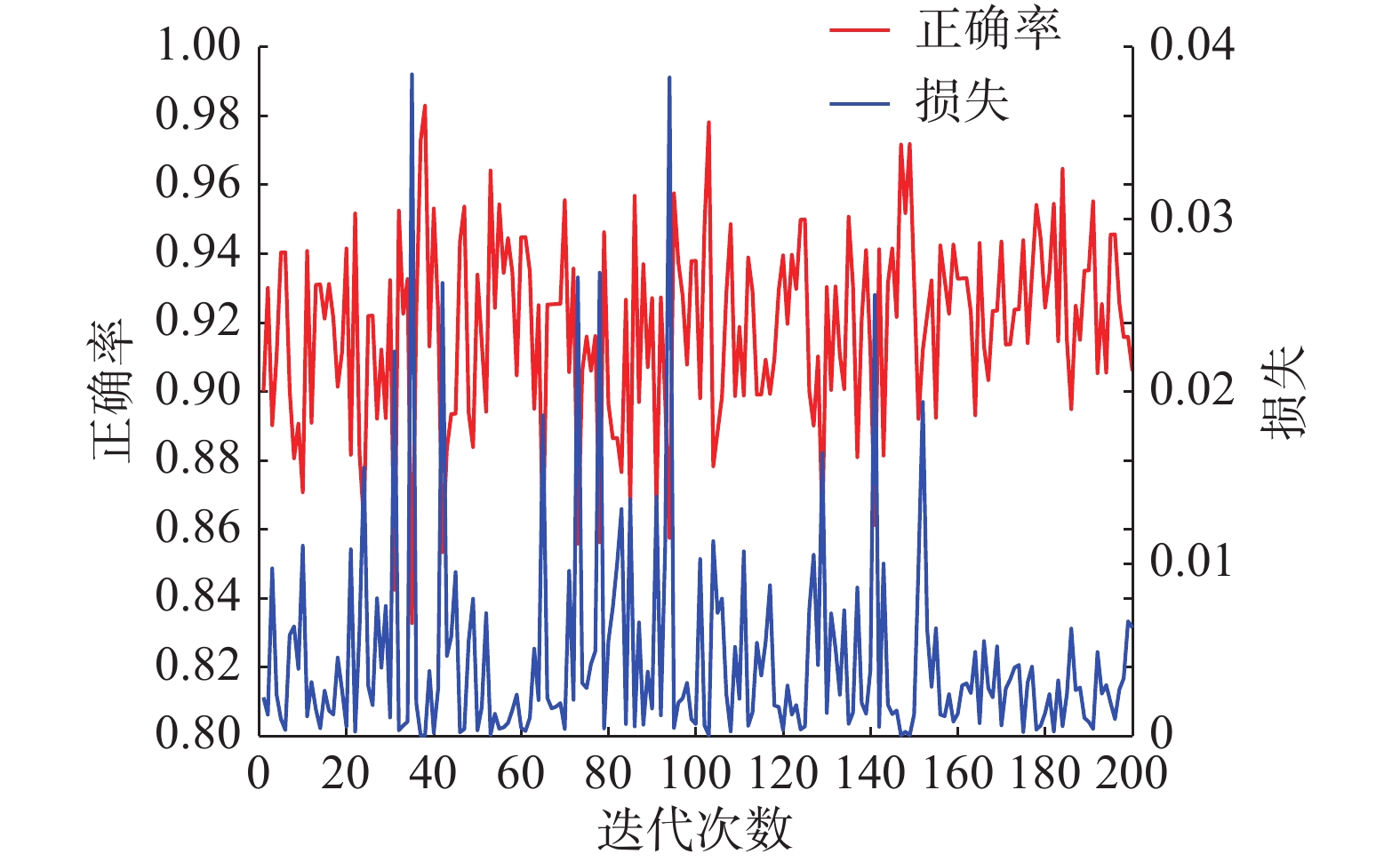
图6~9为本文提出模型的实验结果,主要包括5-way 1-shot、5-way 5-shot、20-way 1-shot和20-way 5-shot的测试错误率以及损失函数值的结果。结合表1中的平均正确率,从图6中5-way 1-shot的测试实验结果可以看出,整体样本正确率达到98.0%,一部分样本可以100%地识别出来,与原始孪生网络相比,分类正确率提高了4.3%。结合图8可以看出,当样本类别数量增加到20类时,20-way 1-shot场景下整体测试样本正确率达到了94.1%,与原始孪生网络相比,分类正确率提高了 5.9%。
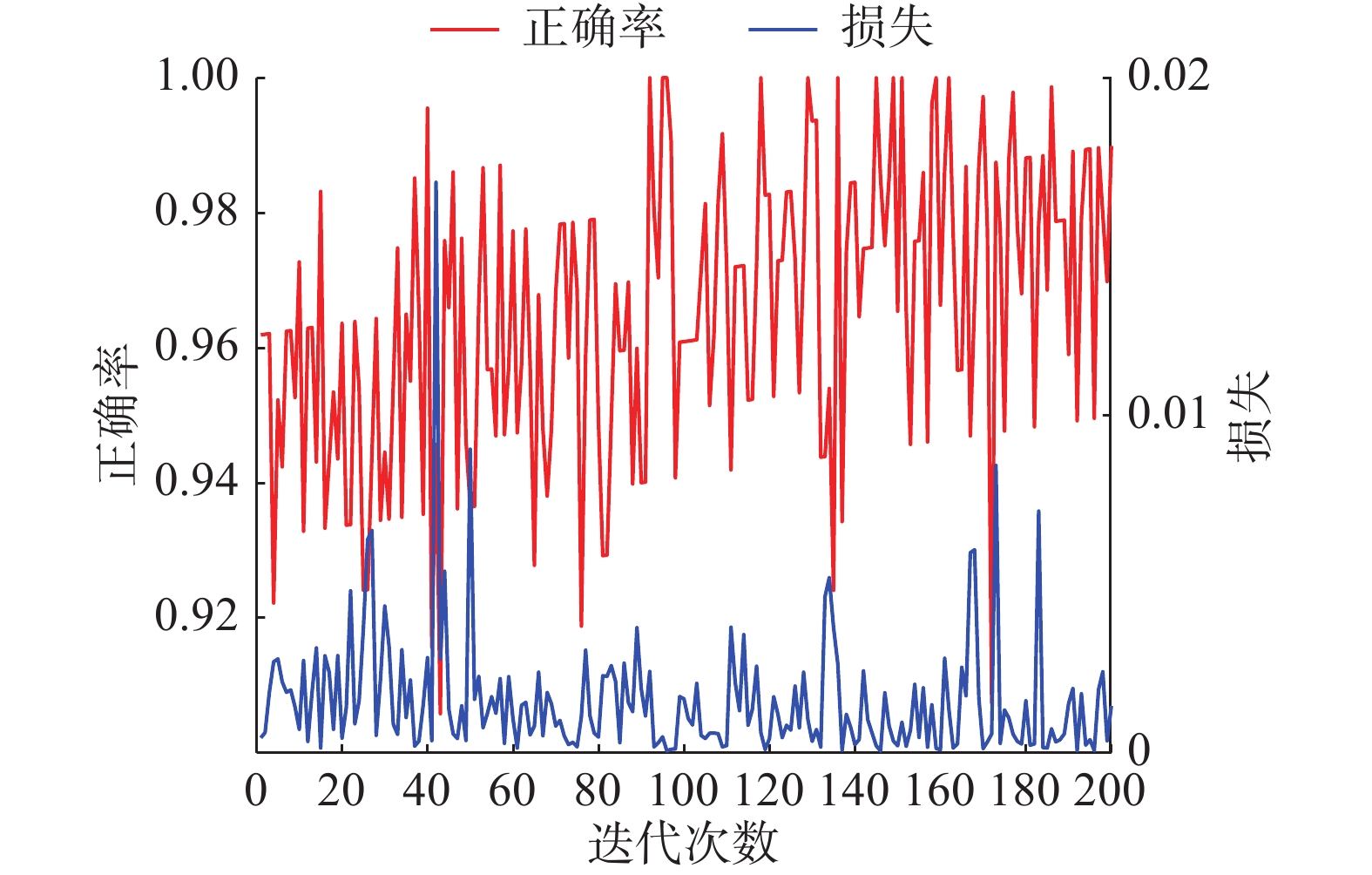
|
Download:
|
| 图 6 5-way 1-shot测试正确率和损失函数值 Fig. 6 Test accuracy and loss of 5-way 1-shot | |
|
Download:
|
| 图 7 5-way 5-shot测试正确率和损失函数值 Fig. 7 Test accuracy and loss of 5-way 5-shot | |
|
Download:
|
| 图 8 20-way 1-shot测试正确率和损失函数值 Fig. 8 Test accuracy and loss of 20-way 1-shot | |

|
Download:
|
| 图 9 20-way 5-shot测试正确率和损失函数值 Fig. 9 Test accuracy and loss of 20-way 5-shot | |
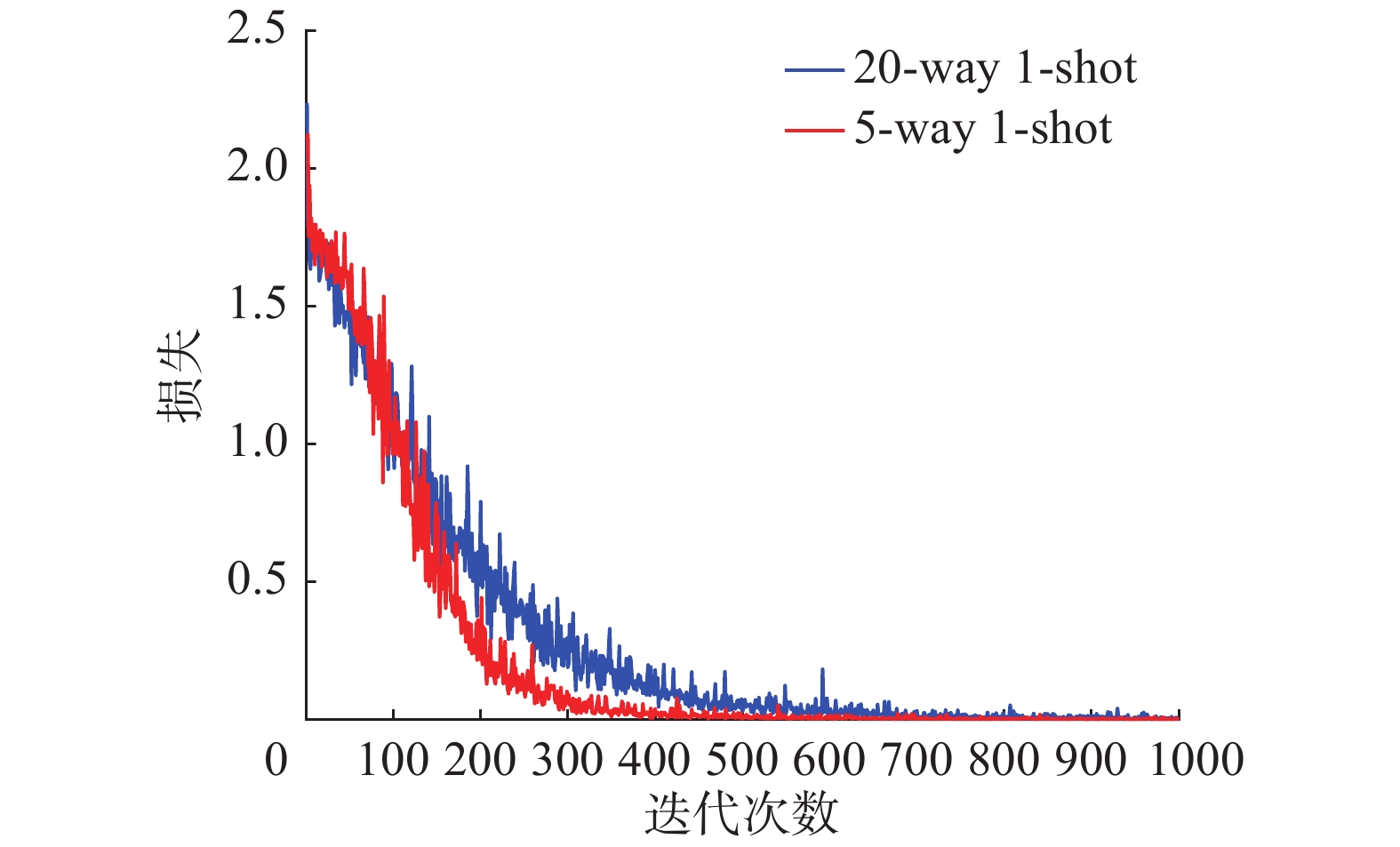
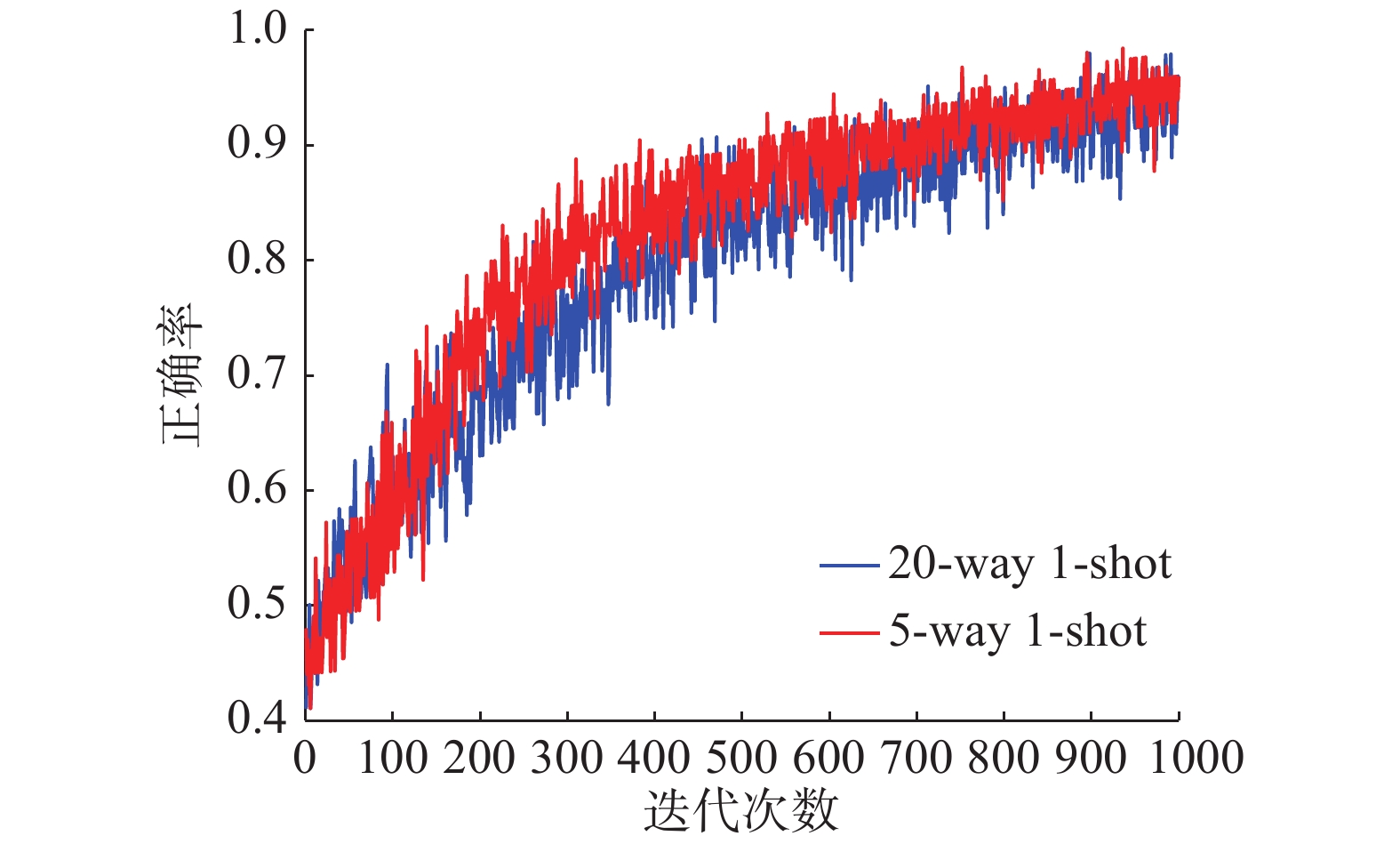
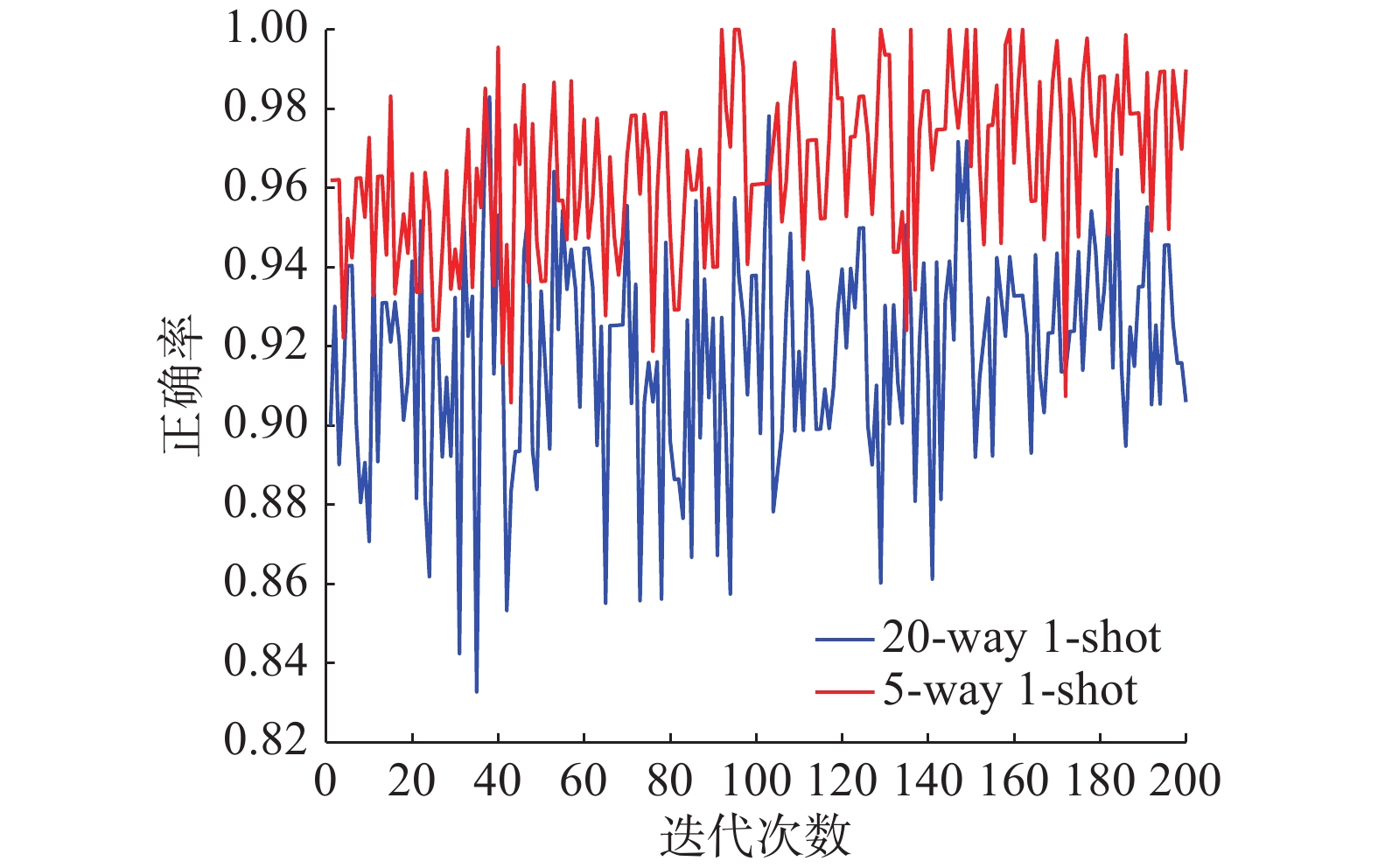
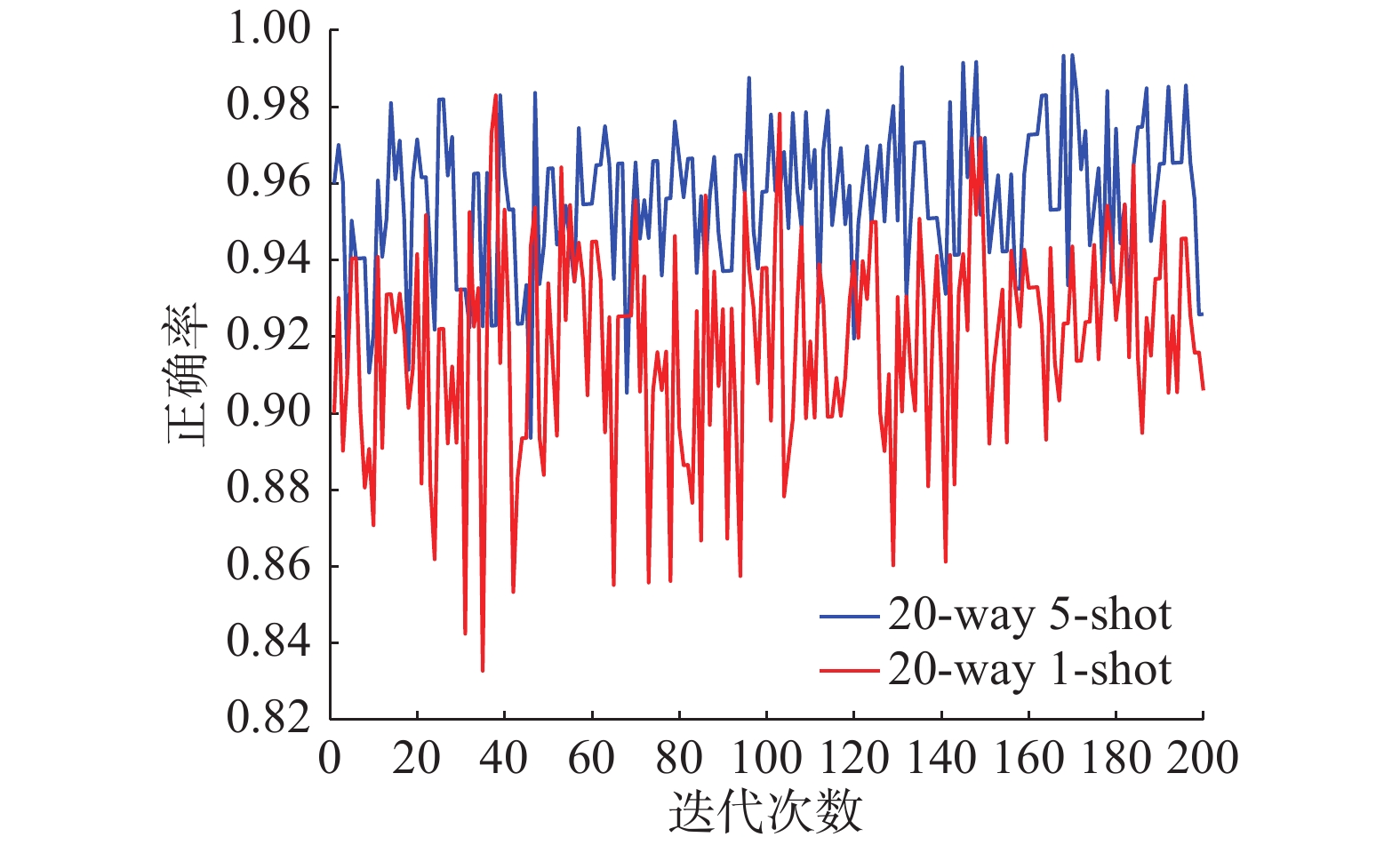
图10~12是以20-way 1-shot和5-way 1-shot为例,反映了不同类别,相同的训练样本数据集经过测试后的结果有着明显差距。当训练数据集样本数相同时,随着训练样本类别的增加,最终识别难度变大,分类正确率下降。当样本类别达到20,训练样本只有一个时,训练难度最大,图10体现出20-way 1-shot收敛速度明显慢于5-way 1-shot 条件下的收敛速度,正确率也略微下降。结合图7以及表1中的平均正确率可以看出在难度最大的20-way 1-shot条件下,样本在迭代700次之后收敛,测试正确率达到94.1%。
|
Download:
|
| 图 10 different-way 1-shot训练损失函数值 Fig. 10 Training loss of different-way 1-shot | |
|
Download:
|
| 图 11 different-way 1-shot训练正确率 Fig. 11 Training accuracy of different-way 1-shot | |
|
Download:
|
| 图 12 different-way 1-shot测试正确率 Fig. 12 Test accuracy of different-way 1-shot | |
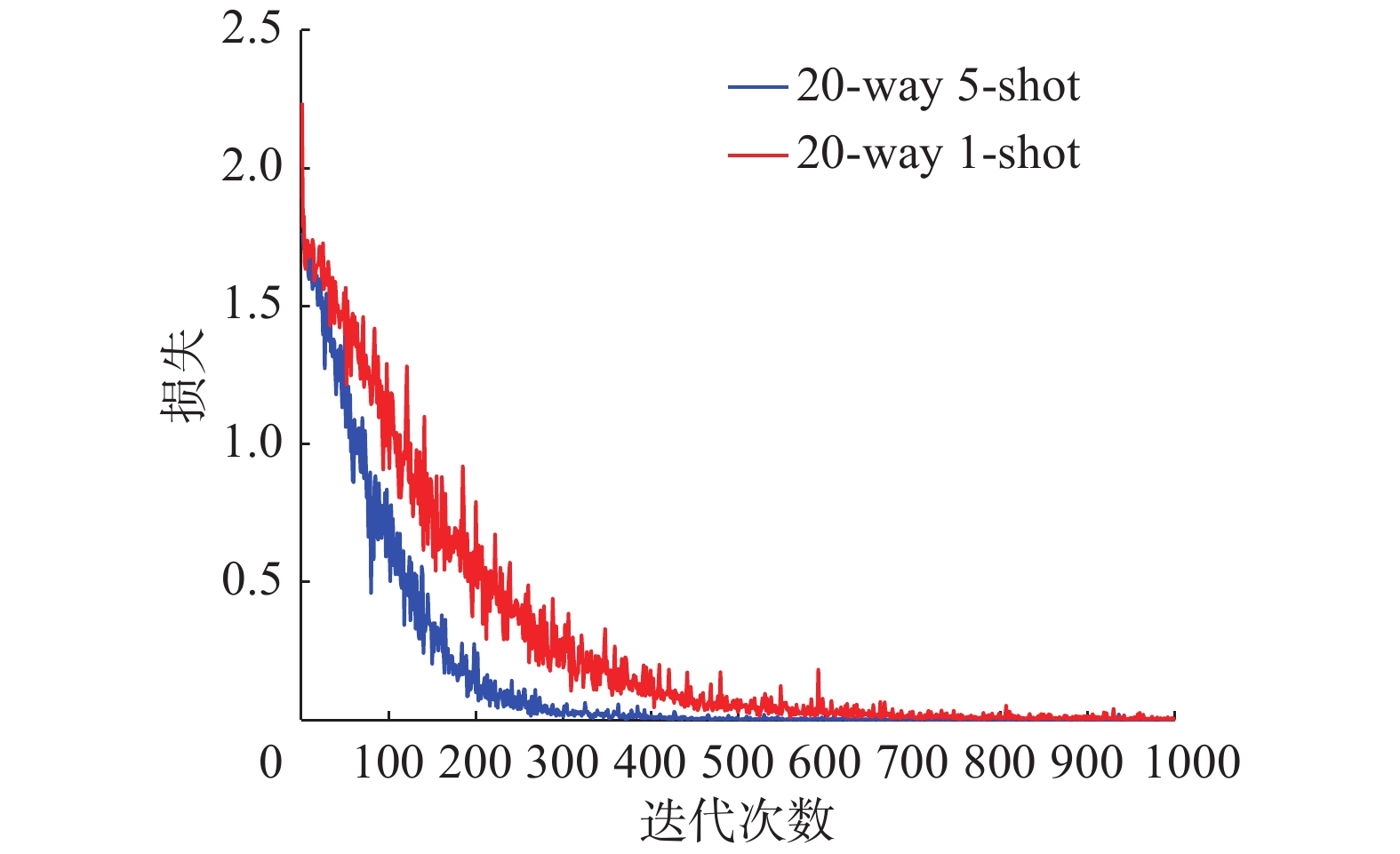
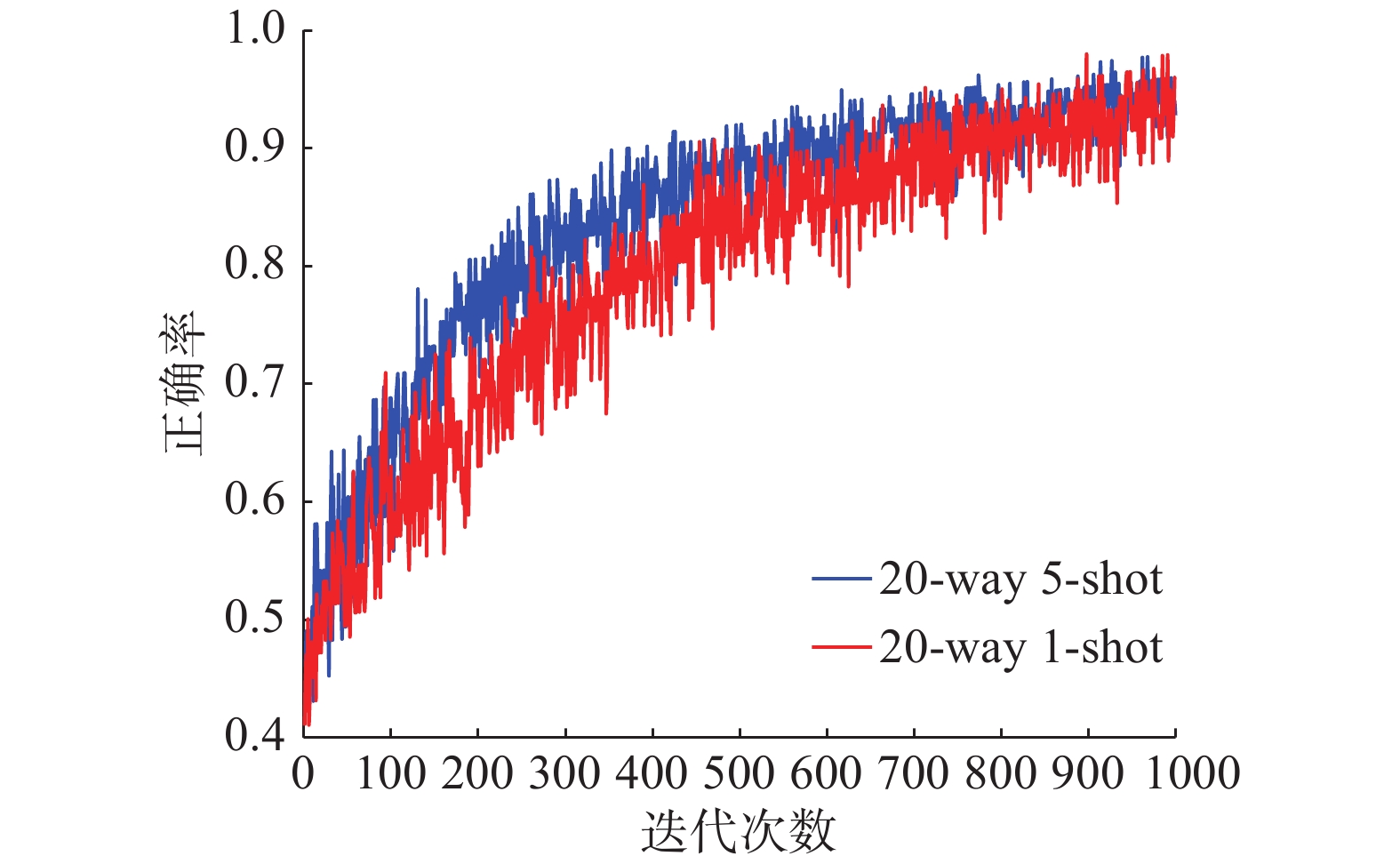
图13~15是以20-way 5-shot和20-way 1-shot为例,反映了相同类别,不同的训练样本数据集经过测试后的结果。当训练数据集样本数相同时,随着训练样本类别的增加,最终识别难度变大,分类正确率下降。结合表1中平均正确率的实验结果对比,与原始的Siamese Net[25]相比,在难度最高的20-way 1-shot情况下,孪生变分自编码器分类正确率提高了5.9%,其他情况下最低提高了0.3%,可以在说明本文所提出的混合模型的先进性。与Lake等[26]提出的分层贝叶斯学习结构相比,孪生变分自编码器正确率低0.9%,但是Lake的方法使用的不是原始图像的像素,而是Omniglot的笔画数据,虽然在Omniglot数据集上具有极高的分类正确率却失去了向其他数据集拓展的能力,本文所提出的模型与之相比具有更好的泛化能力。从4种条件下的损失函数结合表2中几个方法的训练时间对比,孪生变分自编码器可以很快速的收敛,在训练1000次后就已经达到了比较不错的分类效果。
|
Download:
|
| 图 13 20-way different-shot训练损失函数值 Fig. 13 Training loss of 20-way different-shot | |
|
Download:
|
| 图 14 20-way different-shot训练正确率 Fig. 14 Training accuracy of 20-way different-shot | |
|
Download:
|
| 图 15 20-way different-shot测试正确率 Fig. 15 Test accuracy of 20-way different-shot | |
针对小样本图像分类问题,本文提出了孪生变分自编码器网络模型。首先对训练样本数据使用变分自编码器进行降维处理,提取样本的隐含特征,然后通过孪生网络,对成对输入的两个样本进行相似度匹配,返回与待测样本标签为同类的样本类别以及正确率,完成物体的分类。通过Omniglot数据集对模型效果进行4组实验验证,本文提出的改进模型与原始孪生神经网络相比最高提高了5.9%,平均提高3.1%。
下一步工作将本文方法拓展应用到实际问题中。在电力设备故障诊断中,只有很少的实际采集样本,因此,通常会额外生成模拟数据进行实验,本文下一步工作即通过孪生变分自编码器在仅使用实际采集样本的情况下对故障类型进行分类。
| [1] |
胡越, 罗东阳, 花奎, 等. 关于深度学习的综述与讨论[J]. 智能系统学报, 2019, 14(1): 1-19. HU Yue, LUO Dongyang, HUA Kui, et al. Overview on deep learning[J]. CAAI transactions on intelligent systems, 2019, 14(1): 1-19. (  0) 0)
|
| [2] |
马世龙, 乌尼日其其格, 李小平. 大数据与深度学习综述[J]. 智能系统学报, 2016, 11(6): 728-742. MA Shilong, WUNIRI Qiqige, LI Xiaoping. Deep learning with big data: state of the art and development[J]. CAAI transactions on intelligent systems, 2016, 11(6): 728-742. (  0) 0)
|
| [3] |
王昊, 刘高军, 段建勇, 等. 基于特征自学习的交通模式识别研究[J]. 哈尔滨工程大学学报, 2019, 40(2): 354-358. WANG Hao, LIU GaoJun, DUAN Jianyong, et al. Transportation mode detection based on self-learning of features[J]. Journal of Harbin Engineering University, 2019, 40(2): 354-358. (  0) 0)
|
| [4] |
张程熠, 唐雅洁, 李永杰, 等. 适用于小样本的神经网络光伏预测方法[J]. 电力自动化设备, 2017, 37(1): 101-106, 111. ZHANG Chengyi, TANG Yajie, LI Yongjie, et al. Photovoltaic power forecast based on neural network with a small number of samples[J]. Electric power automation Equipment, 2017, 37(1): 101-106, 111. (  0) 0)
|
| [5] |
洪雁飞, 魏本征, 刘川, 等. 基于深度学习的椎间孔狭窄自动多分级研究[J]. 智能系统学报, 2019, 14(4): 1-9. HONG Feiyan, WEI Benzheng, LIU Chuan, et al. Deep learning based automatic multi-classification algorithm for intervertebral foraminal stenosis[J]. CAAI transactions on intelligent systems, 2019, 14(4): 1-9. (  0) 0)
|
| [6] |
王翔, 胡学钢. 高维小样本分类问题中特征选择研究综述[J]. 计算机应用, 2017, 37(9): 2433-2438, 2448. WANG Xiang, HU Xuegang. Overview on feature selection in high-dimensional and small-sample-size classification[J]. Journal of computer applications, 2017, 37(9): 2433-2438, 2448. DOI:10.11772/j.issn.1001-9081.2017.09.2433 (  0) 0)
|
| [7] |
LI Feifei, FERGUS R, PERONA P. One-shot learning of object categories[J]. IEEE trans pattern anal mach intell, 2006, 28(4): 594-611. DOI:10.1109/TPAMI.2006.79 ( 0) 0)
|
| [8] |
LAKE B M, SALAKHUTDINOV R, TENENBAUM J B. Human-level concept learning through probabilistic program induction[J]. Science, 2015, 350(6266): 1332-1338. DOI:10.1126/science.aab3050 ( 0) 0)
|
| [9] |
宋丽丽. 迁移度量学习行人再识别算法[J]. 计算机工程与应用, 2019, 55(20): 170-176, 201. SONG Lili. Transfer metric learning for person re-identification[J]. Computer engineering and applications, 2019, 55(20): 170-176, 201. DOI:10.3778/j.issn.1002-8331.1808-0145 (  0) 0)
|
| [10] |
任俊, 胡晓峰, 朱丰. 基于深度学习特征迁移的装备体系效能预测[J]. 系统工程与电子技术, 2017, 39(12): 2745-2749. REN Jun, HU Xiaofeng, ZHU Feng. Effectiveness prediction of weapon equipment system-of-systems based on deep learning feature transf[J]. Systems engineering and electronics, 2017, 39(12): 2745-2749. DOI:10.3969/j.issn.1001-506X.2017.12.17 (  0) 0)
|
| [11] |
谭本东, 杨军, 赖秋频, 等. 基于改进CGAN的电力系统暂态稳定评估样本增强方法[J]. 电力系统自动化, 2019, 43(1): 149-160. TAN Bendong, YANG Jun, LAI QiuPin, et al. Data augment method for power system transient stability assessment based on improved conditional generative adversarial network[J]. Automation of electric power systems, 2019, 43(1): 149-160. (  0) 0)
|
| [12] |
王建敏, 吴云洁. 基于聚类云模型的小样本数据可信度评估[J]. 系统仿真学报, 2019, 31(7): 1263-1271. WANG Jianmin, WU Yunjie. Credibility evaluation method of small sample data based on cluster cloud model[J]. Journal of system simulation, 2019, 31(7): 1263-1271. (  0) 0)
|
| [13] |
杨懿男, 齐林海, 王红, 等. 基于生成对抗网络的小样本数据生成技术研究[J]. 电力建设, 2019, 40(5): 71-77. YANG Yinan, QI Linhai, WANG Hong, et al. Research on generation technology of small sample data based on generative adversarial network[J]. Electric power construction, 2019, 40(5): 71-77. DOI:10.3969/j.issn.1000-7229.2019.05.009 (  0) 0)
|
| [14] |
韩冬, 马进, 贺仁睦. 基于Bootstrap的实测负荷模型参数优选[J]. 电工技术学报, 2012, 27(8): 141-146. HAN Dong, MA Jin, HE Renmu. Parameter optimization of measurement-based load model based on bootstrap[J]. Transactions of China electrotechnical society, 2012, 27(8): 141-146. (  0) 0)
|
| [15] |
马晓, 张番栋, 封举富. 基于深度学习特征的稀疏表示的人脸识别方法[J]. 智能系统学报, 2016, 11(3): 279-286. MA Xiao, ZHANG Fandong, FENG Jufu. Sparse representation via deep learning features based face recognition method[J]. Transactions of China electrotechnical society, 2016, 11(3): 279-286. (  0) 0)
|
| [16] |
马忠丽, 刘权勇, 武凌羽, 等. 一种基于联合表示的图像分类方法[J]. 智能系统学报, 2018, 13(2): 220-226. MA Zhongli, LIU Quanyong, WU Lingyu, et al. Syncretic representation method for image classification[J]. CAAI transactions on intelligent systems, 2018, 13(2): 220-226. (  0) 0)
|
| [17] |
赵春晖, 齐滨, Eunseog Youn. 基于蒙特卡罗特征降维算法的小样本高光谱图像分类[J]. 红外与毫米波学报, 2013, 32(1): 62-67. ZHAO Chun Hui, QI Bin, EUNSEOG Youn. Hyperspectral image classification based on Monte Carlo feature reduction method[J]. Journal of infrared and millimeter waves, 2013, 32(1): 62-67. DOI:10.3724/SP.J.1010.2013.00062 (  0) 0)
|
| [18] |
CHOPRA S, HADSELL R, LECUN Y. Learning a similarity metric discriminatively, with application to face verification[C]//2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05), San Diego, USA, 2005: 539−546.
( 0) 0)
|
| [19] |
KOCH G, ZEMEL R, SALAKHUTDINOV R. Siamese neural networks for one-shot image recognition[C]// Proc of the ICML Deep Learning Workshop, Lille, France 2015.
( 0) 0)
|
| [20] |
KINGMA D P, WELLING M. Auto-encoding variational bayes[C]//International Conference on Learning Representations, [S.l.], 2014.
( 0) 0)
|
| [21] |
LIU Guojun, LIUYang, GUO Maozu, et al. Variational inference with Gaussian mixture model and householder flow[J]. Neural networks, 2019, 109: 43-55. ( 0) 0)
|
| [22] |
宋辉, 代杰杰, 张卫东, 等. 基于变分贝叶斯自编码器的局部放电数据匹配方法[J]. 中国电机工程学报, 2018, 38(19): 5869-5877, 5945. SONG Hui, DAI Jiejie, ZHANG Weidong, et al. A data matching method of partial discharge data based on auto-encoding briational Bayes[J]. Proceedings of the CSEE, 2018, 38(19): 5869-5877, 5945. (  0) 0)
|
| [23] |
Lu Guangquan, Zhao Xishun, Yin Jian, et al. Multi-task learning using variational auto-Encoder for sentiment classification[J]. Pattern recognition letters, 2018. ( 0) 0)
|
| [24] |
ZAKHAROV N, SU H, ZHU J, et al. Towards controllable image descriptions with semi-supervised VAE[J]. Journal of visual communication and image representation, 2019, 63: 102574. DOI:10.1016/j.jvcir.2019.102574 ( 0) 0)
|
| [25] |
VINYALS O, BLUNDELL C, LILLICRAP T, et al. Matching networks for one shot learning [C]// Proc of the Advances in Neural Information Processing Systems, 2016: 3630−3638
( 0) 0)
|
| [26] |
LAKE B M, SALAKHUTDINOV R, TENENBAUM J B. One-shot learning by inverting a compositional causal process[C]// International Conference on Neural Information Processing Systems. Curran Associates Inc 2013.
( 0) 0)
|
| [27] |
ZHANG Ling, lIU Jun, LUO Minnan, et al. Hauptmann, Scheduled sampling for one-shot learning via matching network[J]. Pattern Recongnition, 2019, 96: 106962. DOI:10.1016/j.patcog.2019.07.007 ( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16


