度量学习作为机器学习领域的重要分支，已广泛应用于多个领域，如图像检索^[1-4]、目标检测^[5-7]、亲属关系验证^[8]、音乐推荐^[9]等，目的是学习数据间的相似性关系使相似样本间距离尽可能小，不相似样本间距离尽可能大^[10]。

在度量学习中，样本之间的相似性通常用马氏距离进行度量，即 ${{{d_M}}}({{{x}}_i},{{{x}}_j}) = {({{{x}}_i} - {{{x}}_j})^{\rm{T}}}{{M}}({{{x}}_i} - {{{x}}_j})$ ，其中M要求为半正定矩阵，以保证距离的有效性。Xing等^[10]使用所有样本构成二元组约束，首次提出了关于马氏距离的度量学习算法，但当样本规模较大时，约束数量呈爆炸式增长，导致算法效率降低。为了提高算法效率，Ying等^[11]将学习度量的过程转化为特征值优化问题，提出基于特征值优化的距离度量学习算法(distance metric learning witheigenvalue optimization, DML-eig)，该算法每次迭代只关注最近的不相似样本。为减少约束的规模，Davis等^[12]随机选择二元组，提出关于度量参数正则化的信息理论度量学习算法(information-theoretic metric learning, ITML)，由于随机选择约束，该算法的结果不稳定；Zadeh等^[13]随机选择约束，在相似样本与不相似样本中使用不同的度量方法提出几何平均度量学习算法(geometric mean metric learning, GMML)，该算法存在闭式解，当样本规模较大时，随着迭代次数的增加，部分样本对在训练中不产生作用。针对该问题，Omara等^[14]提出了动态生成二元组的算法。然而，当二元组样本间的相似性或相异性存在较大差异时，也将相同阈值应用于所有约束。因此，Weinberger等^[15-16]基于样本与其最近的同类样本间的距离和不同类样本之间尽可能以一个间隔分开的原则，提出了大间隔近邻分类算法(distancemetric learning for large margin nearest neighbor classification, LMNN)。Yang等^[17]将自适应地选择近邻个数引入到目标函数中，提出了自适应大间隔近邻分类算法(adaptive large margin nearest neighborclassification algorithm, ALMNN)，但该算法受参数影响较大。Song等^[18]利用特征空间中样本的几何信息对LMNN算法进行改进，提出了只关注距离最近的不同类样本对的无参大间隔最近邻度量学习算法(parameter free large margin nearest neighbor for distance metric learning, PFLMNN)，该算法不需要调参，且考虑的约束相对较少。Liu等^[19]提出一种新的约束构建方法，依据样本的先验信息，针对所有目标样本，只选与其同类距离远的样本及不同类距离近的样本生成固定的三元组，该算法受先验知识影响较大。Capitaine^[20]利用损失的加权选择约束，关注较难区分的区域或类重叠区域，适用于小样本度量学习。为了减少约束数量，Perrot等^[21]提出回 归虚 拟度 量 学习 算法 (regressive virtual metric learning, RVML)，该算法中每个样本逼近先验定义的虚拟点，可以在线性时间内学习度量，但算法受数据分布的影响。由于三元约束与支持向量机出发点一致，都是采用大间隔思想，鉴于支持向量机(support vector machine, SVM)成熟的求解方式，Wang等^[22]提出了距离度量学习的一种核分类框架，所提出的框架可以使用标准支持向量机(SVM)求解器有效地实现，但不能得到全局最优解。Zuo等^[23]将三元组约束形式用SVM表示，提出了新的度量学习算法，该算法可以得到全局最优解。基于三元组约束的度量学习大都通过设置不同的损失函数来学习度量。

基于三元组约束的度量学习通常依据先验知识，采用不同策略构建固定约束。随着迭代次数的增加，部分三元组在训练中不产生作用，于是，一些动态选择三元组的算法被提出。Mei等^[24]提出了使用三元组的基于 Logdet 散度的度量学习算法(logdet divergence based metric learning with triplet constraints, LDMLT)，该算法在每次迭代中选择有效的约束进行度量学习，降低了先验知识对度量学习的影响，但是构成三元组约束的样本都是在原始样本中选择，不能充分利用数据蕴含的三元约束。针对这一问题，研究人员将对抗训练与度量学习进行结合，在度量学习中通过产生对抗样本增强算法性能。Chen等^[25]提出对抗度量学习算法(adversarial metric learning, AML)，通过产生对抗样本对用于混淆学得的度量，提高度量学习算法鲁棒性。

基于二元组约束的对抗度量学习受参数和样本对间相似性差异的影响，使得对所有二元组约束产生对抗样本对是很难实现的，而三元约束解决了样本对间差异性的问题，同时考虑类间样本和类内样本的关系，可以将三元约束与对抗训练进行结合。基于三元组约束的度量学习与对抗训练进行结合的关键问题是如何生成对抗样本。本文借鉴对抗训练中样本扰动的思想，在原始样本附近产生对抗样本以构建对抗三元组约束，提出一种新的三元组约束的构造方法，并构建对抗样本三元组约束的度量学习模型。本文的贡献主要有：

1) 通过在三元组中的入侵样本附近学习对抗样本，构造了间隔更小的对抗样本三元组约束；

2) 构造的对抗样本学习优化模型具有闭式解；

3) 实验结果表明提出算法的性能优于代表性的三元组度量学习算法。

1 约束构建的相关算法 1.1 三元组约束构建

三元组的构建是基于三元组约束的度量学习关键问题之一。Liu等^[19]通过选择位于类边界的样本构建三元组约束，提出了一种有效的三元组约束构建方法。该论文利用任意样本、与其欧氏距离最大的同类样本和与其欧氏距离最小的异类样本构造三元组约束，并随机选择其中的一部分约束用于度量学习，这些约束一旦构造和选择将在整个度量学习的过程中固定不变。然而，这些基于欧氏距离构造并随机选择的三元组约束并不能很好地指导不断更新的度量学习，制约了算法的性能。为了解决这一问题，Mei等^[24]提出了一种面向度量学习的三元组动态选择策略，使每次迭代都能有效地利用约束进行度量学习。该方法基于当前(第t次迭代)的马氏矩阵M_t计算样本的距离矩阵和相似矩阵，根据当前度量下的近邻与先验目标近邻的偏离程度定义了样本的混乱度，并依据样本混乱度选择三元组约束，用于学习下一次(t+1次)迭代时度量矩阵 ${{{M}}_{t + 1}}$ 。

尽管LDMLT算法在每次迭代时动态选择混乱度高的约束，可以提升度量学习算法的性能，但并不能充分挖掘数据蕴含的相似性关系。

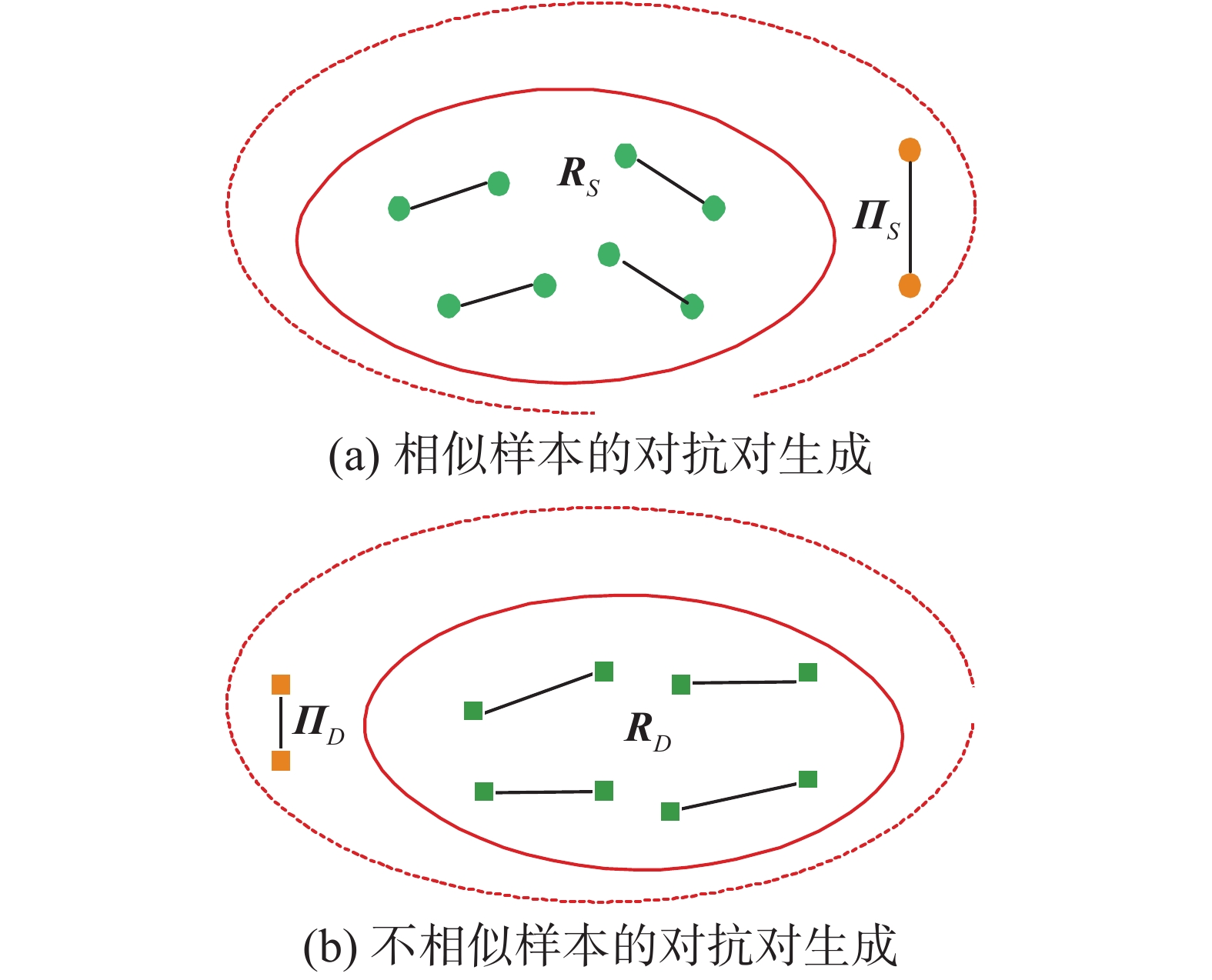
1.2 对抗度量学习

对抗度量学习(AML)算法^[25]基于对抗样本构造二元组约束，用于提高度量学习算法的鲁棒性。AML算法包括2个阶段：混淆阶段和区分阶段。在混淆阶段，通过对每个约束的2个端点产生样本扰动，即学习对抗样本对，不断放大或者缩小当前对抗样本的距离，使得在当前度量下该样本对难以区分，如图1所示。同类样本生成的对抗样本对(即 ${{{\varPi }}_{{S}}}$ )的2个样本彼此相距甚远，其描述对抗样本对为同类的极端情况。类似地，生成的异类样本的2个对抗样本对(即 ${{{\varPi }}_{{D}}}$ )变得非常相似，其描述了对抗样本对仍为异类的极端情况。在区分阶段，实现学得的度量尽可能地区分对抗样本对。

图1中S为相似样本，D为不相似样本，R_S表示相似样本对， ${{{\varPi }}_{{S}}}$ 表示相似样本对产生的对抗样本对，R_D表示不相似样本对， ${{{\varPi }}_{{D}}}$ 表示不相似样本对产生的对抗样本对。

AML算法通过对同类样本生成同类彼此相距甚远的对抗样本对，而异类样本生成异类彼此相对较近的对抗样本对来增强算法的鲁棒性。然而，由于需要为每一个二元约束构建对抗样本对，仅用单个参数来控制对抗样本的学习，使其参数难以调整，且构建的对抗样本对绝大多数是无效的。

2 对抗样本三元组约束的度量学习

现有的方法基于欧氏距离构建三元组约束，并随机选择部分三元组约束用于度量学习。虽然有一些方法提出了动态构造三元组约束的方法，但大多都是从数据中选择或强调部分约束，并没有构造新的约束，受对抗度量学习(AML)的启发，本文提出一种三元对抗约束的构造方法。

2.1 模型构建

通过调整参数动态构建三元组，提出了对抗样三元组约束的度量学习算法 (metric learning algorithm with adversarial sample triples constraints, ASTCML)。算法分为2个阶段：对抗阶段和区分阶段。

对抗阶段，生成对抗样本。初始三元组构建参考文献[15]，针对每个样本 ${{{x}}_i}$ ，选择与其距离最近的K个样本 ${{{x}}_j}$ 及不同类的所有样本 ${{{x}}_l}$ 构成三元组。当 $({{{x}}_i},{{{x}}_j},{{{x}}_l})$ 三元组约束间的距离不满足约束关系 ${{{d_M}}}({{{x}}_i},{{{x}}_l}) - {{{d_M}}}({{{x}}_i},{{{x}}_j}) \geqslant1$ 时，样本 ${{{x}}_l}$ 为入侵样本，三元组 $({{{x}}_i},{{{x}}_j},{{{x}}_l})$ 为违反约束关系的三元组。对初始三元组中违反约束关系的三元组构建对抗三元组，在入侵样本 ${{{x}}_l}$ 的附近生成对抗样本 ${{{\pi}}_{il}}$ ，使 $({{{x}}_i},{{\pi}_{il}})$ 间的距离尽可能小， $({{{x}}_i},{{{x}}_j},{{{{\pi} }}_{il}})$ 之间更加难以区分，如图2所示。通过式(1)中的损失函数计算对抗样本。

$\min \sum\limits_{(i,j,l) \in {\cal{N}}} {{{{d_M}}}({{{x}}_i},{{{{\pi}}} _{il}})} + \alpha \sum\limits_{(i,j,l) \in {\cal{N}}} {{{{d_M}}}({{{{{\pi}}}} _{il}},{{{x}}_l})} $

(1)

式中： ${\cal N}$ 表示初始三元组中违反约束关系的三元组； $\alpha $ 为调控因子，控制 ${{{\pi}} _{il}}$ 是否为对抗样本。

区分阶段，学到的度量尽可能区分对抗三元组。将生成的对抗样本代入初始违反约束关系的三元组中，通过调整参数动态生成新的三元组。在新的三元组 $({{{x}}_i},{{{x}}_j},{{{\pi}}_{il}})$ 中，使相似样本 $({{{x}}_i},{{{x}}_j})$ 间距离尽可能小，相似样本与不相似样本之间以一定的间隔分离开。引入非负的松弛变量 ${\xi _{ijl}}$ ，构建如式(2)所示的损失函数进行度量学习：

$ \begin{array}{l} \min (1 - \mu )\displaystyle\sum\limits_{i,j\sim i} {{{{d_M}}}({{{x}}_i},{{{x}}_j})} + \mu \displaystyle\sum\limits_{i,j\sim i} {\displaystyle\sum\limits_l {(1 - {y_{il}}){\xi _{ijl}}} } \\ \;\;\;\;{\rm{s.t.}}\;\;\;{{{d_M}}}({{{x}}_i},{{{\pi}}_{il}}) - {{{d_M}}}({{{x}}_i},{{{x}}_j}) \geqslant 1 - {\xi _{ijl}}\geqslant 0\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {{M}}\geqslant 0 \end{array} $

(2)

式中：最小化损失函数中的前者表示近邻损失，后者表示三元组损失； $\mu $ 为权衡因子，调节近邻损失与三元组损失在损失函数中的比重；当 ${y_i} = {y_l}$ 时， ${y_{il}} = 1$ ，否则， ${y_{il}} = 0$ ；第1约束条件为三元组约束条件，使相似样本与不相似样本之间以一定的间隔分离开；第2约束条件 ${\xi _{ijl}} \geqslant 0$ 表示违反了三元组约束条件的间隔；第3约束条件 ${{M}}\geqslant 0$ 以保证距离的有效性。

2.2 优化问题求解

该模型的目标函数是一个凸优化问题，可以利用梯度下降方式进行求解。根据式(1)可以得到对抗样本的闭式解：

${{{{\text{π}}}} _{il}} = \frac{1}{{\alpha + 1}}{{{{x}}}_i} + \frac{\alpha }{{\alpha + 1}}{{{{x}}}_l}, (i,j,l) \in {\cal{N}}$

(3)

将对抗样本代入违反约束的初始三元组中。区分阶段的损失函数也可以表示为

$\begin{split} {{L}} =& (1 - \mu )\displaystyle\sum\limits_{i,j \sim i} {{{{d}}_{{M}}}({{{x}}_i},{{{x}}_j})} + \\ &\mu \displaystyle\sum\limits_{i,j \sim i} {\displaystyle\sum\limits_l {(1 - {y_{il}}){{[1 + {{{d}}_{{M}}}({{{x}}_i},{{{x}}_j}) - {{{d}}_{{M}}}({{{x}}_i},{{{{{\pi}} }}_{il}})]}_ + }} } \end{split}$

(4)

利用式(4)得到 ${{M}}$ 的梯度：

$\begin{split} \dfrac{{\partial {{L}}}}{{\partial {{M}}}} =& (1 - \mu )\displaystyle\sum\limits_{i,j \sim i} {{{{X}}_{ij}}} + \\ &\mu \displaystyle\sum\limits_{(i,j,l) \in {\cal J}} {{{{X}}_{ij}} - \left( {\left( {{{\left( {\dfrac{\alpha }{{\alpha + 1}}} \right)}^2} - 1} \right){{[\xi _{ijl}^{{\rm{ori}}}]}_ + } + 1} \right){{{X}}_{il}}} \end{split} $

(5)

式中： ${\cal J}$ 表示以对抗样本构成的三元组中违反约束条件间隔的三元组； ${{{x}}_{ij}} = ({{{x}}_i} - {{{x}}_j}){({{{x}}_i} - {{{x}}_j})^{\rm{T}}}$ ， ${{{x}}_{il}} = $ $ ({{{x}}_i} - {{{x}}_l}){({{{x}}_i} - {{{x}}_l})^{\rm{T}}}$ ，初始三元组中不相似样本间距离小于相似样本间距离 ${[\xi _{ijl}^{{\rm{ori}}}]_ + } = 1$ ，反之 ${[\xi _{ijl}^{{\rm{ori}}}]_ + } = 0$ 。为了便于调整参数，令 $\beta = \dfrac{\alpha }{{\alpha + 1}}$ ，详细过程如算法1所示。

算法1 对抗样本三元组约束的度量学习算法。

输入 ${{X}}$ ：样本集； ${{Y}}$ ：样本标签集； $\beta $ ：调控参数； $\mu $ ：权衡因子。

输出 ${{M}}$ 。

初始化 ${{{M}}_0} = {{I}}$ 。

根据式(3)计算对抗样本，代入初始三元组中。

迭代计算：

1) 根据式(5)计算梯度 $\nabla {{{G}}_{{t}}}$ 。

2) 更新梯度 ${{{M}}_{t + 1}} = {{{M}}_t} - \lambda \nabla {{{G}}_{{t}}}$ 。

3) 将 ${{{M}}_{t + 1}}$ 进行分解，得到 ${{U}},{{{V}}_ + }$ 。

4) ${{{M}}_{t + 1}} = {{{U}}^{\rm{T}}}{{{V}}_ + }{{U}}$ 。

5) 直到收敛。

假定样本个数为 $N$ ，共有 $C$ 类且每个类的样本数相同， $\beta $ 和 $\mu $ 的取值个数分别为 $p$ 和 $q$ ， $t$ 为迭代次数。由式(2)构建的三元组约束个数大致为 $K{N^2}(1 - {1/ C})$ ，并计算每个三元组约束间的距离，对违反约束的三元组进行梯度下降。为取得较高的分类精度，选取合适的 $\beta $ 和 $\mu $ 值进行分类，算法所需次数为 $2pqtK{N^2}(1 - {1 / C})$ 。所以算法1的时间复杂度为 $O({N^2})$ 。

3 实验分析

本节在12个数据集上(如表1所示)，对提出的ASTCML算法与目前几个代表性算法进行比较，并分析了实验中参数的灵敏度与提出算法的收敛性。

3.1 实验数据与设计

本文提出的ASTCML算法与与 K 近邻算法(K-nearest neighbor, KNN)、ITML算法^[12]、GMML算法^[13]、LMNN算法^[16]、PFLMNN算法^[18]、RVML算法^[21]、LDMLT算法^[24]和AML算法^[25]进行了对比。

实验中，对表1数据中的Corel_5k数据集，先用主成分分析(principal component analysis, PCA)进行降维，保留的数据信息大于95%，除Satellite和Wilt数据集外，对其他数据集进行预处理操作，对处理后的数据集进行划分，其中80%的数据为训练集，20%的数据为测试集。采用5折交叉验证的方法进行实验，将训练集随机分为5部分，轮流作为验证集，并对5次实验结果求平均，选择在验证集上达到最高分类精度的参数，在测试集上进行测试。Satellite数据集由4 435个训练样本和2 000个测试样本组成，Wilt数据集是由4 339个训练样本和500个测试样本组成，针对这2个数据集，首先对训练集进行预处理操作，记录下训练集的归一化方法，将该方法应用于测试集进行预处理，在所有参数实验结果中选择分类精度最高的精度，即为当前数据集的分类精度。初始化度量矩阵 ${{M}} = {{I}}$ ，参数 $\beta $ 的取值范围为{0.1, 0.2, ···, 0.9}， $\mu $ 的取值范围为{0.1, 0.2, ···, 1}。此外，由式(8)可以得到，当 $\beta $ 取值为1时，算法精度与LMNN算法的结果相同或相近。使用KNN分类器的分类正确率评价度量学习算法的性能。当样本数大于或等于4500时， $\mu $ 的取值范围为{0.1, 0.3, 0.5, 0.7, 0.9}，且当数据集为Corel_5k时， $\beta $ 的取值范围为{0.2, 0.4, 0.6, 0.8}，同时采用3折进行交叉验证。

3.2 实验结果与分析

实验结果在表2中列出，表2中粗体表示最高的分类正确率，在次高的分类正确率下划横线。当数据集为Corel_5k时，AML算法运行时间相对较长，不参与算法比较。实验结果显示本文算法普遍优于代表性的度量学习方法，相比于动态构建三元组的LDMLT算法，除在German数据集上取得次高的分类精度，在其他数据集上的分类精度明显提高；与LMNN算法相比，提出算法的分类精度最低与其保持一致；相比基于对抗训练的AML算法，分类精度普遍较高。可以得出，本文算法在一定程度上说明区分更加难以区分的三元组约束能够提升算法的性能。

3.3 参数的灵敏度分析

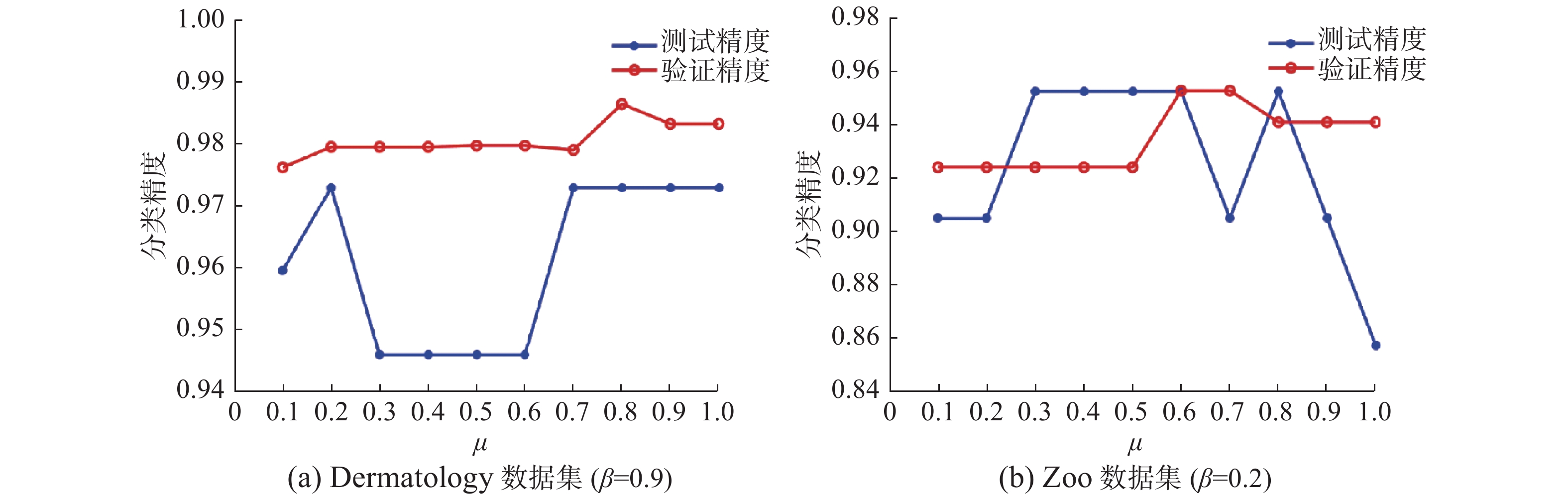
在本文提出的算法中，超参数 $\beta $ 和 $\mu $ 的设置对实验结果会产生一定的影响，其中参数 $\beta $ 控制在入侵样本附近产生对抗样本，参数 $\mu $ 为权衡因子，调节三元组损失在整个损失中的比重。在不同数据集下，只以最高的验证集分类正确率设置超参数 $\beta $ 和 $\mu $ ，通过固定其中的一个超参数，调整另一个超参数，观察在验证集与测试集上分类正确率的变化情况。从图3、4可以看出，当测试集上取得最高分类正确率时，验证集上的分类正确率也最高；在不同的参数设置下，验证集上分类准确率的变化幅度相对较小，而测试集上变化幅度相对较大。

3.4 收敛性分析

在对抗样本三元组约束的度量学习算法迭代优化的过程中，若相邻2次损失值的差小于设定的阈值或迭代次数大于最大迭代次数，则算法结束。本文通过不同数据集分别在测试集上迭代100次的损失值变化情况分析提出算法的收敛性。从图5可以看出，在迭代过程中，随着迭代次数的增加，损失函数的值呈现下降趋势，表明提出算法是可以收敛的。

4 结束语

本文借鉴对抗训练的思想，建立了学习对抗样本的优化模型，构建了对抗样本三元组约束度量学习模型，并提出相应的度量学习算法。理论上，基于对抗训练思想得到的三元组约束更加符合数据的情况，学习对抗样本的模型求解简单，且可以提高分类精度。实验结果验证了提出算法的性能。虽然，与已有代表性算法相比提出算法的性能有所提升，但其对参数较为敏感。如何降低模型对参数的敏感性将是值得进一步研究的问题。