大数据时代政府关于隐私保护的法律法规盛行，如《通用数据保护条例》(general data protection regulation)^[1]，数据在政策的限制下分散在不同的载体/组织中，因此保护隐私的机器学习在学术界和工业界都备受重视。在实现隐私保护机器学习的各种技术中，联邦学习(federated learning，FL)^[2]受到高度重视，它最初由Google提出，目标是基于分布在每个用户手机上的数据学习一个统一的模型，用户的原始信息无需转移到中央服务器，从而实现了隐私保护。经证明，FL与在原始数据上学习到的传统模型相比，预测能力几乎相同^[3]。

随着互联网和电子商务的迅猛发展，推荐系统成为企业提高市场竞争力的重要工具。其中，协同过滤 (collaborative filtering，CF) 是最著名的一种推荐算法^[4]，有2种实现方法：一种是基于近邻^[5]，另一种是基于矩阵分解^[6]。其中基于近邻的协同过滤又分为基于用户的协同过滤和基于物品的协同过滤，分别依据用户消费行为上的相似性或消费产品间的相似性来实现个性化的产品推荐。一般来说，客户的历史信息越详细，推荐结果越准确。

由于没有足够多的客户数据，许多中小型公司无法获得满意的推荐模型。为了解决这个问题，通常采取的解决方案有：1) 请求另一家拥有庞大客户数据库的公司帮助；2) 与其他多家拥有相对较小客户数据库公司合作，共同创建一个大的数据库^[7]。公司间无法简单地共享或允许彼此完全访问其数据库，因为这可能会造成客户隐私数据外泄。文献[8]表明，70%~89.5%的互联网用户认为个人隐私信息面临泄露风险。鉴于联邦学习处理数据孤岛和隐私保护问题的有效性和实用性，与联邦学习相结合的协同过滤推荐算法成为目前推荐系统领域的一个研究热点^[9]。

冷启动是协同过滤算法应用中经常会遇到的问题，分为新用户冷启动、新项目冷启动、系统冷启动等。当系统中有新用户加入时，由于该用户在系统中没有历史评分数据，不能根据传统算法计算用户间的相似度，也就无法为其进行推荐，这就是协同过滤算法的新用户冷启动问题^[10]。在现有的与联邦学习相结合的协同过滤推荐算法的研究中，对用户冷启动问题的研究比较少，因此对联邦学习协同过滤算法中用户冷启动问题的研究具有迫切的意义。

1 相关工作

本文的研究是3个研究主题的交叉点：联邦学习、协同过滤推荐算法中的隐私保护问题和冷启动问题。

1.1 联邦学习

随着信息革命的发展，海量的数据在不断产生，如何合理有效地利用这些数据成为一个热点方向。由于隐私政策的保护，很多数据不能被轻易地获取，数据间相互隔离，形成了一个个数据孤岛。如何建立数据孤岛间沟通的桥梁，打破数据之间的界限，成为一个热点方向。谷歌研究院提出了联邦学习的概念，即通过只在各节点间传递模型参数，而不分享模型间数据的方式训练一个共享的数据模型。联邦学习成为解决数据隐私保护的一个有利工具。联邦学习旨在满足数据隐私保护、数据安全和政府法规的前提下，进行数据的使用和建模。根据数据划分的方式，联邦学习可分为纵向联邦学习以及横向联邦学习^[11]。迄今为止，有许多研究致力于联邦学习算法，以支持更多的机器学习模型，包括深度神经网络（deep neural network，DNN）^[12]、梯度提升树（gradient boosting decision tree，GBDT）^[13]、逻辑回归、支持向量机^[14]。

本文主要关注在纵向联邦的场景下实现推荐系统的冷启动问题。

1.2 推荐系统的隐私保护

推荐系统(recommendation systems, RS)收集和学习用户对一系列项目的偏好信息，并预测用户对新物品或项目的兴趣程度，产生推荐列表。用户的偏好信息可以是显性的(基本上是通过收集用户的评分)或隐性的(基本上是通过监测用户的交互记录，如访问过的网页、购买过的软件、阅读过的书籍和刷过的短视频等隐性推断关于某物品的兴趣程度)^[15-17]。根据输入数据的类型，推荐模型主要分为协同过滤式推荐系统^[17]、基于内容的推荐系统^[18]和基于知识的推荐系统^[19]。在实践中，推荐系统已经被广泛地应用于各种应用中，如电子商务^[20-21]、娱乐^[22-23]、新闻^[24-25]和社交平台^[26-27]。

由于个人对物品的偏好往往涉及到个人的隐私信息，长期以来，推荐系统中如何保护隐私信息受到许多学者关注。许多研究使用差分隐私的方法保护用户评价记录的隐私性^[1]。联邦学习通过数据不出本地、仅传输用户梯度的方式，进一步保障用户的隐私不被窃取。联邦推荐系统可以与差分隐私、多方安全计算等技术结合，灵活有效地在不泄露用户隐私的前提下实现推荐系统性能的提升。

协同过滤是推荐系统中最常用、应用范围最广的算法之一，也是本文讨论的主要算法。针对协同过滤算法中的隐私保护问题，有多种方法可以解决。如文献[15]针对集中式数据，采用随机扰乱技术，提出了一个保护隐私的协同过滤推荐方案；文献[28]在差分隐私框架中提出了协同过滤算法；文献[29]使用同态加密计算协同过滤过程的中间值，中间值解密后通过奇异值分解和因子分析产生推荐建议；文献[30]提出了一种基于同态密码的协同过滤算法；文献[31]提出了一种新的兴趣点推荐隐私保护框,在联邦学习中采用安全聚合的策略来学习特征交互模型；文献[32]提出了一种新的分布式矩阵分解框架用于兴趣点推荐，该框架具有可扩展性，能够保护用户隐私。

1.3 协同过滤及其冷启动问题

协同过滤是一种基于矩阵分解的推荐算法。在已知用户的历史评分矩阵 $ {{R}} $ 的前提下，使用较低维的用户特征矩阵 ${{U}}=\{{{u}}_{1}\; {{u}}_{2}\;\cdots \;{{u}}_{N}\}$ 和物品特征矩阵 ${{V}}=\{{{v}}_{1}\;{{v}}_{2}\; \cdots \;{{v}}_{M}\}$ 的乘积 $ {{{U}}}^{{\rm{T}}}{{V}} $ 拟合评分矩阵。在进行推荐时，通过用户特征和物品特征向量的内积 ${{u}}_{i}^{{\rm{T}}}{{v}}_{j}$ 计算出用户对某一物品的预测评分，即用户可能对该物品感兴趣的程度。其中，用户特征和物品特征都是通过对历史评分的学习训练得到的，当系统中添加新的用户和新的物品时，它们的特征向量是未知的，即产生了初始推荐的问题，相关的算法称为协同过滤的冷启动。

针对协同过滤算法中冷启动问题，文献[33]提出了一种基于协同矩阵分解的用户冷启动推荐算法，来处理用户冷启动问题。文献[34]将计算相似性的不对称方法与矩阵分解和基于典型性的协同过滤(tyco)相结合，实现了一种改进的电影推荐算法。然而目前对冷启动问题的研究一般基于单方数据库，具有一定的局限性，有少数学者对多方参与的协同过滤冷启动问题进行了探索。文献[35]引入联邦多视图矩阵分解方法，将联邦学习框架扩展到具有多个数据源的矩阵分解。经证明，该方法对于多数据源冷启动推荐有较好的预测效果。

本文提出的方法联合多方数据，打通了数据孤岛，在进行隐私保护的同时，解决了协同过滤中的冷启动问题。

2 纵向联邦协同过滤中的冷启动定义

在本节中，对纵向联邦协同过滤中的冷启动问题给出正式的公式定义。

本文考虑采用基于纵向联邦学习的协同过滤方法。其中，联邦协同过滤可以由多方进行联合训练，为了方便起见，本文均以两方为例。假定联邦参与公司A、B都是半诚实的，这意味着他们会遵守协议，但也会尽可能地从执行中推断信息。因此在本文中，由于评分属于隐私信息，A、B双方均不能直接交换评分。在此假定A需要解决新用户冷启动问题，与B联合进行基于物品的协同过滤训练，最终A、B均能获得两方物品的相似度矩阵，B通过相似度矩阵与物品评分对A物品进行评分预测，将预测值排序并返回A推荐物品id。最终，在不泄露评分信息的情况下，A获得了针对新用户的物品推荐顺序。

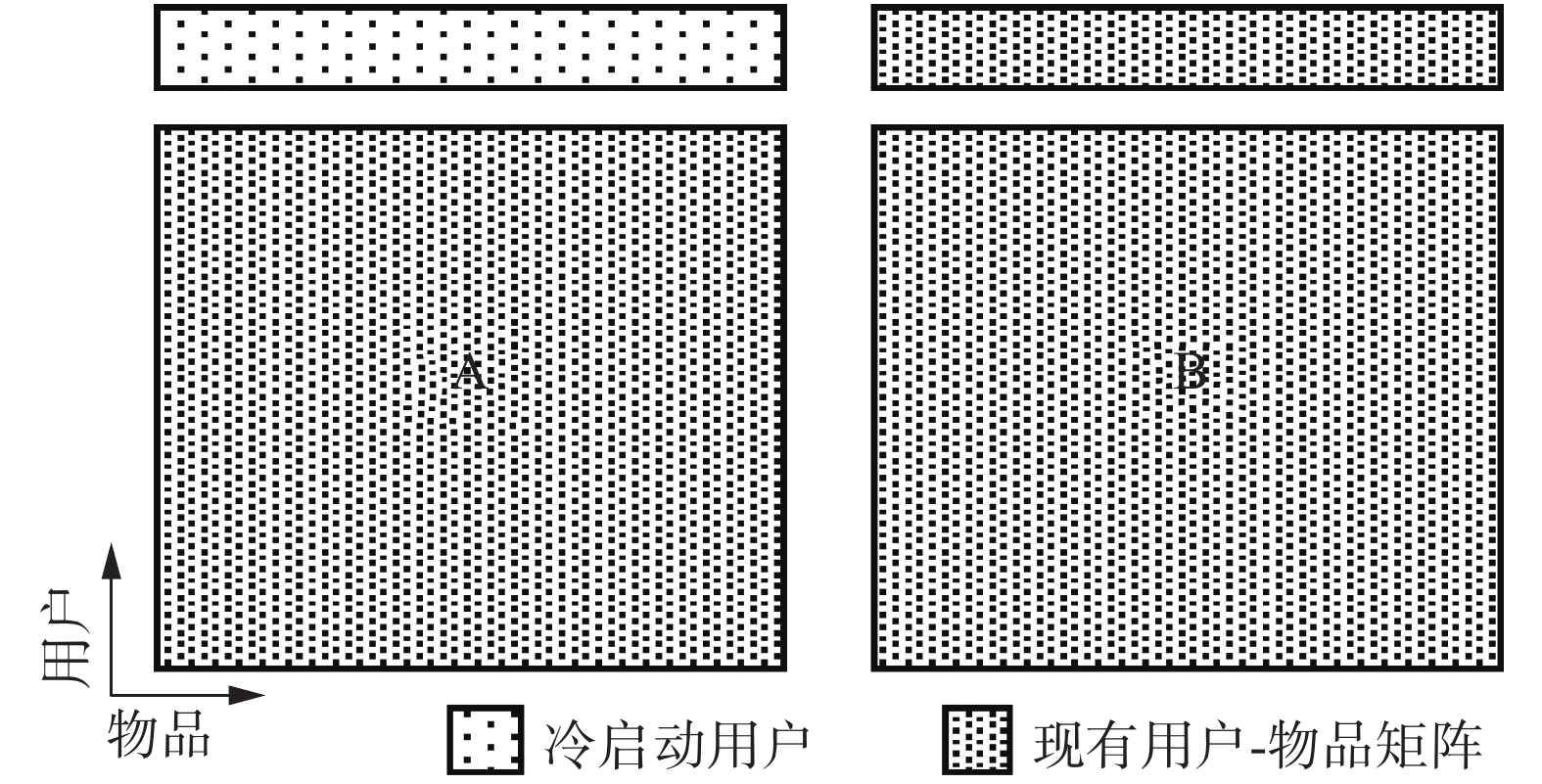
如图1，机构A为了解决本地新用户的冷启动问题，与机构B进行合作。假设A与B是纵向联合，A与B共有用户 $ n $ 个，已经进行了对齐处理；共有 $ m $ 个物品，其中A有 $ m' $ 个物品，B有 $ m-m' $ $ m-m' $ 个物品。令评分为 $ [{v}_{{\rm{min}}},{v}_{{\rm{max}}}] $ $ [{v}_{{\rm{min}}},{v}_{{\rm{max}}}] $ 中的一个整数，对于物品 $ i(1\leqslant i\leqslant m) $ ，评分向量为 ${{{V}}}_{i}=({v}_{1i},{v}_{2i},{ \cdots , v}_{ni})$ ，其中 ${v}_{ui}(1\leqslant u\leqslant n)$ 代表用户 $ u $ 对物品 $ i $ 的评分。假设 $ n $ 个用户中，A有 $ {n}' $ 个新用户，但对于B不为新用户。因此A拥有评分矩阵 $ {{{V}}}_{ui}({n}'+1\leqslant u\leqslant n, 1\leqslant i\leqslant {m}') $ ，相应地，B机构拥有评分矩阵 $ {{{V}}}_{ui}(1\leqslant u\leqslant n,{m}'+1\leqslant i\leqslant m) $ 。该研究问题是设计一个联邦学习纵向协同过滤算法，让A能够在不泄露双方信息的前提下，通过B的信息完成对新用户 $ u (1\leqslant u\leqslant {n}') $ 的推荐。

3 联邦推荐冷启动 3.1 协同过滤冷启动算法

根据文献[36]提出的框架，协同过滤主要分为3个步骤：

1)物品相似度计算：根据评分信息，计算物品i与其他物品相似度；

2)邻近样本选择：这一步主要是为了提高推荐算法的效率和精确度；

3)预测推荐：对用户 $ u $ 的评分预测，并将排序最高的前 $ N $ 个推荐给用户。

1)计算物品相似度：为了计算A方物品与B方物品的相似度，采用皮尔森相关系数进行计算，令 $ i $ 为A方物品， $ j $ 为B方物品，则皮尔森系数为

$ {{\rm{sim}}_{ij}} = \frac{{\displaystyle\sum\limits_{u = {n^\prime } + 1}^n {\left( {{v_{ui}} - \overline {{v_i}} } \right)} \left( {{v_{uj}} - \overline {{v_j}} } \right)}}{{\sqrt {\displaystyle\sum\limits_{u = {n^\prime } + 1}^n {{{\left( {{v_{ui}} - \overline {{v_i}} } \right)}^2}} } \sqrt {\displaystyle\sum\limits_{u = {n^\prime } + 1}^n {\left( {{v_{u,j}} - \overline {{v_j}} } \right)} } }} $

式中： $ {v}_{u,i} $ 表示用户 $ u $ 给物品 $ i $ 的评级； ${\bar{v}}_{i}= \dfrac{{\displaystyle\sum\limits_{u = n' + 1}^n {{v_{ui}}} }}{{n - n'}}$ ； ${{\rm{sim}}}_{ij}$ 代表物品 $ i $ 与 $ j $ 相似度，范围在[−1, 1]。为了使A、B两方能够联合计算，将其分为 $c_{ui} $ 、 $c_{uj} $ 2个部分：

$ {{\rm{sim}}_{ij}} = \sum\limits_{u = n' + 1}^n {{c_{ui}}} {c_{uj}} $

其中：

$ {c_{ui}} \!\!\!=\!\!\! \dfrac{{{v_{ui}} - {{\bar v}_i}}}{{\sqrt {\displaystyle\sum\limits_{u = n'\! +\! 1}^n \!\!{{{\left( {{v_{ui}} \!-\! {{\bar v}_i}} \right)}^2}} } }} $

(1)

$ {c_{uj}} \!\!\!=\!\!\! \dfrac{{{v_{uj}} - {{\bar v}_j}}}{{\sqrt {\displaystyle\sum\limits_{u = n'\! +\! 1}^n \!\!{{{\left( {{v_{uj}} \!-\! {{\bar v}_j}} \right)}^2}} } }} $

(2)

显然，计算 ${c}_{ui}$ ( ${c}_{uj}$ )只需要 ${v}_{ui}\left({v}_{uj}\right)$ 的信息，因此A、B两方均可在本地计算 ${c}_{ui}$ 、 ${c}_{uj}$ 。令 ${C}_{i}= $ $ \left({c}_{{n}'+1i},{c}_{{n}'+2i}, \cdots ,{c}_{ni}\right),{C}_{j}=({c}_{{n}'+1j},{c}_{{n}'+2j}, \cdots ,{c}_{nj})$ ，计算 ${{\rm{sim}}}_{ij}$ 即可转为计算C_i和C_j的内积。

2)选择近邻：由于本文针对的是新用户的冷启动推荐问题，将所有物品都作为邻近样本，允许使用不相似的物品来进行计算，增加推荐覆盖率。

3)预测推荐：为了对机构A的新用户进行推荐，采用B机构里的评分信息进行预测：

$ {{\rm{pred}}_{ui}} = \frac{{\displaystyle\sum\limits_{j = {m^\prime } + 1}^m {{v_{uj}}} {{\rm{sim}}_{ij}}}}{{\displaystyle\sum\limits_{j = {m^\prime } + 1}^m {\left| {{{\rm{sim}}_{ij}}} \right|} }} $

式中： ${{\rm{pred}}}_{ui}$ 代表用户 $ u $ 对物品 $ i $ 的预测评分，对于A机构的新用户，有 $ 1\leqslant u\leqslant {n}', 1\leqslant i\leqslant {m}' $ 。其中预测值计算可在B机构进行，且B机构对预测值结果排序，将排在前N个物品发送给A机构，完成对新用户的推荐。

3.2 安全内积

文献[37]提出了一种基于第3方的一种安全内积计算协议。

为了计算 $ {C}_{i} $ 与 $ {C}_{j} $ 的内积 $ <{C}_{i},{C}_{j}> $ ，加入一个第3方，在不泄露各方数据下进行数据的汇总，如算法1所示。

算法1　安全内积算法 $ <{C}_{i},{C}_{j}> $

多方　 A、B以及第3方T；

输入　 A: $ {C}_{i} $ ；B: $ {C}_{j} $ ；

输出　A: $ {r}_{A} $ ；B: $ {r}_{B} $ ，且有 $ {r}_{A}+{r}_{B}= <{C}_{i},{C}_{j}> $ 。

1) T方随机产生2个随机向量 ${{x}},{{y}}$ ，以及一个随机数 $ r $ ，且令 $z= < {{x}},{{y}} > - r$ ，将 $({{x}}, r)$ 传给A， $({{y}}, z)$ 传给B；

2) A将 ${C}_{i}+{{x}}$ 传给B；

3) B将 ${C}_{j}-{{y}}$ 传给A；

4) A计算可公开信息 ${r}_{A}= < {C}_{i},{C}_{j}-{{y}} > - r$ ；

5) B计算可公开信息 ${r}_{B}= < {C}_{i}+{{x}},{C}_{j} > - z$ 。

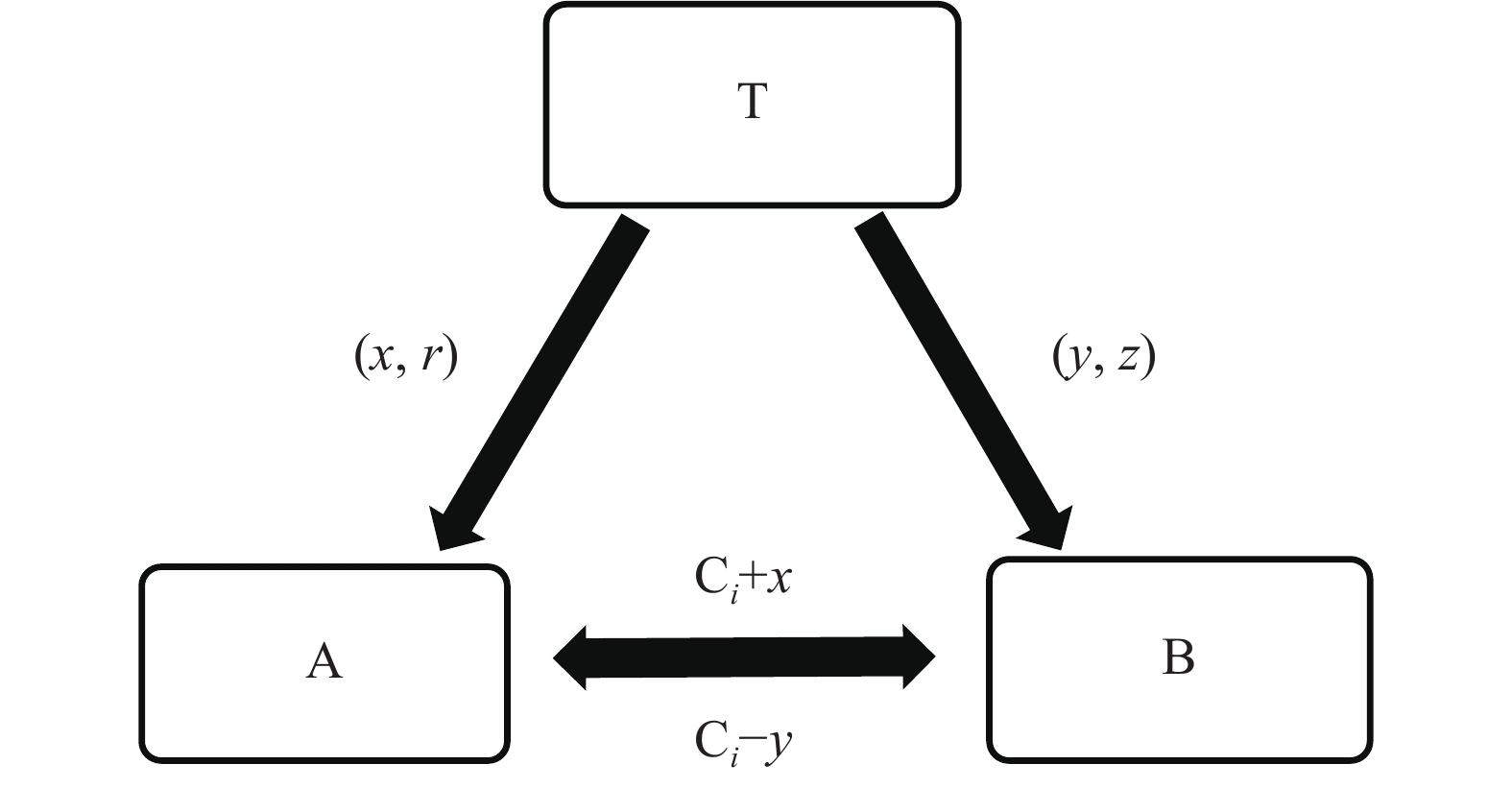
由于 $ {r}_{A} $ 及 $ {r}_{B} $ 里面各包含2个随机项，对 $ {C}_{i} $ 及 $ {C}_{j} $ 的隐私信息均进行了保护，因此不会泄露各方的隐私数据，最终A, B双方均可利用公开的 $ {r}_{A} $ 、 $ {r}_{B} $ 进行内积 $ <{C}_{i},{C}_{j}> $ 的计算，达到了隐私保护的作用，流程如图2所示。

3.3 联邦协同过滤冷启动算法

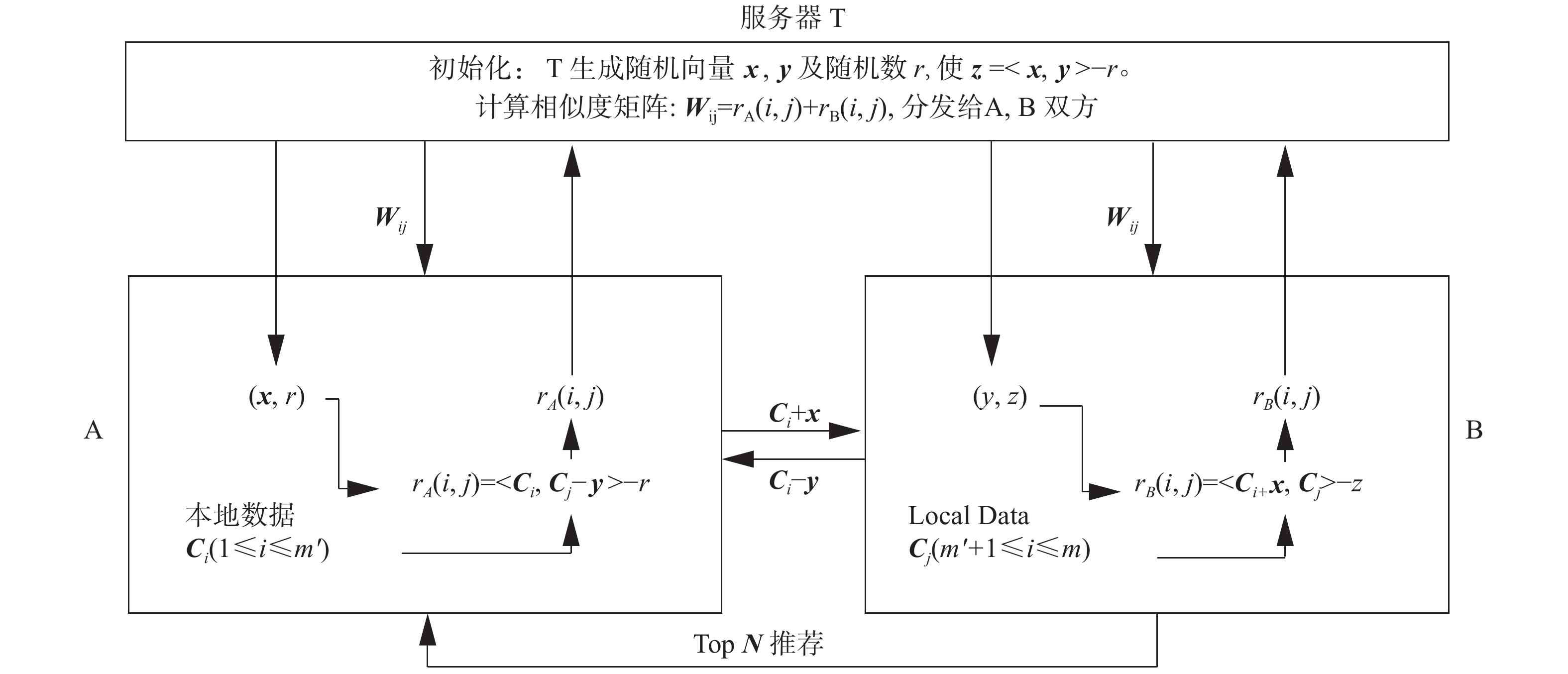
为了使A、B双方能够在数据不泄露的情况下进行新用户的推荐，将协同过滤与安全内积相结合，构建联邦学习协同过滤冷启动解决算法。框架内容如图3所示，由受信任的第3方T以及A、B两方构成。如前文所述，假设A、B两方都是半诚实的，同时第3方T也不与A、B两方勾结。

联邦协同过滤冷启动算法的主要步骤包括：

1) 基于安全内积算法，A、B端根据式(1)、(2)在本地分别计算 $ {C}_{i}(1\leqslant i\leqslant {m}') $ ， $ {C}_{j}({m}'+1\leqslant i\leqslant m) $ ；

2) 第3方T随机产生2个随机向量 ${{x}}$ 、 ${{y}}$ 以及一个随机数 $ r $ ，且令 $z= < {{x}},{{y}} > - r$ ，将 $({{x}}, r)$ 传给A， $({{y}}, z)$ 传给B；

3) A将 ${C}_{i}+{{x}}(1\leqslant i\leqslant {m}')$ 传给B；B将 ${C}_{j}-{{y}} $ $ ({m}'+1\leqslant j\leqslant m)$ 传给A；

4) A分别计算 ${r}_{A}\left(i,j\right)= < {C}_{i},{C}_{j}-{{y}} > - r (1\leqslant i\leqslant {m}', $ $ {m}'+1\leqslant j\leqslant m)$ 传输给T；同理B相应计算 $ {r}_{B}\left(i,j\right) $ 传输给T；

5) T计算 ${{{\rm{sim}}}_{ij}=r}_{A}\left(i,j\right)+{r}_{B}\left(i,j\right)$ ，并构建相应的相似矩阵 ${{{W}}}_{ij}$ (由 ${{\rm{sim}}}_{i,j}$ 元素构成)分发给A、B双方；

6) B根据 ${{{W}}}_{ij}$ 相似矩阵以及本地用户 $ u\in [1,{n}'] $ 对物品 $ j\in [{m}'+1, m] $ 的评分信息，由式(3)对 ${{\rm{pred}}}_{ui},u\in \left[1,{n}'\right], i\in [1,{m}']$ 进行预测，并对预测结果进行排序，最终将预测值最高的前N个物品ID发送给A，完成用户冷启动推荐过程。

由图3中可看出，每一方并不能直接收到对方的原始评分，且由于增加了随机项，不能从中间结果进行对原数据的反推，因此达到了隐私保护的作用。

4 实验与结果 4.1 度量标准

本文采用Top-N推荐，采用2种不同的评估方法进行模型评价。

1) 阈值击中评价

推荐评估指标采用精确率Precision、查全率Recall以及 $F_1-{\rm{score}} $ 。

$ {\rm{Precision}}=\dfrac{\displaystyle\sum_{u=1}^{{n}'}|{R}_{u}\cap {T}_{u}|}{\displaystyle\sum_{u=1}^{{n}'}\left|{R}_{u}\right|} $

$ {\rm{Recall}}=\dfrac{\displaystyle\sum_{u=1}^{{n}'}\left|{R}_{u}\cap {T}_{u}\right|}{\displaystyle\sum_{u=1}^{{n}'}\left|{T}_{u}\right|} $

$ F_1-{\rm{score}} = 2 \dfrac{{{{ {\rm{precision}} }} \times {{ {\rm{recall}} }}}}{{{{ {\rm{precision}} }} + {{ {\rm{recall}} }}}} $

式中： $ {R}_{u} $ 是B方基于相似矩阵以及用户 $ u $ 的评分信息进行对A方的推荐列表； $ {T}_{u} $ 是新用户 $ u $ 对于A中物品的非空且评分大于阈值 $ c $ 的用户行为列表。

2) 留一法 (leave-one-out)评价

对于测试集里的每个用户，都保留其最新一条评分信息进行验证。由于在评价过程中对每个用户都进行排序比较耗时，所以本位采用了常用的策略^[35-36]，即对于每个用户随机抽取30个没有评分的物品，并且对其评分预测排序。在此设定推荐个数为10，将该30个物品与最新评分物品的预测评分进行排序，若最新评分物品排在前10则视为击中。评估指标采用命中率 (hit ratio, HR)^[37]以及归一化折现累计增益(normalized discounted cumulative gain，NDCG)来判断排序列表的性能。HR直观地衡量测试物品是否在前10，而NDCG根据击中的位置进行评估。

4.2 数据集

本文实验采用GroupLens提供的网络开源数据集MovieLens 1M为例，整个数据集包括了6 040个电影用户对3 706部电影的1 000 209条评分，评分范围为1~5。由于本文针对基于物品协同过滤的冷启动问题，因此只取数据集中的用户−电影评分集作为实验数据。

该评分数据集均对用户及电影进行了ID处理，因此在进行计算过程中用户ID及电影ID不视为隐私数据。同时有较多数的电影只被极少数的用户进行评分，该部分电影对新用户的推荐起较少的作用，因此将用户评分率低于10%的电影进行删除，处理后的用户−电影数据维度为6 040 498。

为了衡量冷启动推荐的效果，将用户分割为2部分，新老用户比例为2：8，在新用户与老用户中的数据进行了纵向分割，随机分成A、B 2个部分，并且通过改变A、B的分配比例 $ P\in (0.1, 0.9) $ 进行多组实验。评估时，将A中已有的新用户评分行为与相应的推荐作比较。

4.3 验证

第1个实验是通过变化A、B间分配比例P的取值来观察当联合多方数据训练模型时，取何值效果会比较理想。第2个实验中，将该算法和一个基于物品平均评分的无偏差推荐基线算法进行评估指标的比较。

1) 不同B机构比例的实验结果

令P代表B数据量在总数据量中的占比，当P越大时，代表B所拥有的信息越多。由于在实际场景中，两方机构所含有的物品特征不全是一致的，A可能会与规模较大的机构合作，也可能会与规模较小的机构合作。

从表1中可以看出当B的占比越大，无论阈值c取3或4(当用户评分>=阈值时，才算击中)，对于A机构的冷启动推荐效果都更好，这与直观相符合，当外部提供的信息越多，对自身的帮助会越大。对于HR及NDCG，也可以看到随着B的占比上升，总体趋势也为上升。阈值c为4时召回率均大于阈值为3，这说明本文的方法对于高评分物品推荐的效果较好。

2) 基准算法与本文算法的结果对比

为验证方法可行性，采用一个基准算法来作对比。采用的基准算法为只取A方的数据对各个物品评分取平均，并将其平均分排序最高的前N个对新用户进行无偏差的推荐。本文以A、B机构均占50%，即 $ P=0.5 $ 为例，实验结果如表2、3。

从表2结果可以发现，当阈值取3以及取4时，本文算法均比基准算法有一定的提高。当阈值取3，可以看到无论是精确度还是查全率都有一定的提升，其中F₁值较基准算法提升了约7%。当阈值取4时，F₁值较基准算法提升了约6%。

从表3中可以看到留一法的评估结果，相较基准算法，本文算法的击中率(HR)有较大的提升，约12.5%，但NDCG的提升效果较小，约9.6%。说明该算法对于推荐的击中效果有较大的提升，而对于击中的位置提升的效果较小。

5 结束语

本文首先介绍了基于物品的协同过滤算法以及安全内积算法，并针对新用户的冷启动问题，提出了一种基于联邦学习的协同过滤冷启动解决算法。该算法针对某一方的新用户冷启动问题，通过与其他方数据进行联合，在不泄露信息的情况下进行相似矩阵的计算，最终解决冷启动问题。实验结果表明，本文提出的联邦学习冷启动方法在准确度均有一定的提升，同时实验证明当联合规模较大的数据进行联合训练时，对于本地的推荐效果会有较大的提升。该方法不仅提供了一种解决协同过滤冷启动的方法，也在运用联邦学习解决冷启动的方向带来了一定的启发。