机器人与智能制造是国家制造2025的主攻方向和工业4.0的核心技术，为实施制造业创新驱动发展战略和加速制造业转型升级提供有利支撑。传统的工业机器人工作过程主要以示教或离线编程的方式执行预定指令，不利于加工柔性和智能化程度的提高^[1-3]。机器人按预先编制的模式工作，当环境变化不被机器人感知时，容易造成加工误差，无法满足产品质量要求，或增加产品报废率，影响企业产品质量等级或增加生产成本。因此，基于实时信息感知反馈的机器人柔性位姿控制，是提高机器人智能化水平和产品质量的有利条件^[4-5]。机器人智能化程度的提高有赖于传感器技术和信息技术的发展，其中，将机器视觉感知与机器人反馈控制技术相结合，有效利用视觉传感器信息感知能力，自适应地控制机器人执行决策，已成为提高机器人柔性和智能化水平的一个重要支撑条件^[6-7]。

机器人视觉伺服控制研究领域涉及图像处理、模式识别、机器人运动学、机器人动力学以及控制理论等。20世纪90年代以来，基于信息感知的工业机器人柔性加工方法得到广泛的关注并进入快速发展阶段^[8]。基于视觉的机器人控制形式在很大程度上克服了机器人自身、视觉系统以及外部环境的不确定性，使机器人定位和跟踪精度有极大的提高。Espiau等^[9]较早地开展了机器人视觉伺服控制算法的研究。Belousov等^[10]基于计算机网络远程控制方式对机器人实时目标抓取技术进行了研究，并采用仿真技术研究了目标定位和运动轨迹跟踪方法。Chaumette等^[11]提出了基于21/2D视觉伺服控制方法，对视觉伺服经典控制方法进行了优化，并开展了机器人工业应用测试。Schmidt等^[12]采用“眼在手”方式，将单目相机固定于机器人末端，通过在工件表面粘贴标记物实现定位抓取，目标标记方式可有效提高检测和控制精度。尹湘云等^[13]基于支持向量机回归的机器人视觉定位，简化了控制策略并提高了机器人的控制精度。Ishibashi等^[14]提出了基于双目立体视觉的机器人定位方法，实现了目标对象的快速、非接触三维定位，但该方法存在特征点难以匹配，较适合于特征点显著的目标物体。Wilson等^[15]将单目摄像头安装在机器人执行器末端，借助物体已知特征点，通过扩展卡尔曼滤波器，研究了轨迹控制和目标跟踪技术，该方法可在动态环境中具备一定的可靠性。陈影等^[16]采用点云切片法得到熔覆路径上的点集，运用非均匀有理B样条拟合得到加工点的曲线，从而得到枪头的运动轨迹，该方法提高了算法实现的可行性和可靠性。Park等^[17]采用厚度映射法对物体表面进行三维重建，同时生成磨削路径，主要应用于船舶和飞机螺旋桨磨削加工，该方法验证了机器人数字化对大型雕刻面进行重塑和刀具路径生成的有效性。董铃等^[18]采用基于三维视觉的激光再制造机器人离线自动编程系统，采用梯度重心法提取激光条纹的中心线，依据极限几何理论进行特征匹配，根据三角原理得到零件的表面点云数据，该算法在一定程度上提高了测量精度，具有较好的理论和实用价值。

目前，在面向工业应用的机器人手眼协调技术领域，由于存在外界光照干扰或加工工件形状复杂等因素，提高机器人动态环境适应能力和实现精确路径引导技术仍是研究热点。其中，机器人手眼关系标定、视觉有效信息获取、成像与控制模式以及视觉检测控制精度等仍需开展进一步的研究工作。本文鉴于前人的研究成果，以激光切割机器人视觉引导为研究背景，为克服环境光照干扰、切割工件形状复杂以及检测和控制精度低等问题，提出了一种基于双目CCD激光扫描3D成像的“眼在外”(Eye-to-hand:ETH)工业机器人末端(TCP)运动轨迹在线修正方法。以激光切割机器人视觉引导为研究背景，降低加工过程机器人对物理工装定位精度的依赖。首先，为提高机器人视觉控制精度，研究了目标工件双目3D激光扫描成像空间点云坐标精确提取方法；其次，融合ETH控制特点和扫描成像系统结构，建立了一种机器人TCP运动轨迹相对偏差在线补偿方法。该方法可用于混合多形状物料的识别、抓取与分拣工作。

1 实验系统构建 1.1 手眼关系与目标检测方法

文中机器人视觉信息反馈系统采用了眼在外独立工作方式(Eye-to-hand)，因此，利用检测坐标点调整机器人末端执行器姿态，需将工件坐标系和机器人末端执行器坐标系统一到基坐标系下，确定机器人基座坐标系B和摄像机坐标系D之间的变换关系，转换关系矩阵可由手眼标定完成^[19-20]。本系统由于采用双目激光扫描方式，因此，为便于确定手眼关系，在系统中定义了两个已知坐标原点，如图1所示，一是由示教获得的机器人工作原点，二是双目3D扫描成像系统扫描原点(双目CCD 3D点云数据在系统结构不变的情况由ICP算法进行一次配准，并确定配准变换矩阵参数不变)。基于以上定义可知，系统中视觉坐标系D与机器人基坐标系B位姿相对固定，基坐标系B与工具中心坐标系之间的转换矩阵可由机器人内部参数确定，位于工作原点中的工具中心点坐标系T₁与扫描原点视觉成像坐标系V可通过一次标定获得并确定不变。此处，为便于计算，特将视觉坐标系原点V定义在扫描原点，在双目激光扫描系统标定过程中，将被扫描目标点云坐标确定在V坐标下，具体检测方法不作为本文重点论述。因此，扫描获得的目标物体上某一点 $p({x_i},{y_i},{z_i})$ 可通过式(1)获得：

${}^B{{\boldsymbol{P}}_p} = {}^B{{\boldsymbol{T}}_{{T_1}}}\times{}^{{T_1}}{{\boldsymbol{T}}_V}\times{}^V{{\boldsymbol{P}}_p}$

(1)

式中： ${}^B{{\boldsymbol{P}}_p}$ 为扫描点位于机器人基坐标系下的坐标； ${}^B{{\boldsymbol{T}}_{{T_1}}}$ 为机器人末端工具中心点姿态； ${}^{{T_{\rm{1}}}}{{\boldsymbol{T}}_V}$ 为定义的双目扫描视觉坐标系与工具中心点坐标系转换关系矩阵； ${}^V{{\boldsymbol{P}}_p}$ 为目标扫描点位于在扫描原点定义的视觉坐标系中的坐标值，此处，扫描原点为双目扫描系统归零点，即系统扫描开始和结束编码器指定位置。

依据正运动学求解过程，图1中目标坐标系内点 $P$ ，在视觉坐标系内为 ${}^V{\boldsymbol{P}}$ ，通过旋转和平移变换可获得该点在机器人基座坐标系 $B$ 中的坐标值，变换式可表示为

${}^B{\boldsymbol{P}} = {}_V^B{\boldsymbol{R}}\times{}^V{\boldsymbol{P}} + {}_V^B{\boldsymbol{t}}$

(2)

式中： ${}_V^B{\boldsymbol{R}}$ 表示视觉坐标系V相对于基坐标系B的旋转矩阵； ${}_V^B{\boldsymbol{t}}$ 表示对应的平移向量，因此，获得 ${}^B{\boldsymbol{P}}$ 为目标坐标系相对于基坐标系B的位置，通过正运动学可获取末端工具中心点坐标系的相对位置，关系为

$\begin{split} {}^{{T_1}}{\boldsymbol{P}} = {}_B^{{T_1}}{\boldsymbol{R}}\times{}^B{\boldsymbol{P}} + {}_B^{{T_1}}{\boldsymbol{t}} ={}_B^{{T_1}}{\boldsymbol{R}}\times({}_C^B{\boldsymbol{R}}\times{}^C{\boldsymbol{P}} + {}_C^B{\boldsymbol{t}}) + {}_B^{{T_1}}{\boldsymbol{t}} \end{split} $

(3)

式中： ${}_B^{{T_1}}{\boldsymbol{R}}$ 、 ${}_B^{{T_1}}{\boldsymbol{t}}$ 分别表示工具中心点坐标系T相对于视觉坐标系V的旋转矩阵和平移向量，则 ${}^{{T_1}}P$ 为工具中心点坐标系T₁相对于视觉坐标系V的位姿。

对式(2)和(3)引入齐次坐标变换矩阵如下：

$\left[ {\begin{array}{*{20}{c}} {{}^B{\boldsymbol{P}}} \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{}_V^B{\boldsymbol{R}}}&{{}_V^B{\boldsymbol{t}}} \\ 0&1 \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{}^V{\boldsymbol{P}}} \\ 1 \end{array}} \right]$

(4)

$\left[ {\begin{array}{*{20}{c}} {{}^{{T_1}}{\boldsymbol{P}}} \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{}_B^{{T_1}}{\boldsymbol{R}}}&{{}_B^{{T_1}}{\boldsymbol{t}}} \\ 0&1 \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{}^B{\boldsymbol{P}}} \\ 1 \end{array}} \right]$

(5)

令 ${}^V\tilde {\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {{}^V{\boldsymbol{P}}} \\ 1 \end{array}} \right]$ 、 ${}^B\tilde {\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {{}^B{\boldsymbol{P}}} \\ 1 \end{array}} \right]$ 、 ${}^{{T_1}}\tilde {\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {{}^{{T_1}}{\boldsymbol{P}}} \\ 1 \end{array}} \right]$ ，则：

${}^B\tilde {\boldsymbol{P}} = {}_V^B{\boldsymbol{T}}{}^V\tilde {\boldsymbol{P}}$

(6)

${}^{{T_1}}\tilde {\boldsymbol{P}} = {}_B^{{T_1}}{\boldsymbol{T}}{}^B\tilde {\boldsymbol{P}} = {}_B^{{T_1}}{\boldsymbol{T}}{}_V^B{\boldsymbol{T}}{}^V\tilde {\boldsymbol{P}}$

(7)

式中变换矩阵 ${}_V^B{\boldsymbol{T}}$ 的求解过程需获取相机与工具中心点坐标系的关系矩阵 ${}_{{T_1}}^V{\boldsymbol{T}}$ 。在系统中，由于已设定扫描原点(扫描成像系统归零点)为视觉坐标系V的原点，将机器人示教工作原点作为 ${}_{{T_1}}^V{\boldsymbol{T}}$ 求解的T₁坐标系原点，因此， ${}_{{T_1}}^V{\boldsymbol{T}}$ 变换矩阵可假定为眼在手方式固定变换参数。因此，借助工具中心点坐标系T₁，为便于求解，可将各坐标系的逻辑关系表示为图2所示。

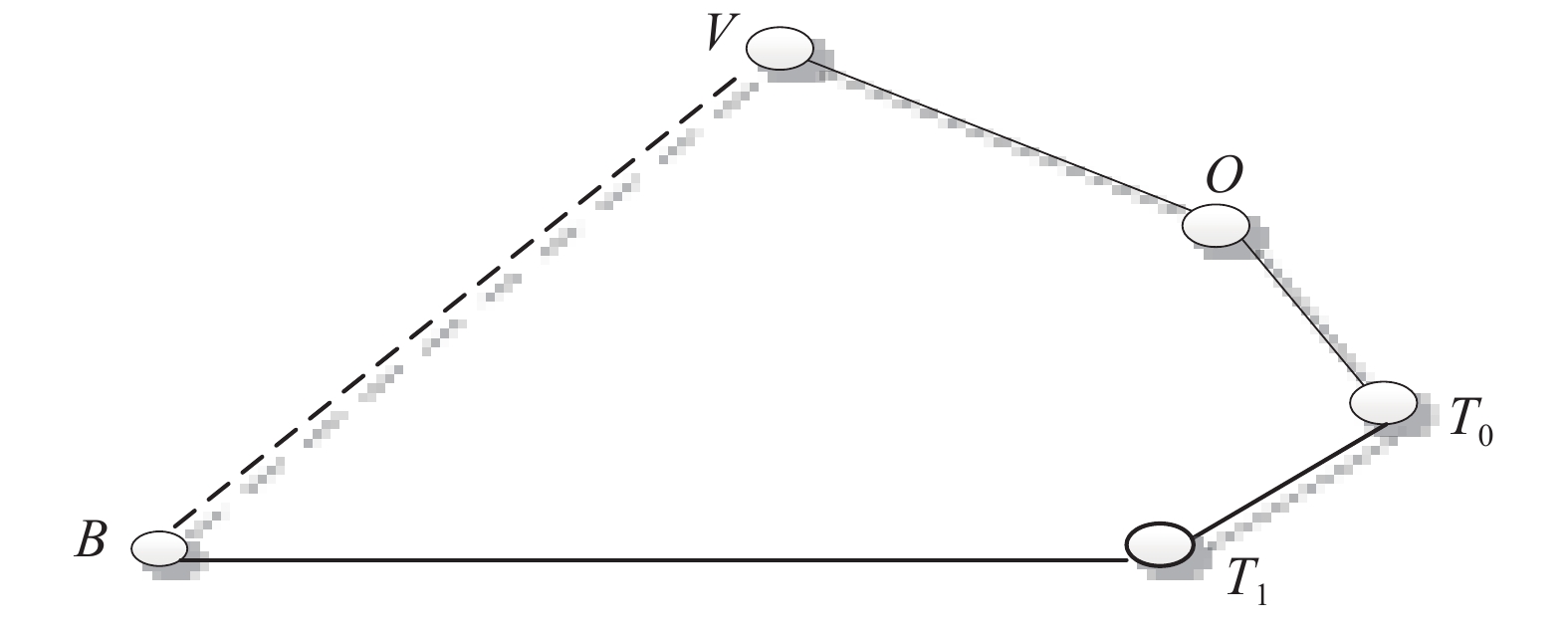
图2中，类似于空间尺寸链计算过程， ${}_V^B{\boldsymbol{T}}$ 为一个封闭的环，其中，B为机械人基坐标系，T₀为末端坐标系，T₁为工具中心点坐标系，V为视觉坐标系，O为目标坐标系，该坐标系可定义为标定板坐标系，用于标定目标点位于视觉坐标系下的点云量化检测结果。待求的基坐标系与视觉坐标系之间虚线路径可以转化为实线B到D的路径，变换关系可表示如下：

$_{\boldsymbol{V}}^{\boldsymbol{B}}{\boldsymbol{T}} = _{{{\boldsymbol{T}}_{\boldsymbol{1}}}}^{\boldsymbol{B}}\!\!{\boldsymbol{T}} \times _{{{\boldsymbol{T}}_{\boldsymbol{0}}}}^{{{\boldsymbol{T}}_{\boldsymbol{1}}}}{\boldsymbol{T}} \times _{\boldsymbol{O}}^{{{\boldsymbol{T}}_{\boldsymbol{0}}}}{\boldsymbol{T}} \times _{\boldsymbol{V}}^{\boldsymbol{O}}{\boldsymbol{T}}$

(8)

式中： ${}_{{T_1}}^B{\boldsymbol{T}}$ 可由机器人内部参数求出； ${}_{{T_0}}^{{T_1}}{\boldsymbol{T}}$ 对同一末端工具坐标系为已知； ${}_V^O{\boldsymbol{T}}$ 为视觉系统标定变换矩阵，通过该变换可得到目标检测点位于视觉坐标系的量化检测值。因此，通过手眼标定，视觉系统扫描测量的目标工件三维姿态可通过 ${}_V^B{\boldsymbol{T}}$ 变换到相对于机械臂基坐标系下的位姿 ${}_O^B{\boldsymbol{T}}$ ：

${}_O^B{\boldsymbol{T}} = {}_C^B{\boldsymbol{T}}{}_O^V{\boldsymbol{T}}$

(9)

由以上推导可知，通过运动学计算，将机械臂的各关节角度输入到机械臂控制器，驱动机械臂完成指定任务。

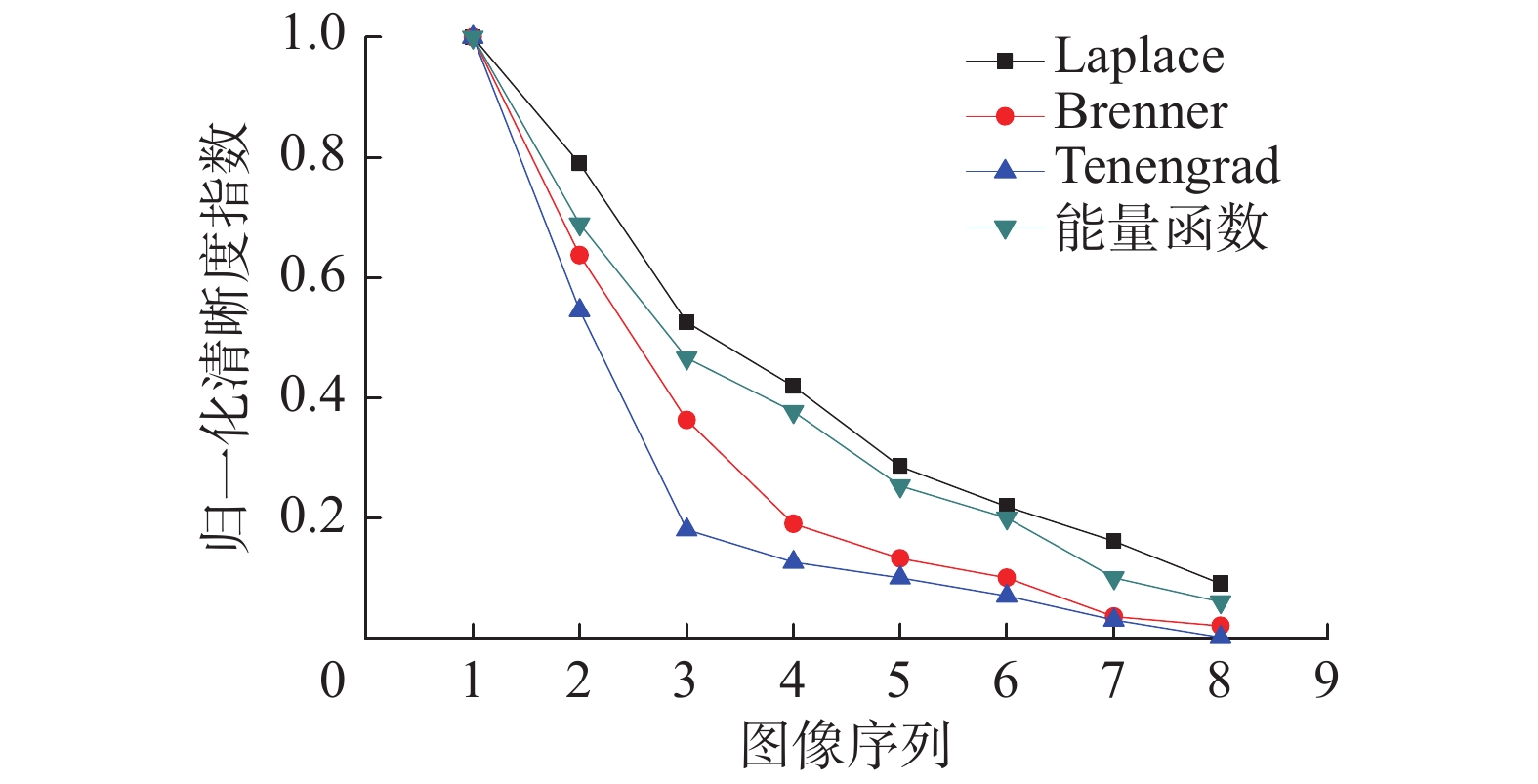
通过机器人视觉引导工作过程可知，视觉系统检测精度是提高机器人加工过程偏差修正可靠性的一个必要条件，本实验系统采用主动成像方法，针对机器人所处光照不均、亮度变化环境下，对不同清晰度评价函数进行了理论分析和实验研究，确定了激光线最佳成像方法。实现CCD在不同光积分时间和聚焦(离焦)状态下有效提取激光线调制信息变化情况，提高扫描系统在复杂变化环境下的鲁棒性。基于此，实验中同时考虑激光线成像清晰度曲线的单峰性和计算实时性因素，综合对比不同图像清晰度评价函数的清晰度指数计算结果，依据图像清晰度变化的灵敏度响应，如图3所示，确定了基于Tenengrad图像梯度的清晰度自适应控制方法。

在实时获取激光线清晰图像的前提下，机器人工作目标点云的精确检测取决于激光线调制信息的精确提取。本文对比研究了目前较为常用的结构光中心线提取算法，包括极值法^[21]、Steger^[22]算法、曲线拟合法^[23]、模板法^[24]以及本文确定的自适应灰度重心法^[25]等。实验中，依据所选激光线特征，首先对激光线条像使用高斯分布动态阈值进行自适应二值化处理，其阈值函数表达式如下：

$T(x) = a{{\rm{e}}^{{{({T_n} - b)}^{2/{c^2}}}}}$

(10)

式中： $ a$ 、 $b$ 、 $c$ 为常数，且 $a > 0$ ， ${T_n}$ 表示激光线光带离散阈值。

根据检测实时性和检测精度需求，文中对于激光线进一步单像素处理采用灰度重心法求出，其重心坐标表达式如下：

$\left\{ \begin{array}{l} {x_o} = \displaystyle\sum\limits_{i = 1}^M {\displaystyle\sum\limits_{j = 1}^N {i \cdot I(i,j)} } /\displaystyle\sum\limits_{i = 1}^M {\displaystyle\sum\limits_{j = 1}^N {I(i,j)} } \\ {y_o} = \displaystyle\sum\limits_{i = 1}^M {\displaystyle\sum\limits_{j = 1}^N {j \cdot I(i,j)} } /\displaystyle\sum\limits_{i = 1}^M {\displaystyle\sum\limits_{j = 1}^N {I(i,j)} } \end{array} \right.$

(11)

式中： $({x_o},{y_o})$ 为条纹中心坐标； $I(i,j)$ 是图像上第 $i$ 行第 $j$ 列的灰度值。

特定环境下，算法的抗噪性能会影响检测精度^[26]，算法设计应根据所选激光线特征以及环境易变情况而定，一般不存在最优或通用性条纹提取算法。图4分别为最佳成像状态下Steger算法、模板法和文中算法激光先中心点提取结果。实际应用中，结构光辅助测量图像中心线提取过程中，光条宽度越小、目标面对比度越高、平顺性越好，算法设计性能会越高。

1.2 基于扫描3D点云的姿态修正方法

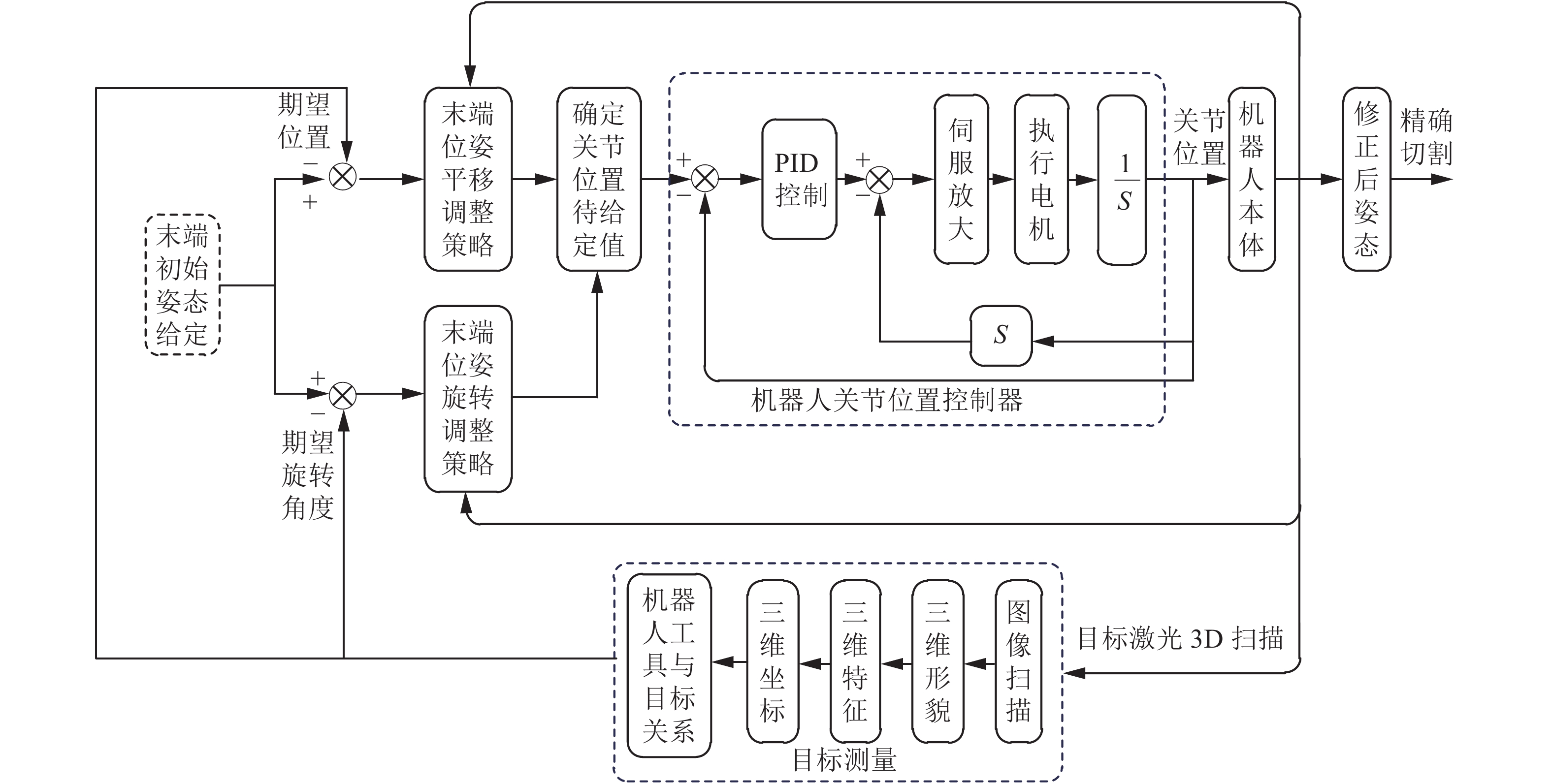
通过双目3D激光扫描成像技术旨在实现被测件的三维形貌和笛卡尔空间姿态的精确检测，输出用于工具中心点位姿的旋转和平移量，并将结果传递给机器人关节控制器修正执行器姿态。该方法便于实现基于图像和位置的机器人混合视觉伺服控制，进一步保证了基于图像和基于位置的伺服控制的优点(本文在该方面不做进一步论述)。图5为文中设计的基于双目激光3D扫描成像机器人加工点修正和控制方法示意图。

该修正方法的优点在于结合了双目激光扫描大视野低遮挡的三维量化检测优势，基于此，在被测目标z方向提取旋转坐标时可采用两个特征值获得，其一是被测目标在z坐标方向的距离值；其二是结合目标投影畸变获得。如图6(a)、(b)所示，当目标定位存在偏差(如一侧高于另一侧)图像将发生投影畸变，此时可根据畸变程度与标准图形反推工件姿态。由于已获得被检测目标三维形貌，因此，被测件与计算机输入的标准件在空间上可以快速进行匹配。另一方面是被加工件在二维平面中姿态的读取，包括二维空间中的平移和旋转量，如图6(c)所示，读取值为实际检测值与标准定位图像在二维平面的平移和旋转偏差。

传统的单目激光三角测量系统，对于复杂三维曲面其测量精度易受激光入射角影响，或在某些区域出现成像遮挡问题，产生视觉盲区。文中采用双目扫描和图像ICP配准方式优化了成像空间，采用激光直射和双目斜射扫描激光调制信息，并根据系统标定参数输出被测目标点云坐标。对于机器人在工件上的连续工作路径，通过选择边界特征点，采用NURBS曲线拟合得到工件边界曲线，拟合方法如下^[27]：

$ P(u) = \frac{{\displaystyle\sum\limits_{i = 0}^n {{N_{i,k}}(u){W_i}{D_i}} }}{{\displaystyle\sum\limits_{i = 0}^n {{N_{i,k}}(u){W_i}} }} $

(12)

式中： ${W_i}$ 为权因子； ${D_i}$ 为控制顶点； ${N_{i,k}}(u)$ 为B样条的基函数( $i = 0,1, \cdots, n$ )，其定义如下所示：

$\begin{aligned}{N_{i,k}}(u) = \frac{{u - {u_i}}}{{{u_{i + k}} - {u_i}}}{N_{i,k - 1}}(u) + \frac{{{u_{i + k + 1}} - u}}{{{u_{i + k + 1}} - {u_{i + 1}}}}{N_{i + 1,k - 1}}(u)\\ {\text{且}}{N_{i,0}}(u) = \left\{ \begin{array}{l} 1,\quad{u_i} \leqslant u \leqslant {u_{i + 1}}\\ 0,\quad{\text{其他}} \end{array} \right. \quad\quad\quad\end{aligned}$

(13)

式中： ${\boldsymbol{U}} = [{u_0}\;{u_1}\;{u_2}\; \cdots \; {u_{n + k + 1}}]$ 为节点矢量； $k$ 为样条基的次数。

通常情况下，采用NURBS曲线拟合，需要控制节点矢量、顶点以及权因子参数，其中，通过控制顶点的位置和数量可以更清晰地调整曲线的形状，为简化计算，假定权因子 ${W_i} = 1$ ，由于B样条的基函数满足 $\displaystyle\sum\limits_{i = 0}^n {{N_{i,k}}(u)}$ =1，故式(12)转化为

$P(u) = \sum\limits_{i = 0}^n {{N_{i,k}}(u)} {D_i}$

(14)

对于每个边界测量离散点 ${P_j}$ ，在进行曲线拟合时曲线上总有点 $P({u_j})$ 与之对应：

${P_j} \approx P({u_j}) = \sum\limits_{i = 0}^n {{N_{i,k}}} (u){D_i}$

(15)

式中： $\left| {P({u_j}) - {p_j}} \right|$ 表示每个离散点与曲线偏差； ${u_j}$ 表示对应参数值。

为使拟合的曲线与离散点的偏差总和最小，偏差总和与控制顶点函数表示为

$P({D_0},{D_1}, \cdots, {D_n}) \!=\! {\sum\limits_{j = 0}^m {\left| {p({u_j}) - {p_j}} \right|} ^2} \!=\! \sum\limits_{j = 0}^m {{{\left| {\sum\limits_{i = 0}^n {{N_{i,k}}({u_j}){D_j} - {p_j}} } \right|}^2}} $

(16)

由式(12)～(15)，可以求解出各个控制顶点的值，故可以确定NURBS拟合的工件边缘路径曲线。采用NURBS进行修正点曲线的拟合，通过调整控制顶点和权值，可以实现复杂曲线的精确拟合。

通过拟合工件加工路径的3D特征点，可精确获取机器人工作路径的3D空间姿态调整信息。根据加工路径曲线拟合数据，完成修正点到机器人坐标系的转化，实现检测点和机器人控制点坐标系的统一。基于此，可通过已知检测点的逆运动学求解，得到加工机器人各个关节旋转角度，并由控制器输出指令完成路径引导。以图1中已定义坐标系为例，机器人的末端坐标系为T₀，工具坐标系为T₁。取边界测量数据中一点作为当前的加工点，其位置矢量为 ${\boldsymbol{P}}$ ，法向矢量为 ${{\boldsymbol{\upsilon}} _n}$ ，切向方向为该点到下一点的连线方向 ${{\boldsymbol{\upsilon}} _{\rm{t}}}$ ，另设一个向量 ${{\boldsymbol{\upsilon}} _{\rm{e}}}$ ，使 ${{\boldsymbol{\upsilon}} _e} = {{\boldsymbol{\upsilon}} _t} \cdot {{\boldsymbol{\upsilon}}_n}$ ，则该加工点的坐标系相对于机器人基坐标系的转换矩阵 ${}_p^B{\boldsymbol{T}}$ 可表示为^[28]

${}_p^B{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{\upsilon}} _t}}&{{{\boldsymbol{\upsilon}} _e}}&{{{\boldsymbol{\upsilon}} _n}}&{\boldsymbol{P}} \\ 0&0&0&1 \end{array}} \right]$

(17)

根据变换式，需要将检测点的数据转换成机器人位姿，转换关系如下：

${}_{{T_0}}^B{{\boldsymbol{T}}_P} \cdot {}_{{T_1}}^{{T_0}}{\boldsymbol{T}} = {}_p^B{\boldsymbol{T}}$

(18)

式中： ${}_{{T_0}}^B{{\boldsymbol{T}}_p}$ 表示切割该点 $p$ 时机器人的位姿矩阵； ${}_{{T_1}}^{{T_0}}{\boldsymbol{T}}$ 表示工具坐标系相对于末端坐标的变换矩阵， ${}_{{T_0}}^{T_1}{\boldsymbol{T}}$ 由工具坐标系标定已知，因此机器人的位姿变化矩阵可表示为

$ {}_{{T_0}}^B{{\boldsymbol{T}}_P} = {}_p^B{\boldsymbol{T}}{}_{{T_1}}^{{T_0}}{{\boldsymbol{T}}^{ - 1}} $

(19)

${\boldsymbol{\varTheta}} = {\Gamma ^{ - 1}}({}_{{T_0}}^B{{\boldsymbol{T}}_P})$

(20)

式中： ${\Gamma ^{{\rm{ - }}1}}$ 表示机器人的逆运动学模型； $\varTheta $ =( ${\theta _1} {\theta _2} \cdots {\theta _6}$ )为机器人各个关节旋转角。

因此，通过遍历各加工路径点，可获得机器人位姿变化矩阵，并通过逆运动学求解各个关节的旋转角度，串联各个边界测量点，完成机器人加工路径引导。

2 实验结果分析

本文通过搭建实验平台，采用越疆Dobot机器人首先对三维混合物料抓取方法进行了实验研究。通过物料的三维形貌测量实现机器人按形状次序(同形状按z值排序)控制夹具坐标系的空间定位。图7(a)、(b)分别为软件实验系统和测试平台，其中，双目CCD采样频率为14帧/s(分辨率：2592×1944)。系统中主要采用双目扫描检测和三维形态坐标提取，与机器人形成闭环控制视觉引导系统，实现物料的识别、抓取和分拣工作。

实验2为注塑件边缘毛刺激光切割路径加工点检测与路径曲线拟合实验，图8为检测目标三维形貌测量与点云坐标重构图像，图8(b)为目标双目扫描与配准过程示意图，系统中考虑到数据处理速度和系统刚性，配准过程中平移和旋转矩阵参数均采用IPC初始化方式进行确定，后续过程仅按确定参数进行配准以完成最终三维图像生产。图8(c)、(d)分别为三维扫描重构图和机器人加工(机器人切割)路径视觉引导三维空间坐标点。通过三维形态特征提取反映工件边界的特征点，NURBS拟合生成切割轨迹并进行视觉坐标系转换到机器人基座坐标系的转换，通过逆运动学求解，得到机器人一系列关节的角度，以此控制激光切割机器人进行末端位姿修正。

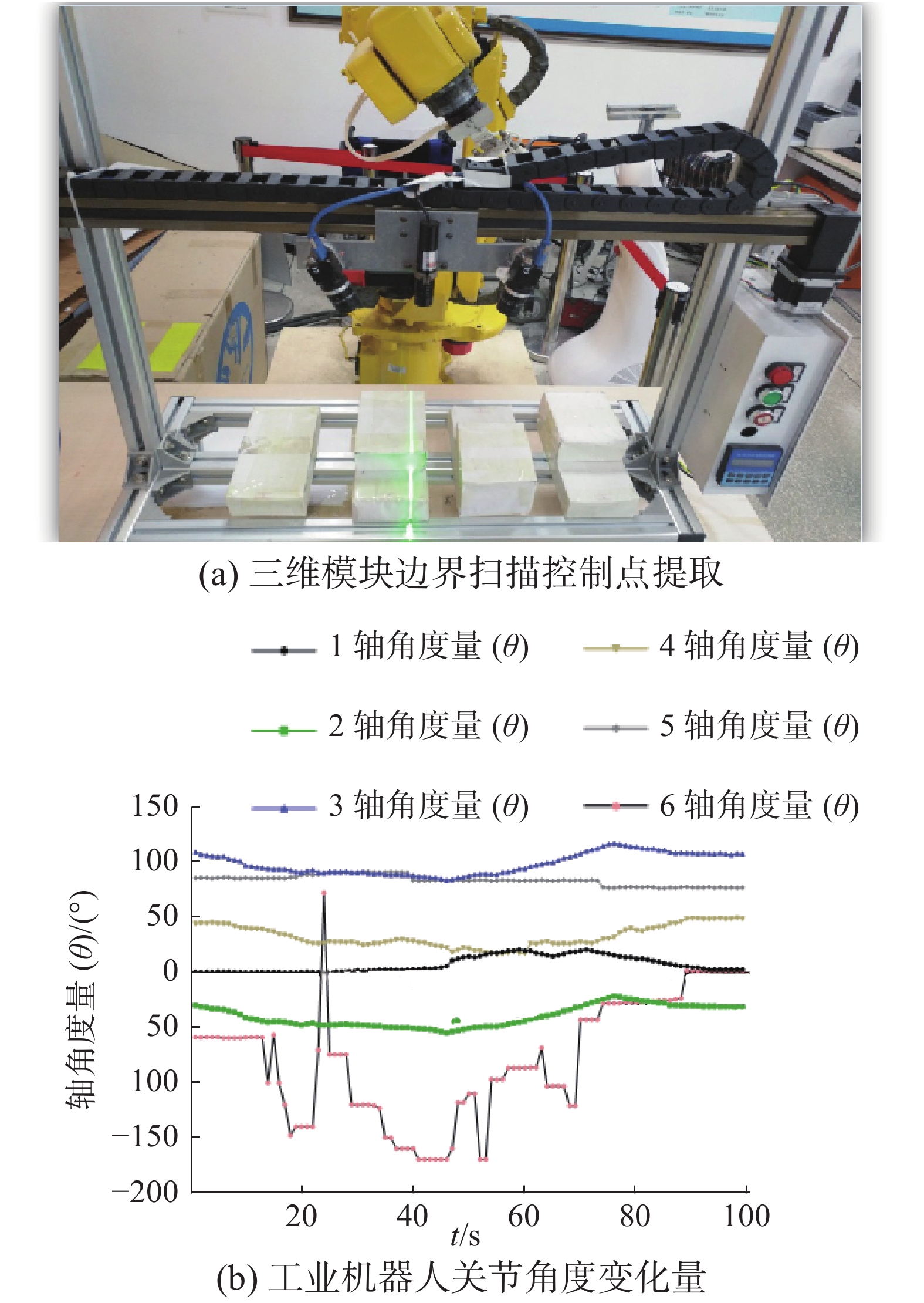
实验3通过FANUC6自由度工业机器人进行了实验测试，基于双目三维扫描方式提取的三维模块边界控制点对机器人工具中心点加工路径进行引导。图9所示为机器人完成切割路径引导后各个关节的角度变化曲线。通过实验研究，证明采用双目三维扫描成像与视觉伺服融合控制的方式，针对特定应用对象，有利于提高工业机器人三维曲面空间的加工柔性。

3 结束语

本文以激光切割机器人视觉引导为研究背景，为克服环境光照干扰、切割工件形状复杂以及检测和控制精度低等问题，基于工业机器人手眼协调控制理论，对机器人眼在外(Eye-to-hand)视觉引导系统的设计和控制方法进行了研究，提出了一种基于双目CCD 激光扫描3D成像的眼在外(Eye-to-hand)TCP切割路径在线修正方法。首先，为提高机器人视觉引导控制点的提取精度，研究了双目3D激光扫描成像目标工件空间点云坐标精确检测方法；其次，融合Eye-to-hand控制特点和三维扫描成像系统结构，构建了一种机器人TCP运动轨迹在线视觉修正方法，并通过实验研究对文中所提方法进行了验证，文中方法同时可应用于机器人混合多形状物料的识别、抓取与分拣工作，提高机器人的工作柔性程度，对工业实际应用奠定了基础。