自然界中，劳动分工现象随处可见。狼群、蚁群、鸟群等生物群体中如捕食、御敌、育幼、筑巢、迁徙等，人类社会中如装备研制、架桥修路、军事战争等，群体通过多个个体之间的分工与协作，即可完成多样化的复杂任务^[1]。

通常而言，群体中不同的个体(通常表现为角色、体型、年龄等方面的差异)一般会专注于相应的某项任务或任务子集，且能根据环境或任务变化动态调整任务分工或执行不同任务的个体规模，从而在任何时刻这些任务都能被并行地执行，形成一种个体任务均衡分配的稳定模式，这种现象即为劳动分工^[2-3]。劳动分工是社会性生物群体在面临复杂环境或繁杂任务时依然能够保持协调有序的重要因素，也是生物群体千百年进化成果和生态稳定的基础。劳动分工行为也是群智能(swarm intelligence, SI)的重要表现形式，具有SI的一般特征，如自组织性、协作性、稳定性、分布式结构、个体和交互规则简单等^[4]。而任务专业化和行为柔性是劳动分工有别于其他群智能方法的显著特点，动态适应性则是其突出优势。任务专业化避免个体频繁地在不同任务之间切换，提高了任务执行效率。行为柔性赋予个体改变原有行为或任务以适应复杂环境变化的能力，从而使种群具备从扰动中恢复稳态的巨大潜力，表现出非常强的动态适应性^[5]。

启发于生物群智能，现实中各种复杂任务系统，如地面群机器人系统、无人机集群系统等，研究热点之一即是如何通过大量简单个体的局部相互作用涌现出复杂的集群行为，并使任务系统可高效完成各种复杂任务^[6]。任务分配(task allocation, TA)是复杂任务系统中的基础问题，指各个体如何高效协作以完成一系列约束下的复杂任务^[7]。目前，典型的有基于市场机制的方法(market-based approaches)和基于优化的方法(optimization-based approaches)^[8]。前者是以协商主义为基础的分布式任务分配方法，如拍卖算法和合同网算法等，适合于确定性环境下中小规模的任务系统的分布式求解，可扩展性和鲁棒性较好，但通信开销和计算代价较大^[9]。后者以一系列群智能启发的最优化算法为代表，如遗传算法(genetic algorithm, GA)^[10]、粒子群算法(particle swarm optimization, PSO)^[11]、蚁群算法(ant colony optimization, ACO)^[12], 狼群算法(wolf pack algorithm, WPA)^[13]等。尽管这些算法某种程度上讲也可求得最优分配方案，但其均基于反复迭代的寻优求解思路，在实时性和动态适应性要求较高的作战应用场景中表现不佳。

生物群体的劳动分工本质即是任务分配，鉴于生物群体与复杂任务系统(诸如地面群机器人系统、无人机集群系统等)在个体的简单性、局部交互规则、自组织分布式结构、群智能能力涌现等方面的相似性^[14]，自然地，可借鉴劳动分工机制研究复杂任务系统的高效任务分配方法。狼是一类认知能力强且组织严密的社会性群居动物，凭借巧妙的劳动分工可以完成复杂的协作捕猎、哺育幼崽、领地维系等一系列群体活动^[15]。这些群体活动中，不同角色的狼个体匹配执行不同的任务，内部或环境变化时也能调整自身角色，表现出高效、灵活、动态适应等特征。模仿狼群智能行为的群智能优化算法不断涌现，如狼群算法(wolf pack algorithm, WPA)^[16], 灰狼优化(grey wolf optimizer，GWO)^[17], 郊狼优化算法(coyote optimization algorithm，COA)^[18]等，无不显示出狼群智能的巨大魅力和应用价值。然而，一方面这些基于狼群智能的优化算法通常存在计算复杂、动态环境适应性不强等问题，应用于复杂系统任务分配时需要设计相应的离散化版本^[19]。另一方面，适合任务分配问题的狼群劳动分工内在机理和形式化模型也尚未见到研究报道。

本文基于对狼群的生物学行为分析，分析了角色−匹配狼群劳动分工的个体角色转换和任务调整机制，研究了狼群角色−任务匹配的柔性劳动分工机制，建立了狼群劳动分工模型，提出了角色−匹配狼群劳动分工方法。最后，通过比较分析，阐述了狼群角色−匹配、蚁群刺激−响应，蜂群激发−抑制3种群智能劳动分工模型的同根同源性和差异性，并展示出角色−匹配的狼群劳动分工的广泛应用前景。

1 狼群生物学行为分析 1.1 生物学背景

狼是一种适应力极强的群居动物，依靠紧密的协作配合实现高效的劳动分工，千百年来一直处于食物链顶端。一般而言，每匹狼都拥有与其自身体型、能力等相匹配的某一角色，这造就了狼群稳定的社会性组织结构。分工明确、信息共享、顺势而动是狼群捕猎的显著特点。分工明确是指头狼负责发起和指挥整个捕猎行动，其他个体根据自身角色执行与之匹配的任务。通常而言，由最为强健而富有智慧的狼作为头狼，头狼拥有繁殖、分配和享用猎物等各项活动的优先权，是整个捕猎行动的组织者和指挥者 ^[14]。探狼是狼群中的少数精锐，感知敏锐而富有耐力，负责根据空气中弥留的气味搜寻猎物。猛狼是狼群中的体力担当，冲击力强，负责快速奔袭绞杀猎物。还有部分巨狼埋伏在猎物逃窜的路线待命增援。如此，狼群中不同角色个体各司其职，形成了完备的猎物打击链条，如图1所示。

狼群具有多样化的群体智能行为，但在协作捕猎中其劳动分工特性表现最为明显，且千百年的进化也造就了其不言而喻的生存优势：1) 狼群中不同角色的狼相互协作即可捕杀单匹狼远不能匹敌的大型猎物；2)大大缩短了捕猎作业时间，提高了捕猎成功概率^[20]。

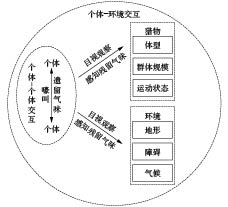
如图2所示，狼群个体的环境学习与认知能力较强，感知与交互方式多样，群体行动中通过有效的“个体−个体”+“个体−环境”交互方式获取和共享信息，为头狼指挥和个体自主决策提供指引。

嚎叫和遗留气味是生物狼群个体−个体交互的主要途径，不同的嚎叫声调和长短可以传达多样化信息；通过主动遗留气味(如狼的粪便、排尿等)宣示领地主权和传达信息给同伴^[21-22]。个体−环境交互主要依靠猎物残留气味和目视观察，通过感知猎物残留的气味可以准确判断猎物状态，个体依靠敏锐的目视观察把握目标的细微特征, 通过对微妙信息的挖掘和关联, 迅速掌握目标整体行为特征^[23]。

狼群具备很强的环境适应性，其领地和群体规模可以根据环境和猎物密度变化而动态调整。在高度变化的复杂捕猎环境中，狼群也能够根据猎物的体型大小和群体规模进行动态重组以形成规模不等的捕猎集群^[24]，具有非常强的动态适应性。

1.2 特性分析

狼群劳动分工主要有以下3个方面的特征：

1) 个体任务的专职化。狼群中的个体一般按照角色分工执行与角色相匹配的任务，简单来讲，就是一般情况下，什么角色干什么事(此种专职化现象在人类社会中也同样普遍存在)。多次执行特定任务的某一角色类型的个体经过学习强化成为该任务的“专家”，下次执行该任务的趋向性越大，且不同角色的个体不会随意转换自身角色而执行其他任务。个体专职化避免了狼群不同角色类型的个体在不同任务间的频繁切换而导致的系统动荡，同时有助于任务经验的积累，降低了个体的学习和适应成本，进而提高了任务的执行效率。

2) 个体角色的可塑性。角色可塑性主要反映狼群在动态复杂环境下的适应能力。在内部变化或环境扰动下，各角色也并不是一成不变的，不同个体的角色也可基于一定条件改变，以适应任务或环境的需求。例如猎物过于强大，承担围攻任务的狼不足以将其捕杀，那么原先承担潜伏或侦察任务的部分个体会自发地迅速转变自身角色为围攻狼，且转换的速度和个体数量随任务紧迫程度而调整。再例如，通常情况下，拥有最佳基因的头狼独享交配权，头狼即“种狼”，如此最大概率地保证了后代的优秀，也控制了狼群的数量；但当灾难来临，例如大面积染病或者气候异常造成狼群锐减，为维持狼群数量，其他狼也拥有交配生育权^[25]。

3) 任务分配的均衡性。一般情况下，通过将复杂任务分解为一系列子任务，狼群中不同角色的个体可以根据自身能力合理承担相应的子任务，各司其职，且狼群每个个体所承担的任务都较为均衡，尤其是面临复杂任务的时候。例如，面对体型巨大的猎物时，狼群不会使用疲劳战术，会以车轮战和接力攻击的方式拖垮猎物，使得参与围攻的狼群个体任务负荷相对均衡，这体现出狼群的群体智慧：一方面可防止能力强的猛狼负载过大而导致加速老化；二是保证能力相对较弱的其他狼也能得到有效的训练和学习，如此，狼群得以能够始终保持其高效的任务执行力和强大的群体竞争力。

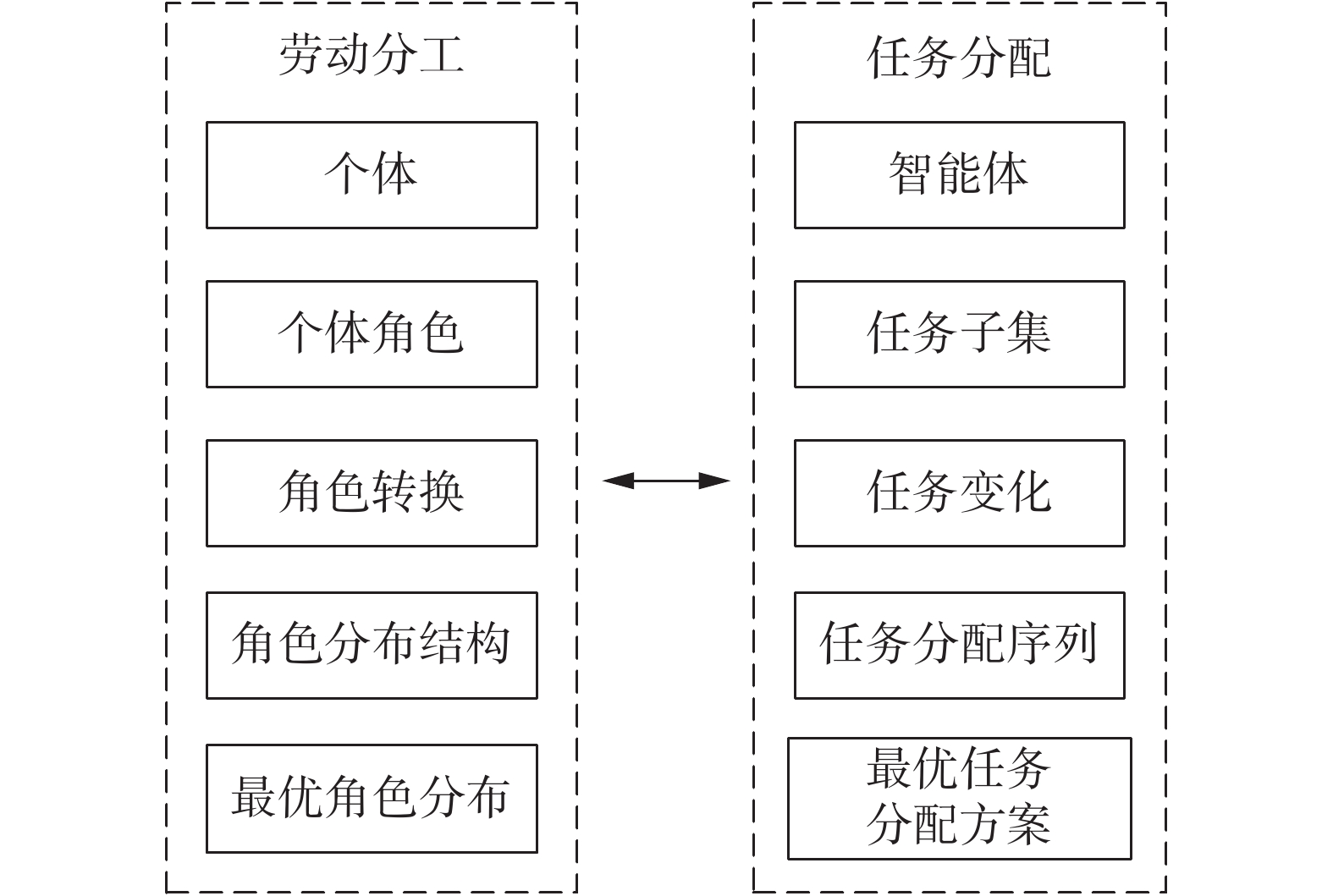
2 角色−匹配狼群劳动分工模型 2.1 基本原理

狼群劳动分工以个体角色区分为基础，即不同角色类型的个体承担与之匹配的任务集，从而在群体中形成一种较为稳定的角色分布结构。当任务需求或群体内部发生变化后，当前狼群的角色分布与环境不相适应时，个体的角色会基于一定条件发生改变，同时更新任务，从而快速响应环境的变化，重新在狼群中形成稳定的角色分布结构。狼个体执行与其角色匹配的任务本质上即是一种任务分配，而响应任务的需求和群体内部的变化进而调整个体角色的过程可视为面向任务的动态重分配，群体的任务分配情况可以通过个体的角色分布情况来描述。将狼个体视为简单智能体，则可建立狼群劳动分工与复杂系统任务分配之间的映射关系，如图3所示。

2.2 角色−匹配狼群劳动分工模型描述

若将每匹狼抽象简化为一个Agent，角色−匹配狼群劳动分工模型中每个Agent的自身角色及其执行任务遵守2条简单调整规则：

1)个体根据与环境和同伴的交互结果决定自身角色的转换；

2)个体根据调整后的角色更新所承担的任务。

2.2.1 角色转换及任务调整机制

群体通过这2个简单规则对个体角色进行调整，直到所有个体将自身角色调整合适，满足变化后的任务需求，形成新的角色分布结构。

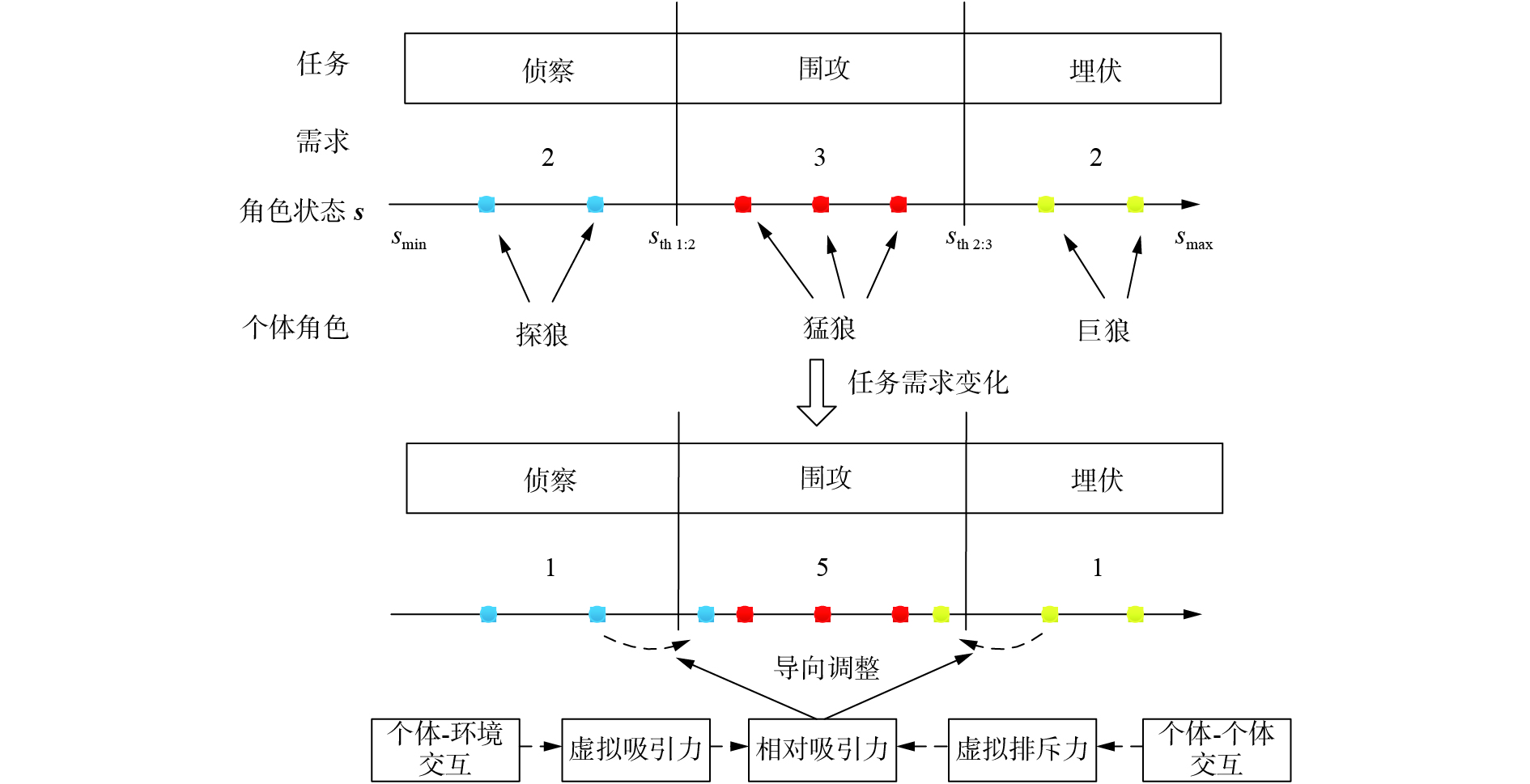
为说明角色−匹配狼群劳动分工的个体角色转换和任务调整机制，图4给出了简化的3类角色个体匹配执行3个任务的示意。狼群在协作捕猎过程中，在头狼的指挥下狼群其他个体可被分成3类角色：探狼、猛狼和巨狼。若定义个体角色状态变量为s，处于区间(s_min，s_th1:2)的个体定义为探狼，处于区间(s_th1:2，s_th2:3)的个体定义为猛狼，处于区间(s_th2:3，s_max)的个体定义为巨狼。其中，s_th1:2和s_th2:3分别为各角色之间的转换阈值。探狼、猛狼和巨狼分别执行与之匹配的侦察、围攻和潜伏任务。基于前期经验，执行侦察、围攻和潜伏任务的个体需求数分别为2、3和2，即执行侦察任务需要分配2匹探狼，执行围攻任务分配3匹探狼，执行潜伏任务分配2匹探狼。

任务需求发生变化后(如猎物过于强大，猛狼子群不能将其捕获)，若当前群体角色分布和个体规模比例不能满足任务需求。通过对猎物的认知判断，侦察、围攻和潜伏任务的需求分别变化为1、5和1，那么原先处于探狼和巨狼角色的部分个体需要快速调整自身角色转变为猛狼，协助执行围攻任务，从而满足任务需求变化将猎物顺利捕杀。具体表现为处于探狼角色类型的个体角色状态变量s逐渐增大，而处于巨狼角色类型的个体角色状态变量s逐渐减小，且角色转换步长随任务紧迫程度而调整，最终当个体的角色状态变量s变换至区间(s_th1:2，s_th2:3)内转变为猛狼角色。

2.2.2 一般模型

假设共有m个任务需要执行，首先对任务进行排序，任取其中任务序号由小到大排列的3个任务task_k-1、task_k和task_k+1 (k=1,2,…,m)，当前匹配执行这3个任务的个体角色分别定义为wolf_k−1、wolf_k和wolf_k+1，如同上述分析中的探狼、猛狼和巨狼。wolf_k−1类型的个体j，wolf_k类型的个体i，wolf_k+1类型的个体p的角色状态分别为 ${s_j}$ ， ${s_i}$ ， ${s_p}$ ，其中 j=1,2,…,n₁，i=1,2,…,n₂，p=1,2,…,n₃。 $s_{}^{lb}$ 和 $s_{_{}}^{lu}$ 分别为3种类型的个体角色状态的上下限阈值。n₁、n₂和n₃分别为3类角色的个体数。

1) 角色转换

以wolf_k类个体i的角色转换为例，其角色状态 ${s_i}$ 调整有3种情况：减小、增大或维持原态。每一种情况由个体i与其他个体和环境(任务)交互的结果所决定。为量化交互结果，分别设计2个变量：虚拟吸引力 $f_{{a_{}}}^{}$ 和虚拟排斥力 ${f_r}$ 。虚拟吸引力 $f_{{a_{}}}^{}$ 是个体i与环境(任务)交互而产生的，表征任务对个体i的吸引程度， $f_{{a_{}}}^{}$ 与任务优先级、任务价值和相对需求等因素有关。任务优先级、任务价值或相对需求越大， $f_{{a_{}}}^{}$ 越大，一如猎物数量多，狼群又好久没有进食了，则此批猎物对狼群的吸引力自然就越大。虚拟排斥力 ${f_r}$ 是个体j与同伴交互而产生的，表征个体j对任务的排斥程度，与任务代价、当前执行该任务的个体数或任务执行情况等因素有关。任务代价和执行该任务的个体数越大， ${f_r}$ 越大，一如某区域内猎物非常具有攻击性，捕获往往需要付出较大代价，而狼群又刚好完成了一次捕猎，并不饥饿，且该区域内狼数量较多，则狼群就会存在一定程度的排斥捕猎行为。令 $f_{{a_i}}^{k'}/f_{{r_i}}^{k'}$ 为任务task_k′(k′=k−1, k, k+1)对个体i的相对吸引力，则个体i受到的最大相对吸引力为

$\tilde f_i^{k*} = \arg {\rm{ max(}}f_{{a_i}}^{k'}/f_{{r_i}}^{k'})$

(1)

式中：k^*为所有任务中对个体i具有最大相对吸引力的任务序号。

个体i在时刻t通过其与环境(任务)和同伴的综合交互结果(即相对吸引力 $f_{{a_i}}^{}/f_{{r_i}}^{}$ )来决定其下一时刻的角色转换方向和步长：

${s_i}(t + 1) = \left\{ \begin{array}{l} {s_i}(t){\rm{ + }}{\delta _i}(t),\;{\rm{ }}\;\tilde f_i^{k^*} > {l_u}{\rm{ ，}}{k^*} > k \\ {s_i}(t){\rm{ - }}{\delta _i}(t),\;{\rm{ }}\;\tilde f_i^{k^*} > {l_u}{\rm{ ，}}{k^*} < k \\ {s_i}(t) + \mu ,\quad{\text{其他}}{\rm{}} \\ \end{array} \right.$

(2)

式中： ${\delta _i}(t){\rm{ = }}\lambda \exp \tanh ({\rm{ }}\tilde f_{_i}^{k^*})$ 为导向因子，可理解为个体i调整 ${s_i}$ 时的移动步长； $\lambda $ 为一常量调节系数； ${l_u}$ 为一固定阈值； $\mu = {\delta _i}(t) {\rm{rand}}( - 1,1)$ 为随机因子； $k$ 为个体i当前执行的任务序号。

从式(1)可以看出，当任务task_k*对个体i的相对吸引力 $\tilde f_i^{k^*}$ 超过阈值 ${l_u}$ ，且其任务序号k^*>k时， ${s_i}$ 通过移动步长 ${\delta _i}(t)$ 正向增大。当任务task_k^*对个体j的相对吸引力 $\tilde f_i^{k^*}$ 超过阈值 ${l_u}$ ，且其任务序号k^*<k时， ${s_i}$ 通过移动步长 ${\delta _i}(t)$ 反向减小。任务越紧急即 $\tilde f_i^{k^*}$ 越大，移动步长 ${\delta _i}(t)$ 越大，导向性作用越明显，个体i的角色转变速度越快。其他情况下， ${s_i}$ 通过随机因子 $\mu $ 进行随机转移，防止死锁。

2) 任务调整

个体i根据调整后的角色状态变量 ${s_i}$ 决定执行与其角色−匹配的任务：

${\rm{new}}\_{\rm{task}} = \left\{ \begin{array}{l} {\rm{tas}}{{\rm{k}}_{k + 1}},\;{\rm{ }}\;s_{_{k + 1}}^{lu}{\rm{ > }}{s_i} > s_{_{k + 1}}^{lb} \\ {\rm{tas}}{{\rm{k}}_{k - 1}},\;{\rm{ }}\;s_{_{k - 1}}^{lu}{\rm{ > }}{s_i} > s_{_{k - 1}}^{lb} \\ {\rm{tas}}{{\rm{k}}_k},\quad{\text{其他}}{\rm{}} \\ \end{array} \right.$

(3)

从式(3)可以看出，当 ${s_i}$ 移动至区间 $\left( {s_{_{k{\rm{ + }}1}}^{lb},s_{_{k{\rm{ + }}1}}^{lu}} \right)$ 内，个体i转变为wolf_k+1角色类型的个体，从而选择执行与wolf_k+1角色−匹配的任务task_k+1。同理，当 ${s_i}$ 处于区间 $\left( {s_{_{k{\rm{ - }}1}}^{lb},s_{_{k{\rm{ - }}1}}^{lu}} \right)$ 内，个体i选择执行与wolf_k-1角色−匹配的任务task_k-1。否则，个体j继续执行task_k。

个体角色状态s的调整受导向因子 $\delta $ 和随机因子 $\mu $ 共同影响。导向因子结果反映了个体−个体和个体−环境交互的综合作用，给个体角色转换提供导向信息，保证个体向着任务需求大的方向转换。随机因子的作用是通过引入随机控制，避免某一时刻大量个体转换角色状态导致的大幅震荡现象。

3 模型扩展

角色−匹配的狼群劳动分工一般模型具有良好的普适性，适用于对动态适应性要求较高的复杂任务系统。一般而言，应用于如群机器人任务分配等实际问题时，仅需要进行扩展和改造。下面以 ${N_r}$ 个Robot协同执行 ${N_M}$ 个任务为例进行说明。

3.1 主要变量设计

1) $f_{{a_i}}^j(t)$ ：t时刻任务j对Robot i的吸引力， $j = 1,2, \cdots ,{N_M}$ 为任务编号， ${N_M}$ 为任务数量。

$f_{{a_i}}^j(t) = \frac{{{V_T}^j(t)}}{{{\omega _1}\overline {{d_i}^j(t)} + {\omega _2}\overline {{T_i}^j(t)} }}$

(4)

式中： ${V_T}^j(t)$ 为任务j在时刻t的价值； $\overline {{d_i}^j(t)} $ 和 $\overline {{T_i}^j(t)} $ 分别为无量纲处理后的Robot i与任务j的距离和 Robot i到达任务j的时间。

由式(4)可以看出，任务j价值越大，Robot i与任务j的距离及其到达任务j的时间越小，任务j对Robot i的吸引力越大，即Robot i选择任务j的趋势越大。反之亦然。

2) $f_{{r_i}}^j(t)$ ：t时刻Robot i对执行任务j的排斥力， $i = 1,2, \cdots ,{N_r}$ 为Robot编号， ${N_r}$ 为Robot数量。

$f_{{r_i}}^j(t) = \frac{{{n_{{\rm{act}}}}^j(t)}}{{C_i^j (1 - \partial _{}^j(t))}}$

(5)

式中： $n_{{\rm{act}}}^j(t)$ 为t时刻参与执行任务j的Robot数量； $C_i^j$ 为Robot i执行任务j的能力。

3) $\partial _{}^j(t)$ ：t时刻任务j的完成度。

$\partial _{}^j(t){\rm{ = }}\frac{{R{'}_T^j(t{\rm{ + }}1)}}{{R_T^j}}$

(6)

式中： $R_T^j$ 为任务j在初始时刻所需资源数； $R{'}_T^j(t{\rm{ + }}1)$ 为任务j在时刻t后仍需资源数， $R{'}_T^j(t{\rm{ + }}1){\rm{ = }}R{'}_T^j(t){\rm{ - }}\displaystyle\sum\limits_{i = 1}^{n_{{\rm{act}}}^j} {({\eta _i}} T)$ 。

4) ${\eta _i}$ ：Robot i单位时间的资源消耗量，T为时刻t+1~t的时间，则 $\displaystyle\sum\limits_{i = 1}^{n_{{\rm{act}}}^j} {({\eta _i}} T)$ 表示在时刻t+1~t所有参与执行任务j的Robot的总资源消耗量。

由式(4)、(5)可知，参与执行任务j的Robot数量越多，Robot i的能力越小及任务完成度越大，任务j对Robot i的排斥力越大，即Robot i选择任务j的趋势越小。反之亦然。

5) ${s_i}^j(t)$ ：t时刻参与执行任务j的Robot i的角色状态变量值。

3.2 基本流程

1) 根据任务数量 ${N_M}$ 将 ${N_r}$ 个体角色变量区间(s_min，s_max)分为 ${N_M}$ 个等距子区间，分别对应 ${N_M}$ 个任务。初始化 ${N_r}$ 个Robot的个体角色变量 ${s_i}^{}(0)$ 。

2) 判断 ${s_i}^{}(0)$ 所处子区间，Robot i预设匹配执行对应的任务，形成任务预分配方案；

3) 依据式(4)、(5)分别计算 $f_{{a_i}}^j(t)$ 和 $f_{{r_i}}^j(t)$ ，依据式(1)确定对于Robot i具有最大相对吸引力 $\tilde f_{_i}^j = \arg {\rm{ max(}}f_{{a_i}}^j/f_{{r_i}}^j)$ 的任务j；

4) Robot i依式(2)进行决策，决策 ${s_i}^j(t)$ 的调整方向和移动步长；

5) Robot i根据调整后的 ${s_i}^j(t)$ 判断自身角色状态，依式(3)更新与之匹配的任务j；

6)评价效能函数。如满足任务需求，则转6)；否则转3)；

7)输出任务分配方案。

4 群智能劳动分工模型机理比较分析

启发于生物群体生存智慧的群智能劳动分工方法已经引起了广泛关注，其中以基于蚁群劳动分工机制的刺激−响应模型(stimulus response model, SRM)^[26]和基于蜂群劳动分工机制的激发−抑制模型(activation inhibition model, AIM)^[27]为代表。

刺激−响应模型可解释蚁群形态行为多型的劳动分工机制，表示个体所执行的任务与其体型大小相关，如小型工蚁主要负责护理、觅食等工作，而大型工蚁主要负责防御、储存食物等^[28]；而激发−抑制模型可解释蜂群时间行为多型的劳动分工机制，表示个体所执行的任务与其生理年龄有关，如蜜蜂能据蜂群的需求，延迟、加速甚至逆转其行为发育^[29]。角色匹配模型中个体的角色与任务对应，属角色行为多型，即个体所执行的任务与其角色有关，如狼群中不同角色的狼(头狼、探狼、猛狼等)一般执行与之匹配的指挥、侦察、围攻等不同任务。

实际中影响个体行为调整和群体任务组织的因素很多，为便于工程应用，劳动分工模型均以简单的交互规则和简化机制来实现个体行为和群体任务的自组织分配。蚁群刺激−响应模型以个体−环境交互规则为基础，由个体感知到的任务需求刺激和个体响应刺激的内部阈值来共同决定个体是否执行任务。蜂群激发−抑制模型以个体−个体交互规则为基础，个体内生长激素(激发剂)和同伴对其传递的保幼激素(抑制剂)来调节其发育情况，进而直接影响其执行任务的类型。单一的交互规则尽管简单，却很难反应群体真实的行为组织影响因素，因此，实际应用中需根据问题设计相关因子来弥补单一交互规则的不足。

角色−匹配狼群劳动分工模型与前述2种模型既同根同源(均属于群智能劳动分工方法体系)，又有其自身特点。表1通过比较分析，列出了狼群角色−匹配模型、蚁群刺激−响应模型和蜂群激发−抑制模型3种群智能劳动分工模型的对比情况。

由表1可以看出，群智能劳动分工模型都是基于对不同生物群体劳动分工机制的深入分析而建立的，一定程度上能模拟实现生物群体通过个体的局部感知和交互反应作用进而涌现整体的自组织行为。群体任务分配的优化与协调基于个体对环境的动态反应来实现。其中的交互机制是决定其动态反应和决策的基础，角色−匹配狼群劳动分工模型同源于自然群体的生物学行为分析，以自然狼群中真实存在的“个体−环境”+“个体−个体”交互规则为基础，以虚拟吸引力和虚拟排斥力分别量化评价2种交互方式，由虚拟力的相对作用来实现个体角色转换和任务调整。其“个体−个体”+“个体−环境”的交互方式既能使个体行为快速适应环境或任务变化，又能保证对群体内部扰动的动态响应。

目前，蜂群刺激−响应模型和蚁群激发−抑制模型均已被成功应用于任务分配、空间分配、区域覆盖、时间分配等领域^[30-33]。相关应用也表明，相对于其他方法，这些模型具有计算简单、无需迭代、动态适应性强等诸多优势，对动态环境下的复杂系统分配问题的即时响应求解具有新的启发意义。

5 结束语

令人惊叹的生物群智能给予了人类很多启示。蚁群优化算法、粒子群优化算法、蜂群优化算法等即是启发于生物群智能，基于迭代寻优、关联求解思路的群智能优化方法在求解静态优化和有限动态优化问题时取得了较好的效果。但对于非结构、大规模、不可预测的动态优化、动态调度和分配问题却越来越显出颓势。以蚁群的刺激−响应和蜂群的激发−抑制为代表的群智能劳动分工方法，基于自然生物群体的劳动分工行为，强调基于局部的交互式作用(元机制：刺激−响应、激发−抑制、角色−匹配)，具有良好的动态适应性，显示出广阔的应用前景。

本文基于对狼群生物学行为的深入剖析，研究狼群如何依靠多样化的智能行为，得以在严酷的环境中成功生存和进化。分析得出其多样化的群体智能行为的完成，归因于高效的劳动分工、信息感知与交互、环境学习与认知、主动响应变化的能力。同时，本文阐述了蚁群刺激−响应，蜂群激发−抑制，狼群角色−匹配3种群智能劳动分工模型的同根同源性和差异性，所研究的角色−匹配狼群劳动分工模型具有角色行为多型特点，该项研究提供了一种柔性化的自底向上(bottom-up)的普适性群智能方法，为复杂系统任务分配问题研究提供了一种新思路。

今后的研究主要从机理分析和应用扩展2个方面着手：1) 角色−匹配的狼群劳动分工模型还处于初步探索阶段，其中涉及的多Agent交互机理、协作分配机制、问题适用性、求解复杂度等方面还有待深入研究；2) 将重点关注任务分配现实问题的应用，潜在应用领域包括军事领域的群机器人协同搜索、目标跟踪、围捕、搜救和察打任务分配，工业生产领域的机器任务调度，物流领域的车辆任务调配等。