聚类分析在图像处理、机器学习、Web搜索等众多领域得到了广泛应用，是机器学习领域一个比较活跃且极具挑战的研究方向。其主要思想是通过计算样本间的相似度把数据集划分成若干个簇，使得“同一个簇内的样本相似度较高，不同簇间的样本相似度较低^[1]”。在实际的聚类分析任务中，由于数据类型和结构分布的复杂性与多样性，单一聚类方法的适用范围、可靠性和稳定性都受到了制约，为此，研究人员结合集成学习技术提出了聚类集成的方法^[2-4]。聚类集成的目的是将数据集的多重基聚类集成为统一的、综合的最终聚类结果^[5]，其过程主要包括两个阶段，首先使用不同的聚类算法或重复同一种聚类算法生成多个基聚类；其次设计有效的一致性函数对基聚类进行集成，获得最终聚类集成结果^[6]。

一致性函数通常用来将基聚类的划分结果进行集成，得到一个统一的聚类结果。现有的一致性函数大体包括以下几种。1)投票法：其基本思想是首先根据得到的基聚类对样本划分结果进行投票，然后计算每个样本被划分到各个簇中的投票比例，若样本归属于某个簇的投票比例超过一定阈值(一般大于等于0.5)，则将样本划分到该簇中^[7-8]。2)证据积累：其基本思想是同一个自然簇中的“样本对”在不同的基聚类中可能属于同一个簇。具体划分过程为：把每个基聚类看作是一个独立的证据，计算“样本对”被分到同一个簇中的次数，从而得到共协矩阵，然后使用基于最小生成树(mininum spaning tree, MST)的层次聚类算法得到最终的聚类结果^[9-10]。3)概率积累^[11]：其基本思想是使用簇密度来计算基聚类中所有“样本对”间的距离，生成p-association矩阵，依据最高寿命标准采用MST合并p-association矩阵得到最终的聚类结果^[12]。4)超图划分：其基本思想是先将聚类集成问题转化为超图的最小切割问题，在此基础上使用基于图论的聚类算法得到最终的聚类结果^[9，13]。其中用超图表示基聚类，超边表示簇，超边的顶点表示归属于该簇的样本，Strehl等^[9]提出HGPA、CSPA和MCLA三种基于超图的划分方法。

1 相关工作 1.1 图神经网络

Scarselli等^[14]于2009年将神经网络和图嵌入模型结合提出了图神经网络(graph neural network，GNN)，该模型对图的信息结构进行编码，将每个节点用一个低维状态向量表示，从而学习图的表征，能以半监督的方式处理各种类型的图，比如无环图、有向图、无向图等。近年来图神经网络已成为一种应用广泛的图分析方法，主要包括^[15]：图递归神经网络(graph recurrent neural networks, Graph RNNs)、图卷积网络(graph confolutional networks, GCN)、图自动编码器(graph autoencoders, GAE)和图强化学习(graph reinforcement learning, Graph RL)。其中图卷积网络为半监督方法，利用节点属性和节点标签训练模型参数，图自动编码器为无监督方法，利用自动编码器的降维技术学习图的低维表征^[16]。

1.2 图自动编码器

图自动编码器(graph autoencoders，GAE)在稀疏自编码器 (sparse autoencoder，SAE)^[17]的启发下被提出，该模型将邻接矩阵或其变体作为节点的原始特征，将自动编码器(autoencoder，AE)作为降维方法来学习低维节点表征。简单来说，图自动编码器的基本思想是：首先输入图的邻接矩阵和节点的特征矩阵；然后通过编码器学习节点低维向量表示的均值和方差；最后利用解码器重构图。因此图自动编码器能很好地处理没有监督信息的图，同时学习图的低维表征。

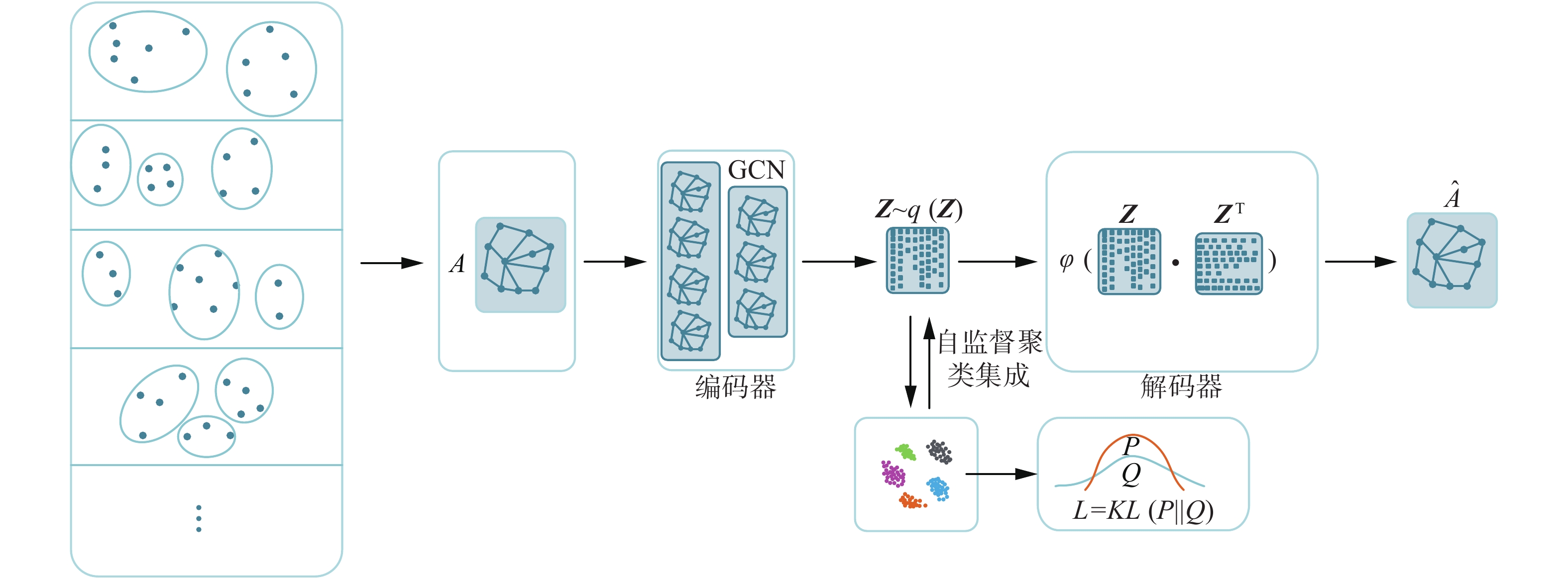
2 图神经网络自监督聚类集成算法

本文提出了一种深度自监督聚类集成算法，该算法首先根据基聚类划分计算样本之间的相似度矩阵以表达样本之间的邻接关系，将基聚类在特征空间的表示转化为图数据表示；然后利用图自动编码器学习图的低维嵌入，由低维嵌入的似然分布监督聚类集成过程，同时通过聚类集成目标指导低维嵌入的学习过程，形成一个聚类集成的自监督优化模型，从而优化聚类集成结果，该算法如图1所示。

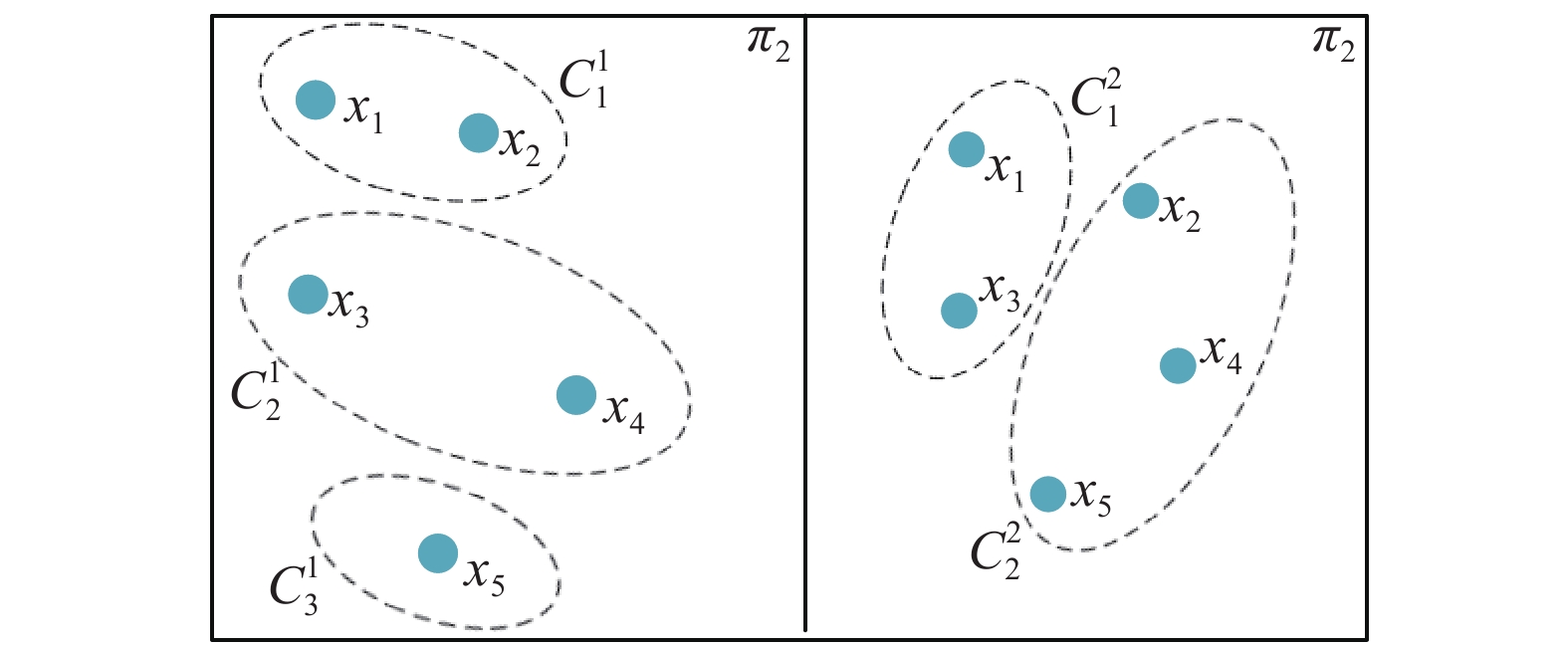
2.1 基聚类的图数据表示

本文基于已有的基聚类划分计算样本之间的相似性，将相似度矩阵作为邻接矩阵把样本数据的拓扑空间表示转化为图数据表示。以下为利用基聚类计算样本相似度矩阵的过程示例，图2给出了5个样本 $({x_1},{x_2}, \cdots ,{x_5})$ 构成的数据集以及在其上生成的基聚类集合 ${\rm{II}} {\rm{ = \{ }}{\pi _{\rm{1}}},\pi {}_2{\rm{\} }}$ ，其中 $ {\pi }_{1}= $ $ \left\{{C}_{1}^{1}{\text{，}}{C}_{2}^{1}{\text{，}}{C}_{3}^{1}\right\}$ ， $ {\pi }_{2}=\left\{{C}_{1}^{2}{\text{，}}{C}_{2}^{2}\right\}$ 。

首先计算相交簇之间的相似度，称为样本之间的一阶全局相似度：

${w_{ij}} = \frac{{\left| {{x_{{C_i}}} \cap {x_{{C_j}}}} \right|}}{{\left| {{x_{{C_i}}} \cup {x_{{C_j}}}} \right|}}$

(1)

式中：C_i、C_j表示不同基聚类中的任意两个簇；w_ij表示簇C_i和簇C_j之间的相似度； ${x_{{C_i}}}$ 表示簇C_i中的任意样本； ${x_{{C_j}}}$ 表示簇C_j中的任意样本。

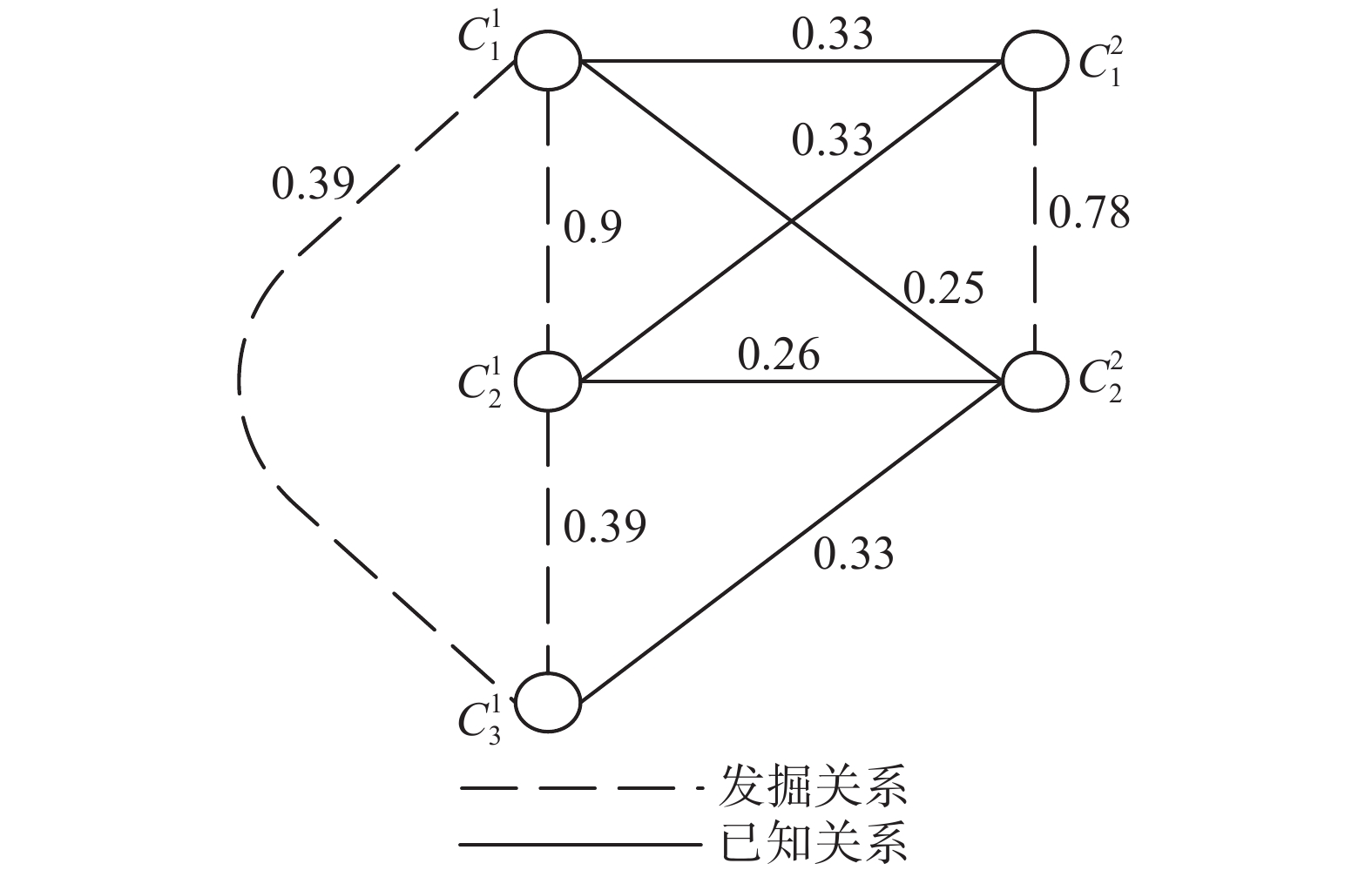
图3为利用基聚类集合Π生成的样本一阶全局相似性关系图，该图中存在两个不相交的簇能同时与第3个簇相连，从而构成三元组。图4表示簇 $C_1^1$ 、 $C_3^1$ 和 $C_2^2$ 之间的三元组。

式(1)只能计算存在交集的簇间的相似度，忽略了不相交的簇间的相似性关系。为此，加权连通三元组(weighted connected-triple，WCT)算法^[18]通过利用三元连通关系来计算不相交簇之间的相似度，即样本间的二阶全局相似度。WCT对簇C_i、C_j、C_k组成的三元组中C_i、C_j的之间的相似度估算值为

${\rm{WCT}}_{ij}^k = \min \left( {{w_{ik}},{w_{jk}}} \right)$

(2)

式中：w_ik为簇C_i和簇C_k之间的相似性；w_jk为簇C_j和簇C_k之间的相似性。WCT算法根据簇C_i、C_j之间存在的所有三元组 $\left( {1,2, \cdots ,q} \right)$ 对C_i、C_j之间相似度的估算值为

$ {\rm{WC}}{{\rm{T}}_{ij}} = \sum\limits_{k = 1}^q {{\rm{WCT}}_{ij}^k} $

(3)

簇C_i、C_j的相似度，即样本的二阶全局相似度计算为

${\rm{sim}}^{\rm{WCT}}\left( {{C_i},{C_j}} \right) = \frac{{{\rm{WC}}{{\rm{T}}_{ij}}}}{{{\rm{WC}}{{\rm{T}}_{\max }}}} \times {\rm{DC}}$

(4)

式(4)中WCT_max是任意两个簇C_p、C_q之间WCT_pq的最大值， ${\rm{DC}} \in \left( {0,1} \right]$ 表示置信度。图5是由图3生成的样本间的二阶全局相似性关系图。

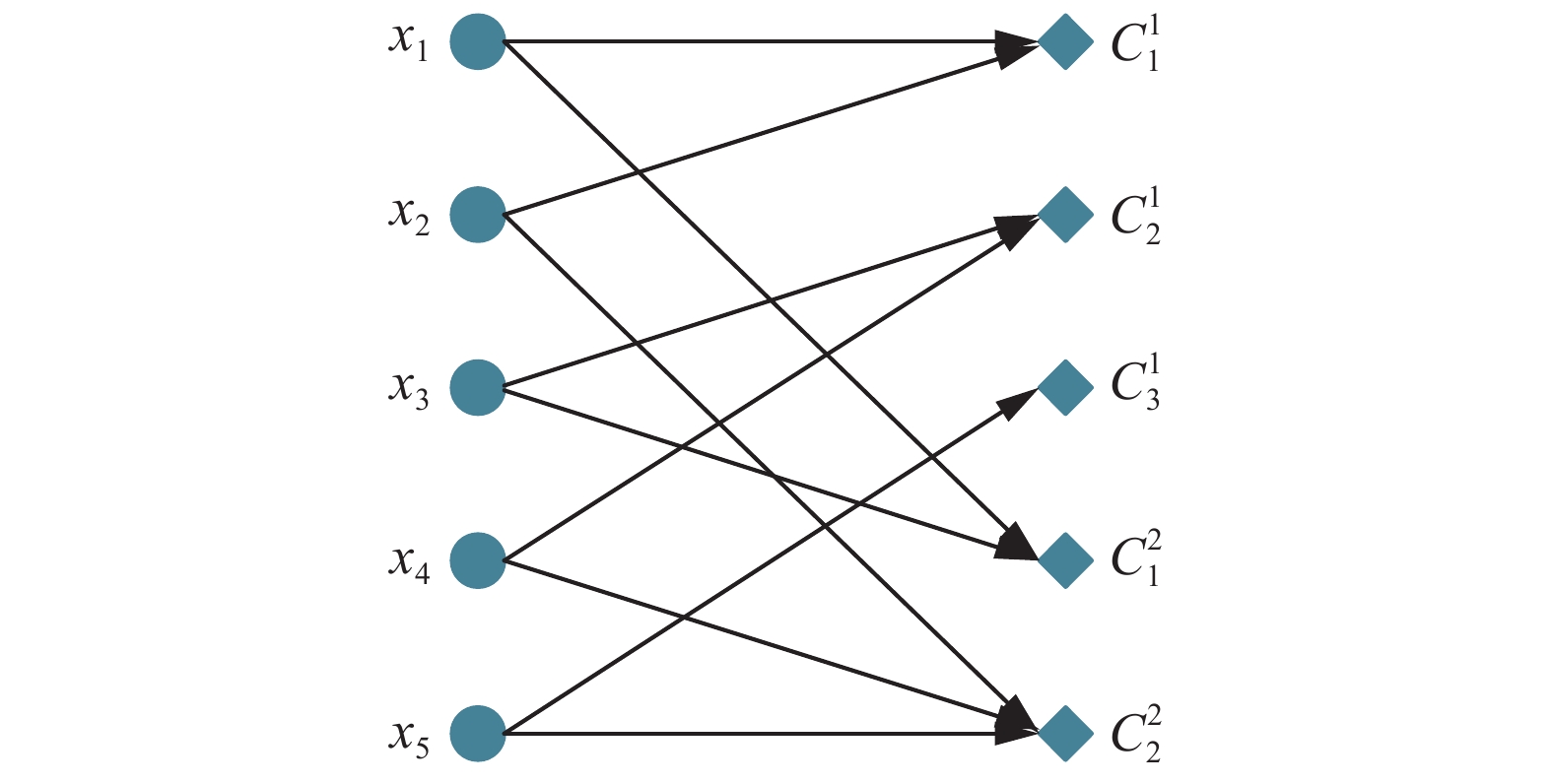
计算得到样本之间的二阶全局相似度之后，依据基聚类划分结果获得样本与簇之间的二分图关系，图6为样本 $\left( {{x_1}, {x_2}, \cdots ,{x_5}} \right)$ 与簇 $C_1^1$ 、 $C_2^1$ 、 $C_3^1$ 、 $C_1^2$ 、 $C_2^2$ 之间的二分图关系，图中数据点与簇相连表示该数据点在基聚类中被划分到该簇中。

利用式(5)计算样本之间的相似度：

$ {\rm{sim}}\left({x}_{i},{x}_{j}\right)=\left\{ \begin{array}{l}1\;\;\;{\text{，}}\;\;{x}_{i}={x}_{j}\\ \dfrac{\rm{DC}}{\left|{\Re }_{{x}_{i}}\right|\left|{\Re }_{{x}_{j}}\right|}{ \displaystyle\sum\limits _{{R}_{{x}_{i}}\in {\Re }_{{x}_{{}_{i}}}}{ \displaystyle\sum\limits _{{R}_{{x}_{j}}\in {\Re }_{{x}_{j}}}{\rm{sim}}\left({R}_{{x}_{i}},{R}_{{x}_{j}}\right){\text{，}}\rm{ }{\text{其他}}}}\end{array} \right.$

(5)

式中：DC∈(0, 1]表示置信度； ${R_{{x_i}}}$ 、 ${R_{{x_j}}}$ 分别表示包含样本x_i、x_j的簇； ${\Re _{{x_i}}}$ 、 ${\Re _{{x_j}}}$ 分别表示包含样本x_i、x_j的簇的集合。

综上，得到样本之间的相似度矩阵表示样本邻接关系，从而将基聚类特征空间表示转化至图数据表示为G=(V, E)，其中V={v_i}是图的节点的集合，E={e_ij}表示两个节点之间的边。

2.2 自监督聚类集成算法

利用图自动编码器与自监督聚类集成模型^[19]对基聚类的图数据表示G进行图聚类，即利用图自动编码器学习G的低维嵌入并由似然分布监督聚类集成，同时利用聚类集成目标指导低维嵌入学习过程，得到最终聚类集成结果。

本文采用的自监督聚类集成算法同时优化图自动编码器和聚类集成过程，得到总体目标函数：

$L = {L_r} + \gamma {L_c}$

(6)

式中：L_r、L_c分别为图自编码器的重构损失和聚类过程中的聚类损失，超参数γ>0。

在自监督聚类集成过程中，首先训练图自动编码器得到低维嵌入 $Z = \left( {{z_1},{z_2}, \cdots ,{z_m}} \right)$ ，图自动编码器由图卷积网络(graph convolutional network，GCN)编码器和简单的内积解码器组成^[20]，编码器定义为

$Z = {{A'}}{\bf{ReLU}}\left( {{{A'X}}{W_0}} \right){W_1}$

(7)

式中：ReLU(·)=max(0,·)和 ${{A'}} = {{{D}}^{{\rm{ - 1/2}}}}{{A}}{{{D}}^{{\rm{ - 1/2}}}}$ 是对称归一化的邻接矩阵，D为度矩阵，X输入为单位矩阵。

解码器定义为

${\hat { A}} = {\rm{sigmoid}}\left( {{{Z}}{{{Z}}^{\rm T}}} \right)$

(8)

由此得到以下重构损失：

${L_r} = \dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {\left\| {{{{\hat { A}}}_{{{ij}}}} - {{{A}}_{{{ij}}}}} \right\|_2^2} $

(9)

式中：n为样本的数量；A为图G的邻接矩阵； $\hat {{A}}$ 为图G的重构邻接矩阵。

然后，在Z上执行k-means聚类获得初始类别中心 $\mu =\left({\mu }_{1},\;{\mu }_{2},\;\cdots ,\;{\mu }_{n}\right)$ ，使用学生t分布测量第i个样本的嵌入点z_i与第u个簇的类别中心μ_u之间相似性^[21]：

${q_{iu}} = \frac{{{{(1 + \left\| {{z_i} - } \right.{\mu _u}\left\| {^2} \right.)}^{ - 1}}}}{{\displaystyle\sum\limits_i {{{\left( {1 + {{\left\| {{z_i} - {\mu _k}} \right\|}^2}} \right)}^{ - 1}}} }}$

(10)

式中：q_iu表示样本i被分配到簇u的概率，Q=[q_iu]表示似然分布。样本i与簇u之间的相似性定义为

${p_{iu}} = \frac{{q_{iu}^2/\displaystyle\sum\limits_i {{q_{iu}}} }}{{\displaystyle\sum\limits_k {\left(q_{ik}^2/\displaystyle\sum\limits_i {{q_{ik}}} \right)} }}$

(11)

式中P=[p_iu]表示目标分布。聚类集成的目标函数定义为

${L_c} = KL\left( {P||Q} \right) = \sum\limits_i {\sum\limits_u {{p_{iu}}\log \frac{{{p_{iu}}}}{{{q_{iu}}}}} } $

(12)

通过最小化分布Q和分布P之间的KL散度使嵌入点更接近类别中心。在这一过程中，由分布Q计算得到分布P，而分布P监督分布Q的更新。

2.3 模型优化

在训练过程中，基于L_c关于u和z的梯度，使用随机梯度下降(stochastic gradient descent，SGD)对簇中心μ和低维嵌入Z进行同步更新^[22]，如式(13)所示。目标分布P在训练过程中监督分布Q的更新，同时依赖于每次迭代时更新的分布Q。由于目标不断变化会阻碍学习和收敛，在每次迭代中用Q更新P会导致自训练过程的不稳定性，因此本文设置了一个迭代间隔T，每T次迭代更新一次P，以避免上述可能出现的不稳定性。

$\begin{array}{l} \dfrac{{\partial L}}{{\partial {z_i}}} = \dfrac{{\alpha + 1}}{\alpha }\displaystyle\sum\limits_u {{{\left( {1 + \dfrac{{{{\left\| {{z_i} + {\mu _u}} \right\|}^2}}}{\alpha }} \right)}^{ - 1}}} \times \left( {{p_{iu}} - {q_{iu}}} \right)\left( {{z_i} - {\mu _u}} \right) \\ \dfrac{{\partial L}}{{\partial {\mu _u}}} = - \dfrac{{\alpha + 1}}{\alpha }{\displaystyle\sum\limits_i {\left( {1{\rm{ + }}\dfrac{{{{\left\| {{z_i} - {\mu _u}} \right\|}^2}}}{\alpha }} \right)} ^{ - 1}} \times \left( {{p_{iu}} - {q_{iu}}} \right)\left( {{z_i} - {\mu _u}} \right) \\ \end{array}$

(13)

综上所述，本文算法流程如算法1所示。

算法1　自监督聚类算法

输入　基聚类 $ \Pi =\left\{{\pi }_{1}，{\pi }_{2}，\cdots ，{\pi }_{n}\right\}$ ，类别数k，迭代次数Iter，目标分布P更新间隔T，超参数γ；

输出　最后聚类集成结果。

1)使用式(1)~(5)计算相似度矩阵A；

2)最小化式(9)得到自动编码器的低维嵌入Z，基于Z计算初始类别中心μ；

3) for l=0 to Iter－1 do

使用式(10)基于Z和μ计算分布Q；

if l% T==0 then

使用式(11)基于分布Q计算分布P；

end if

使用式(12)计算聚类集成损失函数L_c；

最小化式(6)更新整个算法

end if

4)迭代完成后得到聚类集成结果。

3 实验结果与分析 3.1 数据集

为验证算法的有效性，本文选用UCI数据库中的5个真实数据集进行测试，表1给出了实验中选用的UCI数据集描述。

在仿真实验中选取HGPA^[9]、CSPA^[9]、MCLA^[9]、基于投票的聚类集成算法^[13]和谱聚类集成算法^[23]与本文方法进行对比，HGPA、CSPA、MCLA算法属于基于超图的聚类集成算法，其原理是根据基聚类构造超图，对超图进行分割；基于投票的聚类集成算法根据基聚类的划分进行投票，得到样本的集成结果；谱聚类集成算法利用基聚类得到样本的图数据表示，对图进行分割。

3.2 评价指标

本文使用准确率(accuracy，ACC)、调整兰德系数(adjusted rand index，ARI)以及标准互信息(normalized mutual information，NMI)3个指标对各算法的聚类集成结果进行评价与分析。准确率对样本的真实标签和生成标签的匹配程度进行度量：

${\rm{ACC}} = \frac{{\displaystyle\sum\limits_{i = 1}^n {\delta \left( {{s_i},{\rm{map}}\left( {{r_i}} \right)} \right)} }}{n}$

(14)

式中：r_i、s_i分别表示数据x_i聚类得到的标签和真实标签；n表示数据总个数；map表示最佳类标的重现分配；δ表示指示函数，表示为

$\delta \left( {x,y} \right) = \left\{ {\begin{array}{*{20}{c}} {1,} \\ {0,} \end{array}} \right.{\rm{ }}\begin{array}{*{20}{c}} \!\!\!\!{{\rm{ }}x = y} \\ \text{其他} \end{array}$

(15)

调整兰德系数度量真实标签和聚类标签相似性，定义如下：

${\rm{ARI}} = \dfrac{{\displaystyle\sum\limits_{i = 1}^I {\displaystyle\sum\limits_{j = 1}^J {\left( {\begin{array}{*{20}{c}} {{n_{ij}}} \\ 2 \end{array}} \right) - \eta } } }}{{\dfrac{1}{2}\left( {\rho + \vartheta } \right) - \eta }}$

(16)

式中： $\rho = \displaystyle\sum\limits_{i = 1}^I {\left( {\begin{array}{*{20}{c}} {{n_i}} \\ 2 \end{array}} \right)} $ 、 $\vartheta =\displaystyle\sum\limits_{j = 1}^J {\left( {\begin{array}{*{20}{c}} {{n_j}} \\ 2 \end{array}} \right)} $ 、 $\eta = \dfrac{{2\rho \vartheta }}{{n\left( {n - 1} \right)}}$ 。标准互信息用来度量真实样本簇划分与聚类结果之间的相近程度：

${\rm{NMI}} = \dfrac{{\displaystyle\sum\limits_{i = 1}^I {\displaystyle\sum\limits_{j = 1}^J {{n_{ij}}{\rm{lb}}\dfrac{{n{n_{ij}}}}{{{n_i}{n_j}}}} } }}{{\sqrt {\displaystyle\sum\limits_{i = 1}^I {{n_i}{\rm{lb}}\dfrac{{{n_i}}}{n}\displaystyle\sum\limits_{j = 1}^J {{n_j}{\rm{lb}}\dfrac{{{n_j}}}{n}} } } }}$

(17)

式中：n_ij表示聚类结果的第i个簇中包含原数据集类标签为j的样本总数；n_i表示聚类结果的第i个簇的样本总数；n_j表示原数据集类标签为j的样本总数；n表示样本总数；I和J分别表示聚类得到的簇个数和原数据集的类个数。

ACC、ARI、NMI的取值范围为[0,1]，且取值越接近1，表明算法在数据集中获得的聚类效果越好。

3.3 实验结果与分析

对本文算法进行如下设置：将置信度DC的值设置为0.9，收敛阈值tol设置为0.1%，目标分布P的“更新间隔设置T ”设置为5。为了确定超参数γ的取值，在实验中将γ分别设置为2、4、6、8、10，在不同γ下获得的ARI、NMI和ACC值如图7所示。

由图7可以看出，当超参数γ<8时，本文算法在5个数据集上的ARI、NMI和ACC取值随着γ值的增加整体上呈上升趋势。当超参数γ=8时，取值达到峰值，聚类效果最佳。而当γ的取值继续增加到10时，取值没有呈现明显的增长趋势。这是因为在自监督聚类集成过程中，通过最小化目标损失函数L达到优化图自动编码器与聚类集成模块的目的，通过L的定义可知，如果γ的值过小，会使聚类损失对低维嵌入学习过程影响过大从而导致空间扭曲；而当γ取值过大时，会影响低维嵌入空间对聚类损失的优化，从而导致聚类集成结果变差。分别使用本文算法与5种对比算法在5个数据集上进行聚类划分，各方法聚类集成结果的ARI、NMI和ACC值如表2~4所示。

表2~4中加粗的数字分别表示不同算法在每个数据集上取得的最优值。由这些实验结果可以看出，本文算法在各数据集上获得的ARI、NMI和ACC值整体优于其他5种算法。其中，本文算法在5个数据集上的ARI和NMI取值相较于其他算法均有明显提升，仅在Segment数据集的ACC取值稍逊于Spectral算法。这是由于本文算法生成的基聚类的图数据表示完整反映了样本的全局相似关系，使用了处理属性缺失的图数据更具有优势的图神经网络，并且自监督模型使图自动编码器中的信息传递和数据映射服从最终聚类集成目标，从而使产生的低维嵌入有利于获得最优的聚类集成结果。而HGPA、CSPA、MCLA方法采用的图分割算法趋向于将图形划分为大小相似的簇，对于真实分布大小不一的簇聚类结果较差；投票法只依赖基聚类的划分结果，没有充分挖掘样本之间的相似性关系；谱聚类集成算法的聚类集成结果很大程度上受到相似度矩阵计算结果的影响。

4 结束语

本文针对聚类集成的一致性函数设计问题，提出了一种基于图神经网络的聚类集成算法，主要工作包括：

1)根据基聚类划分结果计算样本之间的相似性，完整地反映了样本之间的一阶与二阶相似性，在此基础上，用相似度矩阵表示样本之间的邻接关系，将基聚类在拓扑空间中的表示转化为图数据表示，通过图聚类获得聚类集成的最优解；

2)利用图神经网络模型构造自监督聚类集成算法，图自动编码器在聚类集成结果中很好地保留了样本在空间中的结构，并且自监督优化模型使图自动编码器中的低维学习服从聚类集成的目标，从而得到最优的聚类集成结果；

3)在数据集上进行了仿真实验，结果表明本文算法提升了聚类集成结果的准确性。

然而，本文算法的空间复杂度较大，在未来的工作中，考虑如何降低算法的空间复杂度并且将算法应用于实际问题。