概念格理论^[1]是在形式背景中进行数据分析的一个重要工具，由Wille教授在1982年提出，从本质上描述了对象集和属性集的内在联系。

目前，概念格理论已在信息检索^[2-4]、数据挖掘^[5-7]、机器学习^[8-10]等领域取得了广泛应用。吴伟志等^[11]将粒计算与概念格理论进行结合，研究了保持概念格的粒结构不变的属性约简。米据生等分别从变精度^[12]和公理化^[13]角度考虑概念格约简问题。针对大型数据集，陈锦坤等^[14-15]将图论理论与概念格理论进行结合，提出了一种快速属性约简方法。邵明文等^[16]从形式概念分析理论角度提出一种从信息表中提取决策规则的方法。李金海等^[17-18]针对决策形式背景提出了一种新的知识认知和约简框架，并给出约简算法，进一步提出了保持由全体对象集构造的决策规则不变的情况下的属性约简方法^[19]。三支形式概念分析^[20]的提出丰富了概念格理论，魏玲和任睿思进一步研究了三支概念格的属性约简^[21]与决策规则提取^[22]。李俊余等^[23]研究了基于同余关系的不协调决策形式背景的属性约简。

如何简化概念格结构，从而便于提取用户所需信息是该领域的一个重要问题。上述研究中，往往默认形式背景中所有属性重要度是相同的，然而在实际问题中，可能仅需针对特定属性进行数据挖掘，即不同属性的重要性是不同的。张继福等^[24]通过对概念格的内涵引入权值，提出一种加权概念格，拓广了概念格的结构。张素兰等^[25]在此基础上提出了一种基于信息熵和偏差分析的加权概念格的内涵权重获取方法。但上述两种加权概念格并没有考虑到对象权重的问题。

概念格需储存由形式背景获取的全部概念及属性间的偏序关系，使概念格构造过程变得异常困难。同时随着大数据时代的到来，需要分析的数据越来越多，如果想要将其中所有概念提取出来，并根据概念间的偏序关系构成概念格，难度进一步加大。因此，如何删除无用的属性和对象，降低构造概念格的难度，使提取的规则更加简洁就成为我们应该考虑的重要问题。本文通过信息熵给出单个属性权重后，进一步给出对象权重和重要度偏差的定义，利用3个阈值对冗余数据进行删除，缩小了概念格的规模，提高了构造概念格的时间效率，并且能够让决策规则的提取过程更为简洁高效。

1 预备知识

首先简单介绍形式背景中的相关知识。

定义1　设 $F = (U,A,I)$ 为形式背景，其中 $U = $ $ \{ {x_1},{x_2}, \cdots ,{x_n}\} $ ， $A = \{ {a_1},{a_2}, \cdots ,{a_m}\} $ ， $I \subseteq U \times A$ 。如果 $(x,a) \in I$ ，则称 $x$ 具有属性 $a$ 。用 $P(U)$ 表示 $U$ 的幂集， $P(A)$ 表示 $A$ 的幂集。 $\forall X \in P(U)$ ， $B \in P(A)$ ，定义：

$f(X) = \{ a \in A:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall x \in X,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (x,a) \in I\} $

$g(B) = \{ x \in U:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall a \in B,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (x,a) \in I\}。$

定义2　设 $F = (U,A,I)$ 为形式背景，对于 ${U'} \subseteq U$ ， ${A'} \subseteq A$ ，可以得到形式背景 ${F'} = ({U'},{A'},{I'})$ ，称为 $F$ 的子背景，其中 ${I'} = I \cap ({U'} \times {C'})$ 。

定义 3　设 $F = (U,A,I)$ 为形式背景，若二元组 $(X,B) \in P(U) \times P(A)$ 能够满足 $f(X) = B$ 且 $g(B) = X$ ，则 $(X,B)$ 称为形式概念或概念。其中， $X$ 称为外延， $B$ 称为内涵。由形式背景 $(U,A,I)$ 构造的概念格记为 $L(U,A,I)$ 。

定义4　设 $({X_{\rm{1}}},{B_{\rm{1}}})$ ， $({X_{\rm{2}}},{B_{\rm{2}}})$ $ \in L(U,A,I)$ ，如果 ${X_{\rm{1}}} \subseteq {X_{\rm{2}}}$ 或者 ${U_2} \subseteq {U_1}$ 则称 $({X_{\rm{1}}},{B_{\rm{1}}})$ 是 $({X_{\rm{2}}},{B_{\rm{2}}})$ 的子概念， $({X_{\rm{2}}},{B_{\rm{2}}})$ 是 $({X_{\rm{1}}},{B_{\rm{1}}})$ 的父概念，记为

$({X_{\rm{1}}},{B_{\rm{1}}}) \leqslant ({X_2},{B_2})$

另外，两个概念的上下确界定义分别为

$({X_{\rm{1}}},{B_{\rm{1}}}) \vee ({X_{\rm{2}}},{B_{\rm{2}}}){\kern 1pt} = (g{\kern 1pt} f({X_{\rm{1}}} \cup {X_{\rm{2}}}{\rm{), }}{B_{\rm{1}}} \cap {B_{\rm{2}}})$

$({X_{\rm{1}}},{B_{\rm{1}}}) \wedge ({X_{\rm{2}}},{B_{\rm{2}}}){\kern 1pt} = ({X_{\rm{1}}} \cap {X_{\rm{2}}}{\rm{, }}fg({B_{\rm{1}}} \cup {B_{\rm{2}}}))$

定义5　设 $F = (U,A,I)$ 为形式背景，其中 $U = $ $ \{ {x_1},{x_2}, \cdots ,{x_n}\} $ ， ${x_i} \in U$ ， $a \in A$ ，则 $P(a/{x_i})$ 表示对象 $x$ 提供给属性 $a$ 的平均信息量，即属性 $a$ 的信息量为

$H(a) = - \sum\limits_{i = 1}^{{n}} {P(a/{x_i})} {\log _2}P(a/{x_i})$

信息熵值越大，表示对象集 $U$ 具有该属性的不确定性越大，也即该属性的信息量越大，信息熵从平均意义上表示了属性的总体特性。

2 对象加权概念格 2.1 对象权重及对象重要度偏差

定义6　设 $F = (U,A,I)$ 为形式背景，且 $U = $ $ \{ {x_1},{x_2}, \cdots ,{x_n}\} $ ， $A = \{ {a_1},{a_2}, \cdots ,{a_m}\} $ ，每个属性 ${a_i}$ 的权重均已知，记为 $w({a_i})$ 。

$\forall x \in U$ ， $f(x) = \{ {a_{{s_1}}},{a_{{s_2}}}, \cdots ,{a_{{s_t}}}\} {\kern 1pt} {\kern 1pt} {\kern 1pt} $ ，对象 $x$ 的权重定义为

$d(x) = \frac{{\displaystyle\sum\limits_{j = 1}^t {w{\kern 1pt} {\kern 1pt} {\kern 1pt} ({a_{{s_j}}})} }}{t}$

通过定义6获取的对象权重能够反映该对象的总体信息量，但是却忽略了该结果可能存在偏差，不利于获得具有一定偏差的信息。

定义7　对象 $x$ 的重要度偏差定义为

$D(x) = \sqrt {\frac{1}{{t - 1}}\sum\limits_{j = 1}^t {{{(w{\kern 1pt} {\kern 1pt} ({a_{{s_j}}}) - d(x))}^2}} } $

由重要度偏差定义，特规定当 $t = 1$ 时，有 $D(x) = 0$ 。

通过定义对象权重和对象重要度偏差能够更全面地考虑形式背景中隐含的知识。

2.2 对象加权概念格及其构造

在无专家给定属性权重时，需通过信息熵公式求出属性对应的信息量，再进行归一化处理获得每个属性的权重。按照对象对于属性是否感兴趣，给出属性权重阈值为 $\alpha $ ( $0 \leqslant \alpha \leqslant 1$ )，对于形式背景 $F = (U,A,I)$ 上的任意属性 $a \in A$ ，如果 $w(a) < \alpha $ ，则称该属性冗余。给定对象权重阈值为 $\beta $ ( $0 \leqslant \;\beta \leqslant 1$ )，对于形式背景 $(U,A,I)$ 上的任意对象 $x \in U$ ，如果 $d(x) < \beta $ ，则称该对象冗余。删除冗余概念及对象获取的子形式背景记为 ${F_d} = ({U_d},{A_d},{I_d})$ ，其构造的概念格称为对象加权概念格。

设对象重要度偏差阈值为 $\delta $ ( $0 \leqslant \delta \leqslant 1$ )，对于形式背景 $(U,A,I)$ 上的任意对象 $x \in U$ ，如果 $D(x) > $ $ \delta $ ，则称 $x$ 为偏差对象。不包含冗余属性、冗余对象、偏差对象的子形式背景，记为 ${F_D} = $ $ ({U_D},{A_D},{I_D})$ 。由此构造的概念格称为对象强加权概念格。

通过删除不满足给定的属性权重阈值 $\alpha $ 的属性和不满足对象权重阈值 $\beta $ 或对象重要度偏差阈值 $\delta $ 的对象能够节省形式背景存储空间，从而获得简化的概念格，提升概念格构造效率，并且获取的概念形式更为简单，有利于规则提取。

算法1　对象强加权概念格的构造算法

输入　 $F = (U,A,I)$ ， $\alpha $ ， $\beta $ ， $\delta $ (其中 $0 \leqslant \alpha \leqslant 1$ ， $0 \leqslant \beta \leqslant 1$ ， $0 \leqslant \delta \leqslant 1$ )；

输出　对象强加权概念格。

1) for $1 \leqslant i \leqslant \left| A \right|$ do

2) $w({a_i}) = \dfrac{{H({a_i})}}{{\displaystyle\sum\limits_{i = 1}^{\left| A \right|} H{\kern 1pt} {\kern 1pt} {\kern 1pt} ({a_i}) }}$

3) end for

4) initialize $d'({x_j}) = 0$

5) for $1 \leqslant i \leqslant \left| A \right|$ ， $1 \leqslant j \leqslant \left| U \right|$ do

6) if $({x_j},{a_i}) \in I$ then

7) $d'({x_j}) \leftarrow w({a_i})$

8) end if

9) compute $d({x_j}) = \dfrac{{d'({x_j})}}{{\left| {f({x_j})} \right|}}$

10) $D({x_j}) = \sqrt {\dfrac{1}{{\left| {f({x_j})} \right| - 1}}\displaystyle\sum {{{(w{\kern 1pt} {\kern 1pt} ({a_i}) - d({x_j}))}^2}} }$

11) end for

12) if $w({a_i}) < \alpha $ ， $d({x_j}) < \beta $ or $D({x_j}) > \delta $ then

13) delete ${x_j}$ ， ${a_i}$

14) end if

15) ${F_D} = (U/{x_j},A/{a_i},I')$

16) return $L({F_D})$

2.3 基于对象强加权概念格的决策规则提取

通过2.2节中给出的对象强加权概念格的构造过程，能够帮助我们获取更为简单的概念格。如在决策形式背景中，利用该方法对于条件概念格进行简化，则能够大大降低概念提取的难度。

定义8　设 $(U,A,I,D,J)$ 为决策形式背景，由 ${R_D} = \{ (x,y) \in U \times U: {d_l}(x) = {d_l}(y){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (\forall {d_l} \in D)\} $ ，可产生 $U$ 上的一个划分：

$U/{R_D} = \{ {[x]_D}:\!\!\!\!\!{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x \in U\} {\rm{ = \{ }}{D_1}{\rm{,}}{D_2}, \cdots ,{D_r}{\rm{\} }}$

其中： ${[x]_D}{\rm{ = \{ }}y \in U: (x,y) \in {R_D}\}$ ； $\forall {d_l} \in D$ 。如 $x$ ， $y \in {D_k}$ ，必有 ${d_l}(x) = {d_l}(y)$ ，显然属于同一决策类的对象具有相同的决策值，记 ${T_k} = \{ {d_1}({D_k}),{d_2}({D_k}), \cdots ,{d_{|D|}}({D_k})\} $ 为 ${D_k}$ 的决策值。 $({D_k},{T_k})$ 称为决策概念。

设 $(U,A,I,D,J)$ 为决策形式背景，则由形式背景 $F = (U,A,I)$ 能够获得子形式背景 ${F_D} = ({U_D},{A_D}, $ $ {I_D})$ ，进一步可构造对象强加权概念格，记为 $L({U_D},{A_D},{I_D})$ 。称 $ (X,B)\in L({U}_{D},{A}_{D},{I}_{D})$ 为条件概念。

$X{\text{、}}B $ 均为非空集合，如果有 $\dfrac{{\left| {X \cap {D_k}} \right|}}{{\left| X \right|}} = 1$ ，则称 $\left( {X,B} \right) \Rightarrow ({D_k},{T_k})$ 为决策形式背景的粒决策规则。简记为 $B \Rightarrow {T_k}$ 。

下面给出具体算法。

算法2　粒决策规则获取算法

输入　 $(U,A,I,D,J)$

输出　粒决策规则

1) compute $L({F_D})$

2) $\forall x,y \in U$

3) for $1 \leqslant k \leqslant \left| D \right|$ do

4) if ${d_k}(x) = {d_k}(y)$ then

5) $(x,y) \in {R_D}$

6) end if

7) $U/{R_D} = \{ {[x]_D}: x \in U\} {\rm{ = \{ }}{D_1}{\rm{,}}{D_2}, \cdots ,{D_r}{\rm{\} }}$

8) end for

9) compute $({D_t},{T_t})$

10) for all $(X,B) \in L({F_D})$ ， $1 \leqslant t \leqslant r$ do

11) if $\dfrac{{\left| {X \cap {D_t}} \right|}}{{\left| X \right|}}{\rm{ = 1}}$ then

12) $\left( {X,B} \right) \Rightarrow ({D_t},{T_t})$

13) end if

3 实验和分析 3.1 应用举例

由表1给出人才市场大学生就业信息，处理后构成形式背景 $F = (U,A,I)$ ，其中对象集为6位求职者。属性集为 $A = \{ a,b,c,d,e{\rm{\} }}$ ，分别代表5个属性，即应届生、数学专业、教师资格证、英语四级、计算机二级。

1)直接构造概念格

由表1给出的形式背景直接构造的概念格如图1所示，共12个概念结点。

2)对象加权概念格

给定 $\alpha = 0.1{\rm{4}}$ ， $\beta = 0.1{\rm{4}}$ 。在表1给定的形式背景中通过信息熵获取属性权重。由表1可获得属性 $a$ 出现的概率为 ${P_{\rm{1}}}(a) = \dfrac{5}{6}$ ，利用定义5可得属性 $a$ 的信息熵：

${H_{\rm{1}}}(a) = - {P_{\rm{1}}}(a) \times {\log _2}{P_{\rm{1}}}(a) = {\kern 1pt} = - \frac{5}{6} \times {\log _2}\frac{5}{6} = 0.219\;2$

由计算可知：

${P_{\rm{1}}}(b) = \dfrac{4}{6}$ ， ${H_{\rm{1}}}(b){\kern 1pt} {\kern 1pt} = - \dfrac{4}{6} \times {\log _2}\dfrac{4}{6} = 0.389\;9$

${P_{\rm{1}}}(c) = \dfrac{1}{6}$ ， ${H_{\rm{1}}}(c){\kern 1pt} {\kern 1pt} = - \dfrac{1}{6} \times {\log _2}\dfrac{1}{6} = 0.430\;8$

${P_{\rm{1}}}(d) = \dfrac{2}{6}$ ， ${H_{\rm{1}}}(d){\kern 1pt} {\kern 1pt} = - \dfrac{2}{6} \times {\log _2}\dfrac{2}{6} = 0.528\;3$

${P_{\rm{1}}}(e) = \dfrac{3}{6}$ ， ${H_{\rm{1}}}(e){\kern 1pt} {\kern 1pt} = - \dfrac{3}{6} \times {\log _2}\dfrac{3}{6} = 0.5$

$H(A) = {H_{\rm{1}}}(a) + {H_{\rm{1}}}(b) + {H_{\rm{1}}}(c) + {H_{\rm{1}}}(d) + {H_{\rm{1}}}(e) = {\rm{2}}{\rm{.068\;2}}。$

可获得各属性权重，分别为： ${w_{\rm{1}}}(a){\rm{ = 0}}{\rm{.11}}$ (小于α，故该属性冗余需删去)， ${w_{\rm{1}}}(b){\rm{ = 0}}{\rm{.19}}$ ， ${w_{\rm{1}}}(c){\rm{ = 0}}{\rm{.21}}$ ， ${w_{\rm{1}}}(d){\rm{ = 0}}{\rm{.25}}$ ， ${w_{\rm{1}}}(e)= {\rm{ 0}}{\rm{.24}}$ 。

对于对象1来说， $f(1) = \{ a,b\} {\kern 1pt} {\kern 1pt} {\kern 1pt} $ 。则

${d_{\rm{1}}}(1) = \frac{{{w_{\rm{1}}}(a){\rm{ + }}{w_{\rm{1}}}(b)}}{2} = 0.{\rm{15}}$

$ {d_{\rm{1}}}(2) = \frac{{{w_{\rm{1}}}(a){\rm{ + }}{w_{\rm{1}}}(d){\rm{ + }}{w_{\rm{1}}}(e)}}{{\rm{3}}} = 0.2 $

$ {d_{\rm{1}}}({\rm{3}}) = \frac{{{w_{\rm{1}}}(a){\rm{ + }}{w_{\rm{1}}}(b) + {w_{\rm{1}}}(c){\rm{ + }}{w_{\rm{1}}}(e)}}{{\rm{4}}} = 0.1{\rm{87\;5}} $

${d_{\rm{1}}}({\rm{4}}) = {w_{\rm{1}}}(a) = 0.11$ (小于β，故该对象冗余需删去)

${d_{\rm{1}}}({\rm{5}}) = \frac{{{w_{\rm{1}}}(b){\rm{ + }}{w_{\rm{1}}}(e)}}{2} = 0.{\rm{215}}$

${d_{\rm{1}}}({\rm{6}}) = \frac{{{w_{\rm{1}}}(a){\rm{ + }}{w_{\rm{1}}}(b) + {w_{\rm{1}}}(d)}}{{\rm{3}}} = 0.183\;{\rm{3}}。$

则可获得子形式背景 ${F_d} = ({U_d},{A_d},{I_d})$ ，其中 ${U_d}= $ $ {\rm{ \{ 1,2,3,5,6\} }}$ ， ${A_d} = \{ b,c,d,e\} $ ，具体数据如表2所示。

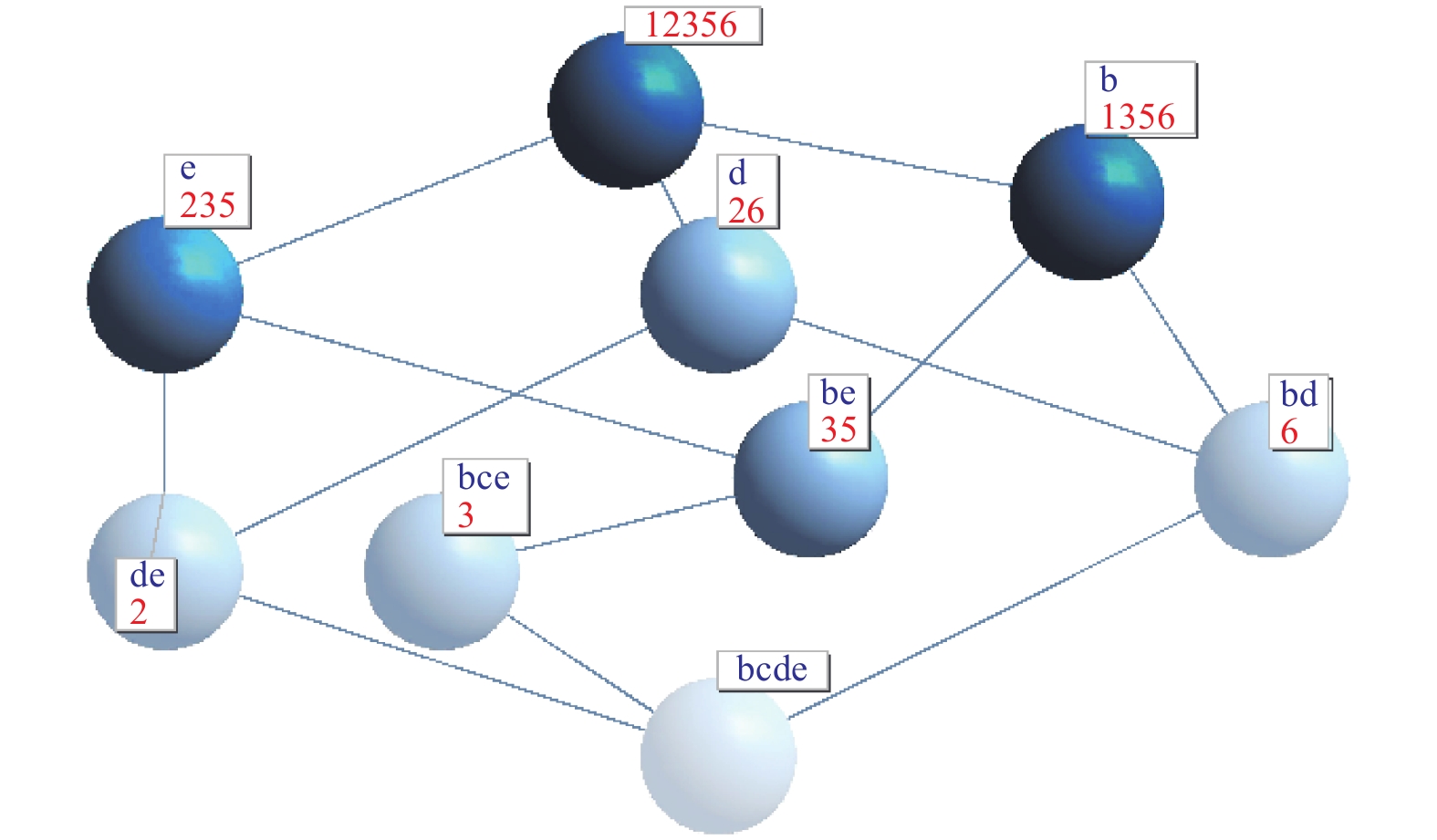
由表2给出的形式背景构造的概念格如图2所示，共9个概念结点，即为对象加权概念格。

3)对象强加权概念格

给定 $\delta = 0.0{\rm{75}}$ ，则通过计算可知

${D_{\rm{1}}}({\rm{1}}) = \sqrt {{{({w_{\rm{1}}}(a) - {d_{\rm{1}}}({\rm{1}}))}^2} + {{({w_{\rm{1}}}(b) - {d_{\rm{1}}}({\rm{1}}))}^2}} {\rm{ = 0}}{\rm{.057}}$

${D_{\rm{1}}}({\rm{2}}) = \sqrt {\frac{{{{({w_{\rm{1}}}(a) - {d_{\rm{1}}}({\rm{2}}))}^2} + {{({w_{\rm{1}}}(d) - {d_{\rm{1}}}({\rm{2}}))}^2} + {{({w_{\rm{1}}}(e) - {d_{\rm{1}}}({\rm{2}}))}^2}}}{{{\rm{3}} - 1}}} {\rm{ = 0}}{\rm{.078}}$

由于 ${D_{\rm{1}}}(2) > \delta {\rm{ = 0}}{\rm{.075}}$ ，则2为偏差对象，需删除。

${D_{\rm{1}}}({\rm{3}}) = \sqrt {\frac{{{{({w_{\rm{1}}}(a) - {d_{\rm{1}}}({\rm{3}}))}^2} + {{({w_{\rm{1}}}(b) - {d_{\rm{1}}}({\rm{3}}))}^2} + {{({w_{\rm{1}}}(c) - {d_{\rm{1}}}({\rm{3}}))}^2} + {{({w_{\rm{1}}}(e) - {d_{\rm{1}}}({\rm{3}}))}^2}}}{{{\rm{4}} - 1}}} {\rm{ = 0}}{\rm{.056}}。$

${D_{\rm{1}}}({\rm{5}}) = \sqrt {{{({w_{\rm{1}}}(b) - {d_{\rm{1}}}({\rm{5}}))}^2} + {{({w_{\rm{1}}}(e) - {d_{\rm{1}}}({\rm{5}}))}^2}} {\rm{ = 0}}{\rm{.035}}。$

${D_{\rm{1}}}({\rm{6}}) = \sqrt {\frac{{{{({w_{\rm{1}}}(a) - {d_{\rm{1}}}({\rm{6}}))}^2} + {{({w_{\rm{1}}}(b) - d({\rm{6}}))}^2} + {{({w_{\rm{1}}}(d) - {d_{\rm{1}}}({\rm{6}}))}^2}}}{{{\rm{3}} - 1}}} {\rm{ = 0}}{\rm{.07}}。$

则可获得子形式背景 ${F_D} = ({U_D},{A_D},{I_D})$ ，其中： ${U_D}{\rm{ = \{ 1,3,5,6\} }}$ ， ${A_D} = \{ b,c,d,e\} $ ，详见表3。

表3给出的形式背景构造的概念格如图3所示，共5个概念结点，即为对象强加权概念格。

通过上述计算能够看到本文提出的对象强加权概念格能够通过删除不必要的对象和属性，缩小形式背景的规模，从而实现简化概念格构造过程的目的。且通过这种方法能够简化概念形式，便于我们在之后进行规则提取。

4)粒决策规则提取

在表1的基础上给出决策形式背景 $(U,A, $ $ I,D,J)$ ，其中对象集为6位求职者。条件属性集仍为 $A = \{ a,b,c,d,e{\rm{\} }}$ ，决策属性集为 $D = \{ f{\rm{\} }}$ ，取值为1代表教育机构工作录取该求职者，否则为拒绝录取。具体数据如表4所示。

由表4可知 $U/{R_D}{\rm{ = \{ }}{D_1}{\rm{,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {D_2}{\rm{\} }}$ ， ${D_1} = \{ 1,2,4,6\} $ ， $ {D}_{\rm{2}}=\left\{3,5\right\}$ 。有两个决策概念： ${{(\{ 1}},{{2,4,6\} ,\{ 0\} )}}$ 和 ${{(\{ 3,5\} ,\{ 1\} )}}$ 。

由上述计算过程可直接获取 $L({U_D},{A_D},{I_D})$ ，共有5个概念，分别为： ${{(\{ 1,3,5,6\} ,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {{\{ }}b{{\} )}}$ 、 ${{(\{ 6\} ,}}{\kern 1pt} {{\{ }}b,d\} {{)}}$ 、 ${{(\{ 3,5\} ,\{ }}b,e\} {{)}}$ 、 ${{(\{ 3\} ,\{ }}b,c,e\} {{)}}$ 、 ${{(}} \text{Ø} ,{{\{ }}b,c,d,e\} {{)}}$ 。

由算法2可获得粒决策规则：

$\{ b,e\} \Rightarrow \{ 1\} $

$\{ b,c,e\} \Rightarrow \{ 1\} $

$\{ b,d\} \Rightarrow \{ 0\} $

可进一步简化规则得:

$\{ b,e\} \Rightarrow \{ 1\} $

$\{ b,d\} \Rightarrow \{ 0\} $

通过本文算法对于概念格进行简化后提取规则，可知本岗位更倾向于招聘数学专业且拥有教师资格证的应聘者，与现实背景相符。

对于没有删除冗余属性、冗余对象、偏差对象的情况，也即直接用表2所示的决策形式背景获取条件概念格，然后利用算法2获取粒决策规则，结果如下：

$\{ a,d\} \Rightarrow \{ 0\} $

$\{ b,e\} \Rightarrow \{ 1\} $

$\{ a,d,e\} \Rightarrow \{ 0\} $

$\{ a,b,d\} \Rightarrow \{ 0\} $

$\{ a,b,c,e\} \Rightarrow \{ 1\} $

进一步简化规则可得

$\{ a,d\} \Rightarrow \{ 0\} $

$\{ b,e\} \Rightarrow \{ 1\} $

可知本岗位更倾向于招聘拥有教师资格证的数学专业的应聘者，这也是符合实际情况的。可见，通过本文构造的对象强加权概念格仍能够保持原决策规则的关键信息，即教育机构更愿意录取数学专业有教师资格证的应聘者，而且能够简化规则获取的过程。

3.2 实验分析

在内存为 8 GB，操作系统为 Windows 10 的计算机上，用Matlab软件实现了本文算法、经典概念格构造算法及文献[25]的算法。选用UCI数据集中的ZOO数据集进行实验，该数据集共有101条记录, 18项属性。对数据集的预处理，包括去掉决策属性，将数值属性布尔化等，最后获取了共100条记录, 20项属性的形式背景，以20条动物记录为单位将其划分为5个子形式背景。将子形式背景依次进行合并，分别采用本文算法、经典算法及文献[25]的算法构造合并后的整体概念格，对比其分别获取的概念结点个数，以此对比其执行效率，具体如表5所示。

由实验结果可知，记录数逐渐增多，概念结点也会随之递增。由于经典算法在构造概念格的过程不会删除任何信息，因此该算法会获得最多的概念结点，同样会导致构造时间最长，执行效率最低。而文献[25]中的算法虽然减少了19.4%的冗余结点，但其构造的概念格规模仍然较为复杂。本文算法相较于经典算法减少了66%的冗余结点，相较于文献[25]中的算法减少了59.2%的冗余结点，极大缩短了构造概念格的时间，提升了概念格的构造效率，有利于提取用户关心的知识信息。

4 结束语

删除冗余概念，提升概念格构造效率是概念格理论的重要问题。本文通过信息熵获取了形式背景中数据隐含的属性权重，利用属性权重给出了对象权重及对象重要度偏差，并进一步给出满足阈值要求的对象强加权概念格的构造算法。本文的方法能够有效避免产生冗余概念，获得结构更简单的概念格，同时也能够进一步简化规则获取过程。

但本文仍有许多不足，比如在给出对象权重时采取的是均值法，把对象具有的属性作为个体去考虑，并没有将考虑对象具有的属性作为一个整体具有的特征。而且本文对于2.3节中给出的决策规则时仅从条件属性集角度出发构造了对象强加权概念格，并没有充分考虑决策属性隐含的信息。未来将进一步研究这些问题。