在现实生活中存在大量多目标优化问题，例如生产制造业、金融投资、航空调度等。多目标优化问题是由多个待优化目标函数组成，当目标个数多于3个时，该问题又被称为高维多目标优化问题(many-objective optimization problem)^[1]。由于各目标之间具有冲突性，传统的优化算法很难得到一组最优解，因此，研究者大多采用启发式方法来求解该问题。目前，用于求解高维多目标优化问题的启发式方法主要分为以下三类^[2]：基于支配关系的进化算法、基于分解的进化算法和基于指标的进化算法。

基于支配关系的进化算法是通过Pareto支配策略来选择非支配解。NSGA-II^[3]算法通过快速非支配解排序策略来获得非支配解，但是该方法无法保证种群的多样性。NSGA-III^[4]作为NSGA-II的改进版本，为了增强算法处理高维多目标优化问题的能力，在筛选同一等级的个体时，采用了基于参考点的方法来代替拥挤距离，然而该算法仅在某些具有特定形状的Pareto前沿问题上表现较优。CNSGA-III^[5]算法在NSGA-III的基础上，通过在非支配解层中添加一个聚类操作来增强算法种群的多样性，实验结果表明，该策略效果较差。Zou等^[6]在NSGA-II框架基础上，提出了一种在关键层中选取非支配解的旋转网格策略，在一定程度上增强了算法的选择压力。Lin等^[7]提出了一种基于平衡适应度估计策略的高维粒子群算法来解决高维多目标优化问题，该策略将目标空间划分为不同的区间并给每个区间中的目标赋予不同的权重，然而过多的权重设置限制了该方法的实际应用。

基于分解的进化算法是通过将多目标问题转化为多个单目标问题来处理。MOEA/D^[8]和MOEA/D-M2M^[9]是两种常用的基于分解的多目标进化算法。MOEA/DD^[10]是通过目标空间分解与自适应权重分配相结合来解决高维多目标优化问题。但上述算法过于依赖权重的选取。此外为了减少Pareto前沿形状对分解算法性能的影响，Liu等^[11]提出了一种基于模糊分解的多目标进化算法，结果表明该算法对于该问题具有较好的处理效果。

基于指标的进化算法是将解的评价标准作为选择支配解的一类算法。IBEA^[12]采用Hypervolume指标选取非支配解，该方法在处理高维多目标问题时无法保证分布性。Bader等^[13]提出了另一种基于Hypervolume指标的进化算法，在一定程度上平衡了高维多目标优化问题的收敛性和分布性，但是Hypervolume指标的计算复杂度随着目标个数的增加呈指数增加^[2]，进一步限制了该算法应用。此外，基于GD^[14]、IGD^[15]和R2^[16]指标的进化算法在求解高维多目标优化问题时都取得了不错的效果。

基于Pareto支配策略的进化算法相对于另外两类算法，可以从搜索的深度上逼近Pareto前沿，因此，对解决高维多目标优化问题方面仍具有巨大潜力。收敛性和分布性作为多目标优化问题中的两个重要指标，在种群演化过程中是相互冲突的^[17]，因此设计一种能有效平衡收敛性和多样性的新型支配策略，对于解决高维多目标优化问题具有重要意义。本文提出了一种目标空间映射策略的高维多目标粒子群优化算法，该策略作为一种新的多样性保持机制，可从众多的候选解中筛选出收敛性和分布性都较优的个体，同时利用一种增强型反向学习策略帮助种群跳出局部最优。

1 粒子群优化算法 1.1 基本粒子群优化算法

粒子群算法(particle swarm optimization, PSO)^[18]是通过研究鸟群觅食规律而发展出的一种群智能优化算法。粒子通过个体最优位置和群体最优位置动态更新自身的位置和速度，速度和位置的更新公式分别为

$ \begin{split} {v_{id}}(t + 1) =& \omega {v_{id}}(t) + {c_1}{r_1}({p_{id}}(t) - {x_{id}}(t)) + \\ & {c_2}{r_2}({p_{gd}}(t) - {x_{id}}(t)) \end{split} $

(1)

${x_{id}}(t + 1) = {x_{id}}(t) + {v_{id}}(t + 1)$

(2)

式中：ω表示权重系数；v_id和x_id分别表示第i个粒子在第d维度上的速度和位置大小；c₁和c₂表示学习因子；r₁和r₂表示(0，1)之间的随机数；p_id和p_gd分别表示个体最优位置和群体最优位置。

1.2 改进粒子群优化算法

粒子群算法在其发展过程中，为了提高算法的寻优性能，主要有以下几种改进策略。

1)调整算法的参数。为了平衡种群勘探与开采的能力，Shi等^[19]将ω引入粒子群算法中，ω值越大，勘探未知区域的能力越强，ω值越小，小范围内的开采能力越强，Clerc等^[20]建议ω的取值为0.729，Venter等^[21]则采用非线性递减的策略来更新ω。此外还有部分研究者通过调整c₁、c₂的取值来增强算法的搜索能力^[22-23]。

2)设计不同类型的拓扑结构。Kennedy^[24]通过分析种群拓扑结构与交互概率的关系，提出了一种bare bones particle swarm (BBPS)的模型。Yue等^[25]提出了一种基于环形拓扑结构的粒子群算法并将其用于求解多模态的多目标问题。

3)与其他策略相结合，形成混合粒子群算法。侯翔等^[26]为了提高算法求解问题的能力，对所有粒子的最优位置进行降维处理，形成一个参考全局最优解，同时使用该解来更新群体当前的最优位置。Lin 等^[27]将 MOPSO 同分解算法相结合，采用两种不同的搜索策略来更新粒子的速度，结果显示，算法对复杂问题的解决性能得到了加强。Zain等^[28]为了降低算法在约束问题上求解的难度，在标准 MOPSO^[29]算法的基础上提出了一种基于动态搜索边界策略的 MOPSO。

2 目标空间映射策略的高维多目标粒子群算法 2.1 高维多目标优化问题

最小化高维多目标优化问题可以表示为

$\begin{array}{l} \min Y({{x}}) = {\rm{\{ }}{f_1}({{x}}), \,{f_2}({{x}}),\, \cdots,\,{f_m}({{x}}){\rm{\} }} \\ {\rm{subject\; to \;}}{{x}} \in {{D}} \end{array} $

(3)

式中：D表示决策空间，x=(x₁,x₂,…,x_n)；Y: D→R^m由m个目标函数f₁,f₂,…f_m组成，R^m表示目标空间；m≥4表示为目标函数的个数。通过式(3)得到一组最优解，即Pareto解集，表示为PS，如果 ${\rm{PF}} = \{ Y(x) \in {{\bf{R}}^m}|x \in{\rm{ PS}}\}$ ，称PF为Pareto前沿。

2.2 目标空间映射策略

由于非支配解个数增加导致算法无法收敛到完整的Pareto前沿，本文采用目标空间映射策略来增强算法对非支配解的选择压力。

首先，对每个个体在目标空间中的收敛性进行评价，采用式(4)计算个体的收敛性：

${F_i} = \frac{{{d_{i,o}}}}{{\sqrt m }},\quad i = 1,2, \cdots,n$

(4)

式中：m表示目标函数的个数；d_i,o表示个体i到参考点o之间的欧式距离，这里将参考点设置为原点。F_i的值越小，个体的收敛性越好。

然后，对每个个体在目标空间上的分布性进行评价，采用式(5)计算个体的分布性：

${\rm{Di}}{{\rm{s}}_i} = \dfrac{{\Bigg(\displaystyle\sum\limits_{s = 1}^m {\frac{{f_s^{i + 1}(x) - f_s^{i - 1}(x)}}{{\max ({f_s}(x)) - \min ({f_s}(x))}}} \Bigg)}}{m},\quad i = 1,2, \cdots,n$

(5)

式中：f_sⁱ⁺¹表示第i+1个个体在第s个目标函数上的目标值；Dis_i越大，则第i个个体的分布越好。

此时，每个非劣解都可以映射为以收敛性和分布性表征的2维空间，即 ${\rm{PS}} \to ({F_i},\;{\rm{Di}}{{\rm{s}}_i})$ 。

最后，计算收敛性评价的平均值F_ave和分布性评价的平均值Dis_ave，F_ave和Dis_ave如式(6)和(7)所示：

${F_{{\rm{ave}}}} = \dfrac{{\displaystyle\sum\limits_{i = 1}^n {{F_i}} }}{n}$

(6)

${\rm{Di}}{{\rm{s}}_{{\rm{ave}}}} = \dfrac{{\displaystyle\sum\limits_{i = 1}^n {\Bigg(\dfrac{1}{{{\rm{Di}}{{\rm{s}}_i}}}\Bigg)} }}{n}$

(7)

其中n表示个体的总数。

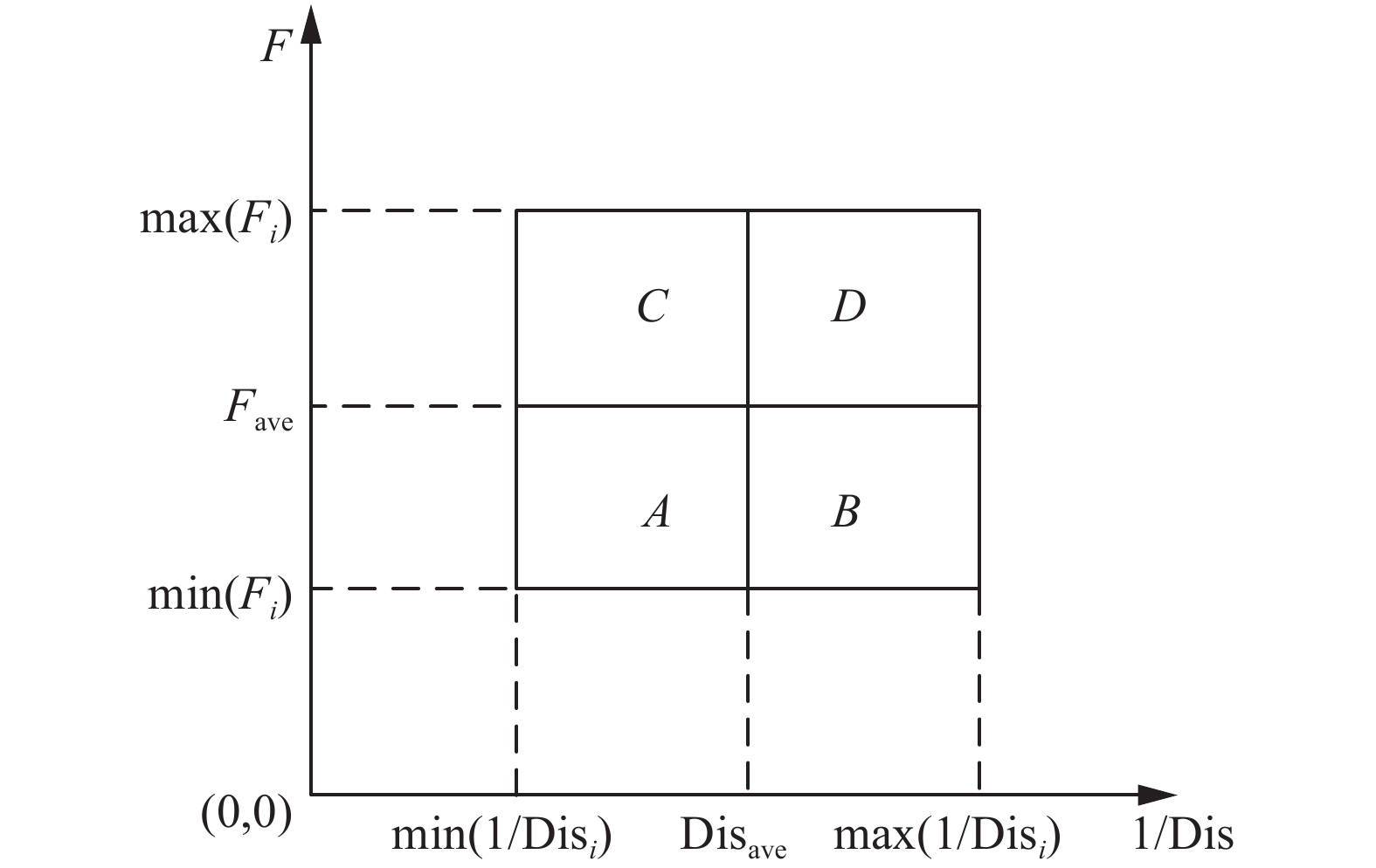
根据F_i、Dis_i、F_ave、Dis_ave这4个参数将映射后的2维空间划分为4个不同的区域，如图1所示。

设个体i对应的目标函数值为Y_i，此时其映射到2维空间后存在以下4种情况：

A： $\{ {Y_i}|{F_i} \leqslant {F_{{\rm{ave}}}} \cap \dfrac{1}{{{\rm{Di}}{{\rm{s}}_i}}} \leqslant {\rm{Di}}{{\rm{s}}_{{\rm{ave}}}},\;{Y_i} \in A\}$ ，处于A区域的个体，其收敛性和分布性均是最优。

B： $\{ {Y_i}|{F_i} \leqslant {F_{{\rm{ave}}}} \cap \dfrac{1}{{{\rm{Di}}{{\rm{s}}_i}}} > {\rm{Di}}{{\rm{s}}_{{\rm{ave}}}},\;{Y_i} \in A\}$ ，处于B区域的个体，其收敛性较好，分布性较差。

C： $\{ {Y_i}|{F_i} > {F_{{\rm{ave}}}} \cap \dfrac{1}{{{\rm{Di}}{{\rm{s}}_i}}} \leqslant {\rm{Di}}{{\rm{s}}_{{\rm{ave}}}},\;{Y_i} \in A\}$ ，处于C区域的个体，其收敛性较差，分布性较好。

D： $\{ {Y_i}|{F_i} > {F_{{\rm{ave}}}} \cap \dfrac{1}{{{\rm{Di}}{{\rm{s}}_i}}} > {\rm{Di}}{{\rm{s}}_{{\rm{ave}}}},\;{Y_i} \in A\}$ ，处于D区域的个体，其收敛性和分布性都较差。

在不同区域内的非支配解质量从好到坏的顺序为： $A > B = C > D$ 。

为进一步评价同区域内或并列区域内个体的优劣，采用式(8)计算个体的序值。

${\rm{Valu}}{{\rm{e}}_i} = \alpha \left( {\frac{1}{{{\rm{Di}}{{\rm{s}}_i}}}} \right) + \beta {F_i}$

(8)

式中：α和β分别为分布性权重和收敛性权重。Value_i越小，个体排序越好。对于处在区域A或D中的个体，设置α=β=1，保证A和D区域中的个体信息不变。对于处在B和C中的个体，其收敛性和分布性互不支配，假设B区域中个体数量为k，当个体处在B区域时，参数设置如下：β=1， $\alpha = $ $ \Bigg(\min \Bigg(\dfrac{1}{{{\rm{Di}}{{\rm{s}}_i}}}\Bigg) + {\rm{rand}}\Bigg({\rm{Di}}{{\rm{s}}_{{\rm{ave}}}} - \min \Bigg(\dfrac{1}{{{\rm{Di}}{{\rm{s}}_i}}}\Bigg)\Bigg)\Bigg){\rm{Di}}{{\rm{s}}_i},i = 1,2,\cdots,k$ ，通过该设置，B区域中个体收敛信息保持不变，分布信息被缩放到 $(\min (1/{\rm{Di}}{{\rm{s}}_i}),{\rm{Di}}{{\rm{s}}_{{\rm{ave}}}}),i = 1,2,\cdots,k$ 区间内。当个体处于C区域时，假设C区域中个体数量为q,参数设置如下： $\beta = (\min ({F_i}) + {\rm{rand}}({F_{{\rm{ave}}}} - $ $ \min ({F_i}))) \dfrac{1}{{{F_i}}},i = 1,2,\cdots q$ ，α=1，该设置将区域C中个体的收敛信息缩放到 $(\min ({F_i}),{F_{{\rm{ave}}}}),i = 1,2,\cdots q$ 区间内，而分布信息保持不变。通过上述操作，处于区域B和C中的个体，其分布信息和收敛信息都被缩放到相同的区间之中，因此两区域中的个体可以被放在一起统一评价。

在选取非支配解时，首先选取区域A中的个体，当区域A中的个体个数大于外部文档大小时，选取Value_i值小的个体进入档案文件；当区域A中的个体个数小于外部文档大小时，再从B和C中选取剩余个体，当B和C中的个体个数大于剩余外部文档大小时，仍然选取Value_i值小的个体进入外部文档。当B和C中的个体个数不能满足条件时，最后选取D中的个体。

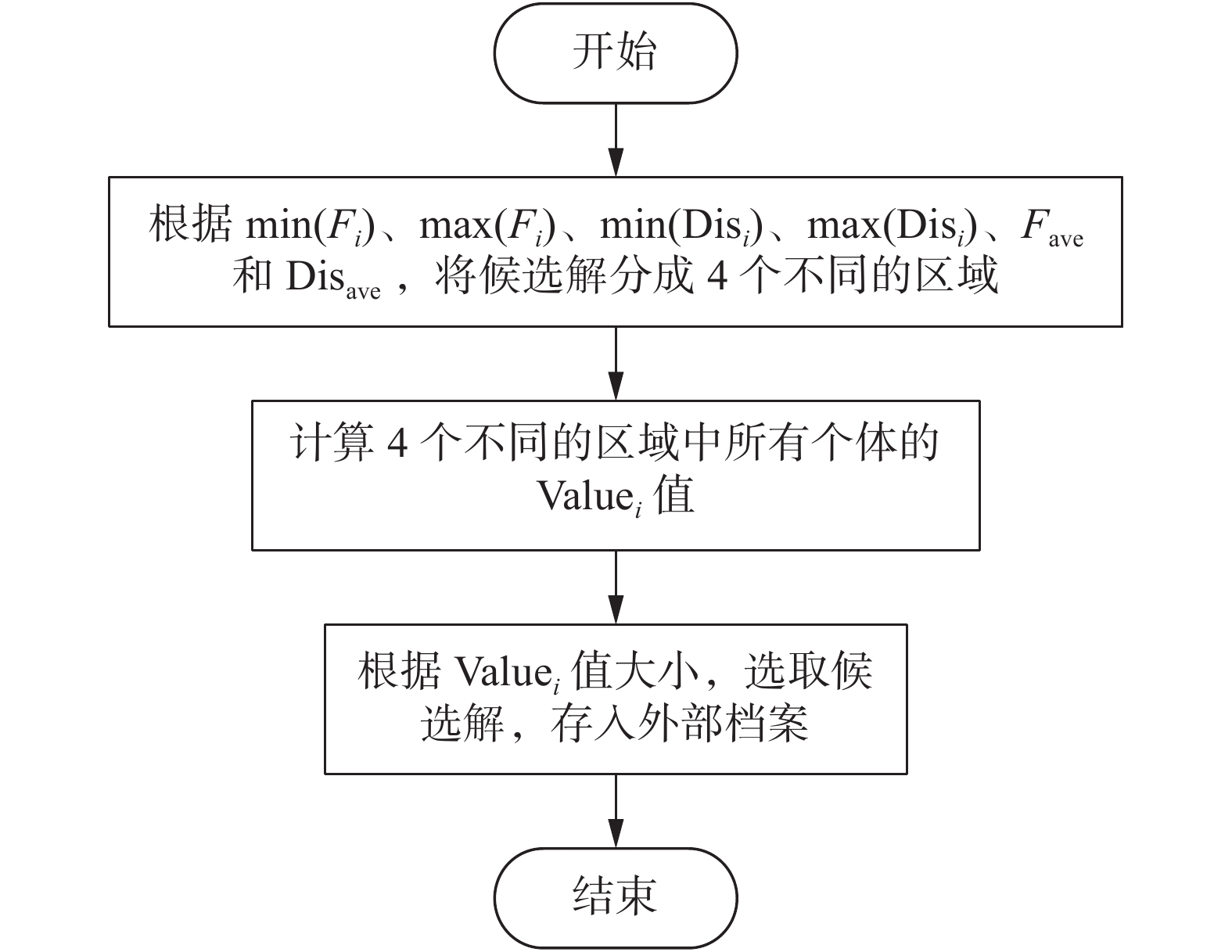
图2给出了目标空间映射策略的流程图。

2.3 反向学习策略

优化过程中如果算法陷入局部最优，则利用反向学习策略作为跳出机制，其中文献[30]的反向学习策略如式(9)所示：

$\left\{ {\begin{array}{*{20}{l}} x_{id}^* = k(\min ({x_d}) + \max ({x_d})) - {x_{id}} \\ x_{id}^* = k({a_d} + {b_d}) - {x_{id}} \\ {x_{id}^* = {\rm{rand}}({a_d},\;{b_d}),\;{\rm{if}}\;x_{id}^* < {x_{d\min }}||x_{id}^* > {x_{d\max }}} \end{array}} \right.$

(9)

式中：x_id^*表示第i个个体在第d维决策向量上得到的新位置；x_d表示所有个体在第d维上的位置；a_d和b_d分别表示种群个体在第d维目标向量上的最小和最大边界值；k表示(0，1)间的随机数；[x_dmin, x_dmax]表示在第d维上的边界约束。

由式(9)可得， $x_{id}^* $ 的取值范围为 $[k({a_d} + {b_d}) - $ $ {b_d},\;k({a_d} + {b_d}) - {a_d}]$ ，当k=1时， $x_{id}^* $ 取得最大值为b_d。因此，当最优解的决策向量位于b_d的右侧时，上述方法不能跳出局部最优。

本文对上述方法进行了改进，为提高算法跳出局部最优的能力，同时不忽略当前收敛信息，当 $x_{id}^* = {x_{d\min }} $ 时，x_id执行式(10)给出的反向学习策略。

$x_{id}^* = {x_{d\min }} + {x_{d\max }} - {x_{id}}$

(10)

从式(10)可以看出， $x_{id}^* $ 的取值范围扩大到了 [x_dmin, x_dmax]，该粒子跳出局部最优区域。

为了判断算法是否陷入局部最优，本文采用文献[31]给出的判断准则作为反向学习的激发条件，如式(11)所示：

$\left\{ {\begin{array}{*{20}{l}} \dfrac{{|\min (f_i^t) - \min (f_i^{t - 10})|}}{{|\min (f_i^t)|}} < 0.005\quad ,\;t > 10 \\ {\dfrac{{|\max (f_i^t) - \max (f_i^{t - 10})|}}{{|\max (f_i^t)|}} < 0.005\quad ,\;t > 10} \end{array}} \right. $

(11)

式中：min(f_i^t)和max(f_i^t)分别表示在第 $t$ 代时，第i个目标维度上的最小和最大值。min(f_i^t−10)和max(f_i^t−10)分别表示在第t−10代时，第i个目标维度上的最小和最大值。对于一个 $m$ 维测试函数，通过式(11)对其所有的目标维度的变化率进行计算，当所有的变化率都小于0.005时，算法陷入局部最优。

2.4 MOPSO-OSM流程

MOPSO-OSM算法具体流程如下：

1)算法初始化；

2)判断是否满足停止条件，若条件满足，算法停止迭代，否则转到3)；

3)判断种群是否陷入局部最优，执行反向学习策略；否则，直接转到4)；

4)利用式(1)和(2)更新个体的速度和位置；

5)计算个体的适应度值；

6)对个体当前适应度值和前代适应度值进行比较来更新个体最优;

7)选择非支配解；

8)利用目标空间映射策略更新外部档案文件；

9)从外部档案中随机选择一个个体来更新种群最优，并转到2)；

3 实验结果与分析 3.1 测试函数

为了评价算法性能的优劣，文中采取了6组WFG测试函数。参数设置如表1所示。

3.2 性能指标

文中利用世代距离(GD)、间距(SP)和逆世代距离(IGD)3个指标来评估算法的性能。GD被用来评价种群的收敛性，GD值越小，收敛性越好，其计算公式为

${\rm{GD}} = \frac{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {d_i^2} } }}{n}$

(12)

式中：n表示非支配解的个数；d_i表示非支配解与Pareto最优解之间的欧式距离。

SP指标通常被用来评价种群的分布性，其计算如式(13)所示，分布性好坏与其计算值成反比。

$SP = \sqrt {\frac{1}{{n - 1}}\displaystyle\sum\limits_{i = 1}^n {{{(\overline d - {d_i})}^2}} } $

(13)

式中 $\overline d $ 为d_i的平均值。

IGD指标被用来同时评价种群分布性和收敛性，IGD越小，算法展现出的性能越好，其计算公式为

${\rm{IGD}} = \frac{{\displaystyle\sum\limits_{{{{x}}^*} \in {{{P}}^*}} {d({{{x}}^*},\;{{P}})} }}{{|{{{P}}^*}|}}$

(14)

式中：P和P^*分别表示Pareto最优解集和非支配解；|P^*|表示非支配个数。

3.3 对比算法及其设置

本文所得结果与目前较为流行的进化算法进行对比，比较算法包括：NSGA-III^[3]、RVEA^[32]、MOEA/DD^[10]、PESA-II^[33]和NMPSO^[7]。所有使用的算法其种群大小都设置为100，外部文档的大小为100，算法进化的次数为700次，算法具体参数设置如表2所示，所有算法均运行30次，计算收敛性和多样性指标，取其平均值。

对于MOPSO-OSM算法，其权重ω是随着迭代次数线性减少的。

3.4 结果与分析

表3和表4分别为所有算法在5目标和10目标测试函数时得到的GD、SP和IGD的平均值。

3.4.1 收敛性分析

从表3中可以看出，对于5目标测试函数，NMPSO算法在WFG1和WFG2测试函数中得到了最好的GD值。NSGA-III算法在WFG4和WFG6问题中取得了最佳的GD值。MOPSO-OSM算法在WFG3和WFG5取得了最优的GD值。对于10目标的测试函数，从表4中可以看出，在WFG1和 WFG2测试函数上，MOEA/DD取得了最佳GD值。NSGA-III在WFG6问题上取得最优GD值，在WFG4和WFG5测试问题上，RVEA取得的GD值排名第一。对于WFG3测试函数，MOPSO-OSM取得了最优的GD值。从以上可以看出，本文所提出的算法在大部分测试函数中并没有取得最优值。原因在于，大多数算法在求解时，仅仅追求收敛性，忽视了分布性，而本文在目标空间分配策略中，同时考虑目标向量的收敛性和分布性，所以在测试函数中，并不能完全保证GD的最优性，这也验证了“没有免费午餐”的原理。

3.4.2 分布性分析

对于5目标测试函数，从表3中可以看出，MOPSO-OSM算法在所有测试函数中都取得了最好的SP值。对于10目标的测试函数，从表4可以看出，MOPSO-OSM算法同样在所有的测试函数中，得到了最好的SP值。以上可以看出，MOPSO-OSM算法在保持种群分布性上面具有很大的优势。

3.4.3 整体性分析

从表3中可以看出，对于5目标测试函数，NSGA-III在WFG1、WFG5和WFG6中取得了最优的IGD值。MOEA/DD在WFG2中取得最好的IGD值。MOPSO-OSM算法在WFG3和WFG4中取得的IGD值排名第一。对于10目标测试函数，从表4可以看出，MOEA/DD在WFG1和WFG2中取得了IGD的最优值。NMPSO在WFG4和WFG5中的IGD值最优。MOPSO-OSM算法在WFG3和WFG6中的IGD取得了最佳值。从以上可以看出，本文所提算法在处理WFG1和WFG2问题时表现出较低的能力，主要原因在于目标映射策略要综合考虑个体的分布性和收敛性，导致了算法在该问题上的收敛性不足，无法得到一组完整的Pareto前沿，所以该算法在处理WFG1和WFG2问题时还有待提高。对于其余测试函数，虽然在部分问题上算法无法得到最优值，但是所得结果仍处于较好的排名。对于不同目标个数的同一个测试函数，本文算法与其余算法相比较，随着目标个数的增加，对比算法的性能都在急剧下降，而本文所提算法展现出了更好的适应性能。通过以上可以看出，本文采用的目标空间映射策略，将收敛性和多样性结合，用这两者对目标向量进行分类选择，最后得到的非支配解具有较好的性能。

图3分别给出了在5目标WFG3测试函数下得到的Pareto前沿。对于WFG3测试函数，所有算法都得不到一个完整的Pareto前沿。但是MOPSO-OSM算法的Pareto前沿相比于另外5种对比算法，其收敛性和分布性都是明显优于其他算法，表现出较好的性能。图4给出了MOPSO-OSM算法在5目标WFG3和WFG4测试问题中得到的GD值曲线。

图4中横坐标为记录的次数，每7次迭代记录一次。从中可以看出，在迭代过程中，GD值都是逐渐减小，算法逐渐收敛。目标映射策略作为一种有效的筛选候选解的方法，对于算法在问题中的收敛性能的表现起到决定性的作用，因此，在高维多目标优化问题中，目标映射策略是可行且有效的。

4 结束语

本文提出了一种基于目标空间映射策略的高维多目标粒子群算法来求解高维多目标问题。该方法利用性能指标对目标空间进行划分，从而达到增强算法选择压力的目的。通过6组标准测试函数的仿真验证，实验结果表明，在处理高维多目标问题时，目标空间映射策略能够有效地提高种群的收敛性和分布性。将该算法应用在工程实例问题将是下一步的研究重点。