2. 同济大学 电子与信息工程学院,上海 201804;
3. 清华大学 计算机科学与技术系,北京 100084;
4. 清华大学 自动化系,北京 100084
2. School of Electronics and Information Engineering, Tongji University, Shanghai 201804, China;
3. Department of Computer Science and Technology, Tsinghua University, Beijing 100084, China;
4. Department of Automation, Tsinghua University, Beijing 100084, China
同步定位与地图构建 (simultaneous localization and mapping, SLAM)问题可以描述为:移动机器人在未知环境中运动时,逐步构建其周围环境的地图,同时运用此地图对机器人位置和姿态进行估计[1]。SLAM技术广泛应用于移动机器人、无人驾驶汽车、无人机、增强现实、导航或水下无人潜航器等领域[2-4]。但是目前已有的SLAM算法,大多是单机器人系统且假设运动轨迹已知,这种被动式SLAM与SLAM问题中的环境未知相矛盾[5]。
多机器人系统在探索能力、鲁棒性、容错性等方面比单机器人更具优势[6],各个机器人通过通信网络进行信息传递与共享,相互协调工作,共享环境信息,极大扩展了机器人系统对环境的感知范围与定位的精度。因此,自20世纪90年代以来,在研究单机器人SLAM的基础上,多机器人SLAM逐步成为移动机器人领域研究的热门[5,7-8]。
由Feder[9]提出的基于信息论的自适应导航与建图方法为主动SLAM奠定了基础。文献[10],基于EKF提出局部子地图的SLAM方法,证明局部子地图与全局地图相互独立,机器人只维护自己所建立的子图,然后周期性地将子图融合到全局地图中,但是其机器人的路径事先指定,建图过程中仅按规定路线进行环境探索,因此缺乏多机协同。文献[11]扩展了基于局部子图的多机器人主动SLAM方法,将主动SLAM问题转为多目标优化问题,并通过EKF对子地图进行融合得到全局地图。文献[12]通过引入吸引因子,实现主动SLAM,但是只适用于单机器人。文献[13]将主动信息收集任务应用于多机器人主动SLAM中,并引入虚拟地标与吸引因子引导多机器人探索,但是没有进行估计的数据融合。
多机器人主动SLAM是指机器人在未知环境下多机器人协同主动感知环境,并通过目标函数选择一系列的控制输入使得机器人能够高效地完成探索与建图的任务,其目标函数的优化的目标一般包括定位与建图的准确、新增探索区域、导航代价等因素。但以上优化目标之间往往是相互制约、相互对立的,例如机器人为了提高自身定位与建图的准确性,常局限于一定的范围内徘徊,而向外探索时,定位与建图的不确定性又会增大[14]。即使进行多目标优化,对常见的优化函数进行线性叠加,在实际中还是会出现不能遍历完整个环境、定位与建图精度不理想的情况,因为,定位所有地标不等于遍历整个环境,不遍历完整个环境,是不知道地标的具体数目位置的。因此,本文扩展了文献[13]的吸引因子,将吸引因子作用域放大,不仅仅用来纠正自身定位不好的机器人,还用于去指导多机器人团队进行环境的探索,使其能够遍历完整个环境,定位环境中所有的未知地标,吸引因子作为媒介促进多机器人系统的交流,增强多机器人系统与环境的交互,使其能够快速协同完成定位建图任务。多机器人主动SLAM中的误差主要来自于两个方面:一是机器人自身位置误差,二是传感器观测误差。当机器人自身定位精准时,其估计的视野范围内的地标精度也比较高。当多个机器人观测到同一地标时,通过凸组合融合[15]利用多个机器人对地标的估计值修正当前地标的状态值,可以大大降低该地标的不确定度,减少多机器人系统定位与建图的误差。
针对上述问题,本文基于EKF-SLAM算法[16]提出一种多机器人主动SLAM算法,其主要创新性工作包含改进吸引因子作用范围和建立信息融合技术为基础的地标估计融合方法,将主动SLAM问题转化为最优控制选取问题,并通过引入吸引因子促进了多机器人间的信息交流,一方面用于提升机器人自身位置估计准确性,另一方面用于指引多机器人进行环境的探索。当多个机器人观测到同一地标时,采用凸组合融合[15],进行地标的估计,降低被估计地标的不确定度,提升建图与定位的精度。
1 问题描述考虑一个拥有n个机器人的系统,符合以下运动模型:
| ${{x}}_{i,t + 1}^r = {{f}}\left( {{{x}}_{i,t}^r,{{{u}}_{i,t}}} \right) + {{{w}}_{i,t}},i \in \{ 1,2, \cdots n\} $ | (1) |
式中:
在主动SLAM任务中要求机器人感知环境主动选择控制量去定位未知环境下的所有地标,地标的状态
| ${{{y}}_{t + 1}} = {{{y}}_t}$ | (2) |
其中
令
| ${{x}}_{i,t + 1}^{} = \left[ {\begin{array}{*{20}{c}} {{{f}}\left( {{{x}}_{i,t}^r,{{{u}}_{i,t}}} \right) + {{{w}}_{i,t}}} \\ {{{{y}}_t}} \end{array}} \right],i \in \{ 1,2, \cdots, n\} $ | (3) |
机器人运动时在每个时刻进行观测,其传感器观测模型如下:
| ${{{z}}_{i,t}} = {{h}}\left( {{{{x}}_{i,t}},{{{y}}_t}} \right) + {{{v}}_{i,t}},i \in \{ 1,2, \cdots, n\} $ | (4) |
式中:
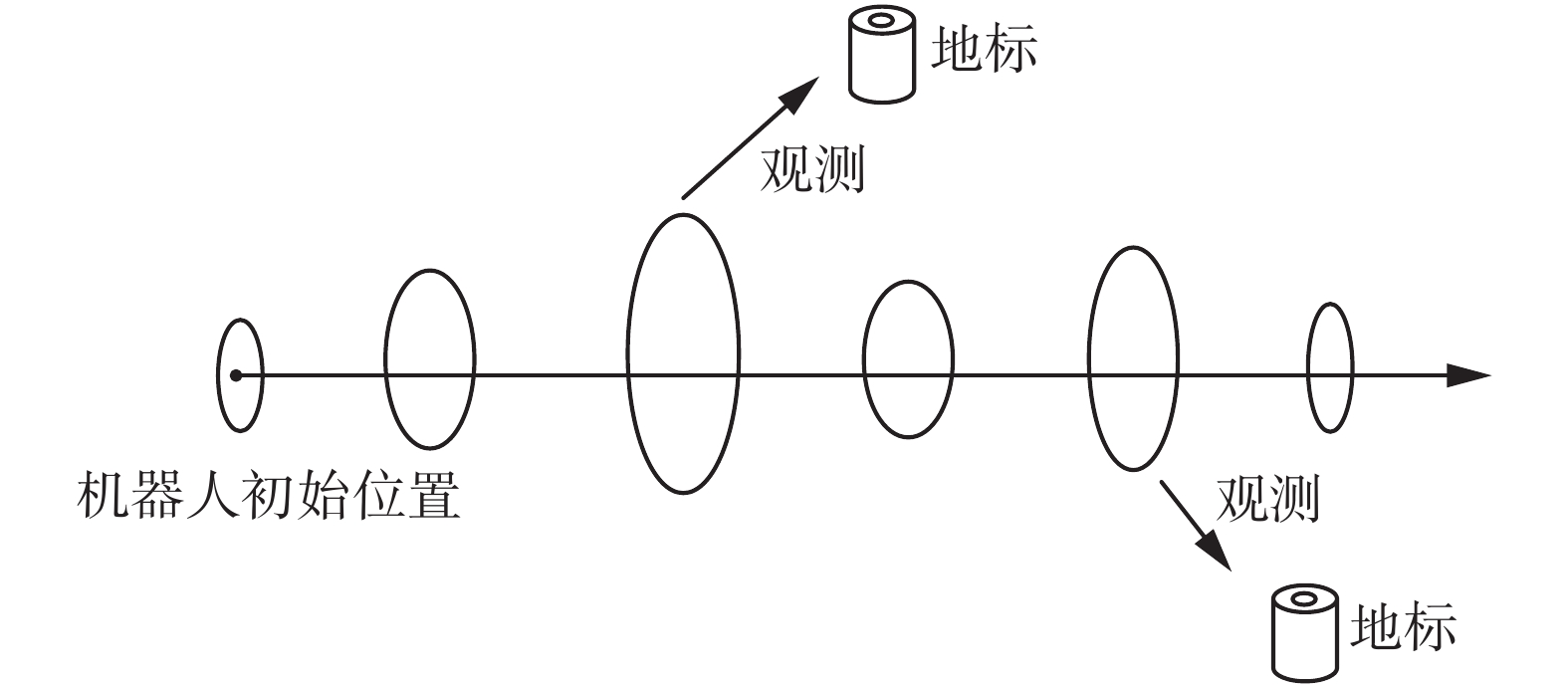
如图1所示为EKF-SLAM简图[17],其中椭圆代表机器人位置估计的不确定度,当机器人沿如图1所示直线运动时,可以看出当机器人一直观测不到地标时,位置估计不确定度会越来越大,在完全未知环境中无法预测机器人定位误差的上限[18],直到观测到新的地标时其不确定度会下降。这也是现有大多数算法不能遍历完环境的原因,因为在完全未知环境下,当没有地标作用时,机器人自身定位误差越来越大,其会倾向于去探索过的地方降低自身不确定度,而不是选择继续探索环境。
|
Download:
|
| 图 1 使用EKF-SLAM进行地标定位简图 Fig. 1 Landmark localization using extended Kalman Filter | |
多机器人主动SLAM问题可以描述为最大化目标
| $\begin{array}{l} \;\;\;\;\;\;\mathop {\max }\limits_{{{u}} \in {{U}}} \;\;J({{u}}): = {I}({{{y}}_t}|{{{z}}_t}) \\ {\rm{s.t.}}\;\;{{{x}}_{i,t + {{1}}}} = {{f}}\left( {{{{x}}_{i,t}},{{{u}}_{i,t}}} \right) + {{{w}}_{i,t}},i \in \{ 1, 2,\cdots, n\} \\ \;\;\;\;\;\;{{{z}}_{i,t}} = {{h}}\left( {{{{x}}_{i,t}},{{{y}}_t}} \right) + {{{v}}_{i,t}},i \in \{ 1,2, \cdots, n\} \\ \end{array} $ | (5) |
互信息可以衡量观测与目标的关联程度,互信息越大说明,目标与观测之前的关联越大,则更有可能从观测中获取更多信息。
2 基于观测融合的主动SLAM主动SLAM可以用式(5)描述为随机最优控制问题,通常,对于此类问题,自适应闭环控制策略比非自适应开环策略具有显著优势。但是,由于观测模型式(4)在目标状态下的线性和高斯噪声假设,可以证明式(5)简化为确定性的最优控制问题,对于该问题,开环策略是最优的[19]。在目标状态是高斯分布的情况下,存在最优控制序列
| $\begin{array}{l} \;\;\;\;\;\mathop {\min }\limits_{{{u}} \in {{U}}} \;\;J({{u}}): = \log \det \left( {{{{P}}_{i,t+1}}} \right) \\ {\rm{s.t.}}\:\:{{{x}}_{i,t + {{1}}}} = {{f}}\left( {{{{x}}_{i,t}},{{{u}}_{i,t}}} \right) + {{{w}}_{i,t}},i \in \{ 1,2, \cdots, n\} \\ \;\;\;\;\;{{{P}}_{i,t + 1}} = {{P}}_{i,t + 1}^ - - {{{K}}_{i,t+1}}{{{H}}_{i,t+1}}{{P}}_{i,t + 1}^ - ,i \in \{ 1, 2,\cdots ,n\} \\ \end{array} $ | (6) |
式中
| $\begin{array}{c} {\hat{ x}}_{i,t + 1}^ - = {{f}}({\hat{ x}}_{i,t}^{},{{{u}}_{i,t}}) \\ {{P}}_{i,t + 1}^ - = {{{F}}_{i,t}}{{{P}}_{i,t}}{{F}}_{i,t}^{\rm{T}} + {{{G}}_{i,t}}{{{Q}}_{i,t}}{{G}}_{i,t}^{\rm{T}} \\ \end{array} $ | (7) |
其中
| $\begin{array}{l} {{{F}}_{i,t}} = {\left. {\dfrac{{\partial {{f}}}}{{\partial {{x}}}}} \right|_{{{x}} = {\hat{ x}}_{i,t}^{}}} \\ {{{G}}_{i,t}} = {\left. {\dfrac{{\partial {{f}}}}{{\partial {{w}}}}} \right|_{{{w}} = 0}} \end{array} $ | (8) |
量测更新:
| $\begin{array}{l} {{{\hat{ x}}}_{i,t + 1}} = {\hat{ x}}_{i,t + 1}^ - + {{{K}}_{i,t+1}}({{{z}}_{t+1}} - {{h}}({\hat{ x}}_{i,t + 1}^ - )) \\ {{{K}}_{i,t+1}} = {{{P}}_{i,t+1}}{{H}}_{i,t+1}^{\rm{T}}{({{{H}}_{i,t+1}}{{{P}}_{i,t+1}^-}{{H}}_{i,t+1}^{\rm{T}} + {{{R}}_{i,t+1}})^{ - 1}} \\ \end{array} $ | (9) |
其中
| ${{{H}}_{i,t+1}} = {\left. {\frac{{\partial {{h}}}}{{\partial {{x}}}}} \right|_{{{x}} = {\hat{ x}}_{i,t + 1}^ - }}$ | (10) |
主动SLAM问题式(6)指多机器人系统在t时刻,主动选取最优控制序列
但是在EKF-SLAM建图中,机器人为了提升自身的估计精度,常会在一定范围局部运动,在探测过的区域进行徘徊。当机器人与两个陆标的距离相等,且到两个陆标的向量正交时,系统更新是最稳定的[14]。因此需要对式(6)进行优化,不仅仅考虑机器人估计误差协方差还要考虑新增探索面积
| $\mathop {\min }\limits_{\mu \in {{U}}} \:\:J({{u}}): = \alpha \coprod \log \det \left( {{{{P}}_{i,t+1}}} \right) + \beta \coprod \Delta S_{t + 1|t}^i$ | (11) |
其中
新增探索面积为相对于已探索区域,机器人视野扫过新增加的面积。
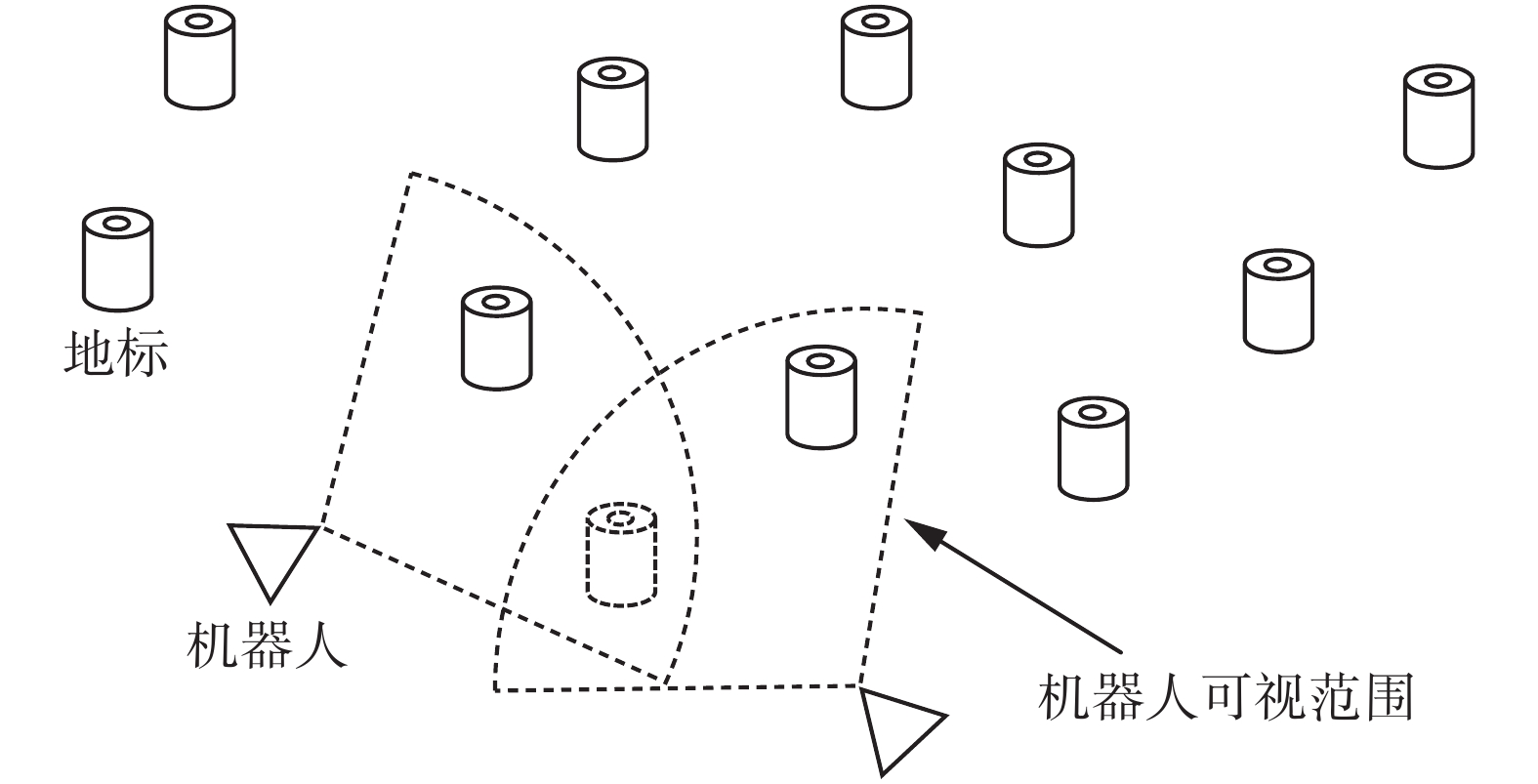
观测阶段中,每个机器人在不同位置对环境中的地标进行观测,如图2所示。
|
Download:
|
| 图 2 地标估计融合示意 Fig. 2 Landmark estimation fusion schematic | |
当多个机器人观测到同一地标时,多机器人系统可以分先后观测到同一地标,每个机器人都会对地标位置产生一个估计,同一地标的估计位置可能有多个,这样会带来更多的不确定性,造成错误的数据关联。因此,在多个机器人观测到同一地标时,采用凸组合融合对各个机器人对地标的估计值融合,从而降低地标的不确定度。地标的不确定度越小其地标估计误差协方差的迹越小,凸组合融合可以表示为
| ${{P}}_{f,t + 1}' = {\left( {{{({{P}}_{i,t + 1}')}^{ - 1}} + {{({{P}}_{j,t + 1}')}^{ - 1}}} \right)^{ - 1}}$ | (12) |
| ${\hat{ x}}_{f,t + 1}' = {{P}}_{f,t + 1}'\left( {{{({{P}}_{i,t + 1}')}^{ - 1}}{\hat{ x}}_{j,t + 1}' + {{({{P}}_{j,t + 1}')}^{ - 1}}{\hat{ x}}_{i,t + 1}'} \right)$ | (13) |
其中
由于多机器人系统不知道环境中地标的数目和位置,基于式(11)的目标函数在机器人视野范围内无新增探索面积时,其会采用估计误差协方差作为主动控制选取的原则,这样会导致机器人在已经探索过的区域徘徊。因此有必要让多机器人团队去探索环境,故增加虚拟探索地标,在机器人所建图的边界上,当机器人扩展环境时虚拟地标会建立,并移除旧的虚拟探索地标,当虚拟探索地标集合为空时证明环境已经遍历完毕。
吸引因子是用于指引机器人进行控制策略选择的一个向量,当其出现时机器人会去选择朝着吸引因子的方向进行运动规划。其发挥作用从出现到消失为3步,满足一定条件后会重新出现。当机器人在t步内无新增探索面积时,吸引因子会出现,其朝向为最近的虚拟探索地标,去引导多机器人团队进行环境探索,如图3所示,当机器人自身的位置估计协方差的迹
吸引因子的作用有两个,一是提升机器人自身的定位精度修正自身位姿估计,二是引导机器人探索环境。吸引因子促进了多机器人团队进行交流与通信。在完全未知的环境下,吸引因子的必要性是保证多机器人团队能够遍历完整个环境,不加吸引因子的主动SLAM算法,会出现局部环境遍历不完全的情况。

|
Download:
|
| 图 3 用于位姿修正的吸引因子 Fig. 3 Attractors for pose correction | |
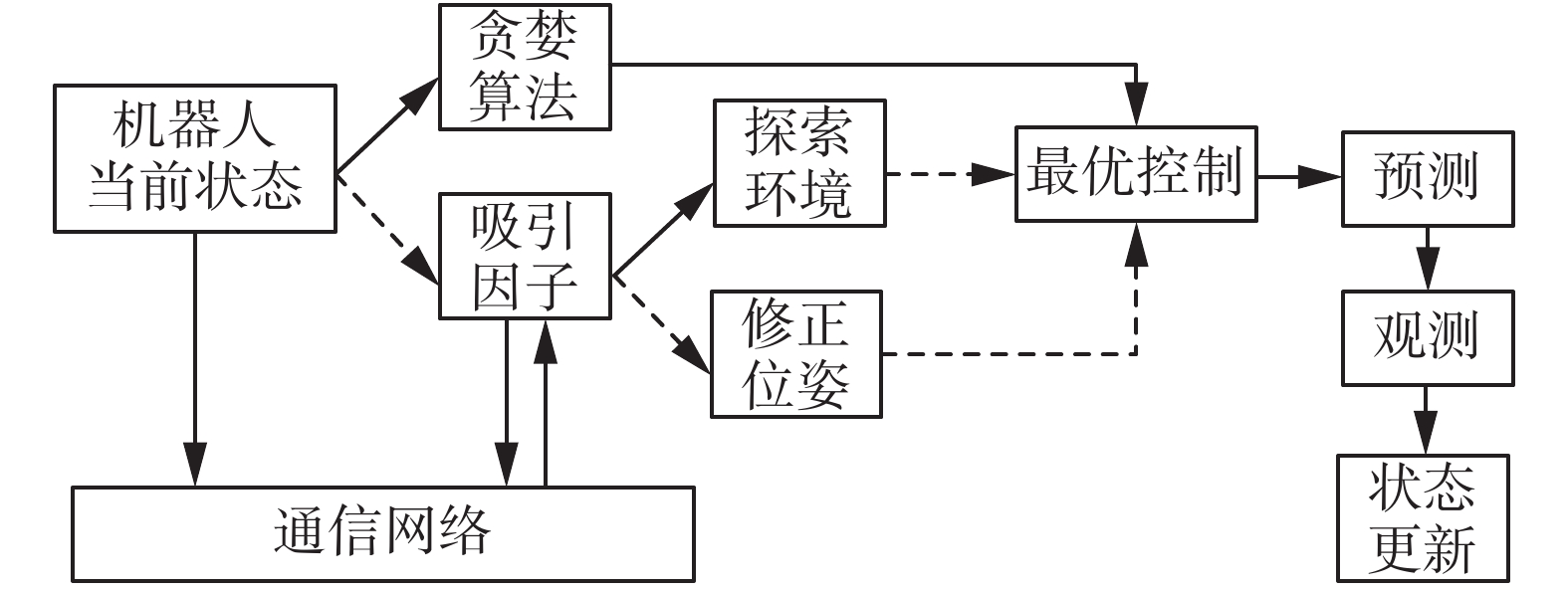
如图4所示,吸引因子的应用范围是位姿修正与探索环境,虚线代表满足一定的条件所采取的控制策略。在机器人位置估计偏差较大时,会触发吸引因子,此时不采用贪婪算法,而吸引因子会去引导机器人修正其位姿,而不会进行环境探索。当机器人在t步内无新增扩展面积时,则会触发吸引因子,引导多机器人团队去探索环境。
|
Download:
|
| 图 4 多机器人主动SLAM算法流程 Fig. 4 Multi-robot active SLAM algorithm | |
为验证多机器人主动SLAM算法有效性,设计仿真进行验证。机器人运动模型如下[18]:
| $\left[ {\begin{array}{*{20}{c}} {{x^\prime }} \\ {{y^\prime }} \\ {{\theta ^\prime }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} x \\ y \\ \theta \end{array}} \right] + \left[ \begin{array}{l} - \dfrac{v}{\omega }\sin \theta + \dfrac{v}{\omega }\sin (\theta + \omega \Delta t) \\ \dfrac{v}{\omega }\cos \theta - \dfrac{v}{\omega }\cos (\theta + \omega \Delta t) \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\omega \Delta t \end{array} \right]$ | (14) |
机器人的状态向量为
目标为静态地标,在
| $\begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{{z}}_{i,t}} = {{h}}\left( {{{{x}}_{i,t}},{{{y}}_t}} \right) + {{{v}}_t} \\ {{h}}\left( {{{x}},{{y}}_t^{}} \right) = \left[ \begin{array}{l} \;\;\;\;\;\sqrt {{{({{y}}_t^x - x)}^2} + {{({{y}}_t^y - y)}^2}} \\ {\rm{arctan}}(({{y}}_t^y - y)/({{y}}_t^x - x)) - \theta \\ \end{array} \right] \\ \end{array} $ | (15) |
机器人所携带的传感器能探测的最大范围为25 m,机器人可视角度为
考虑拥有5台机器人的多机器人团队,初始位置为随机分布于环境中,系统噪声观测噪声设置为
| $\begin{array}{l} {{Q}} = \rm{diag}([0.3,0.3,0.03]) \\ {{R}} = \rm{diag}([0.015,0.015]) \\ \end{array} $ |
为探究本文算法有效性,本文分别对比单机器人主动SLAM、随机SLAM、无吸引因子的多机器人主动SLAM、基于EKF融合的多机器人主动SLAM和带吸引因子的多机器人主动SLAM,这5种方式的SLAM算法以验证本文算法有效性。
图5、6为基于EKF融合的多机器人主动SLAM,图7、8为无吸引因子的多机器人主动SLAM,图9、10带吸引因子的多机器人主动SLAM。其中,绿色三角代表机器人,红色椭圆代表机器人的位置协方差,青色圆圈代表真实的地标位置,蓝色点和椭圆分别代表估计的地标位置与协方差,红色虚线代表机器人可视范围,洋红色的五角星代表吸引因子,黄色方块代表虚拟探索地标。深红色的点和椭圆代表融合估计的地标位置和协方差,初始的地标不确定度为:

|
Download:
|
| 图 5 基于EKF融合的多机器主动SLAM建图80步 Fig. 5 80 steps of multi-robot active SLAM based on EKF fusion | |
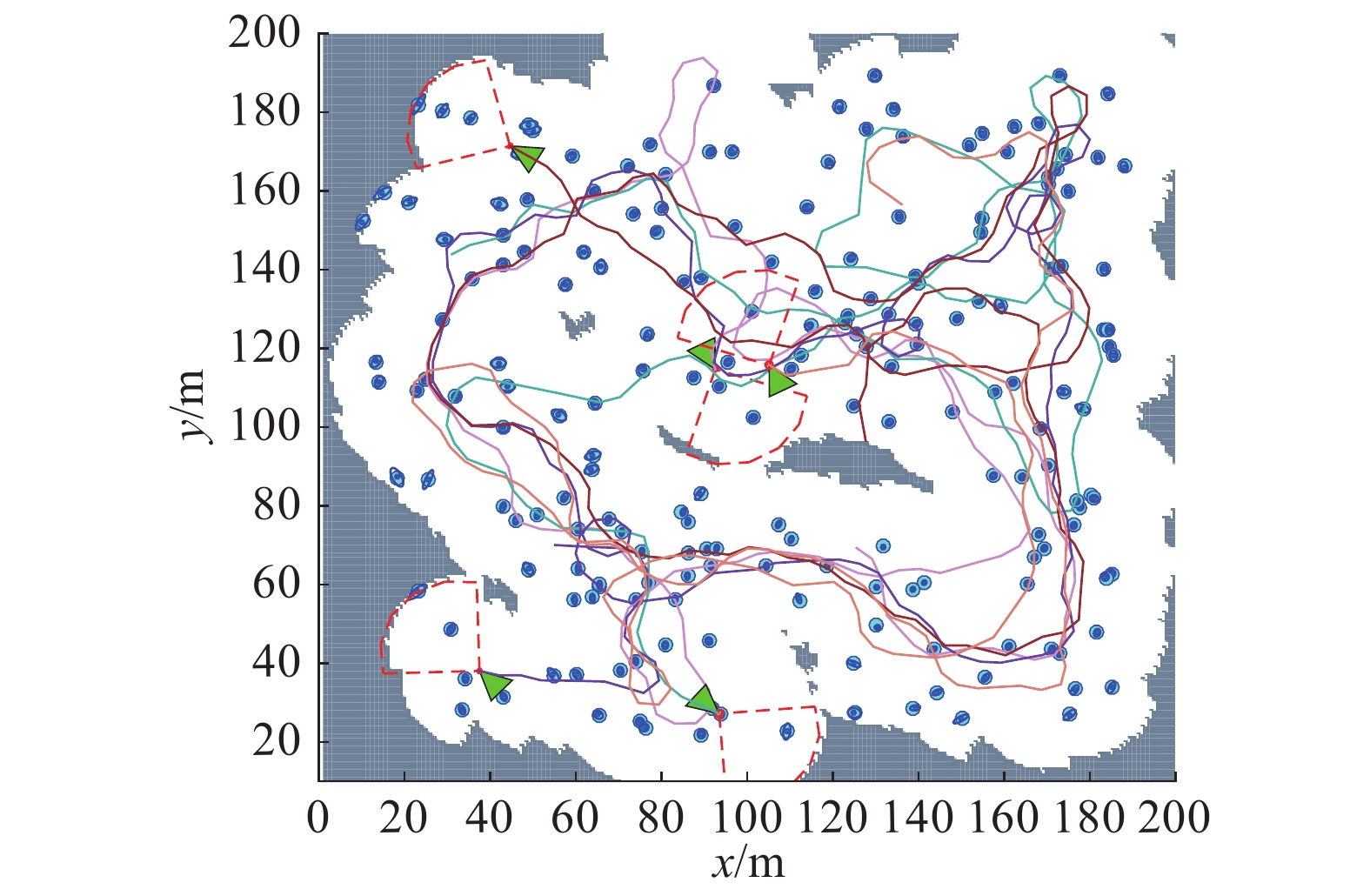
其中图5、图7、图9为建图的中间过程对比,从图6和图8中可以看出这两种方式的主动SLAM可以遍历大部分的环境,但是不能遍历完全部环境。
|
Download:
|
| 图 6 基于EKF融合的多机器主动SLAM建图167步 Fig. 6 167 steps of multi-robot active SLAM based on EKF fusion | |

|
Download:
|
| 图 7 无吸引因子的多机器人主动SLAM建图80步 Fig. 7 80 steps of multi-robot active SLAM without attractor | |

|
Download:
|
| 图 8 无吸引因子的多机器人主动SLAM建图167步 Fig. 8 167 steps of multi-robot active SLAM without attractors | |
对于无吸引因子的主动SLAM来说,即使目标函数式(11)中含有对新增面积的权重,仍然难以对环境进行完全覆盖。因为多机器人团队,在建图过程中,当机器人在已经建图的环境中走动的时候,无新增覆盖面积。因此目标函数式(11)退化成了式(6),这样会导致机器人在已经建图区域徘徊,不能遍历整个环境。

|
Download:
|
| 图 9 带吸引因子的多机器主动SLAM建图80步 Fig. 9 80 steps of multi-robot active SLAM with attractors | |
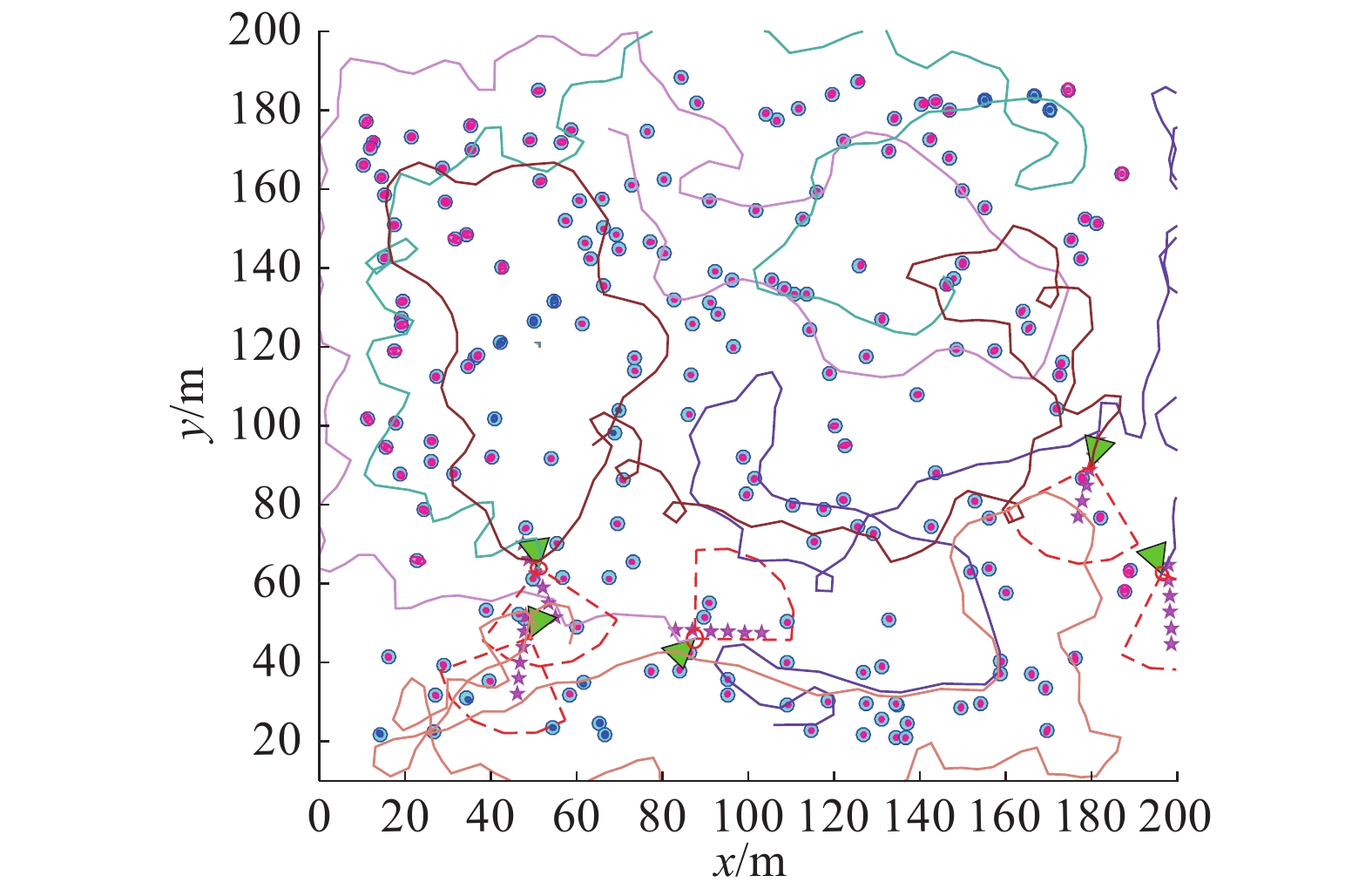
|
Download:
|
| 图 10 带吸引因子的多机器主动SLAM建图完成 Fig. 10 Multi-robot active SLAM with attractors completed | |
如图11所示,为带吸引因子的多机器主动SLAM仿真中凸组合融合前后地标估计误差协方差迹的对比,其中共有184个地标是融合地标,纵坐标为该地标融合前后估计误差协方差的迹的大小,可以看出凸组合融合可以有效地提升地标估计的精度,降低估计的不确定度。

|
Download:
|
| 图 11 凸组合融合前后地标估计误差协方差迹的对比 Fig. 11 Comparison of landmark estimation error covariance trace before and after convex combination | |
表1所示为当仿真步数为167步时5种SLAM方法平均地标估计与环境覆盖率的对比。
| 表 1 5种SLAM方法对比 Tab.1 Comparison of five SLAM methods |
从表1中可以看出,本文改进方法即带吸引因子的多机器人主动SLAM不仅可以覆盖全部环境而且平均地标估计均低于其他方法。通过与单机器人的对比可以看出多机器人系统的优越性,多机器人团队可以同时不同地作业,协作完成任务。通过与无吸引因子的方法对比,说明吸引因子的有效性,带吸引因子的多机器人团队,可以在机器人位置估计大于一定阈值下,通过吸引因子,让机器人先去定位精度较高的地标,修正自己的位姿,然后去扩展环境,自身定位精度提升有利于提升估计地标的精度。无吸引因子的主动SLAM方法和本文改进方法的平均地标估计均低于基于EKF融合的方法,说明凸组合融合可以很好地降低地标估计的不确定度。综上所诉,本文改进方法可以很好地遍历完环境,而且对地标的估计精度有所提升。
5 结束语本文研究基于EKF-SLAM的多机器人主动SLAM问题,将主动SLAM问题转化为最优控制选择问题,通过引入吸引因子,既提升了机器人自身定位建图准确性,又引导多机器人团队机器人探索环境。对于多个机器人观测到的同一地标,采用凸组合融合,降低该地标的不确定度。并通过仿真验证算法有效性,实现多机器人主动SLAM,其鲁棒性、定位建图精度都大大提升。但是本文算法依赖于多机器人之间通信良好,对多机器人在通信受限的情况下的主动SLAM研究还需要进一步完善。
| [1] |
张恒, 樊晓平. 移动机器人同步定位与地图构建过程中的轨迹规划研究[J]. 机器人, 2006, 28(3): 285-290. ZHANG Heng, FAN Xiaoping. Mobile robot trajectory planning in simultaneous localization and mapping problem[J]. Robot, 2006, 28(3): 285-290. DOI:10.3321/j.issn:1002-0446.2006.03.010 (  0) 0)
|
| [2] |
HASHEMIFAR Z S, ADHIVARAHAN C, BALAKRISHNAN A, et al. Augmenting visual SLAM with Wi-Fi sensing for indoor applications[J]. Autonomous robots, 2019, 43(8): 2245-2260. DOI:10.1007/s10514-019-09874-z ( 0) 0)
|
| [3] |
张毅, 陈起, 罗元. 室内环境下移动机器人三维视觉SLAM[J]. 智能系统学报, 2015, 10(4): 615-619. ZHANG Yi, CHEN Qi, LUO Yuan. Three dimensional visual SLAM for mobile robots in indoor environments[J]. CAAI transactions on intelligent systems, 2015, 10(4): 615-619. (  0) 0)
|
| [4] |
权美香, 朴松昊, 李国. 视觉SLAM综述[J]. 智能系统学报, 2016, 11(6): 768-776. QUAN Meixiang, PIAO Songhao, LI Guo. An overview of visual SLAM[J]. CAAI transactions on intelligent systems, 2016, 11(6): 768-776. (  0) 0)
|
| [5] |
沈永福, 王希彬. 基于边界的无人机主动SLAM算法[J]. 海军航空工程学院学报, 2014, 29(5): 461-464. SHEN Yongfu, WANG Xibin. UAV active SLAM algorithm based on boundary[J]. Journal of naval aeronautical and astronautical university, 2014, 29(5): 461-464. DOI:10.7682/j.issn.1673-1522.2014.05.013 (  0) 0)
|
| [6] |
DONG Siyan, XU Kai, ZHOU Qiang, et al. Multi-robot collaborative dense scene reconstruction[J]. ACM transactions on graphics, 2019, 38(4): 84. ( 0) 0)
|
| [7] |
陶通, 黄亚楼, 苑晶, 等. 基于协助校正方法的多机器人主动同时定位与建图[J]. 模式识别与人工智能, 2012, 25(3): 534-543. TAO Tong, HUANG Yalou, YUAN Jing, et al. Multi-robot active simultaneous localization and mapping based on cooperative correction approach[J]. Pattern recognition and artificial intelligence, 2012, 25(3): 534-543. DOI:10.3969/j.issn.1003-6059.2012.03.025 (  0) 0)
|
| [8] |
张国良, 汤文俊, 曾静, 等. 考虑通信状况的多机器人CSLAM问题综述[J]. 自动化学报, 2014, 40(10): 2073-2088. ZHANG Guoliang, TANG Wenjun, ZENG Jing, et al. An overview on the cooperative SLAM problem of multi-robot systems considering communication conditions[J]. Acta automatica sinica, 2014, 40(10): 2073-2088. (  0) 0)
|
| [9] |
FEDER H J S, LEONARD J J, SMITH C M. Adaptive mobile robot navigation and mapping[J]. The International journal of robotics research, 1999, 18(7): 650-668. DOI:10.1177/02783649922066484 ( 0) 0)
|
| [10] |
WILLIAMS S B. Efficient solutions to autonomous mapping and navigation problems[D]. Sydney, Australia: University of Sydney, 2001.
( 0) 0)
|
| [11] |
苑晶, 黄亚楼, 陶通, 等. 基于局部子地图方法的多机器人主动同时定位与地图创建[J]. 机器人, 2009, 31(2): 97-103. YUAN Jing, HUANG Yalou, TAO Tong, et al. Multi-robot active simultaneous localization and mapping based on local submap approach[J]. Robot, 2009, 31(2): 97-103. DOI:10.3321/j.issn:1002-0446.2009.02.001 (  0) 0)
|
| [12] |
LEUNG C, HUANG Shoudong, DISSANAYAKE G. Active SLAM using model predictive control and attractor based exploration[C]//Proceedings of 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. Beijing, China, 2006: 5026−5031.
( 0) 0)
|
| [13] |
ATANASOV N, LE NY J, DANIILIDIS K, et al. Decentralized active information acquisition: theory and application to multi-robot SLAM[C]//Proceedings of 2015 IEEE International Conference on Robotics and Automation. Seattle, USA, 2015: 4775−4782.
( 0) 0)
|
| [14] |
刘杨. 基于激光传感器的移动机器人主动SLAM[D]. 天津: 南开大学, 2009: 24−29. LIU Yang. Mobile robot based on laser sensor active SLAM[D]. Tianjin: Nankai University, 2009: 24−29. (  0) 0)
|
| [15] |
ZHU Hongyan, CHEN Shuo, HAN Chongzhao. Fusion of Gaussian mixture models for possible mismatches of sensor model[J]. Information fusion, 2014, 20: 203-212. DOI:10.1016/j.inffus.2014.02.002 ( 0) 0)
|
| [16] |
THRUN S, BURGARD W, FOX D. Probabilistic robotics[M]. Cambridge, MA: MIT Press, 2005.
( 0) 0)
|
| [17] |
MASINJILA R, PAYEUR P. Consistent multirobot localization using heuristically tuned extended Kalman filter[C]//Proceedings of 2017 IEEE International Symposium on Robotics and Intelligent Sensors. Ottawa, Canada, 2017: 297−303.
( 0) 0)
|
| [18] |
季秀才, 郑志强, 张辉. SLAM问题中机器人定位误差分析与控制[J]. 自动化学报, 2008, 34(3): 323-330. JI Xiucai, ZHENG Zhiqiang, ZHANG Hui. Analysis and control of robot position error in SLAM[J]. Acta automatica sinica, 2008, 34(3): 323-330. (  0) 0)
|
| [19] |
ATANASOV N, LE NY J, DANIILIDIS K, et al. Information acquisition with sensing robots: algorithms and error bounds[C]//Proceedings of 2014 IEEE International Conference on Robotics and Automation. Hong Kong, China, 2014: 6447−6454.
( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16


