自抗扰控制(active disturbance rejection control, ADRC)和PI型广义预测控制(PI type generalized predictive control, PI-GPC)都是为解决系统所受到干扰问题而引入的算法。

1988年韩京清提出ADRC算法^[1-2]，通过对系统受到的总扰动进行估计和补偿，ADRC算法具有较强的克服干扰的能力，也因此有着广泛的应用前景。钟斌等^[3]将ADRC算法应用于交流感应电动机的精确解耦模型，从而改善了交流感应电动机的调速性能并且快速跟踪了负载转矩。王东阳等^[4]将ADRC算法应用于电压型PWM整流器的功率控制，获得了很好的控制效果。荣智林等^[5]使用滑膜自抗扰算法调节永磁同步电动机的转速，改进算法具有更好的抗干扰能力。Cao等^[6]将自抗扰控制用于并网逆变器的电流控制，并研究了其鲁棒性。Ramirez-Neria等^[7]将自抗扰控制和微分平滑算法结合，在欠驱动系统中进行轨迹跟踪，降低了实验过程中对测量噪声的敏感性。Das等^[8]在风能转换系统中使用自抗扰控制算法，增强了向电网传输的有功和无功功率的稳态和瞬态响应，得到了较好的效果。Wang等^[9]将自抗扰控制和矢量谐振控制相结合，用于永磁同步直流电机的电流谐波抑制。从而建立了线性电动机控制平台。Zhou等^[10]使用基于偏差控制原理的线性自抗扰控制进行并网光伏逆变器的控制，提高了控制的稳定性和抗干扰性。

1994年陈增强等^[11]提出了 PI-GPC 算法。通过对过程输出进行多步预测，PI-GPC算法的动态性能和鲁棒性较好，被广泛应用于工业生产。仉宝玉等^[12]提出了一种由遗传算法进行参数优化的PI-GPC算法，它有效地解决了PI-GPC算法的参数优化问题。为了进一步提高非线性系统控制器的性能，朱峰等^[13]提出了一种基于U模型的非线性系统的PI-GPC算法。

尽管有着上述优点，但是ADRC算法在时滞较大的系统中具有局限性；PI-GPC算法在线计算量大，在快速系统中的应用受限。因此，结合两种算法的优势，我们在先前的研究中设计了PI型自抗扰广义预测控制(PI-ADRGPC)算法^[14]。该算法不依赖于受控对象的具体模型，无需在线辨识系统参数，且可以对总扰动进行在线补偿，从而将系统简化成串联积分器形式。该算法可以离线求解Diophantine方程，从而使在线计算量得以减少，克服了PI-GPC算法在线计算量大的问题。利用滚动优化的思想对系统输出进行多步预测，该算法可以克服ADRC算法在大时滞系统中的局限性。

1 PI-ADRGPC介绍

本节将对PI-ADRGPC进行详细介绍，其算法结构如图1所示。

如图1所示，将系统所有外部干扰以及内部未知信息看作总扰动，用扩张状态观测器(extended state observer, ESO)估计该扰动并将其扩张为x_n+1，然后通过线性状态误差反馈控制律(linear states error feedback control laws, LSEF)补偿总扰动，虚线框内部分被化为积分器串联形式。针对该部分设计PI-GPC的控制量u，就完成了整个PI-ADRGPC的设计。和ADRC控制相比，该控制算法将原来PD控制器换成了PI-GPC，从而改善了算法性能。

给出以下形式的离散单输入单输出系统，称为CARIMA模型：

$A({z^{ - 1}})y(k) = B({z^{ - 1}})u(k - 1) + \frac{{C({z^{ - 1}})\zeta (k)}}{\Delta }$

(1)

式中：u(k−1)是被控对象输入；y(k)是被控对象输出；z⁻¹是后移算子； $\zeta (t)$ 是表示扰动的随机序列； $\Delta = 1 - {z^{ - 1}}$ 为差分算子。 $A({z^{ - 1}})$ 、 $B({z^{ - 1}}) $ 、 $C({z^{ - 1}}) $ 分别为

$\left\{ \begin{array}{l} A({z^{ - 1}}) = 1 + {a_1}{z^{ - 1}} + \cdots + {a_{{n_a}}}{z^{ - n}} \\ B({z^{ - 1}}) = {b_0} + {b_1}{z^{ - 1}} + \cdots + {b_{{n_b}}}{z^{ - n}} \\ C({z^{ - 1}}) = 1 + {c_1}{z^{ - 1}} + \cdots + {c_{{n_c}}}{z^{ - n}} \\ \end{array} \right.$

为简单起见，令 $C({z^{ - 1}}) = 1$ 。

在自抗扰算法中，对总扰动进行补偿后，系统简化为串联积分器形式，一阶系统就是单个积分器。传递函数为

$G(s) = \frac{1}{s}$

用零阶保持器对其离散化得到脉冲传递函数：

$G({z^{ - 1}}) = (1 - {z^{ - 1}})Z\Bigg[\frac{{G(s)}}{s}\Bigg] = \frac{{T{z^{ - 1}}}}{{1 - {z^{ - 1}}}}$

(2)

忽略扰动ζ(k)，则式(1)化为

$A({z^{ - 1}})y(k) = B({z^{ - 1}})u(k - 1)$

其脉冲传递函数可以定义为

$G({z^{ - 1}}) = {z^{ - 1}}\frac{{B({z^{ - 1}})}}{{A({z^{ - 1}})}}$

(3)

由式(2)和式(3)对比得：

$A({z^{ - 1}}) = 1 - {z^{ - 1}},B({z^{ - 1}}) = T$

(4)

将丢番图方程写为

$\begin{array}{l} \left\{ \begin{array}{l} 1 = {E_j}({z^{ - 1}})A({z^{ - 1}})\Delta + {z^{ - j}}{F_j}({z^{ - 1}}) \\ {E_j}({z^{ - 1}})B({z^{ - 1}}) = {G_j}({z^{ - 1}}) + {z^{ - j}}{H_j}({z^{ - 1}}) \\ \end{array} \right. \\ \left\{ \begin{array}{l} {E_j}({z^{ - 1}}) = e{}_1 + {e_2}{z^{ - 1}} + \cdots + {e_j}{z^{ - (j - 1)}} \\ {F_j}({z^{ - 1}}) = f_1^j + f_2^j{z^{ - 1}} + \cdots + f_{n{\rm{ + }}1}^j{z^{ - n}} \\ {G_j}({z^{ - 1}}) = {g_1} + {g_2}{z^{ - 1}} + \cdots + {g_j}{z^{ - (j - 1)}} \\ {H_j}({z^{ - 1}}) = h_1^j + h_2^j{z^{ - 1}} + \cdots + h_{n - 1}^j{z^{ - (n - 2)}} \\ \end{array} \right. \\ \end{array} $

(5)

将式(4)代入式(5)，得到一阶系统丢番图方程的解为

$\begin{array}{l} {e_j} = j,{f_1}^j = j + 1,{f_2}^j = - j \\ {g_j} = jT,{H_j}({z^{ - 1}}) = 0 \\ \end{array} $

考虑以下PI-GPC算法的性能指标函数：

$\begin{array}{c} J = E\Bigg\{ \displaystyle\sum\limits_{j = 1}^N {[{K_p}{{(\Delta e(k + j))}^2} + {K_i}e{{(k + j)}^2}]} + \\ \lambda \displaystyle\sum\limits_{j = 1}^{{N_u}} {{{[\Delta u(k + j - 1)]}^2}} \Bigg\} \\ \end{array} $

(6)

式中： ${K_p} \geqslant 0,{K_i} > 0$ 是给定常数，称为比例因子和积分因子； $\Delta u(k + j - 1) = 0$ ( $j = {N_u},{N_u} + 1, \cdots ,N$ )表示当 $j = {N_u},{N_u} + 1, \cdots ,N$ 时，系统输入不变；N是预测步长；N_u是控制步长；而λ(λ>0)是控制加权系数。

$\Delta e(k + j) = e(k + j) - e(k + j - 1)$

式中 $j = 1,2, \cdots ,N$ 。

误差序列的计算如式(7)所示：

$e(k + j) = w(k + j) - y(k + j)$

(7)

设计以下柔化序列w(k + j)来使输出平缓达到给定值：

$\begin{array}{c} \overline {{W}} = {[w(k + 1),\;w(k + 2),\; \cdots,\;w(k + N)]^{\rm{T}}} = \\ {{{F}}_{{\alpha }}}y(k) + {\overline {{F}} _{{\alpha }}}{y_r}(k) \end{array} $

(8)

式中： $\alpha \left( {0 \leqslant \alpha \leqslant 1} \right)$ 是柔化因子；y_r(k)是参考轨迹； ${{{F}}_{{\alpha }}}{\rm{ = [}}\alpha {\rm{,}}\;{\alpha ^2}{\rm{,}}\; \cdots ,\;{\alpha ^N}{{\rm{]}}^{\rm{T}}};\;{\overline {{F}} _{{\alpha }}} = {[1 - \alpha ,\;1 - {\alpha ^2}, \;\cdots ,\;1 - {\alpha ^N}]^{\rm{T}}}$ 。

j步后的预测输出为

$y(k + j) = {G_j}\Delta u(k + j - 1) + {F_j}y(k) + {H_j}\Delta u(k - 1)$

令 ${y_0}(k + j) = {F_j}y(k) + {H_j}\Delta u(k - 1)$ ，所以有

$y(k + j) = {y_0}(k + j) + {G_j}\Delta u(k + j - 1)$

(9)

将式(9)写为向量形式：

$\overline {{Y}} = \overline {{{{Y}}_0}} + {{{G}}_{{i}}}\overline {{U}} $

(10)

其中

$\overline {{Y}} = {[y(k + 1)\;y(k + 2)\; \cdots \;y(k + N)]^{\rm{T}}}$

${\overline {{Y}_0}} = {[{y_0}(k + 1)\;{y_0}(k + 2)\; \cdots \;{y_0}(k + N)]^{\rm{T}}}$

${{{G}}_{{i}}} = \left[ {\begin{array}{*{20}{c}} {{g_0}}&{}&{}&0 \\ {{g_1}}&{{g_0}}&{}&{} \\ \vdots & \vdots &{}&{} \\ {{g_{{N_u} - 1}}}&{{g_{{N_u} - 2}}}& \cdots &{{g_0}} \\ \vdots & \vdots &{}&{} \\ {{g_{N - 1}}}&{{g_{N - 2}}}& \cdots &{{g_{N - {N_u}}}} \end{array}} \right]$

${\overline{ U}} = {[\Delta u(k)\;\Delta u(k + 1)\; \cdots \;\Delta u(k + {N_u} - 1)]^{\rm{T}}}$

根据式(7)和式(10)，可得：

$\overline {{E}} = \overline {{W}} - \overline {{Y}} = \overline {{W}} - \overline {{{{Y}}_0}} - {{{G}}_{{i}}}\overline {{U}} $

$\Delta \overline {{E}} = \Delta \overline {{W}} - \Delta \overline {{Y}} = \Delta \overline {{W}} - \Delta \overline {{{{Y}}_0}} - {{{G}}_p}\overline {{U}} $

其中

$ {\overline{ E}} = {[e(k + 1)\;e(k + 2)\; \cdots \;e(k + N)]^{\rm{T}}} $

$ {{{G}}_{{p}}} = \left[ {\begin{array}{*{20}{c}} {{g_0}}&{}&{}&0\\ {{g_1} - {g_0}}&{{g_0}}&{}&{}\\ \vdots & \vdots &{}&{}\\ {{g_{{N_u} - 1}} - {g_{{N_u} - 2}}}&{{g_{{N_u} - 2}} - {g_{{N_u} - 3}}}& \cdots &{{g_0}}\\ \vdots & \vdots &{}&{}\\ {{g_{N - 1}} - {g_{N - 2}}}&{{g_{N - 2}} - {g_{N - 3}}}& \cdots &{{g_{N - {N_u}}} - {g_{N - {N_u} - 1}}} \end{array}} \right] $

将式(6)写为向量形式：

$\begin{array}{c} {{J}} = {K_p}\Delta {{{\overline{ E}}}^{\rm{T}}}\Delta {\overline{ E}} + {K_i}{{{\overline{ E}}}^{\rm{T}}}{\overline{ E}} + \lambda {{{\overline{ U}}}^{\rm{T}}}{\overline{ U}} = \\ {K_p}{[\Delta {\overline{ W}} - \Delta {{{\overline{ Y}}}_0} - {{{G}}_{{p}}}{\overline{ U}}]^{\rm{T}}}[\Delta {\overline{ W}} - \Delta {{{\overline{ Y}}}_0} - {{{G}}_{{p}}}{\overline{ U}}] + \\ {K_i}{[{\overline{ W}} - {{{\overline{ Y}}}_0} - {{{G}}_{{i}}}{\overline{ U}}]^{\rm{T}}}[{\overline{ W}} - {{{\overline{ Y}}}_0} - {{{G}}_{{i}}}{\overline{ U}}] + \lambda {{{\overline{ U}}}^{\rm{T}}}{\overline{ U}} \\ \end{array} $

当J为最小值时，

$\begin{split}&{\overline{ U}} = {(\lambda {\bf{I}} + {K_{p}}{{{G}}^{{\rm{T}}}_{{p}}} {{{G}}_{{p}}} + {K_i}{{{G}}^{{\rm{T}}}_{{i}}} {{{G}}_{{i}}})^{ - 1}} \cdot\\ &[{K_p}{{{G}}^{{\rm{T}}}_{{p}}} (\Delta {\overline{ W}} - \Delta {\overline Y_0}) + {K_i}{{{G}}^{{\rm{T}}}_{{i}}} ({\overline{ W}} - {{\overline{ Y}}_0})] \end{split}$

(11)

令 ${{K}} = [1,0,0,\cdots ,0]_{{N_u} \times 1}^{\rm{T}}$

$\begin{split}& \Delta u(k) = {{{K}}^{\rm{T}}}{(\lambda {{I}} + {K_p}{{{G}}_{{p}}}^{\rm{T}} {{{G}}_{{p}}} + {K_i}{{{G}}_{{i}}}^{\rm{T}}{{{G}}_{{i}}})^{ - 1}} \cdot \\ &[{K_p}{{{G}}_{{p}}}^{\rm{T}}(\Delta {\overline{ W}} - \Delta {{{\overline{ Y}}}_0}) + {K_i}{{{G}}_{{i}}}^{\rm{T}}({\overline{ W}} - {{{\overline{ Y}}}_0})] \end{split} $

其中， $\Delta u\left( k \right)$ 是 ${\overline{ U}}$ 的第一个分量。

$u(k) = u(k - 1) + {{R}}_{{p}}^{\rm{T}} (\Delta {\overline{ W}} - \Delta {{\overline{ Y}}_0}) + {{R}}_{{i}}^{\rm{T}} ({\overline{ W}} - {{\overline{ Y}}_0})$

其中，

${{{R}}_{{p}}} = {K_p}{{{K}}^{\rm{T}}}{(\lambda {{I}} + {K_p}{{{G}}_{{p}}}^{\rm{T}}{{{G}}_{{p}}} + {K_i}{{{G}}_{{i}}}^{\rm{T}}{{{G}}_{{i}}})^{ - 1}}{{G}}_{{p}}^{\rm{T}} $

${{{R}}_{{i}}} = {K_i}{{{K}}^{\rm{T}} }{(\lambda {{I}} + {K_p}{{{G}}_{{p}}}^{\rm{T}}{{{G}}_{{p}}} + {K_i}{{{G}}_{{i}}}^{\rm{T}}{{{G}}_{{i}}})^{ - 1}}{{G}}_{{i}}^{\rm{T}} $

则可以得到基于CARIMA模型的PI-ADRGPC算法控制律。

为了方便计算，本文把所得控制律进行简化。

先定义：

${{S}} = \left[ {\begin{array}{*{20}{c}} 1& \cdots &0 \\ { - 1}& \quad &0 \\ \vdots & \quad & \vdots \\ 0& \quad &1 \\ 0& \cdots &{ - 1} \end{array}} \right]$

则可得 ${{{G}}_{{p}}} = {{S}}{{{G}}_{{i}}}$ ， $\Delta {\overline{ W}} = {{S\overline W}}$ ， $\Delta {{\overline{ Y}}_0} = {{S}}{{\overline{ Y}}_0}$ 。使用上述公式简化式(11)，可以得到：

$\begin{split} &{\overline{ U}} = {[\lambda {{I}} + {K_p}{{G}}_{{i}}^{\rm{T}} {{{S}}^{\rm{T}} }{{S}}{{{G}}_{{i}}} + {K_i}{{G}}_{{i}}^{\rm{T}} {{{G}}_{{i}}}]^{ - 1}} \cdot\\ & [{K_p}{{G}}_{{i}}^{\rm{T}} {{{S}}^{\rm{T}} }({{S\overline W}} - {{S}}{{{\overline{ Y}}}_0}) + {K_i}{{G}}_{{i}}^{\rm{T}} ({\overline{ W}} - {{{\overline{ Y}}}_0})] = \\ & {(\lambda {{I}} + {{G}}_{{i}}^{\rm{T}} {{\varOmega }}{{{G}}_{{i}}})^{ - 1}}{{G}}_{{i}}^{\rm{T}} {{\varOmega }}({\overline{ W}} - {{{\overline{ Y}}}_0}) \\ \end{split} $

${{\varOmega }} = {K_i}{{I}} + {K_p}{{{S}}^{\rm{T}}}{{S}}$

2 PI-ADRGPC的离散形式

由上述分析可知：

$\Delta u(k) = {{{h}}^{\rm T}}(\overline {{W}} - {\overline {{Y}} _0})$

(12)

其中 ${{{h}}^{\rm T}} = [1,0,0, \cdots ,0]{(\lambda {{I}} + {{G}}_{{i}}^{\rm T}{{\varOmega }}{{{G}}_{{i}}})^{ - 1}}{{G}}_{{i}}^{\rm T}{{\varOmega }}$ 。

将式(8)代入式(12)得：

$\begin{array}{l} \Delta u(k) = {{{h}}^{\rm T}}[{\overline {{F}} _{{\alpha }}}{y_r}(k) - ({{F}} - {{{F}}_{{\alpha }}})y(k) - {{H}}\Delta u(k - 1)] \end{array} $

即

$T\Delta u(k) = R{y_r}(k) - Sy(k)$

(13)

其中 $R = {{{h}}^{\rm T}}{\overline F _\alpha },S = {{{h}}^{\rm T}}(F - {F_\alpha }),T = 1 + {z^{ - 1}}{{{h}}^{\rm T}}{{H}}({z^{ - 1}})$ 。

已知

$y(k) = G({z^{ - 1}})u(k)$

(14)

式(14)两边同乘 $T\Delta $ ，并代入式(13)得：

$y(k) = \frac{{G({z^{ - 1}})D({z^{ - 1}})}}{{1 + G({z^{ - 1}})H({z^{ - 1}})}}{y_r}(k)$

其中 $D({z^{ - 1}}) = \dfrac{R}{{T\Delta }},H({z^{ - 1}}) = \dfrac{S}{{T\Delta }}$ 。

PI-GPC算法可以转化为闭环离散系统的形式，结构如图2所示。

LESO的内模控制结构如图3所示^[15]。

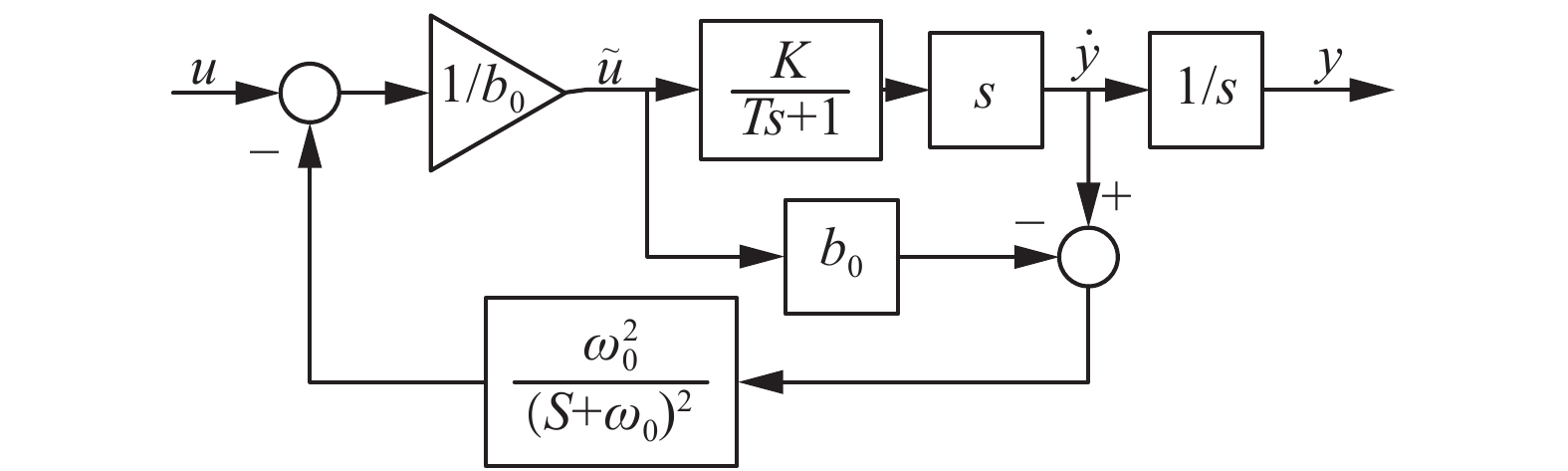
所以PI-ADRGPC下的闭环离散系统结构如图4所示^[16]。

对于一阶惯性环节

${G_p}(s) = \frac{K}{{Ts + 1}}$

ESO内模结构下的闭环传递函数为

$G(s) = \dfrac{{{b_0}{{(s + {w_o})}^2}}}{{T{b_0}{s^3} + (2{w_o}{b_0}T + 1){s^2} + (2{w_o}{b_0} + w_o^2{b_0})s}}$

设

$\begin{array}{c} G({z^{ - 1}}) = \\ Z\Bigg[\dfrac{{1 - {{\rm{e}}^{ - \tau s}}}}{s} \cdot \dfrac{{{b_0}{{(s + {w_o})}^2}}}{{T{b_0}{s^3} + (2{w_o}{b_0}T + 1){s^2} + (2{w_o}{b_0} + w_o^2{b_0})s}}\Bigg] \end{array} $

则闭环系统的特征方程为

$1{\rm{ + }}G({z^{ - 1}})H({z^{ - 1}}) = 0$

因此，只需考虑开环传递函数的频率响应。

$G({z^{ - 1}})H({z^{ - 1}}) = \frac{{{z^{ - 1}}B({z^{ - 1}})S({z^{ - 1}})}}{{A({z^{ - 1}})T({z^{ - 1}})\Delta }}$

3 PI-ADRGPC的稳定性检测

给出以下一阶惯性环节：

$G(s) = \frac{2}{{2s + 1}}$

控制过程中采样时间 $T_0=0.1$ ，控制增益的估值价 $b_0=1$ 。

所以，PI-ADRGPC算法主要受参数N、w_o、α、λ、N_u、K_P、K_I的影响。对参数进行调整，并且通过Bode图来分析参数变化对系统性能的影响。

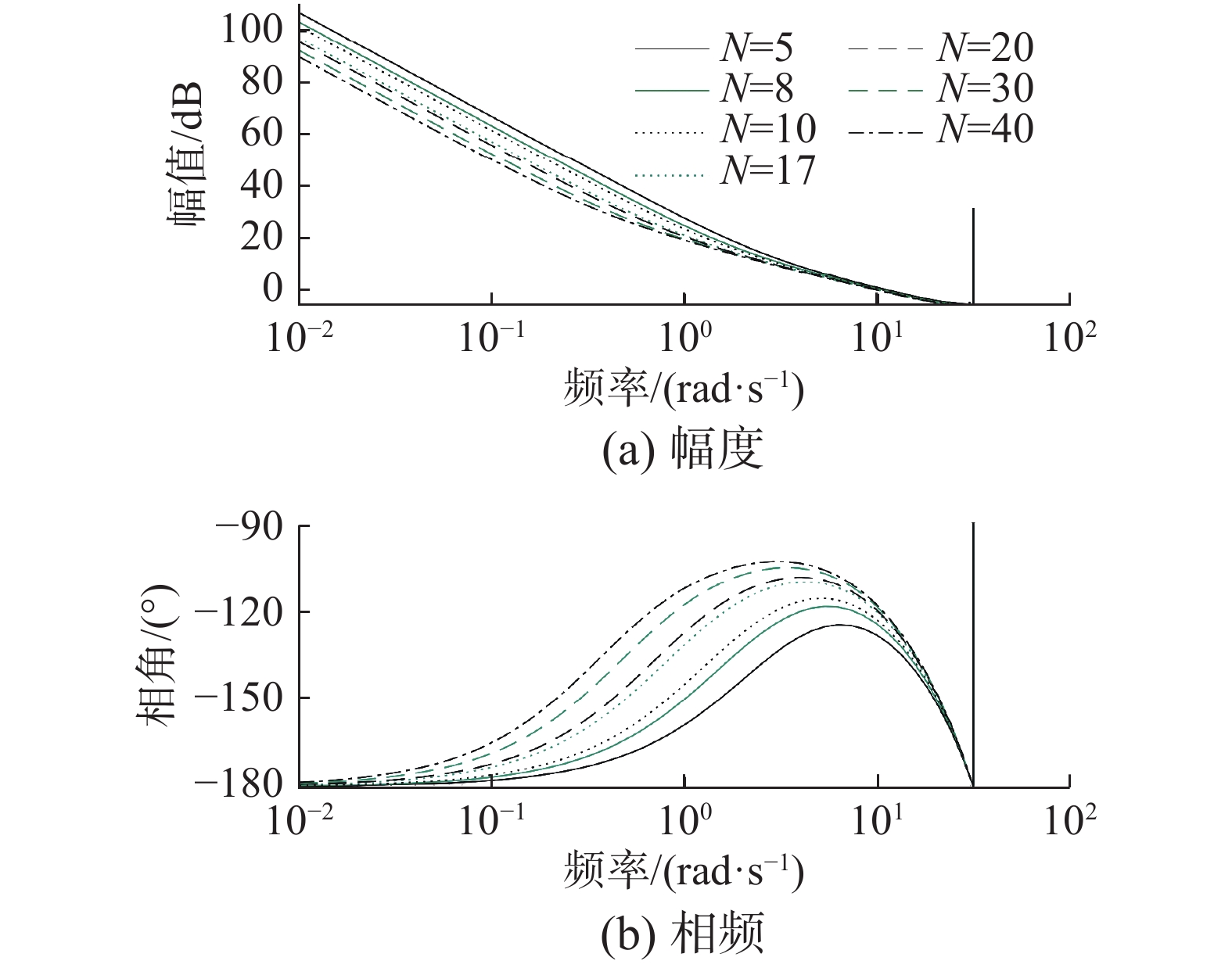
3.1 N改变对系统性能的影响

当N分别取5、8、10、17、20、30、40时，取λ = 0.005, α = 0.2, w_o = 8, N_u = 1, K_P = 0.1, K_I = 1开环系统的Bode图如图5所示。

实验结果显示，当N_u = 1时，N取值较大，系统截止频率小，响应速度慢，但是相角裕度较大，稳定性较好。

当N_u = 2时，开环系统的伯德图如图6所示。对应的相角裕度和截止频率如表1所示。

从图6和表1可得，预测时域的改变会同时影响系统的相角裕度和截止频率。N_u = 2时，N取值较小，系统截止频率小，响应速度慢，但是相角裕度较大，稳定性较好。

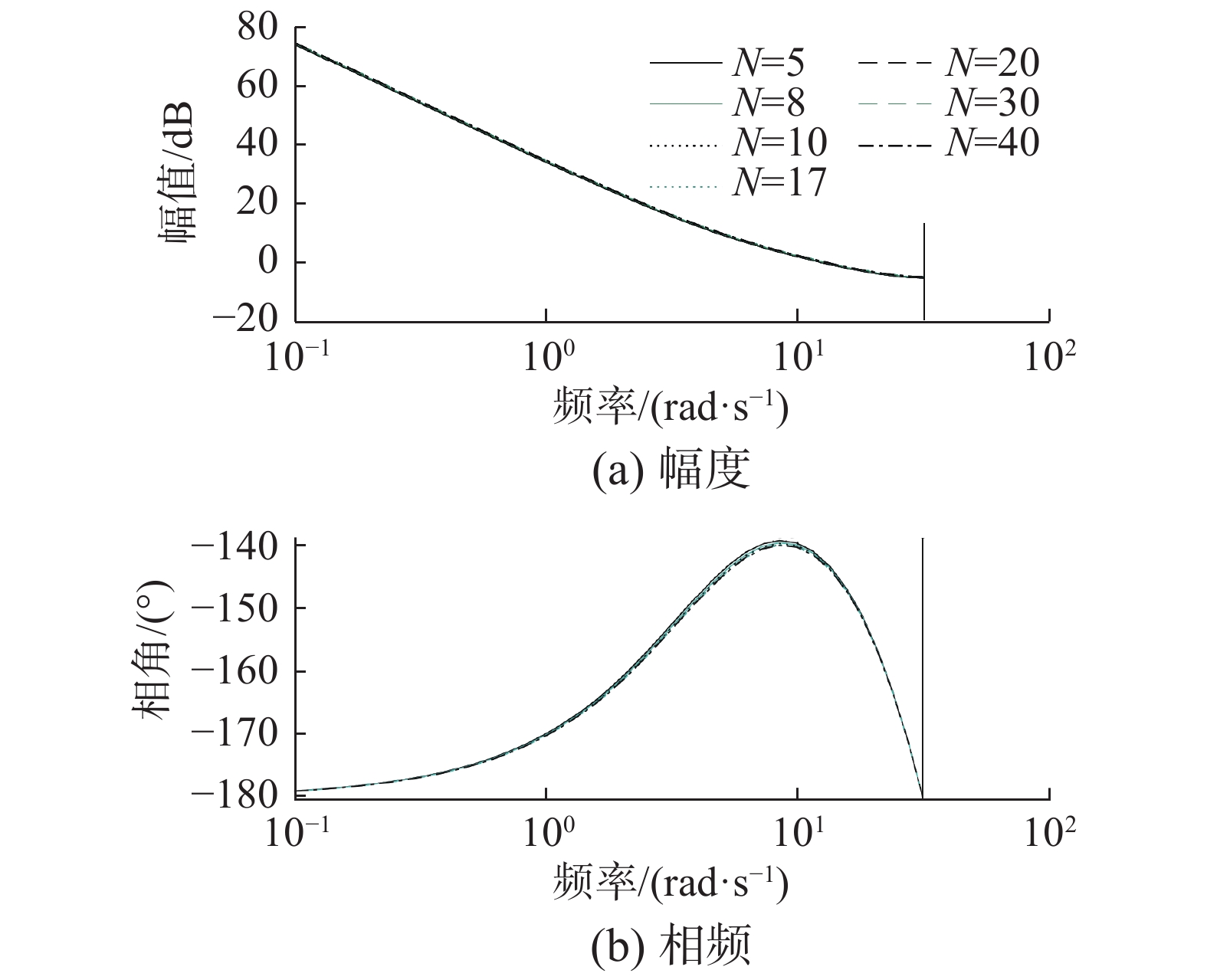
当N_u = 3时，开环系统的Bode图如图7所示。

实验结果显示，当N_u = 3时，随着N的改变，系统性能几乎不发生变化。因此N_u取值越大，N的改变对系统性能的影响越不明显。

N改变对系统性能的影响也和N_u的取值相关。应选择合适的预测时域，使控制过程既能得到较快的响应速度，又具有较好的稳定性。

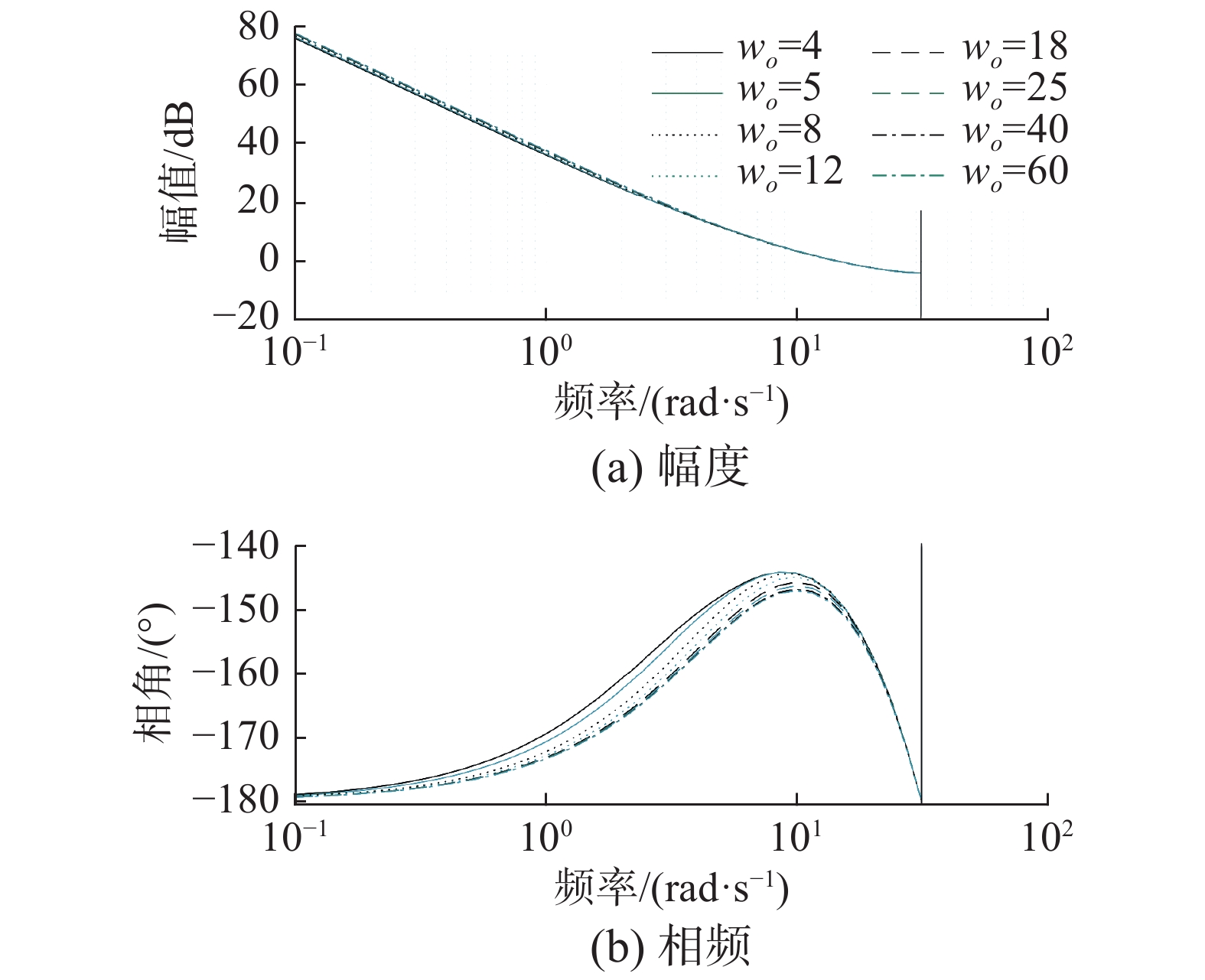
3.2 w_o改变对系统性能的影响

当 ${w_o}$ 分别取4、5、8、12、18、25、40、60时，取N = 17, λ = 0.005, α = 0.2, N_u = 2, K_P = 0.1, K_I = 1，开环系统的Bode图如图8所示。

随着w_o增加，系统的截止频率和相角裕度几乎不变，但是ESO的精度提高了。即w_o起滤波作用，w_o越大，系统的输入输出对噪声就越敏感。因此w_o应该限制在一定范围内以获得较好的控制效果。

3.3 α改变对系统性能的影响

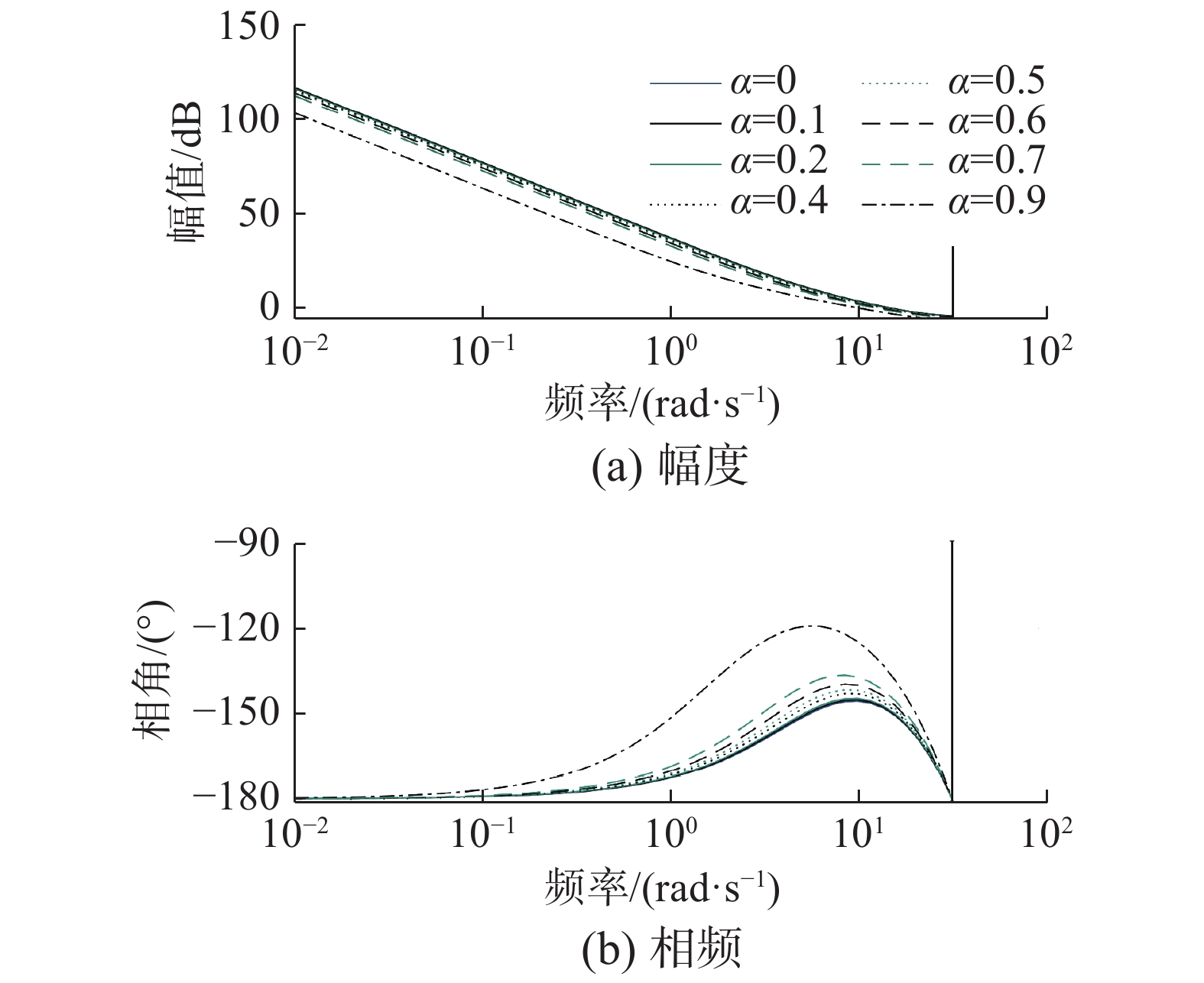
当α分别取0、0.1、0.2、0.4、0.5、0.6、0.7、0.9时，取N = 17, λ = 0.005, w_o = 8, N_u = 2, K_P = 0.1, K_I = 1，开环系统的Bode图如图9所示。

由图9可得，α取较大值时，系统的截止频率较低，响应速度慢，影响了系统的动态性能，但是系统稳定性较好。因此在确定了预测时域值N的基础上进行参数调节，α应在1附近取值，才能获得较好的控制效果。

3.4 λ改变对系统性能的影响

当λ分别取1、0.5、0.1、0.05、0.01、0.005、0.001、0时，取N = 17, α = 0.2, w_o = 8, N_u = 2, K_P = 0.1, K_I = 1,开环系统的Bode图如图10所示。

由图10可得，随着λ减小，系统的截止频率升高，响应速度变快。但同时系统的相角裕度减小，稳定性降低，而且也出现了超调。相反，如果λ增大，则相角裕度增加，超调消失，但响应速度减慢。所以实际会选择较小的λ。

3.5 N_u改变对系统性能的影响

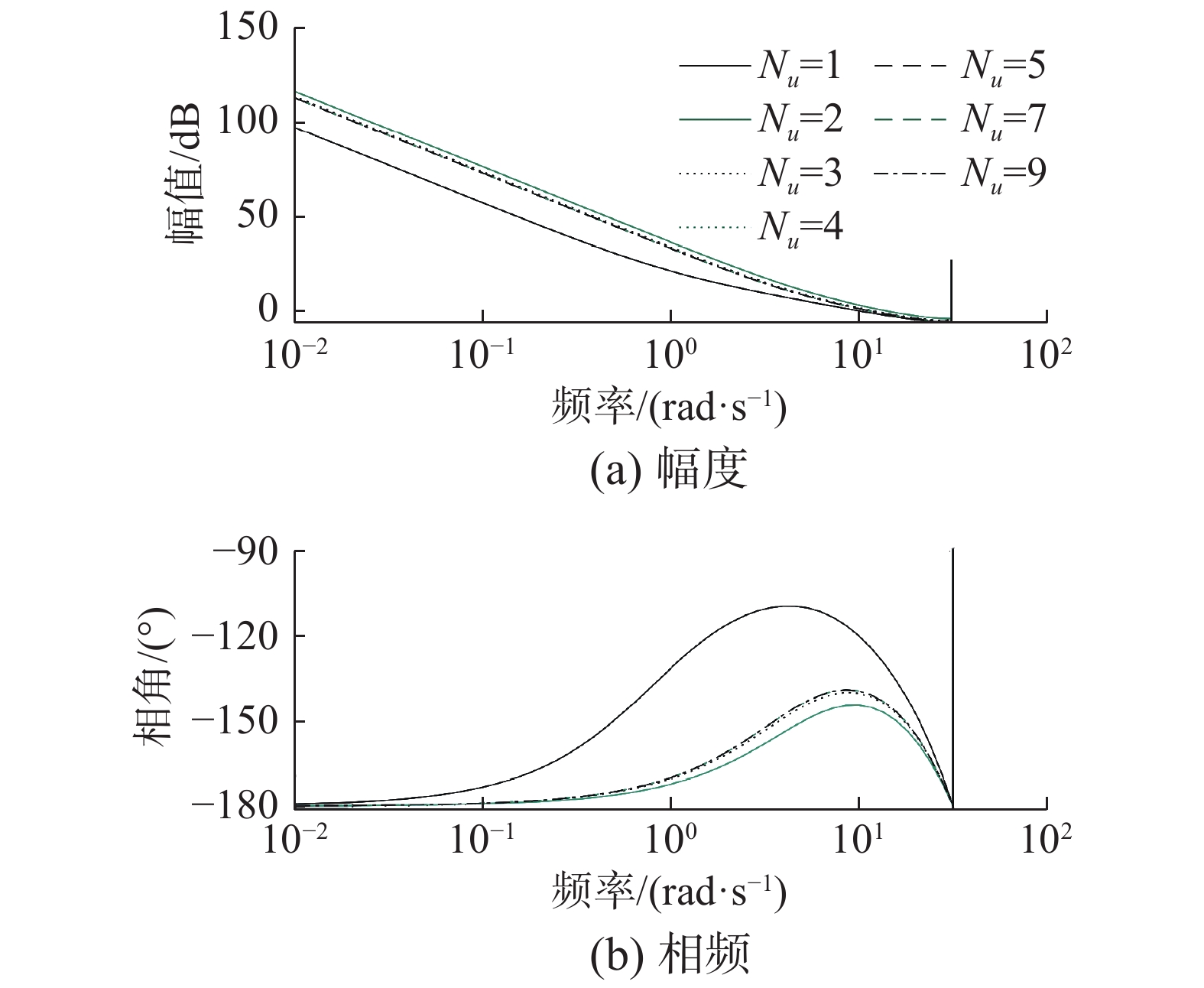
当N_u分别取1、2、3、4、5、7、9时，取N = 17, λ = 0.005, α = 0.2, w_o = 8, K_P = 0.1, K_I = 1。开环系统的Bode图如图11所示。对应的相角裕度和幅值裕度如表2所示。

在PI-GPC中应满足N_u ≤ N。图11和表2显示，当N_u = 1时，截止频率最小，系统响应速度最慢。但是相角裕度最大，稳定性强。当N_u>1时，系统的响应速度比N_u = 1时快。但相角裕度与N_u = 1时相比下降，系统的稳定性降低。当N_u = 2时，截止频率最大，系统响应速度最快。但是相角裕度最小，稳定性差。因此，要根据对控制效果的要求选择合适的N_u值。

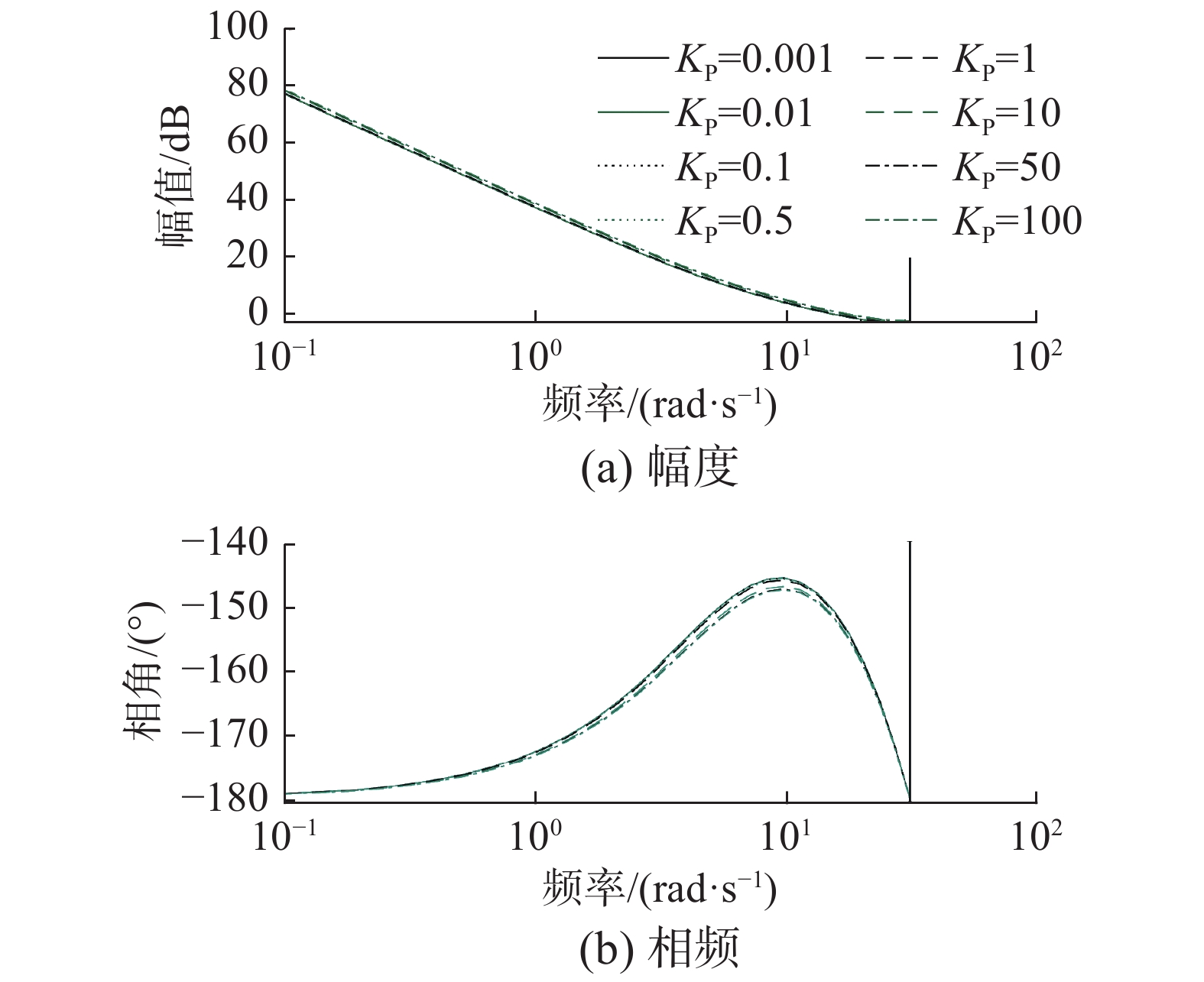
3.6 K_P改变对系统性能的影响

当K_P分别取0.001、0.01、0.1、0.5、1、10、50、100时，取N = 17, λ = 0.005, α = 0.2, w_o = 8, N_u = 2, K_I = 1开环系统的Bode图如图12所示。

从图12中可以看出，随着K_P的变化，系统的截止频率和相角裕度变化不明显。当K_P取值较小时，系统截止频率小，响应速度慢，但相角裕度较大，稳定性较好。应该选择合适的K_P，使控制过程既能得到较快的响应速度，又具有较好的稳定性。

3.7 K_I改变对系统性能的影响

当K_I分别取0.01、0.1、1、5、10、50、100、500时，取N = 17, λ = 0.005, α = 0.2, w_o = 8, N_u = 2, K_P = 0.1开环系统的Bode图如图13所示。

实验结果显示，K_I的改变会同时影响系统的相角裕度和截止频率。当K_I取值较小时，系统截止频率小，响应速度慢，但是相角裕度较大，稳定性较好。但当K_I ≥ 5时，系统的截止频率和相角裕度几乎不随着K_I变化，所以K_I的选择不需要过大。应该选择合适的K_I，使控制过程既能得到较快的响应速度，又具有较好的稳定性。

3.8 实验例证 3.8.1 一阶线性系统验证

对于上述系统，当控制器参数为N = 17, w_o = 8, λ = 0.005, α = 0.2, N_u = 2, K_P = 0.1, K_I = 1时，其离散系统的开环传递函数为

$\begin{array}{c} G({z^{ - 1}})H({z^{ - 1}}) = \\ \dfrac{{1.65{z^{ - 1}} - 2.375{z^{ - 2}} + 1.134{z^{ - 3}} - 0.1798{z^{ - 4}}}}{{1 - 2.859{z^{ - 1}} + 2.911{z^{ - 2}} - 1.243{z^{ - 3}} + 0.192{z^{ - 4}}}} \end{array} $

可以得出离散系统的奈奎斯特图，如图14所示。从图14可以看出，系统的奈氏曲线逆时针绕(−1，j0)点0圈，它的开环传递函数在单位圆外没有特征根，因此离散系统稳定。

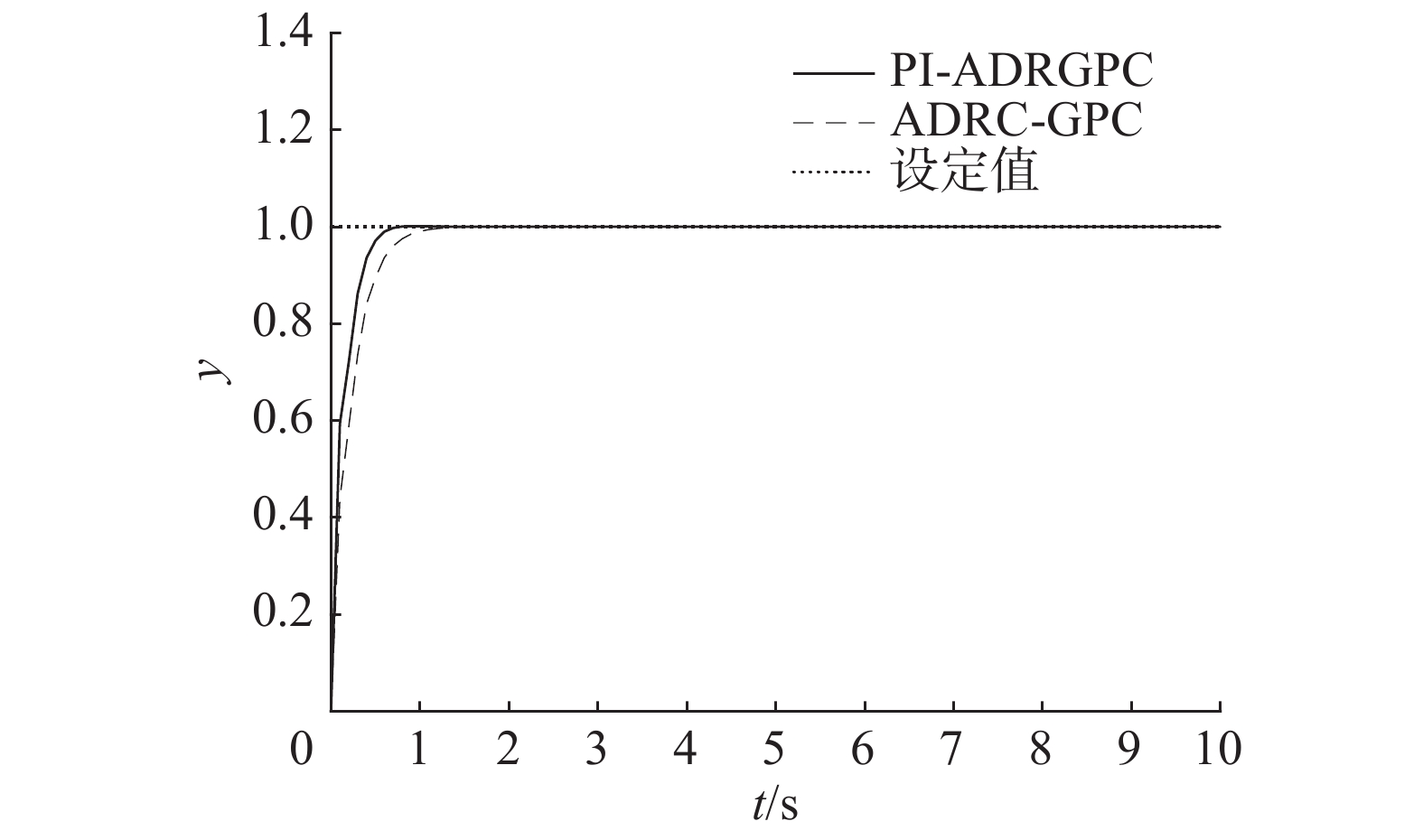
将PI-ADRGPC算法的控制效果和ADRC-GPC算法进行对比，两种算法的参数如表3所示，其输出响应对比如图15所示。

由图15和表4可知，对于一阶线性系统，由PI-ADRGPC算法控制的系统输出上升时间短、调节时间短，控制过程响应速度更快。ITAE性能指标小，PI-ADRGPC具有更好的控制效果。

控制过程中，系统的性能指标如表4所示。表4中数据的计算阈值为±0.5%，即控制量达到100%±0.5%时计算上升时间、调节时间、超调量和静差。其中ITAE为时间与绝对误差乘积积分。

3.8.2 船舶航向控制验证

为检验算法在实际系统中的性能，本文使用PI-ADRGPC控制船舶航向，并将其与使用ADRC-GPC算法的控制效果进行比较。

船舶的非线性响应模型可以表示为

$\left\{ \begin{array}{l} \dot \psi = r \\ \dot r = - \dfrac{1}{T}r - \dfrac{\alpha }{T}{r^3} + \dfrac{K}{T}\delta \\ \dot \delta = {K_E}({\delta _r} - \delta )/{T_E} \end{array} \right.$

式中： $\psi $ 表示船舶的实时航向； $\delta $ 为舵机输出的实际舵角； ${\delta _r}$ 为舵机输出舵角的期望值； $r$ 为航向角速度； $K$ 、 $T$ 为船舶操纵性指数； $\alpha $ 为非线性系数， ${K_E}$ 为舵机控制增益； ${T_E}$ 为舵机时间常数^[17]。

本文选择“育龙轮”为实验对象。当航速为7.2 m/s时，其操纵性指数为 $K = 0.478\;{{{\rm{s}}}^{ - 1}}$ ， $T = 216\;{{\rm{s}}}$ ， $\alpha = 30$ ；舵机特性参数 ${K_E} = 1$ ， ${T_E} = 2.5\;{\rm{s}}$ ，舵机的最大舵角^[18]为 35°。

一般情况下，船舶航行过程中会受到二阶波浪力干扰，在200 s之后给船施加一个频率为 $0.1\;{{{\rm{rad}}} / {\rm{s}}}$ ，幅值为 ${4^ \circ }$ 的等效正弦干扰，如式(15)所示：

$w(t) = 4\sin (0.1t)$

(15)

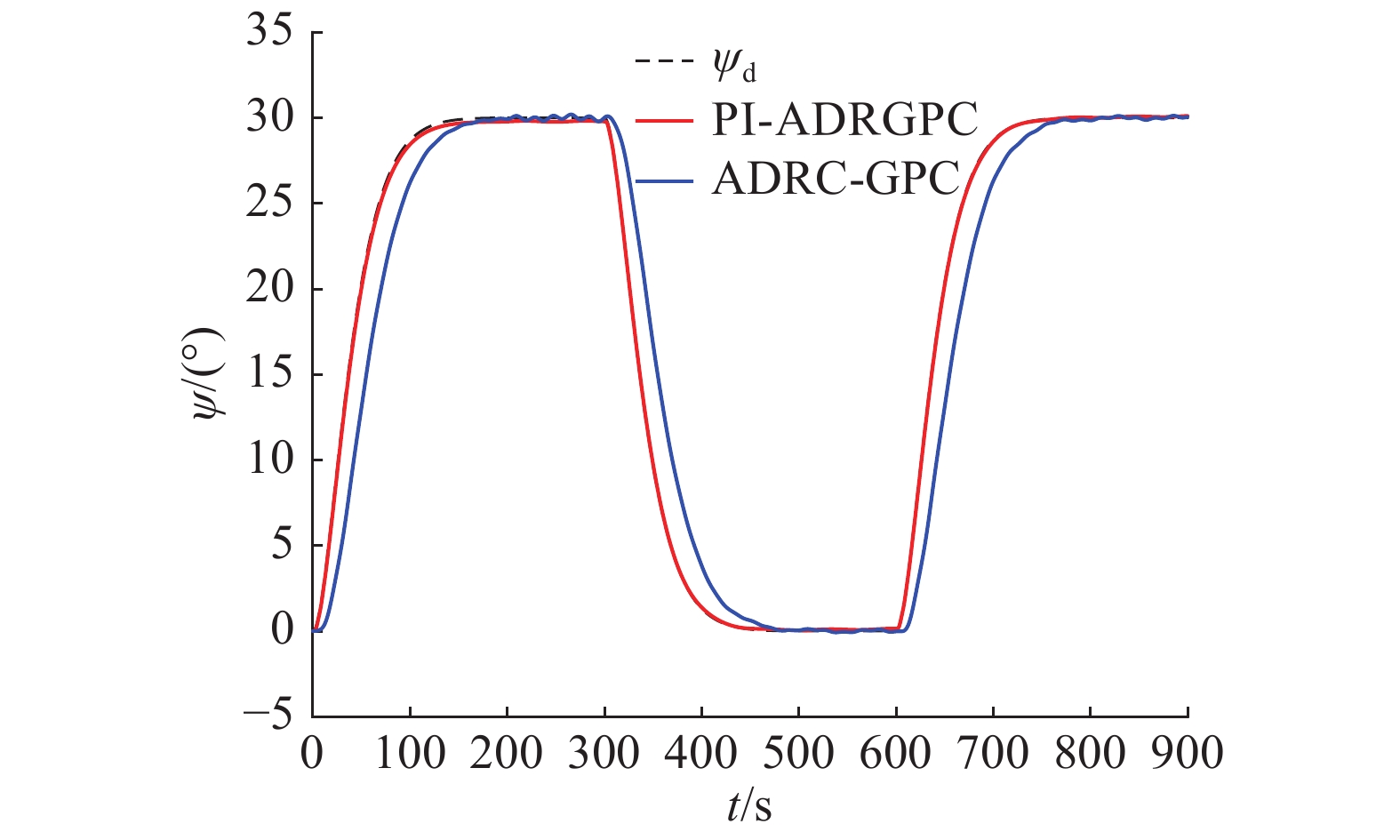
船舶航向控制器参数如表5所示。船舶航向输出曲线如图16所示。

由图16得，PI-ADRGPC控制器对船舶航向的跟踪偏差比ADRC-GPC控制器小。经计算PI-ADRGPC控制器控制船舶航向平均误差(每个采样点误差的绝对值除以采样点个数)为0.1219。ADRC-GPC控制器控制平均误差为1.9048。所以PI-ADRGPC控制器对船舶航向的控制效果优于ADRC-GPC控制器。

4 结束语

为克服ADRC算法在大时滞系统中具有局限性、PI-GPC算法在线计算量大的缺点，我们提出了PI-ADRGPC算法。本文利用频域法对该算法进行了分析。针对一阶线性系统，推导了PI-ADRGPC算法的闭环反馈结构，证明了算法的稳定性；利用开环传递函数的频域特性，分析了参数变化对PI-ADRGPC性能的影响；将所提出的算法应用于一阶线性系统和船舶航向控制系统，验证了算法的性能。仿真结果显示，所提出的算法和传统ADRC和ADRC-GPC算法相比具有更快的响应速度和更短的调节时间。在未来，我们将继续提高算法的性能并加以推广。