机器人、无人机和其他智能系统^[1]无法在建筑物、地下商场和其他室内环境中利用全球导航系统获得准确的位置信息，所以研究室内目标定位变得更加重要。近年来各种基于测距的智能体(机器人等)定位技术已经被提出，根据不同的定位参数，可以分为基于接受信号强度(receive signal strength，RSS)、基于到达时间差(time difference of arrival，TDOA)、基于到达角度(angle of angle，AOA)、基于到达时间(time of arrival，TOA)以及混合参数等。其中，基于TOA测距的定位算法由于测量精度高和抗干扰性能好等优点被广泛应用于室内定位系统。本文主要研究非视距(non line of sight，NLOS)环境下的TOA定位。目前大部分算法在视距(line of sight，LOS)条件下得到了很好的估计值，但是在含有NLOS的环境中，由于NLOS误差一般远大于节点间的测量噪声，传统算法的定位性能大大降低^[2]。另一个原因是在恶劣环境中，目标节点和传感器之间的LOS信号难以提供足够的信息，不得不求助NLOS信号^[3]。因此，抑制NLOS误差成为一项紧迫的任务，解决这个问题最简单的办法是识别出NLOS路径，然后丢掉NLOS测量，用LOS测量定位源位置^[4-5]。然而这种办法有2个缺点：1) 如果LOS测量数量在二维空间小于3，三维空间小于4，则无法定位目标节点的位置；2) 目前的技术下NLOS识别的成功率还不能达到100%，存在一定的虚警和漏警，这会大大地降低定位的性能^[2]。

近年来，基于凸优化的方法得到了广泛的应用。Yang 等^[6]通过利用二次规划(quadratic programming，QP)方法，提出了一种凸优化定位算法，该算法能较好地抑制NLOS误差，并且不需要知道任何NLOS误差分布以及识别NLOS信号。文献[7]提出了一种NLOS环境下RSS和TDOA联合的信源被动定位方法，通过建立加权最小二乘模型来抑制NLOS误差对定位精度的影响，最终的目标节点位置通过二分法迭代得到。Yu等^[8]提出了一种基于非直瞄状态信息的优化问题，并利用序列二次规划算法解决了问题。Lui等^[9]提出了一种最大后验(maximum a posteriori，MAP)方法，该方法假定知道关于NLOS状态的概率和NLOS误差的准确分布的先验信息。王刚等^[2]通过联合估计目标节点的位置和一个平衡参数，用于部分减轻NLOS误差的影响，将估计问题放宽为二阶锥规划(second order cone programming，SOCP)和半定规划(semidefinite programming，SDP)，但是该方法需要知道NLOS误差的上界。Tome等^[10]在王刚等的基础上，将估计问题表述为一个广义信赖域子问题(generalized trust region subproblem，GTRS)，并以全局最优的方式加以解决，算法计算复杂度逼近于线性。Chen等^[11]针对基于估计的方法在测量精确的稀疏NLOS环境中性能更好，当NLOS误差的上界是紧的时候，鲁棒方法在稠密的NLOS环境中表现得更好的问题，通过引入平衡参数，将问题建模为一个鲁棒加权最小二乘问题，并利用凸松弛技术将原问题近似为一个SDP问题求解。目前，虽然基于凸优化的方法显著提高了NLOS环境下的定位精度，但是这些算法的复杂度高，一是对传感器的内存、CPU要求高，二是难以满足实时定位的需求，基于此，本文研究了一种低复杂度的NLOS环境下的定位算法。

1 无线电定位系统模型

在智能体构成的局域网中，假设有 $N$ 个锚节点和一个未知位置的目标节点，定位就是用 $N$ 个锚节点的位置去估计目标节点的位置。假设锚节点的位置坐标为 ${a_i}(i = 1,2, \cdots ,N)$ ，目标节点的位置坐标为 $x$ ，目标节点和锚节点之间的路径有视距(LOS)和非视距(NLOS)2种，第 $i$ 个锚节点到目标节点之间的距离基于TOA模型可以建模为^[12-13]

${d_i} = \left\| {x - {a_i}} \right\| + {e_i} + {n_i}$

(1)

式中： $i \in 1,2, \cdots ,N$ ； ${n_i}$ 表示测量噪声，大量文献中均假设测量噪声服从方差为 ${\delta ^2}$ 的Gaussian零均值分布，即， ${n_i} \sim N(0,{\delta ^2})$ ； ${e_i}(i = 1,2, \cdots ,N)$ 表示NLOS误差，由于NLOS误差 ${e_i}$ 的产生是由于锚节点和目标节点之间的障碍物造成的，所以在文献中均假设NLOS误差 ${e_i}$ 非负，即 ${e_i} \geqslant 0$ ，并且认为NLOS误差 ${e_i}$ 远大于测量噪声 ${n_i}$ ，即 ${e_i} > > {n_i}$ 。

如果NLOS状态已知，式(1)可以变形为

${d_i} = \left\{ {\begin{array}{*{20}{l}} {\left\| {x - {a_i}} \right\| + {e_i} + {n_i}},\quad{{\rm{NLOS}}}\\ {\left\| {x - {a_i}} \right\| + {n_i}},\quad{{\rm{LOS}}} \end{array}} \right.$

(2)

在一些文献中，建模过程中假设NLOS误差 ${e_i}$ 为一些确定的分布，如均匀分布、指数分布、高斯分布等，或者需要对NLOS误差 ${e_i}$ 加入一个约束，如NLOS误差的上界已知等。本文所提的方法不需要知道NLOS误差 ${e_i}$ 的任何信息，适用于所有的分布，也不需要知道NLOS误差 ${e_i}$ 的上界等。

2 NLOS误差抑制的无线电定位算法

在NLOS状态未知的情形下，来考虑目标节点的定位。首先，通过对式(1)进行移项和平方恒等变形，得到：

${({d_i} - {e_i})^2} = {\left\| {x - {a_i}} \right\|^2} + 2{n_i}\left\| {x - {a_i}} \right\| + n_i^2$

(3)

对式(3)进行变形，得：

$\frac{{{{({d_i} - {e_i})}^2} - {{\left\| {x - {a_i}} \right\|}^2}}}{{2\left\| {x - {a_i}} \right\|}} = {n_i} + \frac{{n_i^2}}{{2\left\| {x - {a_i}} \right\|}}$

(4)

由于测量噪声 ${n_i}$ 都比较小，所以可以忽略二阶测量噪声 $n_i^2$ ，这样，由式(4)可以得到：

$\frac{{{{({d_i} - {e_i})}^2} - {{\left\| {x - {a_i}} \right\|}^2}}}{{2\left\| {x - {a_i}} \right\|}} \approx {n_i}$

(5)

由式(5)可以得到极大似然估计的概率密度函数为

$p({{\varsigma}} ) = {(2{\text{π}} )^{ - \frac{N}{2}}}{\left| {{Q}} \right|^{ - \frac{1}{2}}}\exp \left( { - \frac{1}{2}{{{\varsigma}} ^{\rm{T}}}{{{Q}}^{ - 1}}{{\varsigma}} } \right)$

(6)

式中： ${{\varsigma}} = \Bigg[ \dfrac{{{{({d_1} - {e_1})}^2} - {{\left\| {{{x}} - {{{a}}_1}} \right\|}^2}}}{{2\left\| {{{x}} - {{{a}}_1}} \right\|}}\; \dfrac{{{{({d_2} - {e_2})}^2} - {{\left\| {{{x}} - {{{a}}_2}} \right\|}^2}}}{{2\left\| {{{x}} - {{{a}}_2}} \right\|}}\;\cdots \; \dfrac{{{{({d_N} - {e_N})}^2} - {{\left\| {{{x}} - {{{a}}_N}} \right\|}^2}}}{{2\left\| {{{x}} - {{{a}}_N}} \right\|}} \Bigg]$ ； ${{Q}} = {\rm{diag}}([\delta _1^2\;\delta _2^2\;\cdots \;\delta _N^2])$ 。

关于 $x$ 最大化式(6)，得到：

$\hat x = \mathop {\arg \min }\limits_x {\sum\limits_{i = 1}^N {\left( {\frac{{{{({d_i} - {e_i})}^2} - {{\left\| {{{x}} - {{{a}}_i}} \right\|}^2}}}{{2\left\| {{{x}} - {{{a}}_i}} \right\|}}} \right)} ^2}$

(7)

通过研究发现，式(7)是一个高度非凸的表达式，因为其分子和分母均是 $x$ 的函数，本文没有解决式(7)，而是解决了其一个近似问题：

$\hat x = \mathop {\arg \min }\limits_x {\sum\limits_{i = 1}^N {\left( {\frac{{{{({d_i} - {e_i})}^2} - {{\left\| {{{x}} - {{{a}}_i}} \right\|}^2}}}{{2{d_i}}}} \right)} ^2}$

(8)

式(8)可以转化为一个约束最优化问题：

$\begin{array}{l} \mathop {{\rm{minimize}}}\limits_x {\displaystyle\sum\limits_{i = 1}^N {\left( {\dfrac{{{{({d_i} - {e_i})}^2} - {{\left\| {{{x}} - {{{a}}_i}} \right\|}^2}}}{{2{d_i}}}} \right)} ^2}\\ {\rm{s.t.}}\;\;\;\;\;\;\;\;\;\;{e_i} \geqslant 0,\;\;\;\;\; i = 1,2, \cdots ,N \end{array}$

(9)

为了求解式(9)，引入平衡参数 $e$ ，用平衡参数 $e$ 代替式(9)中的NLOS误差 ${e_i}$ 。由于平衡参数 $e$ 可以看成是NLOS误差的均值，这样的优点是只需估计一个平衡参数 $e$ 。与文献[10]不同的是本文并没有联合估计目标节点的位置 $x$ 以及平衡参数 $e$ ，仅仅通过已有的SR-LS^[12]算法进行了建模，求解得到了平衡参数 $e$ 的估计值 $\hat e$ ，这样会降低算法的复杂度，仿真结果表明，这样有助于提高定位的性能。

这样(9)式可以通过已有的方法求解，通过式(9)可以得到：

$\mathop {{\rm{minimize}}}\limits_x {\sum\limits_{i = 1}^N {\left( {\frac{{{{({d_i} - \hat e)}^2} - {{\left\| {{{x}} - {{{a}}_i}} \right\|}^2}}}{{2{d_i}}}} \right)} ^2}$

(10)

把式(10)转化为一个约束最小化问题：

$\begin{array}{l} \mathop {{\rm{minimize}}}\limits_{x,\beta } {\displaystyle\sum\limits_{i = 1}^N {\left( {\frac{{{{({d_i} - \hat e)}^2} - {{\left\| {{{x}} - {{{a}}_i}} \right\|}^2}}}{{2{d_i}}}} \right)} ^2}\;\; {\rm{s.t.}}\;\;{\left\| {{x}} \right\|^2} = {{\beta}} \end{array}$

(11)

式(10)转化为式(11)是直接的，本文的目的是把原问题转化为一个广义信赖域的子问题(GTRS)，这样便可以利用二分法求解该问题。把式(11)用向量的形式表示为

$\begin{array}{l} \mathop {{\rm{minimize}}}\limits_y \;\;\; ({\left\| {{{u}}({{Ay}} - {{b}})} \right\|^2})\;\;\;{\rm{s.t.}}\;\;\;{{{y}}^{\rm{T}}}{{Dy}} + 2{{{f}}^{\rm{T}}}{{y}} = 0 \end{array}$

(12)

式中： ${{y}} = {({{{x}}^{\rm{T}}},{{\beta}} )^{\rm{T}}}$ ； ${{D}} = {\rm{diag}}([1\;1\;0])$ ；

${{b}} = \left[ {\begin{array}{*{20}{c}} {{{\left\| {{{{a}}_1}} \right\|}^2} - {{({d_1} - \hat e)}^2}}\\ {{{\left\| {{{{a}}_2}} \right\|}^2} - {{({d_2} - \hat e)}^2}}\\ \vdots \\ {{{\left\| {{{{a}}_N}} \right\|}^2} - {{({d_N} - \hat e)}^2}} \end{array}} \right];\;{{A}} = \left[ {\begin{array}{*{20}{c}} {2{{a}}_1^{\rm{T}}}&{ - 1}\\ {2{{a}}_2^{\rm{T}}}&{ - 1}\\ \vdots & \vdots \\ {2{{a}}_N^{\rm{T}}}&{ - 1} \end{array}} \right]$

${{f}} = \left[ {\begin{array}{*{20}{c}} 0\\ { - \dfrac{1}{2}} \end{array}} \right];\;{{u}} = {\rm{diag}}\left( {\left[ {\dfrac{1}{{2{d_1}}}, \dfrac{1}{{2{d_2}}},\cdots ,\frac{1}{{2{d_N}}}} \right]} \right){\text{}}$

到此为止，建模过程便完成了，但是有2个问题需要解决，一是如何求解平衡参数 $e$ 的估计值 $\hat e$ ，二是怎么求解该模型。下面便正式提出改进的算法，解决上述2个问题。

式(12)的模型是一个GTRS问题，可以使用二分法进行求解，对于平衡参数，首先假设平衡参数的估计值 ${\hat e_0}$ 的初始值等于0，即不含有任何NLOS测量值，这样便能求出目标节点的一个初始值 ${x_0}$ ，然后计算平衡参数的方式为

${\hat e_1} \approx \frac{{\displaystyle\sum\limits_{i = 1}^N {({d_i} - \left\| {{{{x}}_0} - {{{a}}_i}} \right\|)} }}{N}$

(13)

这样利用平衡参数的估计值 ${\hat e_1}$ 便能计算出源节点的位置 ${x_1}$ ，同理可以计算出第 $m$ 次平衡参数的估计值 ${\hat e_m}$ 与源节点的位置 ${x_m}$ 。算法1中总结了提出的定位方法。

算法1

输入 ${a_i}(i = 1,2, \cdots ,N)$ ， $d$ ， $m$ 。

输出 源节点的位置 ${\hat x_m}$ 。

初始化 $t = 1$ ， ${\hat e_1} = 0$

while $t \leqslant m$

1) 计算区间 $I$ ：

$I = \left( { - \dfrac{1}{{{\lambda _{\max }}\left( {{{({{u}}{{{A}}^{\rm{T}}}{{uA}})}^{ - \frac{1}{2}}}{{D}}{{({{u}}{{{A}}^{\rm{T}}}{{uA}})}^{ - \frac{1}{2}}}} \right)}},\infty } \right) $

式中 ${\lambda _{\max }}( \cdot )$ 代表最大的特征值。

2) 用二分法在区间 $I$ 计算函数 $\psi (\lambda )$ 的零点 ${\lambda _t}$ 。其中：

$\psi (\lambda ) = {{\hat y}}{({{\lambda}} )^{\rm{T}}}{{D}}{{\hat y}}({{\lambda}} ) + 2{{{f}}^{\rm{T}}}{{\hat y}}({{\lambda}} )$

${{\hat y}}({{\lambda}} ) = {({{u}}{{{A}}^{\rm{T}}}{{uA}} + {{\lambda D}})^{ - 1}}({{u}}{{{A}}^{\rm{T}}}{{ub}} - {{\lambda f}})$

3) 计算 ${{\hat y}}({{{\lambda}} _{{t}}})$ 的值，源节点的位置 ${\hat x_t}$ 等于向量 ${{\hat y}}({{{\lambda }}_{{t}}})$ 的前2个分量。

$t = t + 1$

4) 计算平衡参数的估计值 ${\hat e_t}$ ：

${\hat e_t} \approx \frac{{\displaystyle\sum\limits_{i = 1}^N {({d_i} - \left\| {{{{x}}_{t - 1}} - {{{a}}_i}} \right\|)} }}{N}$

if ${\hat e_t} < 0$

${\;\hat e_t}$ = 0

end

end

3 算法的复杂度分析

本节主要给出一些现有算法的复杂度以及本文所提算法的复杂度，参考文献[10-11]中已有的结果，表1给出了所有算法最坏结果下的计算复杂度分析。可以看出，所有方法的计算复杂度主要取决于网络的规模，即锚的数量。

本文算法的计算复杂度虽然与迭代次数 $m$ 有关系，但该算法与锚节点的数量以及迭代次数之间呈现出一种线性关系，在后面的仿真实验中证明，当算法迭代次数 $m = 1$ 时，算法便能取得较为良好的定位性能。

4 仿真结果以及分析

这节主要利用MTLAB仿真验证所提算法的性能。为了更好说明本文算法的性能，与已有的二次规划(quadratic programming，QP)，半定规划(semide- finite programming，SDP)，二阶锥规划(second order cone programming，SOCP)，随机高斯(random Guess)，鲁棒半定规划(robust semidefinite programming，R-SDP)等算法进行了比较。算法的定位性能使用均方根误差(root mean square error，RMSE)来衡量，RMSE计算方式为

${\rm{RMSE}} = \sqrt {\frac{1}{M}\sum\limits_{i = 1}^M {{{\left\| {{{\hat {{x}}}_i} - {{{x}}_i}} \right\|}^2}} } $

(14)

式中 ${x_i}$ 与 ${\hat x_i}$ 分别表示第 $i$ 次定位目标节点的真实位置与估计位置。假设锚节点和目标节点随机地分布在 $20 \;{\rm{m}} \times 20 \;{\rm{m}} $ 的区域，执行 $M$ 个独立的Monte Carlo(MC)运行，并且在每个运行中，使用随机的锚节点拓扑结构来定位随机定位的目标节点位置。在本文的仿真中，设置 $M = 5\;000$ 。假设节点间的测量噪声 ${n_i}$ 服从Gaussian零均值分布，即 ${n_i} \sim N(0,{\delta ^2})$ 。节点间的NLOS误差 ${e_i}$ 在这里假设服从均匀分布，即 $U(0,{B_{\max }})$ 。

为了验证所提算法的性能，主要从以下3个方面进行仿真：1)NLOS测量的数量比较少的情形；2)NLOS测量的数量比较多的情形；3)算法的计算复杂度验证。

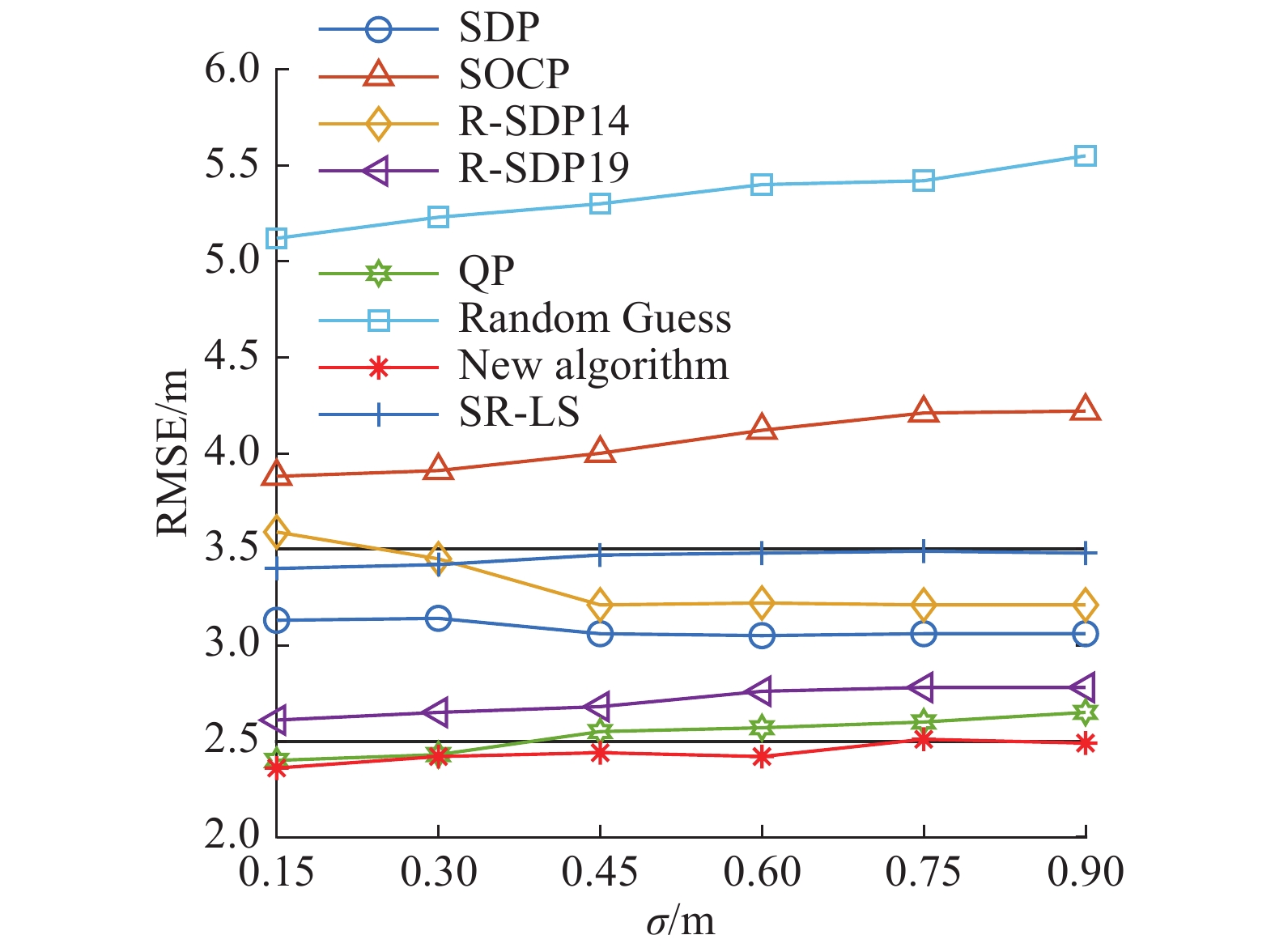
1) 验证NLOS测量的数量比较少的情形下算法的性能。设置锚节点的个数 $N = 5$ ，NLOS测量与LOS测量的数量分别为1、4，等价于NLOS占比为20%， ${B_{\max }} = 7\;{\rm{m}}$ ， $m = 1$ ，这也就意味着本文所提的算法仅仅迭代1次。仿真RMSE随 $\sigma $ 测量噪声的关系，其中设置 $\sigma $ 的范围为0.15~0.90。图1给出了算法的定位性能，可以看出本文所提算法的定位性能最好，QP、R-SDP19算法的定位性能次之。这是由于NLOS测量的数量少，本文所提的算法能计算出比较准确的平衡参数初始值，所以迭代过程中取得了不错的性能。当测量噪声比较小，可以看出本文算法和QP算法的性能基本一致，这是因为当LOS数量比较多，测量噪声比较小的时候，对QP算法的目标函数值影响比较小，从而表现出了优异的性能。本文所提算法在这种环境下性能优于其他的凸优化定位算法，这是因为诸如SDP、SOCP等算法中含有经过凸松弛处理的约束条件，在大量的LOS测量中，定位性能自然会下降。

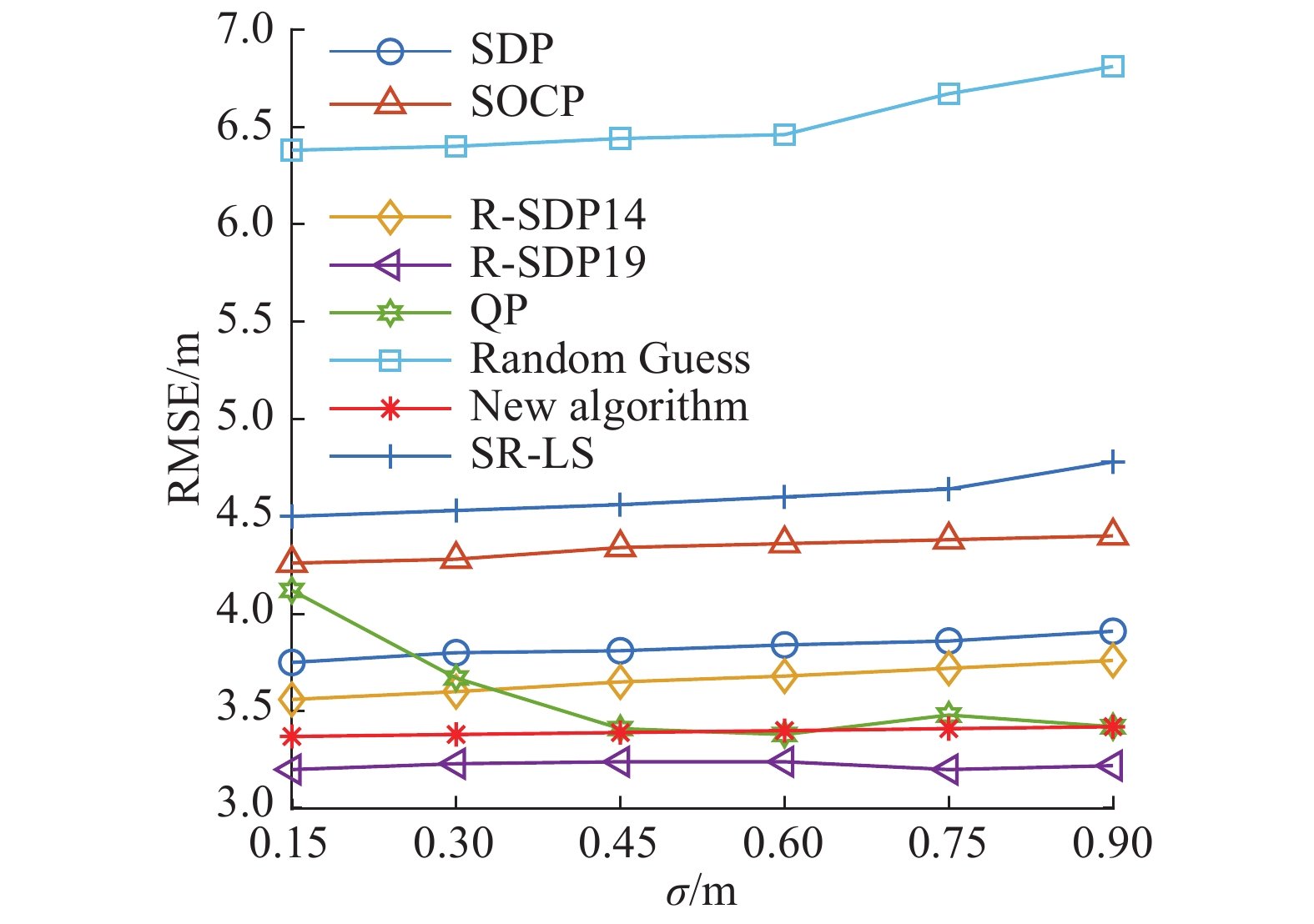
2) 验证NLOS测量的数量比较多的情形下算法的性能。NLOS测量与LOS测量的数量分别为3、2，等价于NLOS占比为60%，其他参数的设置同1)。在图2中显示了算法的定位性能，可以看出，R-SDP19算法的性能最好，这是由于在含有大量的NLOS测量时，大量的约束条件就起到了抑制NLOS误差的作用，能很好地提高算法的定位性能。并且在测量噪声不是很大的情形下，算法R-SDP14、SDP的定位性能也要好于QP，这也是因为其中的约束条件发挥了抑制NLOS误差的作用。本文的算法中由于加入了平衡参数，从图2可以看出，其定位性能仍然要优于一般的凸优化算法，但次于算法R-SDP19。但是当测量噪声增加时，本文算法的性能比较稳定，并且与算法R-SDP19的定位精度相差不大，也表现出了不错的性能。

3)算法的计算复杂度验证。软件：MATALB R2018 b，CPU：Intel(R)Core(TM)i5-7500 3.40 GHZ，内存：4.0 GB， $\delta = 0.2$ ，其他参数设置同1)，平均每次定位时间如表2所示。

从表2可以看出，本文所提算法的定位速度仅次于Random Guess和SR-LS，远快于几种基于凸优化的定位算法。

通过以上仿真实验可以看出，本文算法在NLOS比例不是很高的时候占有很大的优势，在NLOS占比高的情形下虽然定位性能有所下降，但仍然优于一些凸优化算法。综合看来，本文的算法在定位性能和计算复杂度之间有着很好的平衡，可以满足实时定位的需求。

5 结束语

在关于机器人、无人机和其他智能体的位置信息的研究领域中，目标节点的位置信息是至关重要的环节。但是在含有NLOS环境中，节点的定位精度大大下降。为了抑制NLOS误差对定位精度的影响，本文引入了平衡参数这一关键量，将定位问题与一个GTRS问题框架进行对应。与已有算法不同的是，本文所提算法并没有联合估计目标节点的位置和平衡参数，而是采用了一种迭代求精的思想，算法用二分法进行求解，高速有效。本文所提算法与已有的算法相比，不需要任何关于NLOS路径的信息(NLOS状态、NLOS的分布、NLOS误差的上界等)，另外，与大多数现有算法不同，所提算法的计算复杂度低，能够满足实时定位的需求。仿真实验结果表明，该算法具有稳定的NLOS误差抑制能力，在定位性能和算法复杂度之间有着很好的平衡。但不足的是，如果所有的路径均是NLOS，所提算法表现不佳，还有待后续研究。